Long term time series analysis and prediction of waves at Hainan offshore zone based on Prophet algorithm
-
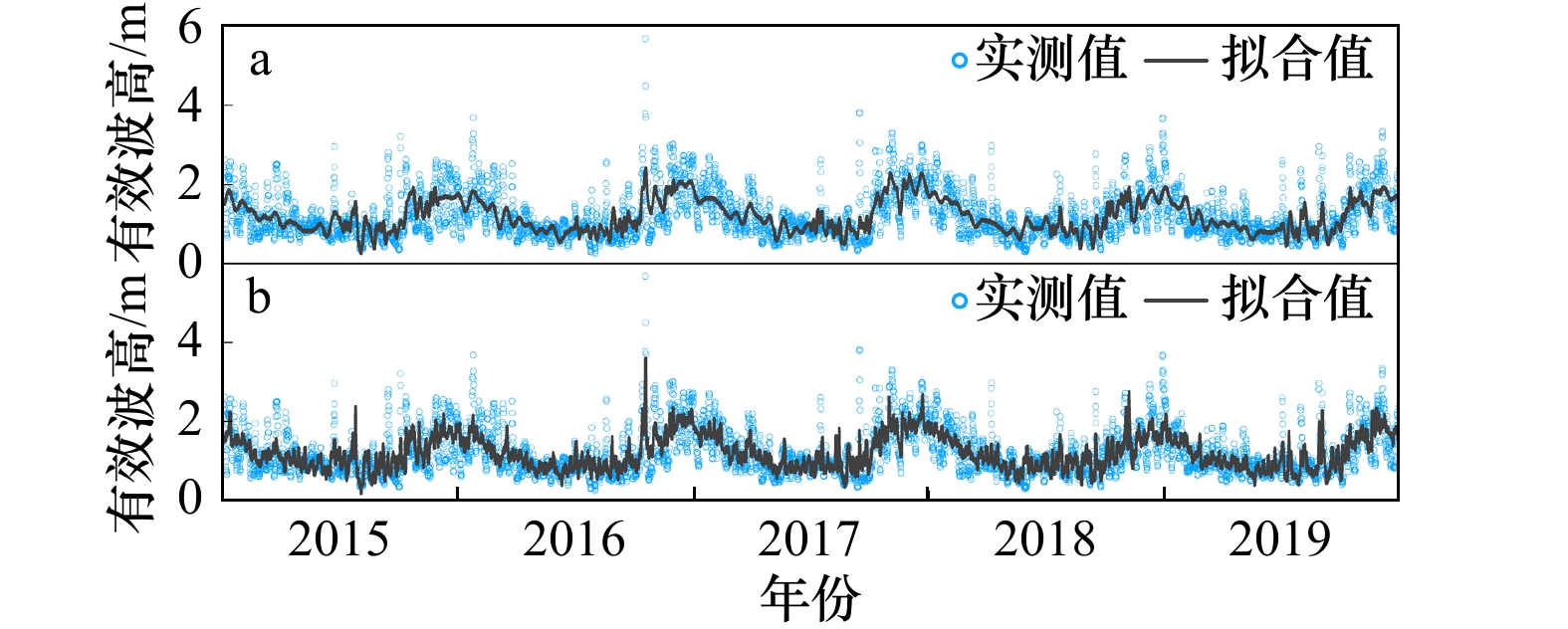
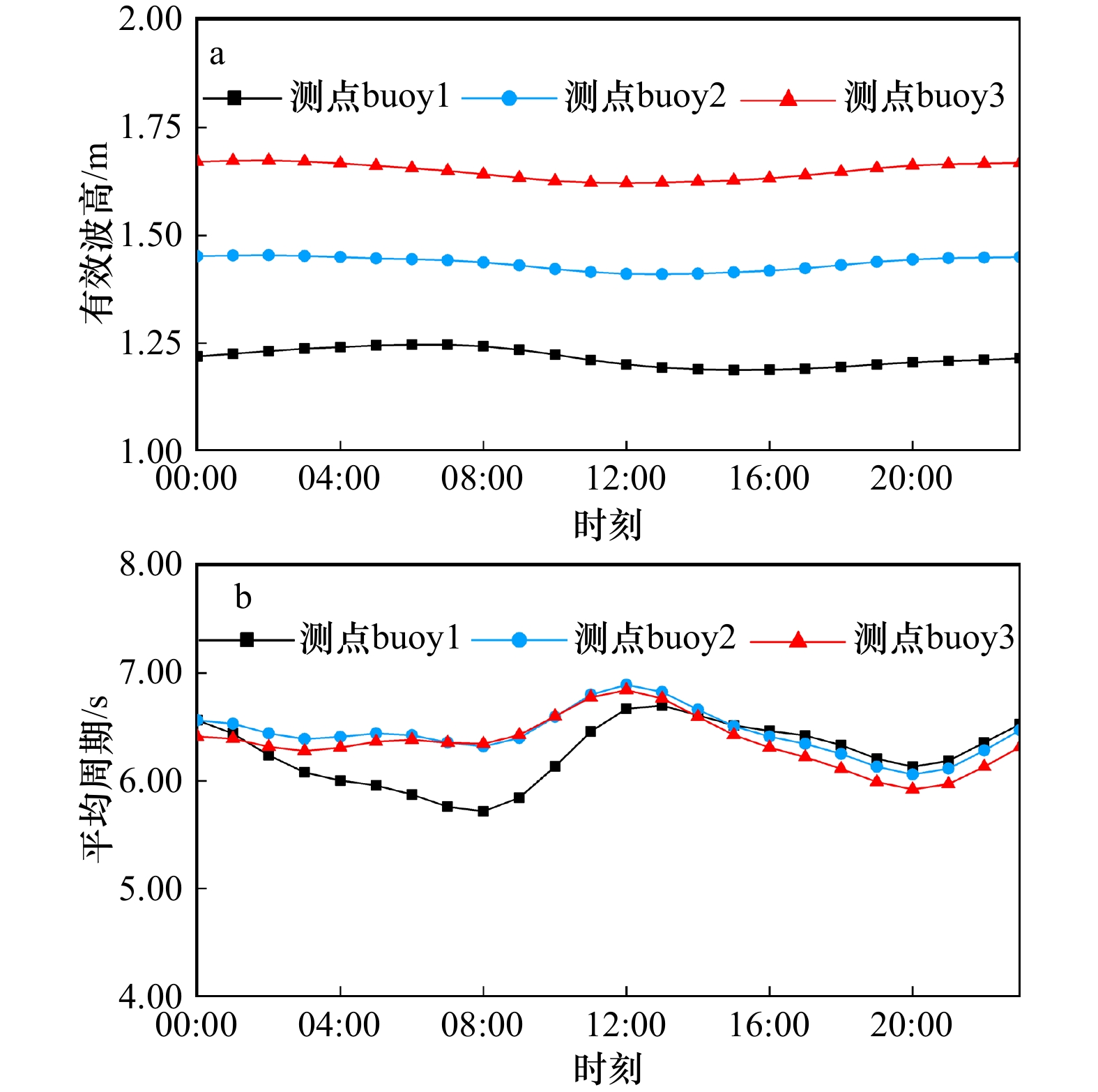
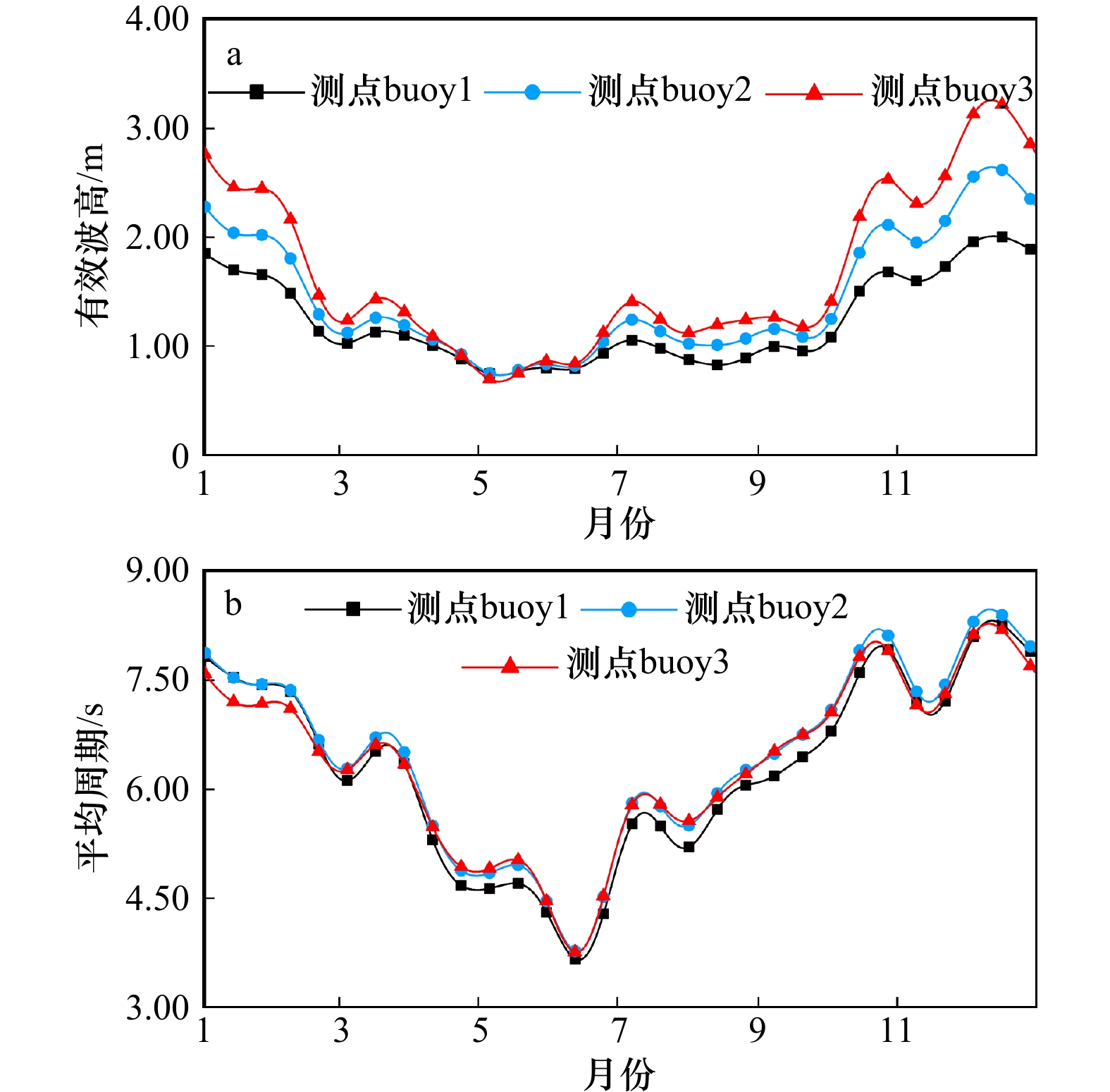
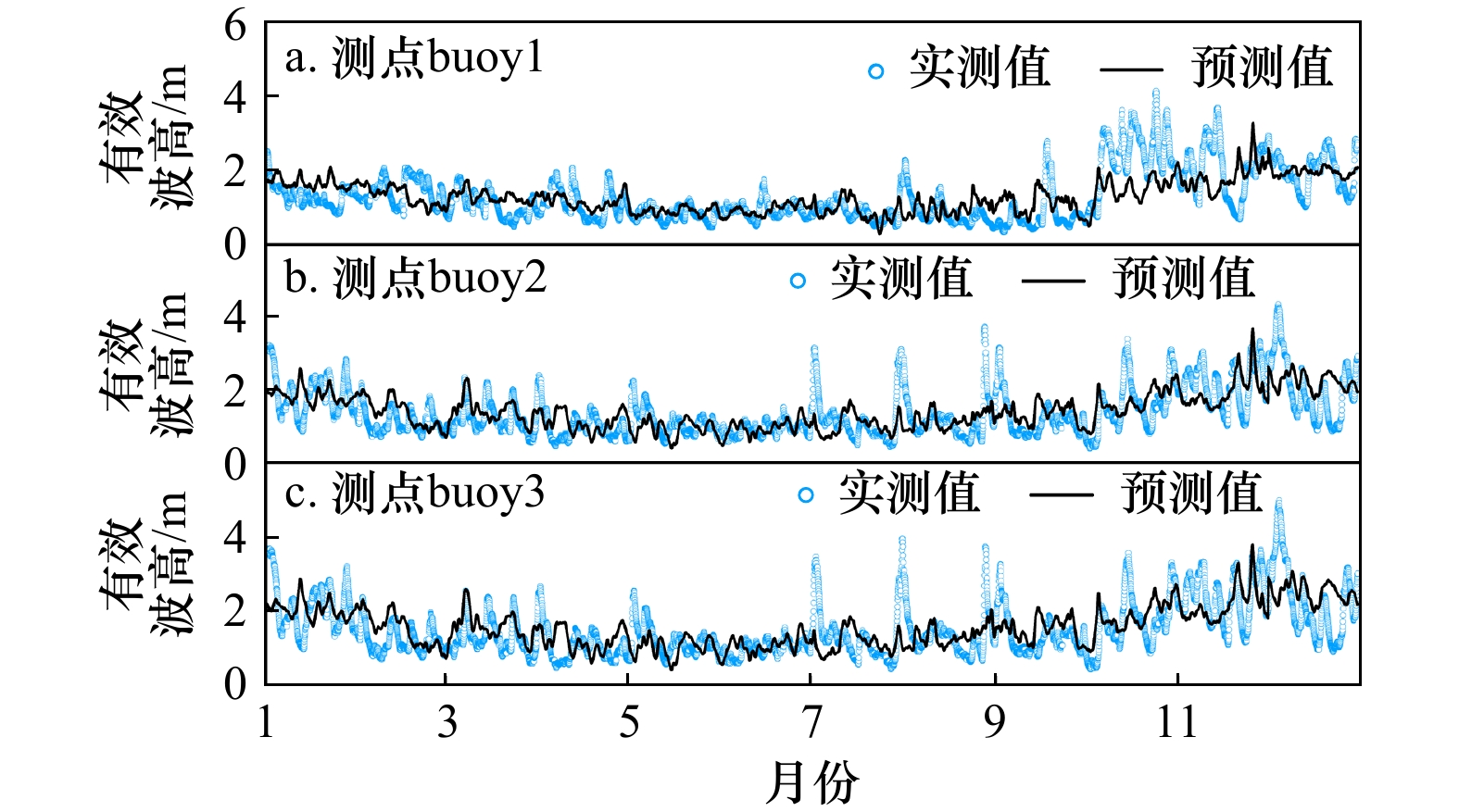
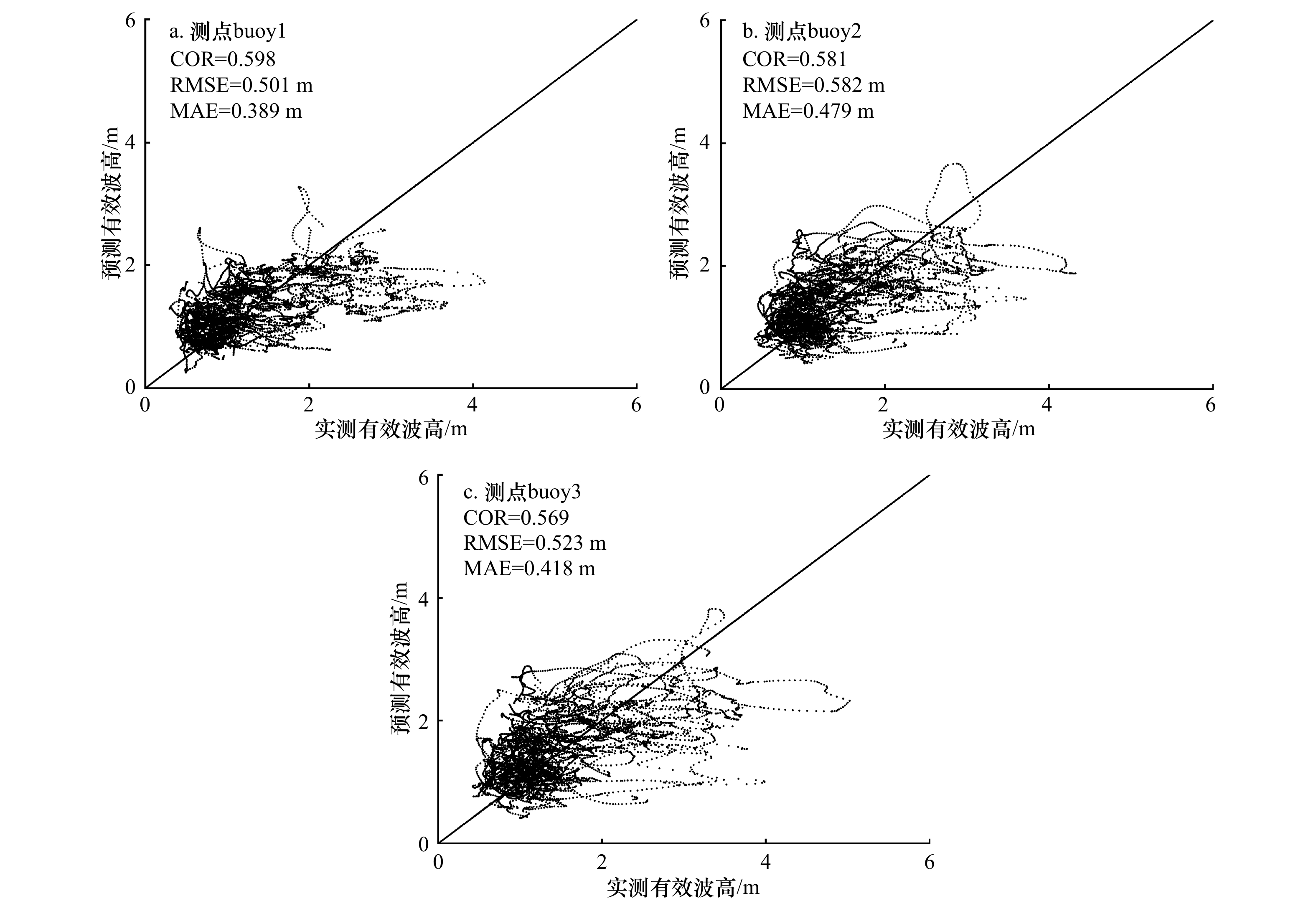
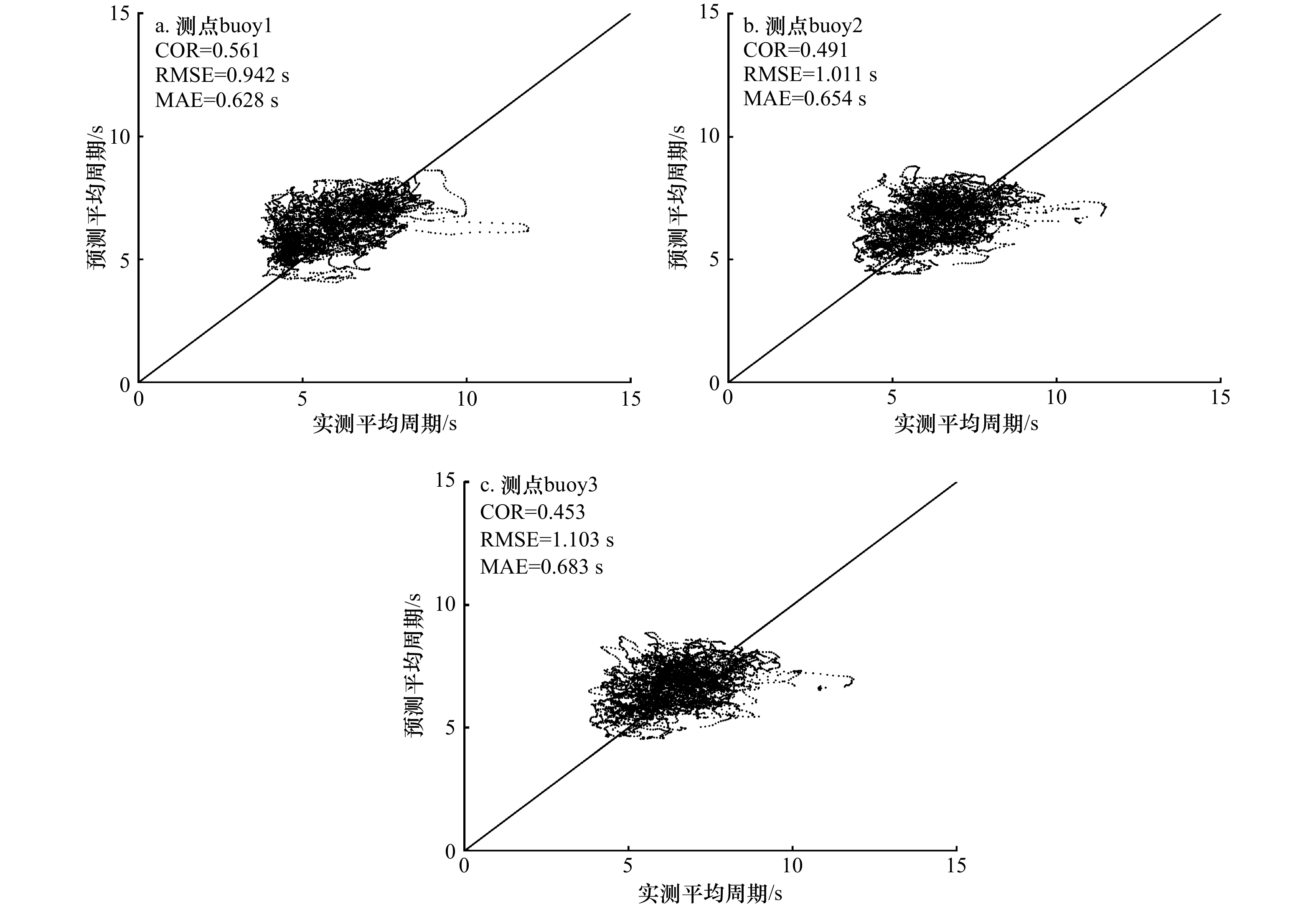
摘要: 近年来，以大数据为基础的人工智能算法逐步兴起并被用于海洋波浪短期预测。本文采用2015−2019年海南近海逐时波浪实测时序数据，基于Prophet算法建立了海南近海波浪长时段时序预测模型，分析了2015−2019年海南近海波浪日、月、年变化特性，并对海南近海2020年波浪变化过程进行了预测。结果显示，Prophet算法模型对波浪波高和周期的预测值和实测值整体吻合良好，可有效用于长时段波浪的特性分析和时序预测。Abstract: In recent years, various artificial intelligence algorithms based on big data have gradually emerged and have been applied in short-term time series wave forecasting. Based on the measured time series data of hourly waves in Hainan offshore from 2015 to 2019, a prediction model for long-term time series waves of Hainan offshore based on Prophet algorithm is established in this paper. The daily, monthly and annual variation characteristics of waves in Hainan offshore from 2015 to 2019 are analyzed, and the waves in Hainan offshore in 2020 are predicted. The results show that the predicted values of wave height and period by prophet algorithm model are in good agreement with the measured values. Prophet algorithm model can be effectively used for long-term wave characteristic analysis and time series prediction.
-
Key words:
- coast and offshore /
- water wave /
- Prophet algorithm /
- big data /
- artificial intelligence
-
1. 引言
波浪是海洋主要环境动力因素，预测波浪长时段时序变化过程并分析其规律，对开展海洋工程建设和海洋防灾、减灾等具有重要价值[1]。
目前，关于波浪运动的预测方法大致分为两类：一类是从波浪传播的物理力学机制出发，基于波浪数值模型模拟预测波浪传播过程，如基于波浪SWAN模型、Boussinesq模型、缓坡方程模型等[2-5]。波浪数值模型预测通常需要外海入射波浪条件或风场等驱动因子，而这些因子在未来时段通常未知，且数值模型计算效率相对较低。另一类是从统计学角度出发，基于以往大量实测数据对未来波浪运动进行统计学经验分析[6-8]，如基于年极值波浪数据对多年一遇波浪进行分析，但不适于波浪的时序预测。近年来，以大数据为基础的人工智能算法逐渐受到关注，如具有良好自适应学习与非线性映射能力的长短期记忆算法（Long Short-Term Memory, LSTM）、神经网络算法（Neural Networks, NN）、支持向量机算法（Support Vector Machine, SVM）等[9-11]已被用于波浪时序预测，相对数值模型而言具有较高计算效率。高丽斌等[12]基于LSTM，利用2016年实测波高资料对未来4 d波高进行预测，实测值与预测值对比的决定系数达0.999。赵凯欣[13]基于支持向量回归算法(Support Vector Regression, SVR)和LSTM，采用卫星散射计和高度计测量资料反演7 d有效波高，结果表明，LSTM更能有效反演散射计下有效波高。阚世宣等[14]基于经验模态分解算法（Empirical Mode Decomposition, EMD）采用渤海实测3个月波浪数据集作为训练测试集建模分析，研究表明，基于EMD和SVR联合的混合算法预测结果比SVR预测结果更精确。Roh等[15]利用联合风浪预报模型（Ensemble Forecast Wave Model, EFWM）对台风“玲玲”期间波浪进行预测，结果表明，该模型的受试者工作特征曲线（Receiver Operating Characteristic, ROC）相关系数（Correlation Coefficient, COR）可达0.9以上。
总体来看，基于大数据的人工智能算法已愈来愈受到关注并逐渐被用于海洋波浪预测，但现有研究主要采用短时段实测波浪资料作为训练集，对未来波浪进行短期时序预测，尚未见其在波浪长时段时序预测的研究和应用。Prophet算法计算效率高，可对大规模的数据进行训练建模分析并对未来长时段数据变化趋势进行预测。本文拟采用Prophet算法，以海南近海2015−2019年逐小时测波时序数据为基础建立海南近海波浪长时段时序预测模型，分析波浪的日、月、年变化特征，并预测2020年波浪时序变化过程，通过与2020年实测波浪对比，验证Prophet算法在波浪长时段时序预测的适用性。
2. 基于Prophet算法的海南近海波浪时序预测模型
2.1 Prophet时序算法
Prophet算法可用于研究数据时序特征和时序变化规律，如长期趋势、周期性趋势、特殊日期及时间段效应等[16-17]，可对未来时段内的数据变化进行预测，通过将这些特征项拟合，可预测数据的时间序列变化。本文采用Prophet算法对长时段时序波浪进行训练并预测未来波浪的时序变化过程。考虑波浪要素年、月、日的非周期变化趋势、周期性变化趋势及极端事件影响，Prophet算法表达式为
$$ y(t) = g(t) + s(t) + h(t) + \varepsilon t \text{，} $$ (1) 式中，
$y(t)$ 为波浪有效波高或平均周期的预测值；$g(t)$ 为波浪非周期变化趋势项，拟合波浪在时间序列上的非周期变化趋势；$s(t)$ 为波浪变化周期项，拟合波浪以年或月为单位的周期性变化；$h(t)$ 表示波浪变化极端事件影响项，拟合极端天气条件对波浪的影响；$ \varepsilon t $ 为误差项，表示突发事件影响，通常将其模拟为高斯噪声。2.1.1 波浪非周期变化趋势项
波浪非周期变化趋势项是算法核心部分，它预测波浪要素在整个时间序列的增长特征以及预期未来时段如何增长。本文经过大量数据测试比较，发现Prophet算法中的线性趋势模型对波浪趋势项拟合良好，该非周期变化趋势项表达式为
$$ g(t) = [k(t) + a{(t)^{\rm{T}}}\delta ]t + [m(t) + a{(t)^{\rm{T}}}]\gamma \text{，} $$ (2) 式中，
$k(t)$ 为随时间$t$ 变化的波浪有效波高或平均周期增长率；$a(t)$ 为拟定的极端天气期$t$ 时刻前预测因子突变点发生变化的次数；$\delta $ 为增长率变化量；$m(t)$ 是偏移量；$\gamma = - s \times \delta $ ，$s$ 与极端天气条件导致的突变点选取有关。2.1.2 波浪变化周期项
Prophet算法采用傅里叶级数模拟波浪时间序列在日、月、年的周期性变化，具体形式如下：
$$ s(t) = \sum\limits_{n = 1}^N {\left(an\cos \frac{{2n\text{π} t}}{P} + bn\sin \frac{{2n\text{π} t}}{P}\right)} \text{，} $$ (3) 式中，
$P$ 为时间序列周期长度；an、bn为傅里叶系数；N为Prophet自调节的傅里叶级数的阶数。若设$P{\text{ = }}30$ 代表以月为周期，$P{\text{ = }}365$ 则代表以年为周期。式（3）可表述为$$ s(t) = \beta X(t) \text{，} $$ (4) 式中，
$$ \beta = {(a_1,b_1, \cdots ,a_N,b_N)^{\rm{T}}} \text{，} $$ (5) $$\begin{split} X(t) =& \left[ \cos \left(\frac{{2\text{π} (1)t}}{P}\right),\sin \left(\frac{{2\text{π} (1)t}}{P}\right), \cdots ,\right.\\ &\left.\cos \left(\frac{{2\text{π} (N)t}}{P}\right),\sin \left(\frac{{2\text{π} (N)t}}{P}\right) \right] \text{，}\end{split} $$ (6) 式中，
$ X(t) $ 为波浪变化的周期；$\ \beta $ 为参数向量，初始化为$\ \beta \sim {{\rm{Normal}}} (0,{\sigma ^2})$ ，$\sigma $ 代表周期项影响系数，$\sigma $ 越大表示模型周期性越明显，反之则影响越小。2.1.3 波浪变化极端事件影响项
台风、风暴潮等极端事件不确定性强且会对波浪预测结果产生重要影响。为了减少这些不确定因素产生的预测误差，Prophet算法单独对这些极端事件进行定义并灵活拟合，即给每个独立极端事件制定一个时间变化窗口，表达式如下：
$$ h(t) = \sum\limits_{i = 1}^L {k_i \times 1} (t \in D_i)\text{，} $$ (7) 式中，
$L$ 为极端事件的集合；$i$ 为第$i$ 个极端事件；ki为对应事件对模型产生影响的因子；Di为窗口期中包含的时间$t$ ，设$$ Z(t) = \left[ {1(t \in D_1),1(t \in D_2), \cdots ,1(t \in D_L)} \right]\text{，} $$ (8) 可得
$$ h(t) = Z(t)k\text{，} $$ (9) 式中，
$Z(t)$ 代表单个极端事件影响，$k \sim {\text{Normal}}(0,{\upsilon ^2})$ ，$\upsilon $ 代表极端事件的影响系数，$\upsilon $ 越大表示该事件对模型影响越大，反之则影响越小。2.2 海南近海波浪预测模型
将海南近海实测波浪时序数据输入Prophet算法模型进行训练。首先按照算法模型的非周期变化趋势项等对模型进行参数分解和解析，以此来进行模型分组件训练；在此基础上，根据拟合值与实测值的COR对比结果人为进行模型参数调整，通过调整模型不同项的影响系数组合来提高模型对训练集拟合的准确度，直至拟合值与实测值的COR系数稳定地收敛于某一具体值，即认为模型拟合精度达标并停止模型训练；最后基于训练好的算法模型预测未来数据时序变化过程。具体流程如图1所示。
本文所采用的实测波浪数据来自于欧洲中尺度气象预报中心（European Centre for Medium-Range Weather Forecasts, ECMWF）提供的ERA-Interim全球再分析数据集。研究测点位于海南东侧海域，位置如图2所示，坐标及水深见表1。为避免资料过少降低预测准确率，因此取2015−2019年的逐时实测波浪时序数据（有效波高、平均波周期）进行模型训练，训练阶段的输入项包括：2015−2019年逐时时刻（例如2015/01/01/000000）和相应时刻的波浪要素（有效波高、平均波周期）。模型经训练拟合后用于预测2020年逐时波浪，预测阶段的输入项为2020年逐时时刻（例如2020/01/01/000000），输出项为2020年逐时时刻和相应时刻的波浪要素（有效波高、平均波周期），取2020年全年逐小时实测波浪数据验证模型的有效性。
表 1 测点坐标及水深Table 1. Location and water depth of survey points测点 纬度 经度 水深/m buoy1 19.05°N 110.35°E 15.5 buoy2 19.05°N 110.70°E 101.4 buoy3 19.05°N 111.05°E 186.7 实际海况中，台风和天文潮等极端事件会对波浪变化产生很大影响。如何有效拟合极端事件时期内波浪时序变化对提升模型预测准确率十分重要。资料显示，海南风暴潮及台风高发期集中在7−11月之间[18]，模型中设置7−11月为极端天气期。当训练的数据时段处于极端天气期时，模型会自动增加训练次数强化训练，并将波浪要素值与非极端天气期内的值进行对比并自动设定判断阈值，若超过判断阈值，模型将自动添加额外回归项，强化对极端天气期波浪数据的敏感度处理，以此来确定极端天气期的影响。
3. 结果分析
3.1 模型训练效果
以buoy1测点为例分析拟合效果，图3和图4分别为考虑与未考虑极端条件影响的2015−2019年测点有效波高（HS）及平均周期（T）拟合图。从图3与图4中可以看出，考虑极端条件影响后的Prophet算法模型对原始数据拟合效果较好，考虑极端天气影响后模型整体复杂度变高，对实际波高及周期情况拟合效果更佳。
图 3 有效波高训练结果a. 未考虑极端天气影响；b. 考虑极端天气影响Figure 3. Training-fitting results of effective wave heightsa. Without considering extreme weather influence; b. considering extreme weather influence
图 4 波浪平均周期训练结果a. 未考虑极端天气影响；b. 考虑极端天气影响Figure 4. Training-fitting results of wave mean periodsa. Without considering extreme weather influence; b. considering extreme weather influence3.2 波浪时序特征
分析波浪长时段周期性变化特征有助于认识波浪长时段的演化规律。Prophet算法基于2015−2019年实测波浪数据，首先将波浪日、月、年时序数据单独分析拟合，根据日历时规律拟合月历时规律，再根据这些历时规律进行分析组合获得多年变化规律，并依此进行最终预测。模型分别给出了2015−2019年波浪的日、月、年历时变化趋势。
3.2.1 波浪日历时变化特征
图5给出了2015−2019年3个测点有效波高及平均周期日历时变化趋势。从图5可以看出，一天中3个测点波高变化不大，测点buoy1波高在1.24 m上下，测点buoy2波高在1.47 m上下，测点buoy3波高在1.70 m上下，3个测点平均变化范围在4%以内，波高随离岸距离呈正相关。3个测点波浪平均周期的变化规律较波高明显，测点buoy1谷值在早上8点，峰值在下午1点前后，峰值谷值相差近1 s；在晚上8点前后有局部谷值出现；测点buoy2及测点buoy3两点峰值与测点buoy1相同，谷值在晚上8点；凌晨3点及早上8点有局部谷值；3个测点整体变化趋势相近。
3.2.2 波浪月历时变化特征
图6给出了2015−2019年3个测点有效波高及平均周期月历时变化趋势。从图6可以看出，3个测点有效波高变化情况相近，在春季即1−4月前后，波高有明显下降趋势，下降1～2 m；4月中旬至5月下旬，波高和周期趋于平缓，无显著变化；在秋冬季10月前后开始，波高有明显的上升趋势，最大达到2.4 m以上，这也与海南地区春冬期易发生天文大潮及台风等的极端天气情况相吻合。3个测点平均波周期变化几乎相同，在1−6月中旬有显著下降，下降接近4 s；在6月后平均波周期开始稳步提升，在12月中旬前后平均波周期达到最大。
3.2.3 波浪年历时变化特征
2015−2019年3个测点有效波高及平均周期年变化趋势如图7所示。从图7a中有效波高多年变化规律可以看出，3个测点有效波高多年的平均值集中在1～2 m之间，波高随离岸距离增大而整体相对增大，近岸点波高每年波动频率不大，远岸及外海波动较大。3个测点2017年全年波高较其他年份相对偏高，2018年开始显著下降，2019年以后预测波高升高。从图7b平均周期多年变化趋势可以看出，周期的多年均值集中在6～7 s之间，变化幅度不大，周期随离岸距离增大而略有增大，波动频率较小，2016年中旬至2019年起伏相对较大，差值接近1.2 s。
3.3 模型预测结果
Prophet算法模型经训练拟合后用于预测2020年逐时波浪，取2020年全年逐小时实测波浪数据验证模型的有效性。图8给出了2020年全年波浪有效波高预测值和实测值的比较，可以看出模型预测结果相对较好地匹配了实测数据。2020年10−12月极端天气期预测效果相对不理想，可能是2020年该月份风暴潮较往年频发且与2015−2019年风暴潮发生时间点重合度低所致。
图 8 2020年测点预测和实测波浪有效波高对比Figure 8. Comparison between predicted and measured significant wave heights in 2020图9展示了测点预测有效波高与实测有效波高对比的散点值及误差值，可以看出 COR介于0.55～0.60，buoy1的相关性系数达0.598。散点均方根误差（Root Mean Squard Error, RMSE）介于0.50～0.59 m，平均绝对误差（Mean Squared Error, MAE）介于0.38～0.48 m，总体误差属于中等偏下水平。由近岸至外海的预测波高与实测波高相关性减小，误差逐渐偏大，这主要是由于外海天气情况较近岸更为多变，预测难度偏大。
图 9 2020年预测和实测波浪有效波高散点图Figure 9. Scatter plot of predicted and measured effective wave heights in 2020图10与图11展示了3个测点波浪平均周期的预测与实测对比及散点值和误差值。图中平均周期预测与实测相比结果与波高类似，整体趋势较好，非风暴潮期效果佳，风暴潮期误差较大。总体上，预测与实测的散点COR系数介于0.45～0.57，较波高预测效果差，但RMSE在1 s左右，MAE在0.6 s左右，误差较小，呈现出与波高相同的趋势，即从远岸至近岸预测准确率逐渐增大，误差逐渐减小。
图 10 2020年测点预测和实测波浪平均周期对比Figure 10. Comparison between predicted and measured wave mean periods in 2020
图 11 2020年预测和实测波浪平均周期散点图Figure 11. Scatter plot of predicted and measured wave mean periods in 20204. 结论
本文采用2015−2019年海南近海实测波浪时序数据，基于Prophet算法对实测波浪数据进行训练，建立了海南近海波浪长时段时序预测模型。依据模型训练结果分析了2015−2019年海南近海波浪日、月、年变化特性，并对海南近海2020年波浪进行了时序预测，采用2020年实测波浪数据验证分析了模型的有效性。结果表明，Prophet算法模型在训练中考虑极端事件—风暴潮影响后可显著提高模型整体预测准确率；模型对波浪有效波高和平均周期的预测值和实测值整体吻合良好，模型对有效波高的预测值与实测值的相关性系数介于0.55～0.60之间，最高达0.598，均方根误差与绝对平均误差分别介于0.50～0.59 m、0.38～0.48 m之间，模型对平均周期的预测值与实测值的相关性系数介于0.45～0.57之间，最高达0.561，均方根误差与绝对平均误差分别介于0.94～1.11 s、0.62～0.69 s之间。Prophet算法模型可有效用于长时段波浪的特性分析和时序预测。
-
图 3 有效波高训练结果
a. 未考虑极端天气影响；b. 考虑极端天气影响
Fig. 3 Training-fitting results of effective wave heights
a. Without considering extreme weather influence; b. considering extreme weather influence
图 4 波浪平均周期训练结果
a. 未考虑极端天气影响；b. 考虑极端天气影响
Fig. 4 Training-fitting results of wave mean periods
a. Without considering extreme weather influence; b. considering extreme weather influence
图 8 2020年测点预测和实测波浪有效波高对比
Fig. 8 Comparison between predicted and measured significant wave heights in 2020
图 9 2020年预测和实测波浪有效波高散点图
Fig. 9 Scatter plot of predicted and measured effective wave heights in 2020
图 10 2020年测点预测和实测波浪平均周期对比
Fig. 10 Comparison between predicted and measured wave mean periods in 2020
图 11 2020年预测和实测波浪平均周期散点图
Fig. 11 Scatter plot of predicted and measured wave mean periods in 2020
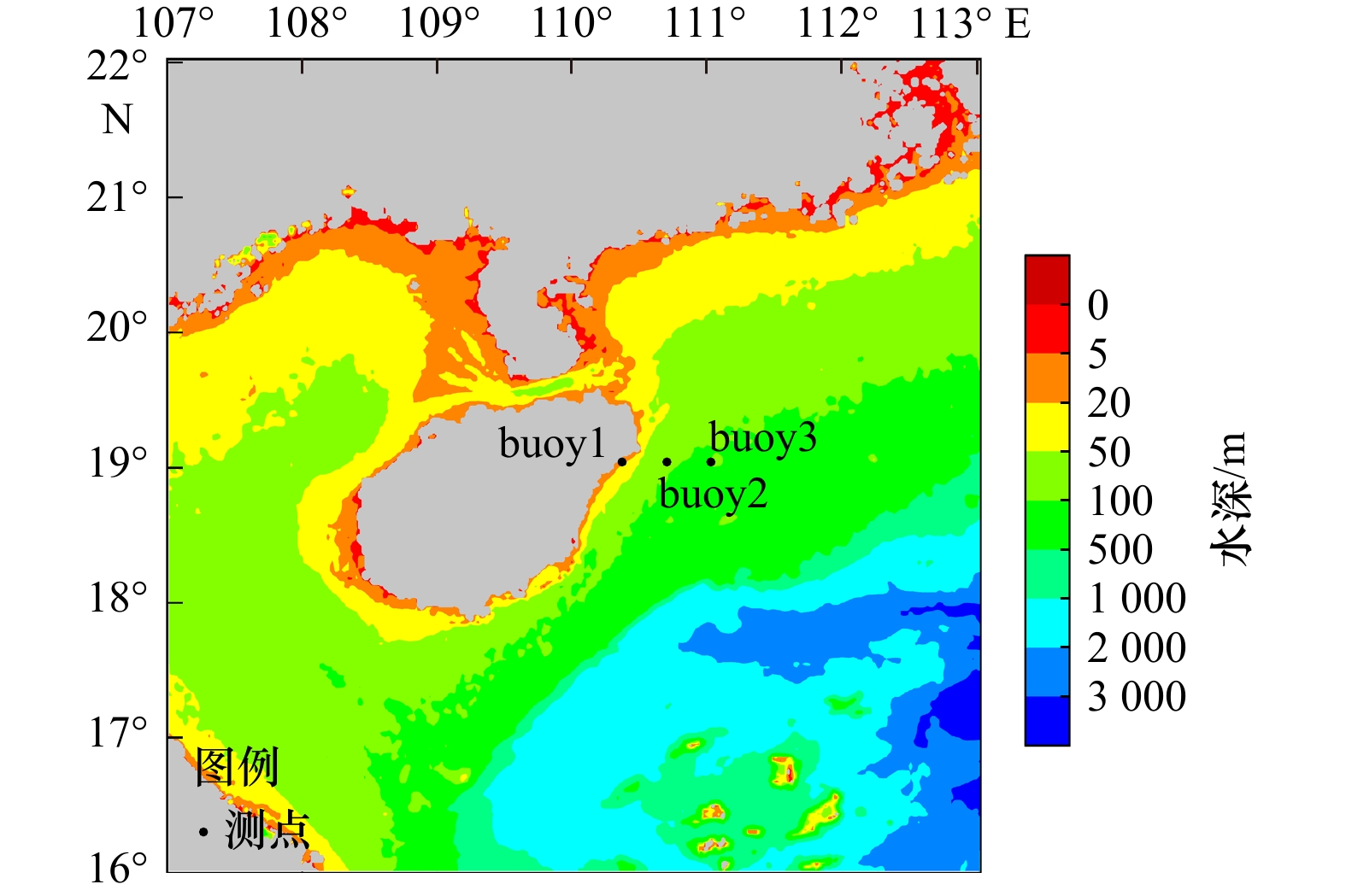
表 1 测点坐标及水深
Tab. 1 Location and water depth of survey points
测点 纬度 经度 水深/m buoy1 19.05°N 110.35°E 15.5 buoy2 19.05°N 110.70°E 101.4 buoy3 19.05°N 111.05°E 186.7 
下载: 导出CSV
-
[1] 李博, 李骏旻, 李毅能, 等. 人工神经网络在岛屿近岸海浪模拟中的应用[J]. 厦门大学学报(自然科学版), 2020, 59(3): 420−427.Li Bo, Li Junmin, Li Yineng, et al. Application of artificial neural network to numerical wave simulation in the coastal region of island[J]. Journal of Xiamen University (Natural Science), 2020, 59(3): 420−427. [2] 莫忠璇, 时闽生, 吕迎雪, 等. 基于SWAN-MIKE21嵌套模型在大连湾某工程区的波浪后报模拟应用[J]. 中国港湾建设, 2021, 41(2): 20−23. doi: 10.7640/zggwjs202102005Mo Zhongxuan, Shi Minsheng, Lü Yingxue, et al. Wave hindcast simulation based on SWAN-MIKE21 nested model in an engineering area in Dalian Bay[J]. China Harbour Engineering, 2021, 41(2): 20−23. doi: 10.7640/zggwjs202102005 [3] 滕陈轲敏, 岳显昌, 吴雄斌, 等. 风场对SWAN模式在台湾海峡后报结果的影响[J]. 海洋学报, 2019, 41(5): 59−69.Teng Chenkemin, Yue Xianchang, Wu Xiongbin, et al. Impacts of wind data on the hindcast of wave height simulated by SWAN model on the Taiwan Strait[J]. Haiyang Xuebao, 2019, 41(5): 59−69. [4] Choi Y K, Seo S N, Choi J Y, et al. Wave prediction in a port using a fully nonlinear Boussinesq wave model[J]. Acta Oceanologica Sinica, 2019, 38(7): 36−47. doi: 10.1007/s13131-019-1456-2 [5] Viitak M, Avilez-Valente P, Bio A, et al. Evaluating wind datasets for wave hindcasting in the NW Iberian Peninsula coast[J]. Journal of Operational Oceanography, 2021, 14(2): 152−165. doi: 10.1080/1755876X.2020.1738121 [6] 李巧生, 唐军, 吕义港. 适于模拟不规则水域波浪的缓坡方程两种数值模型比较[J]. 海洋学报, 2020, 42(1): 31−39.Li Qiaosheng, Tang Jun, Lü Yigang. Comparisons of the two numerical models of elliptic mild-slope equation for wave propagation in irregular coastal zones[J]. Haiyang Xuebao, 2020, 42(1): 31−39. [7] 林毅辉, 郑艺妃, 潘伟然, 等. 西沙湾工程波浪推算及波浪场数值模拟[J]. 应用海洋学学报, 2020, 39(1): 80−86.Lin Yihui, Zheng Yifei, Pan Weiran, et al. Engineering wave calculation and wave field numerical simulation in Xisha Bay[J]. Journal of Applied Oceanography, 2020, 39(1): 80−86. [8] 聂梓超. 广东典型红树林海湾波浪特性数值模拟研究[D]. 大连: 大连理工大学, 2019.Nie Zichao. Numerical study of wave characteristics in typical mangroves bays of Guangdong Province[D]. Dalian: Dalian University of Technology, 2019. [9] 郭云霞, 侯一筠, 齐鹏. Monte-Carlo模拟与经验路径模型预测台风极值风速的对比[J]. 海洋学报, 2020, 42(7): 64−77.Guo Yunxia, Hou Yijun, Qi Peng. Comparison of extreme wind speeds predicted by Monte-Carlo simulation and empirical track model[J]. Haiyang Xuebao, 2020, 42(7): 64−77. [10] Kim T Y, Oh K J, Kim C, et al. Artificial neural networks for non-stationary time series[J]. Neurocomputing, 2004, 61: 439−447. doi: 10.1016/j.neucom.2004.04.002 [11] Sutskever I, Hinton G E. Deep, narrow sigmoid belief networks are universal approximators[J]. Neural Computation, 2008, 20(11): 2629−2636. doi: 10.1162/neco.2008.12-07-661 [12] 高丽斌, 郭民权, 张少涵, 等. 基于长短期记忆网络的波高预报[J]. 福建电脑, 2018, 34(8): 105−107.Gao Libin, Guo Minquan, Zhang Shaohan, et al. Wave height prediction based on long short-term memory network[J]. Fujian Computer, 2018, 34(8): 105−107. [13] 赵凯欣. 基于SVR和LSTM算法反演散射计下有效波高研究[J]. 海洋湖沼通报, 2021, 43(1): 27−32.Zhao Kaixin. Research on retrieval of significant wave height from scatterometer based on SVR and LSTM algorithms[J]. Transactions of Oceanology and Limnology, 2021, 43(1): 27−32. [14] 阚世宜, 于婷, 刘莉. 基于EMD分解的海浪有效波高短期预测研究[J]. 海洋科学前沿, 2019, 6(2): 51−63. doi: 10.12677/AMS.2019.62007Kan Shiyi, Yu Ting, Liu Li. Short-term prediction of significant wave height based on EMD decomposition[J]. Advances in Marine Sciences, 2019, 6(2): 51−63. doi: 10.12677/AMS.2019.62007 [15] Roh M, Kim H S, Chang P H, et al. Numerical simulation of wind wave using ensemble forecast wave model: a case study of Typhoon Lingling[J]. Journal of Marine Science and Engineering, 2021, 9(5): 475. doi: 10.3390/jmse9050475 [16] 杨飞虎, 许国平, 刘贤松, 等. 基于Prophet时序算法的无线网络突变小区识别方法研究[J]. 邮电设计技术, 2021(2): 25−30.Yang Feihu, Xu Guoping, Liu Xiansong, et al. Research on recognition method of abrupt cells in wireless network based on Prophet sequence algorithm[J]. Designing Techniques of Posts and Telecommunications, 2021(2): 25−30. [17] 王晓, 揣锦华, 张立恒. 基于Prophet算法的铁路客流量预测研究[J]. 计算机技术与发展, 2020, 30(6): 130−134,150. doi: 10.3969/j.issn.1673-629X.2020.06.025Wang Xiao, Chuai Jinhua, Zhang Liheng. Research on railway passenger flow forecast based on Prophet time series algorithm[J]. Computer Technology and Development, 2020, 30(6): 130−134,150. doi: 10.3969/j.issn.1673-629X.2020.06.025 [18] 张海燕. 南海区台风风暴潮时空分布特征[J]. 海洋预报, 2019, 36(6): 1−8. doi: 10.11737/j.issn.1003-0239.2019.06.001Zhang Haiyan. Spatio-temporal distribution of typhoon storm surge along the South China Sea coast[J]. Marine Forecasts, 2019, 36(6): 1−8. doi: 10.11737/j.issn.1003-0239.2019.06.001 期刊类型引用(8)
1. 辛唯. LSTM-Prophet混合模型在物料储备需求预测中的应用. 现代计算机. 2024(04): 53-57 . 
百度学术2. 杜红兵，邢梦柯，赵德超. Prophet-LSTM组合模型在运输航空征候预测中的应用. 安全与环境学报. 2024(05): 1878-1885 . 百度学术3. 姚骥，汪雪良，武文华，顾学康，张欣玉. 考虑时间相关性的风速和波浪高度短期预测. 船舶力学. 2024(06): 832-842 . 百度学术4. 赵中伟，吴凌云，高伟健，李伟. 海南岛峨蔓五彩湾内海蚀平台对海蚀崖侵蚀的影响研究. 热带海洋学报. 2024(05): 106-115 . 百度学术5. 宋巍，赵勐，贺琪，胡安铎，张峰. 多要素局部-全局特征关联的有效波高预测模型. 上海海洋大学学报. 2023(03): 669-679 . 百度学术6. 周海涛，王玥，岳婷雨，陈威，胡斌. 基于Prophet等模型的手足口发病预测及对比分析. 医学动物防制. 2023(08): 715-721 . 百度学术7. 郑小罗，李其超，姜浩，宋巍，邓小东. 基于多周期趋势分解和两级融合策略的浪高预测方法. 海洋科学进展. 2023(03): 466-476 . 百度学术8. 李骏旻，李博，陈武阳，刘军亮. 三亚近岸海浪观测特征及其对台风过程的响应. 热带海洋学报. 2023(04): 25-35 . 百度学术其他类型引用(4)
-
下载:
百度学术
计量
- 文章访问数: 799
- HTML全文浏览量: 274
- PDF下载量: 81
- 被引次数: 12
