Inference methods and uncertainty assessment of extreme wave heights
-
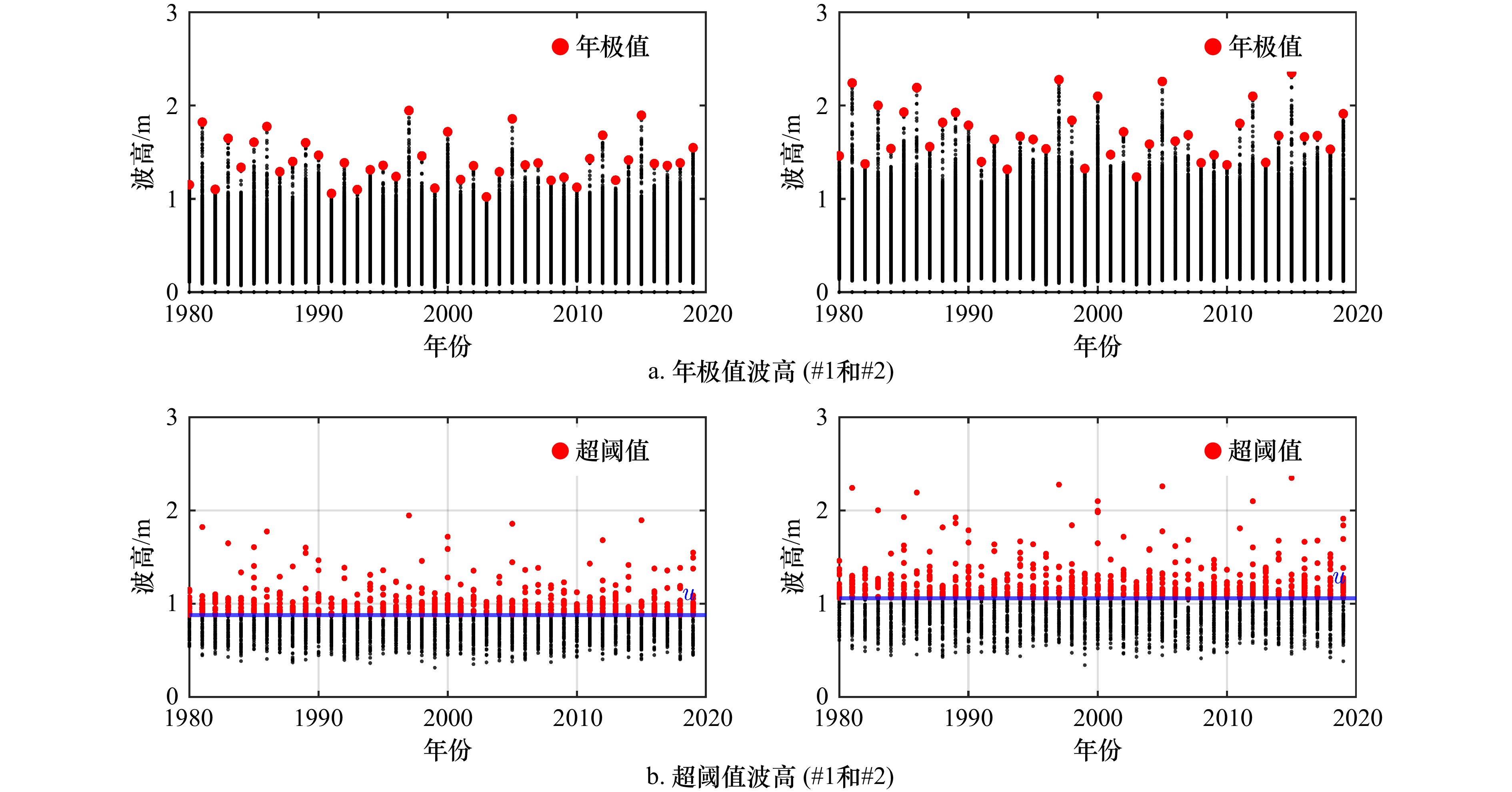
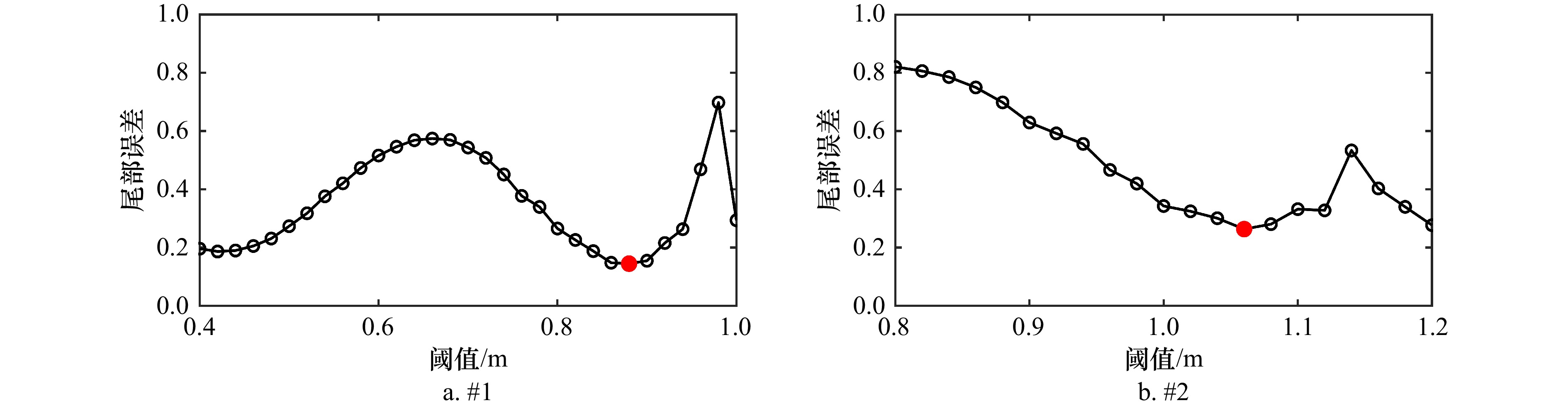
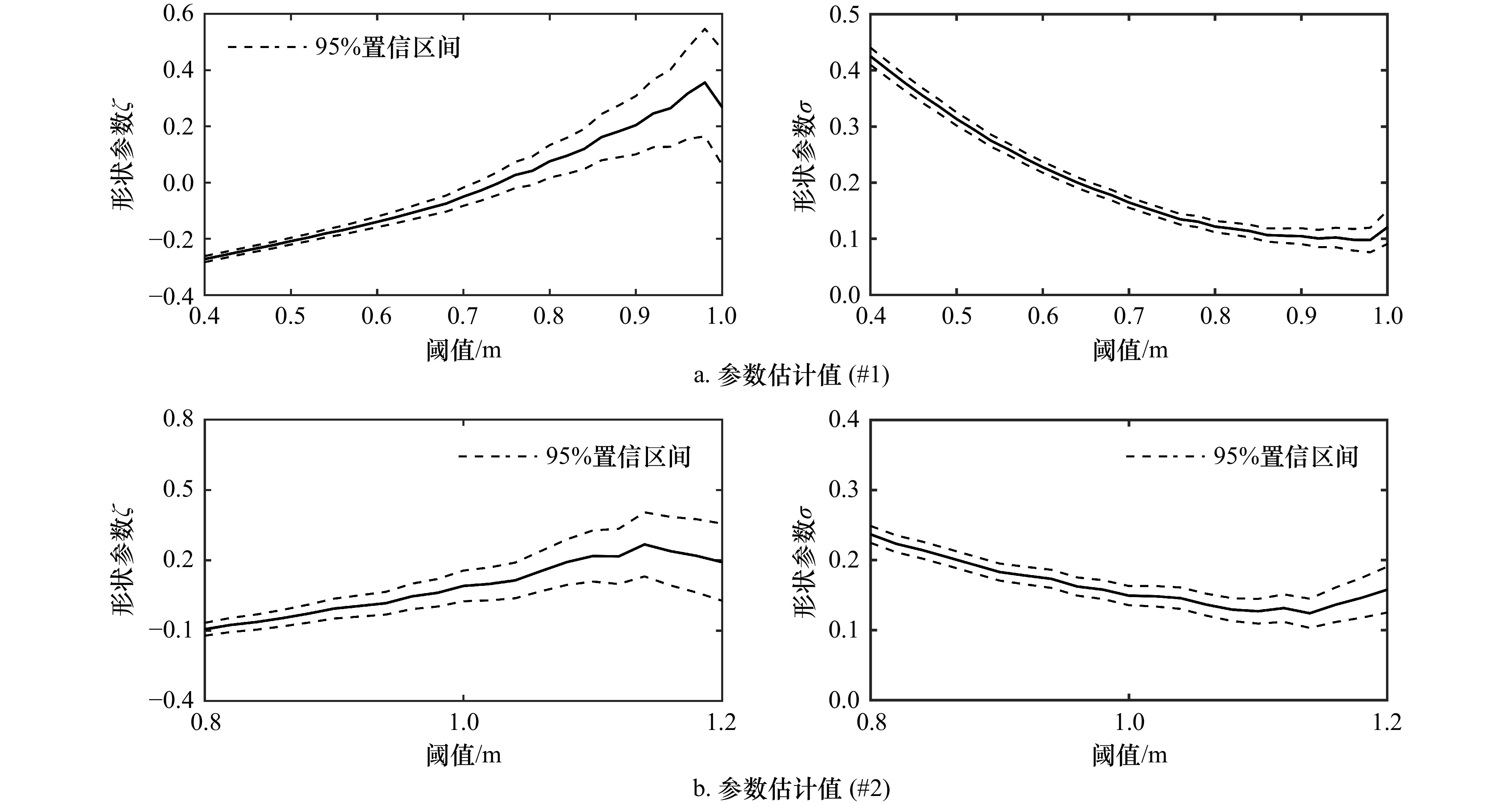
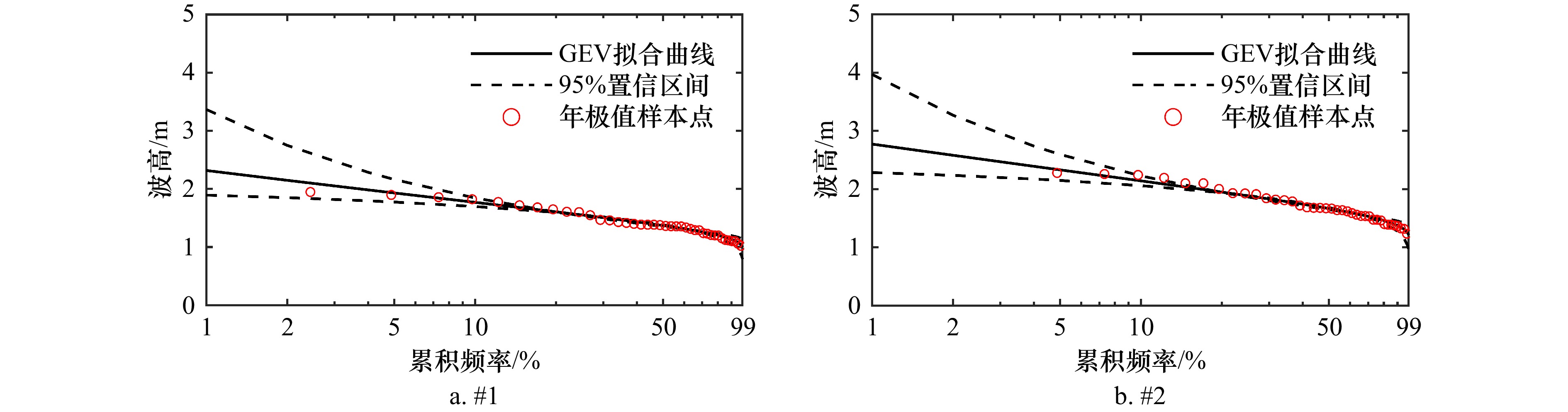
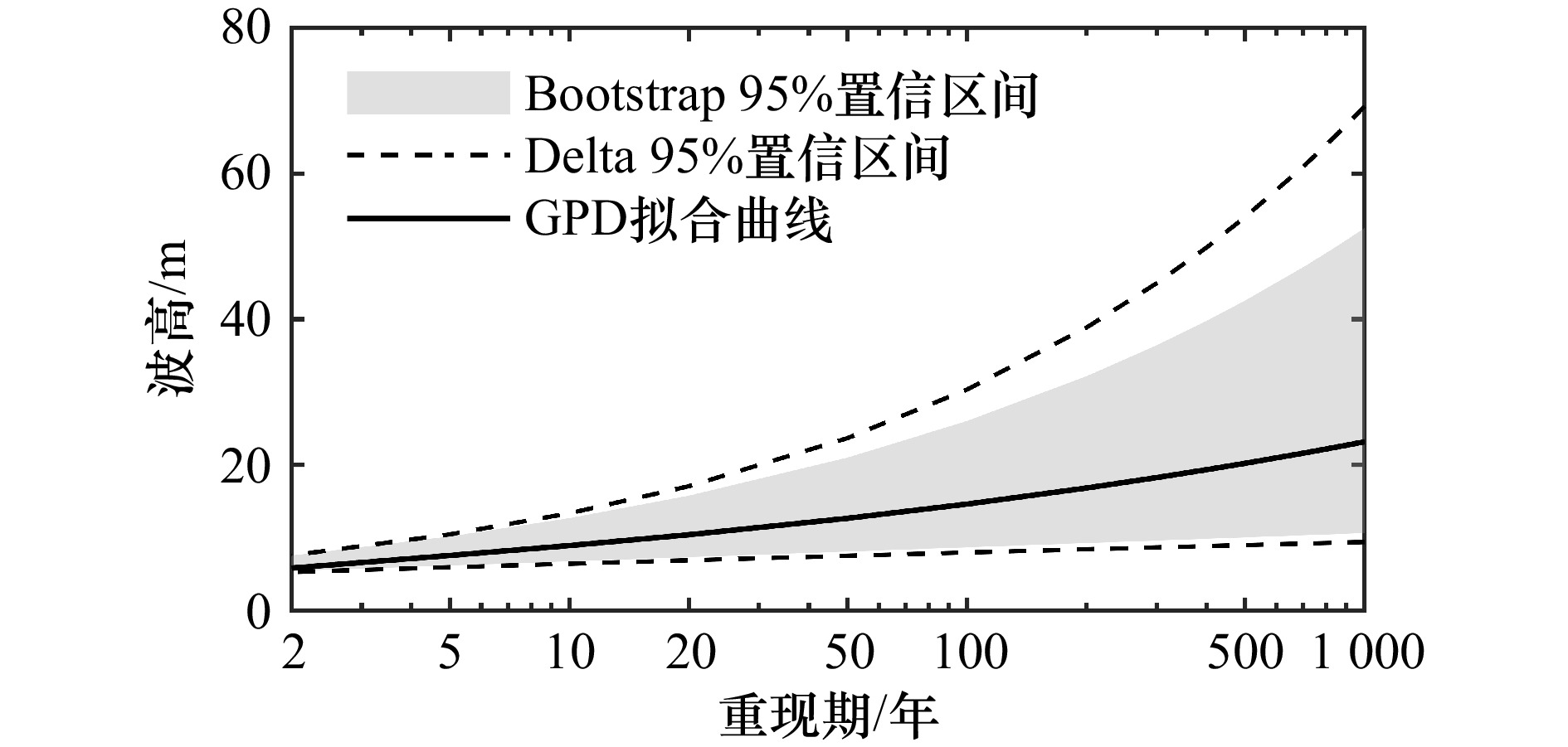
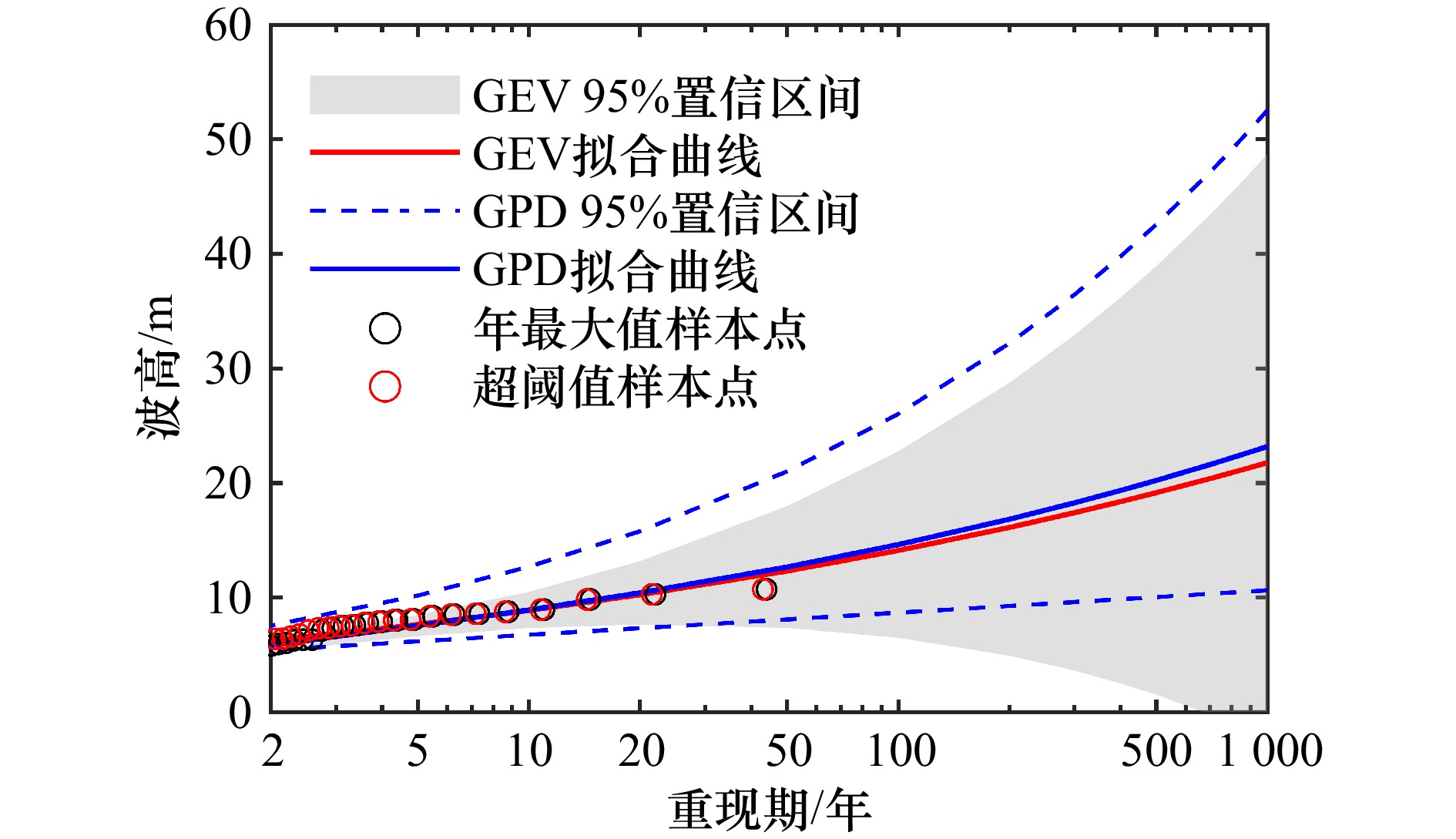
摘要: 针对提升海洋工程中波高极值推算精度的需求，本文系统对比分析了年极值法（AM）与超阈值法（POT）的适用性及其不确定性。基于杭州湾两站点的多年再分析波浪数据，分别构建年极值序列与超阈值样本，并采用广义极值分布（GEV）和广义Pareto分布（GPD）进行建模；其中，POT法通过尾部误差最小化准则优化阈值选择。进一步结合Delta法与Bootstrap法，量化了模型参数与重现期水平波高估计值的置信区间。结果表明，对于高重现期水平，POT法给出的波高估计值更高，置信区间更窄，更适用于对极端事件敏感的工程设计场景；在不确定性分析方面，Bootstrap法较Delta法更能全面反映模型不确定性。本研究为波高极值建模建立了更为稳健的分析框架与参数推算依据。Abstract: To enhance the accuracy and reliability of extreme wave height inference in ocean engineering, this study systematically compares the applicability and uncertainty of the Annual Maxima (AM) method and the Peak Over Threshold (POT) method. Utilizing reanalysis wave data from two representative sites in Hangzhou Bay, annual maxima series and POT samples were constructed. These were modeled using the Generalized Extreme Value (GEV) distribution and the Generalized Pareto Distribution (GPD), respectively; for the POT method, threshold selection was optimized via a tail least squares error (TLSE) criterion. Confidence intervals for model parameters and return period level wave height estimates were further quantified using both the Delta method and the Bootstrap method. The results demonstrate that for high return periods, the POT method yields higher wave height estimates with narrower confidence intervals, rendering it more suitable for engineering design scenarios sensitive to extreme events. In uncertainty analysis, the Bootstrap method more comprehensively captures model uncertainty compared to the Delta method. This work establishes a more robust analytical framework and inferential basis for extreme wave height modeling.
-
Key words:
- extreme wave height /
- uncertainty /
- Peak Over Threshold method /
- bootstrap
-
图 2 年极值和超阈值波高样本选取对比
Fig. 2 Comparison between the annual maximum model and peak-over-threshold model
图 7 波高估计值（100年）和尾部误差随阈值变化图
Fig. 7 Variation of 100-year return period wave heights estimates and the TLSE with thresholds
图 8 Bootstrap计算的平均尾部误差随阈值变化图
Fig. 8 The TLSEB by Bootstrap varies with the thresholds.
图 10 不同方法推算的重现期波高对比
Fig. 10 Comparison of return period wave heights derived from different methods
图 12 不同方法推算的重现期波高对比
Fig. 12 Comparison of return period wave heights derived from different methods
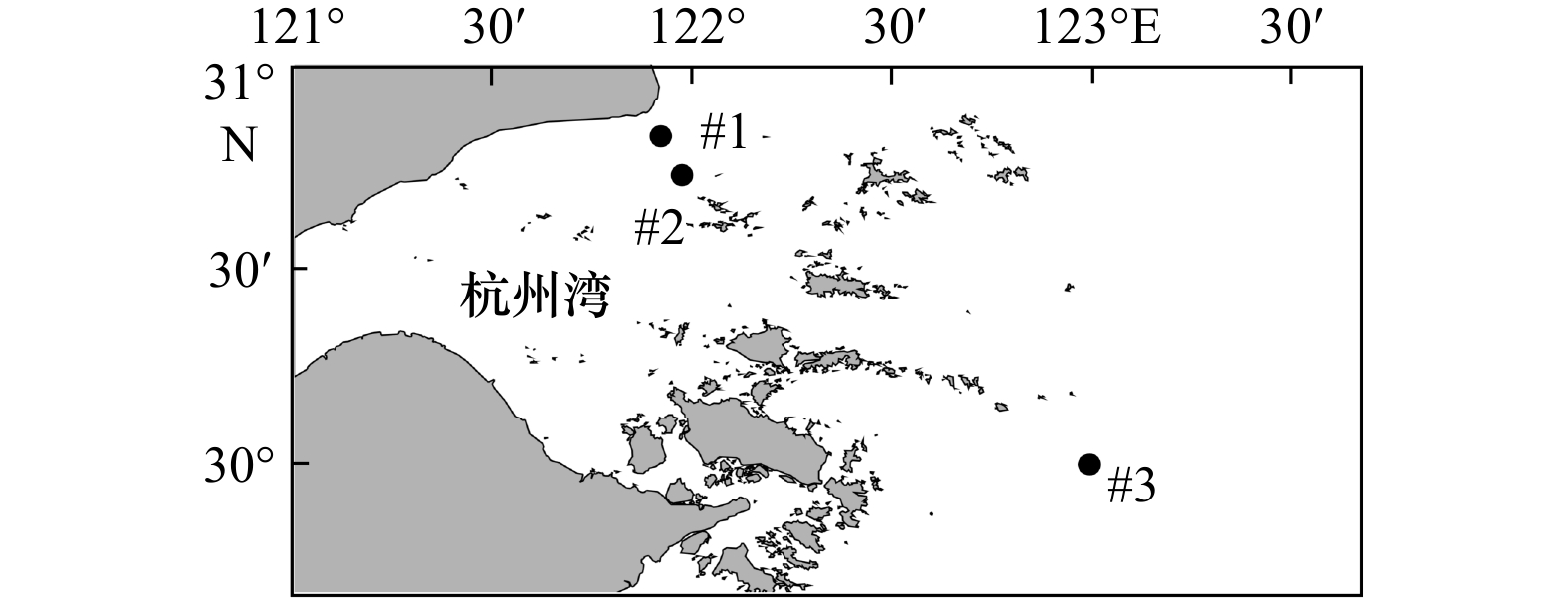
表 1 研究点信息
Tab. 1 Information of Research Stations
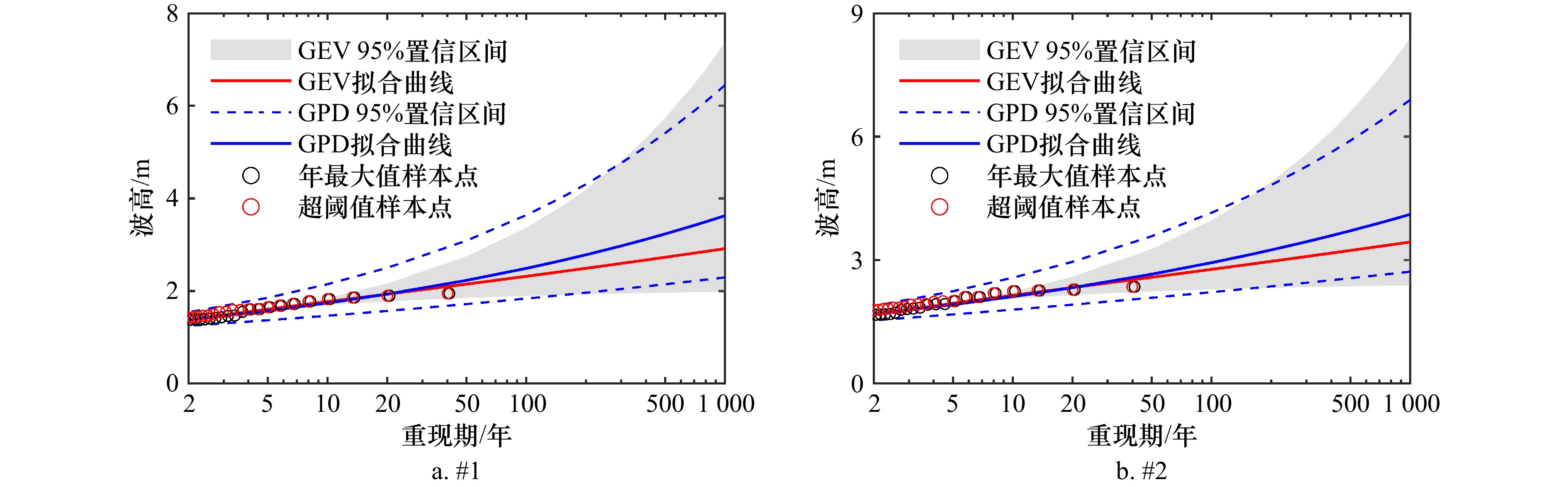
研究点 经度(°E) 纬度(°N) 水深(m) 最大值(m) 最小值(m) 平均值(m) #1 121.92 30.84 5.00 1.95 0.05 0.45 #2 121.99 30.73 5.00 2.35 0.07 0.55 #3 123.00 30.00 50.00 10.72 0.15 1.32 
下载: 导出CSV
表 2 不同极值理论方法参数估计结果及重现期波高比较
Tab. 2 Comparison of parameter estimation and return period wave height using different extreme value theories
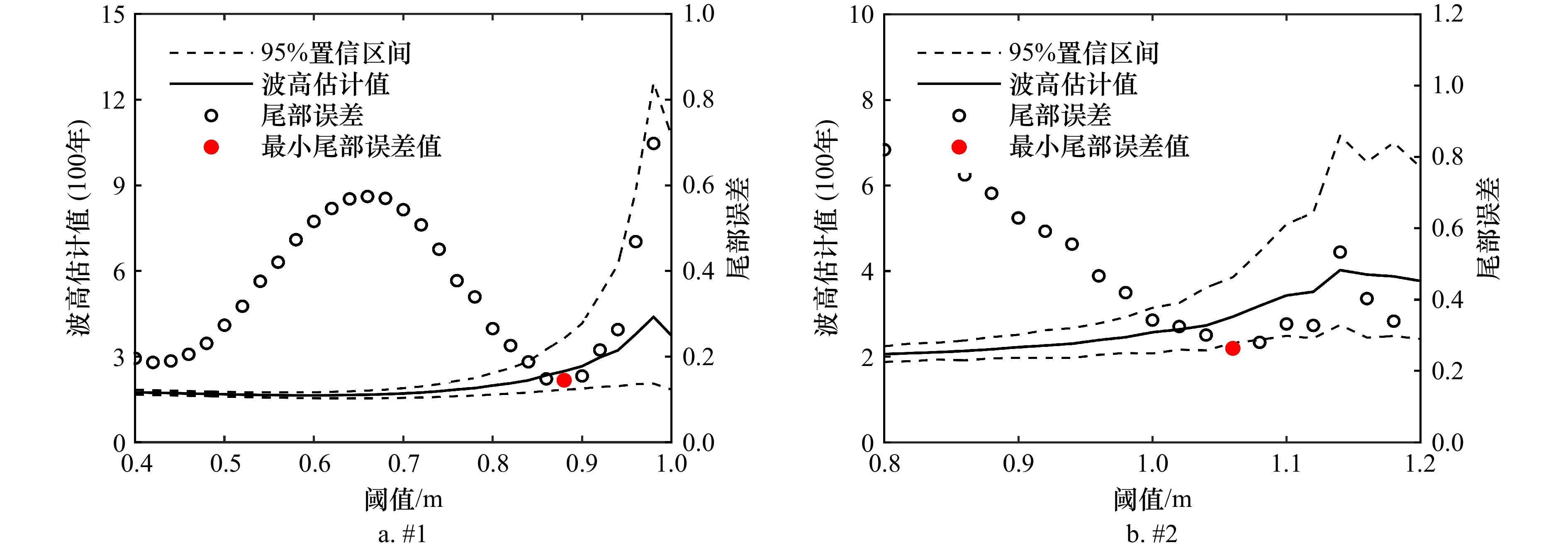
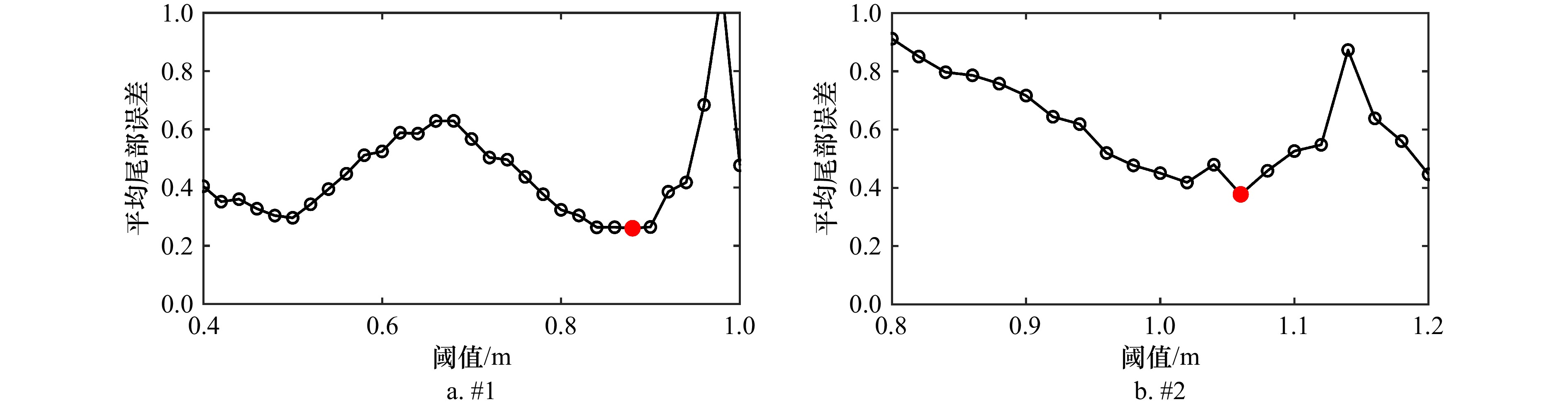
研究点 方法 参数 重现期波高/m μ/u ξ σ 2年 5年 10年 20年 50年 100年 #1 年极值法 1.297 -0.046 0.199 1.37 1.61 1.77 1.93 2.15 2.32 超阈值法 0.88 0.106 0.182 1.37 1.57 1.74 1.93 2.23 2.49 #2 年极值法 1.576 -0.030 0.243 1.67 1.95 2.14 2.33 2.58 2.77 超阈值法 1.06 0.154 0.136 1.69 1.91 2.11 2.33 2.66 2.93
下载: 导出CSV
表 3 不同Bootstrap对应的TLSEB（u = 0.88 m）
Tab. 3 TLSEB corresponding to different Bootstraps (u = 0.88 m)
研究点 Bootstrap 原始样本TLSE 50 100 200 500 1000 2000 #1 TLSEB 0.145 0.228 0.264 0.240 0.241 0.242 0.242 ξ 0.182 0.173 0.176 0.180 0.178 0.180 0.180 σ 0.106 0.106 0.106 0.105 0.106 0.106 0.106 #2 TLSEB 0.263 0.386 0.405 0.397 0.392 0.395 0.396 ξ 0.154 0.162 0.151 0.153 0.155 0.153 0.153 σ 0.136 0.135 0.137 0.136 0.136 0.137 0.137
下载: 导出CSV
表 4 GPD 参数置信区间比较
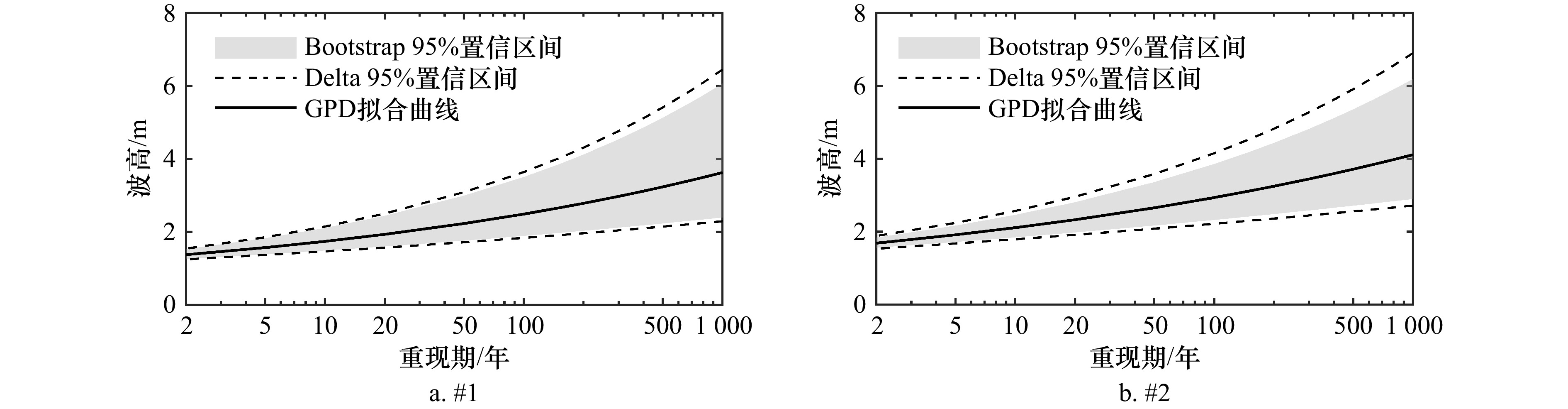
Tab. 4 Comparison of confidence intervals of GPD parameters
研究点 方法 ξ置信区间 σ置信区间 ξ置信区间宽度 σ置信区间宽度 #1 Bootstrap法 [0.101, 0.263] [0.094, 0.119] 0.162 0.025 Delta法 [0.090, 0.274] [0.093, 0.118] 0.184 0.025 #2 Bootstrap法 [0.081, 0.224] [0.125, 0.148] 0.143 0.023 Delta法 [0.068, 0.240] [0.121, 0.152] 0.172 0.031
下载: 导出CSV
-
[1] Chen Baiyu, Zhang Kuangyuan, Wang Liping, et al. Generalized extreme value-pareto distribution function and its applications in ocean engineering[J]. China Ocean Engineering, 2019, 33(2): 127−136. doi: 10.1007/s13344-019-0013-9 [2] Ions K, Karunarathna H, Reeve D E, et al. Gravel barrier beach morphodynamic response to extreme conditions[J]. Journal of Marine Science and Engineering, 2021, 9(2): 135. doi: 10.3390/jmse9020135 [3] Vieira D P, Tannuri E A, Câmara J G A. Availability assessment of a monobuoy-anchored ship to ship offloading system[J]. Applied Ocean Research, 2020, 101: 102291. doi: 10.1016/j.apor.2020.102291 [4] Zheng Siming, Antonini A, Zhang Yongliang, et al. Hydrodynamic performance of a multi-Oscillating Water Column (OWC) platform[J]. Applied Ocean Research, 2020, 99: 102168. doi: 10.1016/j.apor.2020.102168 [5] 中华人民共和国交通运输部. JTS 145-2015(2022版), 港口与航道水文规范[S]. 北京: 人民交通出版社, 2016: 17-20.Ministry of Transport of the People's Republic of China. JTS 145—2015 (2022 Edition), Code of hydrology for harbour and waterway[S]. Beijing: China Communication Press, 2016: 17-20. [6] 刘德辅, 马逢时. 极值分布理论在计算波高多年分布中的应用[J]. 应用数学学报, 1976(1): 23-37.Liu Defu, Ma Fengshi. Application of extreme value distribution theory in computing the multi-year distribution of wave heights[J]. Acta Mathematicae Applicatae Sinica, 1976(1): 23-37. (查阅网上资料, 未找到对应英文翻译信息, 请确认) [7] You Zaijin, Yin Baoshu. Estimation of extreme coastal wave heightsfrom time series of wave data[J]. China Ocean Engineering, 2006, 20(2): 225−241. [8] 王超, 刘德辅. 设计波浪选取中的不确定性分析[J]. 海洋学报, 1991, 13(6): 874−881.Wang Chao, Liu Defu. Uncertainty analysis in the selection of design waves[J]. Haiyang Xuebao, 1991, 13(6): 874−881. (查阅网上资料, 未找到对应英文翻译信息, 请确认) [9] Coles S. An Introduction to Statistical Modeling of Extreme Values[M]. London: Springer, 2001. [10] Silva-González F, Heredia-Zavoni E, Inda-Sarmiento G. Square Error Method for threshold estimation in extreme value analysis of wave heights[J]. Ocean Engineering, 2017, 137: 138−150. doi: 10.1016/j.oceaneng.2017.03.028 [11] Liang Bingchen, Shao Zhuxiao, Li Huajun, et al. An automated threshold selection method based on the characteristic of extrapolated significant wave heights[J]. Coastal Engineering, 2019, 144: 22−32. doi: 10.1016/j.coastaleng.2018.12.001 [12] Shao Zhuxiao, Liang Bingchen, Gao Huijun. Extracting independent and identically distributed samples from time series significant wave heights in the Yellow Sea[J]. Coastal Engineering, 2020, 158: 103693. doi: 10.1016/j.coastaleng.2020.103693 [13] Pickands III J. Statistical inference using extreme order statistics[J]. The Annals of Statistics, 1975, 3(1): 119−131. [14] Mazas F, Hamm L. A multi-distribution approach to POT methods for determining extreme wave heights[J]. Coastal Engineering, 2011, 58(5): 385−394. doi: 10.1016/j.coastaleng.2010.12.003 [15] Zhao Yue, Xie Dongmei, Pan Junning, et al. A threshold determination method for extreme value analysis based on the tail least squares estimation[J]. Ocean Engineering, 2025, 335: 121696. doi: 10.1016/j.oceaneng.2025.121696 [16] 郭怿品, 李典庆, 唐小松, 等. 基于Bootstrap方法的堆石坝坝坡稳定可靠度分析[J]. 武汉大学学报(工学版), 2019, 52(2): 106−115.Guo Yipin, Li Dianqing, Tang Xiaosong, et al. Slope stability reliability of rockfill dams based on Bootstrap method[J]. Engineering Journal of Wuhan University, 2019, 52(2): 106−115. [17] 张艳芳, 赵宜宾, 任晴晴. 广义Pareto分布参数的Bootstrap置信区间及应用[J]. 工程数学学报, 2023, 40(6): 1011−1020. doi: 10.3969/j.issn.1005-3085.2023.06.012Zhang Yanfang, Zhao Yibin, Ren Qingqing. Bootstrap confidence interval for parameters of generalized Pareto distribution and its application[J]. Chinese Journal of Engineering Mathematics, 2023, 40(6): 1011−1020. doi: 10.3969/j.issn.1005-3085.2023.06.012 [18] Makkonen L. Bringing closure to the plotting position controversy[J]. Communications in Statistics-Theory and Methods, 2008, 37(3): 460−467. doi: 10.1080/03610920701653094 [19] Sun Peidong, Xu Bin, Wang Jichao. Long-term trend analysis and wave energy assessment based on ERA5 wave reanalysis along the Chinese coastline[J]. Applied Energy, 2022, 324: 119709. doi: 10.1016/j.apenergy.2022.119709 [20] 杜文彦, 张旭日, 张丽丽, 等. 基于ERA5再分析数据的中国邻近海域极端波高特征分析[J]. 海洋与湖沼, 2022, 53(4): 1007−1014. doi: 10.11693/hyhz20220100003Du Wenyan, Zhang Xuri, Zhang Lili, et al. Characteristics of extreme wave height in China’s marginal seas based on ERA5 reanalysis data[J]. Oceanologia et Limnologia Sinica, 2022, 53(4): 1007−1014. doi: 10.11693/hyhz20220100003 [21] 夏武松, 魏永亮, 陆恒星, 等. 基于ERA5的南大西洋风速和有效波高时空变化特征分析[J]. 海洋湖沼通报, 2024, 46(1): 1−11.Xia Wusong, Wei Yongliang, Lu Hengxing, et al. Analysis of temporal and spatial changes of wind speed and significant wave height in the South Atlantic based on ERA5[J]. Transactions of Oceanology and Limnology, 2024, 46(1): 1−11. [22] Luceño A, Menéndez M, Méndez F J. The effect of temporal dependence on the estimation of the frequency of extreme ocean climate events[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2006, 462(2070): 1683−1697. doi: 10.1098/rspa.2005.1652 [23] Méndez F J, Menéndez M, Luceño A, et al. Estimation of the long‐term variability of extreme significant wave height using a time‐dependent Peak Over Threshold (POT) model[J]. Journal of Geophysical Research: Oceans, 2006, 111(C7): C07024. [24] Feng Jianhong, Jiang Wensheng. Extreme water level analysis at three stations on the coast of the Northwestern Pacific Ocean[J]. Ocean Dynamics, 2015, 65(11): 1383−1397. doi: 10.1007/s10236-015-0881-3 [25] 刘旭, 王峥, 梁颖祺, 等. 我国台风风暴潮灾害损失的时空演变特征分析[J]. 海洋预报, 2023, 40(6): 21−32. doi: 10.11737/j.issn.1003-0239.2023.06.003Liu Xu, Wang Zheng, Liang Yingqi, et al. Spatial-temporal characteristics of the typhoon storm surge damages in China[J]. Marine Forecasts, 2023, 40(6): 21−32. doi: 10.11737/j.issn.1003-0239.2023.06.003 [26] Murphy C, Tawn J A, Varty Z. Automated threshold selection and associated inference uncertainty for univariate extremes[J]. Technometrics, 2025, 67(2): 215−224. doi: 10.1080/00401706.2024.2421744 -
图(12) / 表(4)
计量
- 文章访问数: 19
- HTML全文浏览量: 7
- PDF下载量: 2
- 被引次数: 0
