A multivariate wave forecasting model for the Zhoushan archipelago using Long Short-Term Memory deep neural networks
-
摘要: 本文以2019年1月1日至2021年12月31日舟山群岛南部外海观测点所涵盖的气象、海洋、地形等多种物理量数据为数据基础，使用长短时记忆（Long Short Term Memory，LSTM）神经网络搭建深度学习海浪预报模型，探讨输入输出序列比和输入要素数量对模型预测性能的影响，在舟山海域实现波浪三要素，即有效波高、有效波周期、传播方向的短时预报，并用2022年台风“轩岚诺”和“梅花”期间的数据检验模型对极端海况的预测能力。研究结果表明，根据实测数据所训练的多要素海浪预报模型具有较好的预测准确度和稳定性，能较好地实现对极端海况的预测，当输入输出序列比为1∶1时模型准确度较高，预报时长为1 h的三要素模型对于日常海况中有效波高、有效波周期和波向的预测均方根误差（Root Mean Squared Error，RMSE）分别为0.116 m、0.569 s和24.583°，对于极端海况中有效波高的预测RMSE为0.191 m，输入要素数量的增加可进一步提升模型准确度，但在预测时长较长时也会增加训练成本。Abstract: This study is based on the meteorological, oceanic, terrain and other physical quantity data covered by the observation points in the southern Zhoushan Islands from January 1, 2019 to December 31, 2021, and uses long short-term memory neural network (LSTM) to build deep learning wave forecast model. We explore the impact of the input-output sequence ratio and the number of input elements on the prediction performance of the model, realize the short-term forecast of the three elements of waves in the Zhoushan sea area, that is the significant wave height, the significant wave period and the propagation direction, and use the data during the 2022 typhoons “Hinnamnor” and “Muifa” to test the model’s prediction ability for extreme sea conditions. The research results show that the multi-element deep learning wave forecast model trained based on measured data has good prediction accuracy and stability, and can realize the prediction of extreme sea conditions. When the input-output sequence ratio is 1∶1, the model accuracy is higher. In non-extreme sea conditions, the three-element model with a prediction time of 1 hour accurately predicts significant wave height, significant wave period and direction, with Root Mean Squared Errors (RMSE) of 0.116 m, 0.569 s, and 24.583° respectively. In extreme sea conditions, the prediction RMSE for the significant wave height is 0.191 m. The increase in the number of input elements can further improve the model accuracy but also increase the training cost when the prediction time is long.
-
Key words:
- deep learning /
- Long Short-Term Memory model /
- wave forecasting /
- Zhoushan
-
图 1 16个气象水文观测要素相关系数矩阵
Fig. 1 The Pearson correlation coefficient matrix among sixteen meteorological-hydrological observation elements
图 2 七要素模型中各输入要素的时间序列
a. 有效波高，b. 有效波周期，c. 波向，d. 分钟内瞬时风速，e. 波数，f. 峰值能量，g. 流深
Fig. 2 Time series diagram of each input element in the seven-element model
a. significant wave height, b. significant wave period, c. wave direction, d. instantaneous wind speedper minute, e. wave number, f. peak energy, g. flow depth
图 4 使用15 h历史数据预测未来3 h海浪的模型子样本划分
a. 训练集子样本划分，b. 测试集子样本划分
Fig. 4 Model subsample partitioning for predicting waves in the next 3 hours using 15 hours of historical data
a. Training set subsample division, b. test set subsample division
图 6 三要素海浪预报模型在非极端海况期间的预测结果与实测值的对比验证
Fig. 6 The comparison between the predicted results of the three-element wave prediction model and the measured values during non-extreme sea conditions
图 7 三要素海浪预报模型在台风“轩岚诺”与“梅花”期间的预测结果与实测值的对比验证
Fig. 7 The comparison between the predicted results of the three-element wave forecast model during Typhoon “Hinnamnor” and “Muifa” and the measured values
表 1 2019−2021年舟山南部海域浮标站各要素信息统计表（各数据采样间隔均为1 h）
Tab. 1 Statistical table of each element information of buoy station in the southern waters of Zhoushan from 2019 to 2021, (with a data sampling interval of 1 hour)
观测要素 单位 最大值 平均值 标准差 有效波高 米(m) 7.00 0.98 0.49 有效波周期 秒(s) 15.10 6.00 1.48 波向 度(°) 360.00 113.15 60.46 1 h内最大10 min平均风速 米/秒(m/s) 20.50 6.17 3.07 1 h内最大10 min平均风向 度(°) 360.00 171.29 122.52 分钟内瞬时风速 米/秒(m/s) 25.00 6.58 3.44 分钟内瞬时风向 度(°) 360.00 174.51 123.57 平均波高 米(m) 3.00 0.56 0.25 平均周期 秒(s) 10.6 4.67 0.79 波数 个/千米（km−1） 325.00 209.48 35.48 谱有效波高 米(m) 7.60 1.18 0.54 谱平均波周期 秒(s) 9.90 4.96 0.85 峰值波周期 秒(s) 24.90 11.35 7.57 峰值能量 焦耳(J) 91.50 0.85 2.40 ADCP流量 立方米/秒(m3/s) 41.28 5.16 2.36 流深 米(m) 27.90 25.29 1.11 
下载: 导出CSV
表 2 神经网络模型不同输入输出序列比的训练方案表
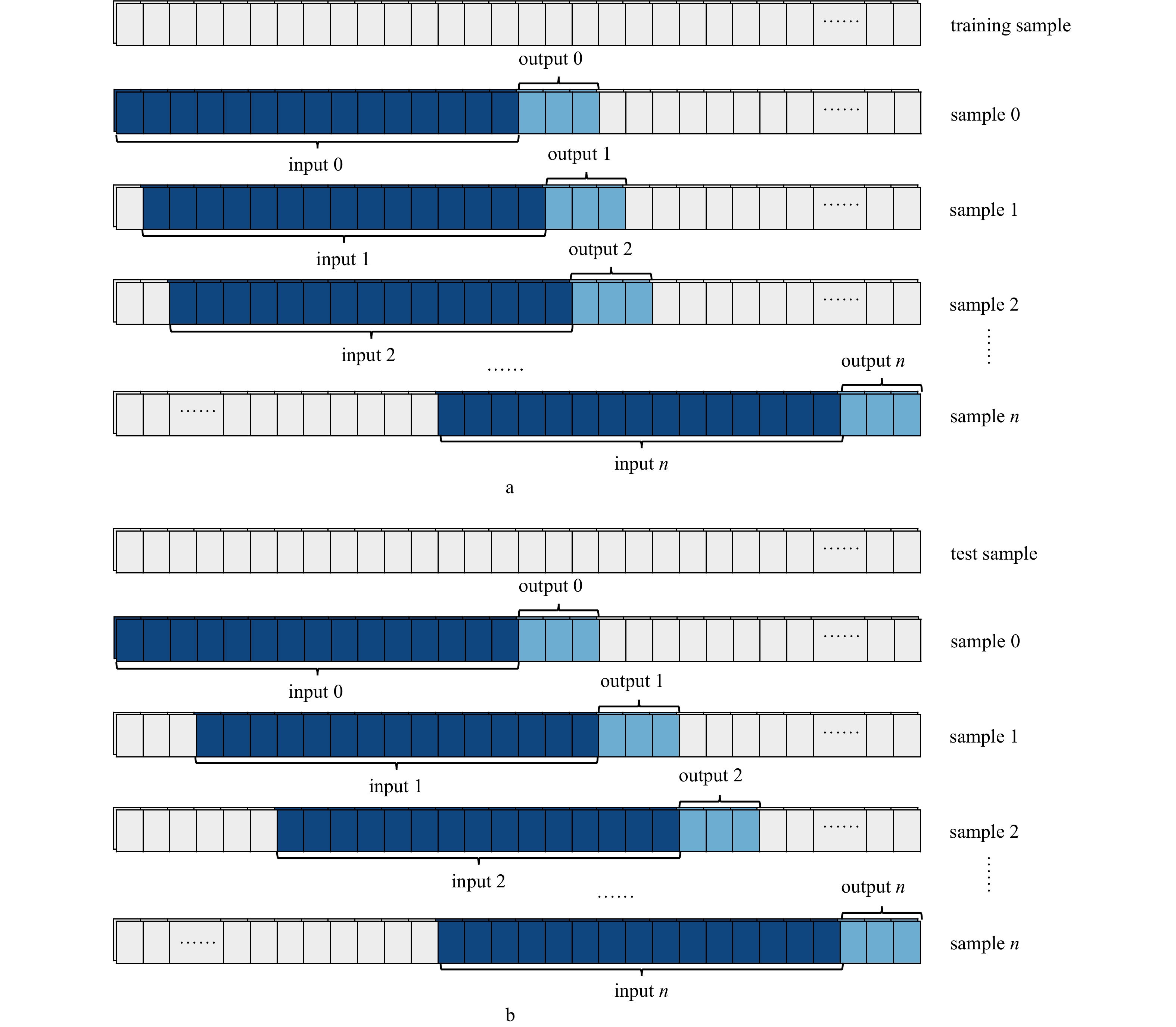
Tab. 2 Table of training schemes for neural network models with different input-output sequence ratios
方案编号 输入序列长度/步 比例 输出序列长度（步）/预报时长（h） M01 1 1∶1 1 M02 3 3∶1 M03 5 5∶1 M04 7 7∶1 M05 3 1∶1 3 M06 9 3∶1 M07 15 5∶1 M08 21 7∶1 M09 6 1∶1 6 M10 18 3∶1 M11 30 5∶1 M12 42 7∶1 M13 12 1∶1 12 M14 36 3∶1 M15 48 5∶1 M16 74 7∶1 M17 18 1∶1 18 M18 54 3∶1 M19 70 5∶1 M20 98 7∶1 M21 24 1∶1 24 M22 72 3∶1 M23 120 5∶1 M24 168 7∶1 M25 48 1∶1 48 M26 144 3∶1 M27 240 5∶1 M28 326 7∶1
下载: 导出CSV
表 3 数据集划分
Tab. 3 Dataset segmentation
数据周期 极端海况 名称 2019年1月1日至2021年9月27日 丹娜丝、利马奇、玲玲、米娜、黑格比、美莎克、烟花、灿都 训练集 2021年9月28日至2021年12月31日 无 非极端海况测试集 2022年8月30日至2022年9月30日 轩岚诺、梅花 极端海况测试集
下载: 导出CSV
表 4 两类模型的RMSE对比
Tab. 4 RMSE comparison of two types of models
方案编号 预报时长/h 比例 有效波高/m 有效波周期/s 波向/（°） 三要素 七要素 三要素 七要素 三要素 七要素 M01 1 1∶1 0.116 0.116 0.569 0.564 24.583 24.296 M02 3∶1 0.116 0.113 0.561 0.548 24.875 24.571 M03 5∶1 0.114 0.112 0.564 0.548 24.568 24.882 M04 7∶1 0.114 0.114 0.566 0.550 24.975 24.746 M05 3 1∶1 0.149 0.146 0.704 0.678 31.565 32.424 M06 3∶1 0.150 0.147 0.701 0.678 32.409 32.086 M07 5∶1 0.149 0.147 0.702 0.676 32.861 33.492 M08 7∶1 0.149 0.147 0.699 0.680 32.682 32.526 M09 6 1∶1 0.181 0.174 0.850 0.818 45.581 44.824 M10 3∶1 0.187 0.173 0.846 0.811 47.467 44.643 M11 5∶1 0.186 0.173 0.836 0.816 48.320 45.477 M12 7∶1 0.182 0.173 0.830 0.818 47.837 45.824 M13 12 1∶1 0.232 0.223 0.954 0.943 48.260 46.127 M14 3∶1 0.231 0.224 0.944 0.938 47.521 46.212 M15 5∶1 0.236 0.230 0.945 0.951 48.184 47.818 M16 7∶1 0.235 0.219 0.941 0.938 47.982 49.797 M17 18 1∶1 0.255 0.244 1.022 1.020 50.168 51.799 M18 3∶1 0.257 0.254 1.007 1.005 49.488 50.330 M19 5∶1 0.258 0.253 1.001 1.005 49.442 51.580 M20 7∶1 0.264 0.260 1.010 1.026 51.358 50.763 M21 24 1∶1 0.295 0.296 1.107 1.120 54.430 50.218 M22 3∶1 0.308 0.294 1.105 1.077 55.247 52.649 M23 5∶1 0.302 0.303 1.085 1.078 54.854 52.503 M24 7∶1 0.292 0.300 1.095 1.080 53.823 52.248 M25 48 1∶1 0.372 0.366 1.218 1.218 58.143 53.154 M26 3∶1 0.381 0.373 1.208 1.170 57.361 53.212 M27 5∶1 0.408 0.389 1.284 1.241 58.145 54.375 M28 7∶1 0.388 0.362 1.258 1.278 57.736 54.693
下载: 导出CSV
-
[1] Qin Yue, Su Changyu, Chu Dongdong, et al. A review of application of machine learning in storm surge problems[J]. Journal of Marine Science and Engineering, 2023, 11(9): 1729. doi: 10.3390/jmse11091729 [2] Mahjoobi J, Mosabbeb E A. Prediction of significant wave height using regressive support vector machines[J]. Ocean Engineering, 2009, 36(5): 339−347. doi: 10.1016/j.oceaneng.2009.01.001 [3] 王燕, 钟建, 张志远. 支持向量回归的机器学习方法在海浪预测中的应用[J]. 海洋预报, 2020, 37(3): 29−34.Wang Yan, Zhong Jian, Zhang Zhiyuan. Application of support vector regression in significant wave height forecasting[J]. Marine Forecasts, 2020, 37(3): 29−34. [4] Mahjoobi J, Etemad-Shahidi A. An alternative approach for the prediction of significant wave heights based on classification and regression trees[J]. Applied Ocean Research, 2008, 30(3): 172−177. doi: 10.1016/j.apor.2008.11.001 [5] Ellenson A, Pei Yuanli, Wilson G, et al. An application of a machine learning algorithm to determine and describe error patterns within wave model output[J]. Coastal Engineering, 2020, 157: 103595. doi: 10.1016/j.coastaleng.2019.103595 [6] Hu R, Fang F, Pain C C, et al. Rapid spatio-temporal flood prediction and uncertainty quantification using a deep learning method[J]. Journal of Hydrology, 2019, 575: 911−920. doi: 10.1016/j.jhydrol.2019.05.087 [7] 石绥祥, 王蕾, 余璇, 等. 长短期记忆神经网络在叶绿素a浓度预测中的应用[J]. 海洋学报, 2020, 42(2): 134−142.Shi Suixiang, Wang Lei, Yu Xuan, et al. Application of long term and short term memory neural network in prediction of chlorophyll a concentration[J]. Haiyang Xuebao, 2020, 42(2): 134−142. [8] Jain P, Deo M C. Real-time wave forecasts off the western Indian coast[J]. Applied Ocean Research, 2007, 29(1/2): 72−79. [9] Gu Chengcheng, Li Hua. Review on deep learning research and applications in wind and wave energy[J]. Energies, 2022, 15(4): 1510. doi: 10.3390/en15041510 [10] Deo M C, Jha A, Chaphekar A S, et al. Neural networks for wave forecasting[J]. Ocean Engineering, 2001, 28(7): 889−898. doi: 10.1016/S0029-8018(00)00027-5 [11] Peres D J, Iuppa C, Cavallaro L, et al. Significant wave height record extension by neural networks and reanalysis wind data[J]. Ocean Modelling, 2015, 94: 128−140. doi: 10.1016/j.ocemod.2015.08.002 [12] James S C, Zhang Yushan, O’Donncha F. A machine learning framework to forecast wave conditions[J]. Coastal Engineering, 2018, 137: 1−10. doi: 10.1016/j.coastaleng.2018.03.004 [13] Law Y Z, Santo H, Lim K Y, et al. Deterministic wave prediction for unidirectional sea-states in real-time using artificial neural network[J]. Ocean Engineering, 2020, 195: 106722. doi: 10.1016/j.oceaneng.2019.106722 [14] Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735−1780. doi: 10.1162/neco.1997.9.8.1735 [15] 赵勇, 苏丹, 邹丽, 等. 基于LSTM神经网络的畸形波预测[J]. 华中科技大学学报(自然科学版), 2020, 48(7): 47−51.Zhao Yong, Su Dan, Zou Li, et al. Rogue wave prediction based on LSTM neural network[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2020, 48(7): 47−51. [16] 高丽斌. 基于深度学习的台湾海峡及周边海域波浪预报研究[D]. 福州: 福建农林大学, 2019.Gao Libin. Wave forecasting of Taiwan Strait and its surrounding waters based on deep learning[D]. Fuzhou: Fujian Agriculture and Forestry University, 2019. [17] Fan Shuntao, Xiao Nianhao, Dong Sheng. A novel model to predict significant wave height based on long short-term memory network[J]. Ocean Engineering, 2020, 205: 107298. doi: 10.1016/j.oceaneng.2020.107298 [18] Minuzzi F C, Farina L. A deep learning approach to predict significant wave height using long short-term memory[J]. Ocean Modelling, 2023, 181: 102151. doi: 10.1016/j.ocemod.2022.102151 [19] 王军, 王国欣. 宁波舟山港沿海航道保护范围研究与探讨[J]. 中国水运, 2020(4): 51−53.Wang Jun, Wang Guoxin. Research and discussion on the protection scope of coastal navigation channels in Ningbo Zhoushan Port[J]. China Water Transport, 2020(4): 51−53. [20] Xu Honghui, Deng Yong. Dependent evidence combination based on shearman coefficient and pearson coefficient[J]. IEEE Access, 2018, 6: 11634−11640. doi: 10.1109/ACCESS.2017.2783320 [21] Jebli I, Belouadha FZ, Kabbaj M I, et al. Prediction of solar energy guided by pearson correlation using machine learning[J]. Energy, 2021, 224: 120109. doi: 10.1016/j.energy.2021.120109 [22] Abadi M, Barham P, Chen Jianmin, et al. TensorFlow: a system for large-scale machine learning[C]//Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation. Savannah: USENIX Association, 2016: 265−283. [23] Ketkar N. Introduction to keras[M]//Ketkar N. Deep Learning with Python: A Hands-on Introduction. Berkeley: Apress, 2017: 97−111. -
计量
- 文章访问数: 101
- HTML全文浏览量: 80
- PDF下载量: 20
- 被引次数: 0
