Asymmetric of anticyclonic jet at the bottom of deep-sea seamounts
-
摘要: 本文旨在利用热带西太平洋采薇海山的底部观测资料和数值模式，分析海山底部反气旋急流的不对称性特征。底部海流的观测结果显示，在海山底部存在东西方向上显著不对称的反气旋急流现象。双层模式再现了理想海山及采薇海山的底部流场结构及其不对称性特征。进一步分析表明，不对称性的主要来源是背景流的能量输入、β效应引发的涡度变化。文中依次分析了海山各个方位的流场特征，并详细解释了涡度变化如何影响底部急流及其不对称特征。此外，本文还讨论了其他环境参数（如底摩擦系数、约化重力）改变时对底部急流的影响。Abstract: This paper studies the asymmetric characteristics and mechanism of the anticyclonic jet at the bottom of seamounts by using the mooring observation data collected at the Caiwei seamount (CS) in the tropical western Pacific Ocean and an ideal two-layer model. The observation of bottom currents shows that there is an asymmetric anticyclonic jet phenomenon in the east-west direction at the bottom of the seamount. The two-layer model reproduces the bottom flow field and its asymmetric characteristics of the ideal seamount and CS, suggesting that the main source of asymmetry is the vorticity change caused by the energy input of background currents and the geostrophic and topographic β effects. The flow field characteristics are analyzed through the principle of potential vorticity conservation, and the mechanism of vorticity change affecting the bottom jet and its asymmetric characteristics is explained. In addition, this paper also discusses the influence of other environmental parameters on the bottom anticyclonic jet.
-
图 1 采薇海山底部的锚系观测
图1a西北太平洋的海底地形。红框处为采薇海山。图1b中白色箭头是双层模式中流场模拟结果。采薇海山山顶水深约−1350 m。其中W、N、E、S是锚系观测点，黄色箭头表征此处锚系观测平均流速相对大小
Fig. 1 Mooring observation at the bottom of Caiwei Seamount
Fig.1a is the seafloor topography of the Northwest Pacific Ocean. The Caiwei Seamount is in red box. In Fig.1b, the white arrow is the flow field in two-layer model in this study. The water depth at the top of the mountain is the shallowest at −1350 m.W, N, E, and S are the mooring observation points. The yellow arrow characterizes the time-average flow velocity.
图 2 双层等密度面模式初始设置
Fig. 2 Initial setting of two-layer isopycnal-coordinate primitive equations model
图 3 采薇海山底部锚系观测的时间系列
Fig. 3 Time series of mooring observation at the bottom of Caiwei Seamount
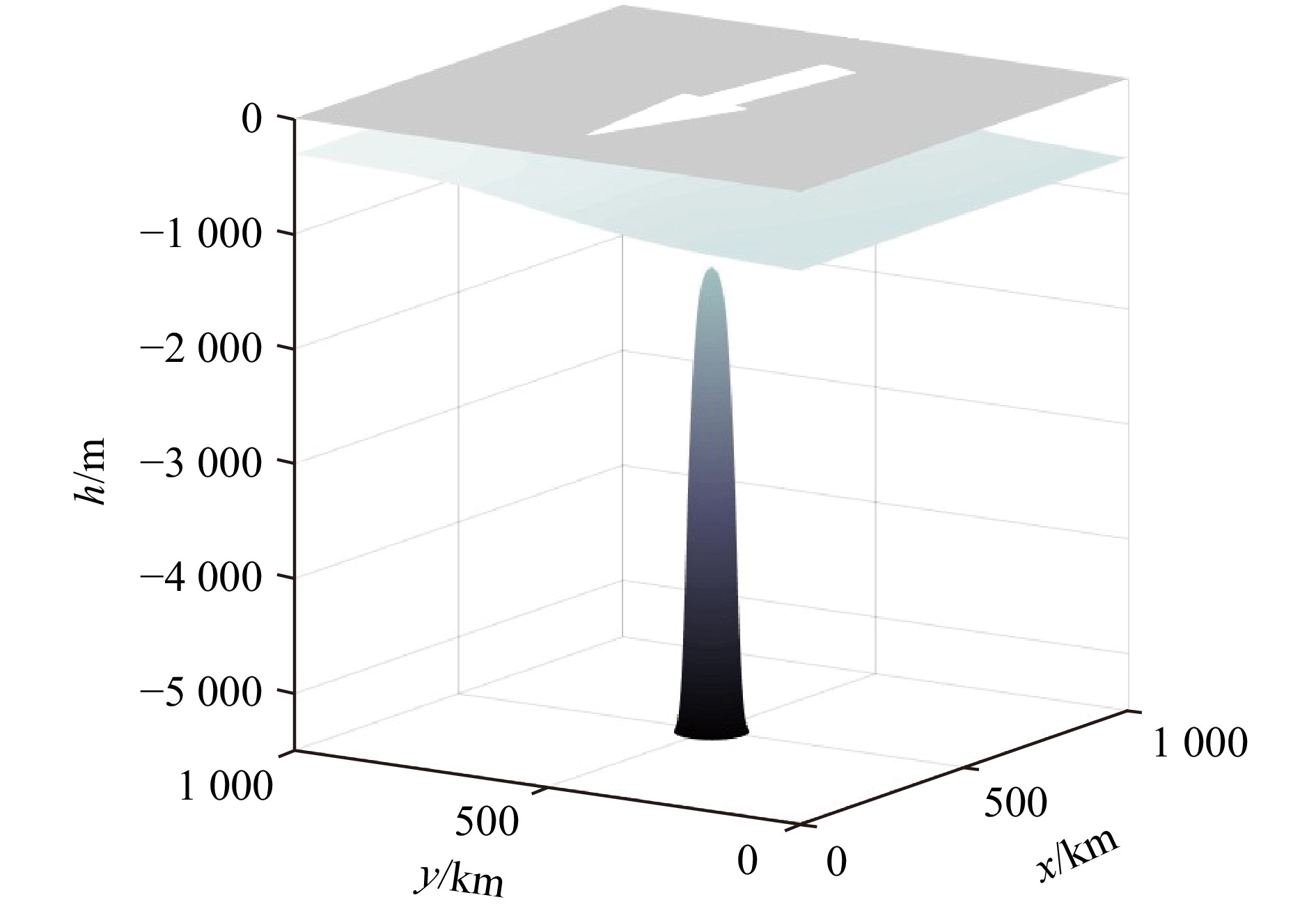
图 4 不同β值下的模式模拟流场
白色箭头表示该点处的流场速度矢量，流速大小与颜色条一致。棕红色线是海山的等高线，范围从
−5500 m至−1250 m，高度间隔250 m。后图一致Fig. 4 The model bottom flow field of the ideal seamount with different β
The white arrow represents the flow field velocity vector, and brown lines are contour lines of the seamount, ranging from
−5500 m to−1250 m, with a height interval of 250 m. The same applies to the subsequent figure
图 5 不同β值下的模式模拟涡度分布
Fig. 5 The vorticity distribution of the model bottom flow of ideal seamount with different β
图 6 不同β值下理想海山的模式底部流场跨等深线分量
Fig. 6 The cross-isobath component of the model bottom flow field of ideal seamount with different β
图 7 地形放大后的模式模拟流场
Fig. 7 The model bottom flow field of ideal seamount with the terrain amplification
图 8 不同程度底摩擦的模式模拟流场
Fig. 8 The model bottom flow field of ideal seamount with different bottom friction
图 9 不同约化重力的模式模拟流场
Fig. 9 The model bottom flow field of ideal seamount with different reduced gravity
图 11 流线的位涡守恒示意图
实心红星表示极限涨点，空心红星表示极限落点；蓝色虚线表示离海山不同距离的流线
Fig. 11 Potential vorticity conservation of streamlines
Solid red star represents the limit up point, hollow red star represents the limit down point; the blue dotted lines represent the streamlines at different distances from the seamount
表 1 锚系潜标的投放信息
Tab. 1 Information of mooring instruments used in this study
站点 坐标 观测水深 观测时间 仪器信息 $ {\mathrm{W}} $ 15.589°N, 154.753°E 5050 m2012年7月至
2013年5月离底15 m ACM $ {\mathrm{N}} $ 16.078°N, 154.905°E 5383 m2013年6月至
2014年1月离底15 m ACM $ {\mathrm{E}} $ 15.955°N, 155.729°E 5666 m2014年7月至
2015年7月离底15 m ACM $ {\mathrm{S}} $ 15.250°N, 155.650°E 5770 m2020年10月至
2021年8月离底30 m ACM 
下载: 导出CSV
表 2 双层等密度面模式的参数
Tab. 2 Parameters of two-layer isopycnal-coordinate primitive equations model
参数符号 参数值 含义 $ {L}_{x} $ 1000 km模式的横向尺度 $ {L}_{y} $ 1000 km模式的纵向尺度 $ {H}_{s} $ 4110 m海山高度 $ {Z}_{s} $ 3500 m半山腰处水深 $ {Y}_{s} $ 40 km 半山腰处离中心轴的距离 $ {W}_{s} $ 50 km 山坡的径向半宽度 $ {\rho }_{0} $ 1000 $ \mathrm{k}\mathrm{g}/{\mathrm{m}}^{3} $标准密度 $ g $ 9.8 $ \mathrm{m}/{\mathrm{s}}^{2} $ 重力加速度 $ {g}_{\mathrm{e}\mathrm{f}\mathrm{f}} $ $ {10}^{-2}\ \mathrm{m}/{\mathrm{s}}^{2} $ 约化重力加速度 $ {f}_{0} $ $ {10}^{-4}\ {\mathrm{s}}^{-1} $ 科氏参数常数 $ \beta $ $ {10}^{-11}\ {\mathrm{m}}^{-1}{\mathrm{s}}^{-1} $ 科氏参数的梯度 $ {R}_{{\mathrm{b}}} $ $ {10}^{-3} $ 线性底摩擦参数
下载: 导出CSV
-
[1] Gevorgian J, Sandwell D T, Yu Yao, et al. Global distribution and morphology of small seamounts[J]. Earth and Space Science, 2023, 10(4): e2022EA002331. doi: 10.1029/2022EA002331 [2] Mai Hongtao, Wang Dongxiao, Chen Hui, et al. Mid-deep circulation in the western South China sea and the impacts of the central depression belt and complex topography[J]. Journal of Marine Science and Engineering, 2024, 12(5): 700. doi: 10.3390/jmse12050700 [3] Jiang Xingliang, Dong Changming, Ji Yuxiang, et al. Influences of deep-water seamounts on the hydrodynamic environment in the northwestern pacific ocean[J]. Journal of Geophysical Research: Oceans, 2021, 126(12): e2021JC017396. doi: 10.1029/2021JC017396 [4] Perfect B, Kumar N, Riley J J. Vortex structures in the wake of an idealized seamount in rotating, stratified flow[J]. Geophysical Research Letters, 2018, 45(17): 9098−9105. doi: 10.1029/2018GL078703 [5] Shu Yeqiang, Wang Jinghong, Xue Huijie, et al. Deep-current intraseasonal variability interpreted as topographic rossby waves and deep eddies in the Xisha Islands of the South China Sea[J]. Journal of Physical Oceanography, 2022, 52(7): 1415−1430. doi: 10.1175/JPO-D-21-0147.1 [6] Carter G S, Gregg M C, Merrifield, M A. Flow and mixing around a small seamount on Kaena Ridge, Hawaii[J]. Journal of Physical Oceanography, 2006, 36(6): 1036−1052. doi: 10.1175/JPO2924.1 [7] Nikurashin M, Ferrari R. Global energy conversion rate from geostrophic flows into internal lee waves in the deep ocean[J]. Geophysical Research Letters, 2011, 38(8): L08610. [8] Taylor G I. Experiments on the motion of solid bodies in rotating fluids[J]. Proceedings of the Royal Society of London - Series A: Containing Papers of a Mathematical and Physical Character, 1923, 104(725): 213−218. [9] Lavelle J W, Mohn C. Motion, commotion, and biophysical connections at deep ocean seamounts[J]. Oceanography, 2010, 23(1): 90−103. doi: 10.5670/oceanog.2010.64 [10] White M, Mohn C. Seamounts: A review of physical processes and their influence on the seamount ecosystem (OASIS Report)[R]. Ireland: NUI, Gaiway, 2004. [11] Chapman D C, Haidvogel D B. Formation of Taylor caps over a tall isolated seamount in a stratified ocean[J]. Geophysical & Astrophysical Fluid Dynamics, 1992, 64(1/4): 31−65. [12] Haidvogel D B, Beckmann A. Chapman D C, et al. Numerical simulation of flow around a tall isolated seamount. Part II: Resonant generation of trapped waves[J]. Journal of Physical Oceanography, 1993, 23(11): 2373−2391. doi: 10.1175/1520-0485(1993)023<2373:NSOFAA>2.0.CO;2 [13] Xu G, Lavelle J W. Circulation, hydrography, and transport over the summit of axial seamount, a deep volcano in the Northeast Pacific[J]. Journal of Geophysical Research: Oceans, 2017, 122(7): 5404−5422. doi: 10.1002/2016JC012464 [14] Guo Binbin, Wang Weiqiang, Shu Yeqiang, et al. Observed deep anticyclonic cap over Caiwei Guyot[J]. Journal of Geophysical Research: Oceans, 2020, 125(10): e2020JC016254. doi: 10.1029/2020JC016254 [15] Beckmann A, Mohn C. The upper ocean circulation at great meteor seamount Part II: retention potential of the seamount induced circulation[J]. Ocean Dynamics, 2002, 52(4): 194−204. doi: 10.1007/s10236-002-0018-3 [16] White M, Bashmachnikov I, Arístegui J, et al. Physical processes and seamount productivity[M]//Pitcher T J, Morato T, Hart P J B, et al. Seamounts: Ecology, fisheries and conservation, Oxford, UK: Wiley Online Library, 2007: 65−84. [17] Ye Ruijie, Shang Xiaodong, Zhao Wei, et al. Circulation driven by multihump turbulent mixing over a seamount in the South China Sea[J]. Frontiers in Marine Science, 2022, 8: 794156. doi: 10.3389/fmars.2021.794156 [18] Owens W B, Hogg N G. Oceanic observations of stratified Taylor columns near a bump[J]. Deep Sea Research Part A. Oceanographic Research Papers, 1980, 27(12): 1029−1045. doi: 10.1016/0198-0149(80)90063-1 [19] Brink K H. Tidal and lower frequency currents above Fieberling Guyot[J]. Journal of Geophysical Research: Oceans, 1995, 100(6): 10817−10832. [20] Lavelle J W. Flow, hydrography, turbulent mixing, and dissipation at Fieberling Guyot examined with a primitive equation model[J]. Journal of Geophysical Research, 2006, 111(C7): C07014. [21] Chapman D C, Haidvogel D B. Generation of internal lee waves trapped over a tall isolated seamount[J]. Geophysical & Astrophysical Fluid Dynamics, 1993, 69(1/4): 33−54. [22] Xie Xiaohui, Wang Yan, Liu Xiaohui, et al. Enhanced near-bottom circulation and mixing driven by the surface eddies over abyssal seamounts[J]. Progress in Oceanography, 2022, 208: 102896. doi: 10.1016/j.pocean.2022.102896 [23] Ma Weidong, Wang Jianing, Wang Fan, et al. The vertical structure and intraseasonal variability of the deep currents in the Southern Philippine Basin[J], Deep Sea Research Part I: Oceanographic Research Papers, 2023, 197: 104043. [24] Saenko O A, Merryfield W J. On the effect of topographically enhanced mixing on the global ocean circulation[J]. Journal of Physical Oceanography, 2005, 35(5): 826−834. doi: 10.1175/JPO2722.1 [25] Stewart A L, Dellar P J. An energy and potential enstrophy conserving numerical scheme for the multi-layer shallow water equations with complete Coriolis force[J]. Journal of Computational Physics, 2016, 313: 99−120. doi: 10.1016/j.jcp.2015.12.042 [26] Stewart R H. Introduction to Physical Oceanography[M]. Austin: The University of Texas, 2006. (查阅网上资料, 未找到本条文献出版信息, 请确认) [27] Sutyrin, G, Herbette S, Carton X. Deformation and splitting of baroclinic eddies encountering a tall seamount[J]. Geophysical & Astrophysical Fluid Dynamics, 2011, 105(4/5): 478−505. [28] Herbette S, Morel Y, Arhan M. Erosion of a surface vortex by a seamount on the β plane[J]. Journal of Physical Oceanography, 2005, 35(11): 2012−2030. doi: 10.1175/JPO2809.1 [29] Fox-Kemper B. Eddies and friction : removal of vorticity from the wind-driven gyre[D]. Cambridge: Massachusetts Institute of Technology, 2003. -
计量
- 文章访问数: 20
- HTML全文浏览量: 7
- PDF下载量: 4
- 被引次数: 0
