Integration of machine learning and physical models for the reconstruction of mesoscale eddy sound speed profile
-
摘要: 针对中尺度涡内声速剖面结构复杂且重构误差显著偏大的问题，本文采用多源卫星遥感数据和Argo剖面，结合随机森林算法和中尺度涡统一结构模型，提出了PIRF-DEN模型。通过将海表面温度、高度异常、盐度、密度等海表环境参数与Argo密度作为输入，建立了“水面-水下”声速映射关系。同时，基于中尺度涡统一结构模型重构涡旋内密度场，将海表环境参数和涡旋重构密度输入映射关系并重构了涡旋内声速剖面。研究结果表明，PIRF-DEN模型显著提高了声速剖面的重构精度，MAE和RMSE分别降至
0.8324 m/s和1.3869 m/s，较传统的sEOF-r方法降低了87.3%和83.7%，且声速重构精度和稳定性优于现有模型。-
关键词:
- 声速重构 /
- 随机森林 /
- 中尺度涡统一结构模型 /
- 垂向密度
Abstract: To address the issue of complex sound speed profile (SSP) structures and significantly large reconstruction errors within mesoscale eddies, this study proposes the PIRF-DEN model by integrating multi-source satellite remote sensing data and Argo profiles with a random forest algorithm and a unified mesoscale eddy structure model. By utilizing sea surface temperature, height anomaly, salinity, density, and other environmental parameters at the sea surface, along with Argo density data as inputs, the model establishes a "surface-to-underwater" sound speed mapping relationship. Additionally, it reconstructs the density field within eddies based on the unified mesoscale eddy structure model and incorporates both surface environmental parameters and reconstructed eddy densities into the mapping relationship to reconstruct the SSP within the eddies. The results demonstrate that the PIRF-DEN model markedly enhances the accuracy of SSP reconstruction, reducing the Mean Absolute Error (MAE) and Root Mean Square Error (RMSE) to0.8324 m/s and1.3869 m/s, respectively. This represents an 87.3% and 83.7% reduction compared to the traditional sEOF-r method. Furthermore, the sound speed reconstruction accuracy and stability of the PIRF-DEN model surpass those of existing models. -
图 4 四种SSP重构方法在各深度层的声速MAE和RMSE
Fig. 4 The MAE and RMSE of sound speed for four SSP reconstruction methods across various depth layers
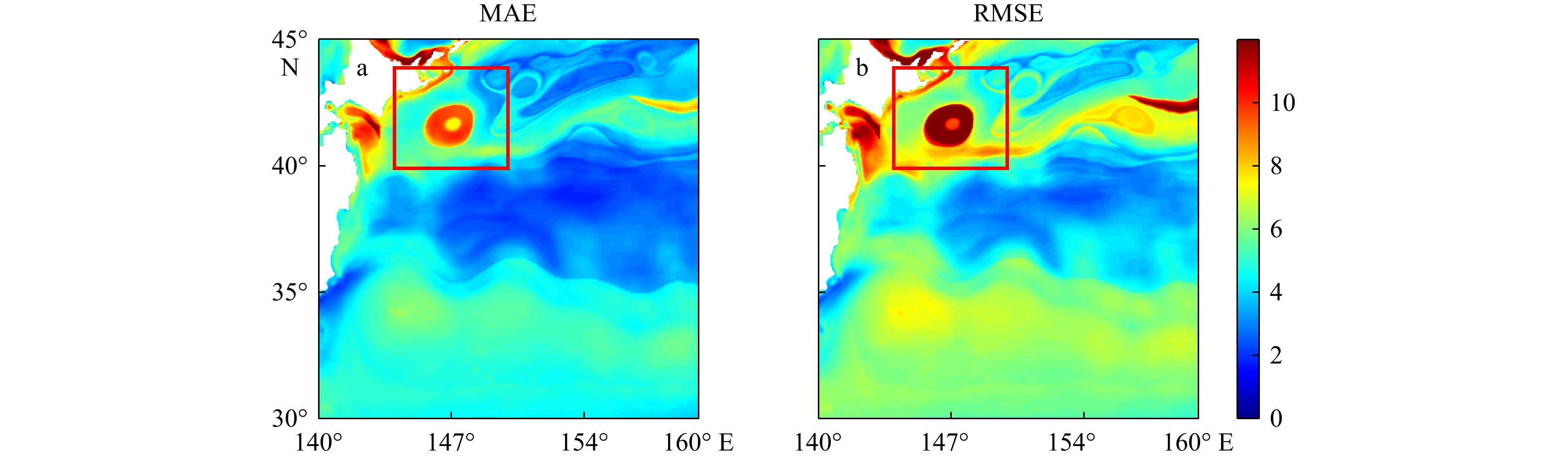
图 5 四种SSP重构方法在各Argo站位处的声速误差，其中1−4行分别为PIRF-DEN、RF、sEOF-RF和sEOF-r的声速平均误差，1−2列分别为四种方法的声速平均MAE和平均RMSE。
Fig. 5 Sound speed errors of the four SSP reconstruction methods at various Argo stations, where rows 1−4 represent the average sound speed errors for PIRF-DEN, RF, sEOF-RF, and sEOF-r, respectively, and columns 1−2 show the MAE and RMSE of sound speed for the four methods.
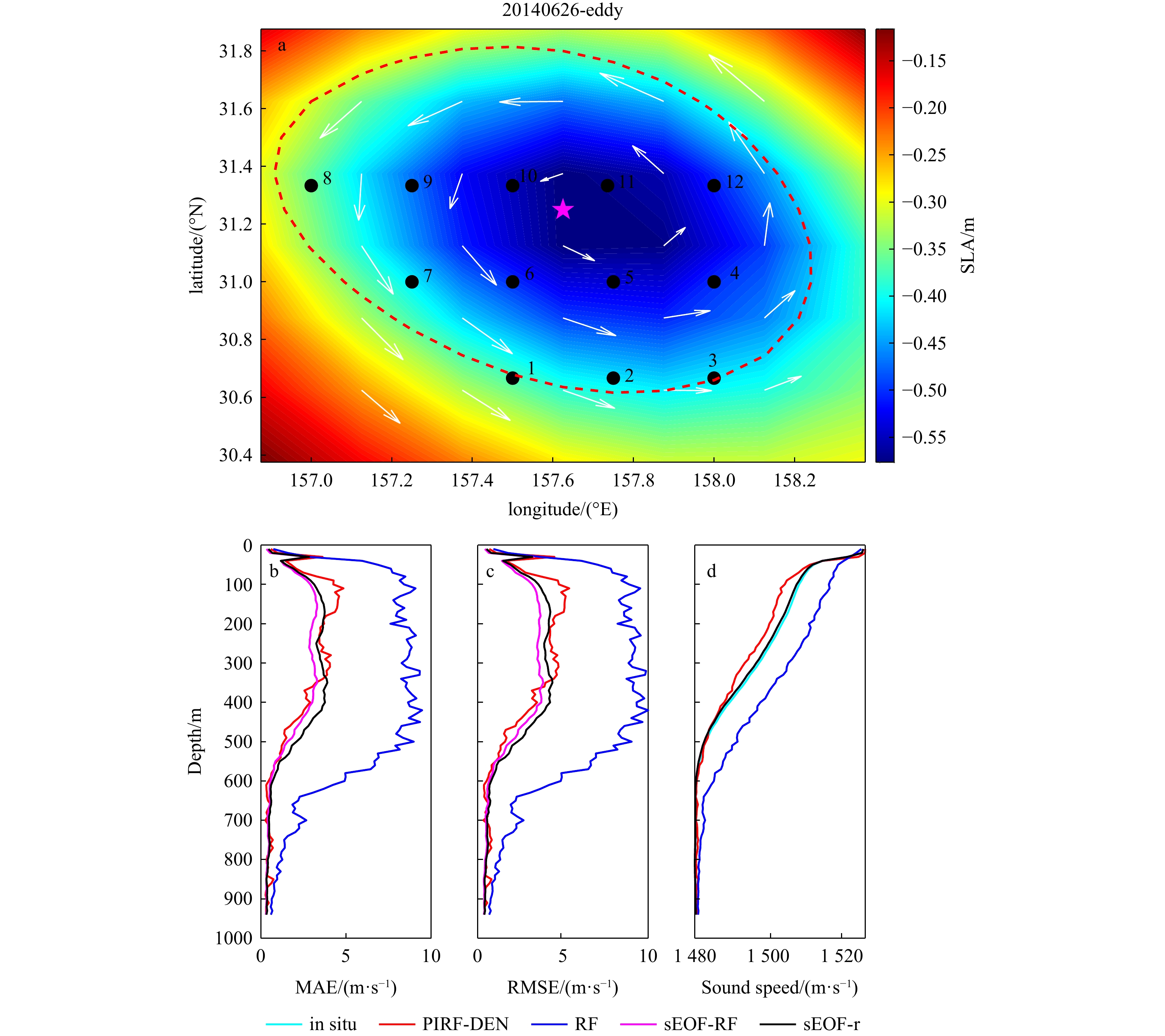
图 6 1号涡SSP重构效果一览图。其中(a)为1号涡及其内部Argo站位示意图，红线为其边缘轮廓，五角星的位置为其涡心所在位置，黑点为Argo观测站位；(b)为声速MAE分布；(c)为声速RMSE分布；(d)为四种方法重构的平均SSP与经验公式计算的平均SSP对比
Fig. 6 Summary of SSP reconstruction of vortex No. 1. (a) Schematic of Vortex No. 1 and Internal Argo Stations. The red line outlines the vortex boundary, the pentagram marks the vortex center, and black dots indicate Argo observation stations; (b) Sound Speed MAE Distribution; (c) Sound Speed RMSE Distribution; (d) Compare the mean SSP reconstructed by the four methods with the mean SSP calculated by the empirical formula
图 7 2号涡SSP重构效果一览图，各分图的具体含义与图9类似。
Fig. 7 Summary of SSP reconstruction of vortex No. 2, the specific meaning of each sub-diagram is similar to Figure 6.
图 8 3号涡SSP重构效果一览图，各分图的具体含义与图9类似
Fig. 8 Summary of SSP reconstruction of vortex No. 3, the specific meaning of each sub-diagram is similar to Figure 6
图 9 密度重构误差与SSP重构误差相关性，其中a～c分别代表1～3号涡
Fig. 9 The correlation between density reconstruction error and SSP reconstruction error, where a~c represent eddies 1 to 3, respectively
表 1 数据信息
Tab. 1 Data Information
数据名称 要素 时间分辨率 覆盖时间 空间分辨率 Argo 温度和盐度 1 d 1997年1月～
2024年3月— DUACS SLA 1 d 0.25°×0.25° GHRSST OISST 1 d 0.05°×0.05° CNR SSS和SSD 1 d 0.125°×0.125° ARMOR 3D 温度和盐度 1 w 0.25°×0.25° 
下载: 导出CSV
表 2 前5模态的方差贡献率（%）
Tab. 2 Variance contribution rates (%) of the first five modes
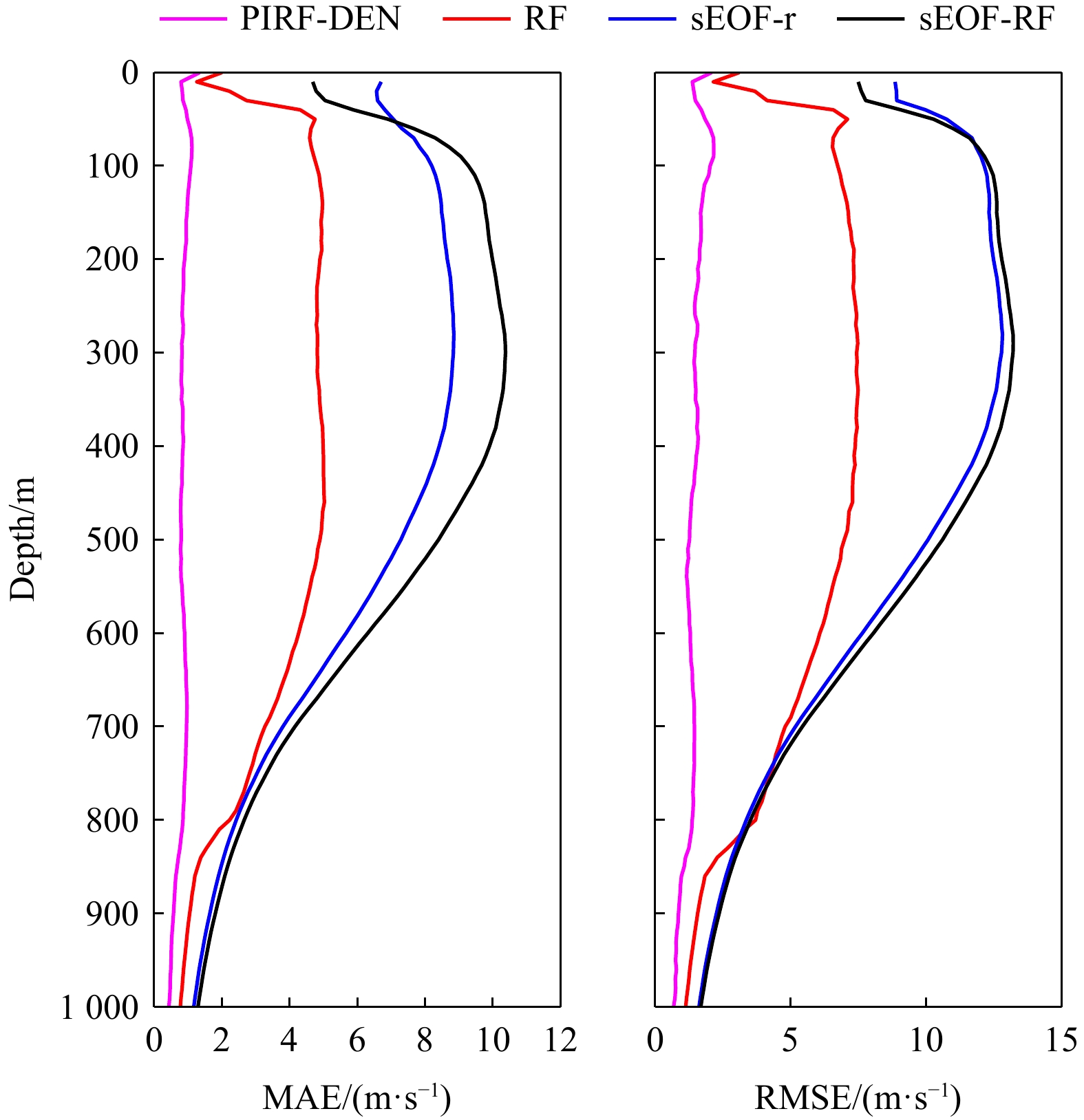
模态数 1 2 3 4 5 方差贡献率 91.76 4.97 1.81 0.76 0.29
下载: 导出CSV
表 3 四种SSP重构方法的评估系数
Tab. 3 Evaluation metrics for the four SSP reconstruction methods
评估系数 SSP重构方法 PIRF-DEN RF sEOF-RF sEOF-r MAE 0.83 3.66 5.84 6.56 RMSE 1.39 5.42 8.28 8.51
下载: 导出CSV
表 5 观测涡旋信息
Tab. 5 Observation of vortex information
编号 涡旋类型 涡心坐标 半径/km 观测仪器 观测时间 站位数/个 1 反气旋涡 29.625°N, 147.168°E 101.38 Argo 2014.3.29 15 2 气旋涡 31.25°N, 157.625°E 63.14 XCTD 2014.6.26 12 3 反气旋涡 35.5°N, 155.5°E 99.34 XCTD 2022.6.23 11
下载: 导出CSV
表 6 四种SSP重构方法在实测涡处的重构效果
Tab. 6 Reconstruction performance of the four SSP reconstruction methods at observed vortex locations
重构方法 MAE/(m/s) RMSE/(m/s) 1号涡 2号涡 3号涡 1号涡 2号涡 3号涡 PIRF-DEN 1.06 1.90 2.60 1.39 2.30 3.23 RF 0.80 5.53 2.88 1.01 5.92 3.38 sEOF-r 1.50 1.95 2.07 1.80 2.28 2.36 sEOF-RF 6.10 1.66 6.97 6.62 1.99 7.34
下载: 导出CSV
-
[1] Chen Wen, Zhang Yongchui, Liu Yuyao, et al. Parametric model for eddies-induced sound speed anomaly in five active mesoscale eddy regions[J]. Journal of Geophysical Research: Oceans, 2022, 127(8): e2022JC018408. doi: 10.1029/2022JC018408 [2] Chen Cheng, Yang Kunde, Duan Rui, et al. Acoustic propagation analysis with a sound speed feature model in the front area of Kuroshio Extension[J]. Applied Ocean Research, 2017, 68: 1−10. doi: 10.1016/j.apor.2017.08.001 [3] Lin Y T, Lynch J F. Three-dimensional sound propagation and scattering in an ocean with surface and internal waves over range-dependent seafloor[J]. The Journal of the Acoustical Society of America, 2017, 141(5): 3753. [4] Alexander P, Duncan A, Boce N, et al. Modelling acoustic propagation beneath Antarctic sea ice using measured environmental parameters[J]. Deep Sea Research Part II: Topical Studies in Oceanography, 2016, 131: 84−95. doi: 10.1016/j.dsr2.2016.04.026 [5] Wu Shuanglin, Li Zhenglin, Qin Jixing, et al. The effects of sound speed profile to the convergence zone in deep water[J]. Journal of Marine Science and Engineering, 2022, 10(3): 424. doi: 10.3390/jmse10030424 [6] 刘玉耀, 陈伟, 陈羽, 等. 水下声速剖面构建方法研究进展[J]. 信息对抗技术, 2024, 3(5): 1−18.Liu Yuyao, Chen Wei, Chen Yu, et al. Research progress on methods for constructing underwater sound speed profile[J]. Information Countermeasure Technology, 2024, 3(5): 1−18. [7] Liu Lei, Peng Shiqiu, Huang Ruixin. Reconstruction of ocean's interior from observed sea surface information[J]. Journal of Geophysical Research: Oceans, 2017, 122(2): 1042−1056. doi: 10.1002/2016JC011927 [8] Wang Jinbo, Flierl G R, LaCasce J H, et al. Reconstructing the Ocean's Interior from Surface Data[J]. Journal of Physical Oceanography, 2013, 43(8): 1611−1626. doi: 10.1175/JPO-D-12-0204.1 [9] Leblanc L R, Middleton F H. An underwater acoustic sound velocity data model[J]. The Journal of the Acoustical Society of America, 1980, 67(6): 2055−2062. doi: 10.1121/1.384448 [10] Chen Cheng, Ma Yuanliang, Liu Ying. Reconstructing sound speed profiles worldwide with sea surface data[J]. Applied Ocean Research, 2018, 77: 26−33. doi: 10.1016/j.apor.2018.05.002 [11] Liu Yuyao, Chen Yu, Meng Zhou, et al. Performance of single empirical orthogonal function regression method in global sound speed profile inversion and sound field prediction[J]. Applied Ocean Research, 2023, 136: 103598. doi: 10.1016/j.apor.2023.103598 [12] Fox D N, Teague W J, Barron C N, et al. The modular ocean data assimilation system (MODAS)[J]. Journal of Atmospheric and Oceanic Technology, 2002, 19(2): 240−252. doi: 10.1175/1520-0426(2002)019<0240:TMODAS>2.0.CO;2 [13] Park J C, Kennedy R M. Remote sensing of ocean sound speed profiles by a perceptron neural network[J]. IEEE Journal of Oceanic Engineering, 1996, 21(2): 216−224. doi: 10.1109/48.486796 [14] 刘杨范, 王振杰, 赵爽. 多波束测深中声速剖面的分层EOF自适应重构[J]. 声学技术, 2020, 39(3): 372−378.Liu Yangfan, Wang Zhenjie, Zhao Shuang. Layered-EOFs based adaptive reconstruction of sound velocity profile in multi-beam sounding[J]. Technical Acoustics, 2020, 39(3): 372−378. [15] Li Haipeng, Qu Ke, Zhou Jianbo. Reconstructing sound speed profile from remote sensing data: nonlinear inversion based on self-organizing map[J]. IEEE Access, 2021, 9: 109754−109762. doi: 10.1109/ACCESS.2021.3102608 [16] Ou Zhenyi, Qu Ke, Wang Yafen, et al. Estimating sound speed profile by combining satellite data with in situ sea surface observations[J]. Electronics, 2022, 11(20): 3271. doi: 10.3390/electronics11203271 [17] 李倩倩, 李宏琳, 曹守莲, 等. 基于遥感数据和表层声速的全海深声速剖面反演[J]. 海洋学报, 2022, 44(12): 84−94.Li Qianqian, Li Honglin, Cao Shoulian, et al. Inversion of the full-depth sound speed profile based on remote sensing data and surface sound speed[J]. Haiyang Xuebao, 2022, 44(12): 84−94. [18] Zhao Yu, Xu Pan, Li Guangming, et al. Reconstructing the sound speed profile of South China Sea using remote sensing data and long short-term memory neural networks[J]. Frontiers in Marine Science, 2024, 11: 1375766. doi: 10.3389/fmars.2024.1375766 [19] Liu Yuyao, Chen Yu, Chen Wei, et al. Inversion of sound speed profile in the Luzon strait by combining single empirical orthogonal function and generalized regression neural network[J]. IEEE Geoscience and Remote Sensing Letters, 2024, 21: 1502405. [20] Feng Xiao, Tian Tian, Zhou Mingzhang, et al. Sound speed inversion based on multi-source ocean remote sensing observations and machine learning[J]. Remote Sensing, 2024, 16(5): 814. doi: 10.3390/rs16050814 [21] 李洪臣, 李明, 陈希, 等. 基于机器学习和经验正交函数法的声速剖面快速重构[J]. 海洋与湖沼, 2025, 56(1): 101−111.Li Hongchen, Li Ming, Chen Xi, et al. Fast reconstruction of sound speed profile based on machine learning and empirical orthogonal function method[J]. Oceanologia et Limnologia Sinica, 2025, 56(1): 101−111. [22] 朱凤芹, 张海刚, 屈科. 南海东北部中尺度暖涡对声传播的影响[J]. 哈尔滨工程大学学报, 2021, 42(10): 1496−1502. doi: 10.11990/jheu.202007077Zhu Fengqin, Zhang Haigang, Qu Ke. Influence of mesoscale warm eddies on sound propagation in the northeastern South China Sea[J]. Journal of Harbin Engineering University, 2021, 42(10): 1496−1502. doi: 10.11990/jheu.202007077 [23] Chen Wen, Zhang Yongchui, Liu Yuyao, et al. Observation of a mesoscale warm eddy impacts acoustic propagation in the slope of the South China Sea[J]. Frontiers in Marine Science, 2022, 9: 1086799. doi: 10.3389/fmars.2022.1086799 [24] Li Ming, Liu Yuhang, Sun Yiyuan, et al. Quantitative analysis and prediction of the sound field convergence zone in mesoscale eddy environment based on data mining methods[J]. Acta Oceanologica Sinica, 2024, 43(5): 110−120. doi: 10.1007/s13131-024-2328-5 [25] Ma Xiaodong, Zhang Lei, Xu Weishuai, et al. Analysis of acoustic field characteristics of mesoscale eddies throughout their complete life cycle[J]. Frontiers in Marine Science, 2025, 11: 1471670. doi: 10.3389/fmars.2024.1471670 [26] White W B, Mccreary J P. On the formation of the Kuroshio meander and its relationship to the large-scale ocean circulation[J]. Deep Sea Research and Oceanographic Abstracts, 1976, 23(1): 33−47. doi: 10.1016/0011-7471(76)90806-8 [27] Yasuda I, Okuda K, Hirai M. Evolution of a Kuroshio warm-core ring—variability of the hydrographic structure[J]. Deep Sea Research Part A. Oceanographic Research Papers, 1992, 39: S131−S161. doi: 10.1016/S0198-0149(11)80009-9 [28] Chen C T, Millero F J. Speed of sound in seawater at high pressures[J]. The Journal of the Acoustical Society of America, 1977, 62(5): 1129−1135. doi: 10.1121/1.381646 [29] Wong G S K, Zhu Shiming. Speed of sound in seawater as a function of salinity, temperature, and pressure[J]. The Journal of the Acoustical Society of America, 1995, 97(3): 1732−1736. doi: 10.1121/1.413048 [30] 卢少磊, 刘增宏, 李宏, 等. 全球海洋Argo网格资料集(BOA_Argo)用户手册[Z]. 中国Argo实时资料中心, 28. (查阅网上资料, 未找到本条文献信息, 请确认)Lu Shaolei, Liu Zenghong, Li Hong, et al. User Manual of global ocean Argo gridded dataset (BOA_Argo)[Z]. 28. [31] Chen Xi, Hu Dong, Mao Kefeng, et al. Detailed investigation of the three-dimensional structure of a mesoscale cold eddy in the Kuroshio extension region[J]. Journal of Operational Oceanography, 2018, 11(2): 87−99. doi: 10.1080/1755876X.2018.1505069 [32] Wang Penghao, Mao Kefeng, Chen Xi, et al. The three-dimensional structure of the mesoscale eddy in the Kuroshio extension region obtained from three datasets[J]. Journal of Marine Science and Engineering, 2022, 10(11): 1754. doi: 10.3390/jmse10111754 [33] Scott R B, Wang Faming. Direct evidence of an oceanic inverse kinetic energy cascade from satellite altimetry[J]. Journal of Physical Oceanography, 2005, 35(9): 1650−1666. doi: 10.1175/JPO2771.1 [34] Lapeyre G, Klein P. Dynamics of the upper oceanic layers in terms of surface quasigeostrophy theory[J]. Journal of Physical Oceanography, 2006, 36(2): 165−176. doi: 10.1175/JPO2840.1 [35] 张正光. 中尺度涡[D]. 青岛: 中国海洋大学, 2014.Zhang Zhengguang. Mesoscale eddy[D]. Qingdao: Ocean University of China, 2014. [36] Vu B L, Stegner A, Arsouze T. Angular momentum eddy detection and tracking algorithm (AMEDA) and its application to coastal eddy formation[J]. Journal of Atmospheric and Oceanic Technology, 2018, 35(4): 739−762. doi: 10.1175/JTECH-D-17-0010.1 [37] Isern-Fontanet J, García-Ladona L E, Font J. Identification of marine eddies from altimetric maps[J]. Journal of Atmospheric and Oceanic Technology, 2003, 20(5): 772−778. doi: 10.1175/1520-0426(2003)20<772:IOMEFA>2.0.CO;2 -
计量
- 文章访问数: 21
- HTML全文浏览量: 6
- PDF下载量: 4
- 被引次数: 0
