Multiscale interactions among the background flow, mesoscale eddy and high-frequency perturbation in the Bay of Bengal
-
摘要: 基于一套涡分辨模式数据，本文利用一种新的泛函工具—多尺度子空间变换—将孟加拉湾（BOB）海域的环流系统分解到背景流（>96 d）、中尺度（24～96 d）和高频尺度（<24 d）3个子空间，并用正则传输理论探讨了3个尺度子空间之间内在的非线性相互作用。结果表明，BOB西北部边界和斯里兰卡岛东部是BOB海域多尺度相互作用最显著的区域，中部则较弱。前两个区域的背景流大多正压、斜压不稳定，动能和有效位能正则传输主要表现为正向级串；后者则以逆尺度动能级串为主。具体来说，在BOB西北部与斯里兰卡东部，中尺度涡动能（EKE）主要来源于正压能量路径（即背景流动能向EKE传输），其次来源于斜压能量路径（即背景流有效位能向中尺度有效位能传输，并进一步转换为EKE）。通过这两个能量路径得到的EKE向更高频的扰动传输能量，起到了耗散中尺度涡的作用。不同于此二者，BOB中部海域的EKE和高频尺度动能主要通过斜压路径获得，随后通过逆尺度级串将动能返还给背景流。苏门答腊岛的西北部也是中尺度和高频尺度扰动较强的海域，正压能量路径和斜压能量路径均是该海域扰动能的来源，但以斜压能量路径为主。Abstract: This study utilizes a new functional analysis tool, multiscale window transform (MWT), to decompose the ocean circulation system in the Bay of Bengal (BOB) into three scale windows, namely, the background flow window (>96 days), the mesoscale window (24–96 days) and the high-frequency window (<24 days), and then uses the canonical energy transfer theory to investigate the intrinsic nonlinear multiscale interactions among these windows, on the basis of an eddy-resolving model simulation. It is found that multiscale interactions are strongest along the northwestern boundary and east of Sri Lanka. With intense barotropic and baroclinic instabilities, the canonical transfers of kinetic energy (KE) and available potential energy (APE) are mainly forward in these two regions. Mesoscale eddy kinetic energy (EKE) reservoir is mainly filled by the barotropic energy pathway with the kinetic energy of the background flow transferring to EKE, and secondarily from the baroclinic energy pathway with APE of the background flow transferring to the mesoscale APE and further converting to EKE. The gained EKE is found to further cascade to high-frequency motions, acting as an important dissipation mechanism of the mesoscale eddies in these regions. In contrast, the central BOB is mainly characterized by inverse KE cascades, where EKE and high-frequency kinetic energy (HKE) are gained via the baroclinic energy pathway, and then feed the background flow through inverse cascade processes. The northwest of Sumatra is also an area with strong mesoscale and high-frequency variability. Both barotropic and baroclinic energy pathways are the sources for EKE and HKE reservoirs in this region, with the baroclinic energy pathway playing the dominant role.
-
图 1 孟加拉湾及其周边海域海底地形
数据来自ETOPO1，区域1~4分别代表孟加拉湾西北部边界（EICC的流经区域）、孟加拉湾中部海域、斯里兰卡岛的东部海域和苏门答腊岛的西北部海域，详细的区域选取说明见2.3节
Fig. 1 The bathymetry in the Bay of Bengal and its adjacent regions
The data from ETOPO1. The numbered boxes from 1 to 4 denote the northwestern boundary of Bay of Bengal (EICC region), the central Bay of Bengal , the east of Sri Lank and northwest of Sumatra, respectively. See Section 2.3 for detailed description of the region selection
图 2 3个尺度子空间框架下的能量循环
红色箭头表示跨尺度能量传输（${\Gamma _K^\varpi} $和${\Gamma _A^\varpi} $）和浮力转换过程（${{b^\varpi }}$），绿色箭头表示同尺度输运（${\nabla \cdot {\boldsymbol{Q}}_K^\varpi }$、${\nabla \cdot {\boldsymbol{Q}}_P^\varpi }$和${\nabla \cdot {\boldsymbol{Q}}_A^\varpi }$），灰色箭头表示同尺度外强迫、耗散等过程（${F_K^\varpi }$和${F_A^\varpi }$）
Fig. 2 The energy cycle for a three-window decomposition
Red arrows denote canonical transfers (${\Gamma _K^\varpi }$ and ${\Gamma _A^\varpi} $) and buoyancy conversions (${{b^\varpi }}$), green arrows denote nonlocal transport processes (${\nabla \cdot {\boldsymbol{Q}}_K^\varpi }$, ${\nabla \cdot {\boldsymbol{Q}}_P^\varpi }$ and ${\nabla \cdot {\boldsymbol{Q}}_A^\varpi }$), and grey arrows stand for forcing/dissipation processes (${F_K^\varpi }$ and ${F_A^\varpi} $)
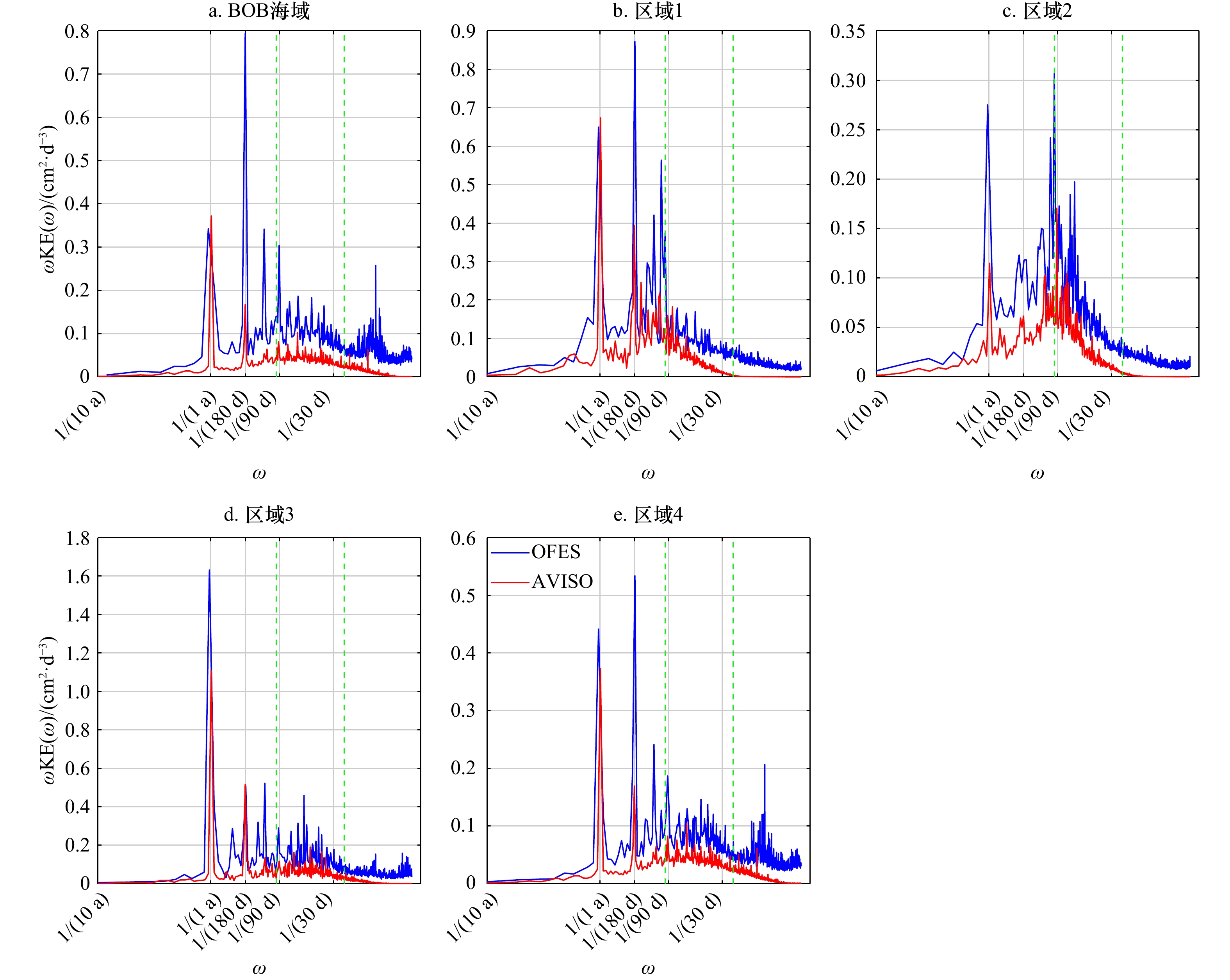
图 3 孟加拉湾（BOB）海域不同区域平均的表层流场动能（KE）谱
动能谱采用了方差保持的形式。蓝色实线表示OFES数据，红色实线表示AVISO数据。绿色垂直虚线从左到右表示周期为96 d和24 d
Fig. 3 The area-mean kinetic energy (KE) spectra of the surface currents in various domains in Bay of Bengal (BOB) sea area
The spectra are in variance-preserving form. The blue and red curves are estimated from the velocity fields from OFES and AVISO, respectively. The green dashed vertical lines from left to right denote the periods of 96 d and 24 d, respectively
图 4 基于AVISO和OFES数据计算得到的1999–2007年表层海洋多尺度动能的气候态空间分布
Fig. 4 Temporally averaged surface multiscale kinetic energy components based on AVISO and OFES of 1999–2007
图 5 经过时间平均（1997–2017年）和垂向积分（上300 m）的多尺度动能和有效位能水平分布
Fig. 5 Horizontal distributions of the temporally averaged (1999–2017) and vertically (upper 300 m) integrated multiscale kinetic energy and available potential energy components
图 6 孟加拉湾（BOB）不同区域平均的多尺度动能和有效位能气候态垂直分布
Fig. 6 The vertical distributions of the long-term mean multiscale kinetic energy and available potential energy components in various domains in Bay of Bengal (BOB)
图 7 经时间平均（1997–2017年）和垂向积分（上300 m）的正则传输和浮力转换的水平分布
Fig. 7 Horizontal distributions of the temporally averaged (1999–2017) and vertically (upper 300 m) integrated canonical transfers and buoyancy conversions
图 8 孟加拉湾（BOB）不同区域平均的多尺度相互作用项的气候态垂直分布
Fig. 8 The vertical distributions of the long-term mean multiscale interaction terms in various domains in Bay of Bengal (BOB)
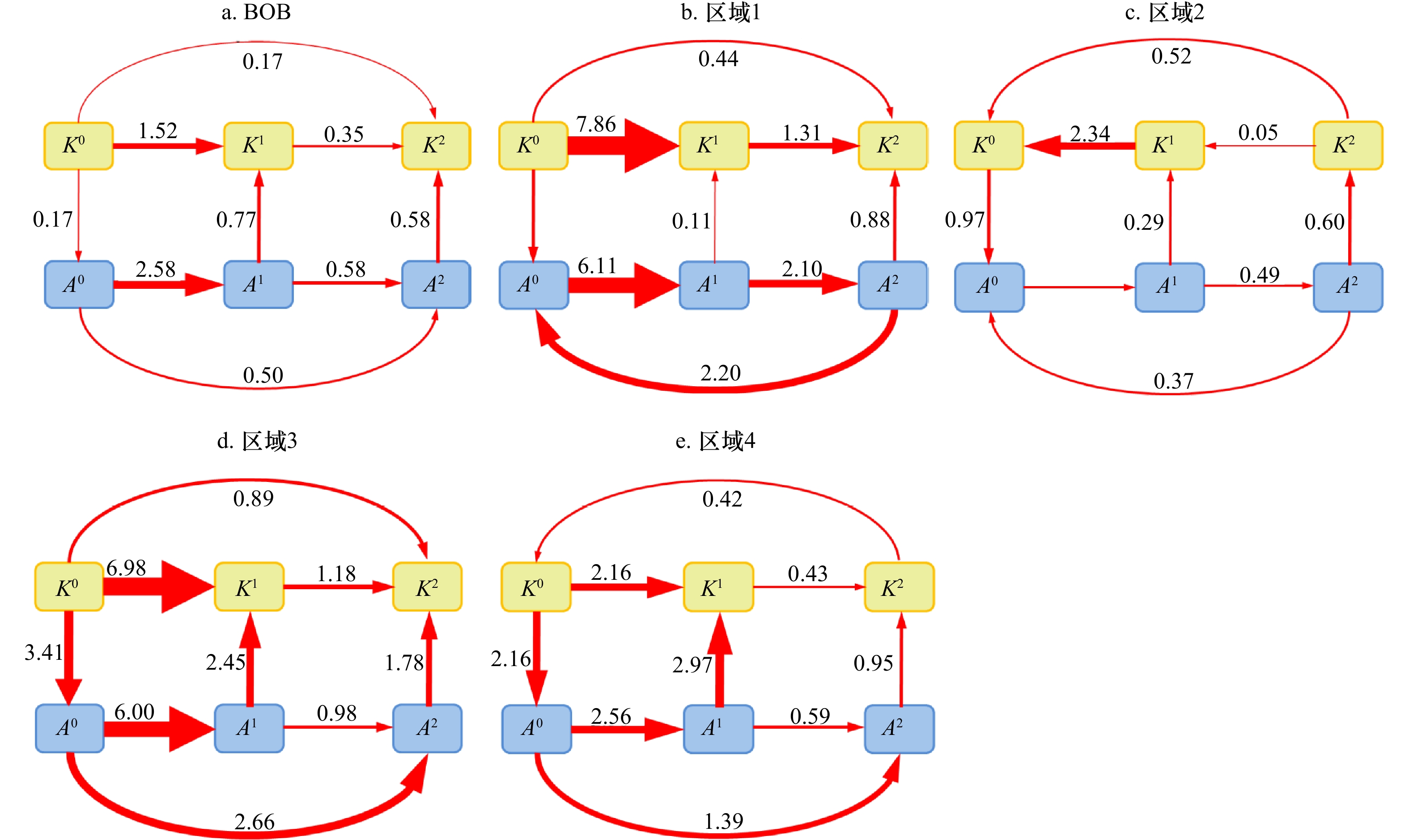
图 9 孟加拉湾（BOB）不同区域的洛伦兹能量循环
箭头上的数字表示1999–2017年上层海洋（0~300 m）体积平均值，箭头的粗细刻画了能量传输的大小（单位：10−6 W/m3）
Fig. 9 Schematics of the Lorenz energy cycle in various domains in Bay of Bengal (BOB)
The numbers above the arrows are obtained from temporally and volume-averaged energy terms of 1999–2017, with the arrow size indicating the strength of the energy terms (unit: 10−6 W/m3)
-
[1] Shankar D, McCreary J P, Han W, et al. Dynamics of the East India coastal current: 1. Analytic solutions forced by interior Ekman pumping and local alongshore winds[J]. Journal of Geophysical Research: Oceans, 1996, 101(C6): 13975−13991. doi: 10.1029/96JC00559 [2] Schott F A, Xie Shangping, McCreary J P Jr. Indian Ocean circulation and climate variability[J]. Reviews of Geophysics, 2009, 47(1): RG1002. [3] Cui Wei, Yang Jungang, Ma Yi. A statistical analysis of mesoscale eddies in the Bay of Bengal from 22–year altimetry data[J]. Acta Oceanologica Sinica, 2016, 35(11): 16−27. doi: 10.1007/s13131-016-0945-3 [4] Subrahmanyam B, Roman-Stork H L, Murty V S N. Response of the Bay of Bengal to 3−7−day synoptic oscillations during the southwest monsoon of 2019[J]. Journal of Geophysical Research: Oceans, 2020, 125(6): e2020JC016200. [5] Hood R R, Beckley L E, Wiggert J D. Biogeochemical and ecological impacts of boundary currents in the Indian Ocean[J]. Progress in Oceanography, 2017, 156: 290−325. doi: 10.1016/j.pocean.2017.04.011 [6] Prasanna Kumar S, Nuncio M, Ramaiah N, et al. Eddy-mediated biological productivity in the Bay of Bengal during fall and spring intermonsoons[J]. Deep Sea Research Part I: Oceanographic Research Papers, 2007, 54(9): 1619−1640. doi: 10.1016/j.dsr.2007.06.002 [7] Sanchez-Franks A, Kent E C, Matthews A J, et al. Intraseasonal variability of air-sea fluxes over the Bay of Bengal during the southwest monsoon[J]. Journal of Climate, 2018, 31(17): 7087−7109. doi: 10.1175/JCLI-D-17-0652.1 [8] Durand F, Shankar D, Birol F, et al. Spatiotemporal structure of the East India coastal current from satellite altimetry[J]. Journal of Geophysical Research, 2009, 114(C2): C02013. [9] Shetye S R, Gouveia A D, Shenoi S S C, et al. The western boundary current of the seasonal subtropical gyre in the Bay of Bengal[J]. Journal of Geophysical Research: Oceans, 1993, 98(C1): 945−954. doi: 10.1029/92JC02070 [10] Eigenheer A, Quadfasel D. Seasonal variability of the Bay of Bengal circulation inferred from TOPEX/Poseidon altimetry[J]. Journal of Geophysical Research: Oceans, 2000, 105(C2): 3243−3252. doi: 10.1029/1999JC900291 [11] McCreary J P, Han W, Shankar D, et al. Dynamics of the East India coastal current: 2. Numerical solutions[J]. Journal of Geophysical Research: Oceans, 1996, 101(C6): 13993−14010. doi: 10.1029/96JC00560 [12] Potemra J T, Luther M E, O’Brien J J. The seasonal circulation of the upper ocean in the Bay of Bengal[J]. Journal of Geophysical Research: Oceans, 1991, 96(C7): 12667−12683. doi: 10.1029/91JC01045 [13] Vinayachandran P N, Kagimoto T, Masumoto Y, et al. Bifurcation of the East India coastal current east of Sri Lanka[J]. Geophysical Research Letters, 2005, 32(15): L15606. doi: 10.1029/2005GL022864 [14] Babu M T, Sarma Y V B, Murty V S N, et al. On the circulation in the Bay of Bengal during northern spring inter-monsoon (March–April 1987)[J]. Deep Sea Research Part II: Topical Studies in Oceanography, 2003, 50(5): 855−865. doi: 10.1016/S0967-0645(02)00609-4 [15] Cheng Xuhua, Xie Shangping, McCreary J P, et al. Intraseasonal variability of sea surface height in the Bay of Bengal[J]. Journal of Geophysical Research: Oceans, 2013, 118(2): 816−830. doi: 10.1002/jgrc.20075 [16] Chen Gengxin, Wang Dongxiao, Hou Yijun. The features and interannual variability mechanism of mesoscale eddies in the Bay of Bengal[J]. Continental Shelf Research, 2012, 47: 178−185. doi: 10.1016/j.csr.2012.07.011 [17] Cheng Xuhua, McCreary J P, Qiu Bo, et al. Intraseasonal-to-semiannual variability of sea-surface height in the astern, equatorial Indian Ocean and southern Bay of Bengal[J]. Journal of Geophysical Research: Oceans, 2017, 122(5): 4051−4067. doi: 10.1002/2016JC012662 [18] Nuncio M, Kumar S P. Life cycle of eddies along the western boundary of the Bay of Bengal and their implications[J]. Journal of Marine Systems, 2012, 94: 9−17. doi: 10.1016/j.jmarsys.2011.10.002 [19] Kumar S P, Nuncio M, Narvekar J, et al. Are eddies nature’s trigger to enhance biological productivity in the Bay of Bengal?[J]. Geophysical Research Letters, 2004, 31(7): L07309. [20] Arunraj K S, Jena B K, Suseentharan V, et al. Variability in eddy distribution associated with East India coastal current from high-frequency radar observations along southeast coast of India[J]. Journal of Geophysical Research: Oceans, 2018, 123(12): 9101−9118. doi: 10.1029/2018JC014041 [21] Kurien P, Ikeda M, Valsala V K. Mesoscale variability along the east coast of India in spring as revealed from satellite data and OGCM simulations[J]. Journal of Oceanography, 2010, 66(2): 273−289. doi: 10.1007/s10872-010-0024-x [22] Chen Gengxin, Li Yuanlong, Xie Qiang, et al. Origins of eddy kinetic energy in the Bay of Bengal[J]. Journal of Geophysical Research: Oceans, 2018, 123(3): 2097−2115. doi: 10.1002/2017JC013455 [23] Patnaik K V K R K, Maneesha K, Sadhuram Y, et al. East India coastal current induced eddies and their interaction with tropical storms over Bay of Bengal[J]. Journal of Operational Oceanography, 2014, 7(1): 58−68. doi: 10.1080/1755876X.2014.11020153 [24] Babu M T, Kumar P S, Rao D P. A subsurface cyclonic eddy in the Bay of Bengal[J]. Journal of Marine Research, 1991, 49(3): 403−410. doi: 10.1357/002224091784995846 [25] Yang Yang, Liang X S. New perspectives on the generation and maintenance of the Kuroshio large meander[J]. Journal of Physical Oceanography, 2019, 49(8): 2095−2113. doi: 10.1175/JPO-D-18-0276.1 [26] Yang Yang, Weisberg R H, Liu Yonggang, et al. Instabilities and multiscale interactions underlying the loop current eddy shedding in the gulf of Mexico[J]. Journal of Physical Oceanography, 2020, 50(5): 1289−1317. doi: 10.1175/JPO-D-19-0202.1 [27] Liang X S, Anderson D G M. Multiscale window transform[J]. Multiscale Modeling & Simulation, 2007, 6(2): 437−467. [28] Liang X S, Robinson A R. Localized multi-scale energy and vorticity analysis: II. Finite-amplitude instability theory and validation[J]. Dynamics of Atmospheres and Oceans, 2007, 44(2): 51−76. doi: 10.1016/j.dynatmoce.2007.04.001 [29] Liang X S. Canonical transfer and multiscale energetics for primitive and quasigeostrophic atmospheres[J]. Journal of the Atmospheric Sciences, 2016, 73(11): 4439−4468. doi: 10.1175/JAS-D-16-0131.1 [30] Masumoto Y, Sasaki H, Kagimoto T, et al. A fifty-year eddy-resolving simulation of the world ocean−Preliminary outcomes of OFES (OGCM for the Earth Simulator)[J]. Journal of the Earth Simulator, 2004, 1: 35−56. [31] Sasaki H, Nonaka M, Masumoto Y, et al. An eddy-resolving hindcast simulation of the quasiglobal ocean from 1950 to 2003 on the earth simulator[M]//Hamilton K, Ohfuchi W. High Resolution Numerical Modelling of the Atmosphere and Ocean. New York, NY: Springer, 2008: 157−185. [32] Gonaduwage L P, Chen Gengxi, McPhaden M J, et al. Meridional and zonal eddy-induced heat and salt transport in the Bay of Bengal and their seasonal modulation[J]. Journal of Geophysical Research: Oceans, 2019, 124(11): 8079−8101. doi: 10.1029/2019JC015124 [33] Yang Yang, Liang X S. The intrinsic nonlinear multiscale interactions among the mean flow, low frequency variability and mesoscale eddies in the Kuroshio region[J]. Science China Earth Sciences, 2019, 62(3): 595−608. doi: 10.1007/s11430-018-9289-4 [34] Renault L, Molemaker M J, McWilliams J C, et al. Modulation of wind work by oceanic current interaction with the atmosphere[J]. Journal of Physical Oceanography, 2016, 46(6): 1685−1704. doi: 10.1175/JPO-D-15-0232.1 [35] Arbic B K, Müller M, Richman J G, et al. Geostrophic turbulence in the frequency–wavenumber domain: eddy-driven low-frequency variability[J]. Journal of Physical Oceanography, 2014, 44(8): 2050−2069. doi: 10.1175/JPO-D-13-054.1 [36] Cheng Xuha, McCreary J P, Qiu Bo, et al. Dynamics of eddy generation in the central Bay of Bengal[J]. Journal of Geophysical Research: Oceans, 2018, 123(9): 6861−6875. doi: 10.1029/2018JC014100 [37] von Storch J S, Eden C, Fast I, et al. An estimate of the Lorenz energy cycle for the world ocean based on the 1/10° STORM/NCEP simulation[J]. Journal of Physical Oceanography, 2012, 42(12): 2185−2205. doi: 10.1175/JPO-D-12-079.1 -
下载:
点击查看大图
计量
- 文章访问数: 336
- HTML全文浏览量: 188
- PDF下载量: 96
- 被引次数: 0
