Comparison of extreme wind speeds predicted by Monte-Carlo simulation and empirical track model
-
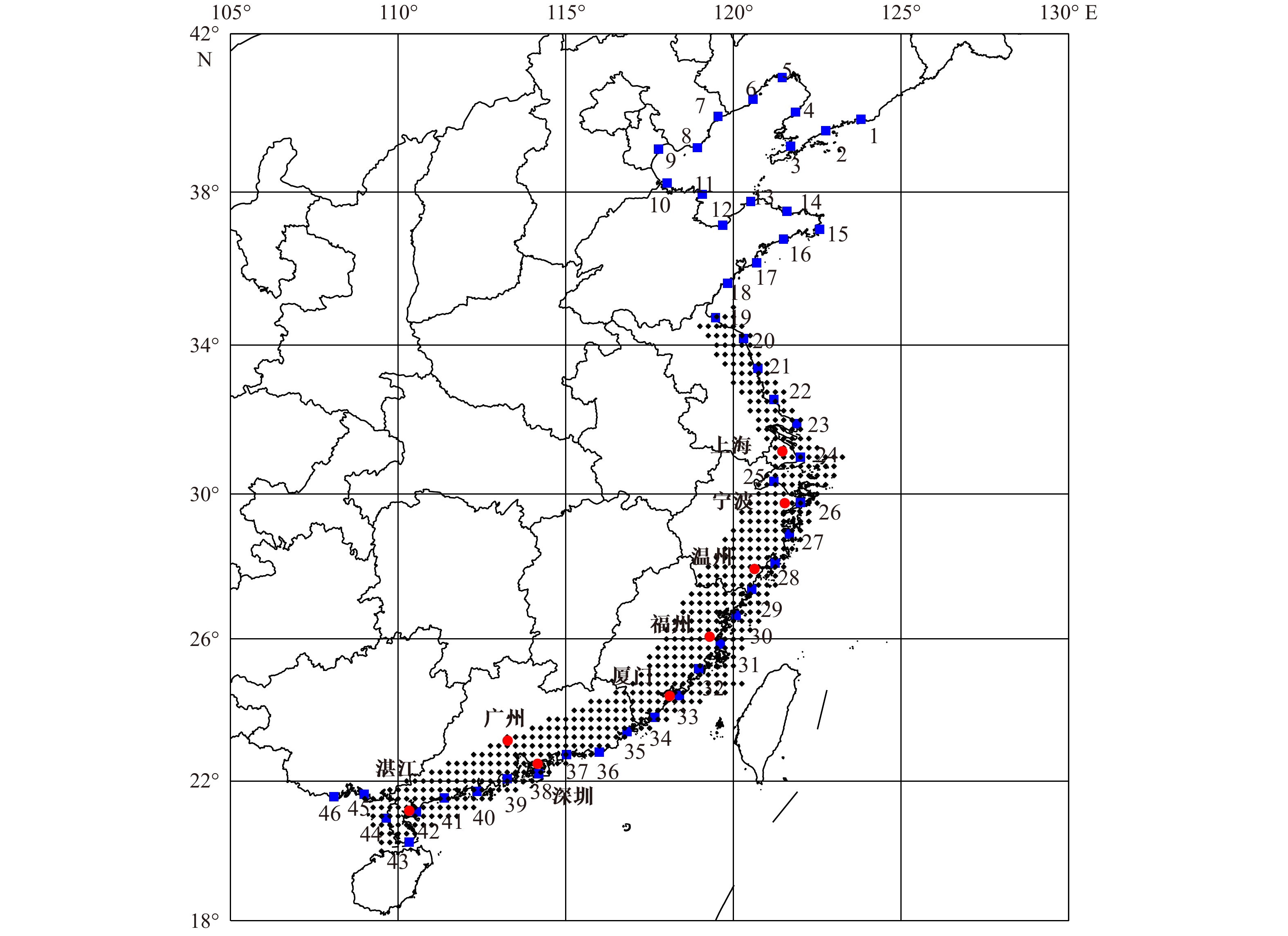
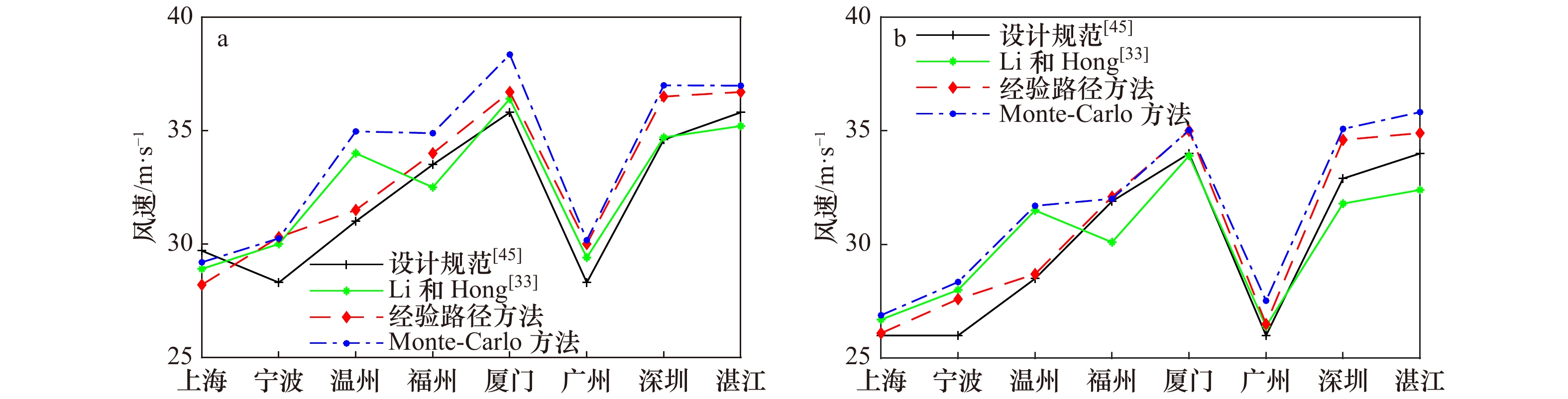
摘要: 台风是我国东南沿海区域每年发生的严重自然灾害之一。本文分别采用传统的Monte-Carlo模拟方法以及较为先进的经验路径模拟方法预测中国东南沿海区域台风的极值风速(10 m高度处10 min平均值)，并对两种方法的预测结果进行了对比。本文将东南海岸线向内陆扩展约200 km的区域划分为0.25°×0.25°的网格，以每个网格点作为研究点。首先采用Monte-Carlo模拟方法产生每个研究点1 000年间的虚拟台风事件。然后采用经验路径模型方法构建了西北太平洋1 000年的热带气旋事件集，采用模拟圆方法从中提取对各个研究站点有影响的台风事件。接着采用Yan Meng风场模型计算每个研究点台风的最大风速，构成极值风速序列。最后采用极值分布模型预测每个研究点不同重现期的极值风速，并对两种不同方法预测的结果进行了对比。研究发现在研究区域的内陆侧经验路径方法预测的风速略高于Monte-Carlo模拟方法预测的结果，而在海岸沿线一带经验路径方法预测的结果略低，这主要是由两种方法构造的虚拟台风的中心压强存在差异以及模型本身的不确定性造成的。本文的研究结果可以为防灾减灾系统提供有益的参考。
-
关键词:
- 台风 /
- Monte-Carlo模拟 /
- 经验路径模型 /
- 风场模型 /
- 极值风速
Abstract: Typhoon is one of the most serious natural disasters in southeast coastal region of China. In this paper, the traditional Monte-Carlo simulation and the advanced empirical track model are respectively used to predict the extreme wind speed (10-min mean at 10 m height) of typhoons in the southeast coastal region of China, and the prediction results of two methods are compared. An area extending 200 km inland from the coastline is divided into 0.25°×0.25° grid cells and each grid is taken as the research point. Firstly, the Monte-Carlo method is used to generate virtual typhoons of 1 000-year for each research point. Then, we use the empirical track model to construct virtual typhoons of 1 000-year in the Northwest Pacific Ocean, from which typhoon events affecting each research site are extracted by using the simulation circle method. Next, the Yan Meng wind field model is used to calculate the wind speed of the extracted typhoons, from which samples of maximum wind speed can be derived. Finally, the extreme wind speed of different return periods for each research point is predicted by the extreme value distribution. Through comparison, we find that in some inland areas, the predicted wind speeds by empirical track model are slightly higher than those by Monte-Carlo method, and in most coastal areas the opposite is true. This is mainly caused by the difference of the central pressure of the virtual typhoons constructed by two methods and the uncertainty of the model itself. The research results of this paper can provide useful reference for the disaster prevention and mitigation system.-
Key words:
- typhoon /
- Monte-Carlo simulation /
- empirical track model /
- wind field model /
- extreme wind speed
-
1. 引言
中国东南沿海区域是世界上遭受台风灾害严重的地区之一。台风，在东太平洋和大西洋被称为飓风，常常引起狂风、暴雨、巨浪和风暴潮等自然灾害。利用台风风场模型与数值模拟方法分析台风灾害风险具有十分重要的意义。
20世纪下半叶，为了解决台风风速观测数据匮乏的问题，Monte-Carlo模拟作为可替代以及可行的方法被广泛用来分析台风的危险性。它利用台风风场模型和台风关键参数资料，采用数值模拟方法构造大量虚拟台风，进而对台风影响区域进行极值风速的预测（又称为台风危险性分析）。采用Monte-Carlo随机抽样构造虚拟台风的具体过程是：首先给定特定地点台风关键参数的统计概率模型，包括台风中心气压差、最大风速半径、移动速度、移动方向以及台风路径与研究点的最小距离。给定这些参数的概率模型之后，用Monte-Carlo方法对这些模型进行随机抽样，台风在满足抽样出来的关键参数的同时沿着直线路径发展，同时模拟的风速被记录下来。在该过程中台风的强度保持不变直到登陆，当台风登陆后则采用衰减模型描述中心压差的变化，由此即可得到虚拟台风路径[1]。
美国[2]和澳大利亚[3]均采用Monte-Carlo模拟方法编制设计风速图。该模拟方法最初是由Russell[4-5]提出并应用于德克萨斯州海岸飓风风速的预测。自此以后，许多学者都对该方法进行了扩展与改进。Batts等[6]和Shapiro[7]相继提出了Batts飓风风场模型以及Shapiro模型。Georgiou[8]通过对台风历史数据进行统计分析，结合Georgiou台风模型，发展了基于Monte-Carlo方法的台风数值模拟方法。Vickery和Twisdale[9]研究表明Shapiro风场模型要优于Batts风场模型。Meng等[10]研究了台风边界层的风场，建立了Yan Meng（YM）台风风场模型。Simiu和Scanlan[11]回顾了在结构设计中描述风气候的问题，并对设计风速的定义提出了相应的标准。Thompson和Cardone[12]采用数值后报方法反演墨西哥湾历史上发生的台风个例，从而获得相应台风引起的最大风速序列。Vickery和Twisdale[13]指出虽然这些研究使用的方法是相似的，但在风场模型、衰减模型、研究区域大小以及历史台风提取方法等方面存在显著差异。
自2000年以来，多位学者[14-20]逐步发展了全路径模型方法。Vickery等[14]首次开发了经验路径模型，该模型可以生成台风从产生到消亡的完整轨迹，允许台风在发展过程中改变移动方向、移动速度和强度。Vickery等[14]利用经验路径模型构造虚拟台风的过程是：根据历史台风资料，抽样产生虚拟台风初始时刻的关键参数；基于大西洋海域5°×5°网格内历史台风数据，拟合得到经验路径模型的系数；结合初始时刻台风关键参数以及台风所处相应网格的经验路径模型可以预测下一时刻台风的位置与强度，以此类推可以产生完整的虚拟台风路径。Vickery等[14]指出，与Monte-Carlo模拟方法相比，经验路径模拟方法的优点在于它不需要依赖子区域气候一致性的假设。因此，即使是在台风气候学变化较大的区域也可以采用经验路径模型进行台风灾害分析，这有助于分析大型系统的台风风险。而Monte-Carlo模拟方法更加适合分析单个站点的台风危险性。美国建筑结构荷载规范[21]推荐的设计风速也是基于Vickery等[14]的经验路径模型。
自Vickery等[14]以来，台风危险性分析方法得到了一些重要改进。Li和Hong[22]采用地理加权回归方法对Vickery等[14]的经验路径模型进行了简化，并对简化后模型进行了充分的验证。Vickery和Wadhera[23]及Vickery等[24]利用飓风侦察飞机测得的压力数据和飓风研究部门提供的飓风风场照片信息，更新了最大风速半径（Rmax）和Holland气压剖面参数（B）的统计模型。Vickery[25]开发了一种新的飓风登陆后的衰减模型。Mudd等[26]采用飓风预测模型模拟了未来气候变化情景下2100年的飓风。Lee和Rosowsky[27]分别在2005年以及未来的气候情景下为美国西北部沿岸区域建立了飓风风速数据库。Rosowsky等[28]对Mudd等[26]的研究进行了相应的改善。此外，Powell等[29]、Legg等[30]、Apivatanagul等[31]、Pei等[32]、Li和Hong[33]都对经验路径模型进行了其他一些衍生研究。
过去几十年，我国在台风风险分析领域也开展了许多研究。欧进萍等[34]利用Batts风场模型分析了我国东南沿海重点城市的台风危险性。Xiao等[1]结合Thompson和Cardone[12]台风模型和Monte-Carlo模拟方法对我国东南沿海地区11个重点城市进行台风风灾分析。Li和Hong[22]对经验路径模型进行了简化并使用该模型分析了我国东南沿海的台风灾害。这些研究为沿海重点城市的抗风设计提供了有益的参考。
利用Monte-Carlo模拟与经验路径模型分析台风危险性的思路是相似的。两种方法都是首先构造大量虚拟台风，然后采用适当的风场模型计算这些台风的风速，从中提取最大风速构成极值风速序列，最后采用极值分布进行拟合并预测不同重现期的极值风速。只是在构造虚拟台风的具体过程上两种方法有所不同。本文分别采用Monte-Carlo模拟方法以及经验路径模拟方法预测了中国东南沿海区域台风的极值风速，并对两种方法的预测结果以及产生差异的原因进行了分析。
2. 数据与方法
Monte-Carlo模拟与经验路径模型都需要以历史台风数据为统计基础，本文采用的历史台风数据来源于中国气象局−上海台风研究所（ China Meteorological Administration and Shanghai Typhoon Institute, CMA-STI）西北太平洋热带气旋最佳路径数据集（1949–2017年，www.typhoon.gov.cn）。该数据集由中国气象局负责维护并进行更新。数据集包括台风每6 h间隔的位置与强度信息，具体包括台风名称、编号、台风中心位置（经度与纬度）、中心压强、近台风中心的2 min平均最大风速。
台风模型通常用一组参数进行参数化，称之为台风关键参数，主要包括台风年发生率（λ）、中心气压差（Δp）、最大风速半径（Rmax）、移动速度（VT）、移动方向（θ）、台风移动路径与模拟点间的最小距离（Dmin），这些参数表征了台风的结构和强度。
2.1 Monte-Carlo模拟方法
采用Monte-Carlo模拟方法分析台风危险性可分为以下5个步骤：（1）确定研究地点，采用模拟圆方法从历史台风事件集中提取对该研究点有影响的台风事件。模拟圆方法是以研究点为圆心，划定一定的半径，当一个台风路径与模拟圆相交或是位于模拟圆里面的时候，则该台风被提取出来作为对该研究点有影响的台风[8,13]。Li和Hong[22]以及Vickery等[15]通过参数化实验，建议模拟圆半径采用250 km。在本文中我们也设定模拟圆的半径为250 km，在该范围内认为台风气候是一致的。（2）基于提取的台风事件，拟合台风各个关键参数的概率模型。基于前人研究[11,13,35]，台风年发生率可以用泊松分布、二项分布或负二项分布来描述；中心气压差可以用对数正态分布、伽马分布或是威布尔分布来拟合；台风中心移动速度可以用正态分布、对数正态分布或伽马分布来描述；台风中心移动方向可以用正态分布、双峰分布或是Von Mises分布来拟合；最小距离可以用均匀分布或梯形分布来描述。（3）采用Monte-Carlo随机抽样从关键参数概率模型中抽取一组台风关键参数，组成一个虚拟台风事件，以此类推可以产生大量的虚拟台风事件。（4）采用台风风场模型计算虚拟台风的风速与风向，从中提取极值风速序列。（5）利用极值分布模型对极值风速序列进行拟合进而估计台风不同重现期的极值风速。
其中通过Monte-Carlo随机抽样产生虚拟台风的步骤如下：（1）判断从概率分布随机抽取的关键参数是否在合理的范围内：Δp为[0, 135] hPa，VT为[2, 65] km/h，θ为[−180°, 180°]，|Dmin|≤250 km。（2）用Dmin和θ确定台风的直线路径，该直线路径与模拟圆的交点即为虚拟台风的起始点，如图1所示。（3）在台风移动过程中移动速度与方向保持不变，以此来确定台风其他时刻的中心位置。（4）在台风登陆前，中心压强保持不变，登陆后采用衰减模型来描述中心压差Δp的变化。（5）当台风中心离开模拟圆范围则认为台风消失。该过程示意图如图1所示。
2.2 衰减模型
台风登陆后，由于海洋能量来源的损失和地面摩擦的增加，台风强度会减弱。台风衰减的速率与台风本身、登陆的位置以及登陆时的中心压差有关。采用合适的衰减模型描述台风的衰减规律，对于预测台风登陆后的风速有重要影响。本文采用Vickery和Twisdale[9]提出的衰减模型，即
$$ \Delta p(t) = \Delta {p_0}\exp ( - at), $$ (1) $$ a = {a_0} + {a_1}\Delta {p_0} + \varepsilon, $$ (1) 式中，Δp（t）是台风登陆后t时刻的中心压差（单位：hPa）；Δp0是登陆时刻的中心压差（单位：hPa）；a是特定点衰减系数；ε是正态分布的误差项，均值为0；标准偏差为σε。通过拟合登陆的台风数据，可以得到研究点或区域的台风衰减模型的系数。
2.3 风场模型
台风风场模型是进行台风数值求解的关键。本文采用了Yan Meng (YM)风场模型，该模型是Meng等[10]在1995年提出的解析模型，其数值形式如下：
$$ \frac{{\partial {{V}}}}{{\partial t}} + {{V}} \cdot \nabla {{V}} = - \frac{1}{\rho }\nabla p - f{{k}} \times {{V}} + {{F}}, $$ (2) 式中，V代表台风风速；ρ代表空气密度；k代表垂向单位向量；f代表科氏参数；F代表边界层摩擦力。该模型以扰动平衡方程和经过边界层摩擦力修正的压力梯度平衡方程为基础，引入了可以考虑地貌等复杂因素的“等效粗糙长度”，能够很好地表示出台风风场中各种力之间的相互关系，并且能够比较直观地求解梯度风方程，得到完整的解析解。基于之前的研究[3，36-37]不同地形地貌的粗糙度如表1所示。
表 1 不同地形地貌的粗糙度Table 1. Roughness length of different geomorphology地形等级 下垫面特征 粗糙度/m I 海面、泥滩、冰雪覆盖的平原，
无障碍海岸地区等0.000 5～0.003 II 平坦开阔的田野、乡村及丛林等
（气象学标准）0.003～0.2 III 丘陵和房屋比较稀疏的
乡镇及城市郊区0.2～1.0 IV 密集建筑群的城市 1.0～2.0 V 密集建筑群且房屋较高的城市 2.0～4.0 YM模型具有足够的精度并被Matsui等[38]、谢汝强等[39]所采用。关于风场模型的详细内容请参考文献[10]。
气压是台风风场模型的重要输入参数，YM风场模型采用Holland[40]气压模型，其形式为
$$ p(r) = {p_0} + \Delta p\exp [ - {({R_{\max }}/r)^B}], $$ (3) 式中，p(r)是距台风中心径向距离为r处的海平面压强；p0是台风中心的气压值。式中有两个未知的参数，分别是最大风速半径（Rmax）和气压剖面参数（B）。这两个参数是台风风场模型中的重要参数，它们的计算公式直接决定风场模型计算风速的大小，进而影响极值风速的预测。本文采用的计算公式取自Vickery和Wadhera[23]，该公式同时被Li和Hong[22, 33, 41]以及Hong等[42]所使用，形式如下：
$$ \ln {R_{\max }} = 3.015 - 6.291 \times {10^{ - 5}}\Delta {p^2} + 0.033\;7\psi + {\varepsilon _{\ln R_{\max} }}, $$ (4) $$ B = 1.833 - 0.326\sqrt {1\;000f{R_{\max }}} + {\varepsilon _B}, $$ (5) 式中，
${\varepsilon _{\ln R_{\max} }} $ 为标准偏差，当Δp≤87 hPa时，${\varepsilon _{\ln R_{\max} }} $ =0.448；当87 hPa<Δp≤120 hPa时，${\varepsilon _{\ln R_{\max} }} $ =1.137−0.007 92Δp；当Δp>120 hPa时，${\varepsilon _{\ln R_{\max} }} $ =0.186；ψ为纬度；εB=0.221。2.4 经验路径模型
Vickery等[14]发展了经验路径模型，对台风的移动速度、移动方向以及相对强度进行了建模。模型表达式如下：
$$ \Delta \ln c = {a_1} + {a_2}\psi + {a_3}\lambda + {a_4}\ln {c_i} + {a_5}{\theta _i} + {\varepsilon _c}, $$ (6) $$ \Delta \theta = {b_1} + {b_2}\psi + {b_3}\lambda + {b_4}{c_i} + {b_5}{\theta _i} + {b_6}{\theta _{i - 1}} + {\varepsilon _\theta }, $$ (7) $$ \begin{split} \ln ({I_{i + 1}}{\rm{) = }}& {d_1} + {d_2}\ln ({I_i}) + {d_3}\ln ({I_{i - 1}}) + {d_4}\ln ({I_{i - 2}}) +\\ & {d_5}T{s_i} + {d_6}(T{s_{i + 1}} - T{s_i}) + {\varepsilon _I}, \end{split} $$ (8) 式中，c表示台风移动速度；θ表示台风移动方向；I表示台风相对强度(台风压强)；ai (i =1, 2,···,5)是移动速度系数；bi (i =1,2,···,6)是移动方向系数；di(i =1,2,···,6)是相对强度系数；ψ和λ是台风的纬度与经度；ci是i时刻的移动速度；θi、θi−1是i与i−1时刻的移动方向；Ii+1、Ii,、Ii−1、Ii−2分别是时刻i+1、i、i−1以及i−2的相对强度；Tsi+1、Tsi是i+1与i时刻海表面温度（单位：K）；ε是误差项。
台风相对强度的概念是由Darling[43]建立的，
$$ I = {{\Delta p} / {({p_{da}} - {p_{dc}})}}, $$ (9) 式中，pda和pdc分别表示环境和最小可持续干空气分子压强。台风中心压强可以用相对强度I来表示，反之也是一样。关于相对强度的具体计算方法可以查看Darling[43]附录。
Vickery等[14]首先将大西洋海盆划分成5°×5°的网格，然后通过对各个网格单元中历史台风的移动速度、移动方向和相对强度数据回归分析得到东向与西向运动台风的ai、 bi、 di的两套数值。然后采用直接抽样方法从HURDAT[44]台风数据集中抽取台风起始时刻的位置、日期、移动方向和移动速度，以此来初始化模拟过程。接着根据公式（7）至公式（9）计算得到的台风移动速度与方向，可以计算下一个6 h间隔的台风位置与强度，以此类推可以得到完整的台风路径。对于那些没有台风数据或是台风数据比较少的网格点，可以用最邻近网格中的模型来代替。当台风登陆后，采用Vickery和Twisdale[9]提出的衰减模型描述中心压强的衰减。如果台风再次回到海里，则采用公式（10）继续计算台风在新的网格位置的中心压强。
在Vickery等[14]模型中，每个网格单元需要确定的系数比较多。Li和Hong[22]在模型回归分析中消除了一些次要的解释变量，对经验路径模型进行了简化，克服了变量多重相关性问题，形式如下：
$$ \Delta \ln c = {a_1} + {a_2}\ln {c_i} + {a_3}{\theta _i} + {\varepsilon _c}, $$ (10) $$ \Delta \theta = {b_1} + {b_2}{c_i} + {b_3}{\theta _i} + {\varepsilon _\theta }, $$ (11) $$ \ln ({I_{i + 1}}{\rm{) = }}{d_1} + {d_2}\ln ({I_i}) + {d_3}T{s_i} + {d_4}(T{s_{i + 1}} - T{s_i}) + {\varepsilon _I}. $$ (12) Li和Hong[22]对简化的路径模型进行了充分的验证，并将其用于分析中国东南沿海区域台风的危险性[33]。
在本文中，我们将简化的经验路径方法应用到整个西北太平洋区域，构造了该海域1 000年热带气旋事件集。台风年频数服从泊松分布，均值为27.27 个/a。台风发生的起始位置和日期是从CMA数据集中直接抽样而得到。图2给出了CMA数据集中所有台风的起始点分布以及西北太平洋区域5°×5°的网格划分。基于历史台风数据，台风的初始移动速度符合伽马分布，形状参数为3.74，尺度参数为5.07；台风初始移动方向符合双峰分布，均值为−69.28 和−17.71，标准偏差为18.80和62.78，权重系数为0.514，拟合的结果分别如图3a和图3b所示。泊松分布、伽马分布以及双峰分布都在5%的显著性水平上通过了Kolmogorov–Smirnov（KS）拟合优度检验。台风的初始移动速度与移动方向分别从上述伽马分布与双峰分布中随机抽样而得到，台风初始相对强度是从经验分布抽取得到。
图 2 CMA数据中台风的起始点以及西北太平洋区域5°×5°的网格Figure 2. Spatial distribution of genesis based on the CMA best-track dataset and the grid cell of 5°×5° in the Northwest Pacific Ocean
图 3 观测的台风初始移动速度（a）与移动方向（b）的概率分布拟合Figure 3. Modeled and observed statistical distributions of translation speed (a) and storm heading (b)给定台风初始移动方向、移动速度以及强度后，路径模型可以基于当前时刻的移动速度与移动方向估计台风新的位置。基于CMA数据集我们拟合的公式（11）中东向与西向运动台风的系数ai和εc如图4所示。同样我们也拟合了公式（12）以及公式（13）中的系数b和d，限于文章篇幅，不再给出这些系数的数值分布。
图 4 对于东向与西向运动的台风拟合的公式（11）中的系数ai和εc的分布Figure 4. Illustration of regression coefficients ai and εc in Eq.(11) for easterly and westerly headed storms为了拟合衰减模型，将西北太平洋台风登陆区域划分成5部分：30°N以北温带气旋区域（区域1），25°～30°N台湾岛以北区域（区域2），20°～25°N包含台湾岛区域（区域3），菲律宾群岛区域（区域5），剩下的区域（区域4）。对衰减模型中拟合的系数如表2所示。
表 2 公式(2)的衰减常数aTable 2. Decay constant a in Eq. (2)区域 N $a = {a_0} + {a_1}\Delta {p_0} + \varepsilon $ a0 a1 R2 σε 区域1 36 0.0078 0.00075 0.0928 0.0198 区域2 66 0.0161 0.00055 0.0946 0.0203 区域3 159 0.0137 0.0012 0.2139 0.0247 区域4 82 −0.0035 0.0019 0.4768 0.0216 区域5 40 −0.0026 0.00052 0.5321 0.0116 注：N代表各个区域中用于回归分析的样本个数，R2是回归分析的相关系数，σε是误差项的标准差。 基于台风的初始化过程以及拟合的经验路径模型与衰减模型构造了西北太平洋1 000年的虚拟台风数据集。为了验证该数据集的可靠性，对比了中国沿岸46个站点（图5）观测与虚拟的台风关键参数。用于验证的观测台风来源于CMA数据集。首先将每个站点250 km范围内的观测与虚拟台风数据分别提取出来，然后统计这些台风事件在距离各个站点最近时（除了中心压差）的关键参数，包括台风年发生率的平均值、移动速度、移动方向与最小距离（当台风经过研究点的右侧时，最小距离取正值，反之取负值）的平均值与标准差。中心压差取台风事件在距各站点250 km范围内的压差最小值。验证结果如图6所示，可以看出模拟的我国沿海台风的特征与实测数据吻合较好，说明经验路径模型能够较好地再现西北太平洋台风的统计特征。
图 5 研究站点（黑色星号）、用于验证经验路径模型的站点（蓝色方框）以及8个沿岸城市（红点）的位置分布Figure 5. Locations of research points (black asterisks), stations for validation of empirical track model (blue squares) and 8 coastal cities (red dots)
图 6 沿岸46个站点虚拟与观测的台风关键参数的对比Figure 6. Comparison of key parameters of simulated and observed typhoons at 46 coastal stations3. 特定点虚拟台风的模拟与计算
我们将中国东南沿海台风多发区域作为本文的研究区域。采用网格法来确定研究点，网格的分辨率是0.25°×0.25°（参考Hong等[42]）。一共有579个网格点（研究点）覆盖整个研究区域（图5）。
首先采用Monte-Carlo方法模拟每个研究点的虚拟台风事件，模拟的时间长度为1 000年。采用模拟圆方法从CMA历史台风数据集中提取对各个点有影响的台风事件，通过统计，每个研究站点有25～267个不等的历史台风样本。提取这些台风的关键参数，用相应的概率分布进行拟合，采用卡方检验与KS检验两个非参数检验方法对台风关键参数的拟合优度进行检验，检验的显著性水平为5%。如果理论分布没有通过检验，则采用经验分布。由此我们确定了每个研究点各个台风关键参数的最优概率模型。利用第2节介绍的Monte-Carlo方法以及衰减模型，为每个研究点构造了1 000年间的虚拟台风事件。再利用YM风场模型可以计算每一个虚拟台风的风速与风向。在利用YM模型计算风场时，根据实际地形标记了每个研究点的粗糙度，如图7所示。
为了比较Monte-Carlo方法与经验路径方法预测的极值风速的异同，我们从第2.4节采用经验路径方法构造的西北太平洋1 000年的台风数据集中提取了对各个研究点有影响的虚拟台风事件。同样采用YM风场模型计算了每一个虚拟台风在研究点处产生的风速与风向。
4. 极值风速的预测与对比
基于第3节计算的虚拟台风风速，可以从中提取每个台风在研究点产生的最大风速，从而构成极值风速序列。极值风速序列通常会用威布尔（Weibull）分布、耿贝尔（Gumbel）分布或经验分布来进行描述，采用这些极值分布可以预测不同重现期的极值风速。
对于经验分布，推导出的重现期为T的风速表达式为
$$ {v_i} = \left\{ {i = \left( {m + 1} \right)\left[ {1 + \frac{{\ln (1 - {1 / T})}}{\lambda }} \right]} \right\}, $$ (8) 式中，m是极值风速序列的样本容量，大括号中的公式是下标i的计算公式，当风速样本从小到大排列时，i是重现期为T时极值风速对应的秩序。
对于Weibull分布，推导出的重现期为T的风速表达式为
$$ {v_i} = \gamma + \eta {\left\{ { - \ln \left[ { - {{\ln (1 - {1 / T})}/ \lambda }} \right]} \right\}^{{1 / \beta }}}, $$ (9) 式中，β为形状参数；η为尺度参数；γ为位置参数；λ为台风发生率。
对于Gumbel分布，推导出的重现期为T的风速表达式为
$$ {v_i} = \mu - {{\ln \left\{ { - \ln \left[ {1 + {{\ln \left( {{{1 - 1} / T}} \right)} / \lambda }} \right]} \right\}} / \alpha }, $$ (10) 式中，μ为位置参数；α为尺度参数；λ为 台风发生率。
为了验证本文采用Monte-Carlo方法与经验路径方法预测的极值风速的准确性，我们将本文预测的8个沿岸重点城市（上海、宁波、温州、福州、厦门、广州、深圳、湛江，如图5所示）的极值风速与Li和Hong[33]的结果以及中国《建筑结构荷载规范》[45]中的数值进行了对比，结果如图8所示。本文的预测结果与Li和Hong[33]以及设计规范的值吻合较好。
本文对Monte-Carlo方法与经验路径方法预测的不同重现期极值风速进行了对比。图9a为采用Monte-Carlo方法以及经验分布预测的50年重现期极值风速等值线图，图9b是相同条件下采用经验路径方法预测的极值风速与Monte-Carlo方法预测的风速的差值。正值表示经验路径方法预测结果高于Monte-Carlo方法预测的结果。可以看出在研究区域的内陆侧，经验路径方法预测的结果略高于Monte-Carlo方法预测的结果；在余下的大部分区域尤其是海岸沿线一带，经验路径方法预测的结果比Monte-Carlo方法预测的结果低0～5 m/s，最大差值为−13.3 m/s，最大相对差值为31.5%。图10为采用Monte-Carlo方法以及经验分布预测的100年重现期极值风速等值线图以及经验路径方法与Monte-Carlo方法预测结果的差值。可以看出100年重现期极值风速普遍比50年重现期极值风速高0～5 m/s，同样在内陆侧少数地区经验路径方法预测的结果略高，在余下的大部分区域尤其是海岸沿线一带经验路径方法预测的结果偏低，最大差值为−16.8 m/s，最大相对差值为33.5%。
图 9 采用Monte-Carlo方法以及经验分布预测的50年重现期的极值风速（a）以及经验路径方法与Monte-Carlo方法预测结果的差值(b)Figure 9. Extreme wind speeds for 50-year return period by Monte-Carlo simulation and empirical distribution (a) and the wind speed difference between empirical track model and Monte-Carlo simulation (b)
图 10 采用Monte-Carlo方法以及经验分布预测的100年重现期的极值风速（a）以及经验路径方法与Monte-Carlo方法预测结果的差值（b）Figure 10. Extreme wind speeds for 100-year return period by Monte-Carlo simulation and empirical distribution (a) and the wind speed difference between empirical track model and Monte-Carlo simulation (b)图11、图12与图9类似，只是极值分布分别采用的是威布尔分布和耿贝尔分布。对比图9a、图11a以及图12a可以看出威布尔分布预测的极值风速略低于经验分布的预测结果，最大差值为−5.1 m/s，最大相对差值为11.4%；而耿贝尔分布预测的极值风速略高于经验分布的结果，最大差值为5.3 m/s，最大相对差值为11.6%。图11b与图12b对比的经验路径方法与Monte-Carlo方法预测的极值风速的差异与图9b是类似的，最大差值分别为−11.0 m/s和−10.2 m/s，最大相对差值分别为27.4%和25.3%。
图 11 采用Monte-Carlo方法以及威布尔分布预测的50年重现期的极值风速（a）以及经验路径方法与Monte-Carlo方法预测结果的差值（b）Figure 11. Extreme wind speeds for 50-year return period by Monte-Carlo simulation and Weibull distribution (a) and the wind speed difference between empirical track model and Monte-Carlo simulation (b)
图 12 采用Monte-Carlo方法以及耿贝尔分布预测的50年重现期的极值风速（a）以及经验路径方法与Monte-Carlo方法预测结果的差值（b）Figure 12. Extreme wind speeds for 50-year return period by Monte-Carlo simulation and Gumbel distribution (a) and the wind speed difference between empirical track model and Monte-Carlo simulation (b)为了解释经验路径方法与Monte-Carlo方法预测的极值风速的差异，计算了对各个站点产生影响的台风在距离各站点最近时的中心压差的平均值。因为中心压差表征了台风的强度，直接影响各个站点极值风速的大小。其中对各个站点产生影响的台风数据分别来自Monte-Carlo方法与经验路径方法构造的虚拟台风事件集。计算了基于这两种方法得到的579个研究站点的中心压差的平均值的差值，结果如图13a所示，其中正值表示经验路径方法得到的中心压差的平均值大于Monte-Carlo方法的结果。对比图13a与图9b可以看出，两者有着类似的正负分布，图13b给出了两者正负号一致的站点（红点）与不一致的站点（蓝点）分布。可以看出对于绝大多数研究站点，经验路径方法得到的中心压差的平均值偏大的地方，其预测的极值风速也偏大。因此我们认为经验路径方法与Monte-Carlo方法预测的极值风速的差异，主要是由两者构造的虚拟台风的中心压强存在差异造成的。这可能是由于Monte-Carlo方法假定台风登陆前压强保持不变，因此在台风登陆时中心压强差偏大，导致其预测的靠近海边的站点极值风速也偏大。对于还有少数站点不能用压强差解释的风速差异可能是模型本身的不确定性造成的，比如台风路径的不确定性、衰减模型的差异等。
5. 结论
本文分别采用Monte-Carlo模拟方法以及经验路径模拟方法预测了中国东南沿海区域台风的极值风速。将整个东南沿海区域划分为0.25°×0.25°的网格，将每个网格点作为研究点。基于历史台风数据，采用Monte-Carlo方法产生每个研究点1 000年间的虚拟台风事件。采用经验路径模型方法构建了整个西北太平洋1 000年的热带气旋事件集，并对构造的虚拟台风的特征进行了验证。从构造的热带气旋事件集中可以提取对各个研究站点有影响的台风事件。采用YM风场模型计算虚拟台风的风场，采用极值分布模型预测每个研究点不同重现期的极值风速。对比两种方法预测的极值风速，研究发现在研究区域内陆侧，经验路径方法预测的结果略高于Monte-Carlo方法预测的结果；在大部分海岸沿线一带，经验路径方法预测的结果比Monte-Carlo方法预测的结果略低，这主要是由两种方法构造的虚拟台风的中心压强存在差异以及模型本身的不确定性造成的。本文研究结果可以为相关部门防灾减灾提供一定的参考。
-
图 2 CMA数据中台风的起始点以及西北太平洋区域5°×5°的网格
Fig. 2 Spatial distribution of genesis based on the CMA best-track dataset and the grid cell of 5°×5° in the Northwest Pacific Ocean
图 3 观测的台风初始移动速度（a）与移动方向（b）的概率分布拟合
Fig. 3 Modeled and observed statistical distributions of translation speed (a) and storm heading (b)
图 4 对于东向与西向运动的台风拟合的公式（11）中的系数ai和εc的分布
Fig. 4 Illustration of regression coefficients ai and εc in Eq.(11) for easterly and westerly headed storms
图 5 研究站点（黑色星号）、用于验证经验路径模型的站点（蓝色方框）以及8个沿岸城市（红点）的位置分布
Fig. 5 Locations of research points (black asterisks), stations for validation of empirical track model (blue squares) and 8 coastal cities (red dots)
图 6 沿岸46个站点虚拟与观测的台风关键参数的对比
Fig. 6 Comparison of key parameters of simulated and observed typhoons at 46 coastal stations
图 9 采用Monte-Carlo方法以及经验分布预测的50年重现期的极值风速（a）以及经验路径方法与Monte-Carlo方法预测结果的差值(b)
Fig. 9 Extreme wind speeds for 50-year return period by Monte-Carlo simulation and empirical distribution (a) and the wind speed difference between empirical track model and Monte-Carlo simulation (b)
图 10 采用Monte-Carlo方法以及经验分布预测的100年重现期的极值风速（a）以及经验路径方法与Monte-Carlo方法预测结果的差值（b）
Fig. 10 Extreme wind speeds for 100-year return period by Monte-Carlo simulation and empirical distribution (a) and the wind speed difference between empirical track model and Monte-Carlo simulation (b)
图 11 采用Monte-Carlo方法以及威布尔分布预测的50年重现期的极值风速（a）以及经验路径方法与Monte-Carlo方法预测结果的差值（b）
Fig. 11 Extreme wind speeds for 50-year return period by Monte-Carlo simulation and Weibull distribution (a) and the wind speed difference between empirical track model and Monte-Carlo simulation (b)
图 12 采用Monte-Carlo方法以及耿贝尔分布预测的50年重现期的极值风速（a）以及经验路径方法与Monte-Carlo方法预测结果的差值（b）
Fig. 12 Extreme wind speeds for 50-year return period by Monte-Carlo simulation and Gumbel distribution (a) and the wind speed difference between empirical track model and Monte-Carlo simulation (b)
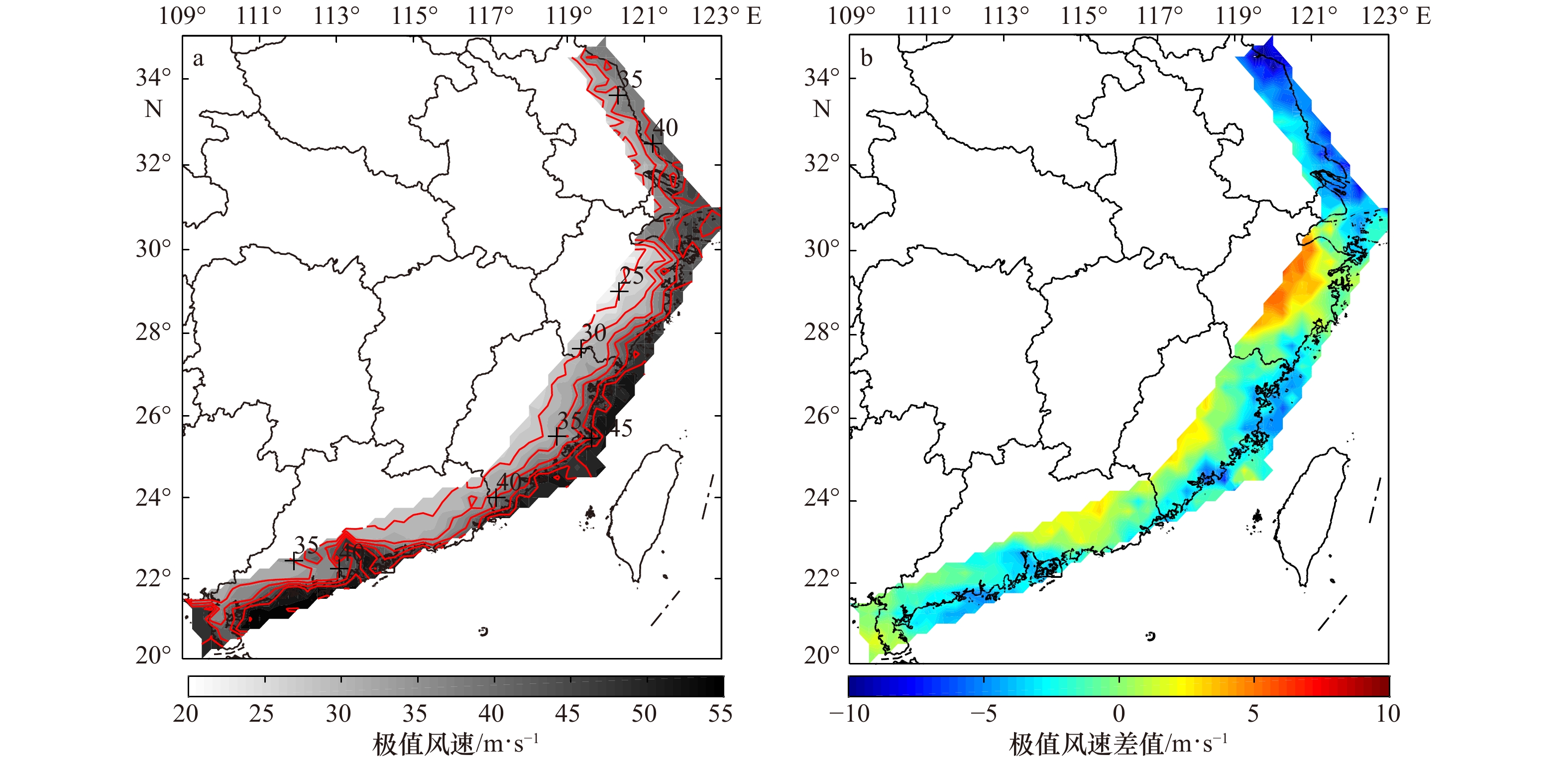
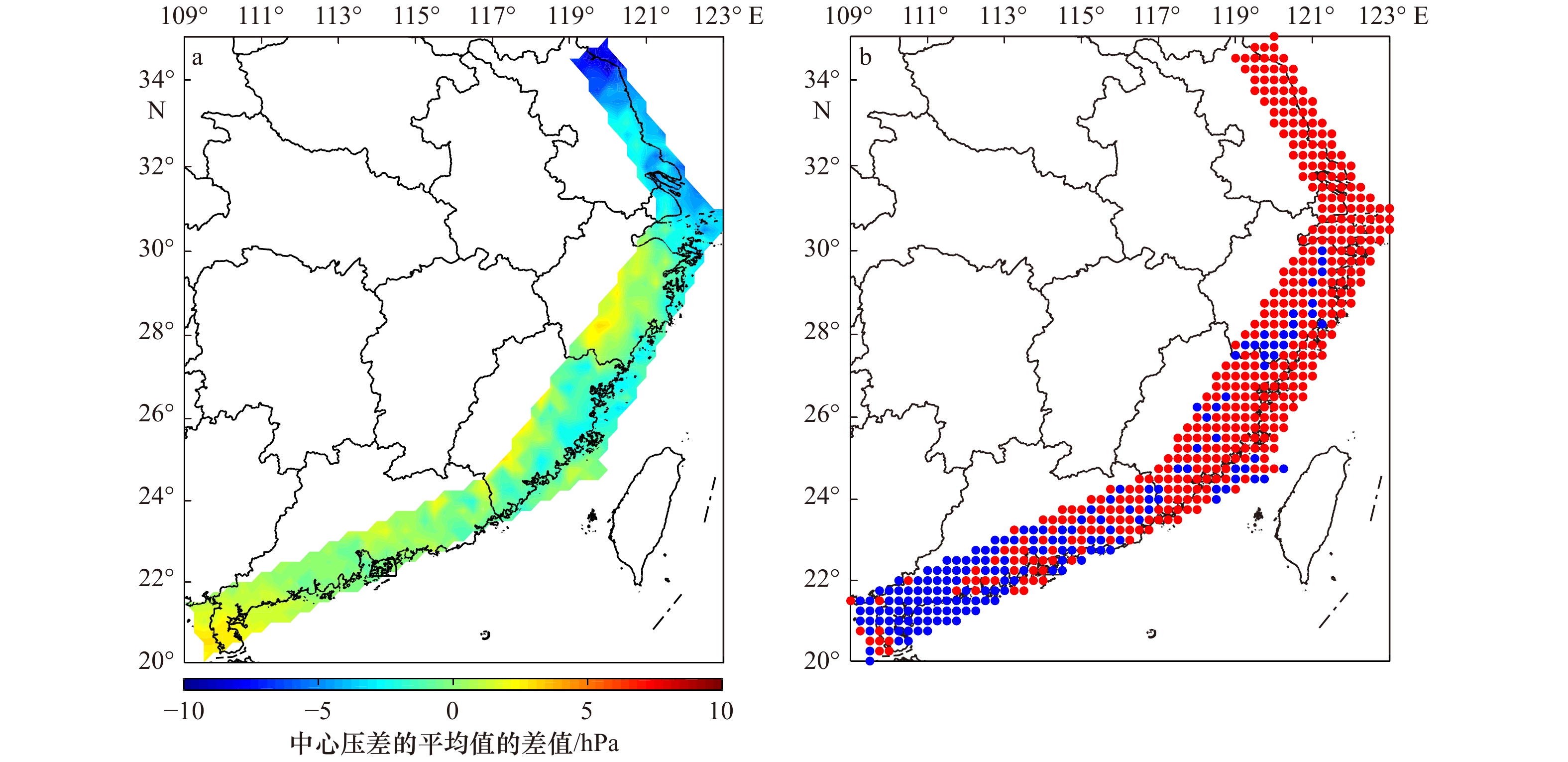
图 13 采用Monte-Carlo方法以及经验路径方法得到的579个研究站点的中心压差的平均值的差值（a）以及图13a与 图9b正负号一致的站点（红点）与不一致的站点（蓝点）（b）
Fig. 13 The difference of the mean value of the central pressure difference for 579 research stations between Monte-Carlo simulation and empirical track method (a), and stations with the same (red dots) and different (blue dots) signs in Fig.13a and Fig.9b (b)
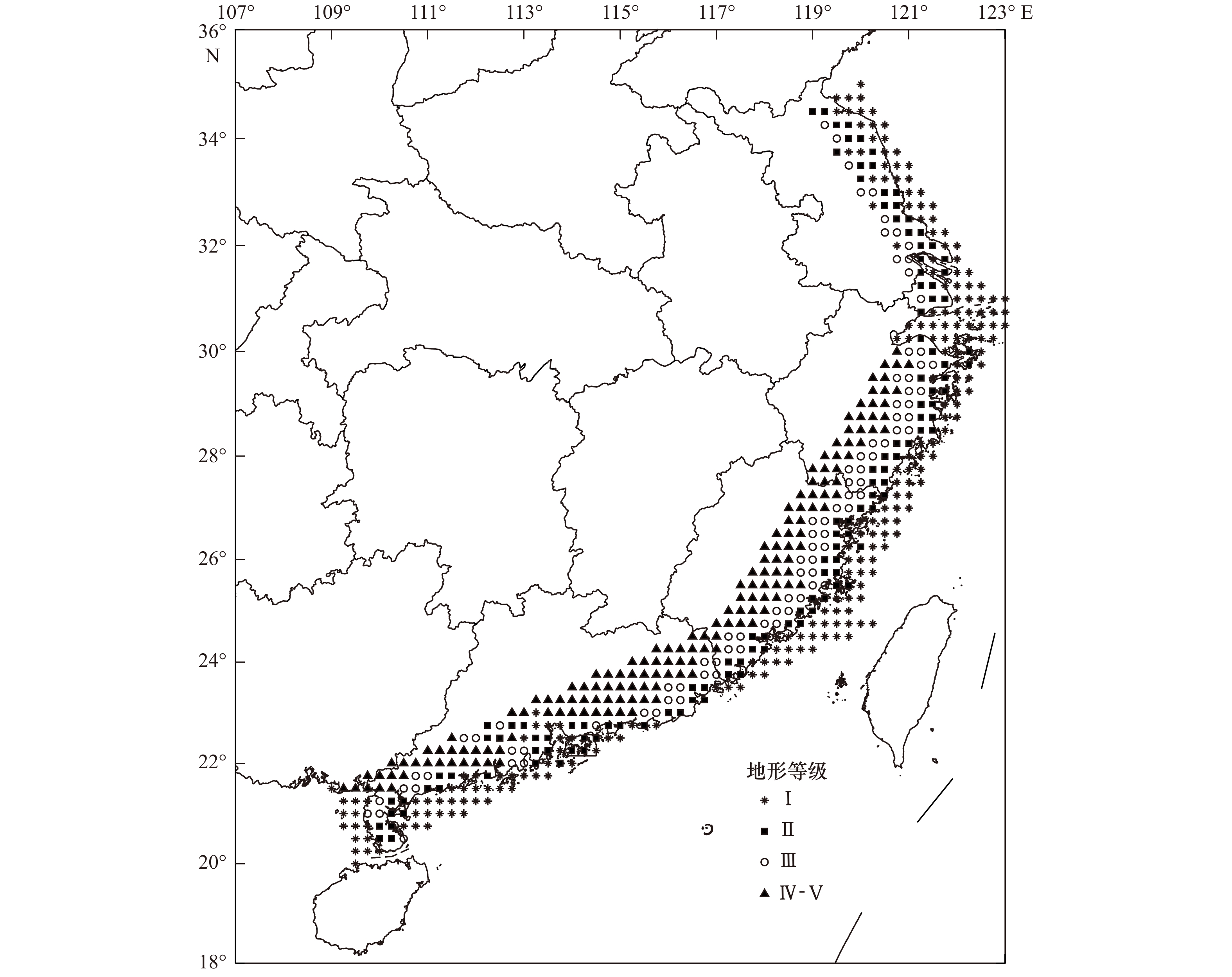
表 1 不同地形地貌的粗糙度
Tab. 1 Roughness length of different geomorphology
地形等级 下垫面特征 粗糙度/m I 海面、泥滩、冰雪覆盖的平原，
无障碍海岸地区等0.000 5～0.003 II 平坦开阔的田野、乡村及丛林等
（气象学标准）0.003～0.2 III 丘陵和房屋比较稀疏的
乡镇及城市郊区0.2～1.0 IV 密集建筑群的城市 1.0～2.0 V 密集建筑群且房屋较高的城市 2.0～4.0 
下载: 导出CSV
表 2 公式(2)的衰减常数a
Tab. 2 Decay constant a in Eq. (2)
区域 N $a = {a_0} + {a_1}\Delta {p_0} + \varepsilon $ a0 a1 R2 σε 区域1 36 0.0078 0.00075 0.0928 0.0198 区域2 66 0.0161 0.00055 0.0946 0.0203 区域3 159 0.0137 0.0012 0.2139 0.0247 区域4 82 −0.0035 0.0019 0.4768 0.0216 区域5 40 −0.0026 0.00052 0.5321 0.0116 注：N代表各个区域中用于回归分析的样本个数，R2是回归分析的相关系数，σε是误差项的标准差。
下载: 导出CSV
-
[1] Xiao Yufeng, Duan Zhongdong, Xiao Yiqing, et al. Typhoon wind hazard analysis for southeast China coastal regions[J]. Structural Safety, 2011, 33(4/5): 286−295. [2] American Society of Civil Engineers. ASCE/SEI 7-05, Minimum design loads for buildings and other structures[S]. Reston, VA: ASCE, 2005. [3] Standards Australia. AS/NZS 1170.2: 2002, Structural design actions part 2: wind actions[S]. Sydeney: Standards Australia International Ltd, 2002. [4] Russell L B. Probability distributions for Texas Gulf coast hurricane effects of engineering interest[D]. Stanford, CA: Stanford University, 1969. [5] Russell L R. Probability distributions for hurricane effects[J]. Journal of the Waterways, Harbors and Coastal Engineering Division, 1971, 97(1): 139−154. [6] Batts M E, Simiu E, Russell L R. Hurricane wind speeds in the United States[J]. Journal of the Structural Division, 1980, 106(10): 2001−2016. [7] Shapiro L J. The asymmetric boundary layer flow under a translating hurricane[J]. Journal of the Atmospheric Sciences, 1983, 40(8): 1984−1998. doi: 10.1175/1520-0469(1983)040<1984:TABLFU>2.0.CO;2 [8] Georgiou P N. Design wind speeds in tropical cyclone-prone regions[D]. London, Ontario, Canada: Western University, 1986. [9] Vickery P J, Twisdale L A. Wind-field and filling models for hurricane wind-speed predictions[J]. Journal of Structural Engineering, 1995, 121(11): 1700−1709. doi: 10.1061/(ASCE)0733-9445(1995)121:11(1700) [10] Meng Yan, Matsui M, Hibi K. An analytical model for simulation of the wind field in a typhoon boundary layer[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 56(2/3): 291−310. [11] Simiu E, Scanlan R H. Wind Effects on Structures: Fundamentals and Applications to Design[M]. 3rd ed. New York: John Wiley & Sons, Inc., 1996. [12] Thompson E F, Cardone V J. Practical modeling of hurricane surface wind fields[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1996, 122(4): 195−205. doi: 10.1061/(ASCE)0733-950X(1996)122:4(195) [13] Vickery P J, Twisdale L A. Prediction of hurricane wind speeds in the United States[J]. Journal of Structural Engineering, 1995, 121(11): 1691−1699. doi: 10.1061/(ASCE)0733-9445(1995)121:11(1691) [14] Vickery P J, Skerlj P F, Twisdale L A. Simulation of hurricane risk in the U. S. using empirical track model[J]. Journal of Structural Engineering, 2000, 126(10): 1222−1237. doi: 10.1061/(ASCE)0733-9445(2000)126:10(1222) [15] Vickery P J, Wadhera D, Twisdale L A, et al. U. S. hurricane wind speed risk and uncertainty[J]. Journal of Structural Engineering, 2009, 135(3): 301−320. doi: 10.1061/(ASCE)0733-9445(2009)135:3(301) [16] Huang Zhigang, Rosowsky D V, Sparks P R. Hurricane simulation techniques for the evaluation of wind-speeds and expected insurance losses[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(7/8): 605−617. [17] James M K, Mason L B. Synthetic tropical cyclone database[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2005, 131(4): 181−192. doi: 10.1061/(ASCE)0733-950X(2005)131:4(181) [18] Emanuel K. Climate and tropical cyclone activity: a new model downscaling approach[J]. Journal of Climate, 2006, 19(19): 4797−4802. doi: 10.1175/JCLI3908.1 [19] Emanuel K, Ravela S, Vivant E, et al. A statistical deterministic approach to hurricane risk assessment[J]. Bulletin of the American Meteorological Society, 2006, 87(3): 299−314. doi: 10.1175/BAMS-87-3-299 [20] Hall T M, Jewson S. Statistical modelling of North Atlantic tropical cyclone tracks[J]. Tellus A: Dynamic Meteorology and Oceanography, 2007, 59(4): 486−498. doi: 10.1111/j.1600-0870.2007.00240.x [21] American Society of Civil Engineers. ASCE/SEI 7-10, Minimum design loads for buildings and other structures[S]. Reston, VA: ASCE, 2010. [22] Li Sihan, Hong H P. Observations on a hurricane wind hazard model used to map extreme hurricane wind speed[J]. Journal of Structural Engineering, 2015, 141(10): 04014238. doi: 10.1061/(ASCE)ST.1943-541X.0001217 [23] Vickery P J, Wadhera D. Statistical models of Holland pressure profile parameter and radius to maximum winds of hurricanes from flight-level pressure and H*Wind data[J]. Journal of Applied Meteorology and Climatology, 2008, 47(10): 2497−2517. doi: 10.1175/2008JAMC1837.1 [24] Vickery P J, Wadhera D, Powell M D, et al. A hurricane boundary layer and wind field model for use in engineering applications[J]. Journal of Applied Meteorology and Climatology, 2009, 48(2): 381−405. doi: 10.1175/2008JAMC1841.1 [25] Vickery P J. Simple empirical models for estimating the increase in the central pressure of tropical cyclones after landfall along the coastline of the United States[J]. Journal of Applied Meteorology, 2005, 44(12): 1807−1826. doi: 10.1175/JAM2310.1 [26] Mudd L, Wang Yue, Letchford C, et al. Assessing climate change impact on the U. S. east coast hurricane hazard: temperature, frequency, and track[J]. Natural Hazards Review, 2014, 15(3): 04014001. doi: 10.1061/(ASCE)NH.1527-6996.0000128 [27] Lee K H, Rosowsky D V. Synthetic hurricane wind speed records: development of a database for hazard analyses and risk studies[J]. Natural Hazards Review, 2007, 8(2): 23−34. doi: 10.1061/(ASCE)1527-6988(2007)8:2(23) [28] Rosowsky D V, Mudd L, Letchford C. Assessing climate change impact on the joint wind-rain hurricane hazard for the northeastern U. S. coastline[M]//Gardoni P, Murphy C, Rowell A. Risk Analysis of Natural Hazards: Interdisciplinary Challenges and Integrated Solutions. Heidelberg: Springer, 2016: 113−134. [29] Powell M, Soukup G, Cocke S, et al. State of Florida hurricane loss projection model: atmospheric science component[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2005, 93(8): 651−674. doi: 10.1016/j.jweia.2005.05.008 [30] Legg M R, Nozick L K, Davidson R A. Optimizing the selection of hazard-consistent probabilistic scenarios for long-term regional hurricane loss estimation[J]. Structural Safety, 2010, 32(1): 90−100. doi: 10.1016/j.strusafe.2009.08.002 [31] Apivatanagul P, Davidson R, Blanton B, et al. Long-term regional hurricane hazard analysis for wind and storm surge[J]. Coastal Engineering, 2011, 58(6): 499−509. doi: 10.1016/j.coastaleng.2011.01.015 [32] Pei Bin, Pang W, Testik F Y, et al. Mapping joint hurricane wind and surge hazards for Charleston, South Carolina[J]. Natural Hazards, 2014, 74(2): 375−403. doi: 10.1007/s11069-014-1185-5 [33] Li Sihan, Hong H P. Typhoon wind hazard estimation for China using an empirical track model[J]. Natural Hazards, 2016, 82(2): 1009−1029. doi: 10.1007/s11069-016-2231-2 [34] 欧进萍, 段忠东, 常亮. 中国东南沿海重点城市台风危险性分析[J]. 自然灾害学报, 2002, 11(4): 9−17. doi: 10.3969/j.issn.1004-4574.2002.04.002Ou Jinping, Duan Zhongdong, Chang Liang. Typhoon risk analysis for key coastal cities in southeast China[J]. Journal of Natural Disasters, 2002, 11(4): 9−17. doi: 10.3969/j.issn.1004-4574.2002.04.002 [35] Yasui H, Ohkuma T, Marukawa H, et al. Study on evaluation time in typhoon simulation based on Monte Carlo method[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(12/15): 1529−1540. [36] Counihan J. Adiabatic atmospheric boundary layers: a review and analysis of data from the period 1880–1972[J]. Atmospheric Environment, 1975, 9(10): 871−905. doi: 10.1016/0004-6981(75)90088-8 [37] Choi H, Kanda J. Characteristics of the vertical wind profile for wind load estimation[J]. Journal of Wind Engineering, 1990, 45: 23−43. [38] Matsui M, Ishihara T, Hibi K. Directional characteristics of probability distribution of extreme wind speeds by typhoon simulation[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(12/15): 1541−1553. [39] 谢汝强, 李利孝, 王艳华, 等. 广东省台风数值模拟与危险性分析[J]. 安徽建筑大学学报, 2015, 23(4): 51−55. doi: 10.11921/j.issn.2095-8382.20150411Xie Ruqiang, Li Lixiao, Wang Yanhua, et al. Typhoon wind numerical simulation and hazard analysis for Guangdong Province[J]. Journal of Anhui Jianzhu University, 2015, 23(4): 51−55. doi: 10.11921/j.issn.2095-8382.20150411 [40] Holland G J. An analytic model of the wind and pressure profiles in hurricanes[J]. Monthly Weather Review, 1980, 108(8): 1212−1218. doi: 10.1175/1520-0493(1980)108<1212:AAMOTW>2.0.CO;2 [41] Li Sihan, Hong H P. Use of historical best track data to estimate typhoon wind hazard at selected sites in China[J]. Natural Hazards, 2015, 76(2): 1395−1414. doi: 10.1007/s11069-014-1555-z [42] Hong H P, Li Sihan, Duan Z D. Typhoon wind hazard estimation and mapping for coastal region in mainland China[J]. Natural Hazards Review, 2016, 17(2): 04016001. doi: 10.1061/(ASCE)NH.1527-6996.0000210 [43] Darling R W R. Estimating probabilities of hurricane wind speeds using a large-scale empirical model[J]. Journal of Climate, 1991, 4(10): 1035−1046. doi: 10.1175/1520-0442(1991)004<1035:EPOHWS>2.0.CO;2 [44] Jarvinen B R, Neumann C J, Davis M A S. A tropical cyclone data tape for the North Atlantic Basin, 1886–1983: contents, limitations, and uses[R]. Miami, FL, USA: National Hurricane Center, 1984. [45] 中华人民共和国住房和城乡建设部. GB 50009–2012, 建筑结构荷载规范[S]. 北京: 中国建筑工业出版社, 2012.Ministry of Housing and Urban-Rural Construction of the People's Republic of China. GB 50009–2012, Load code for the design of building structures[S]. Beijing: China Architecture & Building Press, 2012. 期刊类型引用(6)
1. 黄铭枫，杜海，王卿，王立忠，卞荣，张华杰，赵梦石，郭一凡. 我国东南沿海城市和近海海域的台风极值风速预测. 建筑结构学报. 2024(05): 104-114 . 
百度学术2. 孙建鹏，吕冠军，黄文锋，赵健. 考虑大气环境影响的台风极值风速研究. 西安建筑科技大学学报(自然科学版). 2023(03): 342-349 . 百度学术3. 孔莉莎，张秀芝. 西北太平洋历史台风风场重建模型参数试验. 应用气象学报. 2022(01): 56-68 . 百度学术4. 杜诗嘉，郭创新，俞啸玲，赵福林，邢海青，方赟朋. 台风灾害下的弹性配电网研究综述与展望. 电力自动化设备. 2022(02): 176-186+209 . 百度学术5. 黄心裕，唐军，王晓宇. 基于Prophet算法的海南近海波浪长时段时序分析与预测. 海洋学报. 2022(04): 114-121 . 
本站查看6. 沈菲菲，闵锦忠，李泓，许冬梅，邢建勇，束艾青，宋丽欣. GPM微波成像仪资料同化对台风“麦德姆”路径预报的影响研究. 海洋学报. 2021(10): 124-136 . 本站查看其他类型引用(3)
-
下载:
百度学术
计量
- 文章访问数: 577
- HTML全文浏览量: 119
- PDF下载量: 80
- 被引次数: 9
