Physical properties of the seabed inversed based on Chirp data and the Biot-Stoll model in the northern continental slope of the South China Sea
-
摘要: 浅地层剖面是基于声学信号(频率在几百至几千赫兹)在沉积物中的传播得到可反映沉积地层结构的数据,海底反射系数与沉积物物理性质密切相关。Biot-Stoll声波传播理论模型可以预测海底沉积物的物理性质,构建反射系数等声学参数与物理参数之间的关系,但在不同的海域采用不同的参数所获得的效果不同。为此,本文基于南海北部陆坡海底表层沉积物的实测物理参数,利用Biot-Stoll模型建立研究区海底反射系数和沉积物物理性质之间的关系,结果表明模型计算值与样品实测值吻合度总体较好,偏差在0.1%~4.9%之间,并建立了频率3.5 kHz时海底反射系数与沉积物孔隙度、密度、平均粒径之间的关系方程,且方程拟合度较高,可决系数R2均大于0.99。在对典型Chirp剖面数据计算其海底反射系数的基础上,反演了海底表层沉积物的孔隙度、密度、颗粒平均粒径等物理性质,其中反演孔隙度、密度、平均粒径与实测孔隙度、密度、平均粒径相对误差均小于5%,结果与实测值基本相符,表明该反演方法在南海北部陆坡区的应用是可行的。
-
关键词:
- Chirp浅剖数据 /
- Biot-Stoll模型 /
- 海底反射系数 /
- 沉积物物理性质 /
- 南海北部陆坡
Abstract: Sub-bottom profile is based on the acoustic signal (frequency in hundreds to thousands Hz) in the sediment propagation to reflect the sedimentary formation structure. The seabed reflection coefficient is closely related to the sediments physical properties. The Biot-Stoll theoretical model can predict the physical properties of seabed sediments and establish the relationship between acoustic parameters such as reflection coefficient and physical parameters, but the results obtained by using different parameters in different sea areas are different. For this, this article is based on the measured sediments physical parameters in the northern slope of the South China Sea to establish the relationship between the reflection coefficient and the sediments physical parameters based on Biot-Stoll model. The results show that the calculated value of the model is in good agreement with the measured value of the sample, and the equation for the relationship between the bottom reflection coefficient and the porosity, density, mean grain size of sediments at a frequency of 3.5 kHz is established. The equation has a high fitting degree, and the determination coefficient R2 is all greater than 0.99. On the basis of calculating the seabed reflection coefficient by the typical Chirp profile data, the porosity, density and mean grain size of the sub-bottom sediments are inversed. The relative errors of the inversion porosity, density, mean grain size and the measured porosity, density, mean grain size are all less than 5%, and the results are basically consistent with the measured values, indicating that the inversion method is feasible in the northern continental slope area of the South China Sea. -
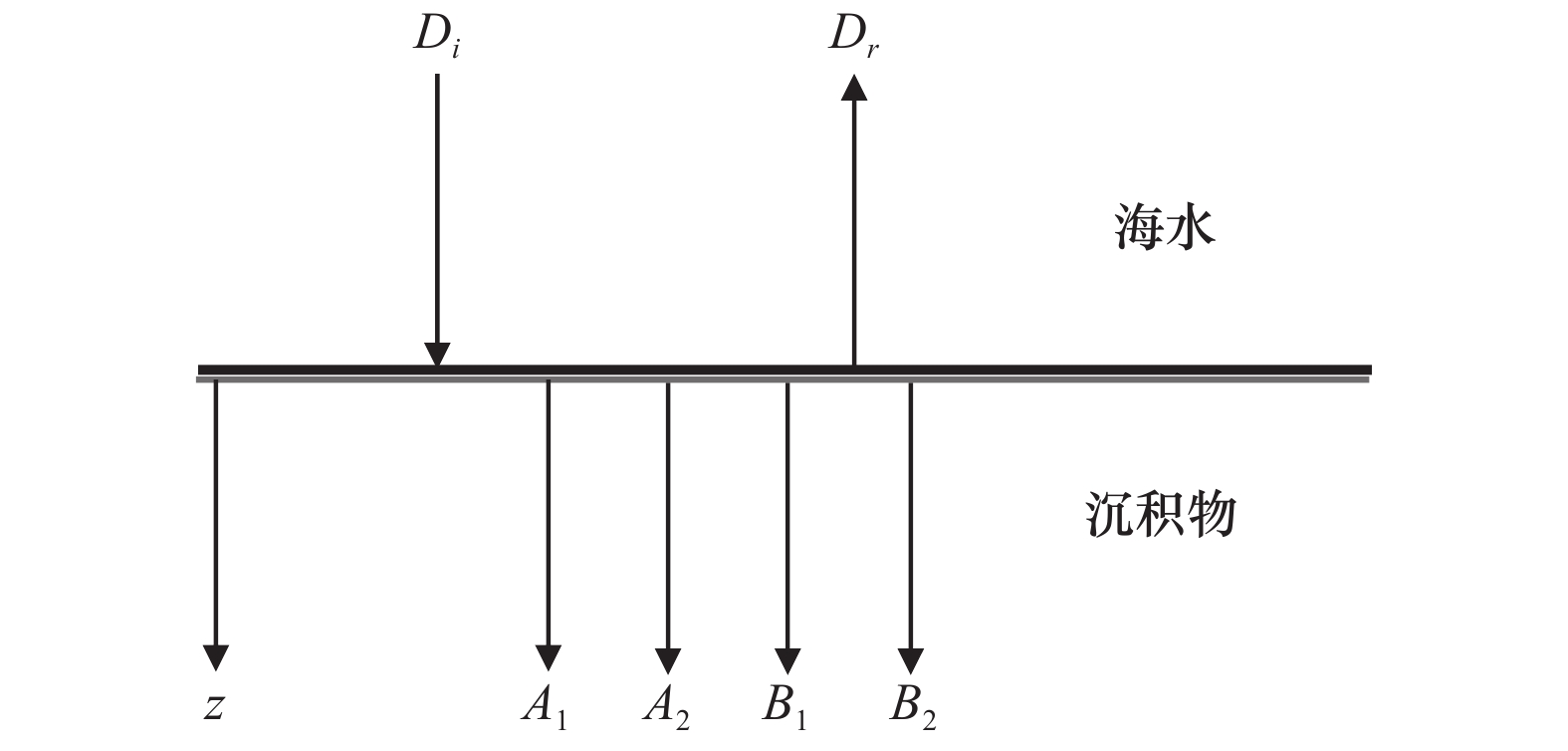
图 1 Biot参数计算反射系数的几何示意图(据文献[2])
${D_i}$和${D_r}$分别为入射波和反射波的复位移振幅值;${A_1}$和${A_2}$分别为沉积物骨架在快波和慢波作用下的复位移振幅值;${B_1}$和${B_2}$分别为快波和慢波作用下孔隙流体相对于骨架运动的复相对位移
Fig. 1 Geometric sketch of reflection coefficient calculated by Biot parameter (according to reference [2])
${D_i}$ and ${D_r}$ are the reset amplitude values of incident wave and reflected wave respectively; ${A_1}$ and ${A_2}$are the resetting amplitude of sediment skeleton under the action of fast wave and slow wave respectively; ${B_1}$ and ${B_2}$ are the complex relative displacement of pore fluid relative to skeleton motion under the action of fast wave and slow wave respectively
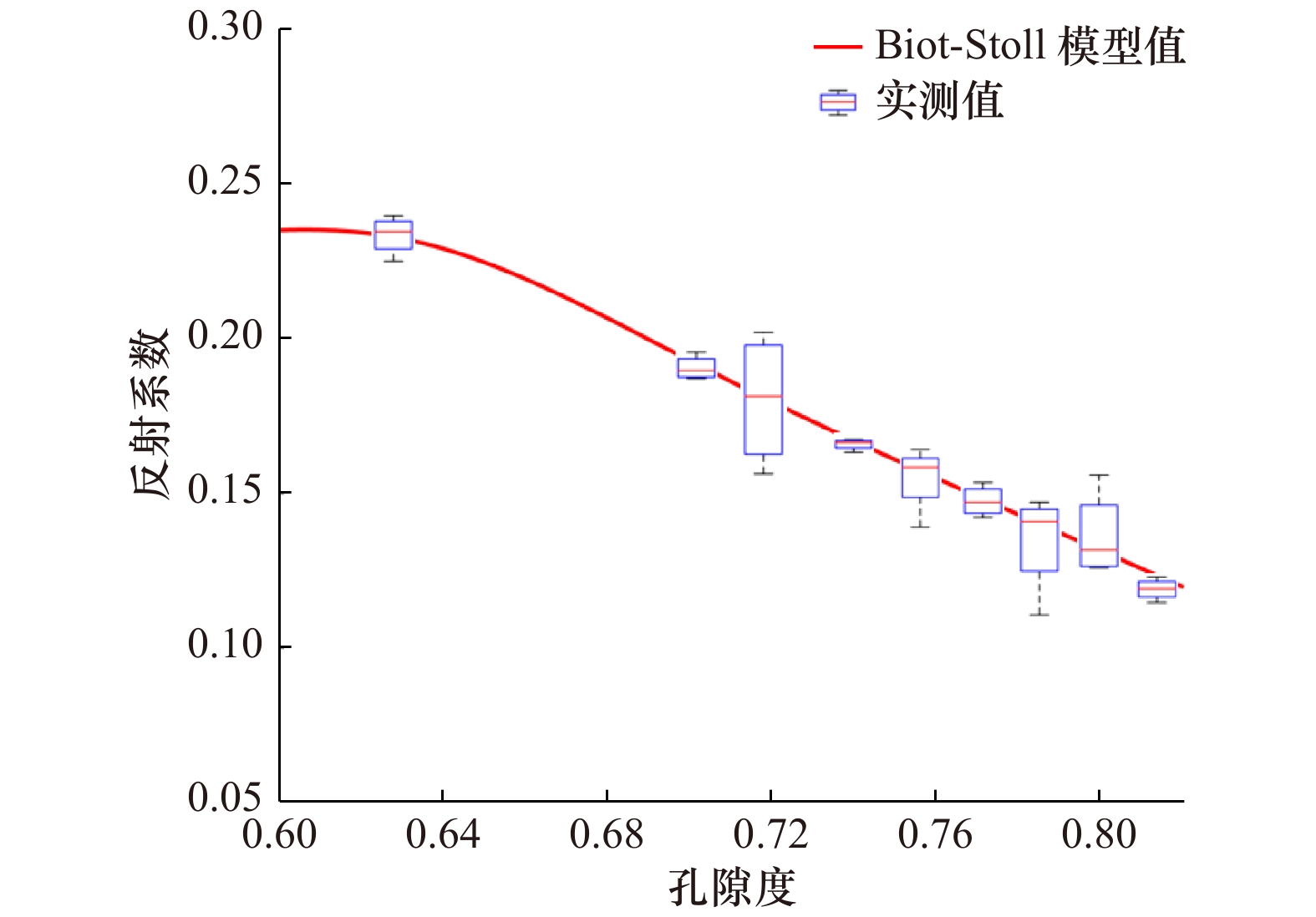
图 5 反射系数与孔隙度的关系
盒图为海底表层沉积物样品测试数据计算的反射系数;红色实线为Biot-Stoll模型计算的反射系数,样品测试频率与模型计算频率均为25 kHz
Fig. 5 The relationship between reflection coefficient and porosity
The boxplot is the reflection coefficient calculated from the test data of seabed surface sediment samples; the red solid line is the reflection coefficient calculated by the biot-stoll model, and the sample test frequency and model calculation frequency are both 25 kHz
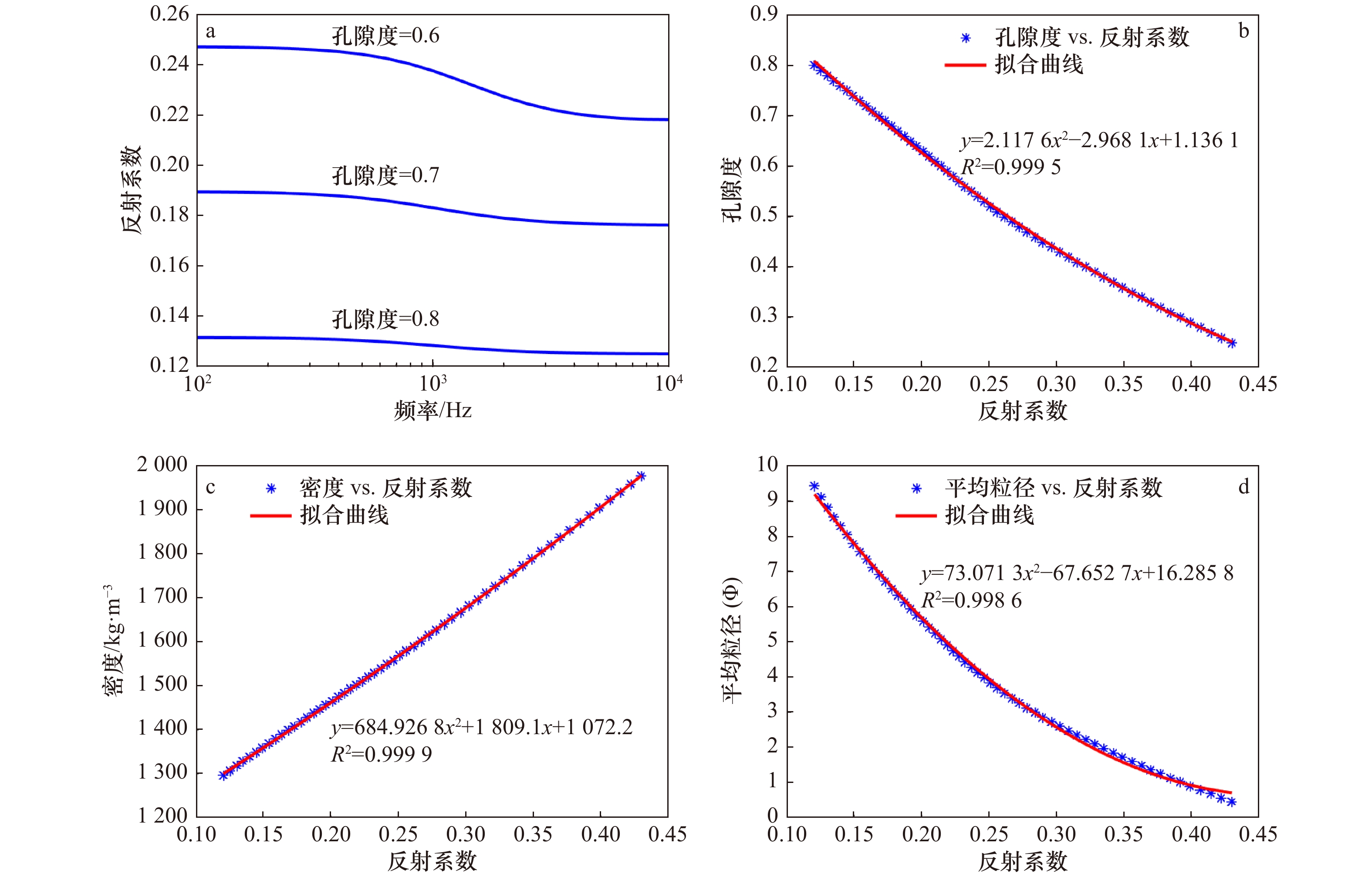
图 6 海底反射系数与沉积物物理性质的相关关系
a. 反射系数随频率的变化;b. 反射系数随孔隙度的变化(f=3.5 kHz);c. 反射系数随密度的变化(f=3.5 kHz);d. 反射系数随平均粒径的变化(f=3.5 kHz)
Fig. 6 Correlation between bottom reflection coefficients and sediment physical properties
a. Variation of reflection coefficient with frequency; b. variation of reflection coefficient with porosity (f = 3.5 kHz); c. variation of reflection coefficient with density (f = 3.5 kHz); d. variation of reflection coefficient with mean grain size (f = 3.5 kHz)
表 1 Biot-Stoll模型输入的沉积物物理参数
Tab. 1 The input sediment physical parameters of the Biot-Stoll model
参数 Biot-Stoll模型取值 颗粒密度${\rho _g}/ {\rm {kg\cdot{m^{-3}}}}$ 实测 孔隙度$n$ 实测 孔隙曲折度$\alpha $ $\alpha = \left\{ {\begin{aligned}& {\begin{array}{*{20}{c}} {1.35}&{\varphi \leqslant 4} \end{array}} \\ & {\begin{array}{*{20}{c}} {{\rm{ - }}0.3 + 0.412\;5\varphi }&{4 < \varphi < 8} \end{array}} \\ & {\begin{array}{*{20}{c}} {3.0}&{\varphi \geqslant 8} \end{array}} \end{aligned}} \right.\;\;\;\;\;\varphi = {\rm{ - lo}}{{\rm{g}}_2}d$,$\varphi $为中值粒径;d为颗粒直径,单位:mm 渗透率$\kappa /{\rm {m}^2}$ $\kappa = \dfrac{{{d^2}{n^3}}}{{180{{(1 - n)}^2}}}\dfrac{1}{{\sqrt {10} }}$ 海水动力黏度$\eta /{\rm {Pa}} \cdot {\rm s}$ 0.001 颗粒体积模量${K_g}/{\rm {Pa}}$ 3.2×1010 海水体积模量${K_w}/{\rm {Pa}}$ 2.395×109 海水密度${\rho _w}/ {\rm {kg\cdot{m^{-3}}}}$ 1 023 框架剪切模量${\mu _0}/{\rm {Pa}}$ ${\mu _0} = 1.835 \times {10^5}{\left(\dfrac{n}{{1 - n}}\right)^{ - 1.12}}\sqrt {{\tau _a}(z)} $${\tau _a}(z) = (1 - n)({\rho _s} - {\rho _f})gz$,${\tau _a}(z)$为沉积物平均有效压力,重力加速度$g = 9.8\;{\rm {m/{s^{ 2} } } }$,z为海底以下沉积物深度,单位:m,ρs为颗粒密度,ρf为孔隙流体密度 框架体积模量${K_0}/{\rm {Pa}}$ ${K_0} = \dfrac{{2{\mu _0}(1 + \sigma )}}{{3(1 - 2\sigma )}}$,$\sigma $为沉积物骨架的泊松比 孔隙大小$a$ $ a = \dfrac{d}{3}\cdot \dfrac{n}{{1 - n}} \cdot \dfrac{1}{{1.8}}$ 体积对数衰减${\delta _f}$ ${\delta _f}({z_s}) = {\delta _f}({z_0})\sqrt {{z_0}/{z_s}} $,z0,zs分别为浅表层和表层沉积物深度 表 2 Chirp子波相关参数
Tab. 2 The relevant parameters of Chirp wavelet
属性 子波特征 频带宽度 1 000~6 000 Hz 脉冲长度 5 ms 脉冲幅度 2.5 ms 采样间隔 13 µs 表 3 站位实测物理性质与反演结果对比
Tab. 3 Comparison between the measured physical properties and the inversion results
取样站位 表层沉积物类型 孔隙度 密度/kg·m−3 平均粒径(Φ) 实测值 反演值 相对误差/% 实测值 反演值 相对误差/% 实测值 反演值 相对误差/% GLW3101 粉砂质黏土 0.651 0.645 −0.92 1 440 1 450 0.69 5.5 5.7 3.63 GLW3102 粉砂质黏土 0.747 0.738 −1.20 1 368 1 374 0.43 6.2 6.5 4.84 GLW3103 粉砂质黏土 0.783 0.758 −3.19 1 350 1 343 −0.52 8.3 8.2 −1.20 GLW3105 粉砂质黏土 0.798 0.792 −0.75 1 310 1 306 −0.31 8.4 8.6 2.38 GLW3108 黏土 0.806 0.812 0.74 1 290 1 303 1.01 8.7 9.1 4.60 注:Φ=−log2d,d为颗粒粒径,单位: mm。 -
[1] 何起祥. 中国海洋沉积地质学[M]. 北京: 海洋出版社, 2006.He Qixing. Marine Sedimentary Geology of China[M]. Beijing: China Ocean press, 2006. [2] Schock S G. A method for estimating the physical and acoustic properties of the sea bed using chirp sonar data[J]. IEEE Journal of Oceanic Engineering, 2004, 29(4): 1200−1217. doi: 10.1109/JOE.2004.841421 [3] Schock S G. Remote estimates of physical and acoustic sediment properties in the South China Sea using chirp sonar data and the biot model[J]. IEEE Journal of Oceanic Engineering, 2004, 29(4): 1218−1230. doi: 10.1109/JOE.2004.842253 [4] 曹正良, 张叔英, 马在田. BICSQS模型与Biot-Stoll模型海底界面声波反射和散射的比较[J]. 声学学报, 2006, 31(5): 389−398. doi: 10.3321/j.issn:0371-0025.2006.05.002Cao Zhengliang, Zhang Shuying, Ma Zaitian. Comparison of reflections and interface scatterings from BICSQS model and Biot-Stoll model seafloors[J]. Acta Acustica, 2006, 31(5): 389−398. doi: 10.3321/j.issn:0371-0025.2006.05.002 [5] 朱祖扬, 王东, 周建平, 等. 基于非饱和Biot-Stoll模型的海底沉积物介质声频散特性研究[J]. 地球物理学报, 2012, 55(1): 180−188. doi: 10.6038/j.issn.0001-5733.2012.01.017Zhu Zuyang, Wang Dong, Zhou Jianping, et al. Acoustic wave dispersion and attenuation in marine sediment based on partially gas-saturated Biot-Stoll model[J]. Chinese Journal of Geophysics, 2012, 55(1): 180−188. doi: 10.6038/j.issn.0001-5733.2012.01.017 [6] 陈静, 阎贫, 王彦林, 等. 基于Biot-Stoll模型声速反演中的参数选择——以南海南部沉积物为例[J]. 热带海洋学报, 2012, 31(1): 50−54.Chen Jing, Yan Pin, Wang Yanlin, et al. Choice of parameters for Biot-Stoll model-based inversion of sound velocity of seafloor sediments in the southern South China Sea[J]. Journal of Tropical Oceanography, 2012, 31(1): 50−54. [7] 王景强, 郭常升, 刘保华, 等. 基于Buckingham模型和Biot-Stoll模型的南沙海域沉积物声速分布特征[J]. 地球学报, 2016, 37(3): 359−367. doi: 10.3975/cagsb.2016.03.13Wang Jingqiang, Guo Changsheng, Liu Baohua, et al. Sound speed distribution of seafloor sediments in Nansha Islands sea based on Buckingham model and Biot-Stoll model[J]. Acta Geoscientica Sinica, 2016, 37(3): 359−367. doi: 10.3975/cagsb.2016.03.13 [8] 陶春辉. 海底沉积物声学原位测试和特性研究[D]. 杭州: 浙江大学, 2005.Tao Chunhui. In situ acoustic experiment and properties study in marine sediments[D]. Hangzhou: Zhejiang University, 2005. [9] 陈静, 吕修亚, 陈亮, 等. 基于Chirp数据反演琼州海峡海底沉积物物性[J]. 热带地理, 2017, 37(6): 874−879.Chen Jing, Lü Xiuya, Chen Liang, et al. Physical properties of the seabed inversed by chirp data in the Qiongzhou Strait[J]. Tropical Geography, 2017, 37(6): 874−879. [10] Velis D R. Stochastic sparse-spike deconvolution[J]. Geophysics, 2008, 73(1): 1−9. [11] Puryear C I, Castagna J P. Layer-thickness determination and stratigraphic interpretation using spectral inversion: Theory and application[J]. Geophysics, 2008, 73(2): R37−R48. doi: 10.1190/1.2838274 [12] Zhang Rui, Castagna J. Seismic sparse-layer reflectivity inversion using basis pursuit decomposition[J]. Geophysics, 2011, 76(6): R147−R158. doi: 10.1190/geo2011-0103.1 [13] Yuan Sanyi, Wang Shangxu. Spectral sparse Bayesian learning reflectivity inversion[J]. Geophysical Prospecting, 2013, 61(4): 735−746. doi: 10.1111/1365-2478.12000 [14] Li X S, Zhou Q J, Su T Y, et al. Slope-confined submarine canyons in the Baiyun deep-water area, northern South China Sea: variation in their modern morphology[J]. Marine Geophysical Research, 2016(2): 95−112. [15] 丁巍伟, 黎明碧, 何敏, 等. 南海中北部陆架-陆坡区新生代构造-沉积演化[J]. 高校地质学报, 2009, 15(3): 339−350. doi: 10.3969/j.issn.1006-7493.2009.03.006Ding Weiwei, Li Mingbi, He Min, et al. Cenozoic tectono-sedimentary evolution in the middle part of northern continental shelf-slope region, South China Sea[J]. Geological Journal of China Universities, 2009, 15(3): 339−350. doi: 10.3969/j.issn.1006-7493.2009.03.006 [16] Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range[J]. The Journal of the Acoustical Society of America, 1956, 28(2): 168−178. doi: 10.1121/1.1908239 [17] Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. Ⅱ. Higher frequency range[J]. The Journal of the Acoustical Society of America, 1956, 28(2): 179−191. doi: 10.1121/1.1908241 [18] Stoll R D. Acoustic waves in saturated sediments[M]//Hampton L. Physics of Sound in Marine Sediments. Boston, MA: Springer, 1974: 19−39. [19] 朱林, 傅命佐, 刘乐军, 等. 南海北部白云凹陷陆坡海底峡谷地形地貌与沉积地层特征[J]. 海洋地质与第四纪地质, 2014, 34(2): 1−9.Zhu Lin, Fu Mingzuo, Liu Lejun, et al. Canyon morphology and sediments on northern slope of the Baiyun Sag[J]. Marine Geology & Quaternary Geology, 2014, 34(2): 1−9. [20] 周庆杰, 李西双, 徐元芹, 等. 一种基于水深梯度原理的海底滑坡快速识别方法——以南海北部陆坡白云深水区为例[J]. 海洋学报, 2017, 39(1): 138−147.Zhou Qingjie, Li Xishuang, Xu Yuanqin, et al. A rapid method to recognize submarine landslides based on the principle of water depth gradient: A case of Baiyun deep-water area, north slope of the South China Sea[J]. Haiyang Xuebao, 2017, 39(1): 138−147. [21] 秦蕴珊. 中国陆棚海的地形及沉积类型的初步研究[J]. 海洋与湖沼, 1963, 5(1): 71−85.Qin Yunshan. A preliminary study on the topography and sedimentary types of continental shelf seas in China[J]. Oceanologia et Limnologia Sinica, 1963, 5(1): 71−85. [22] 杨涛, 薛紫晨, 杨竞红, 等. 南海北部地区海洋沉积物中孔隙水的氢、氧同位素组成特征[J]. 地球学报, 2003, 24(6): 511−514. doi: 10.3321/j.issn:1006-3021.2003.06.005Yang Tao, Xue Zichen, Yang Jinghong, et al. Oxygen and hydrogen isotopic compositions of pore water from marine sediments in the northern South China Sea[J]. Acta Geoscientica Sinica, 2003, 24(6): 511−514. doi: 10.3321/j.issn:1006-3021.2003.06.005 [23] 卢博. 东沙群岛海域沉积物及其物理学性质的研究[J]. 海洋学报, 1996, 18(6): 82−89.Lu Bo. Study on sediments and their physical properties in the waters of Dongsha Islands[J]. Haiyang Xuebao, 1996, 18(6): 82−89. [24] 李傲仙, 李延河, 乐国良. 深海沉积物中碲异常的成因[J]. 地球学报, 2005, 26(S1): 186−189.Li Aoxian, Li Yanhe, Le Guoliang. The cause for tellurium enrichment in deep-sea sediments[J]. Acta Geoscientica Sinica, 2005, 26(S1): 186−189. [25] Liu Jianguo, Xiang Rong, Chen Zhong, et al. Sources, transport and deposition of surface sediments from the South China Sea[J]. Deep Sea Research Part I: Oceanographic Research Papers, 2013, 71: 92−102. doi: 10.1016/j.dsr.2012.09.006 [26] Zhao Hongquan, Jian Zhimin, Li Baohua, et al. Microtektites in the Middle Pleistocene deep-sea sediments of the South China Sea[J]. Science in China Series D: Earth Sciences, 1999, 42(5): 531−535. doi: 10.1007/BF02875247 [27] 业治铮, 何起祥, 张明书, 等. 西沙石岛晚更新世风成生物砂屑灰岩的沉积构造和相模式[J]. 沉积学报, 1985, 3(1): 1−15.Ye Zhizheng, He Qixiang, Zhang Mingshu, et al. Sedimentary structure and facies pattern of bioarenaceous limestone in late pleistocene of Xisha Shidao[J]. Acta Sedimentologica Sinica, 1985, 3(1): 1−15. [28] 刘乐军, 傅命佐, 李家钢, 等. 荔湾3-1气田海底管道深水段地质灾害特征[J]. 海洋科学进展, 2014, 32(2): 162−174. doi: 10.3969/j.issn.1671-6647.2014.02.006Liu Lejun, Fu Mingzuo, Li Jiagang, et al. Geologic hazards in the deep pipeline routing area of the Liwan 3-1 Gas Field in the South China Sea[J]. Advances in Marine Science, 2014, 32(2): 162−174. doi: 10.3969/j.issn.1671-6647.2014.02.006 [29] Zhou Qingjie, Li Xishuang, Zhou Hang, et al. Characteristics and genetic analysis of submarine landslides in the northern slope of the South China Sea[J]. Marine Geophysical Research, 2018, 40(3): 303−314. [30] 卢博, 李赶先, 黄韶健, 等. 中国黄海、东海和南海北部海底浅层沉积物声学物理性质之比较[J]. 海洋技术, 2005, 24(2): 28−33. doi: 10.3969/j.issn.1003-2029.2005.02.008Lu Bo, Li Ganxian, Huang Shaojian, et al. The comparing of seabed sediment acoustic-physical properties in the Yellow Sea, the East China Sea and northern the South China Sea[J]. Ocean Technology, 2005, 24(2): 28−33. doi: 10.3969/j.issn.1003-2029.2005.02.008 [31] 黄绪德. 计算机在地学中的应用[J]. 物探化探计算技术, 1991, 13(2): 93−97.Huang Xude. Computer applications to geoscience[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1991, 13(2): 93−97. [32] 刘财, 刘洋, 王典, 等. 一种频域吸收衰减补偿方法[J]. 石油物探, 2005, 44(2): 116−118. doi: 10.3969/j.issn.1000-1441.2005.02.005Liu Cai, Liu Yang, Wang Dian, et al. A method to compensate strata absorption and attenuation in frequency domain[J]. Geophysical Prospecting for Petroleum, 2005, 44(2): 116−118. doi: 10.3969/j.issn.1000-1441.2005.02.005 [33] 张志军, 周东红, 孙成禹, 等. 基于三维模型数据的地震振幅补偿处理技术的保幅性分析[J]. 物探与化探, 2015, 39(3): 621−626. doi: 10.11720/wtyht.2015.3.32Zhang Zhijun, Zhou Donghong, Sun Chengyu, et al. An analysis of the amplitude preservation of seismic amplitude compensation processing technology based on 3D model data[J]. Geophysical and Geochemical Exploration, 2015, 39(3): 621−626. doi: 10.11720/wtyht.2015.3.32 [34] Park C, Kim W, Shin J, et al. Study on acoustic impedance conversion using an optimal chirplet analyzed in chirp SBP raw data[J]. Marine Geophysical Research, 2019, 40(3): 385−393. doi: 10.1007/s11001-019-09377-7 [35] 赵利, 彭学超, 钟和贤, 等. 南海北部陆架区表层沉积物粒度特征与沉积环境[J]. 海洋地质与第四纪, 2016, 36(6): 111−122.Zhao Li, Peng Xuechao, Zhong Hexian, et al. Characteristics of grain size distribution of surface sediments and depositional environments in the northern shelf region of the South China Sea[J]. Marine Geology & Quaternary Geology, 2016, 36(6): 111−122. -




 下载:
下载: