Effects of seasonal environmental variation on surface acoustic localization in the half convergence zone area of deep sea
-
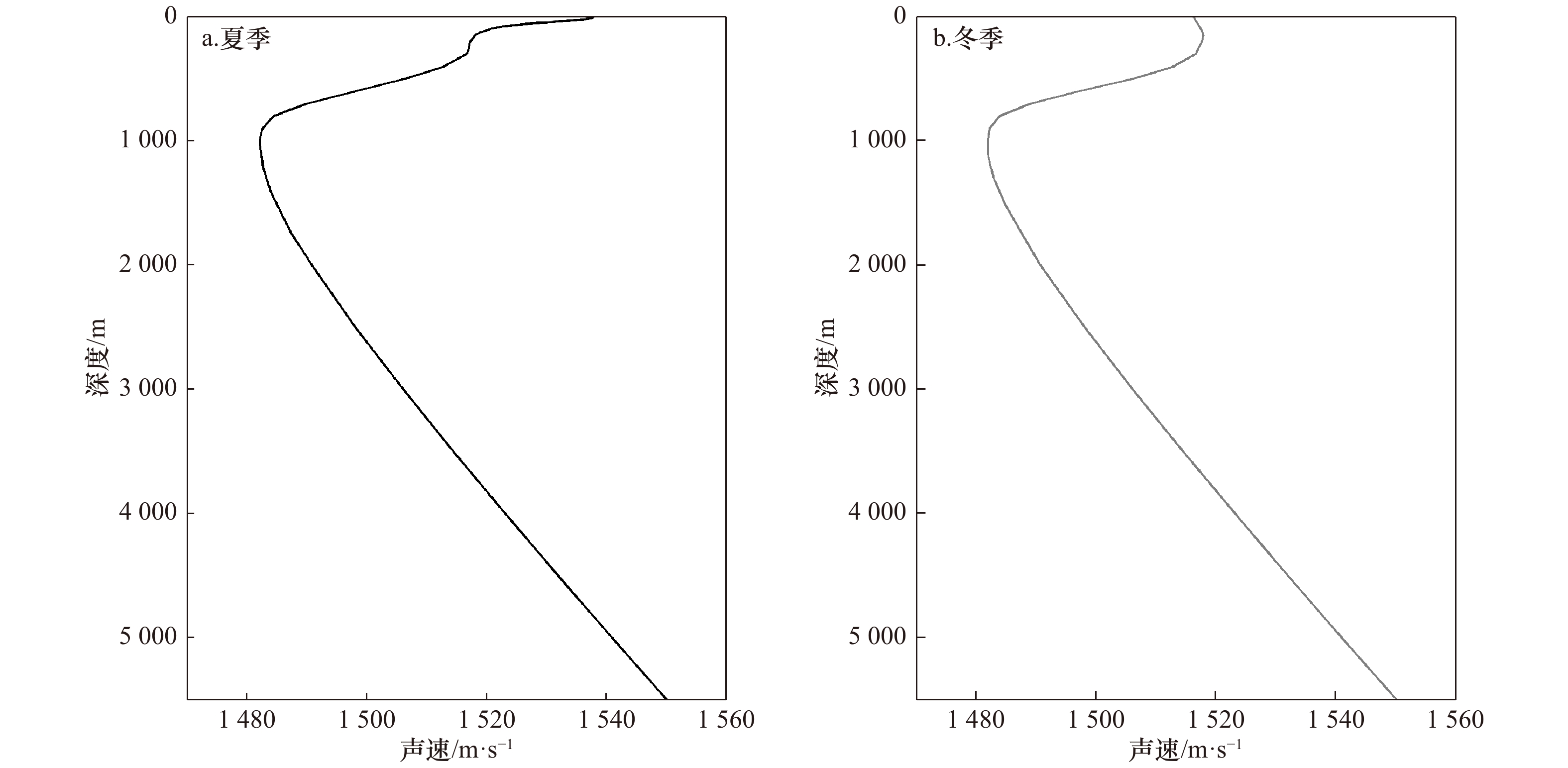
摘要: 针对深海声定位受海洋环境变化影响明显、需考虑测量系统的环境适应性和宽容性设计问题,提出一种评估海水环境变化对定位性能影响的仿真分析方法,将声场计算、误差传播与交会解算联合建模,以西太平洋中纬度海域夏季和冬季环境为代表性场景讨论了季节性环境变化对定位性能的影响方式和影响程度。仿真结果表明,当接收器位于海洋近表层时,在夏季和冬季呈现出两种不同的声信道样式,夏季季节性温跃层影响下的定位精度较差,冬季表面波导影响下的定位精度相对较好,两者均方根误差(RMSE)相差超过50 m;当接收器位于海洋中上层时,直达波有效作用范围的季节性变化引起定位性能差异,冬季定位精度优于夏季,两者RMSE相差15~20 m;当接收器位于海洋近底层时,利用可靠声路径定位精度较高,定位性能季节性变化不明显。研究认为,海水的季节性环境变化能够改变半会聚区尺度水面声定位的声信道特性以及到达声信息、误差传播、交会求解等测量因素,进而对接收深度位于海洋上层的声定位性能产生明显影响。Abstract: To recognize the environmental effects on underwater acoustic localization in deep sea and improve the measurement system performance against environmental variations, an simulation method for localization performance evaluation under different oceanographic conditions was presented, in which the sound filed calculation, error propagation and crossing solution were integrated by modelling, and the effects of seasonal environmental variation on localization performance were discussed in the case of Western Pacific. According to simulation results, when the receiving depth was near the surface, the sound channel showed different models in summer and winter, such that the accuracy was worse in summer influnced by seasonal thermocline and better in winter influnced by surface duct, the difference of root mean square error (RMSE) beyond 50 m; when the receiving depth was in the upper ocean, the localization performance had an obviously seasonal change caused by the active range of direct wave, and the accuracy was better in winter than that in summer, the difference of RMSE was 15−20 m; when the receiving depth was near the bottom, the better accuracy was obtained using reliable acoustic path, and the localization performance had little change with season. This work indicates that the seasonal environmental variation induces differences in the sound channel as well as the arrival acoustic information, the error propagation and crossing solution for the localization in the half convergence zone area of deep sea, then exert significant effects on localization performance as the receiving depth in the upper ocean.
-
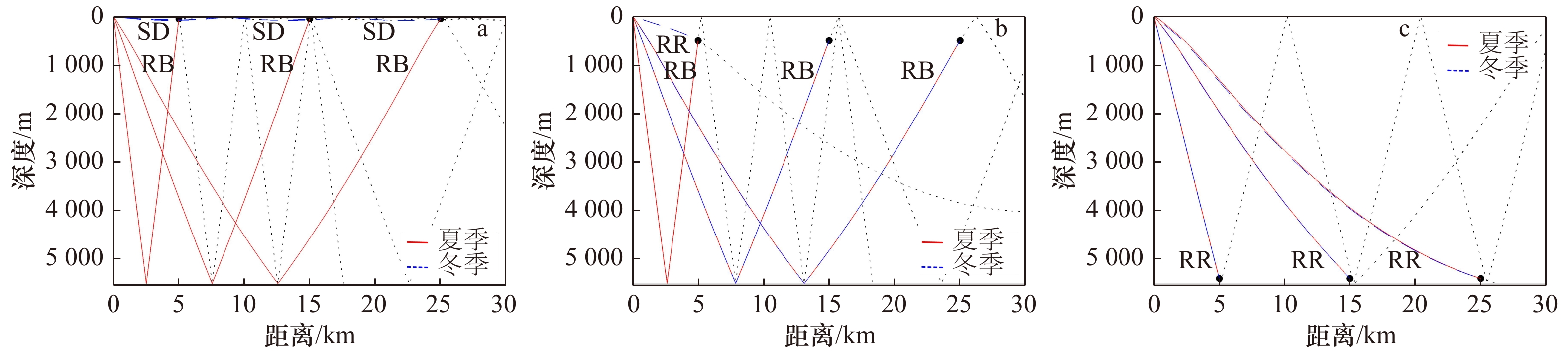
图 5 不同接收深度条件下的本征声线比较
a. RD=50 m,b. RD=500 m,c. RD=5 400 m;RR. 直达波声路径,RB. 一次海底反射波声路径,SD. 表面波导声路径;点线表示声路径到达接收器之后的部分
Fig. 5 Comparison of eigen-rays in different receiving depth
a. RD=50 m, b. RD=500 m, c. RD=5 400 m; RR. Direct wave ray path, RB: seabed first-reflected wave ray path, SD: surface duct ray path; the dotted line denotes the ray paths after receivers
图 6 不同接收深度条件下的信噪比随距离变化曲线比较
a. RD=50 m,b. RD=500 m,c. RD=5 400 m;RR. 直达波声路径,RB. 一次海底反射波声路径,SD. 表面波导声路径;信噪比为10 dB的虚线表示检测阈
Fig. 6 Comparison of signal to noise ratio curve with range under different receiving depth conditions
a. RD=50 m, b. RD=500 m, c. RD=5 400 m; RR. Direct wave ray path, RB. seabed first-reflected wave ray path, SD. surface duct ray path; the dotted line denotes the detection threshold of signal to noise ratio is 10 dB
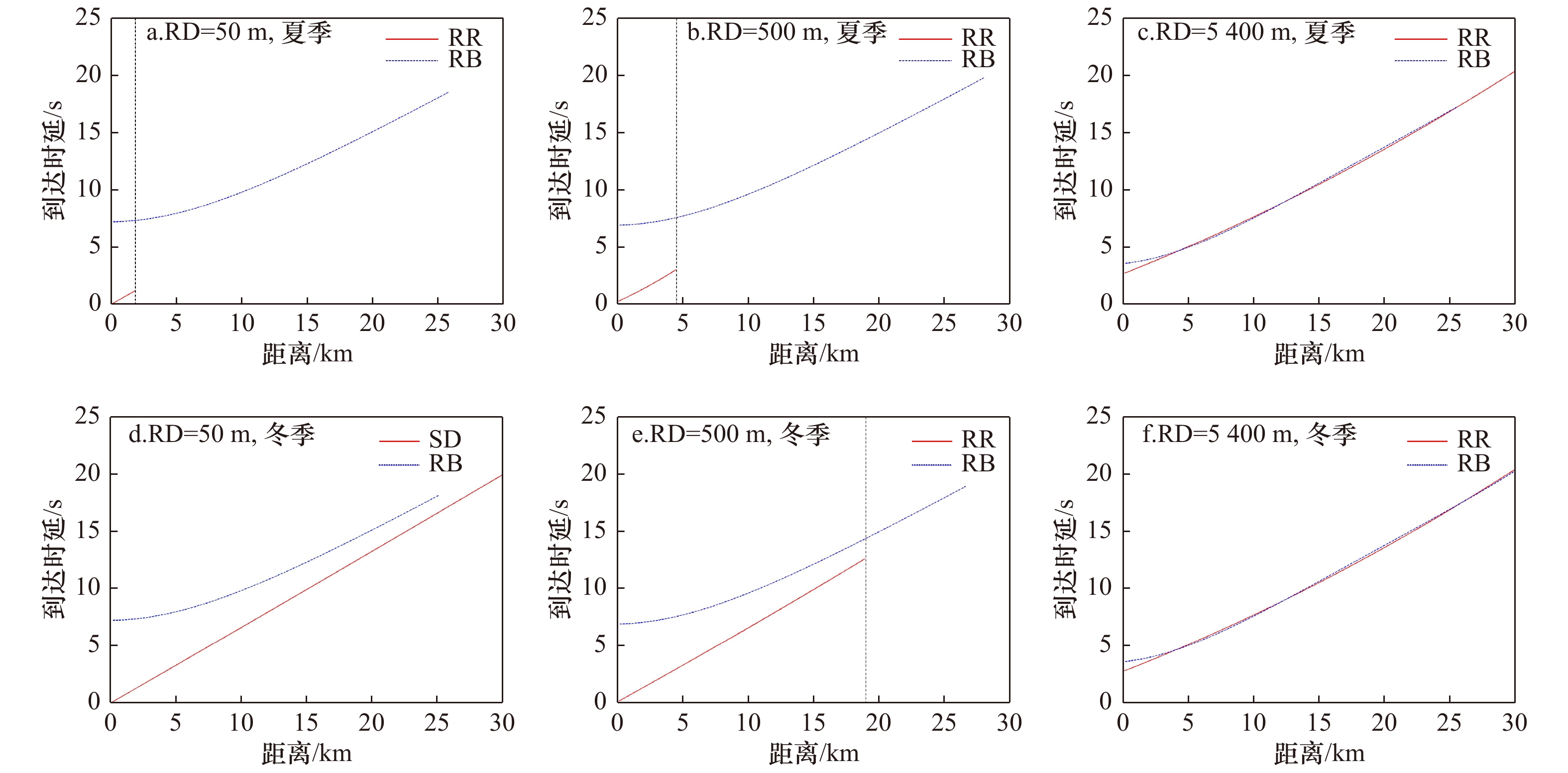
图 7 不同接收深度条件下的到达时延随距离变化曲线比较
RR. 直达波声路径,RB. 一次海底反射波声路径,SD. 表面波导声路径;垂向虚线位置表示直达波作用距离边界
Fig. 7 Comparison of time delay curve with range under different receiving depth conditions
RR. Direct wave ray path, RB. seabed first-reflected wave ray path, SD. surface duct ray path; the dotted line in vertical denotes the maximum active range of direct waves
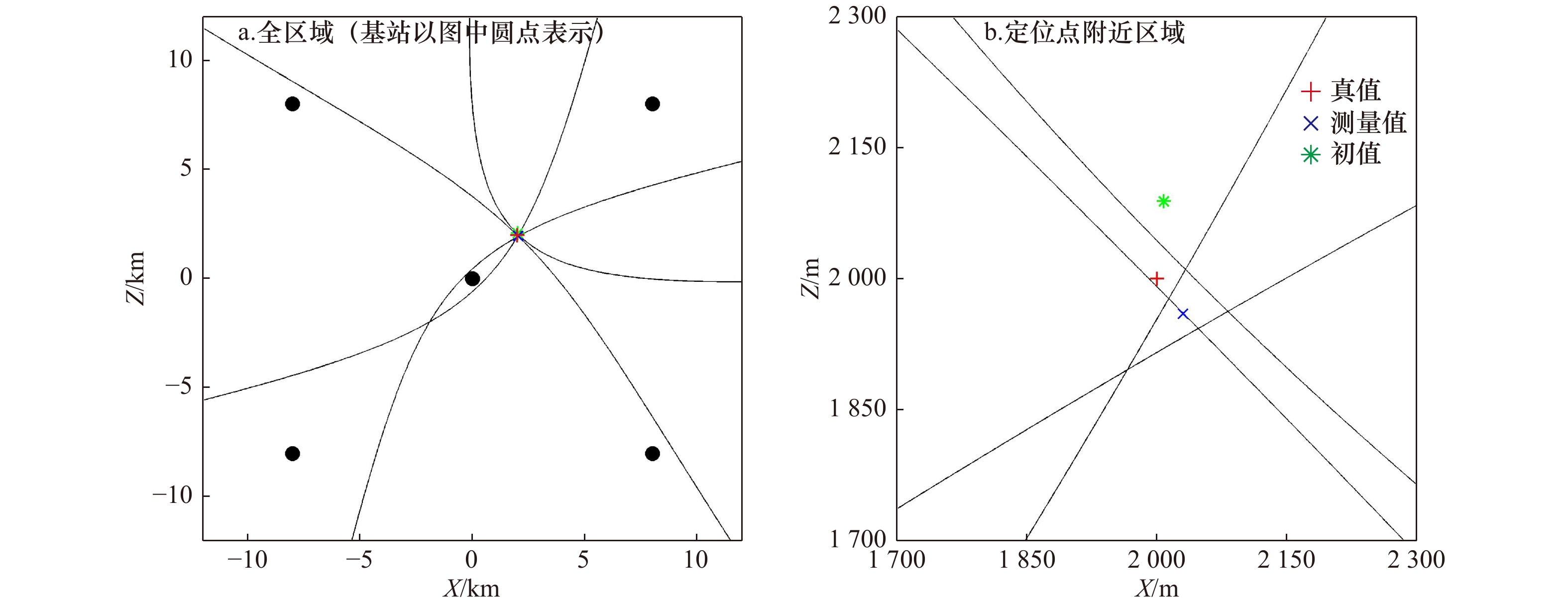
图 8 夏季和冬季信噪比水平分布比较
目标位于X=2 km,Z=2 km处,由黑色三角形表示;基站位置由黑色正方形表示;测量区域由虚线表示;直达波作用距离由圆型实线表示
Fig. 8 Comparison of signal to noise ratio horizontal distribution in summer and winter
The target locates at X=2 km, Z=2 km, marked by black triangle; the base stations are marked by black square; the test sea area is marked by dashed line; the active range of direct wave is marked by circular full line
表 1 不同接收深度夏季和冬季环境下的RMSE比较
Tab. 1 Comparison of RMSE in different receiving depth under summer and winter environment
接收深度 季节 未迭加站址误差 迭加站址误差 RMSE的X分量/m RMSE的Z分量/m RMSE/m RMSE的X分量/m RMSE的Z分量/m RMSE/m RD=50 m 夏季 59.3 59.5 84.0 59.7 60.5 85.1 冬季 23.0 23.0 32.5 23.1 23.1 32.7 RD=500 m 夏季 27.9 28.0 39.6 28.2 28.4 40.0 冬季 14.9 14.7 20.9 15.3 15.3 21.6 RD=5 400 m 夏季 8.2 8.1 11.5 20.2 20.1 28.5 冬季 8.3 8.1 11.6 20.1 20.0 28.3 表 2 目标声信号到达各基站参数比较(真值)
Tab. 2 Comparison of arrival parameters to each base station (the truth value)
接收深度 季节 参数类型 1#基站 2#基站 3#基站 4#基站 5#基站 RD=50 m 夏季 本征声线类型 RB RB RB RB RB 到达时延/s 7.27 10.69 11.85 10.69 9.33 冬季 本征声线类型 SD SD SD SD SD 到达时延/s 1.87 7.70 9.35 7.70 5.60 RD=500 m 夏季 本征声线类型 RR RB RB RB RB 到达时延/s 1.88 10.53 11.70 10.53 9.17 冬季 本征声线类型 RR RR RR RR RR 到达时延/s 1.92 7.70 9.37 7.70 5.60 RD=5 400 m 夏季 本征声线类型 RR RR RR RR RR 到达时延/s 3.99 8.58 10.00 8.58 6.85 冬季 本征声线类型 RR RR RR RR RR 到达时延/s 4.03 8.58 10.00 8.58 6.86 -
[1] 鲍筱玲, 汤渭霖. 击水声特性研究[J]. 哈尔滨船舶工程学院学报, 1981(1): 27−39.Bao Xiaoling, Tang Weilin. Investigations of the impact noise[J]. Journal of Harbin Shipbuilding Engineering Institute, 1981(1): 27−39. [2] 李关防, 赵安邦, 惠俊英, 等. 基于经验模态分解的物体入水声检测及测向研究[J]. 声学学报, 2008, 33(6): 548−554. doi: 10.3321/j.issn:0371-0025.2008.06.010Li Guanfang, Zhao Anbang, Hui Junying, et al. Research on detection and azimuth estimation for the splash sound for target's water entry based on empirical mode decomposition[J]. Acta Acustica, 2008, 33(6): 548−554. doi: 10.3321/j.issn:0371-0025.2008.06.010 [3] 刘德耀, 陈志菲, 郭心伟, 等. 基于声学传感网络的弹着点定位系统[J]. 弹道学报, 2017, 29(2): 85−89. doi: 10.3969/j.issn.1004-499X.2017.02.014Liu Deyao, Chen Zhifei, Guo Xinwei, et al. Measurement system for projectile impact-points based on acoustic sensor network[J]. Journal of Ballistics, 2017, 29(2): 85−89. doi: 10.3969/j.issn.1004-499X.2017.02.014 [4] 张玉涛, 薛飞, 李鹏. 火箭助飞鱼雷海上落点测控系统测量误差分析[J]. 鱼雷技术, 2012, 20(5): 392−395.Zhang Yutao, Xue Fei, Li Peng. Error analysis of measuring water entry point for rocket-assisted torpedo[J]. Torpedo Technology, 2012, 20(5): 392−395. [5] Ainslie M A. 声呐性能建模原理[M]. 张静远, 颜冰, 译. 北京: 国防工业出版社, 2015: 468-473.Ainslie M A. Principles of Sonar Performance Modeling[M]. Zhang Jingyuan, Yan Bing, trans. Beijing: National Defense Industry Press, 2015: 468−473. [6] Voronovich A G, Ostashev V E, Group T N, et al. Horizontal refraction of acoustic signals retrieved from North Pacific Acoustic Laboratory billboard array data[J]. The Journal of the Acoustical Society of America, 2005, 117(3): 1527−1537. doi: 10.1121/1.1854435 [7] Colosi J A, Baggeroer A B, Cornuelle B D, et al. Analysis of multipath acoustic field variability and coherence in the finale of broadband basin-scale transmissions in the North Pacific Ocean[J]. The Journal of the Acoustical Society of America, 2005, 117(3): 1538−1564. doi: 10.1121/1.1854615 [8] Sagers J D, Ballard M S, Knobles, D P. Evidence of three-dimensional acoustic propagation in the Catoche Tongue[J]. The Journal of the Acoustical Society of America, 2014, 136(5): 2453−2462. doi: 10.1121/1.4896469 [9] Heaney K D, Campbell R L. Three-dimensional parabolic equation modeling of mesoscale eddy deflection[J]. The Journal of the Acoustical Society of America, 2016, 139(2): 918−926. doi: 10.1121/1.4942112 [10] Dushaw B D, Sagen H, Besszczynska-Möller A. On the effects of small-scale variability on acoustic propagation in Fram Strait: The tomography forward problem[J]. The Journal of the Acoustical Society of America, 2016, 140(2): 1286−1299. doi: 10.1121/1.4961207 [11] 李整林, 张仁和, 鄢锦, 等. 大陆斜坡海域宽带声源的匹配场定位[J]. 声学学报, 2003, 28(5): 425−428. doi: 10.3321/j.issn:0371-0025.2003.05.008Li Zhenglin, Zhang Renhe, Yan Jin, et al. Broadband matched-field source localization in the continental slope environment[J]. Acta Acustica, 2003, 28(5): 425−428. doi: 10.3321/j.issn:0371-0025.2003.05.008 [12] Li Wen, Li Zhenglin, Zhang Renhe, et al. The effects of seamounts on sound propagation in deep water[J]. Chinese Physics Letters, 2015, 32(6): 064302. doi: 10.1088/0256-307X/32/6/064302 [13] 胡治国, 李整林, 张仁和, 等. 深海不平海底对声场水平纵向相关性的影响[J]. 声学学报, 2016, 41(5): 758−767.Hu Zhiguo, Li Zhenglin, Zhang Renhe, et al. The effects of the uneven bottom on horizontal longitudinal correlations of acoustic field in deep water[J]. Acta Acustica, 2016, 41(5): 758−767. [14] 胡治国, 李整林, 秦继兴, 等. 深海海底斜坡环境对声传播规律的影响[J]. 中国科学: 物理学力学天文学, 2016, 46(9): 18−27.Hu Zhiguo, Li Zhenglin, Qin Jixing, et al. The effects of the sloping bottom environment on sound propagation in deep water[J]. SCIENTIA SINICA Physica, Mechanica & Astronomica, 2016, 46(9): 18−27. [15] 田中成, 刘聪锋. 无源定位技术[M]. 北京: 国防工业出版社, 2015.Tian Zhongcheng, Liu Congfeng. Passive Locating Technology[M]. Beijing: National Defense Industry Press, 2015. [16] 张旭. 深海分层介质中的无源声定位时差交会特性[J]. 科学通报, 2019, 64(24): 2523−2536. doi: 10.1360/N972019-00210Zhang Xu. Time difference intersection characteristics of passive underwater acoustic localization in the stratified deep sea[J]. Chinese Science Bulletin, 2019, 64(24): 2523−2536. doi: 10.1360/N972019-00210 [17] 杨坤德, 李辉, 段睿. 深海声传播信道和目标被动定位研究现状[J]. 中国科学院院刊, 2019, 34(3): 314−320.Yang Kunde, Li Hui, Duan Rui. Research on acoustic propagation and passive localization in deep water[J]. Bulletin of the Chinese Academy of Sciences, 2019, 34(3): 314−320. [18] Tolstoy A. Matched Field Processing for Underwater Acoustics[M]. Singapore: World Scientific, 1992. [19] Vaccaro R J. The past, present, and the future of underwater acoustic signal processing[J]. IEEE Signal Processing Magazine, 1998, 15(4): 21−51. doi: 10.1109/79.689583 [20] Westwood E K. Broadband matched-field source localization[J]. The Journal of the Acoustical Society of America, 1992, 91(5): 2777−2789. doi: 10.1121/1.402958 [21] 陈连荣, 彭朝晖, 南明星. 高斯射线束方法在深海匹配场定位中的应用[J]. 声学学报, 2013, 38(6): 715−723.Chen Lianrong, Peng Zhaohui, Nan Mingxing. The application of Gaussian beam method in deep ocean matched-field localization[J]. Acta Acustica, 2013, 38(6): 715−723. [22] 翁晋宝, 杨燕明. 深海海面目标单水听器被动测距方法与验证[J]. 海洋学报, 2017, 39(1): 36−45.Weng Jinbao, Yang Yanming. A passive sea-surface source ranging method by single hydrophone in deep sea[J]. Haiyang Xuebao, 2017, 39(1): 36−45. [23] 翁晋宝, 杨燕明. 深海中利用单水听器的影区声源无源测距测深方法[J]. 声学学报, 2018, 43(6): 905−914.Weng Jinbao, Yang Yanming. A passive source range and depth estimation method by single hydrophone in shadow zone of deep water[J]. Acta Acustica, 2018, 43(6): 905−914. [24] Duan Rui, Yang Kunde, Ma Yuanliang, et al. Moving source localization with a single hydrophone using multipath time delays in the deep ocean[J]. The Journal of the Acoustical Society of America, 2014, 136(2): EL159−EL165. doi: 10.1121/1.4890664 [25] 吴俊楠, 周士弘, 张岩. 利用深海海底反射声场特征的水面声源被动测距[J]. 中国科学: 物理学力学天文学, 2016, 46(9): 76−82.Wu Junnan, Zhou Shihong, Zhang Yan. Passive ranging of surface source using bottom bounced sound in deep water[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2016, 46(9): 76−82. [26] Locarnini R A, Mishonov A V, Antonov J I, et al. World ocean atlas 2009 volume 1: temperature[R]. Washington, D. C.: U. S. Government Printing Office, 2010. [27] Antonov J I, Seidov D, Boyer T P, et al. World ocean atlas 2009 volume 2: salinity[R]. Washington, D. C.: U. S. Government Printing Office, 2010. [28] Mackenzie K V. Nine-term equation for sound speed in the oceans[J]. The Journal of the Acoustical Society of America, 1981, 70(3): 807−812. doi: 10.1121/1.386920 [29] Porter M B, Bucker H P. Gaussian beam tracing for computing ocean acoustic fields[J]. The Journal of the Acoustical Society of America, 1987, 82(4): 1349−1359. doi: 10.1121/1.395269 [30] Porter M B. The BELLHOP manual and user’s guide: preliminary draft[R]. La Jolla: Heat, Light and Sound Research, Inc., 2011. [31] Hamilton E L. Geoacoustic modeling of the sea floor[J]. The Journal of the Acoustical Society of America, 1980, 68(5): 1313−1340. doi: 10.1121/1.385100 [32] 孙大军, 郑翠娥, 张居成, 等. 水声定位导航技术的发展与展望[J]. 中国科学院院刊, 2019, 34(3): 331−338.Sun Dajun, Zheng Cuie, Zhang Jucheng, et al. Development and prospect for underwater acoustic positioning and navigation technology[J]. Bulletin of the Chinese Academy of Sciences, 2019, 34(3): 331−338. [33] Argo. Argo float data and metadata from Global Data Assembly Centre (Argo GDAC)[Z]. SEANOE, 2000. [34] 张旭, 程琛, 刘艳. 西北太平洋副热带模态水形成区声传播特性分析[J]. 海洋学报, 2014, 36(9): 94−102.Zhang Xu, Cheng Chen, Liu Yan. Acoustic propagation effect caused by subtropical mode water of northwestern Pacific[J]. Haiyang Xuebao, 2014, 36(9): 94−102. [35] Carter G C. Coherence and time delay estimation[J]. Proceedings of the IEEE, 1987, 75(2): 236−255. doi: 10.1109/PROC.1987.13723 [36] 张学森, 冯海泓, 黄敏燕, 等. 两步法提高时延差估计精度的分析和实验验证[J]. 声学学报, 2013, 38(2): 153−159.Zhang Xuesen, Feng Haihong, Huang Minyan, et al. Analysis and experimental verification on improving time-delay difference estimation accuracy with two-step algorithm[J]. Acta Acustica, 2013, 38(2): 153−159. -





 下载:
下载: