Evolution characteristics of surf zone eddies in a strong alongshore current
-
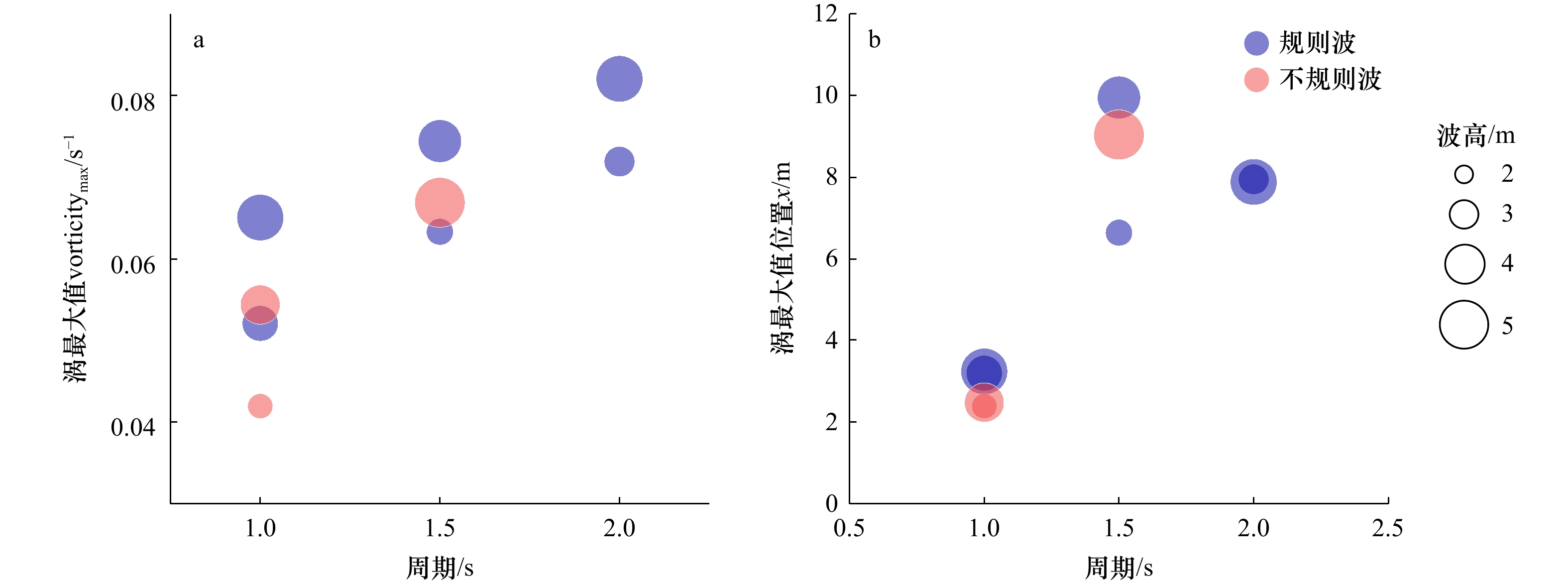
摘要: 破波带涡对物质输运、岸滩演变、生态环境等具有重要影响，但其产生机制及演变特性尚不明晰，特别是强波生流条件下破波带涡的时空演变特性仍需深入研究。本文采用破波带内污染物示踪试验和基于Boussinesq方程的Funwave数值模型，分析了强波生流条件下破波带内涡时空演变。试验结果表明在强波生流条件下破波带向岸和离岸一侧都有大尺度涡团出现，具有瞬时性，涡团从污染团中脱离出来，向岸一侧的涡团尺度受岸线约束，离岸一侧的则逐渐发展演化，有向破波带外输移的趋势。数值模拟结果表明强涡主要集中在破波线附近；破波带内涡场可以分为前剪切区与后剪切区，二者在沿岸方向上具有相似的空间周期和涡分布，涡强度随着波高和周期的增大而增强，且强涡向海侧偏移；不规则波入射条件下，涡强度减弱，并使涡最大值向岸线偏移。Abstract: The surf zone eddies play a vital role in material transport, coastal morphology, and ecological environment. However, the formation mechanisms and evolution characteristics of surf zone eddies, especially their spatiotemporal evolution under strong wave-induced currents, remain insufficiently understood. This study integrates pollutant tracer experiments and numerical simulations using the Funwave model based on the Boussinesq equations to investigate the evolution of surf zone eddies under strong wave-driven currents. The experimental results demonstrate that large eddy patches form both onshore and offshore within the surf zone under strong wave-induced currents, exhibiting transient behavior. Onshore eddies are constrained by the shoreline, whereas offshore eddies gradually expand and migrate seaward. The numerical simulations indicate that strong eddies concentrate near the breaking line, with the surf zone eddy field characterized by upstream and downstream shear zones, both exhibiting similar alongshore spacing and eddy structures. Vorticity positively correlates with wave height and period, and the stronger eddies are shifted to the seaward side. Under irregular wave conditions, vorticity decreases, accompanied by a shoreward shift in the locations of maximum vorticity.
-
Key words:
- Surf zone /
- strong wave-induced currents /
- eddy evolution /
- Funwave /
- vorticity wavenumber spectra
-
图 3 波况3在（4.5 m，8 m）位置处垂直岸线方向（a）和沿岸方向（b）的流速时间历程，蓝线表示滤波后的结果；3条红线分别表示墨水开始释放、释放15 s、释放75 s时对应的时间
Fig. 3 Time series of cross-shore velocity (a) and alongshore velocity (b) at (4.5 m, 8 m) for case 3, the blue line represents the filtered results; the three red lines correspond to the time of dye release onset, 15 s, and 75 s after release
图 4 波况3下采集的墨水运动图像，红色实线框和虚线框分别表示沿岸流和涡驱动的墨水
Fig. 4 Dye patch images collected in case 3. The solid red and dashed boxes indicate the dye patches driven by alongshore currents and vorticity respectively.
图 5 不同时刻采集的墨水运动图像
a. 波况7；b. 波况8；c. 波况9
Fig. 5 Dye patch images at different times
a. case 7; b. case 8; c. case 9
图 7 不同网格分辨率下模拟的沿岸流速及波高同实验数据的比较
Fig. 7 Comparisons of the numerical simulation results for alongshore current profile and wave height with experimental data regarding different grid sizes.
图 8 波况3下不同参数条件下模拟的沿岸流速及波高同实验数据的比较
Fig. 8 Comparison of the numerical simulation results for alongshore current profile and significant wave height with experimental data for case 3
图 9 波况3下的模拟结果
a. 时均流场，b. 时均有效波高，c. t = 400 s时的瞬时波面
Fig. 9 Simulated results for Case 3
a. time-averaged current field; b. time-averaged significant wave height; c. instantaneous surface elevations at t = 400 s
图 10 波况1下不同时刻的涡场，白色虚线表示破波线
Fig. 10 Vorticity fields at different time instants for case 1, with the white dashed line indicating the breaking line
图 11 t = 400 s时各波况下的涡场，其中白色虚线为破波线
Fig. 11 Vorticity fields at t = 400 s for different cases, with the white dashed line indicating the breaking line
图 12 各波况下涡最大值及其位置分布，其中蓝色表示规则波况、红色表示不规则波况；圆的大小表示波高的尺度
Fig. 12 Maximum vorticity and their locations under different cases, with blue indicating regular waves, red indicating irregular waves, and the size of the circle indicates the scale wave height
图 13 不同波况下3个分区的沿岸涡度波数谱密度
Fig. 13 Cross-shore average of the alongshore wavenumber spectra of vorticity for different cases
表 1 实验波浪参数
Tab. 1 Wave parameters under different experimental conditions
波况 入射波 坡度 水深D/m 波高H/m 周期T/s 1 规则波 1∶100 0.18 0.035 1.0 2 规则波 1∶100 0.18 0.045 1.0 3 规则波 1∶100 0.18 0.027 1.5 4 规则波 1∶100 0.18 0.042 1.5 5 规则波 1∶100 0.18 0.030 2.0 6 规则波 1∶100 0.18 0.045 2.0 7 不规则波 1∶100 0.18 0.024 1.0 8 不规则波 1∶100 0.18 0.039 1.0 9 不规则波 1∶100 0.18 0.050 1.5 
下载: 导出CSV
-
[1] 邹志利. 海岸动力学[M]. 4版. 北京: 人民交通出版社, 2009.Zou Zhili. Coastal Hydrodynamics[M]. 4th ed. Beijing: China Communications Press, 2009. [2] Reniers A J H M, Battjes J A, Falqués A, et al. A laboratory study on the shear instability of longshore currents[J]. Journal of Geophysical Research: Oceans, 1997, 102(C4): 8597−8609. doi: 10.1029/96JC03863 [3] Feddersen F, Clark D B, Guza R T. Modeling surf zone tracer plumes: 1. Waves, mean currents, and low-frequency eddies[J]. Journal of Geophysical Research: Oceans, 2011, 116(C11): C11027. [4] Li Shuo, Li Wenxin, Shi Huabin, et al. Hydrodynamics and sediment transport under solitary waves in the swash zone[J]. Journal of Marine Science Engineering, 2024, 12(9): 1686. doi: 10.3390/jmse12091686 [5] Clark D B, Feddersen F, Guza R T. Cross-shore surfzone tracer dispersion in an alongshore current[J]. Journal of Geophysical Research: Oceans, 2010, 115(C10): C10035. [6] Clark D B, Feddersen F, Guza R T. Modeling surf zone tracer plumes: 2. Transport and dispersion[J]. Journal of Geophysical Research: Oceans, 2011, 116(C11): C11028. [7] Spydell M S, Feddersen F, Guza R T. Observations of drifter dispersion in the surfzone: the effect of sheared alongshore currents[J]. Journal of Geophysical Research: Oceans, 2009, 114(C7): C07028. [8] Suanda S H, Feddersen F. A self-similar scaling for cross-shelf exchange driven by transient rip currents[J]. Geophysical Research Letters, 2015, 42(13): 5427−5434. doi: 10.1002/2015GL063944 [9] Rilov G, Dudas S E, Menge B A, et al. The surf zone: a semi-permeable barrier to onshore recruitment of invertebrate larvae?[J]. Journal of Experimental Marine Biology and Ecology, 2008, 361(2): 59−74. doi: 10.1016/j.jembe.2008.04.008 [10] Shanks A L, Morgan S G, MacMahan J, et al. Surf zone physical and morphological regime as determinants of temporal and spatial variation in larval recruitment[J]. Journal of Experimental Marine Biology and Ecology, 2010, 392(1/2): 140−150. [11] Feddersen F. The generation of surfzone eddies in a strong alongshore current[J]. Journal of Physical Oceanography, 2014, 44(2): 600−617. doi: 10.1175/JPO-D-13-051.1 [12] Brown J A, MacMahan J H, Reniers A J H M, et al. Observations of mixing and transport on a steep beach[J]. Continental Shelf Research, 2019, 178: 1−14. doi: 10.1016/j.csr.2019.03.009 [13] Castelle B, Almar R, Dorel M, et al. Rip currents and circulation on a high-energy low-tide-terraced beach (Grand Popo, Benin, West Africa)[J]. Journal of Coastal Research, 2014, 70: 633−638. doi: 10.2112/SI70-107.1 [14] Long J W, Özkan-Haller H T. Low-frequency characteristics of wave group–forced vortices[J]. Journal of Geophysical Research: Oceans, 2009, 114(C8): C08004. [15] Choi J, Kirby J T, Yoon S B. Boussinesq modeling of longshore currents in the SandyDuck experiment under directional random wave conditions[J]. Coastal Engineering, 2015, 101: 17−34. doi: 10.1016/j.coastaleng.2015.04.005 [16] Bowen A J, Holman R A. Shear instabilities of the mean longshore current: 1. Theory[J]. Journal of Geophysical Research: Oceans, 1989, 94(C12): 18023−18030. doi: 10.1029/JC094iC12p18023 [17] Oltman-Shay J, Howd P A, Birkemeier W A. Shear instabilities of the mean longshore current: 2. Field observations[J]. Journal of Geophysical Research: Oceans, 1989, 94(C12): 18031−18042. doi: 10.1029/JC094iC12p18031 [18] Reniers A J H M, MacMahan J H, Thornton E B, et al. Surf zone surface retention on a rip-channeled beach[J]. Journal of Geophysical Research: Oceans, 2009, 114(C10): C10010. [19] Noyes T J, Guza R T, Elgar S, et al. Field observations of shear waves in the surf zone[J]. Journal of Geophysical Research: Oceans, 2004, 109(C1): C01031. [20] Zhang Xuan, Simons R, Zheng Jinhai, et al. A review of the state of research on wave-current interaction in nearshore areas[J]. Ocean Engineering, 2022, 243: 110202. doi: 10.1016/j.oceaneng.2021.110202 [21] Noyes T J, Guza R T, Feddersen F, et al. Model-data comparisons of shear waves in the nearshore[J]. Journal of Geophysical Research: Oceans, 2005, 110(C5): C05019. [22] Zhang Yu, Shi Fengyan, Kirby J T, et al. Phase-resolved modeling of wave interference and its effects on nearshore circulation in a large ebb shoal-beach system[J]. Journal of Geophysical Research: Oceans, 2022, 127(10): e2022JC018623. doi: 10.1029/2022JC018623 [23] Boffetta G, Ecke R E. Two-dimensional turbulence[J]. Annual Review of Fluid Mechanics, 2012, 44: 427−451. doi: 10.1146/annurev-fluid-120710-101240 [24] Clark D B, Elgar S, Raubenheimer B. Vorticity generation by short-crested wave breaking[J]. Geophysical Research Letters, 2012, 39(24): L24604. [25] Baker C M, Moulton M, Chickadel C C, et al. Two-dimensional inverse energy cascade in a laboratory surf zone for varying wave directional spread[J]. Physics of Fluids, 2023, 35(12): 125140. doi: 10.1063/5.0169895 [26] Baker C M. Surfzone vorticity dynamics in a directional wave basin[D]. Washington: University of Washington, 2023. [27] Elgar S, Raubenheimer B. Field evidence of inverse energy cascades in the surfzone[J]. Journal of Physical Oceanography, 2020, 50(8): 2315−2321. doi: 10.1175/JPO-D-19-0327.1 [28] Elgar S, Dooley C, Gorrell L, et al. Observations of two-dimensional turbulence in the surfzone[J]. Physics of Fluids, 2023, 35(8): 085142. doi: 10.1063/5.0159170 [29] Xia H, Francois N. Two-dimensional turbulence in three-dimensional flows[J]. Physics of Fluids, 2017, 29(11): 111107. doi: 10.1063/1.5000863 [30] Colombi R, Schlüter M, von Kameke A. Three dimensional flows beneath a thin layer of 2D turbulence induced by Faraday waves[J]. Experiments in Fluids, 2021, 62(1): 8. doi: 10.1007/s00348-020-03099-y [31] Baker C M, Moulton M, Chickadel C C, et al. Wave breaking eddies and transient rip current dynamics in large-scale wave basin experiments[C]// 9th International Conference on Physical Modelling in Coastal Engineering. Delft: Delft University of Technology, 2024. [32] Spydell M S. The suppression of surfzone cross-shore mixing by alongshore currents[J]. Geophysical Research Letters, 2016, 43(18): 9781−9790. doi: 10.1002/2016GL070626 [33] Bondehagen A, Roeber V, Kalisch H, et al. Wave-driven current and vortex patterns at an open beach: insights from phase-resolving numerical computations and Lagrangian measurements[J]. Coastal Engineering, 2024, 193: 104591. doi: 10.1016/j.coastaleng.2024.104591 [34] Baker C M, Moulton M, Raubenheimer B, et al. Modeled three-dimensional currents and eddies on an alongshore-variable barred beach[J]. Journal of Geophysical Research: Oceans, 2021, 126(7): e2020JC016899. doi: 10.1029/2020JC016899 [35] Zheng Jinhai, Yao Yu, Chen Songhui, et al. Laboratory study on wave-induced setup and wave-driven current in a 2DH reef-lagoon-channel system[J]. Coastal Engineering, 2020, 162: 103772. doi: 10.1016/j.coastaleng.2020.103772 [36] 任春平. 沿岸流不稳定运动的实验研究及理论分析[D]. 大连: 大连理工大学, 2009.Ren Chunping. A laboratory study and theoretical analysis on the instabilities of alongshore currents[D]. Dalian: Dalian University of Technology, 2009. [37] Chen Qin, Kirby J T, Dalrymple R A, et al. Boussinesq modeling of longshore currents[J]. Journal of Geophysical Research: Oceans, 2003, 108(C11): 26. [38] Hally-Rosendahl K, Feddersen F. Modeling surfzone to inner-shelf tracer exchange[J]. Journal of Geophysical Research: Oceans, 2016, 121(6): 4007−4025. doi: 10.1002/2015JC011530 [39] Kennedy A B, Chen Qin, Kirby J T, et al. Boussinesq modeling of wave transformation, breaking, and runup. I: 1D[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2000, 126(1): 39−47. doi: 10.1061/(ASCE)0733-950X(2000)126:1(39) [40] Wei Ge, Kirby J T, Sinha A. Generation of waves in Boussinesq models using a source function method[J]. Coastal Engineering, 1999, 36(4): 271−299. doi: 10.1016/S0378-3839(99)00009-5 [41] 李绍武, 黄筱云. 用Boussinesq方程计算沿岸流的数值方法[J]. 天津大学学报, 2004, 37(12): 1059−1062. doi: 10.3969/j.issn.0493-2137.2004.12.005Li Shaowu, Huang Xiaoyun. Numerical method for calculation of longshore current by using Boussinesq equations[J]. Journal of Tianjin University, 2004, 37(12): 1059−1062. doi: 10.3969/j.issn.0493-2137.2004.12.005 [42] 王国玉, 张琪, 赵银林. 不规则波作用下沿岸流流速分布规律分析[J]. 海洋工程, 2021, 39(3): 11−20.Wang Guoyu, Zhang Qi, Zhao Yinlin. Analysis of alongshore current velocity generated by irregular waves[J]. The Ocean Engineering, 2021, 39(3): 11−20. [43] O’Dea A, Kumar N, Haller M C. Simulations of the surf zone eddy field and cross-shore exchange on a nonidealized bathymetry[J]. Journal of Geophysical Research: Oceans, 2021, 126(5): e2020JC016619. doi: 10.1029/2020JC016619 [44] Spydell M S, Feddersen F, Suanda S. Inhomogeneous turbulent dispersion across the nearshore induced by surfzone eddies[J]. Journal of Physical Oceanography, 2019, 49(4): 1015−1034. doi: 10.1175/JPO-D-18-0102.1 -
计量
- 文章访问数: 6
- HTML全文浏览量: 3
- PDF下载量: 1
- 被引次数: 0
