Energy analysis of submesoscale processes in the Agulhas current system
-
摘要: 本文基于(1/48)°MITgcm数值模拟结果，通过频率−波数谱分析等方法分离地转平衡和非地转运动，分析了阿古拉斯流域亚中尺度的分布特征，讨论了其季节性变化的主要影响因素。结果表明，阿古拉斯流域亚中尺度过程具有冬强夏弱的显著季节变化特征，混合层斜压不稳定是影响该流域亚中尺度季节性差异的主要原因。此外，在涡动能较强的区域，地转平衡运动始终主导亚中尺度过程，季节性变化较小；在涡动能较弱的区域，地转平衡与非地转分量具有明显的季节性差异，局地混合层浅化可能是导致夏季非地转分量贡献增加的主要机制。本文研究结果有助于进一步探究阿古拉斯流域亚中尺度的季节性变化及其主导因素，地转平衡与非地转运动的有效分离加强了我们对海洋多尺度之间能量传递的理解。Abstract: Based on the high-resolution oceanic numerical model product of MITgcm with a resolution of (1/48)°, the geostrophic balanced motion and unbalanced wave motion are decomposed via the frequency-wavenumber spectrum analysis method to analyze the distribution of submesoscale characteristics and diagnose the main factors affecting their seasonal variations in the Agulhas current system. The results show that the submesoscale processes in the Agulhas current system have a significant seasonal distribution with strong features in winter but weak features in summer. The mixed layer baroclinic instability is the main reason affecting the submesoscale seasonal differences in the area. In addition, the geostrophic balanced motions are predominant in the submesoscale process in the regions with stronger eddy kinetic energy (EKE) and have no obvious seasonality. For the regions with weaker EKE, the balanced and unbalanced geostrophic motions show significant seasonality, where the local mixing layer shallowness is responsible for the increase of the unbalanced kinetic energy in summer. Our analysis helps to further clarify the characteristics of submesoscale seasonal variation and its primary factors in the Agulhas current system. The effective separation of geostrophic balanced and unbalanced motion enhances our understanding of energy transformation between multiscale processes in the ocean.
-
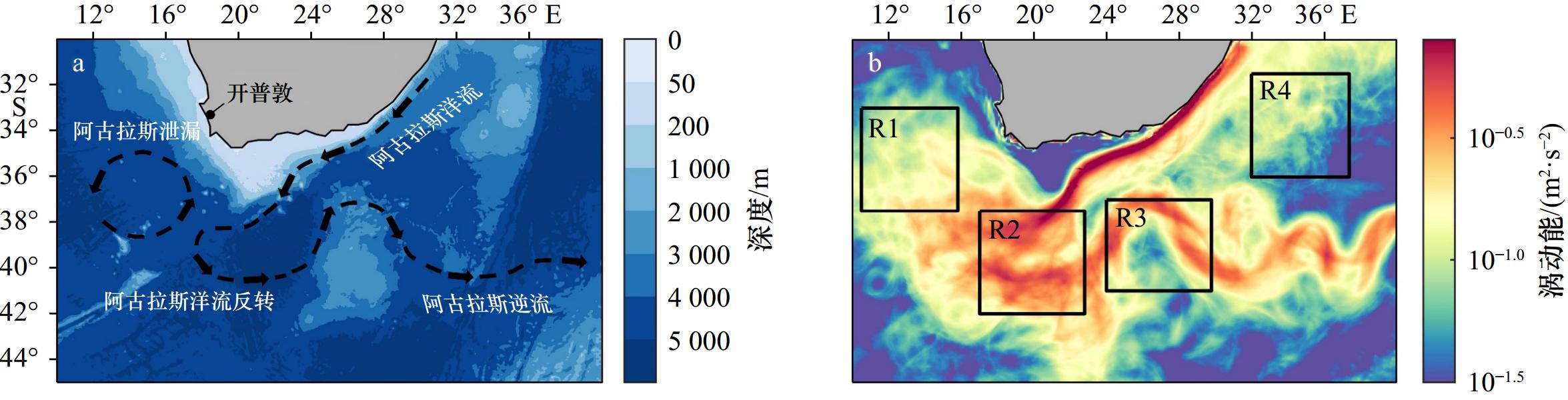
图 1 阿古拉斯流域水深及主要流场分布（a）与2011年10月至2012年9月海表面时间平均涡动能分布（b）
图b中黑色矩形框为选取的研究子区域
Fig. 1 The distribution of water depth and main flow field in Agulhas Current (a) and the surface time average eddy kinetic energy from October 2011 to September 2012 (b)
The black contours in figure b are the selected research subregions
图 2 研究海域海表层相对涡度
$ \zeta $ （a, c）与中尺度水平应变率MSR（b, d）在1月15日（a, b）和7月15日（c, d）日平均水平分布情况（数据均以行星涡度$ f $ 标准化）黑色矩形框为选取的研究子区域
Fig. 2 The daily mean distributions of surface relative vorticity
$ \zeta $ (a, c) and horizontal mesoscale strain rate MSR (b, d) on January 15 (a, b) and on July 15 (c, d) in study sea area (the data are standaridized by planetary vorticity f)Black rectangular boxes are the selected research subregions
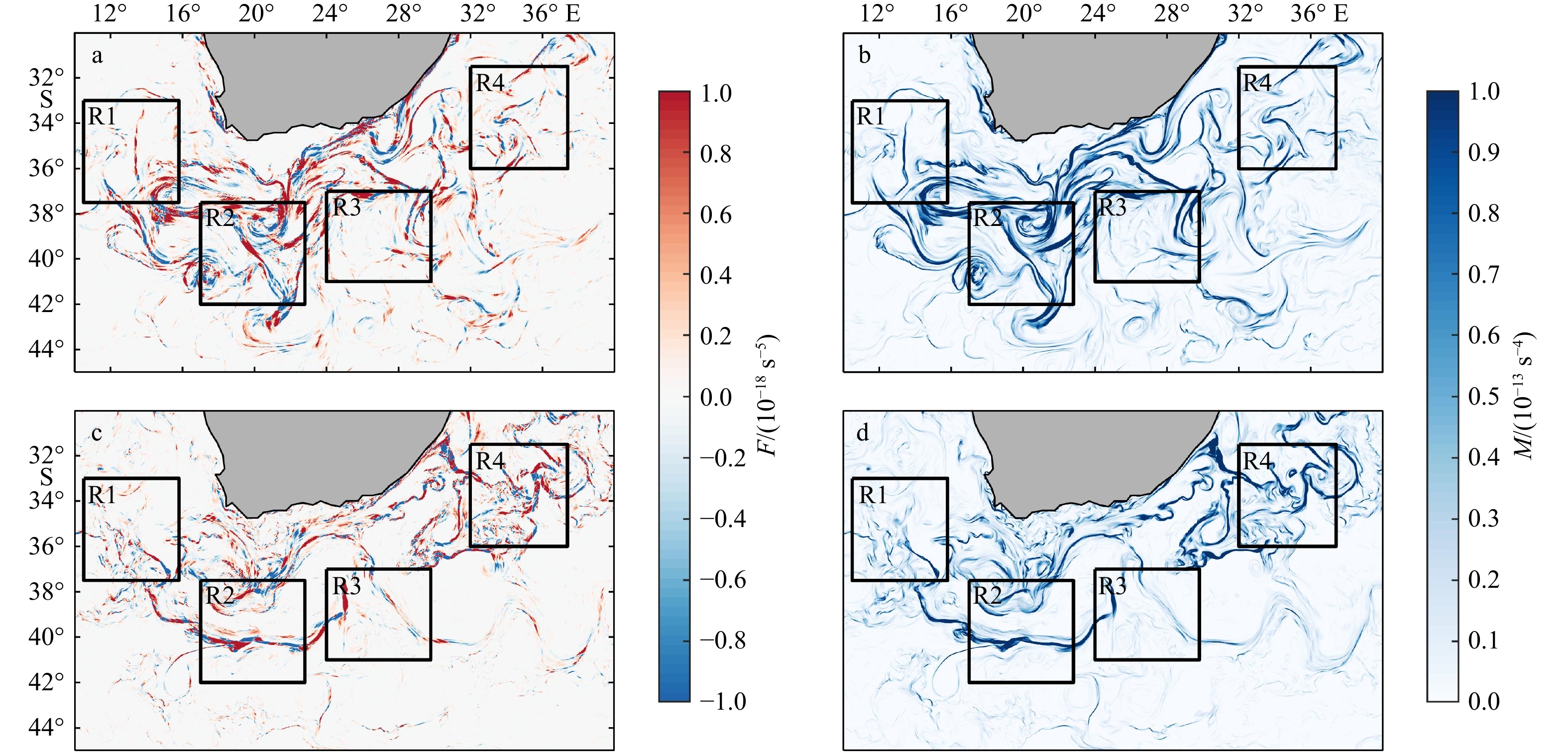
图 3 研究海域海表层中尺度锋生趋势F（a, c）和锋面强度M（b, d）在1月15日（a, b）和7月15日（c, d）日平均水平分布情况
黑色矩形框为选取的研究子区域
Fig. 3 The daily mean distributions of mesoscale frontal tendency F (a, c) and frontal sharpness M (b, d) on January 15 (a, b) and on July 15 (c, d) in study sea area
Black rectangular boxes are the selected research subregions
图 4 R1（a）、R2（b）、R3（c）和R4（d）各区域中尺度锋生趋势F（蓝色曲线）和锋面强度M（红色曲线）的时间变化
Fig. 4 Time series of mesoscale frontal tendency F (blue line) and frontal sharpness M (red line) in R1 (a), R2 (b), R3 (c) and R4 (d)
图 5 研究海域海表层位涡PV（a, d）及其垂向分量
$ {q}_{{\mathrm{vert}}} $ （b, e）和水平斜压分量$ {q}_{{\mathrm{bc}}} $ （c, f）在1月15日（a−c）和7月15日（e−f）日平均水平分布情况黑色矩形框为选取的研究子区域
Fig. 5 The daily mean distributions of surface potential vorticity PV (a, d) and its vertical component
$ {q}_{{\mathrm{vert}}} $ (b, e) and horizontal baroclinic component$ {q}_{{\mathrm{bc}}} $ (c, f) on January 15 (a−c) and on July 15 (e−f) in research sea areaBlack rectangular boxes are the selected research subregions
图 6 R1（a, e）、R2（b, f）、R3（c, g）和R4（d, h）各区域平均相对涡度
$ \zeta /f $ 均方根（a−d）与PKE（e−h）随时间和深度的变化情况黑色实线为混合层深度
Fig. 6 Variations of averaged the RMS of
$ \zeta /f $ (a−d) and the PKE (e−h) over time and depth in R1 (a, e), R2 (b, f), R3 (c, g) and R4 (d, h)Solid black lines denote the averaged mixed-layer depth
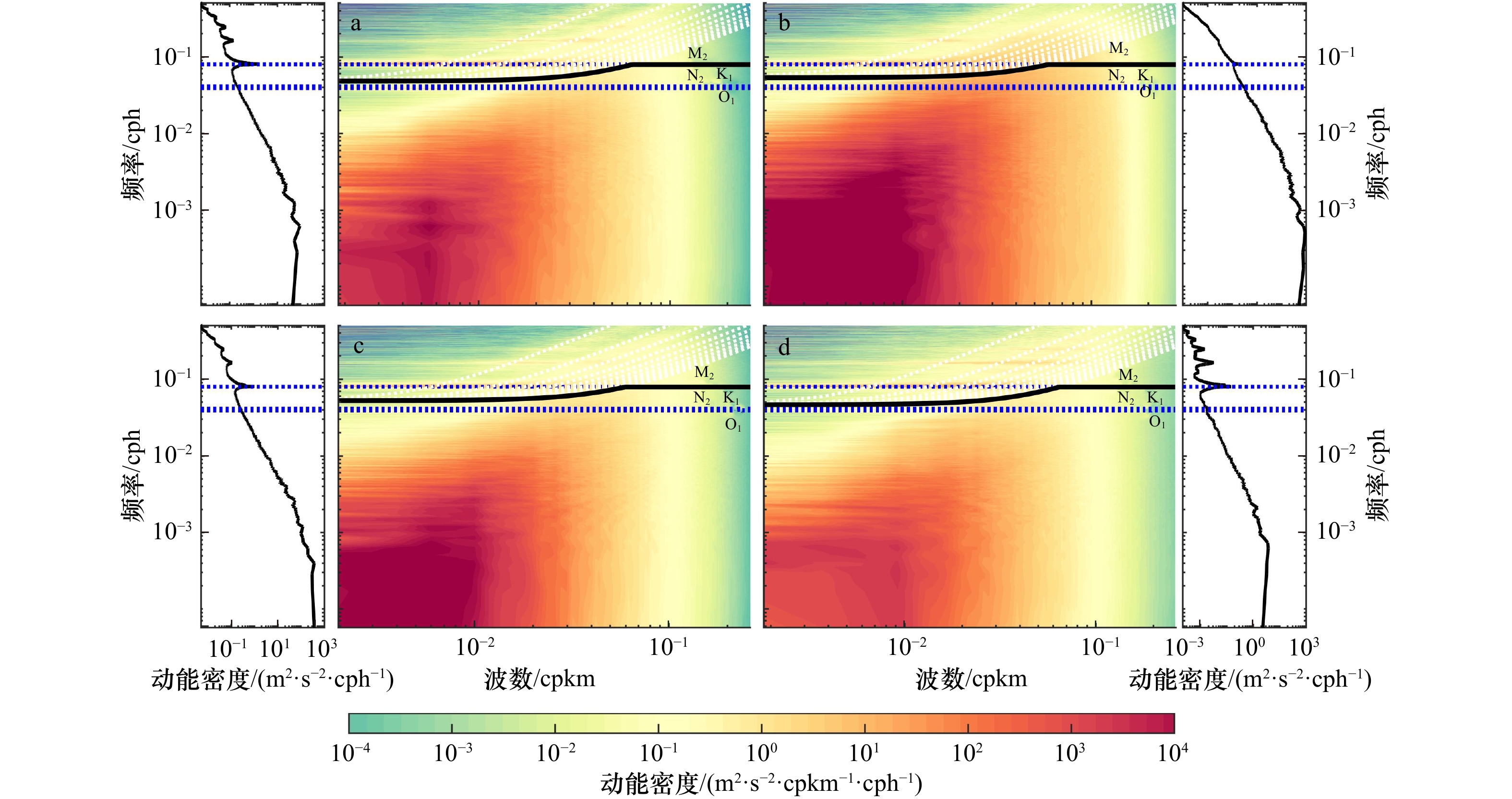
图 7 R1（a）、R2（b）、R3（c）和R4（d）各子区域年涡动能频率−波数谱分析结果及其对应频率谱
蓝色虚线代表潮汐频带M2、N2、K1和O1，白色虚线为第1～10斜压模态下的惯性重力波频散曲线，黑色实线为动态频率以划分地转与非地转运动的频率上（下）限
Fig. 7 The frequency-wavenumber spectra distributions of surface eddy kinetic energy and their frequency spectra in R1 (a), R2 (b), R3 (c) and R4 (d)
Dashed bule lines denote the tidal constituent M2, N2, K1, O1, and the dashed white lines denote inertia-gravity frequencies, solid black lines denote the dynamic frequency to divide the upper (lower) frequency limits of geostrophic balanced and unbalanced motion
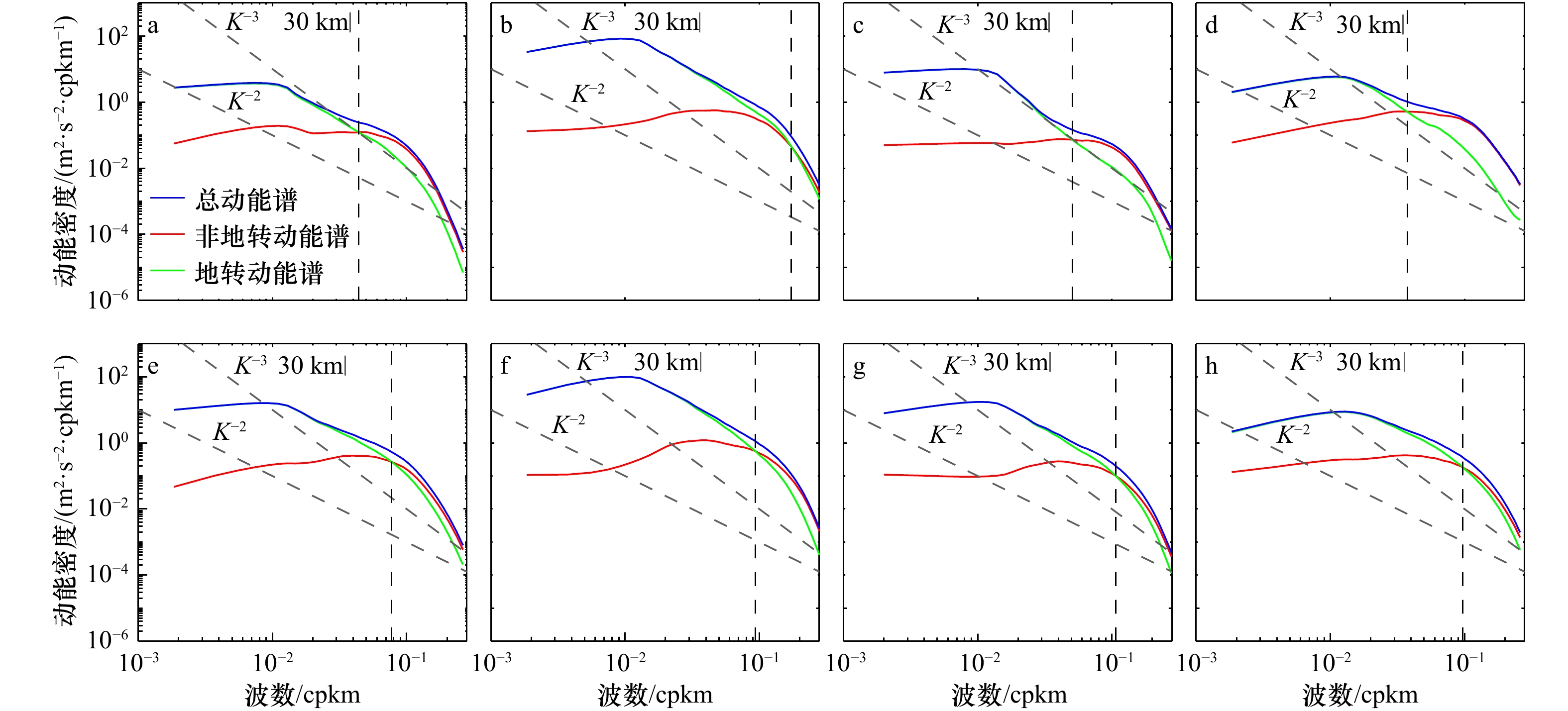
图 8 R1（a, e）、R2（b, f）、R3（c, g）和R4（d, h）各区域夏（a−d）、冬（e−h）两季波数谱
灰色虚线表示${K^{-3}} $和${K^{-2}} $斜率参考线；黑色虚线为过渡尺度Lt
Fig. 8 Wave number spectrum in R1 (a, e), R2 (b, f), R3 (c, g) and R4 (d, h) in summer (a−d) and winter (e−h)
Gray dashed lines denote the ${K^{-3}} $ and ${K^{-2}} $ reference spectra, vertical black dashed lines denote the Lt
图 9 R1、R2、R3和R4各区域亚中尺度动能占总动能比（a）和亚中尺度非地转动能占亚中尺度动能比（b）
Fig. 9 The ratio of submesoscale kinetic energy to total kinetic energy (a) and submesoscale unbalanced kinetic energy to submesoscale kinetic energy (b) in subregions R1, R2, R3, and R4
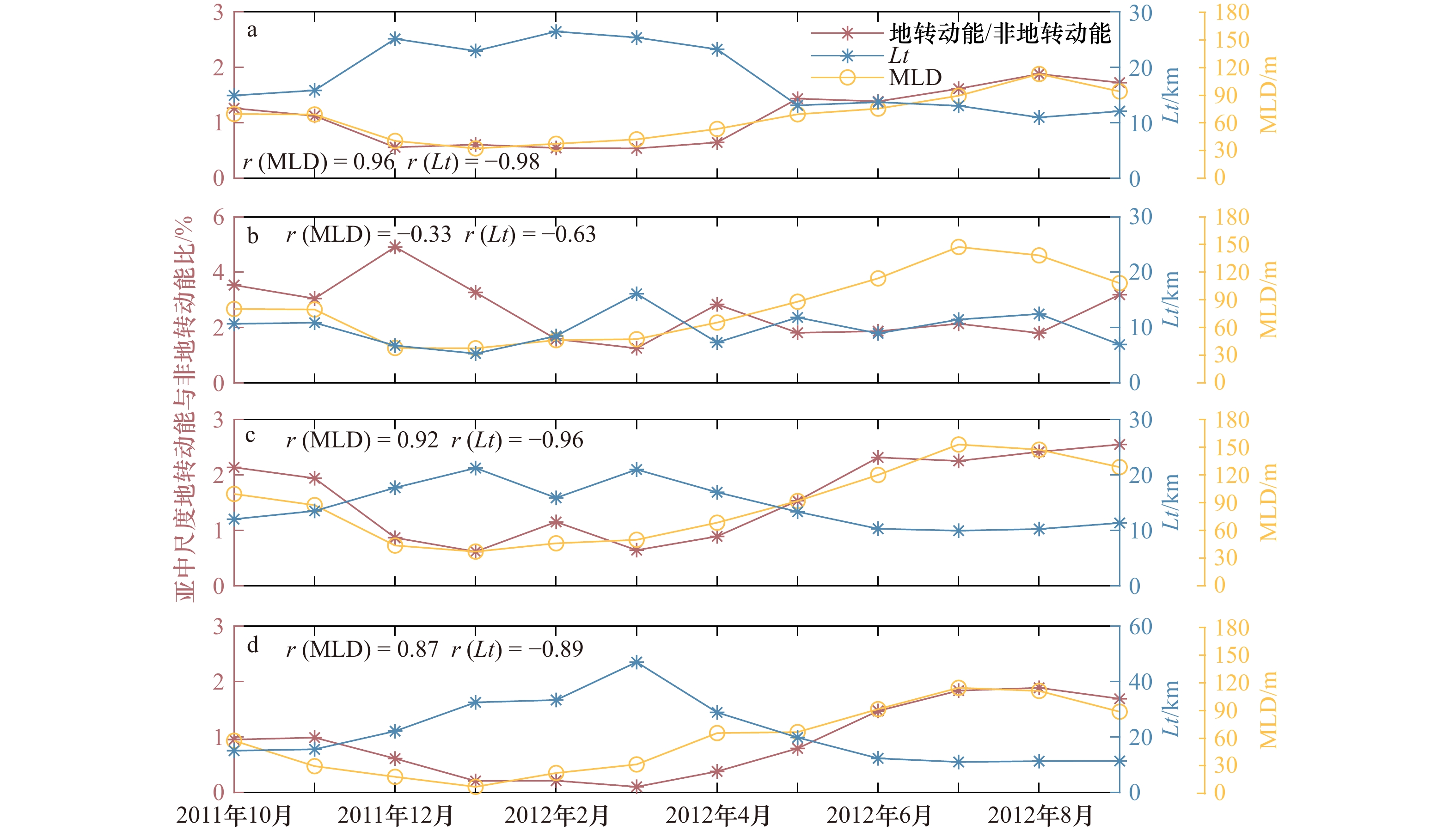
图 10 R1（a）、R2（b）、R3（c）和R4（d）各区域亚中尺度下地转动能与非地转动能比值（红色折线）、过渡尺度
$ Lt $ （蓝色折线）和混合层深度（黄色折线）逐月分布Fig. 10 Monthly variation of the ratio of submesoscale geostrophic balanced energy to unbalanced energy (red line), transition scale
$ Lt $ (blue line) and mixed layer depth (yellow line) in R1 (a), R2 (b), R3 (c) and R4 (d) -
[1] Bracco A, Liu Guangpeng, Sun Daoxun. Mesoscale-submesoscale interactions in the Gulf of Mexico: from oil dispersion to climate[J]. Chaos, Solitons & Fractals, 2019, 119: 63−72. [2] Thomas L N, Taylor J R, Ferrari R, et al. Symmetric instability in the Gulf Stream[J]. Deep-Sea Research Part II: Topical Studies in Oceanography, 2013, 91: 96−110. doi: 10.1016/j.dsr2.2013.02.025 [3] McWilliams J C. Submesoscale currents in the ocean[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2016, 472(2189): 20160117. [4] Gula J, Blacic T M, Todd R E. Submesoscale coherent vortices in the gulf stream[J]. Geophysical Research Letters, 2019, 46(5): 2704−2714. doi: 10.1029/2019GL081919 [5] 郑瑞玺, 经志友, 罗士浩. 南海北部反气旋涡旋边缘的次中尺度动力过程分析[J]. 热带海洋学报, 2018, 37(3): 19−25.Zheng Ruixi, Jing Zhiyou, Luo Shihao. Analysis of sub-mesoscale dynamic processes in the periphery of anticyclonic eddy in the northern South China Sea[J]. Journal of Tropical Oceanography, 2018, 37(3): 19−25. [6] Cao Haijin, Jing Zhiyou, Fox-Kemper B, et al. Scale transition from geostrophic motions to internal waves in the northern South China Sea[J]. Journal of Geophysical Research: Oceans, 2019, 124(12): 9364−9383. doi: 10.1029/2019JC015575 [7] Zhang Zhiwei, Zhang Yuchen, Qiu Bo, et al. Spatiotemporal characteristics and generation mechanisms of submesoscale currents in the northeastern South China Sea revealed by numerical simulations[J]. Journal of Geophysical Research: Oceans, 2020, 125(2): e2019JC015404. doi: 10.1029/2019JC015404 [8] Dong Jihai, Fox-Kemper B, Zhang Hong, et al. The seasonality of submesoscale energy production, content, and cascade[J]. Geophysical Research Letters, 2020, 47(6): e2020GL087388. doi: 10.1029/2020GL087388 [9] 罗士浩, 经志友, 闫桐, 等. 黑潮延伸体海域次中尺度过程的季节变化研究[J]. 热带海洋学报, 2021, 40(1): 1−11.Luo Shihao, Jing Zhiyou, Yan Tong, et al. Seasonal variability of submesoscale flows in the Kuroshio Extension[J]. Journal of Tropical Oceanography, 2021, 40(1): 1−11. [10] Mensa J A, Garraffo Z, Griffa A, et al. Seasonality of the submesoscale dynamics in the Gulf Stream region[J]. Ocean Dynamics, 2013, 63(8): 923−941. doi: 10.1007/s10236-013-0633-1 [11] Buckingham C E, Garabato A C N, Thompson A F, et al. Seasonality of submesoscale flows in the ocean surface boundary layer[J]. Geophysical Research Letters, 2016, 43(5): 2118−2126. doi: 10.1002/2016GL068009 [12] Dong Jihai, Zhong Jihai. The spatiotemporal features of submesoscale processes in the northeastern South China Sea[J]. Acta Oceanologica Sinica, 2018, 37(11): 8−18. doi: 10.1007/s13131-018-1277-2 [13] Haine T W N, Marshall J. Gravitational, symmetric, and baroclinic instability of the ocean mixed layer[J]. Journal of Physical Oceanography, 1998, 28(4): 634−658. doi: 10.1175/1520-0485(1998)028<0634:GSABIO>2.0.CO;2 [14] Su Zhan, Wang Jinbo, Klein P, et al. Ocean submesoscales as a key component of the global heat budget[J]. Nature Communications, 2018, 9(1): 775. doi: 10.1038/s41467-018-02983-w [15] Beal L M, De Ruijter W P M, Biastoch A, et al. On the role of the Agulhas system in ocean circulation and climate[J]. Nature, 2011, 472(7344): 429−436. doi: 10.1038/nature09983 [16] Schubert R, Gula J, Biastoch A. Submesoscale flows impact Agulhas leakage in ocean simulations[J]. Communications Earth & Environment, 2021, 2(1): 197. [17] Schubert R, Schwarzkopf F U, Baschek B, et al. Submesoscale impacts on mesoscale Agulhas dynamics[J]. Journal of Advances in Modeling Earth Systems, 2019, 11(8): 2745−2767. doi: 10.1029/2019MS001724 [18] Schubert R, Gula J, Greatbatch R J, et al. The submesoscale kinetic energy cascade: mesoscale absorption of submesoscale mixed layer eddies and frontal downscale fluxes[J]. Journal of Physical Oceanography, 2020, 50(9): 2573−2589. doi: 10.1175/JPO-D-19-0311.1 [19] Capuano T A, Speich S, Carton X, et al. Mesoscale and submesoscale processes in the Southeast Atlantic and their impact on the regional thermohaline structure[J]. Journal of Geophysical Research: Oceans, 2018, 123(3): 1937−1961. doi: 10.1002/2017JC013396 [20] Schubert R. The impact of submesoscale flows on mesoscale Agulhas dynamics[D]. Kiel: Christian-Albrechts-Universität zu Kiel, 2020. [21] de Ruijter W P M, Biastoch A, Drijfhout S S, et al. Indian-Atlantic interocean exchange: dynamics, estimation and impact[J]. Journal of Geophysical Research: Oceans, 1999, 104(C9): 20885−20910. doi: 10.1029/1998JC900099 [22] Zhang Ruize, Sun Shantong, Chen Zhaohui, et al. Rapid 21st century weakening of the Agulhas current in a warming climate[J]. Geophysical Research Letters, 2023, 50(4): e2022GL102070. doi: 10.1029/2022GL102070 [23] Taylor J R, Thompson A F. Submesoscale dynamics in the upper ocean[J]. Annual Review of Fluid Mechanics, 2023, 55: 103−127. doi: 10.1146/annurev-fluid-031422-095147 [24] Torres H S, Klein P, Menemenlis D, et al. Partitioning ocean motions into balanced motions and internal gravity waves: a modeling study in anticipation of future space missions[J]. Journal of Geophysical Research: Oceans, 2018, 123(11): 8084−8105. doi: 10.1029/2018JC014438 [25] Qiu Bo, Chen Shuiming, Klein P, et al. Seasonality in transition scale from balanced to unbalanced motions in the world ocean[J]. Journal of Physical Oceanography, 2018, 48(3): 591−605. doi: 10.1175/JPO-D-17-0169.1 [26] Menemenlis D, Campin J M, Heimbach P, et al. ECCO2: high resolution global ocean and sea ice data synthesis[J]. Mercator Ocean Quarterly Newslettel, 2008, 31: 13−21. [27] Zhang Zhiwei, Liu Yuelin, Qiu Bo, et al. Submesoscale inverse energy cascade enhances Southern Ocean eddy heat transport[J]. Nature Communications, 2023, 14(1): 1335. doi: 10.1038/s41467-023-36991-2 [28] Chelton D B, Deszoeke R A, Schlax M G, et al. Geographical variability of the first baroclinic rossby radius of deformation[J]. Journal of Physical Oceanography, 1998, 28(3): 433−460. doi: 10.1175/1520-0485(1998)028<0433:GVOTFB>2.0.CO;2 [29] Jing Zhiyou, Fox-Kemper B, Cao Haijin, et al. Submesoscale fronts and their dynamical processes associated with symmetric instability in the Northwest Pacific Subtropical Ocean[J]. Journal of Physical Oceanography, 2021, 51(1): 83−100. doi: 10.1175/JPO-D-20-0076.1 [30] Zhang Zhiwei, Zhang Xincheng, Qiu Bo, et al. Submesoscale currents in the subtropical upper ocean observed by long-term high-resolution mooring arrays[J]. Journal of Physical Oceanography, 2021, 51(1): 187−206. doi: 10.1175/JPO-D-20-0100.1 [31] Sullivan P P, McWilliams J C. Frontogenesis and frontal arrest of a dense filament in the oceanic surface boundary layer[J]. Journal of Fluid Mechanics, 2018, 837: 341−380. doi: 10.1017/jfm.2017.833 [32] Gula J, Molemaker M J, McWilliams J C. Submesoscale dynamics of a gulf stream frontal eddy in the South Atlantic Bight[J]. Journal of Physical Oceanography, 2016, 46(1): 305−325. doi: 10.1175/JPO-D-14-0258.1 [33] Hoskins B J. The role of potential vorticity in symmetric stability and instability[J]. Quarterly Journal of the Royal Meteorological Society, 1974, 100(425): 480−482. doi: 10.1002/qj.49710042520 [34] Thomas L N, Tandon A, Mahadevan A. Submesoscale processes and dynamics[M]//Hecht M W, Hasumi H. Ocean Modeling in an Eddying Regime. Washington: American Geophysical Union, 2013. [35] Cao Haijin, Fox-Kemper B, Jing Zhiyou. Submesoscale eddies in the upper ocean of the Kuroshio Extension from high-resolution simulation: energy budget[J]. Journal of Physical Oceanography, 2021, 51(7): 2181−2201. [36] 张晓璐, 熊学军. 渤海夏季第一斜压罗斯贝变形半径的计算与分析[J]. 海洋科学进展, 2015, 33(3): 295−304. doi: 10.3969/j.issn.1671-6647.2015.03.003Zhang Xiaolu, Xiong Xuejun. Calculation and analysis of the first Baroclinic Rossby deformation radius in summer in the Bohai Sea[J]. Advances in Marine Science, 2015, 33(3): 295−304. doi: 10.3969/j.issn.1671-6647.2015.03.003 [37] Capet X, McWilliams J C, Molemaker M J, et al. Mesoscale to submesoscale transition in the California current system. Part I: flow structure, eddy flux, and observational tests[J]. Journal of Physical Oceanography, 2008, 38(1): 29−43. doi: 10.1175/2007JPO3671.1 [38] Dong Jihai, Jing Zhiyou, Fox-Kemper B, et al. Effects of symmetric instability in the Kuroshio Extension region in winter[J]. Deep Sea Research Part II: Topical Studies in Oceanography, 2022, 202: 105142. doi: 10.1016/j.dsr2.2022.105142 [39] Taylor J R, Ferrari R. On the equilibration of a symmetrically unstable front via a secondary shear instability[J]. Journal of Fluid Mechanics, 2009, 622: 103−113. doi: 10.1017/S0022112008005272 [40] Callies J, Ferrari R, Klymak J M, et al. Seasonality in submesoscale turbulence[J]. Nature Communications, 2015, 6(1): 6862. doi: 10.1038/ncomms7862 [41] Rocha C B, Gille S T, Chereskin T K, et al. Seasonality of submesoscale dynamics in the Kuroshio Extension[J]. Geophysical Research Letters, 2016, 43(21): 11304−11311. -
下载:
计量
- 文章访问数: 272
- HTML全文浏览量: 69
- PDF下载量: 67
- 被引次数: 0
