抛物型对称海脊引导波完整解析理论

刘建豪; 王岗; 郭海; 郑金海; 杜齐鲁

doi:10.12284/hyxb2023095

抛物型对称海脊引导波完整解析理论

doi: 10.12284/hyxb2023095

刘建豪^{1, 2,},
王岗^{1, 2, ,},
郭海³,
郑金海^{1, 2},
杜齐鲁⁴

1.
河海大学海岸灾害及防护教育部重点实验室，江苏南京 210098
2.
河海大学港口海岸与近海工程学院，江苏南京 210098
3.
国家海洋技术中心，天津 300112
4.
南京交通职业技术学院，江苏南京 211188

基金项目: 国家自然科学基金委−山东联合基金(U1906230)；国家自然科学基金面上项目(52071128)；江苏省自然科学基金杰出青年基金(BK20220082)；江苏省高职院校青年教师企业实践培训项目(2021QYSJ049)。

详细信息

作者简介:
刘建豪（1998-），女，湖南省娄底市人，主要从事海啸传播变形与数值模拟研究。E-mail：jianhao_liu@hhu.edu.cn

通讯作者:
王岗（1982-），男，河北省张家口市人，教授，主要从事波浪传播变形研究。E-mail：gangwang@hhu.edu.cn

中图分类号: TV139.2
计量
- 文章访问数: 210
- HTML全文浏览量: 90
- PDF下载量: 34
- 被引次数: 0
出版历程
- 收稿日期: 2022-10-08
- 修回日期: 2023-01-30
- 网络出版日期: 2023-04-27
- 刊出日期: 2023-06-30

Complete analytical solutions for guided waves along a parabolic symmetrical ridge

Liu Jianhao^{1, 2
,},
Wang Gang^{1, 2
, ,},
Guo Hai³,
Zheng Jinhai^{1, 2},
Du Qilu⁴

1.
Key Laboratory of Coastal Disaster and Defence, Ministry of Education, Hohai University, Nanjing 210098, China
2.
College of Harbour, Coastal and Offshore Engineering, Hohai University , Nanjing 210098, China
3.
National Ocean Technology Center, Tianjin 300112, China
4.
Nanjing Communications Institute of Technology, Nanjing 211188, China

摘要

摘要: 越洋海啸能够被大洋海脊引导并沿海脊传播至远场地区，虽然传播速度较慢，但携带较大的能量，会对远场地区造成灾害影响，相关研究对于提高海啸传播特性本质的认识具有重要意义。本文基于线性长波方程，推导出了抛物型对称海脊引导波完整解析理论。研究表明对称型海脊同时存在对称与反对称引导波，其自由水面波动可以表示为虚宗量Bessel函数形式。利用海脊中心对称条件给出了描述其频率与波数的频散关系。基于所提理论进一步分析讨论了引导波的运动特性，包括频散关系、波速度、能量传播速度与波面空间分布等。本研究为揭示地形坡度由脊顶至两侧逐渐增加的海脊引导波运动特征，预测实际越洋海啸中最具威胁性海啸波的到达时间提供了理论依据。
- 海啸 /
- 海脊引导波 /
- 俘获波 /
- 解析解 /
- 线性长波
Abstract: Transoceanic tsunamis can be guided by oceanic ridges and transferred large energy with slower velocity, hitting far-field regions and causing disaster effects. Therefore, the study on guided waves is crucial to improve the understanding of tsunami propagation characteristics. Based on the linear shallow water equation, the complete analytical solutions for guided waves over a parabolic symmetric ridge are derived. It is shown that both symmetric and anti-symmetric guided waves can exist along symmetric ridges and the free surface is described using the modified Bessel functions. Dispersion relationships, determining the relationship between the wave frequency and the wavenumber, are obtained from the continuity of water surface and velocity at the top of the ridge. The kinematic characteristics of guided waves, such as phase velocity, group velocity and surface spatial distribution are further revealed. This paper theoretically elaborates the guided waves over the ridge with its topographic slope generally increasing from the top to the bottom and provides the formulas to predicate the arrival time of the most threatening waves for the actual transoceanic tsunamis.
- tsunamis /
- oceanic guided waves /
- trapped waves /
- analytical solutions /
- linear shallow water equations

HTML全文

图 1 抛物型海脊剖面

Fig. 1 Schematic of parabolic ridge profile

下载: 全尺寸图片幻灯片

图 2 抛物型海脊引导波的频散关系

实线表示偶对称模式，虚线表示奇对称模式

Fig. 2 Dispersion relationships for guided waves over a parabolic ridge

The solid lines indicate the even-symmetric mode and the dashed lines represent the odd-symmetric mode

下载: 全尺寸图片幻灯片

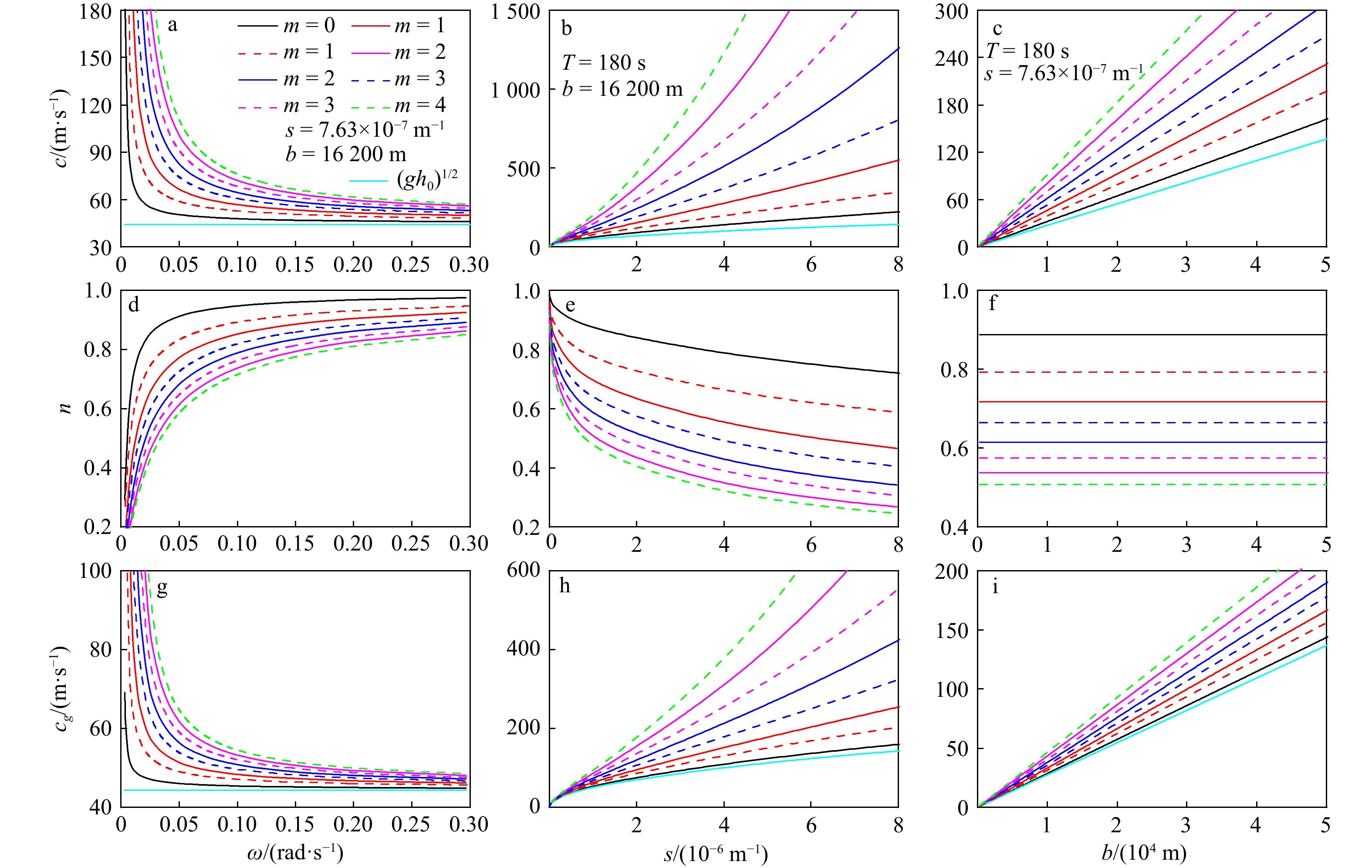
图 3 引导波的相位速度、能量传播速度因子与能量传播速度随角频率ω和地形参数s、b变化示意图

实线表示偶对称模式，虚线表示奇对称模式

Fig. 3 Phase velocity, energy velocity factor and group velocity against angular frequency ω, and ridge shape parameters s, b for guided waves

The solid lines indicate the even-symmetric mode and the dashed lines represent the odd-symmetric mode

下载: 全尺寸图片幻灯片

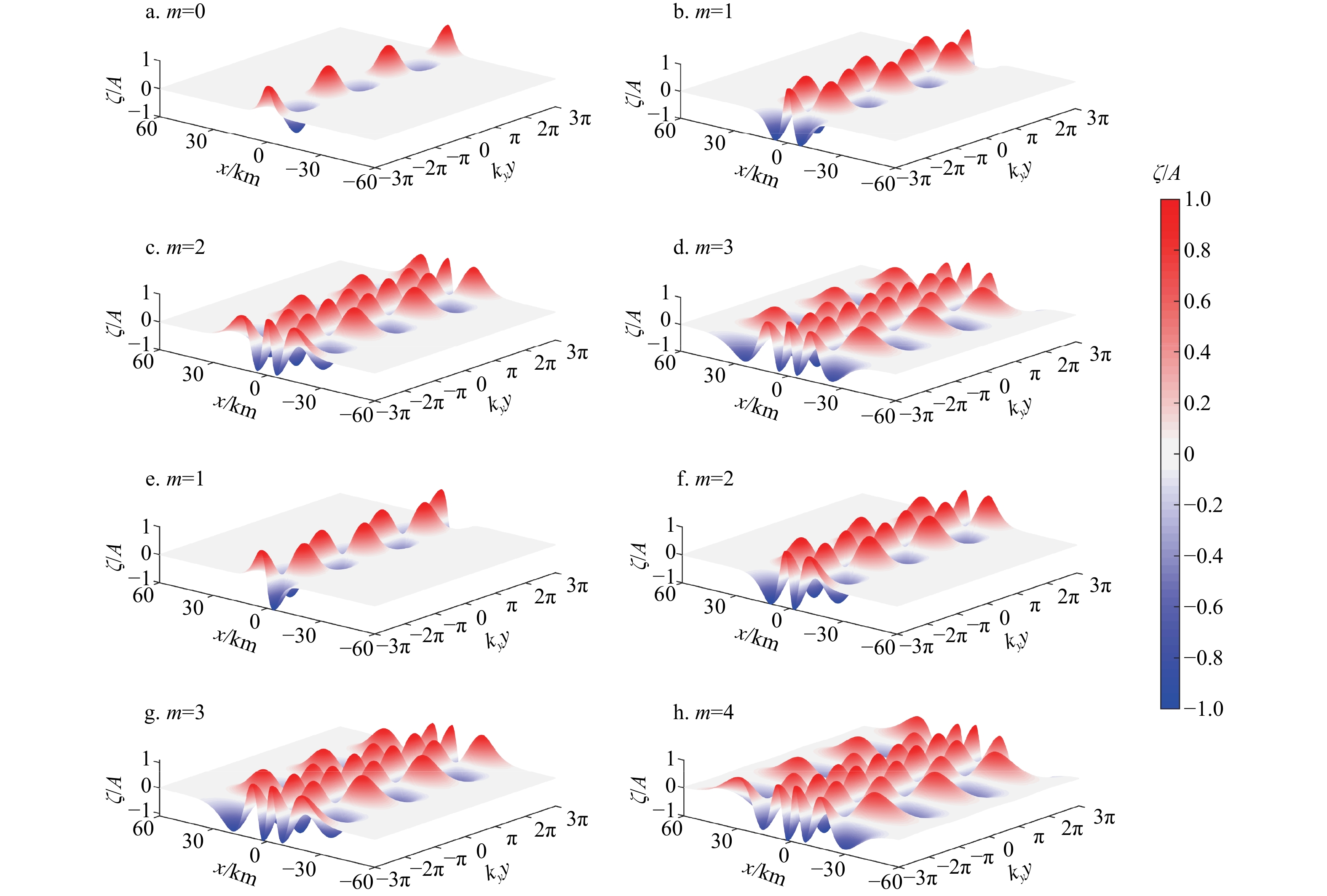
图 4 抛物型海脊引导波沿x方向的空间分布

实线表示偶对称模式，虚线表示奇对称模式（s = 7.63×10⁻⁷ m⁻¹，b = 1.62×10⁴ m，h₀ = 200 m，T = 180 s）

Fig. 4 Spatial distribution of guided waves over a parabolic ridge along the x-axis

The solid lines indicate the even-symmetric mode and the dashed lines represent the odd-symmetric mode (s = 7.63×10⁻⁷ m⁻¹, b = 1.62×10⁴ m, h₀ = 200 m, T = 180 s)

下载: 全尺寸图片幻灯片

图 5 引导波的三维空间分布（s = 7.63×10⁻⁷ m⁻¹，b = 1.62×10⁴ m，h₀ = 200 m，T = 180 s）

a–d为偶对称模式，e–h为奇对称模式

Fig. 5 Three-dimensional spatial distribution of guided waves (s = 7.63×10⁻⁷ m⁻¹，b = 1.62×10⁴ m，h₀ = 200 m，T = 180 s)

a–d indicates the even-symmetric mode and the e–h represents the odd-symmetric mode

下载: 全尺寸图片幻灯片

参考文献(26)

[1]	王岗, 高俊亮, 王培涛, 等. 港湾共振研究综述[J]. 海洋学报, 2017, 39(11): 1−13. Wang Gang, Gao Junliang, Wang Peitao, et al. Review on harbor resonance[J]. Haiyang Xuebao, 2017, 39(11): 1−13.
[2]	Grilli S T, Tappin D R, Carey S, et al. Modelling of the tsunami from the December 22, 2018 lateral collapse of Anak Krakatau volcano in the Sunda Straits, Indonesia[J]. Scientific Reports, 2019, 9(1): 11946. doi: 10.1038/s41598-019-48327-6
[3]	Hu Gui, Feng Wanpeng, Wang Yuchen, et al. Source characteristics and exacerbated tsunami hazard of the 2020 Mw 6.9 Samos earthquake in eastern Aegean Sea[J]. Journal of Geophysical Research: Solid Earth, 2022, 127(5): e2022JB023961.
[4]	Kubota T, Saito T, Nishida K. Global fast-traveling tsunamis driven by atmospheric Lamb waves on the 2022 Tonga eruption[J]. Science, 2022, 377(6601): 91−94. doi: 10.1126/science.abo4364
[5]	Satake K. Effects of bathymetry on tsunami propagation: application of ray tracing to tsunamis[J]. Pure and Applied Geophysics, 1988, 126(1): 27−36. doi: 10.1007/BF00876912
[6]	Koshimura S I, Imamura F, Shuto N. Characteristics of tsunamis propagating over oceanic ridges: numerical simulation of the 1996 Irian Jaya earthquake tsunami[J]. Natural Hazards, 2001, 24(3): 213−229. doi: 10.1023/A:1012038121972
[7]	Wang Yuchen, Satake K, Cienfuegos R, et al. Far-field tsunami data assimilation for the 2015 Illapel earthquake[J]. Geophysical Journal International, 2019, 219(1): 514−521. doi: 10.1093/gji/ggz309
[8]	Heidarzadeh M, Satake K, Takagawa T, et al. A comparative study of far-field tsunami amplitudes and ocean-wide propagation properties: insight from major trans-Pacific tsunamis of 2010−2015[J]. Geophysical Journal International, 2018, 215(1): 22−36. doi: 10.1093/gji/ggy265
[9]	Carvajal M, Sepúlveda I, Gubler A, et al. Worldwide signature of the 2022 Tonga volcanic tsunami[J]. Geophysical Research Letters, 2022, 49(6): e2022GL098153.
[10]	Titov V, Rabinovich A B, Mofjeld H O, et al. The global reach of the 26 December 2004 Sumatra Tsunami[J]. Science, 2005, 309(5743): 2045−2048. doi: 10.1126/science.1114576
[11]	Kowalik Z, Horrillo J, Knight W, et al. Kuril Islands tsunami of November 2006: 1. Impact at Crescent City by distant scattering[J]. Journal of Geophysical Research: Oceans, 2008, 113(C1): C01020.
[12]	He Jianfeng, Zhang Fang, Lin Ling, et al. Effects of the 2010 Chile and 2011 Japan tsunamis on the Antarctic coastal waters as detected via online mooring system[J]. Antarctic Science, 2012, 24(6): 665−671. doi: 10.1017/S0954102012000326
[13]	Gusiakov V K. Strongest tsunamis in the world ocean and the problem of marine coastal security[J]. Izvestiya, Atmospheric and Oceanic Physics, 2014, 50(5): 435−444. doi: 10.1134/S0001433814050041
[14]	Jones D S. The eigenvalues of $\nabla^2 $u + λu=0 when the boundary conditions are given on semi-infinite domains[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1953, 49(4): 668−684. doi: 10.1017/S0305004100028875
[15]	Longuet-Higgins M S. On the trapping of waves along a discontinuity of depth in a rotating ocean[J]. Journal of Fluid Mechanics, 1968, 31(3): 417−434. doi: 10.1017/S0022112068000236
[16]	Buchwald V T. Long waves on oceanic ridges[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1969, 308(1494): 343−354.
[17]	许洋, 王岗, 王培涛, 等. 台阶型海脊俘获波的实验研究[J]. 海洋预报, 2020, 37(2): 29−37. doi: 10.11737/j.issn.1003-0239.2020.02.004 Xu Yang, Wang Gang, Wang Peitao, et al. Experimental investigation on trapped waves over the stepped ridge[J]. Marine Forecasts, 2020, 37(2): 29−37. doi: 10.11737/j.issn.1003-0239.2020.02.004
[18]	Shaw R P, Neu W. Long-wave trapping by oceanic ridges[J]. Journal of Physical Oceanography, 1981, 11(10): 1334−1344. doi: 10.1175/1520-0485(1981)011<1334:LWTBOR>2.0.CO;2
[19]	万鹏, 王岗, 于洪荃, 等. 基于射线理论的海脊俘获波机制[J]. 海洋学报, 2019, 41(11): 35−39. Wan Peng, Wang Gang, Yu Hongquan, et al. Mechanism of trapped wave over an ocean ridge based on the ray theory[J]. Haiyang Xuebao, 2019, 41(11): 35−39.
[20]	于洪荃, 胡见, 王岗, 等. 海啸俘获波在弯曲海脊上的传播规律[J]. 海洋学报, 2020, 42(1): 40−45. Yu Hongquan, Hu Jian, Wang Gang, et al. Trapped tsunami waves propagation over curved ocean ridges[J]. Haiyang Xuebao, 2020, 42(1): 40−45.
[21]	Wang Gang, Liang Qiuhua, Shi Fengyan, et al. Analytical and numerical investigation of trapped ocean waves along a submerged ridge[J]. Journal of Fluid Mechanics, 2021, 915: A54. doi: 10.1017/jfm.2020.1039
[22]	王岗, 胡见, 王培涛, 等. 双曲余弦海脊上海啸俘获波的解析与数值研究[J]. 海洋学报, 2018, 40(5): 15−23. Wang Gang, Hu Jian, Wang Peitao, et al. Analytical and numerical investigation of tsunami trapped waves over a hyperbolic-cosine squared ocean ridge[J]. Haiyang Xuebao, 2018, 40(5): 15−23.
[23]	Killworth P D. How much of a baroclinic coastal kelvin wave gets over a ridge?[J]. Journal of Physical Oceanography, 1989, 19(3): 321−341. doi: 10.1175/1520-0485(1989)019<0321:HMOABC>2.0.CO;2
[24]	Zheng Jinhai, Xiong Mengjie, Wang Gang. Trapping mechanism of submerged ridge on trans-oceanic tsunami propagation[J]. China Ocean Engineering, 2016, 30(2): 271−282. doi: 10.1007/s13344-016-0017-7
[25]	王竹溪, 郭敦仁. 特殊函数概论[M]. 北京: 北京大学出版社, 2012. Wang Zhuxi, Guo Dunren. Introduction to Special Function[M]. Beijing: Peking University Press, 2012.
[26]	张善杰, 金建铭. 特殊函数计算手册[M]. 南京: 南京大学出版社, 2011. Zhang Shanjie, Jin Jianming. Computation of Special Functions[M]. Nanjing: Nanjing University Press, 2011.