Research on laboratory generation method of controllable deep water breaking waves
-
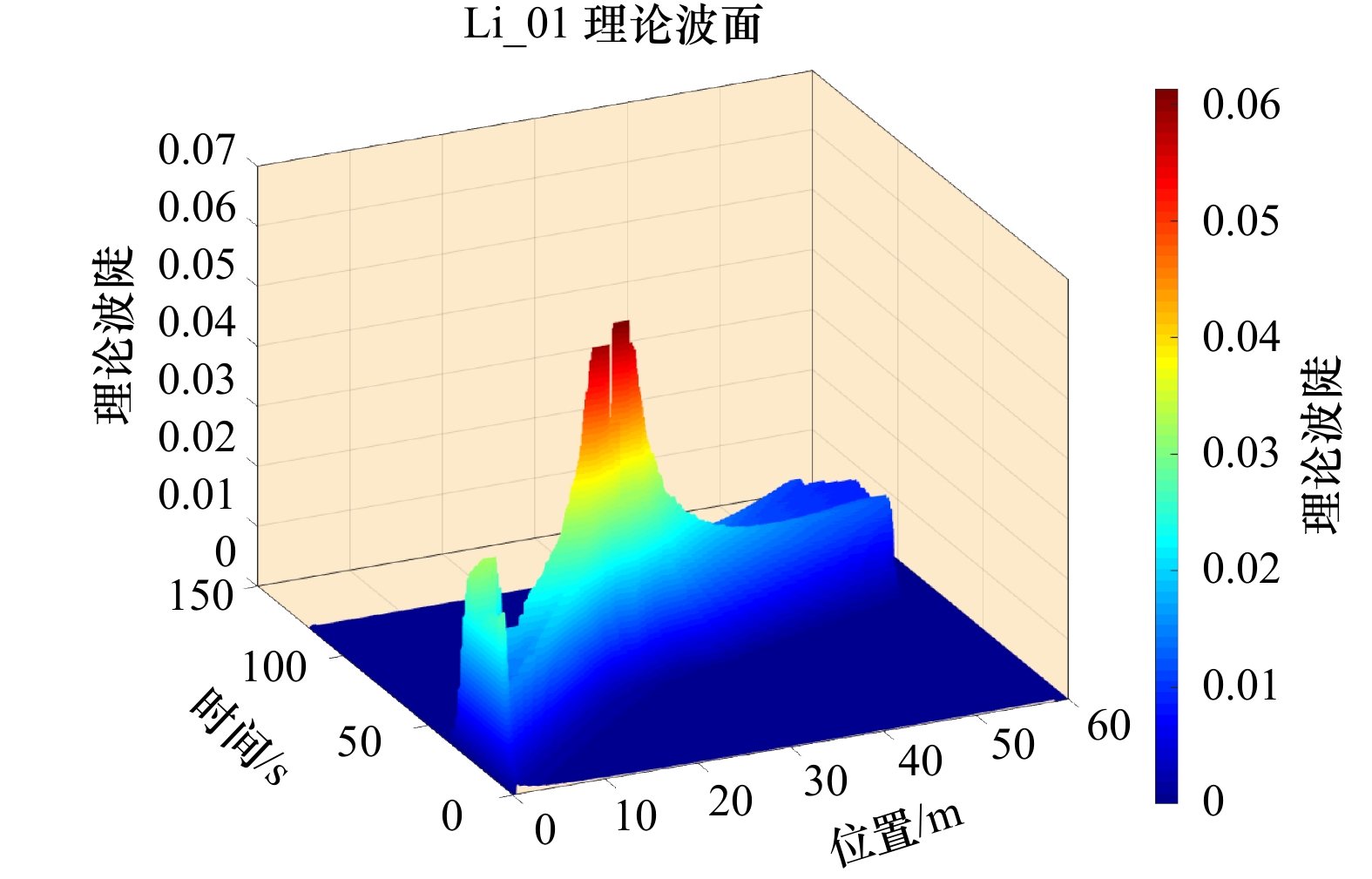
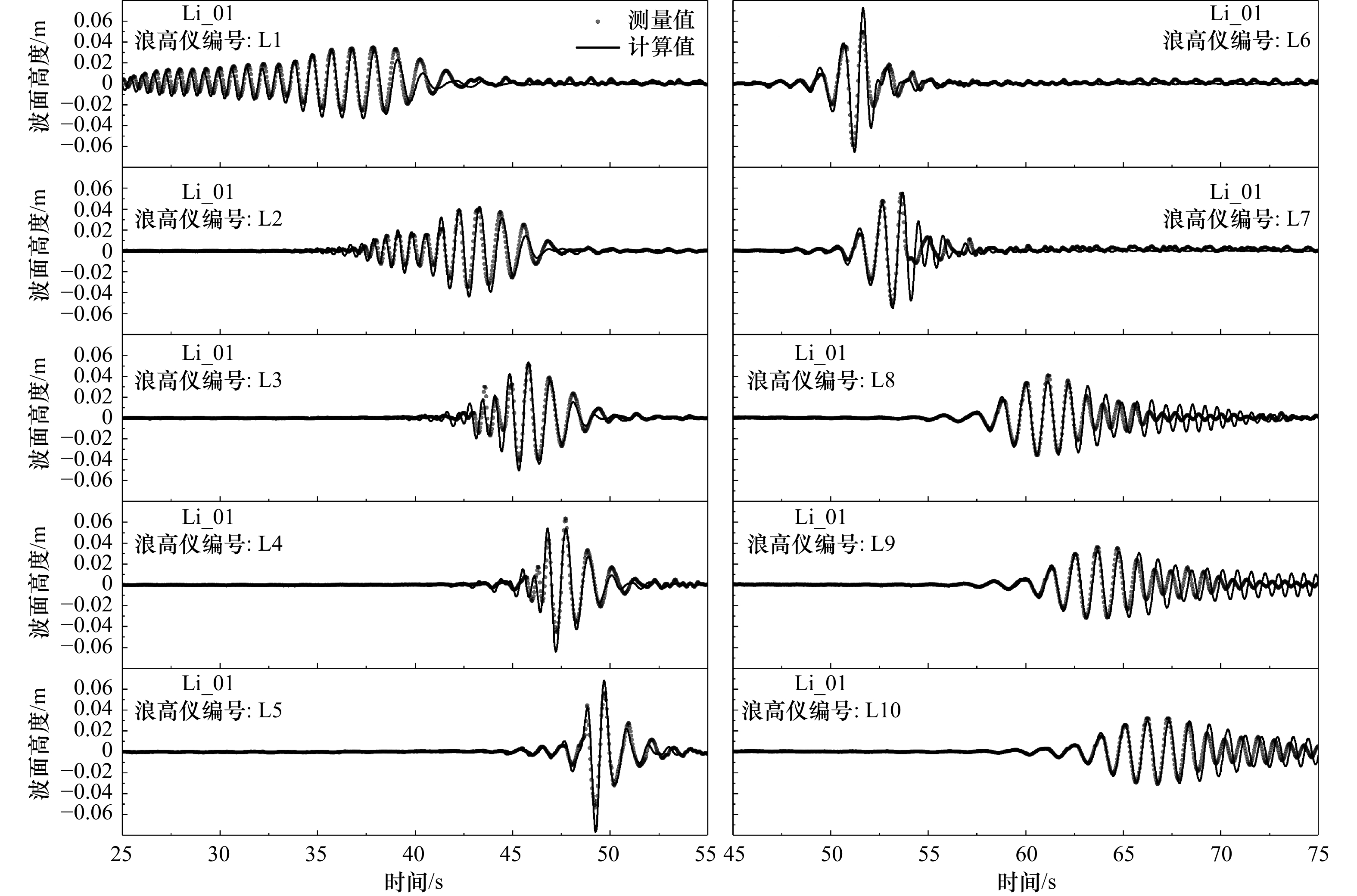
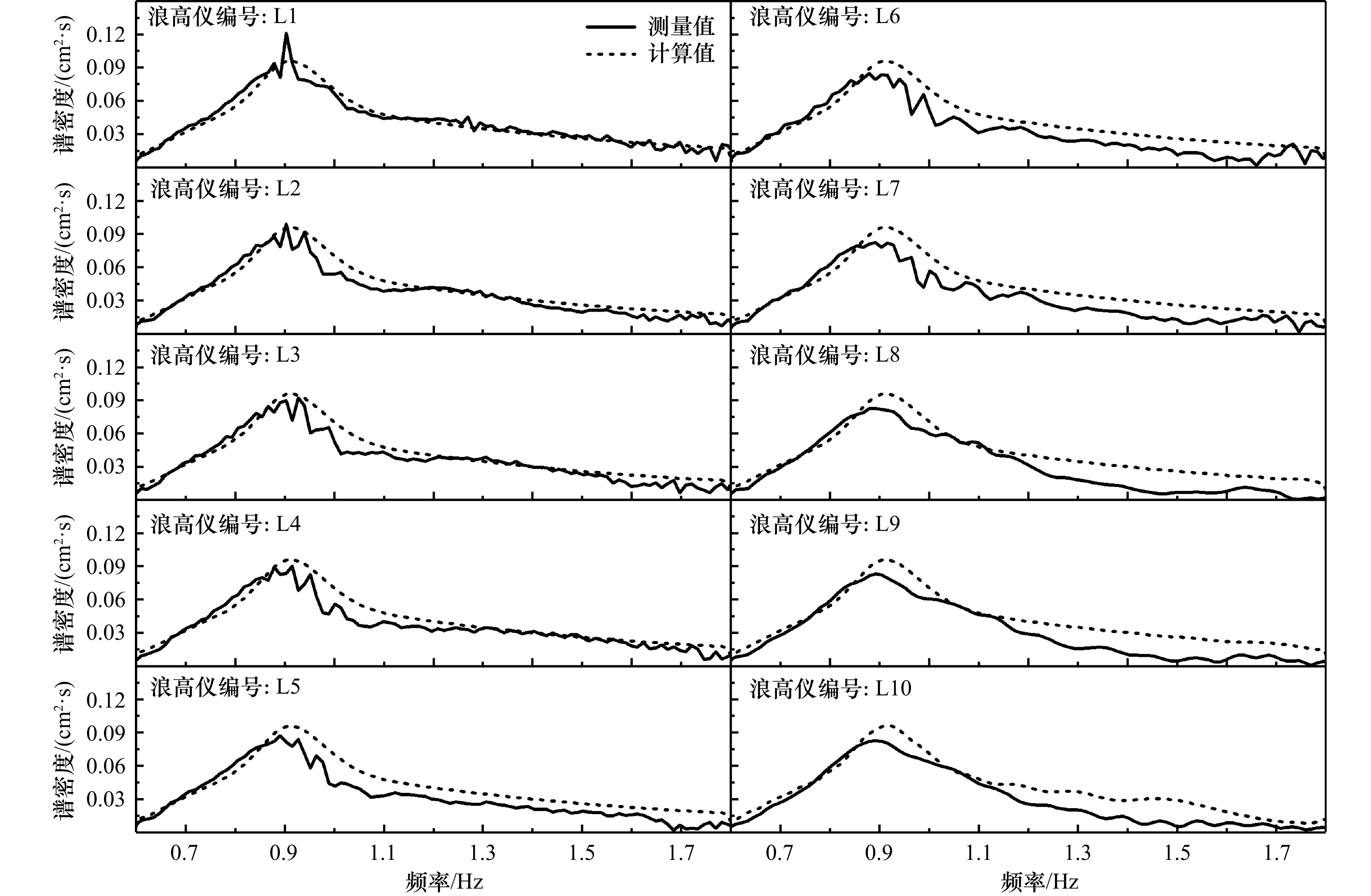
摘要: 实验室一般采用波浪聚焦方法生成深水破碎波，通过各组分波浪的波幅叠加生成一个波高显著增大的大波，使其波陡超过极限波陡发生破碎。利用该方法生成深水破碎波浪的破碎次数通常并不唯一，导致波浪破碎后的流场特征不明显；造波参数不易于选取导致研究工况的设置难度大，直接影响深水破碎精细化实验的效果和效率。本文采用聚焦波理论计算波面，并利用上跨零点法定义的波高和波长计算理论波陡，结合物理模型实验统计波浪沿程破碎次数与剧烈程度，研究以JONSWAP谱为造波输入谱型时，聚焦波幅、谱峰频率、频宽等造波输入参数对于波浪破碎情况的影响，从而建立深水波浪破碎次数与造波输入参数之间的近似定量关系，为实验造波参数的选取提供参考，提高实验效率。Abstract: Deep water breaking wave is usually generated by the wave focusing method in laboratory. A wave with a significantly increased height can be generated by the superposition of components so that wave breaks when the steepness exceeds the limit value. However, using this method, the number of wave breaking is usually not unique leading to less obvious field characteristics after breaking and it’s hard to set research cases due to the difficulty in selecting wave-making parameters. As a result, the effect and efficiency of elaborate deep water wave breaking experiments is affected directly. Theoretical wave surface was calculated by the theory of wave focusing method and theoretical wave steepness was calculated using the wave height and wavelength defined by up-cross-zero method in this paper. On the other hand, wave breaking times and intensity were obtained from the physical experiments. The JONSWAP spectrum was used as the input spectrum and the effects of wave-making parameters, such as focusing amplitude, spectrum peak frequency, frequency bandwidth, on wave breaking were discussed so as to establish an approximate quantitative relationship between breaking times and input parameters. The research conclusions can provide a reference for selection of wave-making parameters so that the efficiency of the experiment can be improved.
-
Key words:
- wave focusing method /
- JONSWAP spectrum /
- deep water wave breaking /
- breaking times
-
图 1 工况Li_01理论波面时空分布
Fig. 1 Spatial and temporal distribution of theoretical wave surface of case Li_01
图 2 工况Li_01理论波陡时空分布
Fig. 2 Spatial and temporal distribution of theoretical wave steepness of case Li_01
图 4 工况Li_01实测波面与理论计算波面对比
Fig. 4 Comparison of wave surface between measurement and theory of case Li_01
图 5 工况Li_01实测波谱与理论波谱对比
Fig. 5 Comparison of wave spectrum between measurement and theory of case Li_01
图 6 工况Li_01、Li_04、Li_07和Li_10波浪沿程理论最大波陡
Fig. 6 Theoretical maximum wave steepness along the tank of case Li_01, Li_04, Li_07 and Li_10
图 7 无量纲化聚焦波幅Ak对波浪全程理论最大波陡的影响
Fig. 7 The effect of the dimensionless focusing-wave-amplitiude Ak on the theoretical maximum wave steepness
图 8 谱峰频率
$ {f_p} $ 对系数$ \alpha $ 的影响Fig. 8 The effect of spectrum peak frequency
$ {f_p} $ on coefficient$ \alpha $ 
图 9 波浪沿程理论最大波陡对破碎次数的影响
Fig. 9 The effect of maximum wave steepness in theory on the wave breaking times along the tank
图 10 工况Li_11、Li_13、Li_15、Li_17和Li_19波浪沿程理论最大波陡
Fig. 10 Theoretical maximum wave steepness along the tank of case Li_11, Li_13, Li_15, Li_17 and Li_19
图 11 谱峰频率fp引起的fp/Δf变化对波浪全程理论最大波陡的影响
Fig. 11 The effect of fp/Δf change induced by the spectrum peak frequency fp on the maximum wave steepness in theory
图 12 谱峰频率fp引起的Smax变化对波浪全程破碎次数的影响
Fig. 12 The effect of Smax change induced by the spectrum peak frequency fp on the wave breaking times along the tank
图 13 频宽∆f引起的fp/∆f变化对波浪全程理论最大波陡的影响
Fig. 13 The effect of fp/∆f change induced by the frequency bandwidth ∆f on the maximum wave steepness in theory
图 14 频宽
$ \Delta f $ 引起的$ f_p/\Delta f $ 变化对波浪全程破碎次数的影响Fig. 14 The effect of
$f_p/\Delta f $ change induced by the frequency bandwidth$ \Delta f $ on the wave breaking times along the tank
图 15 波浪仅发生一次破碎时，聚焦波幅A实测值与计算值对比
Fig. 15 Comparison of focusing wave amplitude A between measurement and theory under the condition of single break
图 16 利用计算造波参数作参考值生成的仅一次破碎波浪入水过程（卷破）
Fig. 16 The process of single break entrying into water with input calculated parameters (plunging)
表 1 实验工况设置
Tab. 1 Experiment cases setting
工况 聚焦波幅A/m 峰频fp/Hz 最小截止频率
F1/Hz最大截止频率
FN/Hz聚焦位置xb/m 聚焦时间tb/s Li_01−Li_10 0.08,
0.10～0.13, △=0.01 m,
0.15,
0.17～0.20, △=0.01 m0.91 0.60 1.80 20 50 Li_11−Li_28 0.12 0.70～0.90, △=0.05 Hz,
0.95～1.35, △=0.05 Hz,
1.40～1.70, △=0.1 Hz0.60 1.80 20 50 Li_29−Li_35 0.12 0.91 0.50～0.55, △=0.05 Hz
0.65～0.85, △=0.05 Hz1.80 20 50 Li_36−Li_50 0.12 0.91 0.60 1.00～1.35, △=0.05 Hz,
1.40～2.00, △=0.1 Hz20 50 注：“△”表示对应参数取值步长。 
下载: 导出CSV
表 2 浪高仪编号与位置
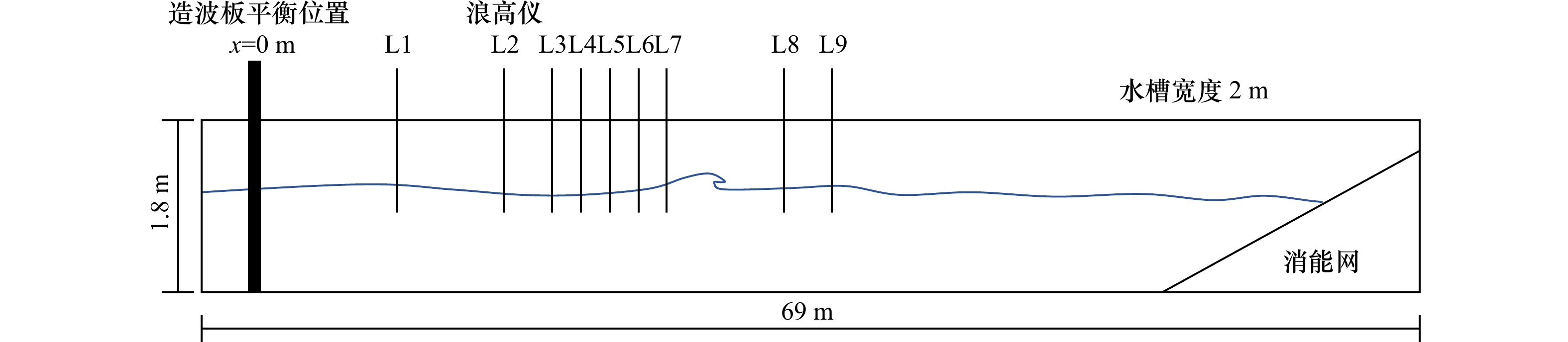
Tab. 2 Wave gauges number and locations
浪高仪编号 L1 L2 L3 L4 L5 L6 L7 L8 L9 安装位置/m 8.9 14.5 17 18.5 20 21.5 23 30 32.5
下载: 导出CSV
表 3 各实验工况实际破碎次数统计
Tab. 3 Actual breaking times statistics of each case
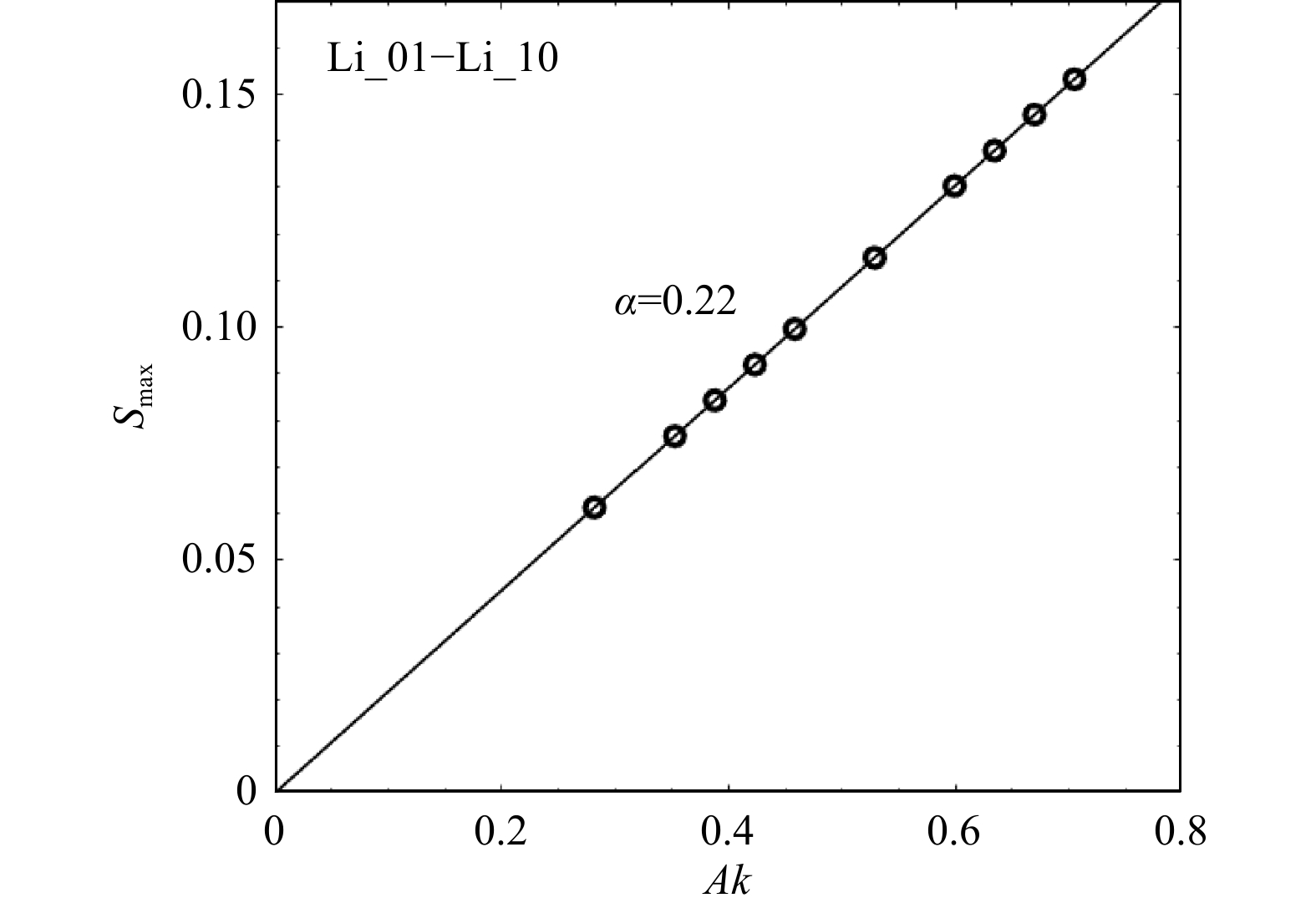
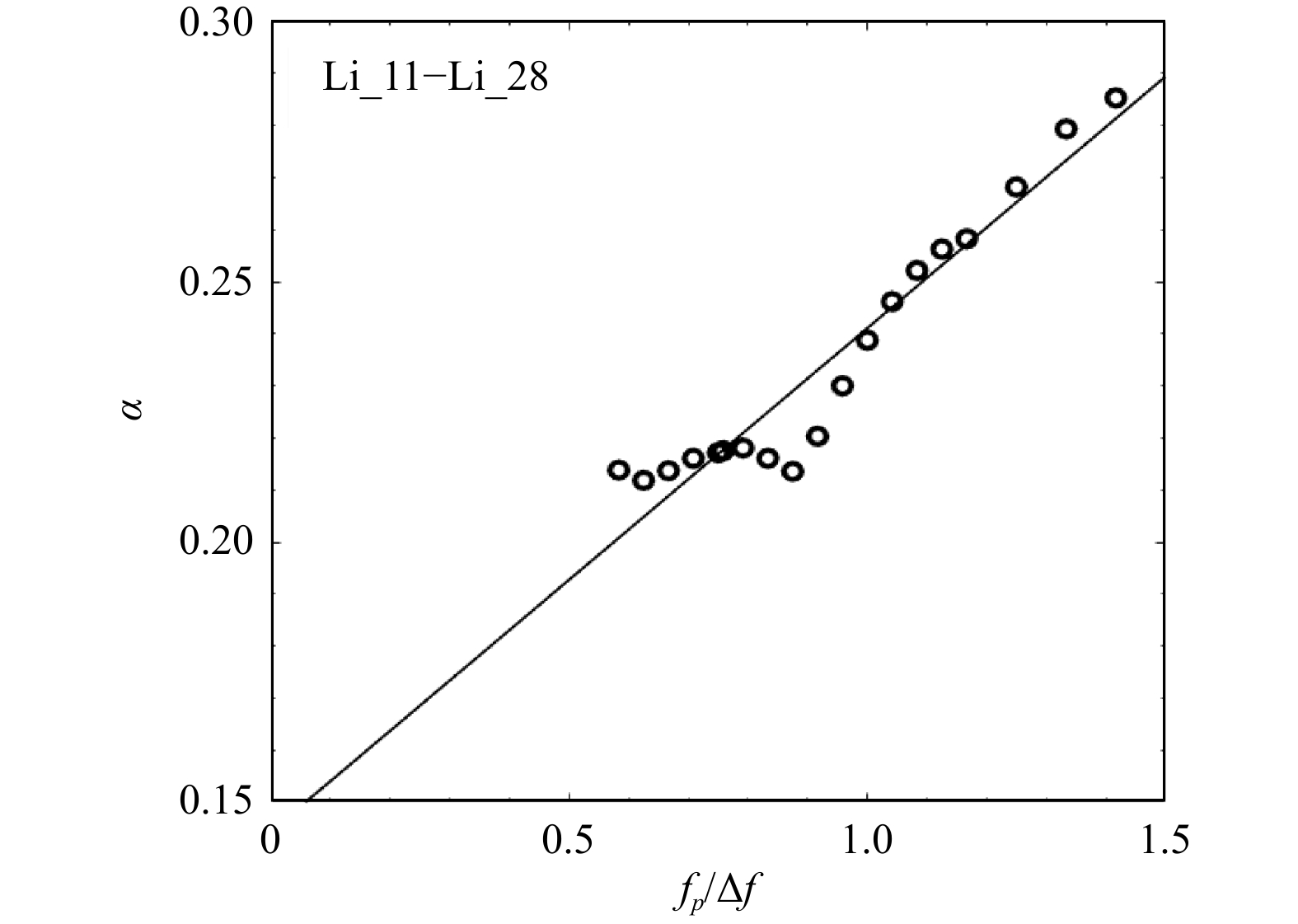
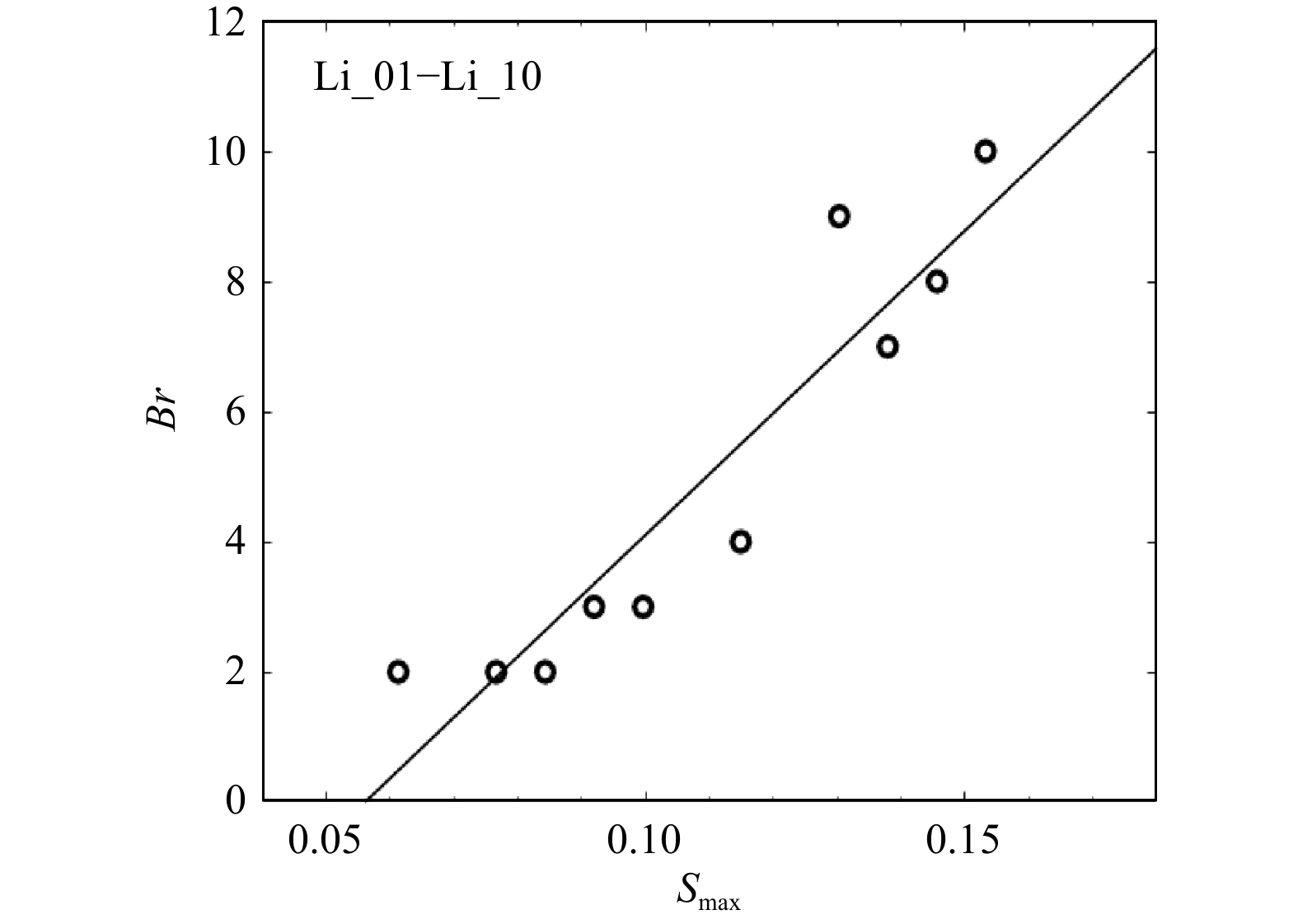
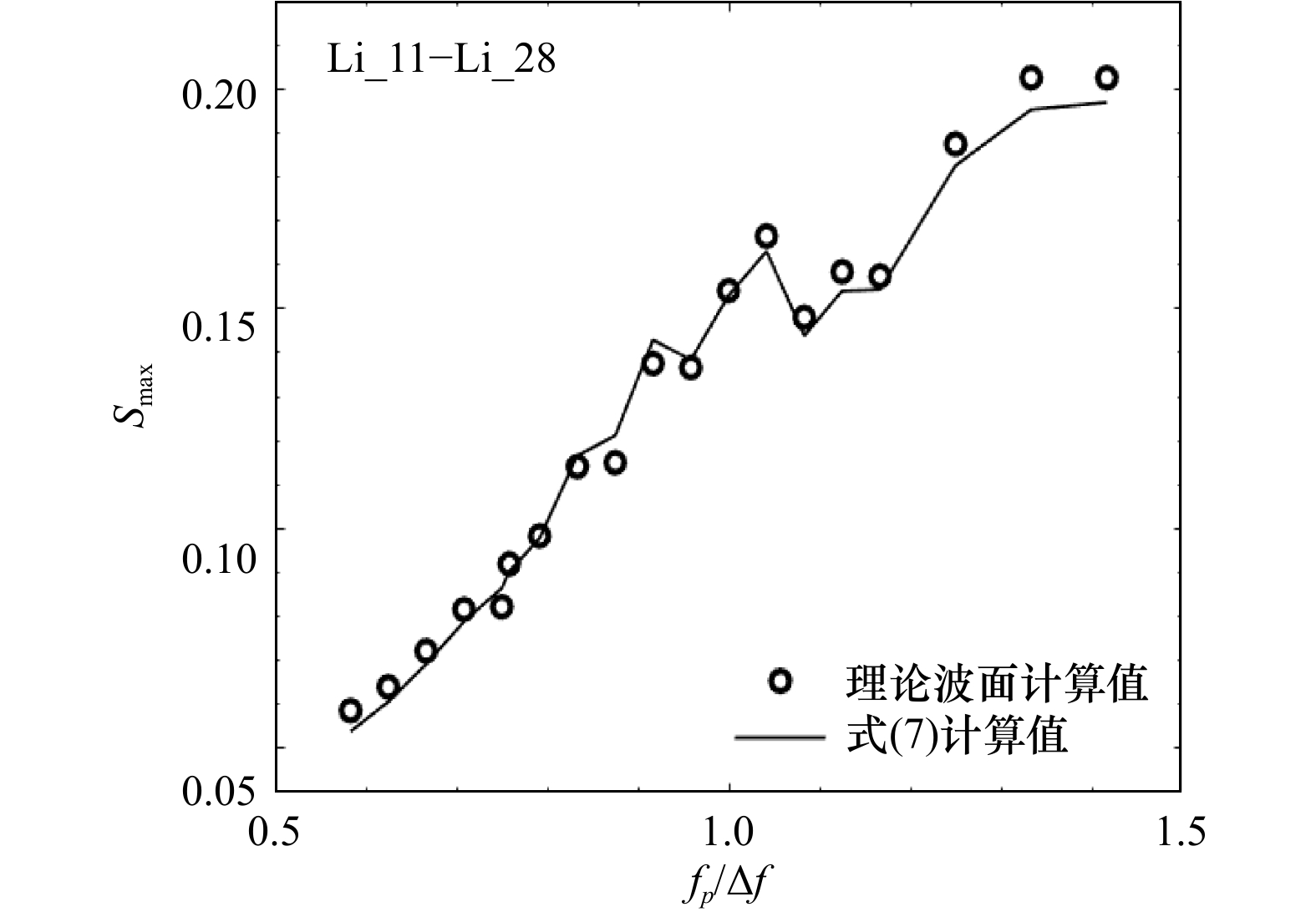
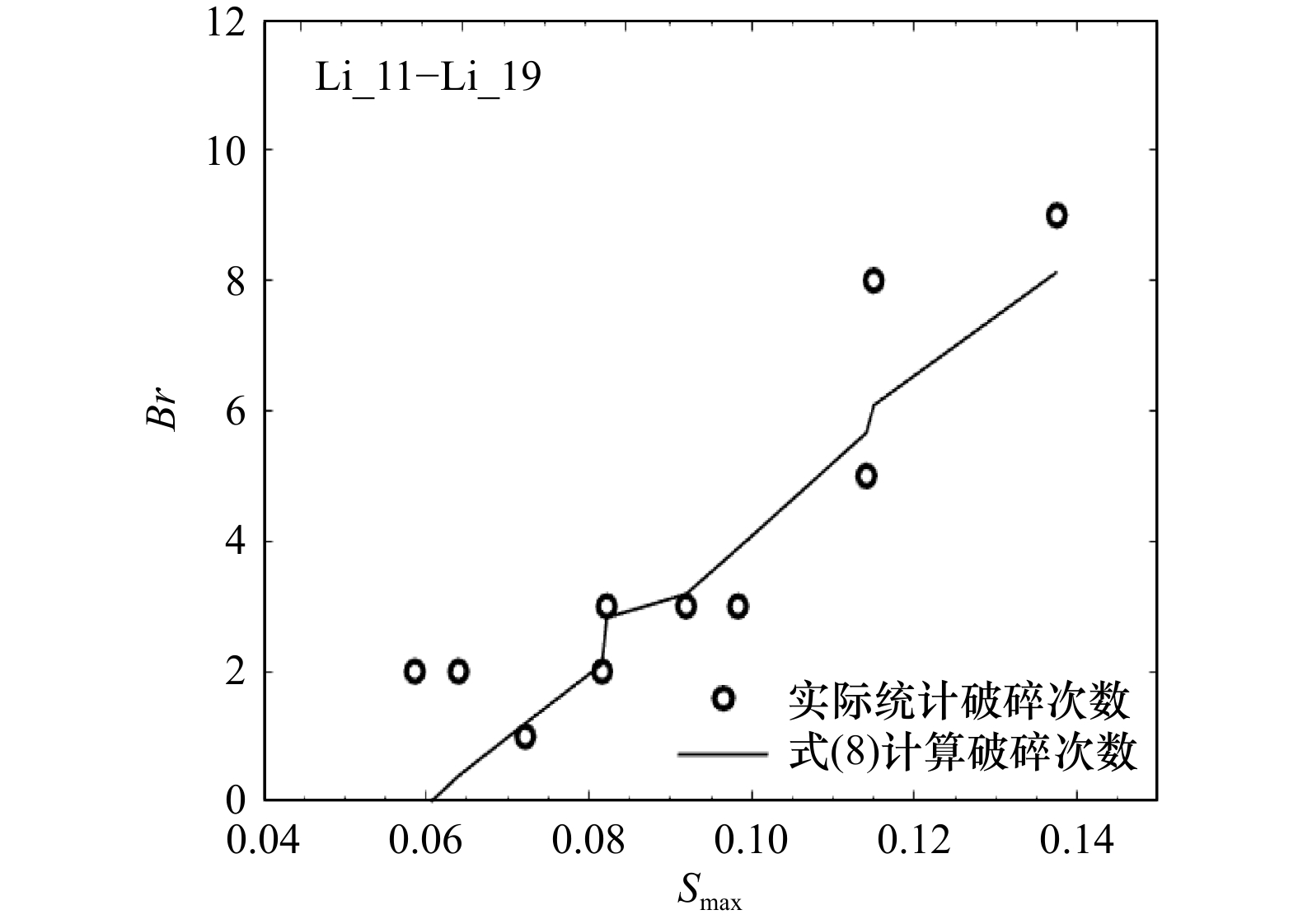
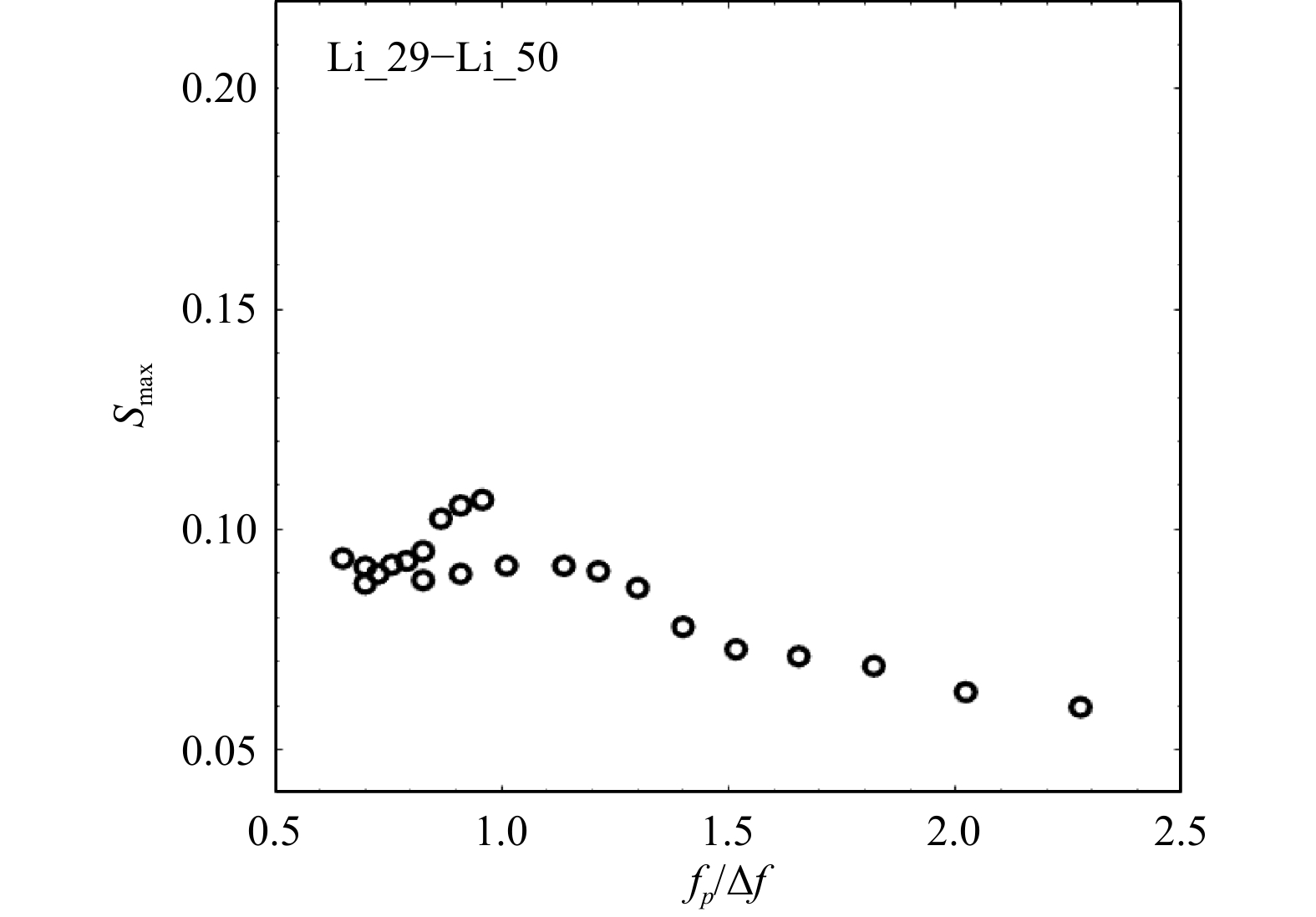
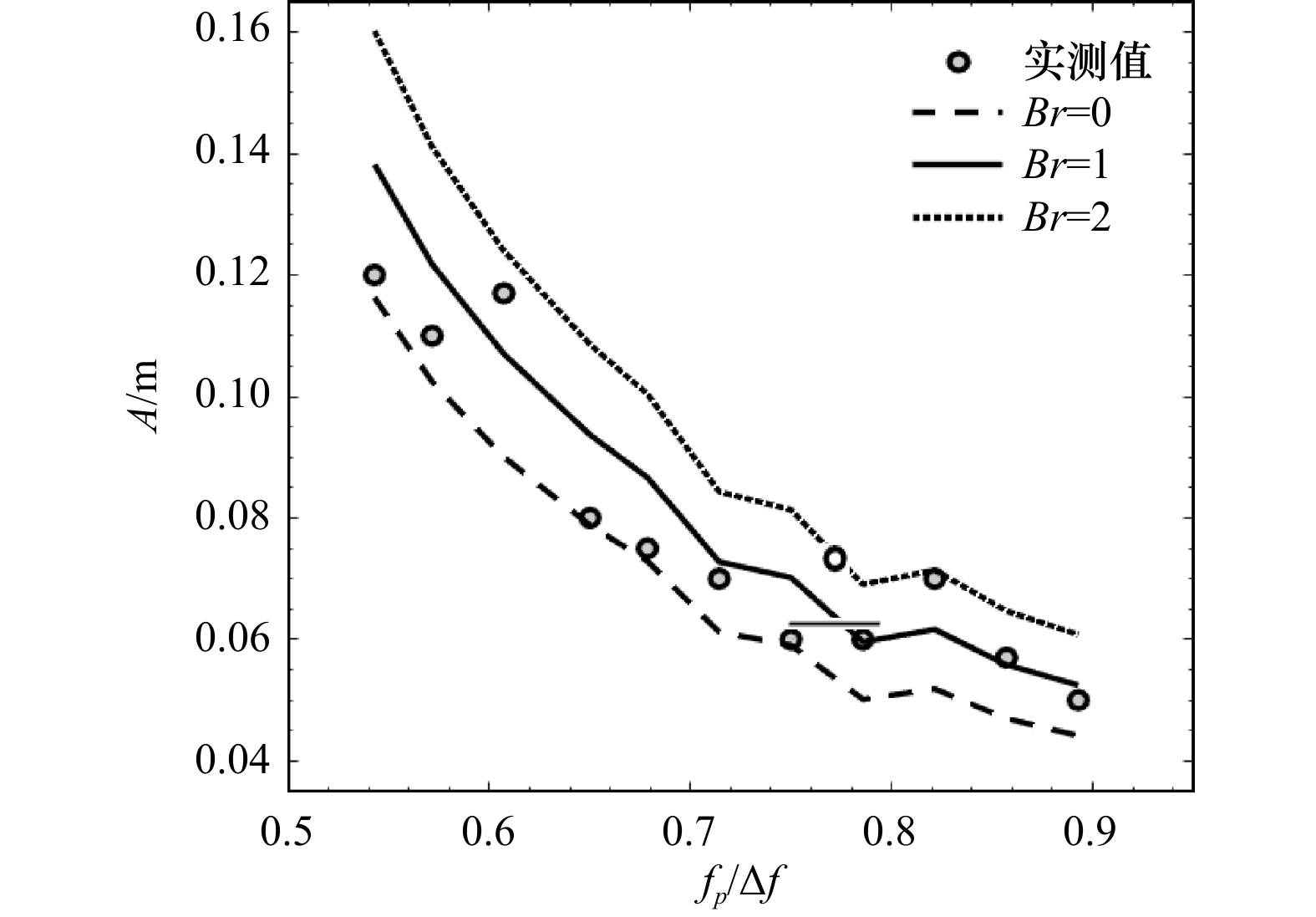
工况 前 中 后 合计 参数变化 参数值 工况 前 中 后 合计 参数变化 参数值 Li_01 1 1 0 2 聚焦波幅A递增（m） 0.08 Li_26 沿程连续破碎破碎次数无法统计 峰频fp递增（Hz） 1.50 Li_02 1 0 1 2 0.10 Li_27 1.60 Li_03 1 0 1 2 0.11 Li_28 1.70 Li_04 1 1 1 3 0.12 Li_29 1 1 1 3 最小截止频率 F1递增（Hz） 0.50 Li_05 1 1 1 3 0.13 Li_30 1 1 1 3 0.55 Li_06 3 1 0 4 0.15 Li_04 1 1 1 3 0.60 Li_07 4 1 4 9 0.17 Li_31 1 1 1 3 0.65 Li_08 4 1 2 7 0.18 Li_32 1 1 1 3 0.70 Li_09 5 1 2 8 0.19 Li_33 2 1 1 4 0.75 Li_10 5 1~2 4 10~11 0.20 Li_34 3 1 0 4 0.80 Li_11 0 1 1 2 峰频fp递增（Hz） 0.70 Li_35 4 1 0 5 0.85 Li_12 0 1 1 2 0.75 Li_36 3 1 2 6 最大截止频率FN递增（Hz） 1.00 Li_13 0 1 0 1 0.80 Li_37 4 0 2~3 6~7 1.05 Li_14 1 1 0 2 0.85 Li_38 5 1 4~5 10~11 1.10 Li_15 1~2 1 0 2~3 0.90 Li_39 5 0 5~6 10~11 1.15 Li_04 1 1 1 3 0.91 Li_40 5 0 5 10 1.20 Li_16 2 1 0 3 0.95 Li_41 5 0 4 9 1.25 Li_17 4 1 0 5 1.00 Li_42 4 0 4 8 1.30 Li_18 6 1 1 8 1.05 Li_43 4 1 3 8 1.35 Li_19 6 0 3 9 1.10 Li_44 4 1 1 6 1.40 Li_20 6 2 >6 >14 1.15 Li_45 3 1 1 5 1.50 Li_21 >7 2 >5~6 >15 1.20 Li_46 2 1 1 4 1.60 Li_22 >9 1 >5 >15 1.25 Li_47 1 1 1 3 1.70 Li_23 >10 1 >5 >16 1.30 Li_04 1 1 1 3 1.80 Li_24 >11 1 >9 >21 1.35 Li_49 1 1 1 3 1.90 Li_25 沿程连续破碎破碎次数无法统计 1.40 Li_50 1 1 0 2 2.00
下载: 导出CSV
-
[1] Terray E A, Donelan M A, Agrawal Y C, et al. Estimates of kinetic energy dissipation under breaking waves[J]. Journal of Physical Oceanography, 1996, 26(5): 792−807. doi: 10.1175/1520-0485(1996)026<0792:EOKEDU>2.0.CO;2 [2] Lueck R G, Huang D, Newman D, et al. Turbulence measurement with a moored instrument[J]. Journal of Atmospheric and Oceanic Technology, 1997, 14(1): 143−161. doi: 10.1175/1520-0426(1997)014<0143:TMWAMI>2.0.CO;2 [3] Ticona Rollano F, Brown A, Ellenson A, et al. Breaking waves in deep water: measurements and modeling of energy dissipation[J]. Ocean Dynamics, 2019, 69(10): 1165−1179. doi: 10.1007/s10236-019-01301-2 [4] Callaghan A H, Deane G B, Stokes M D, et al. Observed variation in the decay time of oceanic whitecap foam[J]. Journal of Geophysical Research: Oceans, 2012, 117(C9): C09015. [5] Sutherland G, Ward B, Christensen K H. Wave-turbulence scaling in the ocean mixed layer[J]. Ocean Science, 2013, 9(4): 597−608. doi: 10.5194/os-9-597-2013 [6] Sullivan P P, McWilliams J C, Melville W K. Surface gravity wave effects in the oceanic boundary layer: large-eddy simulation with vortex force and stochastic breakers[J]. Journal of Fluid Mechanics, 2007, 593: 405−452. doi: 10.1017/S002211200700897X [7] 詹杰民, 李熠华. 波浪破碎的一种混合湍流模拟模式[J]. 力学学报, 2019, 51(6): 1712−1719. doi: 10.6052/0459-1879-19-321Zhan Jiemin, Li Yihua. A hybrid turbulence model for wave breaking simulation[J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(6): 1712−1719. doi: 10.6052/0459-1879-19-321 [8] Kudryavtsev V, Shrira V, Dulov V, et al. On the vertical structure of wind-driven sea currents[J]. Journal of Physical Oceanography, 2008, 38(10): 2121−2144. doi: 10.1175/2008JPO3883.1 [9] Lamarre E, Melville W K. Air entrainment and dissipation in breaking waves[J]. Nature, 1991, 351(6326): 469−472. doi: 10.1038/351469a0 [10] Lim H, Chang Kuangan, Huang Zhicheng, et al. Experimental study on plunging breaking waves in deep water[J]. Journal of Geophysical Research: Oceans, 2015, 120(3): 2007−2049. doi: 10.1002/2014JC010269 [11] Tian Zhigang, Perlin M, Choi W. Energy dissipation in two-dimensional unsteady plunging breakers and an eddy viscosity model[J]. Journal of Fluid Mechanics, 2010, 655: 217−257. doi: 10.1017/S0022112010000832 [12] Rapp R J. Laboratory measurements of deep water breaking waves[D]. Cambridge: Massachusetts Institute of Technology, 1986. [13] 张怡辉. 海浪模式白浪耗散项的改进和海洋水体混合过程的研究[D]. 大连: 大连理工大学, 2016.Zhang Yihui. The study of whitecapping dissipation improvement in wave model and the ocean mixing process[D]. Dalian: Dalian University of Technology, 2016. [14] Banner M L, Peirson W L. Wave breaking onset and strength for two-dimensional deep-water wave groups[J]. Journal of Fluid Mechanics, 2007, 585: 93−115. doi: 10.1017/S0022112007006568 [15] Longuet-Higgins M S. Breaking waves in deep or shallow water[C]//Proceedings of the 10th Symposium on Naval Hydrodynamics. Washington: Government Printing Office, 1974. [16] Melville W K, Veron F, White C J. The velocity field under breaking waves: coherent structures and turbulence[J]. Journal of Fluid Mechanics, 2002, 454: 203−233. doi: 10.1017/S0022112001007078 [17] 常艳玲. 波浪破碎过程周期演化特征的试验研究[D]. 大连: 大连理工大学, 2016.Chang Yanling. Experimental study on the evolution characteristics of wave periods of breaking waves[D]. Dalian: Dalian University of Technology, 2016. [18] 黄金刚. 二维聚焦极限波浪的模拟研究[D]. 大连: 大连理工大学, 2004.Huang Jin’gang. The study of numerical and physical simulation of two-dimensional focusing waves[D]. Dalian: Dalian University of Technology, 2004. [19] 俞聿修. 随机波浪及其工程应用[M]. 大连: 大连理工大学出版社, 2003.Yu Yuxiu. Random Wave and Its Applications for Engineering[M]. Dalian: Dalian University of Technology Press, 2003. [20] Goda Y. A comparative review on the functional forms of directional wave spectrum[J]. Coastal Engineering, 1999, 1(41): 1−20. -
计量
- 文章访问数: 401
- HTML全文浏览量: 183
- PDF下载量: 33
- 被引次数: 0
