Separation method of wind-wave and swell based on the multilayer perceptron
-
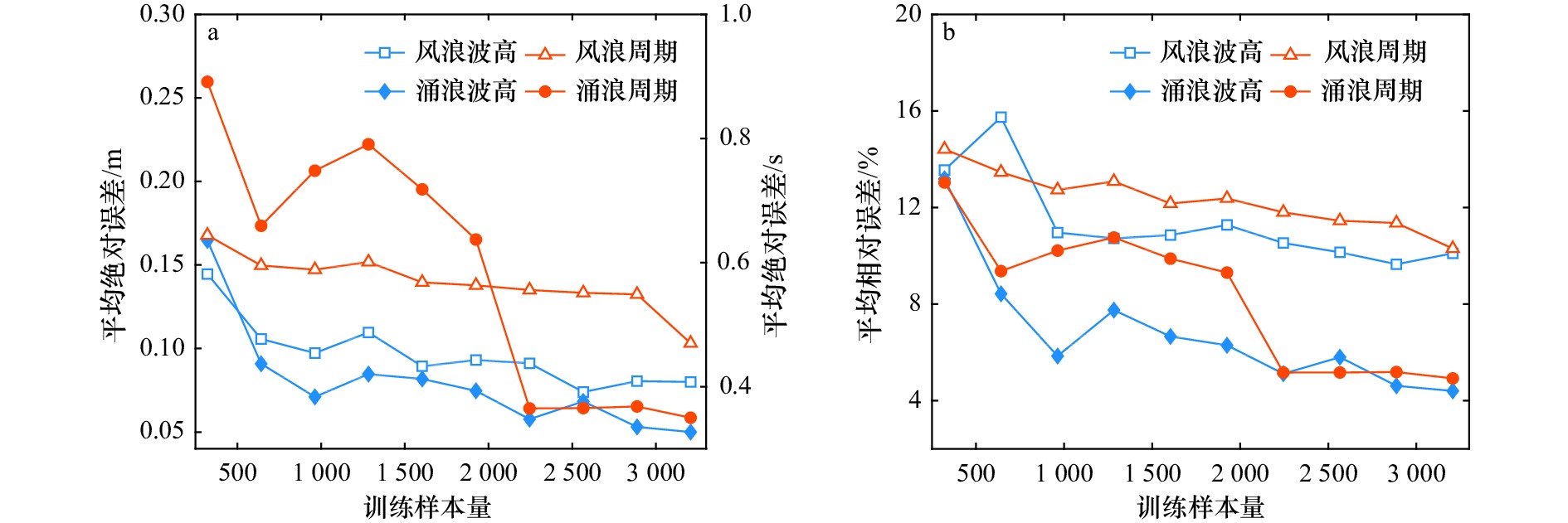
摘要: 风涌浪分离是研究风浪、涌浪各自特性的基础，但受限于海浪谱数据的匮乏，基于海浪谱的风涌浪分离方法难以普及应用，有效的解决办法是采用波浪观测中容易获取的基本波要素进行风涌浪分离。现有方法无法利用基本波要素全面计算出风浪、涌浪的比例及其特征参数，为此本文将机器学习引入到风涌浪分离中，以多层感知器模型为基础，提出了一种利用基本波要素、风要素准确计算出风涌浪参数的方法。该方法需要每个测站提供至少466笔、建议766笔及以上的实测波浪数据作为训练样本，适用于台湾海峡3个测站，在计算精度上显著优于基于海浪频谱的传统风涌浪分离方法，可为本海域缺乏海浪谱的测站提供替代性的风涌浪计算方案，有助于扩大实测风涌浪资料的来源，进而加强风涌浪分布特性以及预警预报研究。Abstract: Separation of wind-wave and swell is the basis for studying the respective characteristics of wind-wave and swell. However, due to the lack of wave spectrum data, it is difficult to popularize and apply separation methods based on wave spectrums. An effective solution is to use wave observations that are easy to obtain, namely basic wave elements to separate wind-wave and swell. Existing methods cannot use basic wave elements to comprehensively calculate the proportions and characteristic parameters of wind-wave and swell. For this reason, this paper introduces machine learning into the separation of wind-wave and swell. Based on the multi-layer perceptron model, a method using wave elements and wind elements to accurately estimate wind-wave and swell parameters is proposed. This method requires each station to provide at least 466 training samples of wave data and 766 or more training samples are recommended. The method is suitable for 3 stations in the Taiwan Strait with its accuracy significantly better than traditional methods based on wave spectrums. The proposed method can provide alternative calculation schemes of wind-wave and swell for stations lacking wave spectrums in this sea area. It helps expand the source of measured data of wind-wave and swell, therefore strengthening the research on the characteristics and early warning and forecasting of wind-wave and swell.
-
Key words:
- separation of wind-wave and swell /
- Taiwan Strait /
- machine learning /
- swell /
- wind-wave
-
1. 引言
在实际的海洋中，波浪往往是以混合浪的形式存在，混合浪由风浪和涌浪相互叠加而成。风浪是在风的吹拂下直接形成的波浪，涌浪是风浪离开风区或外海传播而来的波浪。由于风浪和涌浪在动力成因、外观形态、传播特性、破碎条件等诸多方面均有明显区别，因此在进行相关研究时，有必要将风浪和涌浪分开处理。以涌浪为例，由于涌浪具有长周期的特性，容易与船舶、海洋平台发生共振，影响正常的海上施工、生产作业[1]，浅水涌浪形成的拍岸浪也威胁着近岸人员的生命安全，对于台湾海峡等涌浪普遍存在的海域[2]，提出精确易用的风涌浪分离方法，有助于开展涌浪特性研究进而规避涌浪灾害，保护人民生命财产安全。
学术界已针对风涌浪分离的问题进行了诸多探索，目前学者们提出的风涌浪分离方法主要可以分为两类：波要素法与海浪谱法。汪炳祥等[3]、郭佩芳等[4]基于风速、有效波高等基本风、浪要素定义了特征因子，可判别纯风浪、纯涌浪、风涌浪并存等简单情形。Yang等[5]提出了一种查表法，可根据风速和混合浪有效波高快速查出对应的风浪波高。上述波要素法能快速判别混合浪中是否存在涌浪，但无法全面计算风浪、涌浪的特征参数。海浪谱法常使用频谱（一维谱）或方向谱（二维谱），所以可以根据海浪谱的维数将海浪谱法分为一维谱法和二维谱法。Earle[6]基于PM风浪谱提出一种可以快速计算风浪、涌浪分割频率的方法（PM法）。Wang和Hwang [7]利用涌浪波陡小于风浪波陡的性质构造了一个波陡函数，并给出了波陡函数的峰值频率与风涌浪分割频率之间的定量关系式（WH法），后来Hwang等[8]又对该方法做了改进（改进的WH法）。Portilla等[9]按照一定的标准将海浪频谱划分为多个波系统，依据风浪的超射特性将每个波系统识别为风浪或涌浪（JP法）。上述4种方法是具有代表性的传统一维谱法，近年来，朱绍华等[10]以Jonswap谱模拟海浪谱的高频峰和低频谱，分别表示双峰谱的风浪成分和涌浪成分。林伊楠等[11]将Earle和Hwang的方法相结合，提出了一种适用于台湾海峡的风涌浪分离方法。二维谱法[12]以海浪方向谱作为判据，通过分析不同方向、频率的波浪与风之间的相对关系实现风浪、涌浪的分离，被公认为目前最准确、稳定的风涌浪分离方法[13]。由于现有的国家海洋观测标准[14]只要求海浪观测提供基本波要素、海况和波型数据，加上波浪观测技术的限制，一些波浪测站仅有基本波要素数据，缺少海浪谱资料，导致准确性相对较高的海浪谱法常常无法使用，以致于关于实测风涌浪的研究工作难以开展，为此迫切需要一种既有数据易于获取的优点，也能保证较高的计算精度的新的风涌浪分离方法。
近年来，机器学习的发展为波浪研究提供了新思路。作为数据驱动的统计模型，机器学习无需理解海洋物理过程的复杂机制，而是通过大量样本的训练，直接拟合输入因子和输出结果之间的函数关系。Meng等[15]以气压、距台风中心距离等气象因子作为输入，基于循环神经网络准确预报了台风浪波高，Nikoo等[16]依据模糊K最近邻算法，利用历史风数据建立了高精度的有效波高预报模型。这表明机器学习模型具有较好的自适应学习和非线性映射能力，有应用于风涌浪分离的潜力。
基于以上背景，本文将机器学习引入到风涌浪分离中，以多层感知器模型为基础，提出了一种利用基本波要素、风要素就能准确计算出风浪、涌浪特征参数的方法，而且在准确性上高于现有的一维谱法。该方法兼具了易用性和准确性，可在海浪谱资料缺失的条件下实现高精度的风涌浪分离，从而扩大实测风浪、涌浪资料的来源，为进一步的研究提供数据保证，也有助于评估机器学习在风涌浪计算上的表现。
2. 传统风涌浪分离方法介绍
2.1 二维谱法
Hanson和Phillips [12]提出的二维谱法得到了广泛的认可，该方法采用Komen等[17]提出的判别式作为区分风浪和涌浪的标准，如式（1）所示：
$$ {f_s} = \frac{g}{{2{\text{π}} }}{\left[ {C{U_{10}}\cos \left( {\theta - {\theta _{{\rm{wind}}}}} \right)} \right]^{ - 1}}\qquad \left| {\theta - {\theta _{{\rm{wind}}}}} \right| < \frac{{\text{π}} }{2} \text{，} $$ (1) 式中，
$ {f_s} $ 是分割频率；$ g $ 是重力加速度；$ C $ 是可调系数，一般取1.0～1.9之间的值；$ {U_{10}} $ 表示10 m高度处的风速；$ {\theta _{{\rm{wind}}}} $ 代表风向，是定值；$ \theta $ 代表波向，是变量，当$ \theta $ 一定时，将海浪方向谱中频率高于$ {f_s} $ 的成分判定为风浪，频率低于$ {f_s} $ 的成分判定为涌浪。根据式（1）完成风涌浪分离后，为了计算风浪、涌浪的特征参数，参考海浪数值模式WAVEWATCH III的技术手册[18]，先按照式（2）分别求出风浪波系统和涌浪波系统的海浪谱n阶矩
$ {m_n} $ ，再基于$ {m_n} $ 进一步求得两个波系统的有效波高H和平均周期T，作为风浪、涌浪的有效波高和平均周期。$$ {m_n} = \int {{f^n}S(f,\theta )} {\text{ d}}f{\text{d}}\theta \text{，} $$ (2) $$ H = 4\sqrt {{m_0}} \text{，} $$ (3) $$ T = \sqrt {\frac{{{m_0}}}{{{m_2}}}} \text{，} $$ (4) 式中，
$ S(f,\theta ) $ 是海浪方向谱；$ f $ 是频率；$ \theta $ 是波向；$ {m_n} $ 是海浪谱n阶矩；H和T分别是基于谱计算出的有效波高和平均周期。2.2 一维谱法
二维谱法考虑的海浪信息全面、准确性高，然而由于波浪观测技术的限制，大量海洋波浪站无法提供二维谱数据，进而导致二维谱法常常无法应用。相比之下，一维谱法所需要的海浪频谱数据，相对更易观测，因此一维谱法的普及度更高。上文提及的PM法[6]、WH法[7]、改进的WH法[8]和JP法[9]是4种应用广泛的一维谱法，林伊楠等[11]又在PM法和改进的WH法基础上提出了一种新的一维谱法，这些方法的实现过程可参考原文献。本文5.5节将本文提出的多层感知器法与上述5种一维谱法做了对比。
3. 实测数据介绍与处理
本文获取了M1、M2和M3测站的实测波浪数据，3个测站位于台湾海峡的不同区域（图1a）。各测站的水深信息、数据量及时间范围见表1。各测站均记录了逐时的混合浪波要素和风要素数据，包括混合浪有效波高、混合浪平均周期、混合浪平均波向、10 m高度的风速和风向。此外，每个测站还提供了2016年7–9月期间的逐时海浪方向谱数据。相比于实测风要素、波要素，实测海浪方向谱数据在部分时刻存在缺失，因此后续的研究只分析重叠时段的数据。从谱型特征来看，各站的二维谱主要呈现单峰和双峰特性，很少出现3个峰及以上的情况。
图 1 波浪站位置（a）和二维谱法的可视化展示（b）Figure 1. Location of the buoy （a） and visualization of 2D spectrum method （b）表 1 测站数据信息表Table 1. Statistics of station data information站名 数据时间范围 方向谱数据量 风、浪要素数据量 重叠时段数据总量 水深/m M1 2016年7月1日至9月30日 2 030 2 208 2 030 58 M2 2016年7月1日至9月15日 1 185 1 826 1 185 25 M3 2016年7月1日至9月27日 2 130 2 130 2 130 27 二维谱法是目前最准确的风涌浪分离方法，现以一个算例展示二维谱法在台湾海峡的适用性。图1b展示了M1测站2016年8月31日16时的实测方向谱以及基于二维谱法计算出的风涌浪分割线，图中有两个主要的椭圆状等高线结构，分别对应于不同的波系统。其中一个波系统的频率主要集中在0.29～0.37 Hz之间，由于它位于二维谱法确定的分割线内部，因此被判定为风浪。另一个波系统的频率主要集中在0.08～0.20 Hz之间，它位于二维谱法确定的分割线外部因而被判定为涌浪。可以看出，二维谱法确定的风涌浪分割线与风浪系统的分布范围较为吻合，该方法对台湾海峡的实测波浪特性表现出了较好的适应性。
基于二维谱法对3个测站重叠时段的海浪方向谱数据实施风涌浪分离，并按式（3）、式（4）计算风浪、涌浪的有效波高和平均周期，考虑到二维谱法具有公认的准确性，因此按二维谱法计算出的风浪、涌浪参数可被视为标准实测值，用于评估其他风涌浪分离方法的精度。
4. 多层感知器模型构建
4.1 模型结构设计
本文计划提出一种利用基本的风、浪要素实现风涌浪分离的方法，具体目标是能够计算出风浪、涌浪的有效波高和平均周期。在模型选择时，采用机器学习中常用的多层感知器（Multilayer Perceptron, MLP），原因是MLP具有较强的非线性拟合能力和较好的并行性[19]。MLP是一种经典的人工神经网络，常使用反向传播算法（Back Propagation, BP）作为训练算法，因而又被称为BP神经网络，关于MLP的计算、训练原理可参考文献[20]。
在建立MLP模型时，以混合浪要素以及风要素作为模型的输入因子，以目标风浪/涌浪要素作为模型的输出变量。针对每个风浪/涌浪要素的计算，都单独建立一个MLP模型，从而一共建立了4个MLP模型，各模型的输入、输出设置以及命名见表2。为了更加直观地展示模型结构，图2给出了风浪有效波高计算模型的结构示意图。由图可知：MLP模型由输入层、隐藏层和输出层构成，其中隐藏层的层数可以大于1。由于输入变量个数为4，输出变量个数为1，因此输入层神经元个数确定为4，输出层神经元个数确定为1，至此，MLP的结构参数只剩隐藏层层数L和每个隐藏层的神经元个数N未定，下文将分析结构参数L、N的最优组合。隐藏层激活函数选用Relu[21]，输出层不设置激活函数。为了MLP更快地收敛，输入数据要做归一化处理，可以加快模型训练的收敛速度。选用线性归一化方法将原始数据映射到[0，1]区间内，线性归一化公式如式（5）所示。搭建模型采用的编程语言是Python，开发过程使用了深度学习框架Tensorflow。
表 2 多层感知器模型的输入输出设置Table 2. Input and output settings of multilayer perceptron model模型命名 输入因子 输出因子 模型1 风速，风向，混合浪波高，混合浪波向 风浪有效波高 模型2 风速，风向，混合浪波高，混合浪波向 涌浪有效波高 模型3 风速，风向，混合浪周期，混合浪波向 风浪平均周期 模型4 风速，风向，混合浪周期，混合浪波向 涌浪平均周期 
图 2 风浪有效波高计算模型的结构示意图Figure 2. Structure diagram of calculation model of the significant height of wind-wave$$ X = \frac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}} \text{，} $$ (5) 式中，
$ x $ 是归一化前的样本数据；$ X $ 是归一化后的样本数据；$ {x_{\min }} $ 和$ {x_{\max }} $ 分别代表样本数据的最小值和最大值。以往的研究[22-24]一般针对每个测站都建立独立的机器学习模型，以最大限度地学习各地差异化的波浪特征，提升预报精度。本文将3个测站的数据整合到一起，建立统一的、适用于多测站的模型，以学习区域海浪的共性规律，具有局部海域的适用性。
4.2 数据集划分
以往的研究在建立数据集时，往往将实测波浪数据按时间顺序排序，选择时间上靠前的一部分数据作为训练集，剩下的数据作为测试集，这种做法简单直接、较为通用。比如王燕等[25]利用支持向量机模型预报渤海有效波高时，就选取了时间上靠前的约60%的数据作为训练集，剩下的数据作为测试集。本文参考王燕等[25]的做法，将每个测站时间上靠前的60%的数据取出，共同组成训练集，将每个测站剩下的40%数据取出，共同组成测试集。训练集的数据在时间上早于测试集，是因为实际预报中，总是基于已有的历史数据对未来的波浪做预报。训练集和测试集对不同测站的数据进行了取样，保证了数据来源的空间均衡性，而且训练集和测试集完全独立、没有重叠。由于测试集的数据并未参与模型的训练，对于模型来说，测试集的数据属于全新的数据，因此在测试集上计算出的各项误差指标能够客观地评估模型的性能。最终训练集的样本总数为3 207笔，测试集的样本总数为2 138笔。图3中用不同颜色的线对训练集和测试集的样本来源进行了标注，线段不连续之处代表实测数据缺失。
4.3 误差指标建立
为了客观评价模型的性能，需建立相应的评价指标，选择了3种较为常用的评价指标，包括平均绝对误差（MAE）、平均相对误差（MRE）、皮尔逊相关系数（R）来量化模型的性能。MAE反映模型输出值
$ y $ 与实测值$ \widehat y $ 的绝对偏离程度，MRE能反映模型输出值与实测值之间的相对偏离程度，相关系数R是研究变量之间线性相关程度的重要统计量。3个评价指标的计算公式如下所示：$$ {\rm{MAE}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^N \left| {{y_i} - {{\widehat y}_i}} \right|\; \text{，} $$ (6) $$ {\rm{MRE}}=\frac{1}{M}\displaystyle \sum\limits_ {i=1}^{N}\left|\frac{{y}_{i}-{\widehat{y}}_{i}}{{\widehat{y}}_{i}}\right|\times 100\text{%}\text{} \quad {\widehat y_i} \geqslant a \text{，} $$ (7) $$ R = \frac{{{cov} (y,\widehat y)}}{{\sqrt {Var[y]Var[\widehat y]} }} \text{，} $$ (8) 式中，
$ y $ 代表MLP模型计算出的波参数；$ \widehat y $ 代表实测波参数；下标$ i $ 是样本编号；N是测试集样本总数；$ a $ 是阈值；M是测试集中满足$ {\widehat y_i} \geqslant a $ 的样本数量；$ {cov} (y,\widehat y) $ 代表$ y $ 与$ \widehat y $ 的协方差；Var是方差符号。特别强调：MRE的计算中设定了
$ {\widehat y_i} \geqslant a $ 的前提，在计算有效波高的MRE时a取0.5 m，在计算波周期的MRE时a取0 s。原因是实测有效波高数据中，存在部分偏小值，容易导致MRE的计算结果偏大，从而无法合理地反映实际误差情况[26]，所以要设置一个合理的阈值筛除偏小的波高数据。中国国家标准化管理委员会于2020年发布的海浪等级标准文件中，将有效波高介于0.1～0.5 m的波浪定义为小浪。小浪的波高较小，容易导致相对误差的计算结果偏大，故将阈值a设定为小浪有效波高的上限即0.5 m。因为本文获取的实测波周期数据基本大于2 s，一般不会导致MRE的计算结果偏大，所以计算波周期的MRE时，阈值a设置为0 s即可。5. 模型性能评价
5.1 模型结构影响分析
目前，神经网络的结构优化尚缺乏严密的理论指导，没有确定的理论公式能够给出网络结构与模型性能之间的关系。本文将设计多种典型的网络结构，分析每个隐藏层的神经元个数N以及隐藏层层数L的变化对模型性能的影响，进而确定最优的模型结构。
对隐藏层层数L，设计3种典型情况：1、2、3。对于每个隐藏层的神经元个数N，设计4种典型情况：5、10、15、20。图4展示了随着L和N的改变，各MLP模型的MRE指标的变化情况。由图4可知：当N逐渐增大时，模型一的MRE整体上呈现下降趋势，说明增加神经元个数有助于模型一充分学习样本数据的内在规律，提升计算精度。对于模型二，当N取15时，MRE整体最小。对于模型三，MRE在L取2、N取20时达到最低。至于模型四，不论L、N如何变化，模型四的MRE始终维持在4.9%～5.3%之间，没有特别显著的差异，这说明模型四不需要太高的复杂度，已经能够较好地学习样本数据背后的关系。
图 4 各多层感知器模型的平均相对误差（MRE）随模型结构的变化子图a、b、c、d分别对应于模型一、二、三、四Figure 4. Variation of the mean relative error (MRE) of each multilayer perceptron model with the model structureSubgraphs a, b, c and d correspond to model 1, 2, 3 and 4 respectively在确定最终的模型结构时，不宜只考虑模型的准确率，还应当兼顾模型的复杂程度。因为模型的复杂度越高，计算量也越大，更容易产生过拟合的现象[27]。过拟合意味着模型将训练样本中的噪声和异常数据也一并学习了，从而缺乏泛化能力，当输入新的样本进行预测时易产生较大的误差。经过权衡，将模型一的最优结构定为L=2且N=20，将模型二的最优结构定为L=1且N=15，将模型三的最优结构定为L=2且N=20，将模型四的最优结构定为L=1且N=10。这样的结构选择既保证了较低的计算误差，又避免了过高的模型复杂度。
输出层变量个数也会影响模型精度。上文建立的模型采用单变量输出，为了对比，又建立了可同时预报4种风涌浪要素的四变量输出模型，它的相对误差MRE相对于单变量输出模型普遍偏大（表3），因此MLP模型采用单变量输出的结构是合理的。
表 3 四变量输出模型与单变量输出模型的平均相对误差（MRE）对比Table 3. Comparision of mean relative error (MRE) between 4 output model and 1 output model预报模式 风浪有效波高 涌浪有效波高 风浪平均周期 涌浪平均周期 四变量预报 12.7% 6.6% 13.1% 6.6% 单变量预报 10.1% 4.4% 10.3% 4.9% 5.2 空间适应性检验
上文针对3个测站建立了统一的风涌浪分离模型，具有较低的整体误差，但较低的整体误差并不能保证在每个测站都有较低的误差，有必要进一步分析模型在不同测站的误差表现，进而检验模型的空间适应性。
选取5.1节确定的最优结构MLP模型，计算这些模型在不同测站、不同物理量的各项误差指标，绘制成图5。由图可知：各测站风涌浪参数的MRE均低于13%，大多数物理量的相关系数R高于0.9，误差水平总体较低。在各项波参数中，风浪平均周期的R相对略低，但MRE指标良好。为了分析风浪周期R值相对较低的原因，画出风浪周期预报值与实测值的对比图（图6），由图可知：当实测风浪周期平稳变化时，模型的预报较为准确；当实测风浪周期在短时间内快速变化、出现反复震荡现象时，模型的预报不够精确。因为本模型的输入因子是基本的波要素和风要素，只能反映波浪的整体性质，不能探知海浪的内部结构，因而难以预见风浪周期在短期内的迅速变化。对比来看，由于波浪本身的特性，实测涌浪波高、实测风浪波高基本呈现平稳变化，因此它们的预报相关系数R相对较高，普遍高于0.95。M2测站的训练样本数仅有其他两个测站样本数的约55%，但仍保持了较高的计算精度，相比其他两个测站并未产生明显的误差增大现象，样本少、精度高也是有可能的，推测是因为数据的分布并不复杂，模型能够学习到其中的规律。
图 5 多层感知器模型在不同测站的误差指标Figure 5. Error indices of multilayer perceptron models in different stations
图 6 风浪平均周期预报值与实测值对比Figure 6. Contrast of predicted mean wind-wave period with measured data综上可知：模型在不同的测站均有较好表现，具有跨测站的空间适应性，能够胜任台湾海峡不同区域的风涌浪分离任务，在数据量较少的测站也有良好表现。
5.3 样本量影响分析
MLP本质上是非机理的统计学模型，具有数据依赖性，需要多少训练样本才能让模型产生良好性能，是具有实用意义、值得探讨的问题。本节将分析训练样本量对模型计算精度的影响，提出MLP风涌浪分离模型的最低样本量和推荐样本量。
采用控制变量法，保持测试集样本数量不变，建立10个新的训练集，每个新训练集的样本量分别是原有训练集样本总量的10%、20%、···、90%、100%，在每个新训练集上训练MLP风涌浪分离模型，并在测试集上计算误差指标MAE、MRE，绘制得到图7。
图 7 各多层感知器模型的平均绝对误差（a）和平均相对误差（b）随训练样本量的变化Figure 7. Variation of mean absolute error (a) and mean relative error (b) of multilayer perceptron models with training set size观察图中误差曲线的变化趋势可知：随着训练样本量的增加，计算误差整体上呈现下降趋势。特别注意的是：在训练样本量从600增加到1 400的过程中，部分波参数比如涌浪周期、风浪波高的预报误差不降反升，这是因为训练样本量太小，模型尚未达到稳定的状态。当训练样本量超过1 400后，随着训练样本量的增加，MLP风涌浪分离模型不会出现明显的误差反升现象，说明模型达到了相对稳定的状态，因此MLP模型的最低样本量建议设为1 400，即每个测站提供至少466笔样本。当样本量超过2 300后，风浪波高、涌浪波高、涌浪周期的误差曲线趋表现出小范围波动的形态，说明继续增加样本量对于降低它们的计算误差作用有限，但风浪周期的预报误差仍有下降趋势。综合考虑，将MLP风涌浪分离模型的推荐样本量定为2 300及以上，相当于每个测站应当提供766笔及以上的样本。
当测试集数据减少时，各模型的表现可能会下降，对于这种情况有必要做分析，因此随机抽取原有测试集10%、20%、···、90%、100%的样本建立10个新测试集，在各新测试集上计算误差指标MAE，绘制得到图8。由图可知，当测试集样本量变化时，风涌浪参数的计算误差变化较小，可见模型的稳定性较强，不会因为测试集样本量的减少而降低性能。
图 8 各多层感知器模型的平均绝对误差随测试样本量的变化Figure 8. Variation of mean absolute error of multilayer perceptron models with test set size5.4 台风期间模型性能验证
7–9月是台湾海峡台风多发期，极端天气有可能影响到模型表现。在2016年9月14日6时至15日8时期间，台风“莫兰蒂”经过台湾海峡，该台风的路径如图1所示。筛选出上述时段MLP法计算出的风涌浪参数，与实测数据进行对比，绘制在图9中。由图可知：MLP法计算出的涌浪有效波高、涌浪平均周期和风浪平均周期与实测数据吻合良好，但风浪有效波高的计算值与实测值偏离较大。
图 9 台风期间多层感知器法风涌浪参数计算值与实测值对比Figure 9. Comparision of measured wave data with wind-wave and swell computation values using multilayer perceptron method during typhoon passage由式（3）定义的风浪、涌浪、混合浪有效波高存在如下关系：
$$ H_{{\rm{swell}}}^2 + H_{{\rm{windsea}}}^2 = H_{\rm{s}}^2 \text{，} $$ (9) 式中，
$ {H_{{\rm{swell}}}} $ 是涌浪有效波高；$ {H_{{\rm{windsea}}}} $ 是风浪有效波高；$ {H_{\rm{s}}} $ 是混合浪有效波高。由于MLP法直接得到的风浪有效波高误差较大，但MLP法直接得到的涌浪有效波高误差较小，可以将MLP法得到的涌浪有效波高带入式（9）中，计算出风浪有效波高，这样间接得到风浪有效波高的方法称为“改进的MLP法”。由图9c可知，相比于MLP法，改进的MLP法对风浪有效波高的计算误差明显减小，MAE从0.29 m降至0.17 m，MRE从14.2%降至8.6%。综上所述，改进后的MLP法能够较准确地计算台风期间的风涌浪参数。
5.5 与现有一维谱法的对比
本节使用前文所述的4种传统一维谱法、林伊楠等[11]提出的一维谱法以及基于MLP的方法对3个测站的所有测试集波浪数据进行风涌浪分离，计算出相应的风浪、涌浪参数分离值，绘在图10中。图中横轴代表波浪参数的实测值，纵轴代表各种方法计算出的波浪参数分离值，图中的散点距离1∶1线越近，意味着该散点对应的波浪参数分离值越接近于实测值。可以直观地看出，在这6种方法中，MLP法对应的散点与1∶1线的聚拢度最高，意味着它的风涌浪分离准确性也最高。
图 10 不同方法计算出的波参数与实测数据对比Figure 10. Comparison of the wave parameters calculated by different methods with measured data直观的判断需要客观的指标加以佐证，进一步计算出机器学习法以及5种一维谱法的各项误差指标，列在表4中。对比发现，MLP法在3种误差指标R、MAE和MRE上均表现出了最低的整体误差。以平均相对误差MRE为例，MLP法的MRE最高为10.3%，而5种一维谱法的MRE最低也有11.8%。特别是在涌浪有效波高的计算中，MLP法的MRE仅有4.4%，显著地优于一维谱法。基于散点图的直观对比以及误差指标的量化评估，可以得出结论：本文提出的MLP法在风涌浪分离的准确性上高于传统的一维谱法。
表 4 不同风涌浪分离方法的误差指标Table 4. Error indices of different separation methods of wind-wave and swell目标变量 风涌浪分离方法 相关系数 平均绝对误差 平均相对误差 风浪有效波高 MLP法 0.97 0.08 m 10.1% PM法 0.98 0.28 m 50.9% WH法 0.83 0.28 m 20.3% 改进的WH法 0.86 0.54 m 56.7% JP法 0.77 0.30 m 50.2% 林伊楠等[11]的方法 0.96 0.34 m 45.6% 涌浪有效波高 MLP法 0.99 0.05 m 4.4% PM法 0.60 0.42 m 38.9% WH法 0.92 0.20 m 17.9% 改进的WH法 0.76 0.63 m 60.6% JP法 0.55 0.24 m 18.5% 林伊楠等[11]的方法 0.83 0.43 m 41.7% 风浪平均周期 MLP法 0.82 0.47 s 10.3% PM法 0.57 0.85 s 17.0% WH法 0.18 1.20 s 25.9% 改进的WH法 0.25 1.00 s 26.1% JP法 0.45 2.96 s 67.3% 林伊楠等[11]的方法 0.37 0.83 s 18.9% 涌浪平均周期 MLP法 0.92 0.35 s 4.9% PM法 0.43 2.28 s 34.6% WH法 0.80 0.77 s 11.8% 改进的WH法 0.73 3.37 s 52.5% JP法 0.37 1.53 s 22.4% 林伊楠等[11]的方法 0.28 2.52 s 40.4% 需补充说明的是，改进的WH法在本文收集数据上效果尚不如WH法，原因可能有二：其一是改进的WH法基于大西洋和墨西哥沿岸的浮标波浪数据提出，但不同海域的气候、水深相差较大，因而改进的WH法应用于台湾海峡的测站时，未必有原先的效果；其二是提出改进的WH法的Hwang等人，以海浪一维谱中高频峰与低频峰之间波谷的频率作为风涌浪的真实分割频率，而本文以目前认可度较高的二维谱法划定的分割域作为风涌浪的分割依据，意味着本文与Hwang等判断风涌浪准确分离的标准有所不同，因而在本文的计算下，改进的WH法准确性确有可能不如WH法。
6. 结论
传统的风涌浪分离方法大多使用海浪谱，但海浪谱数据较为匮乏，因而本文建立了以基本波要素和风要素作为输入因子、能够准确计算风涌浪参数的MLP模型，在缺乏海浪谱的情况下依然能够使用。由于MLP模型很好地适用于台湾海峡3个测站，而且这3个测站的位置、水深、风区各不相同，一定程度上具有区域的代表性，可见该模型能够捕捉区域波浪的共性特征，故将其应用于台湾海峡其他测站时，应当也有相对较高的精度，至少在邻近测站使用时本模型的结果是较为可靠的。但需指出的是，由于本文采用的训练数据集中在夏季（6–9月），而台湾海峡的波候存在显著的季节变化，因而该MLP模型在秋冬季的适用性尚需进一步检验。
在海洋观测昂贵、实测数据稀缺的背景下，本文试图探讨机器学习模型的空间普适性，能否利用有限的海洋实测资料训练出具有区域适用性的模型。尽管机器学习是纯数据驱动的统计模型，不能真正地理解物理机制，但局部海域由于气候相近，海洋物理过程可能会存在相似的数据规律，而挖掘数据规律正是机器学习的长处。若一个机器模型能够适用于多个有代表性的站点，说明它能捕捉不同地点差异性波浪特征中的共性，那么在邻近站点使用时应当有一定准确性和参考价值。
本文的主要结论如下：
（1）提出了一种基于多层感知器的风涌浪分离方法，称为“MLP法”。该方法仅需要基本的风要素、波要素就能以较高精度计算出风浪、涌浪的波高和周期参数，可为台湾海峡缺乏海浪谱数据的测站提供替代性的风涌浪分离方案。
（2）MLP法在台湾海峡的不同测站表现良好，具有较强的空间适应性。通过分析训练样本量对风涌浪分离精度的影响，给出MLP法的最低训练样本量为每个测站466笔数据，推荐训练样本量为每个测站至少766笔数据。
（3）以实测风浪、涌浪数据做标定，对比了MLP法与5种现有一维谱法的计算精度，结果表明MLP法的准确性高于现有的一维谱法，说明MLP模型能够充分学习研究区域的波浪特征，从而实现对风浪、涌浪要素的准确计算。
-
图 1 波浪站位置（a）和二维谱法的可视化展示（b）
Fig. 1 Location of the buoy （a） and visualization of 2D spectrum method （b）
图 2 风浪有效波高计算模型的结构示意图
Fig. 2 Structure diagram of calculation model of the significant height of wind-wave
图 4 各多层感知器模型的平均相对误差（MRE）随模型结构的变化
子图a、b、c、d分别对应于模型一、二、三、四
Fig. 4 Variation of the mean relative error (MRE) of each multilayer perceptron model with the model structure
Subgraphs a, b, c and d correspond to model 1, 2, 3 and 4 respectively
图 5 多层感知器模型在不同测站的误差指标
Fig. 5 Error indices of multilayer perceptron models in different stations
图 6 风浪平均周期预报值与实测值对比
Fig. 6 Contrast of predicted mean wind-wave period with measured data
图 7 各多层感知器模型的平均绝对误差（a）和平均相对误差（b）随训练样本量的变化
Fig. 7 Variation of mean absolute error (a) and mean relative error (b) of multilayer perceptron models with training set size
图 8 各多层感知器模型的平均绝对误差随测试样本量的变化
Fig. 8 Variation of mean absolute error of multilayer perceptron models with test set size
图 9 台风期间多层感知器法风涌浪参数计算值与实测值对比
Fig. 9 Comparision of measured wave data with wind-wave and swell computation values using multilayer perceptron method during typhoon passage
图 10 不同方法计算出的波参数与实测数据对比
Fig. 10 Comparison of the wave parameters calculated by different methods with measured data
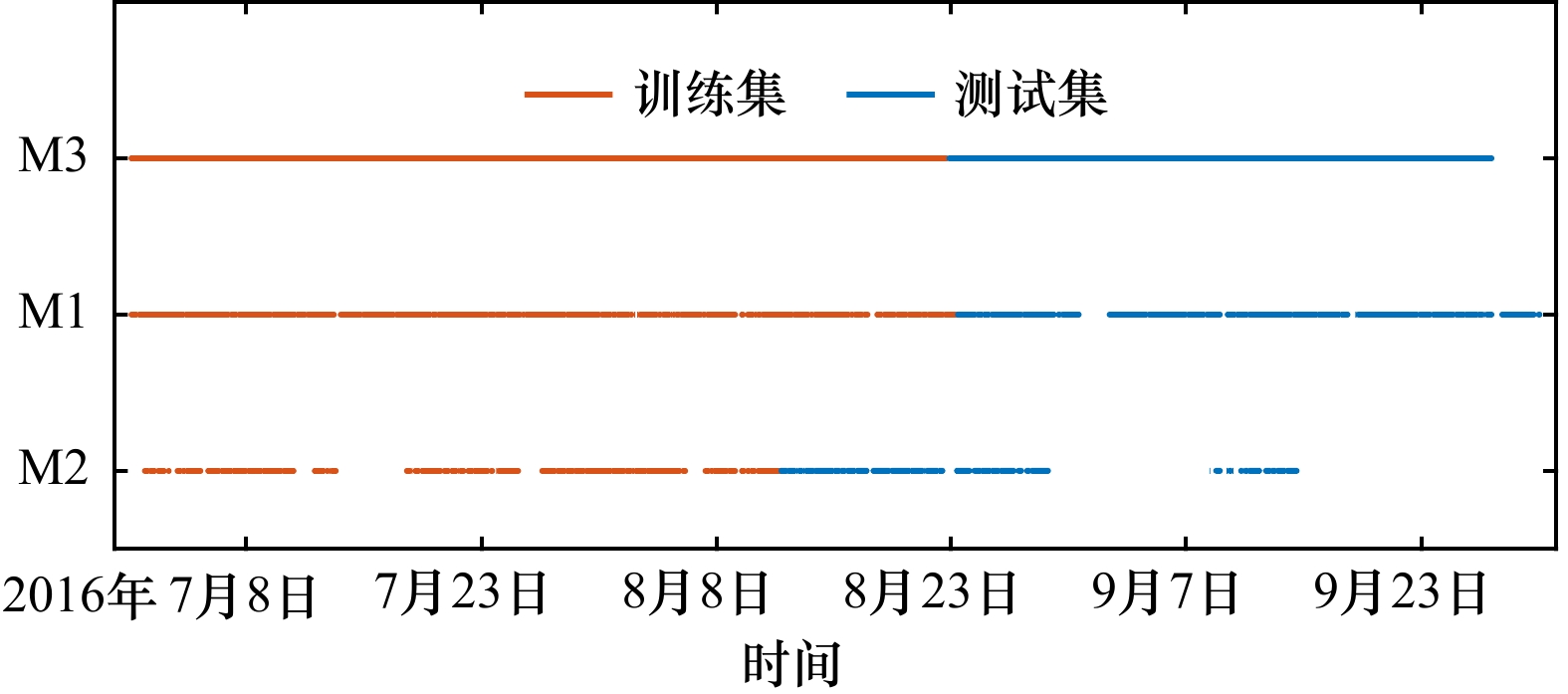
表 1 测站数据信息表
Tab. 1 Statistics of station data information
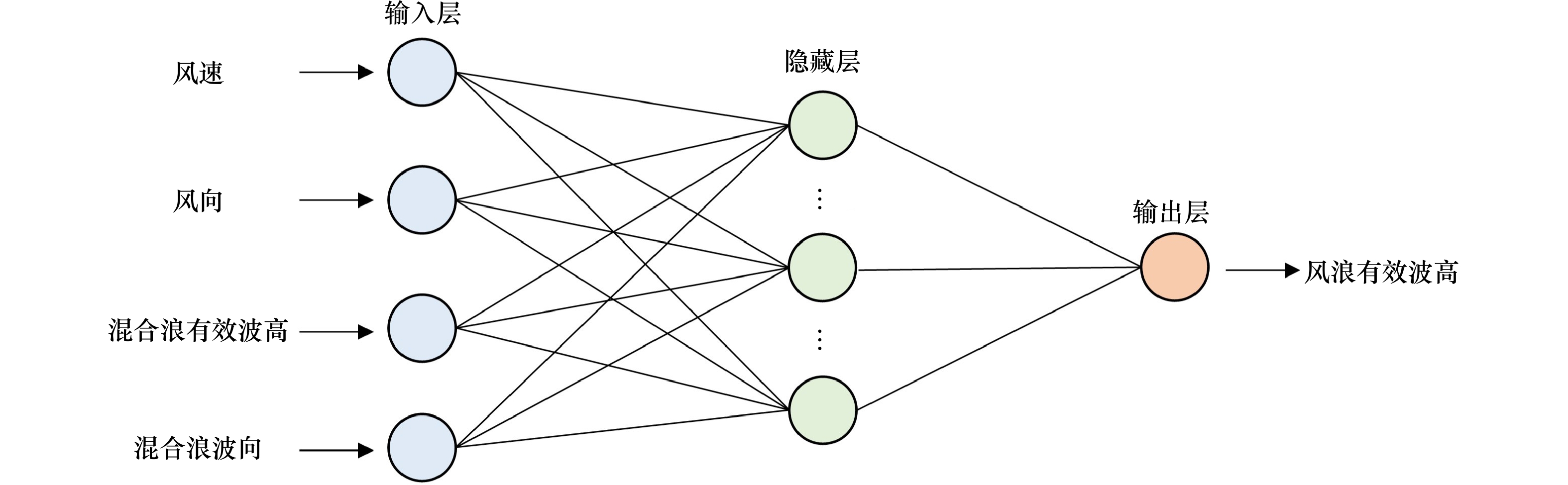
站名 数据时间范围 方向谱数据量 风、浪要素数据量 重叠时段数据总量 水深/m M1 2016年7月1日至9月30日 2 030 2 208 2 030 58 M2 2016年7月1日至9月15日 1 185 1 826 1 185 25 M3 2016年7月1日至9月27日 2 130 2 130 2 130 27 
下载: 导出CSV
表 2 多层感知器模型的输入输出设置
Tab. 2 Input and output settings of multilayer perceptron model
模型命名 输入因子 输出因子 模型1 风速，风向，混合浪波高，混合浪波向 风浪有效波高 模型2 风速，风向，混合浪波高，混合浪波向 涌浪有效波高 模型3 风速，风向，混合浪周期，混合浪波向 风浪平均周期 模型4 风速，风向，混合浪周期，混合浪波向 涌浪平均周期
下载: 导出CSV
表 3 四变量输出模型与单变量输出模型的平均相对误差（MRE）对比
Tab. 3 Comparision of mean relative error (MRE) between 4 output model and 1 output model
预报模式 风浪有效波高 涌浪有效波高 风浪平均周期 涌浪平均周期 四变量预报 12.7% 6.6% 13.1% 6.6% 单变量预报 10.1% 4.4% 10.3% 4.9%
下载: 导出CSV
表 4 不同风涌浪分离方法的误差指标
Tab. 4 Error indices of different separation methods of wind-wave and swell
目标变量 风涌浪分离方法 相关系数 平均绝对误差 平均相对误差 风浪有效波高 MLP法 0.97 0.08 m 10.1% PM法 0.98 0.28 m 50.9% WH法 0.83 0.28 m 20.3% 改进的WH法 0.86 0.54 m 56.7% JP法 0.77 0.30 m 50.2% 林伊楠等[11]的方法 0.96 0.34 m 45.6% 涌浪有效波高 MLP法 0.99 0.05 m 4.4% PM法 0.60 0.42 m 38.9% WH法 0.92 0.20 m 17.9% 改进的WH法 0.76 0.63 m 60.6% JP法 0.55 0.24 m 18.5% 林伊楠等[11]的方法 0.83 0.43 m 41.7% 风浪平均周期 MLP法 0.82 0.47 s 10.3% PM法 0.57 0.85 s 17.0% WH法 0.18 1.20 s 25.9% 改进的WH法 0.25 1.00 s 26.1% JP法 0.45 2.96 s 67.3% 林伊楠等[11]的方法 0.37 0.83 s 18.9% 涌浪平均周期 MLP法 0.92 0.35 s 4.9% PM法 0.43 2.28 s 34.6% WH法 0.80 0.77 s 11.8% 改进的WH法 0.73 3.37 s 52.5% JP法 0.37 1.53 s 22.4% 林伊楠等[11]的方法 0.28 2.52 s 40.4%
下载: 导出CSV
-
[1] Tao Aifeng, Yan Jin, Pei Ye, et al. Swells of the East China Sea[J]. Journal of Ocean University of China, 2017, 16(4): 674−682. doi: 10.1007/s11802-017-3406-5 [2] 徐啸, 陶爱峰, 李雪丁, 等. 基于实测数据的台湾海峡中部波浪特征分析[J]. 热带海洋学报, 2021, 40(1): 12−20.Xu Xiao, Tao Aifeng, Li Xueding, et al. Analysis of wave characteristics in the central Taiwan Strait based on measured data[J]. Journal of Tropical Oceanography, 2021, 40(1): 12−20. [3] 汪炳祥, 常瑞芳, 王一飞. 风浪与涌浪的划分判据[J]. 黄渤海海洋, 1990, 8(1): 16−24.Wang Bingxiang, Chang Ruifang, Wang Yifei. Criteria of differentiating swell from wind waves[J]. Journal of Oceanography of Huanghai & Bohai Seas, 1990, 8(1): 16−24. [4] 郭佩芳, 施平, 王华, 等. 划分风浪与涌浪的一个新判据—海浪成份及其在南海的应用[J]. 青岛海洋大学学报, 1997, 27(2): 131−137.Guo Peifang, Shi Ping, Wang Hua, et al. A new criterion between wind wave and swell wave-by mixed wave composition factors and its application to the South China Sea[J]. Journal of Ocean University of Qingdao, 1997, 27(2): 131−137. [5] Yang Zheng, Song Lili, Mu Lin, et al. Separation of wind-sea and swell wave heights using altimeter data[C]//2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS. Brussels, Belgium: IEEE, 2021: 7564−7567. [6] Earle M D. Development of algorithms for separation of sea and swell[R]. [S.l.]: National Data Buoy Center Tech, 1984: 53. [7] Wang D W, Hwang P A. An operational method for separating wind sea and swell from ocean wave spectra[J]. Journal of Atmospheric and Oceanic Technology, 2001, 18(12): 2052−2062. doi: 10.1175/1520-0426(2001)018<2052:AOMFSW>2.0.CO;2 [8] Hwang P A, Ocampo-Torres F J, García-Nava H. Wind sea and swell separation of 1D wave spectrum by a spectrum integration method[J]. Journal of Atmospheric and Oceanic Technology, 2012, 29(1): 116−128. doi: 10.1175/JTECH-D-11-00075.1 [9] Portilla J, Ocampo-Torres F J, Monbaliu J. Spectral partitioning and identification of wind sea and swell[J]. Journal of Atmospheric and Oceanic Technology, 2009, 26(1): 107−122. doi: 10.1175/2008JTECHO609.1 [10] 朱绍华, 于文太, 李广帅, 等. 基于双峰海浪谱的风浪和涌浪分离应用研究[J]. 中国造船, 2017, 58(4): 160−167. doi: 10.3969/j.issn.1000-4882.2017.04.019Zhu Shaohua, Yu Wentai, Li Guangshuai, et al. Separation of wind wave and swell based on double peak spectrum[J]. Shipbuilding of China, 2017, 58(4): 160−167. doi: 10.3969/j.issn.1000-4882.2017.04.019 [11] 林伊楠, 陶爱峰, 李雪丁, 等. 台湾海峡风涌浪分离方法研究[J]. 海洋学报, 2019, 41(11): 25−34.Lin Yi’nan, Tao Aifeng, Li Xueding, et al. Study on separation method of wind-wave and swell in the Taiwan Strait[J]. Haiyang Xuebao, 2019, 41(11): 25−34. [12] Hanson J L, Phillips O M. Automated analysis of ocean surface directional wave spectra[J]. Journal of Atmospheric and Oceanic Technology, 2001, 18(2): 277−293. doi: 10.1175/1520-0426(2001)018<0277:AAOOSD>2.0.CO;2 [13] 李水清, 赵栋梁. 风浪和涌浪分离方法的比较[J]. 海洋学报, 2012, 34(2): 23−29.Li Shuiqing, Zhao Dongliang. Comparisons on partitioning techniques to identify wind-wave and swell[J]. Haiyang Xuebao, 2012, 34(2): 23−29. [14] 国家市场监督管理总局, 国家标准化管理委员会. GB/T 14914.2-2019, 海洋观测规范 第2部分: 海滨观测[S]. 北京: 中国标准出版社, 2019.State Administration of Market Supervision and Administration, State Standardization Administration Commission. GB/T 14914.2-2019, The specification for marine observation-Part 2: offshore observation[S]. Beijing: Standards Press of China, 2019. [15] Meng Fan, Song Tao, Xu Danya, et al. Forecasting tropical cyclones wave height using bidirectional gated recurrent unit[J]. Ocean Engineering, 2021, 234: 108795. doi: 10.1016/j.oceaneng.2021.108795 [16] Nikoo M R, Kerachian R, Alizadeh M R. A fuzzy KNN-based model for significant wave height prediction in large lakes[J]. Oceanologia, 2018, 60(2): 153−168. doi: 10.1016/j.oceano.2017.09.003 [17] Komen G J, Hasselmann K, Hasselmann K. On the existence of a fully developed wind-sea spectrum[J]. Journal of Physical Oceanography, 1984, 14(8): 1271−1285. doi: 10.1175/1520-0485(1984)014<1271:OTEOAF>2.0.CO;2 [18] Tolman H L, Abdolali A, Accensi M, et al. User manual and system documentation of WAVEWATCH III (R) version 6.07[M]. USA: NOAA, 2019. [19] 张驰, 郭媛, 黎明. 人工神经网络模型发展及应用综述[J]. 计算机工程与应用, 2021, 57(11): 57−69. doi: 10.3778/j.issn.1002-8331.2102-0256Zhang Chi, Guo Yuan, Li Ming. Review of development and application of artificial neural network models[J]. Computer Engineering and Applications, 2021, 57(11): 57−69. doi: 10.3778/j.issn.1002-8331.2102-0256 [20] 周志华. 机器学习[M]. 北京: 清华大学出版社, 2016.Zhou Zhihua. Machine Learning[M]. Beijing: Tsinghua University Press, 2016. [21] Nair V, Hinton G E. Rectified linear units improve restricted Boltzmann machines[C]// Proceedings of the 27th International Conference on International Conference on Machine Learning. Haifa, Israel: Omnipress, 2010. [22] Berbić J, Ocvirk E, Carević D, et al. Application of neural networks and support vector machine for significant wave height prediction[J]. Oceanologia, 2017, 59(3): 331−349. doi: 10.1016/j.oceano.2017.03.007 [23] Fan Shuntao, Xiao Nianhao, Dong Sheng. A novel model to predict significant wave height based on long short-term memory network[J]. Ocean Engineering, 2020, 205: 107298. doi: 10.1016/j.oceaneng.2020.107298 [24] Kaloop M R, Kumar D, Zarzoura F, et al. A wavelet-particle swarm optimization-extreme learning machine hybrid modeling for significant wave height prediction[J]. Ocean Engineering, 2020, 213: 107777. doi: 10.1016/j.oceaneng.2020.107777 [25] 王燕, 钟建, 张志远. 支持向量回归的机器学习方法在海浪预测中的应用[J]. 海洋预报, 2020, 37(3): 29−34. doi: 10.11737/j.issn.1003-0239.2020.03.004Wang Yan, Zhong Jian, Zhang Zhiyuan. Application of support vector regression in significant wave height forecasting[J]. Marine forecasts, 2020, 37(3): 29−34. doi: 10.11737/j.issn.1003-0239.2020.03.004 [26] 李本霞, 吴淑萍, 邢闯, 等. 近海近岸高精度海浪业务化数值预报系统[J]. 海洋预报, 2010, 27(5): 1−6. doi: 10.3969/j.issn.1003-0239.2010.05.001Li Benxia, Wu Shuping, Xing Chuang, et al. High precision operational numerical prediction system for offshore and nearshore waves[J]. Marine Forecasts, 2010, 27(5): 1−6. doi: 10.3969/j.issn.1003-0239.2010.05.001 [27] Aertsen W, Kint V, Van Orshoven J, et al. Comparison and ranking of different modelling techniques for prediction of site index in mediterranean mountain forests[J]. Ecological Modelling, 2010, 221(8): 1119−1130. doi: 10.1016/j.ecolmodel.2010.01.007 -
下载:
计量
- 文章访问数: 758
- HTML全文浏览量: 283
- PDF下载量: 78
- 被引次数: 0
