Numerical simulation of storm surge in the coast of Zhejiang based on parametric wind field model
-
摘要: 针对台风参数化风场模型中最大风速半径
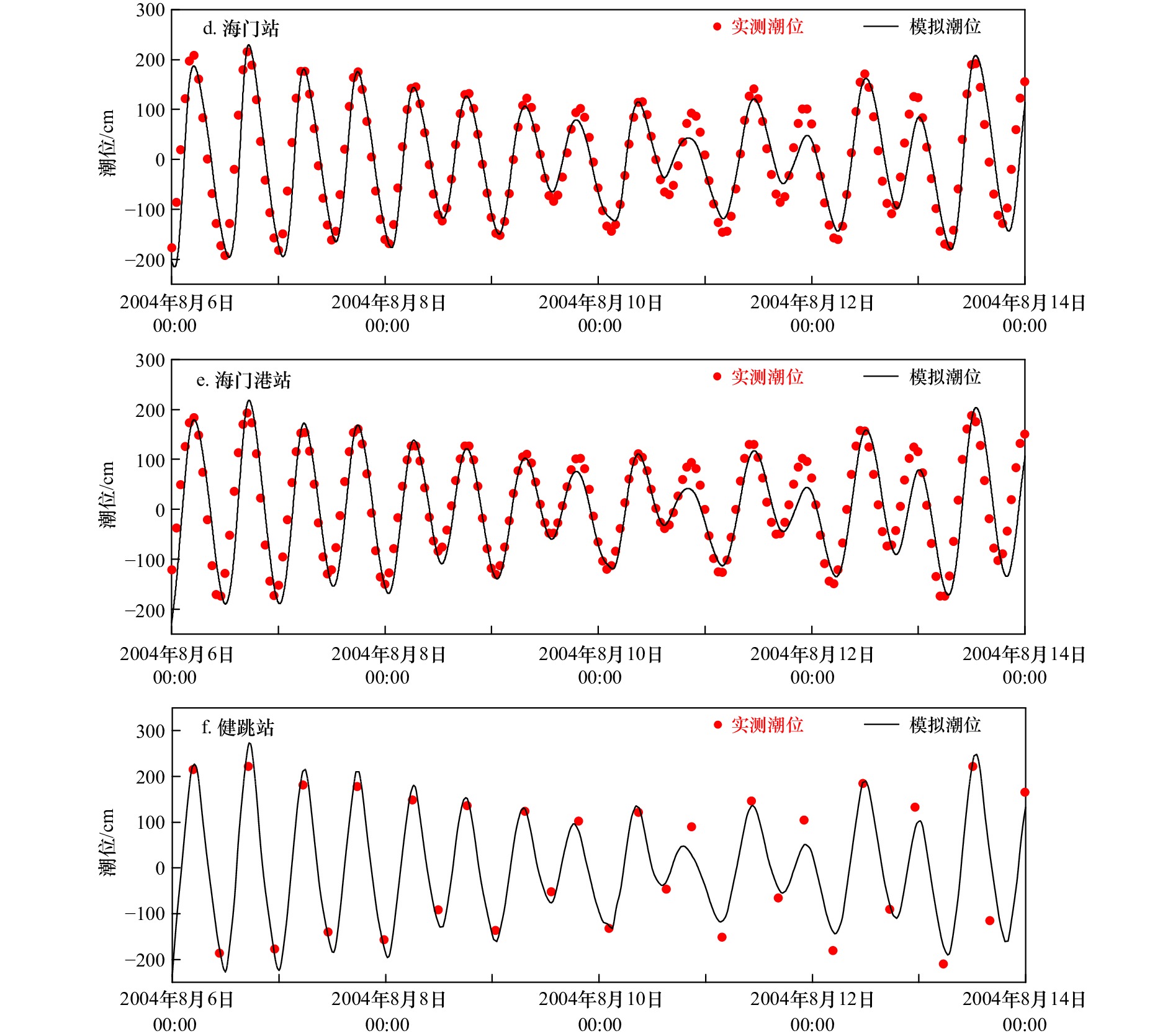
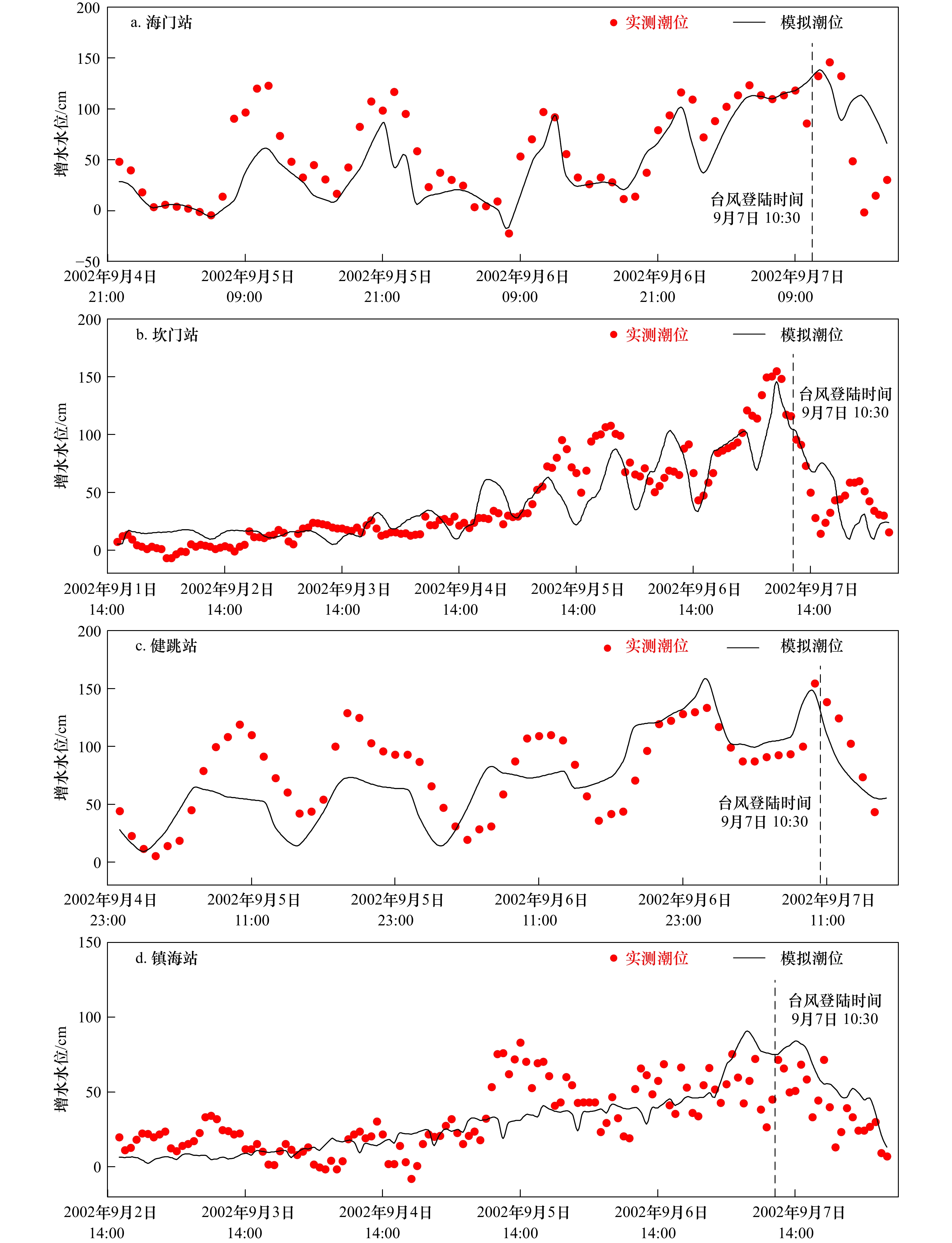
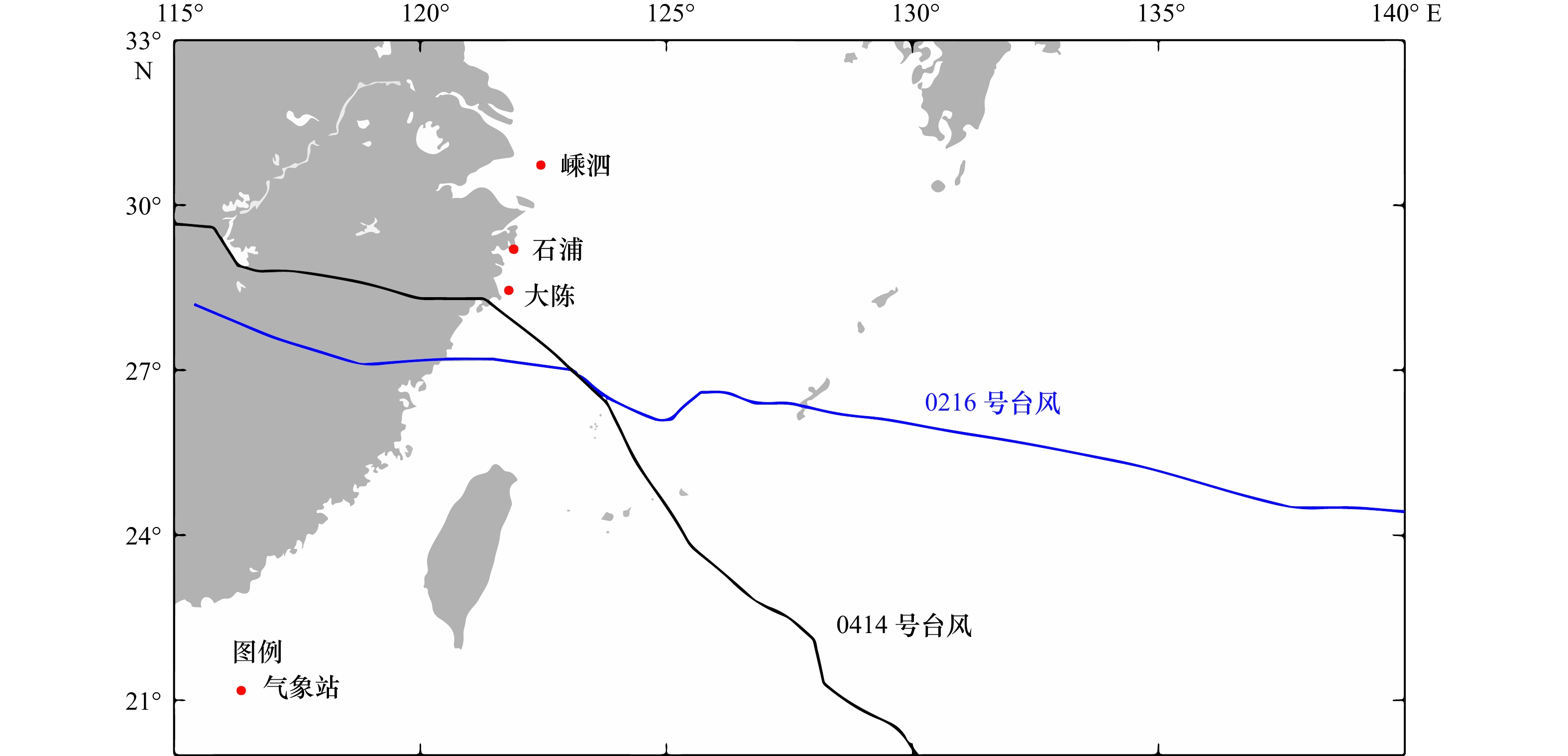
$（{R}_{\mathrm{m}\mathrm{a}\mathrm{x}}）$ 和径向气压分布系数$（B）$ 两个关键参数，以0216（“森拉克”台风）和0414（“云娜”台风）两场台风为例，采用多种$ {R}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ 和$ B $ 计算方法的组合方案，再现台风过程，并提取3处观测站点的模拟数据，与实测结果进行比对。将所得的台风风场作为风暴潮模型的驱动风场，利用MIKE 21模型进行浙江沿海两场台风的风暴潮数值模拟，结合实测资料，验证并分析天文潮位和风暴潮增水水位。结果表明，本文选取的参数化风场模型适用于计算影响浙江海域的台风风场，以此为基础建立的风暴潮模型的模拟结果满足精度要求。Abstract: Aiming at two types of typhoon field parameters used in parametric typhoon wind field model, such as radius to maximum wind speed${R}_{{\rm{max}}}$ and radial pressure distribution coefficient$(B)$ , the process of two typhoon was reproduced with different combinations of parameters${R}_{{\rm{max}}}$ and$ B $ , and compared with the field observation data of three observation sites. The constructed typhoon wind field was used as the driving wind field in the MIKE 21 model, which was used to complete numerical simulation of the storm surge of two typhoons in Zhejiang Province. The tide level and storm tide level were verified and analyzed with the observation data. The results show that the parametric model selected in this paper is suitable for calculating typhoon wind field which affect the coast of Zhejiang, and the simulation results of storm surge model established on this basis meet the requirement of accuracy. -
图 2 0216号台风风速数值模拟结果与实测对比
图中时间均采用世界时（UTC）
Fig. 2 Comparison of Typhoon 0216 wind speed between simulated and observed results
The time in the figure is universal time (UTC)
图 3 0414号台风风速数值模拟结果与实测对比
图中时间均采用世界时（UTC）
Fig. 3 Comparison of Typhoon 0414 wind speed between simulated and observed results
The time in the figure is universal time (UTC)
图 6 0216号台风期间天文潮位数值模拟结果与潮汐表对比
潮位起算面：平均海平面；图中时间均采用世界时（UTC）
Fig. 6 Comparison of tide level between simulated and tide table value during Typhoon 0216
Starting surface of tide: mean sea level; the time in the figure is universal time (UTC)
图 7 0414号台风期间天文潮位数值模拟结果与潮汐表对比
潮位起算面：平均海平面；图中时间均采用世界时（UTC）
Fig. 7 Comparison of tide level between simulated value and tide table value during Typhoon 0414
Starting surface of tide: mean sea level; the time in the figure is universal time (UTC)
图 8 0216号台风期间增水水位数值模拟结果与实测对比
图中时间均采用世界时（UTC）
Fig. 8 Comparison of storm tide between simulated and observed results during Typhoon 0216
The time in the figure is universal time (UTC)
图 9 0414号台风期间增水水位数值模拟结果与实测对比图
图中时间均采用世界时（UTC）
Fig. 9 Comparison of storm tide between simulated and observed results during Typhoon 0414
The time in the figure is universal time (UTC)
表 1 径向气压分布系数
$ B $ 的主要计算表达式Tab. 1 Main calculation methods of radial pressure profile coefficient
$ B $ 海域 $ B $函数表达式 数据来源 编号 西北太
平洋${ {V}_{\mathrm{m}\mathrm{a}\mathrm{x}}={K}_{P}{\left(\mathrm{\Delta }P\right)}^{\beta }} $
${B=\dfrac{{\rm{e}}}{ {\gamma }_{2}^{2} }\dfrac{ {\rho }_{{\rm{A}}} }{100\mathrm{\Delta }P}{\left[\dfrac{1}{3.6}{K}_{P}{\left(\mathrm{\Delta }P\right)}^{\beta }\right]}^{2} }$文献[15] B1 ${\begin{array}{l}B=1.128\;58+8.639\;6\times {10}^{-3}\mathrm{\Delta }P\\\quad\;\; -8.774\;5\times {10}^{-3}\phi \end{array}}$ 文献[17] B2 南太
平洋${ B=0.25+0.3\mathrm{l}\mathrm{n}\mathrm{\Delta }P} $ 文献[12] − $ {B=1.5+(980-P_{\rm{c}})/120 }$ 文献[13] − ${ B=2.0+(P_{\rm{c}}-900)/160 }$ 文献[14] − 大西洋 ${ B=1.881-0.005\;57{R}_{\mathrm{m}\mathrm{a}\mathrm{x}}-0.011\phi }$ 文献[10] B3 ${\begin{array}{l}B=-0.365-0.152\mathrm{l}\mathrm{n}{R}_{\mathrm{m}\mathrm{a}\mathrm{x} }+ 0.082\mathrm{l}\mathrm{n}\mathrm{\Delta }P\\ \quad\;\;\;-0.117\mathrm{l}\mathrm{n}\phi +0.674\mathrm{l}\mathrm{n}T \end{array}}$ 文献[26] − 注：T为海面温度；“−”为无编号；Vmax为最大风速；KP和β为回归系数；γ2为常数1.05 s。 
下载: 导出CSV
表 2 最大风速半径
$ {R}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ 的主要计算表达式Tab. 2 Main calculation methods of maximal wind velocity radius
$ {R}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ 海域 $ {R}_{\mathrm{m}\mathrm{a}\mathrm{x}} $函数表达式 数据来源 编号 西北太
平洋${ {R}_{\mathrm{m}\mathrm{a}\mathrm{x} }=1.119\times {10}^{3}{\mathrm{\Delta }P}^{-0.805} }$ 文献[8] R1 ${ {\mathrm{l}\mathrm{n}R}_{\mathrm{m}\mathrm{a}\mathrm{x}}=5.510{\mathrm{\Delta }P}^{-0.117}+6.707\times {10}^{-3}\phi }$ 文献[27] R2 ${ {R}_{\mathrm{m}\mathrm{a}\mathrm{x}}=110.22-18.04\mathrm{l}\mathrm{n}\mathrm{\Delta }P }$ 文献[28] − 大西洋 ${ {R}_{\mathrm{m}\mathrm{a}\mathrm{x}}=2.097+0.019\mathrm{\Delta }P-1.867\times {10}^{-4}{\mathrm{\Delta }P}^{2}+0.038\phi }$ 文献[26] − ${ {R}_{\mathrm{m}\mathrm{a}\mathrm{x}}=3.015+6.291\times {10}^{-5}{\mathrm{\Delta }P}^{2}+0.034\phi }$ 文献[11] − ${\begin{array}{l}{R}_{\mathrm{m}\mathrm{a}\mathrm{x} }=28.52\mathrm{t}\mathrm{a}\mathrm{n}{\rm h}\left[0.087\;3\left(\phi -28\right)\right]+0.2{V}_{f}\\\qquad\;\;+ 12.22\mathrm{exp}\left(\dfrac{ {P}_{ {\rm{a} } }-1\;013.2}{33.86}\right)+37.22 \end{array} }$ 文献[29] R3 注：“−”为无编号。
下载: 导出CSV
表 3 自匹配模式
Tab. 3 Self-matching patterns
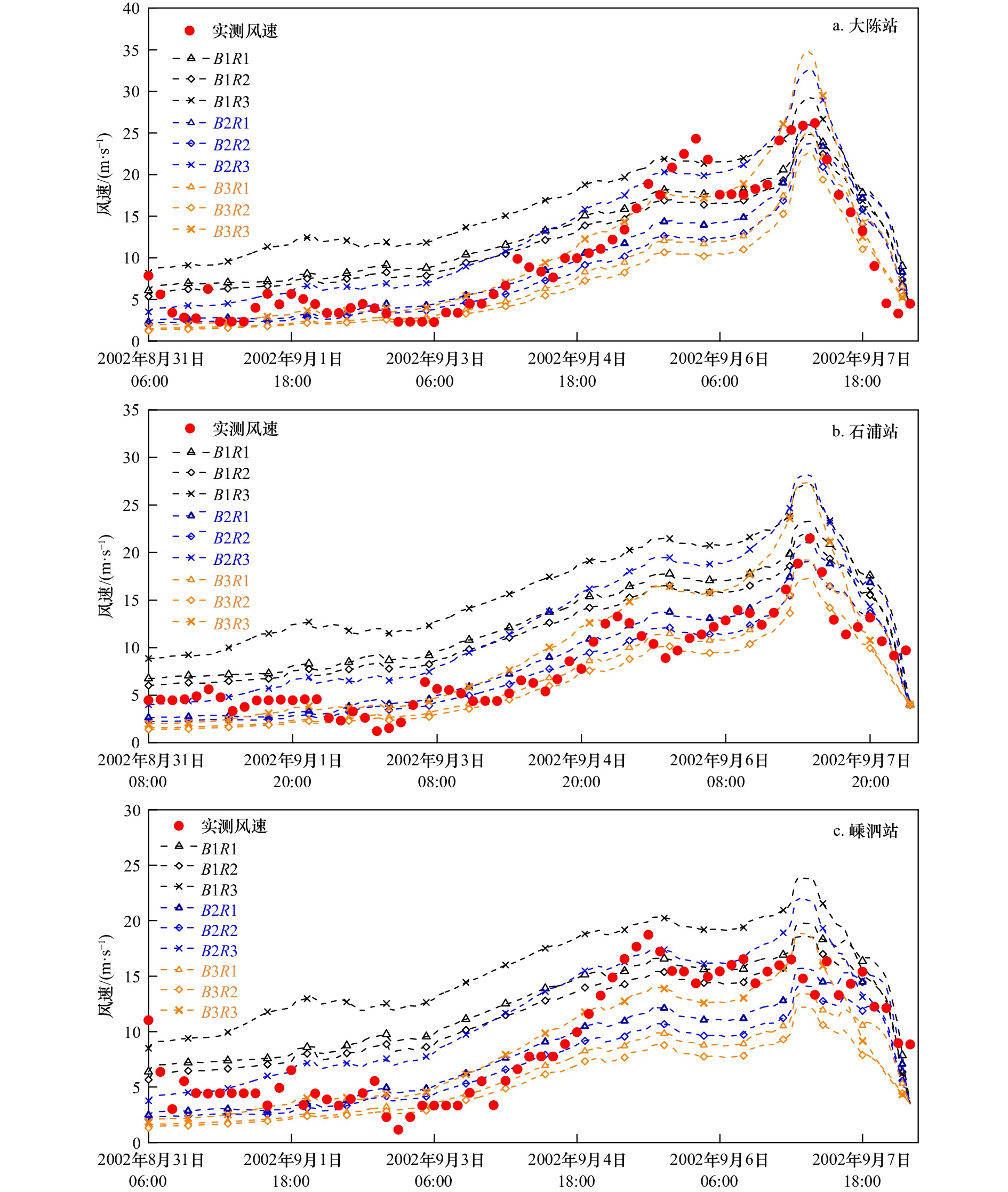
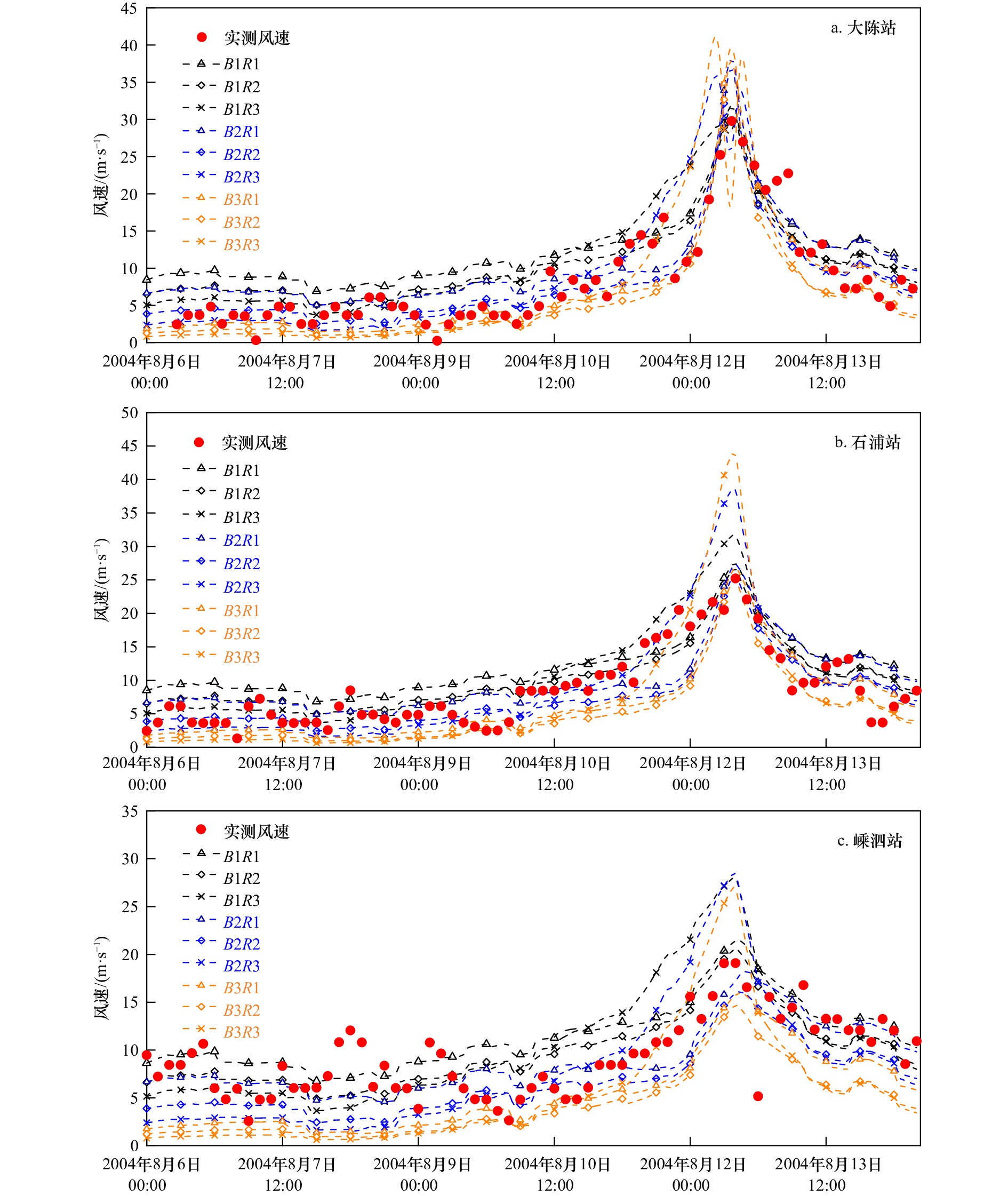
自匹配模式 R1 R2 R3 B1 B1R1 B1R2 B1R3 B2 B2R1 B2R2 B2R3 B3 B3R1 B3R2 B3R3
下载: 导出CSV
表 4 风速计算值与实测值的误差
Tab. 4 Error between simulated and observed results of wind speed
台风名称 测站 误差参数 自匹配模式 B1R1 B1R2 B1R3 B2R1 B2R2 B2R3 B3R1 B3R2 B3R3 0216 大陈 C0 0.92 0.91 0.90 0.89 0.90 0.91 0.89 0.91 0.91 C1 −0.55 −5.14 11.56 −0.93 −9.41 24.28 −4.24 −13.74 33.00 石浦 C0 0.84 0.83 0.74 0.89 0.89 0.85 0.89 0.89 0.88 C1 8.05 2.21 26.08 −2.27 −11.60 30.86 −10.70 −19.82 27.03 嵊泗 C0 0.85 0.84 0.78 0.83 0.82 0.84 0.85 0.84 0.83 C1 5.57 −0.77 27.29 −16.12 −24.51 17.45 −28.28 −34.85 0.85 0414 大陈 C0 0.92 0.91 0.87 0.91 0.91 0.87 0.92 0.91 0.84 C1 3.08 3.92 −0.92 29.4 25.46 21.85 34.85 29.32 40.58 石浦 C0 0.89 0.90 0.94 0.78 0.83 0.93 0.83 0.86 0.90 C1 3.14 5.04 26.95 9.46 3.51 54.62 7.46 1.19 76.38 嵊泗 C0 0.82 0.81 0.78 0.73 0.74 0.73 0.76 0.76 0.74 C1 10.08 7.51 46.89 −5.00 −16.05 49.82 −16.70 −23.02 42.50
下载: 导出CSV
-
[1] 牛海燕, 刘敏, 陆敏, 等. 中国沿海地区近20年台风灾害风险评价[J]. 地理科学, 2011, 31(6): 764−768.Niu Haiyan, Liu Min, Lu Min, et al. Risk assessment of typhoon disasters in China coastal area during last 20 years[J]. Scientia Geographica Sinica, 2011, 31(6): 764−768. [2] 刘倩, 高路, 赵鹏, 等. 2000−2016年中国热带气旋灾害时空特征研究[J]. 中国防汛抗旱, 2020, 30(5): 50−57.Liu Qian, Gao Lu, Zhao Peng, et al. Study on the temporal-spatial characteristics of tropical cyclone disasters in China in 2000−2016[J]. China Flood & Drought Management, 2020, 30(5): 50−57. [3] Holland G J. An analytic model of the wind and pressure profiles in hurricanes[J]. Monthly Weather Review, 1980, 108(8): 1212−1218. doi: 10.1175/1520-0493(1980)108<1212:AAMOTW>2.0.CO;2 [4] 杨万康, 尹宝树, 伊小飞, 等. 基于Holland 风场的台风浪数值计算[J]. 水利水运工程学报, 2017(4): 28−34.Yang Wankang, Yin Baoshu, Yi Xiaofei, et al. Numerical calculation and research of typhoon waves based on Holland wind field[J]. Hydro-Science and Engineering, 2017(4): 28−34. [5] 魏凯, 沈忠辉, 吴联活, 等. 强台风作用下近岸海域波浪−风暴潮耦合数值模拟[J]. 工程力学, 2019, 36(11): 139−146.Wei Kai, Shen Zhonghui, Wu Lianhuo, et al. Coupled numerical simulation on wave and storm surge in coastal areas under strong typhoons[J]. Engineering Mechanics, 2019, 36(11): 139−146. [6] 潘冬冬, 王俊, 周川. 基于“山竹”台风的波浪数值模拟[J]. 水道港口, 2021, 42(2): 194−199, 219. doi: 10.3969/j.issn.1005-8443.2021.02.006Pan Dongdong, Wang Jun, Zhou Chuan. Numerical simulation of wave based on Typhoon Mangkhut[J]. Journal of Waterway and Harbor, 2021, 42(2): 194−199, 219. doi: 10.3969/j.issn.1005-8443.2021.02.006 [7] 李小莉, 潘增弟, 佘军. 一种调整台风参数的方法[J]. 黄渤海海洋, 1995, 13(2): 11−15.Li Xiaoli, Pan Zengdi, She Jun. A method for adjustment of typhoon parameters[J]. Journal of Oceanograpgy of Huanghai & Bohai Seas, 1995, 13(2): 11−15. [8] 江志辉, 华锋, 曲平. 一个新的热带气旋参数调整方案[J]. 海洋科学进展, 2008, 26(1): 1−7. doi: 10.3969/j.issn.1671-6647.2008.01.001Jiang Zhihui, Hua Feng, Qu Ping. A new scheme for adjusting the tropical cyclone parameters[J]. Advances in Marine Science, 2008, 26(1): 1−7. doi: 10.3969/j.issn.1671-6647.2008.01.001 [9] 赵林, 葛耀君, 宋丽莉, 等. 广州地区台风极值风特性蒙特卡罗随机模拟[J]. 同济大学学报(自然科学版), 2007, 35(8): 1034−1038. doi: 10.3321/j.issn:0253-374X.2007.08.007Zhao Lin, Ge Yaojun, Song Lili, et al. Monte-Carlo simulation analysis of typhoon extreme value wind characteristics in Guangzhou[J]. Journal of Tongji University (Natural Science), 2007, 35(8): 1034−1038. doi: 10.3321/j.issn:0253-374X.2007.08.007 [10] Powell M, Soukup G, Cocke S, et al. State of Florida hurricane loss projection model: Atmospheric science component[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2005, 93(8): 651−674. doi: 10.1016/j.jweia.2005.05.008 [11] Vickery P J, Wadhera D. Statistical models of Holland pressure profile parameter and radius to maximum winds of hurricanes from flight-level pressure and H*Wind data[J]. Journal of Applied Meteorology and Climatology, 2008, 47(10): 2497−2517. doi: 10.1175/2008JAMC1837.1 [12] Love G, Murphy K. The operational analysis of tropical cyclone wind fields in the Australian northern region[J]. Northern Territory Region Research Papers, 1984, 85: 44−51. [13] Hubbert G D, Holland G J, Leslie L M, et al. A real-time system for forecasting tropical cyclone storm surges[J]. Weather and Forecasting, 1991, 6(1): 86−97. doi: 10.1175/1520-0434(1991)006<0086:ARTSFF>2.0.CO;2 [14] Harper B A, Holland G J. An updated parametric model of the tropical cyclone[C]// Proceedings of AMS 23rd Conference on Hurricanes and Tropical Meteorology. Dallas: Insititute of Electrical and Electronics Engineers, 1999: 10−15. [15] Jakobsen F, Madsen H. Comparison and further development of parametric tropical cyclone models for storm surge modelling[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2004, 92(5): 375−391. doi: 10.1016/j.jweia.2004.01.003 [16] 李瑞龙. 基于改进的台风关键参数的台风极值风速预测[D]. 哈尔滨: 哈尔滨工业大学, 2007.Li Ruilong. Prediction of typhoon extreme wind speeds based on improved typhoon key parameteters[D]. Harbin: Harbin Institute of Technology, 2007. [17] Fang Pingzhi, Ye Gengjiao, Yu Hui. A parametric wind field model and its application in simulating historical typhoons in the western North Pacific Ocean[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2020, 199: 104131. doi: 10.1016/j.jweia.2020.104131 [18] 唐建, 史剑, 李训强, 等. 基于台风风场模型的台风浪数值模拟[J]. 海洋湖沼通报, 2013(2): 24−30.Tang Jian, Shi Jian, Li Xunqiang, et al. Numerical simulation of typhoon waves with typhoon wind model[J]. Transactions of Oceanology and Limnology, 2013(2): 24−30. [19] 程雨佳, 庞亮, 董胜. 台风条件下南海海域超长重现期波高推算的研究[J]. 中国海洋大学学报, 2019, 49(S2): 125−132.Cheng Yujia, Pang Liang, Dong Sheng. The study on the estimation of very long return-period significant wave height during hurricane in the region of China South Sea[J]. Periodical of Ocean University of China, 2019, 49(S2): 125−132. [20] 方根深, 赵林, 梁旭东, 等. 基于强台风“黑格比”的台风工程模型场参数在中国南部沿海适用性研究[J]. 建筑结构学报, 2018, 39(2): 106−113.Fang Genshen, Zhao Lin, Liang Xudong, et al. Applicability analysis of typhoon field parameters in engineering model for south coastal region of China based on strong typhoon Hagupit 0814[J]. Journal of Building Structures, 2018, 39(2): 106−113. [21] 卢安平, 赵林, 郭增伟, 等. 基于Monte Carlo法的极值分布类型及其参数估计方法比较[J]. 哈尔滨工业大学学报, 2013, 45(2): 88−95. doi: 10.11918/j.issn.0367-6234.2013.02.016Lu Anping, Zhao Lin, Guo Zengwei, et al. A comparative study of extreme value distribution and parameter estimation based on the Monte Carlo method[J]. Journal of Harbin Institute of Technology, 2013, 45(2): 88−95. doi: 10.11918/j.issn.0367-6234.2013.02.016 [22] 孙志林, 钟汕虹, 王辰, 等. 舟山渔港风暴潮模拟分析[J]. 海洋学报, 2020, 42(1): 136−143.Sun Zhilin, Zhong Shanhong, Wang Chen, et al. Simulation and analysis of storm surge at Zhoushan fishing port[J]. Haiyang Xuebao, 2020, 42(1): 136−143. [23] 丁骏, 王晶, 赵鑫. 1323号“菲特”台风过程鳌江站历史最高潮位的数值模拟[J]. 海洋预报, 2014, 31(5): 30−36. doi: 10.11737/j.issn.1003-0239.2014.05.005Ding Jun, Wang Jing, Zhao Xin. Simulation of the highest tidal level in history of Typhoon 1323 “Fitow”[J]. Marine Forecasts, 2014, 31(5): 30−36. doi: 10.11737/j.issn.1003-0239.2014.05.005 [24] 陈洁, 宋城城, 李梦雅, 等. 基于情景的浙江省玉环县台风风暴潮模拟与潜在危险性评估[J]. 华东师范大学学报(自然科学版), 2016(3): 125−135, 155.Chen Jie, Song Chengcheng, Li Mengya, et al. Potential hazard assessment of typhoon storm surge based on scenario simulation methodology in Yuhuan County, Zhejiang Province[J]. Journal of East China Normal University (Natural Science), 2016(3): 125−135, 155. [25] 何威, 姚炎明, 黄森军, 等. 椒江河口形态变化对风暴潮位的影响——以9711号台风为例[J]. 水力发电学报, 2019, 38(7): 21−35. doi: 10.11660/slfdxb.20190703He Wei, Yao Yanming, Huang Senjun, et al. Effects of variations in Jiaojiang estuarine geography on storm tides: Case study of Typhoon 9711[J]. Journal of Hydroelectric Engineering, 2019, 38(7): 21−35. doi: 10.11660/slfdxb.20190703 [26] Vickery P J, Skerlj P F, Twisdale L A. Simulation of hurricane risk in the U. S. using empirical track model[J]. Journal of Structural Engineering, 2000, 126(10): 1222−1237. doi: 10.1061/(ASCE)0733-9445(2000)126:10(1222) [27] Fang Genshen, Zhao Lin, Song Lili, et al. Reconstruction of radial parametric pressure field near ground surface of landing typhoons in Northwest Pacific Ocean[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 183: 223−234. doi: 10.1016/j.jweia.2018.10.020 [28] 林伟, 方伟华. 西北太平洋台风风场模型中Holland B系数区域特征研究[J]. 热带地理, 2013, 33(2): 124−132.Lin Wei, Fang Weihua. Regional characteristics of Holland B parameter in typhoon wind field model for Northwest Pacific[J]. Tropical Geography, 2013, 33(2): 124−132. [29] Graham H E. Meteorological Considerations Pertinent to Standard Project Hurricane, Atlantic and Gulf Coasts of the United States[M]. Washington, D. C. : U. S. Department of Commerce, Weather Bureau, 1959. [30] Ying Ming, Zhang Wei, Yu Hui, et al. An overview of the China meteorological administration tropical cyclone database[J]. Journal of Atmospheric and Oceanic Technology, 2014, 31(2): 287−301. doi: 10.1175/JTECH-D-12-00119.1 [31] Lu Xiaoqin, Yu Hui, Ying Ming, et al. Western north pacific tropical cyclone database created by the China meteorological administration[J]. Advances in Atmospheric Sciences, 2021, 38(4): 690−699. doi: 10.1007/s00376-020-0211-7 [32] 黄山. 琼州海峡风暴潮数值模拟与不同台风路径对增水的影响研究[D]. 广州: 华南理工大学, 2016.Huang Shan. Numerical simulation of storm surges in the Qiongzhou Strait and study on the influence of different typhoon tracks on surges[D]. Guangzhou: South China University of Technology, 2016. [33] 杨玄阁, 朱良生. 琼州海峡台风风暴潮增水过程的数值分析[J]. 人民珠江, 2017, 38(1): 43−47. doi: 10.3969/j.issn.1001-9235.2017.01.010Yang Xuange, Zhu Liangsheng. Numerical simulation and analysis of storm surge in the Qiongzhou Strait[J]. Pearl River, 2017, 38(1): 43−47. doi: 10.3969/j.issn.1001-9235.2017.01.010 [34] 卢美, 严俊. 浙江沿岸“0216”号台风风暴潮特征及预报经验总结[J]. 海洋预报, 2003, 20(2): 15−23. doi: 10.3969/j.issn.1003-0239.2003.02.003Lu Mei, Yan Jun. He characteristics and forecast experience of Typhoon 0216 storm surge in Zhejiang coast[J]. Marine Forecasts, 2003, 20(2): 15−23. doi: 10.3969/j.issn.1003-0239.2003.02.003 [35] 张西琳, 楚栋栋, 张继才, 等. 东南沿海台风风暴潮增水过程中非线性机制和地形的作用研究: 以1509号台风“灿鸿”为例[J]. 海洋与湖沼, 2020, 51(6): 1320−1331. doi: 10.11693/hyhz20191200279Zhang Xilin, Chu Dongdong, Zhang Jicai, et al. Effects of nonlinear terms and topography on storm surges in the southeast seas of China: a case study of Typhoon Chan-hom[J]. Oceanologia et Limnologia Sinica, 2020, 51(6): 1320−1331. doi: 10.11693/hyhz20191200279 [36] 朱婧, 叶龙彬, 陈德花, 等. 1614号台风“莫兰蒂”在厦门湾及其周边海域引发风暴潮的数值模拟[J]. 海洋预报, 2020, 37(6): 20−30.Zhu Jing, Ye Longbin, Chen Dehua, et al. Numerical simulation of storm surge in Xiamen Bay and its adjacent seas caused by Typhoon “Moranti” (1614)[J]. Marine Forecasts, 2020, 37(6): 20−30. -
图(9) / 表(4)
计量
- 文章访问数: 481
- HTML全文浏览量: 197
- PDF下载量: 93
- 被引次数: 0
