A numerical investigation on wave height and wave setup of irregular wave propagation at the reef flat with porous media
-
摘要: 采用
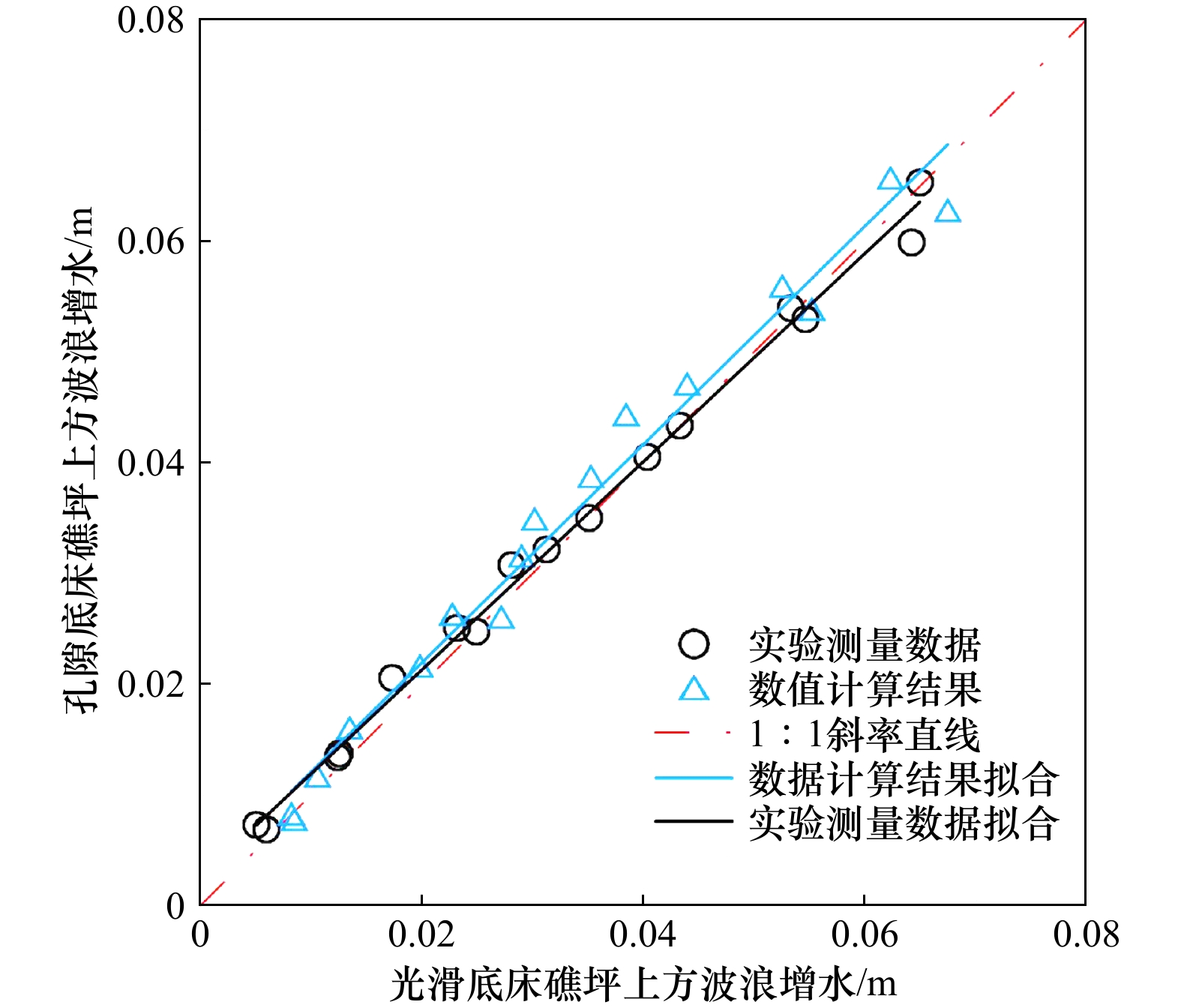
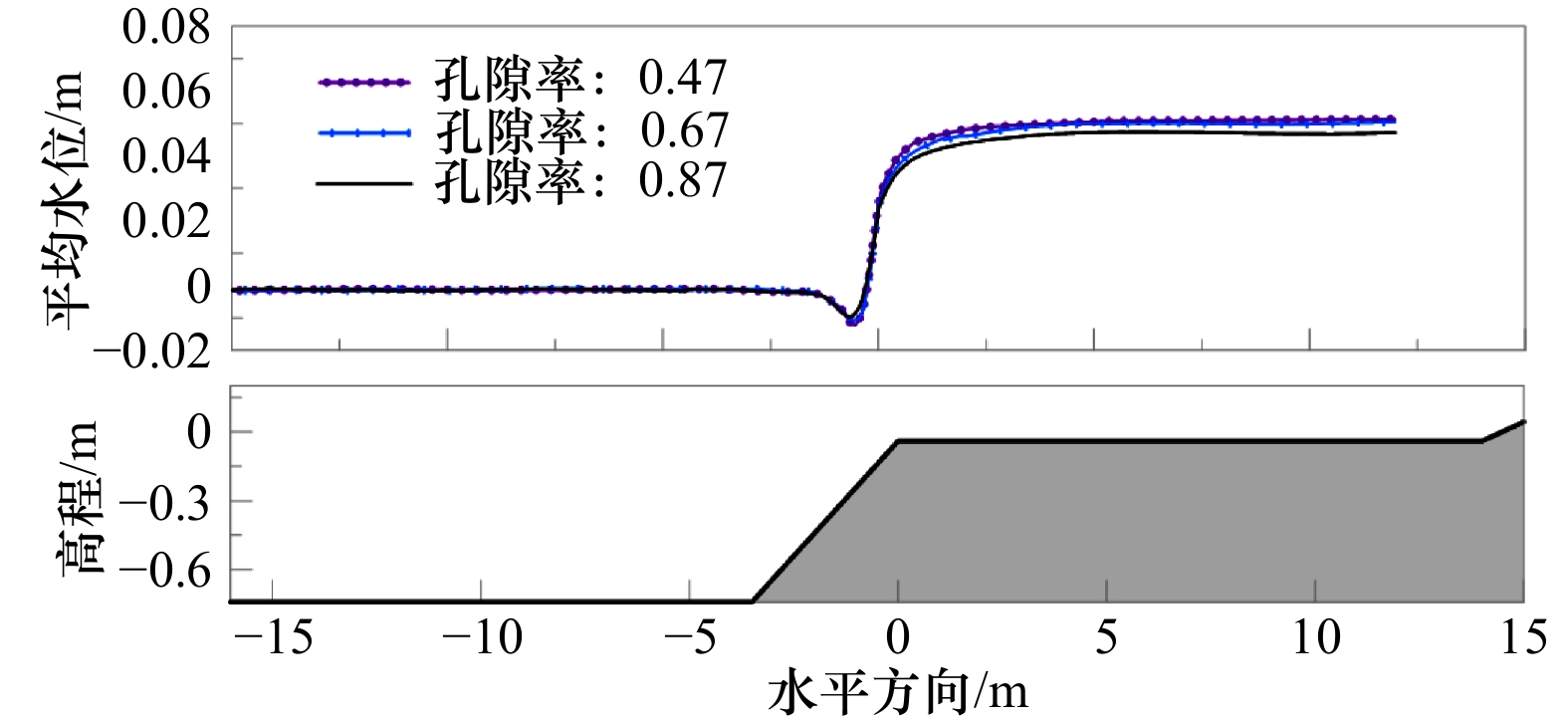
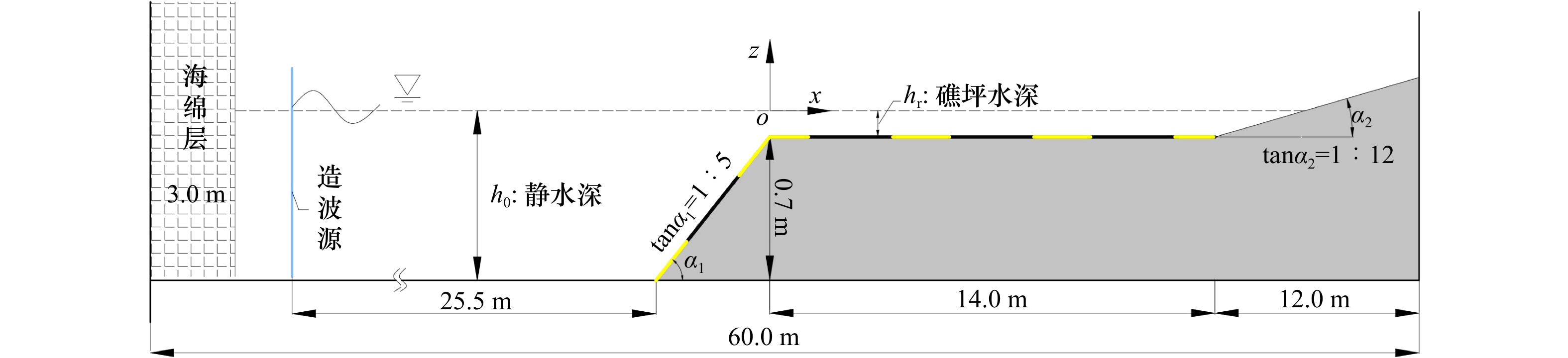
$\sigma $ 坐标系统下以体积平均的雷诺时间平均方程作为控制方程的三维非静压模型，对随机波浪在带有孔隙介质的岛礁地形上的传播过程进行了模拟，重点分析了礁坪上方波高和增水的变化。通过与多个组次工况的物理模型实验数据进行对比，结果显示，本文模型能很好地模拟波浪在孔隙介质上传播演化的过程，与实验结果吻合程度很高。分析结果表明，相比于光滑底床，孔隙介质的存在造成破碎点附近波高平均下降12%，礁坪上方波高平均下降28%。对于平均水位，孔隙底床条件下的最大减水幅值减小了43%，同时礁坪上方增水幅值上升6%。另外，孔隙率在0.47～0.87范围内变化时，对礁坪上方平均水位的变化基本无影响。Abstract: A three-dimensional non-hydrostatic model based on volumed-averaged, Reynolds-averaged Navier-Stokes (VARANS) equations in sigma coordinate, is applied to simulate the propagation process of irregular wave over a typical fringing coral reef profile, with emphasis on the changes of wave height and wave setup on the reef flat. Compared with the laboratory measured data of several groups of wave and water level parameters, the model is shown to be capable of simulating well the wave transformation over the reef profile with and without porous media. Across all cases, the porous cases decrease the wave height by 12% around the breaking point, and by 28% on the reef flat than the smooth cases. As for the mean water level, the results show that the maximum setdown decreases by 43% on average for the porous cases than the smooth cases, while the wave setup on the reef flat for corresponding porous and smooth simulations is found to agree with an average difference of only 6%. In addition, the variation of porosity in the range 0.47−0.87 auses little effect on the wave setup.-
Key words:
- non-hydrostatic model /
- porous media /
- reef profile /
- wave setup
-
图 1 礁坪地形及计算域布置示意图
Fig. 1 Schematic of the reef flat and the computational domain layout
图 2
水平方向网格间距（a）和垂向分层数（b）收敛性分析及地形剖面（c）示意图 Fig. 2 Convergence of grid spacing in horizontal (a) and vertical direction (b) and the sketch of terrain profile (c)
图 3 组合 4测点波面高程历程曲线
Fig. 3 Time series of simulated wave surface elevation for the Case 4
图 4 组合 4光滑和孔隙底床下均方波高（a）、平均水位（b）和地形剖面（c）沿程变化
Fig. 4 Mean square wave height (a) , mean water level (b), and terrain profile (c) for the Case 4 at porous and smooth beds
图 5 孔隙底床和光滑底床在不同区域处均方波高的比较
Fig. 5 Comparisons of the mean square wave heights at different regions for the porous and smooth beds
图 6 孔隙底床和光滑底床在礁坪上方均方波高和水深比（Hrms/h）
Fig. 6 Comparisons of the ratio of mean square wave height to water depth (Hrms/h) on the reef flat for the porous and smooth beds
图 7 孔隙底床和光滑底床条件下最大减水对比
Fig. 7 Comparisons of maximum setdown for the porous and smooth beds
图 8 孔隙底床和光滑底床在礁坪上方波浪增水比较
Fig. 8 Comparisons of wave setup on the reef flat for the porous and smooth beds
图 9 组合4光滑底床（a）和孔隙底床（b）礁坪上方水平方向平均流速分布
Fig. 9 Distribution of horizontal mean current velocities at the reef flat of Case 4 for the smooth (a) and porous (b) beds
图 10 组合4不同孔隙率下平均水位对比及地形剖面示意图
Fig. 10 Comparisons of mean water level for Case 4 with varied porosities and the sketch of terrain profile
表 1 数值实验波浪和水位参数
Tab. 1 Parameters of wave and water level for the numerical experiments
组合 均方波高Hrms/m 谱峰周期Tp/s 礁坪水深hr/m 1 0.03 2.26 0.04 2 0.06 2.26 0.04 3 0.09 2.26 0.04 4 0.12 2.26 0.04 5 0.14 2.26 0.04 6 0.17 2.26 0.04 7 0.06 1.31 0.04 8 0.06 3.20 0.04 9 0.06 2.26 0.00 10 0.06 2.26 0.02 11 0.06 2.26 0.06 12 0.06 2.26 0.09 13 0.12 2.26 0.00 14 0.12 2.26 0.02 15 0.12 2.26 0.06 16 0.12 2.26 0.09 
下载: 导出CSV
表 2 孔隙底床上均方波高和平均水位相对于光滑底床的变化百分比
Tab. 2 Relative percentage changes of mean square wave heights and average water levels between the porous beds and the smooth beds
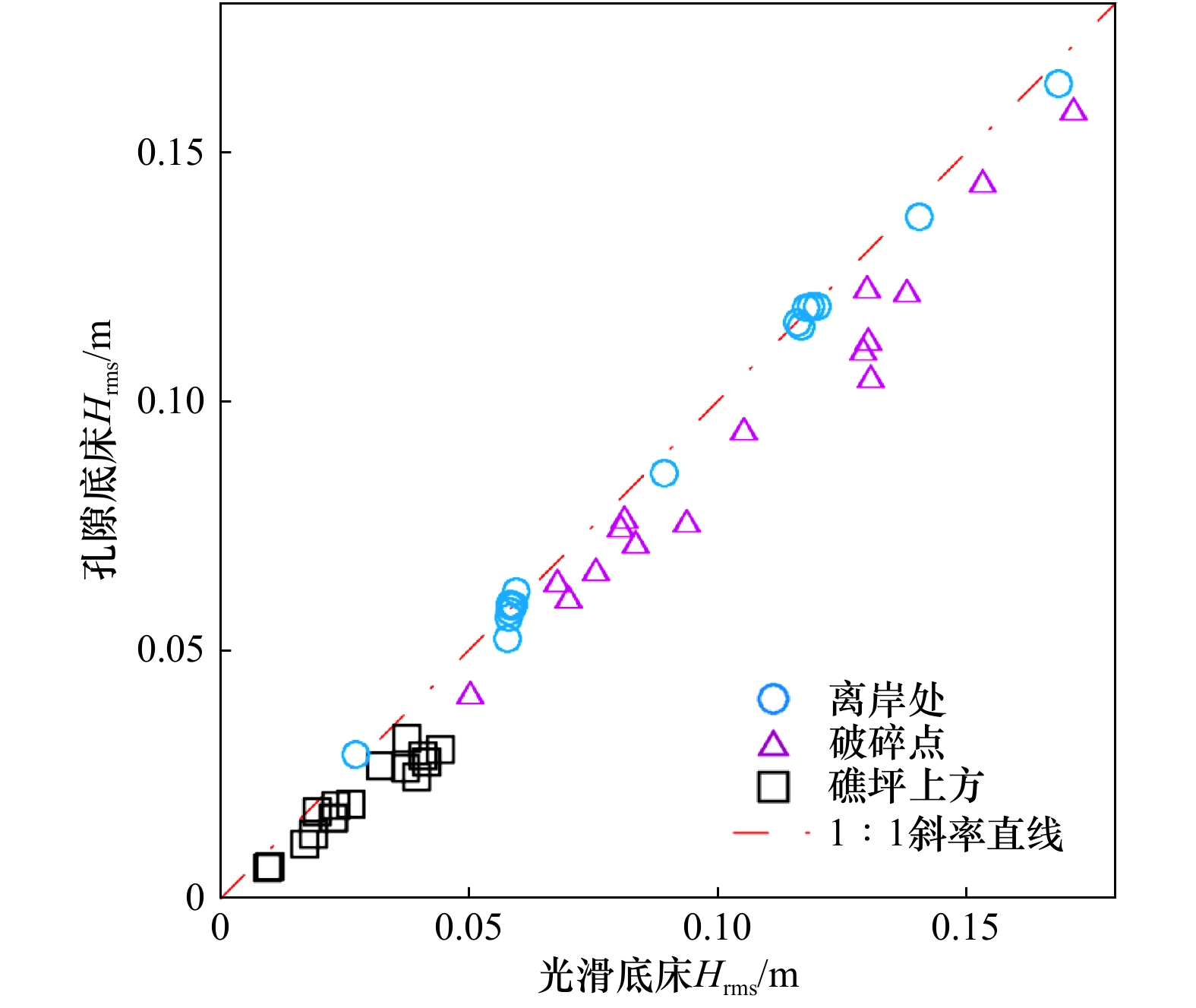
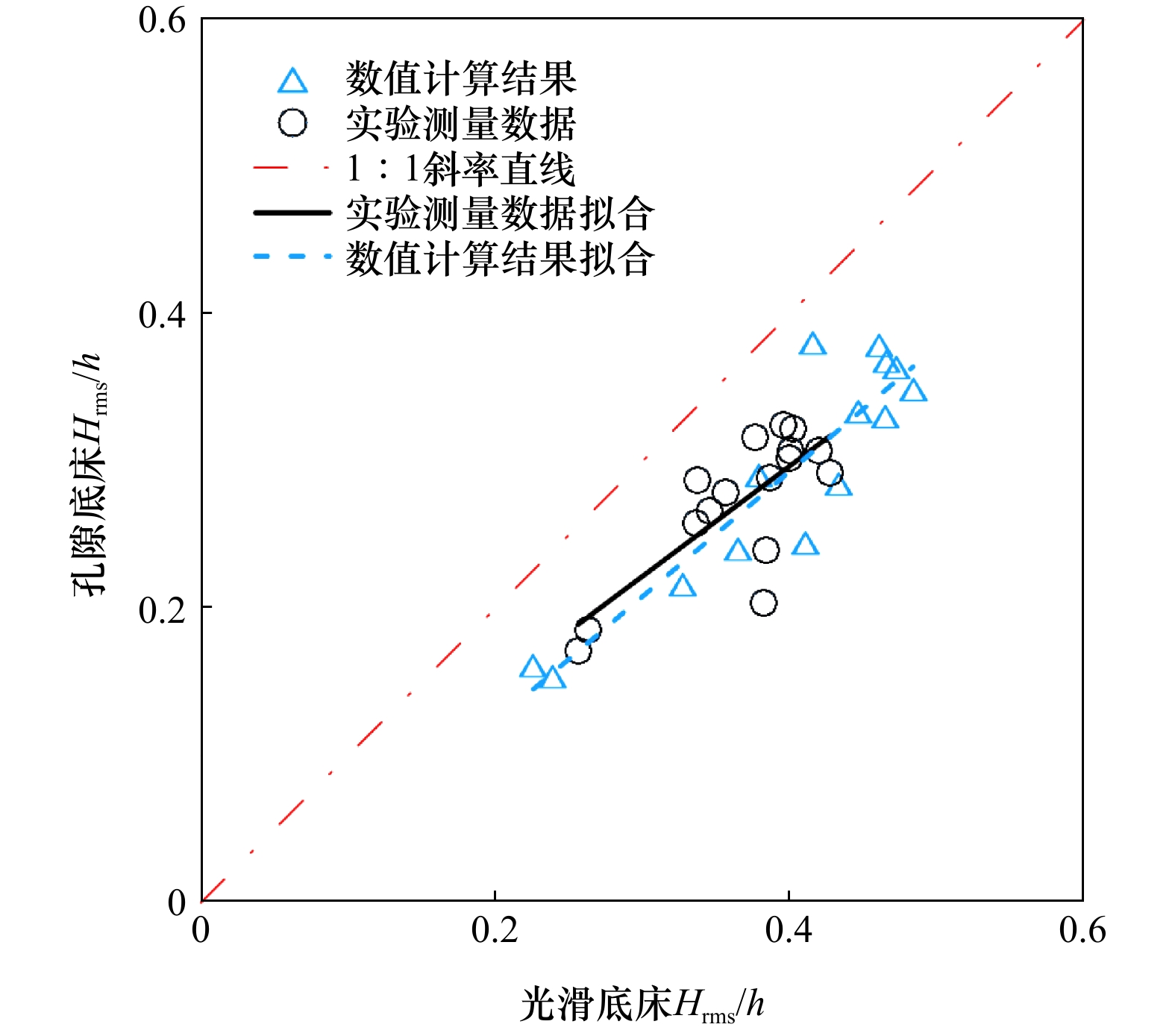
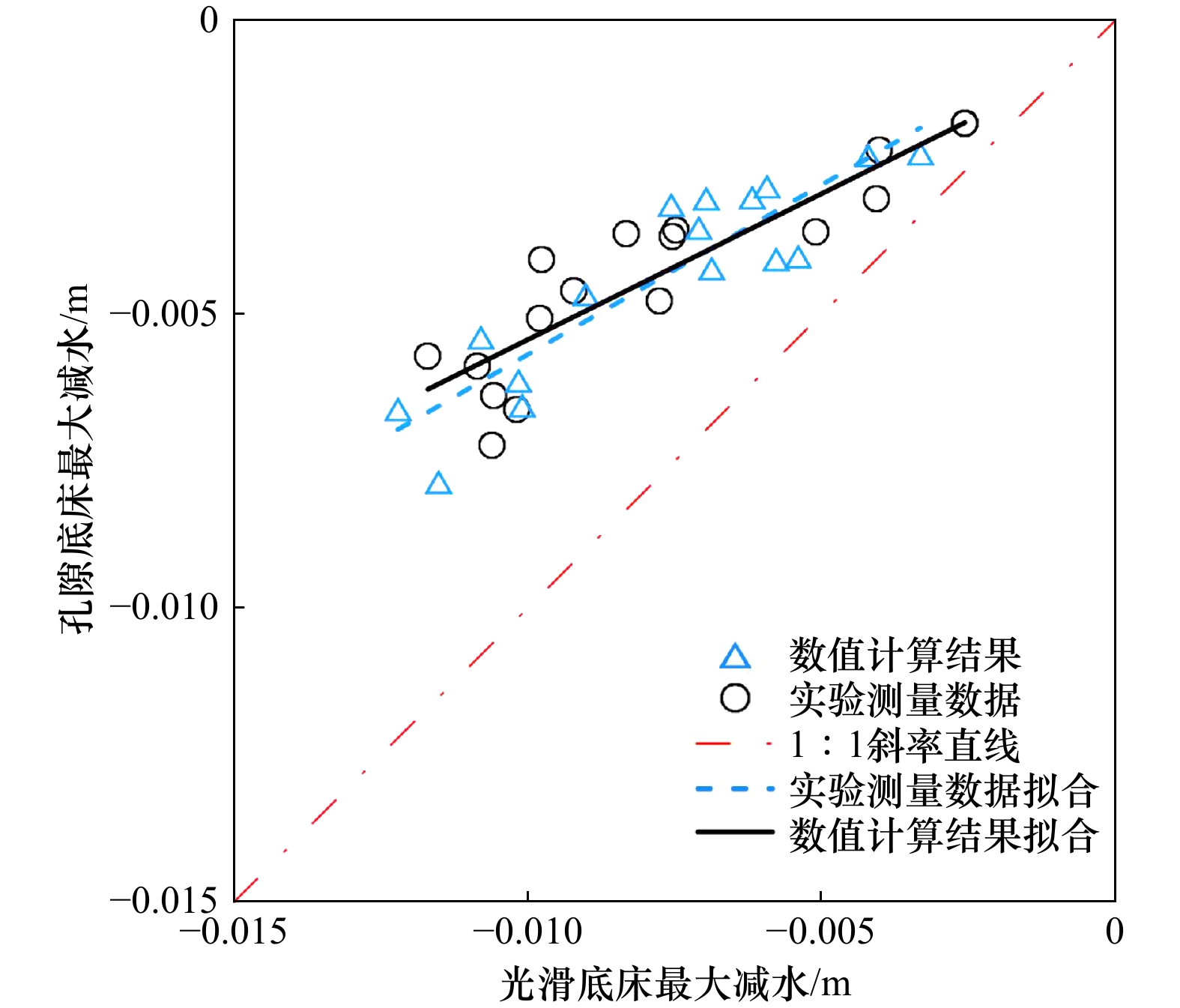
离岸处 破碎点 礁坪上方 均方波高 光滑底床 1.0 1.0 1.0 孔隙底床 −0.7% −12.0% −28.0% 平均水位 光滑底床 1.0 1.0 1.0 孔隙底床 −0.3% −43.0% 6.0%
下载: 导出CSV
-
[1] 陈洪洲, 毕春伟, 高俊亮. 波浪在珊瑚岸礁礁坪上传播变形的数值研究[J]. 水科学进展, 2018, 29(2): 252−259. doi: 10.14042/j.cnki.32.1309.2018.02.013Chen Hongzhou, Bi Chunwei, Gao Junliang. Numerical study of wave transformation over fringing reef flat[J]. Advances in Water Science, 2018, 29(2): 252−259. doi: 10.14042/j.cnki.32.1309.2018.02.013 [2] Grant W D, Madsen O S. Combined wave and current interaction with a rough bottom[J]. Journal of Geophysical Research: Oceans, 1979, 84(C4): 1797−1808. doi: 10.1029/JC084iC04p01797 [3] Feddersen F, Guza R T. Observations of nearshore circulation: alongshore uniformity[J]. Journal of Geophysical Research: Oceans, 2003, 108(C1): 3006. doi: 10.1029/2001JC001293 [4] 刘铁威, 屈科, 黄竞萱, 等. 孤立波在透水岸礁上水动力特性数值模拟研究[J]. 水动力学研究与进展(A辑), 2021, 36(2): 180−191.Liu Tiewei, Qu Ke, Huang Jingxuan, et al. Numerical investigation of hydrodynamic characteristics of solitary wave over permeable fringing reef[J]. Chinese Journal of Hydrodynamics (A), 2021, 36(2): 180−191. [5] Losada I J. Recent advances in the modeling of wave and permeable structure interaction[M]//Liu P L F. Advances in Coastal and Ocean Engineering. Signapore: World Scientific, 2001: 163−202. [6] Bear J. Dynamics of fluids in porous media[J]. Soil Science Society of America Journal, 1973, 37(4): 195−208. [7] Polubarinova-Kochina P Y. Theory of Ground Water Movement[M]. Princeton: Princeton University Press, 1962. [8] Van Gent M R A. Wave interaction with permeable coastal structures[D]. Delft: Technische Universiteit Delft, 1995. [9] Hsu T J, Sakakiyama T, Liu P L F. A numerical model for wave motions and turbulence flows in front of a composite breakwater[J]. Coastal Engineering, 2002, 46(1): 25−50. doi: 10.1016/S0378-3839(02)00045-5 [10] Ma Gangfeng, Shi Fengyan, Hsiao S C, et al. Non-hydrostatic modeling of wave interactions with porous structures[J]. Coastal Engineering, 2014, 91: 84−98. doi: 10.1016/j.coastaleng.2014.05.004 [11] Liu P L F, Lin Pengzhi, Chang K A, et al. Numerical modeling of wave interaction with porous structures[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1999, 125(6): 322−330. doi: 10.1061/(ASCE)0733-950X(1999)125:6(322) [12] Hieu P D, Tanimoto K. Verification of a VOF-based two-phase flow model for wave breaking and wave-structure interactions[J]. Ocean Engineering, 2006, 33(11/12): 1565−1588. [13] Nakayama A, Kuwahara F. A macroscopic turbulence model for flow in a porous medium[J]. Journal of Fluids Engineering, 1999, 121(2): 427−433. doi: 10.1115/1.2822227 [14] 张少华, 马玉祥, 艾丛芳, 等. 基于数值模拟的非线性波浪在直立墙上爬高的研究[J]. 水动力学研究与进展(A辑), 2020, 35(5): 575−583.ZhangShaohua, Ma Yuxiang, Ai Congfeng, et al. Study of nonlinear wave run-up on a vertical structure based on numerical simulation[J]. Chinese Journal of Hydrodynamics (A), 2020, 35(5): 575−583. [15] 马小舟, 马建兴, 马玉祥, 等. 基于非静压模型的波浪空间聚焦研究[J]. 中国海洋大学学报(自然科学版), 2020, 50(4): 128−135.Ma Xiaozhou, Ma Jianxing, Ma Yuxiang, et al. Research on spatial wave focusing based on non-hydrostatic wave model[J]. Periodical of Ocean University of China, 2020, 50(4): 128−135. [16] 张景新. 基于非静压模型的波浪破碎模拟[J]. 水科学进展, 2017, 28(3): 438−444. doi: 10.14042/j.cnki.32.1309.2017.03.015Zhang Jingxin. Wave breaking simulation by non-hydrostatic numerical model[J]. Advances in Water Science, 2017, 28(3): 438−444. doi: 10.14042/j.cnki.32.1309.2017.03.015 [17] Ai Congfang, Jin Sheng. A multi-layer non-hydrostatic model for wave breaking and run-up[J]. Coastal Engineering, 2012, 62: 1−8. doi: 10.1016/j.coastaleng.2011.12.012 [18] He Dongbin, Ma Yuxiang, Dong Guohai, et al. Predicting deep water wave breaking with a non-hydrostatic shock-capturing model[J]. Ocean Engineering, 2020, 216: 108041. doi: 10.1016/j.oceaneng.2020.108041 [19] Derakhti M, Kirby J T, Shi Fengyan, et al. NHWAVE: consistent boundary conditions and turbulence modeling[J]. Ocean Modelling, 2016, 106: 121−130. doi: 10.1016/j.ocemod.2016.09.002 [20] Buckley M L, Lowe R J, Hansen J E, et al. Wave setup over a fringing reef with large bottom roughness[J]. Journal of Physical Oceanography, 2016, 46(8): 2317−2333. doi: 10.1175/JPO-D-15-0148.1 [21] 何文润, 姚宇, 唐政江, 等. 粗糙珊瑚岸礁礁面附近波浪增水实验研究[J]. 海洋科学进展, 2019, 37(3): 409−416. doi: 10.3969/j.issn.1671-6647.2019.03.005He Wenrun, Yao Yu, Tang Zhengjiang, et al. Experimental study on the wave-induced setup around rough fringing reef[J]. Advances in Marine Science, 2019, 37(3): 409−416. doi: 10.3969/j.issn.1671-6647.2019.03.005 [22] 杨笑笑, 姚宇, 何天城, 等. 大糙率珊瑚礁附近规则波非线性特征实验研究[J]. 海洋学研究, 2020, 38(2): 9−15. doi: 10.3969/j.issn.1001-909X.2020.02.002Yang Xiaoxiao, Yao Yu, He Tiancheng, et al. Laboratory study of monochromatic wave nonlinear characteristics around reefs with large bottom roughness[J]. Journal of Marine Sciences, 2020, 38(2): 9−15. doi: 10.3969/j.issn.1001-909X.2020.02.002 [23] Lowe R J, Falter J L, Bandet M D, et al. Spectral wave dissipation over a barrier reef[J]. Journal of Geophysical Research: Oceans, 2005, 110(C4): C04001. [24] Nepf H M, Vivoni E R. Flow structure in depth-limited, vegetated flow[J]. Journal of Geophysical Research: Oceans, 2000, 105(C12): 28547−28557. doi: 10.1029/2000JC900145 [25] Bouws E, Günther H, Rosenthal W, et al. Similarity of the wind wave spectrum in finite depth water: 1. Spectral form[J]. Journal of Geophysical Research: Oceans, 1985, 90(C1): 975−986. doi: 10.1029/JC090iC01p00975 [26] Willmott C J. On the validation of models[J]. Physical Geography, 1981, 2(2): 184−194. doi: 10.1080/02723646.1981.10642213 [27] Apotsos A, Raubenheimer B, Elgar S, et al. Effects of wave rollers and bottom stress on wave setup[J]. Journal of Geophysical Research: Oceans, 2007, 112(C2): C02003. [28] Franklin G, Mariño-Tapia I, Torres-Freyermuth A. Effects of reef roughness on wave setup and surf zone currents[J]. Journal of Coastal Research, 2013, 65(S2): 2005−2010. [29] Lowe R J, Falter J L, Koseff J R, et al. Spectral wave flow attenuation within submerged canopies: Implications for wave energy dissipation[J]. Journal of Geophysical Research: Oceans, 2007, 112(C5): C050185. [30] Yao Yu, Liu Yicheng, Chen Long, et al. Study on the wave-driven current around the surf zone over fringing reefs[J]. Ocean Engineering, 2020, 198: 106968. doi: 10.1016/j.oceaneng.2020.106968 [31] Lara J L, del Jesus M, Losada I J. Three-dimensional interaction of waves and porous coastal structures: Part II: experimental validation[J]. Coastal Engineering, 2012, 64: 26−46. doi: 10.1016/j.coastaleng.2012.01.009 [32] Wu Yunta, Hsiao S C. Propagation of solitary waves over a submerged permeable breakwater[J]. Coastal Engineering, 2013, 81: 1−18. doi: 10.1016/j.coastaleng.2013.06.005 -
计量
- 文章访问数: 284
- HTML全文浏览量: 134
- PDF下载量: 44
- 被引次数: 0
