Numerical simulation of wave dissipation characteristics of permeable submerged breakwater under focused wave
-
摘要: 基于非静压数值计算模型，本文系统研究了聚焦波作用下透水潜堤的消波特性，通过设置合理的计算工况，详细分析了波高、堤顶水深、谱峰周期、孔隙率以及堤顶宽度5种因素对透水潜堤消波特性的影响。与此同时，本文将透水潜堤的计算结果同不透水潜堤的计算结果进行了对比分析。计算结果表明：透水潜堤对聚焦波的消减作用要强于不透水潜堤，从而说明，透水潜堤能更有效地降低畸形波对海岸基础设施的影响；波高和堤顶水深是影响潜堤消波特性的重要因素，随入射波高增加、堤顶水深减小，透水潜堤对波浪的消减作用逐渐增强。透水潜堤对长周期波浪的消波效果较差。在本文考虑的孔隙率范围内，孔隙率越大，透水潜堤消波效果越好；当孔隙率为0.4，堤顶宽度为0.612 5 m时，透水潜堤可消减54%的入射波能，比不透水潜堤对入射波能的消减增加36.1%。本文研究结果可为进一步认识透水潜堤的消波特性和海岸防护工程设计提供相应的参考。Abstract: Based on the non-hydrostatic numerical calculation model, this paper systematically studies the wave dissipation characteristics of permeable submerged breakwater under the impact of focused wave. By setting reasonable calculation conditions, the effects of wave height, water depth above the submerged breakwater, spectral peak period, porosity and the crest width of submerged breakwater on the wave dissipation characteristics of permeable submerged breakwater are analyzed in detail. At the same time, the calculation results of permeable submerged breakwater are compared with those of impermeable submerged breakwater. The calculation results show that the attenuation effect of permeable submerged breakwater on focused wave is stronger than that of impermeable submerged breakwater, which shows that permeable submerged breakwater can more effectively reduce the impact of freak wave on coastal infrastructure; wave height and the water depth above the submerged breakwater are important factors affecting the wave dissipation characteristics of submerged breakwater. With the increase of incident wave height and the decrease of the water depth above the submerged breakwater, the wave dissipation effect of permeable submerged breakwater increases gradually. The permeable submerged breakwater has poor wave dissipation effect on large-spectrum peak period waves. Within the range of porosity considered in this paper, as the porosity increases, the wave dissipation effect of permeable submerged breakwater is better; when the porosity is 0.4 and the crest width is 0.6125 m, the permeable submerged breakwater can reduce 54% of the incident wave energy, which is 36.1% higher than that of the impermeable submerged breakwater. The research results of this paper can provide corresponding reference for further understanding the wave dissipation characteristics of permeable submerged breakwater and the design of coastal protection engineering.
-
图 1 聚焦波与不透水潜堤作用数值计算布置
Fig. 1 Computational layout of focused wave impacting impermeable breakwater
图 2 聚焦波作用下不同水位测点自由液面时程曲线图
Fig. 2 Time series of water elevation recorded at different wave gauges under focused wave
图 3 规则波与透水潜堤作用数值计算布置
Fig. 3 Computational layout of regular wave impacting permeable breakwater
图 4 规则波作用下不同水位测点自由液面时程曲线图
Fig. 4 Time series of water elevation recorded at different wave gauges under regular wave
图 5 聚焦波与透水潜堤作用数值计算布置
Fig. 5 Computation layout of focused wave impacting permeable breakwater
图 6 不同水位测点自由液面时程曲线
Fig. 6 Time series of water elevation recorded at different wave gauges
图 7 不同时刻流场速度分布云图
a, c：不透水潜堤；b, d：透水潜堤
Fig. 7 Snapshots of water body velocity distribution at different time instances
a, c: Impermeable breakwater; b, d: permeable breakwater
图 8 聚焦波与潜堤作用最大波幅变化
Fig. 8 Variations of the largest wave amplitude of focused wave along the breakwater
图 9 水体动能（a）、势能（b）、总能量（c）时程曲线
Fig. 9 Time series of kinetic energies (a), potential energies (b), total wave energies (c) of the whole water body
图 10 不同波高条件下最大波幅衰减系数（DA）（a）和总能量耗散系数（DE）（b）变化
Fig. 10 Variations of maximum amplitude attenuation coefficient (DA) (a) and total energy dissipation coefficient (DE) (b) under different wave height
图 11 不同堤顶水深条件下最大波幅衰减系数（DA）（a）和总能量耗散系数（DE）（b）变化
Fig. 11 Variations of maximum amplitude attenuation coefficient (DA) (a) and total energy dissipation coefficient (DE) (b) under different water depth above the submerged breakwater
图 12 不同谱峰周期条件下最大波幅衰减系数（DA）（a） 和总能量耗散系数（DE）（b）变化
Fig. 12 Variations of maximum amplitude attenuation coefficient (DA) (a) and total energy dissipation coefficient (DE) (b) under different spectral peak period
图 13 不同孔隙率条件下最大波幅衰减系数（DA）（a）和总能量耗散系数（DE）（b）变化
Fig. 13 Variations of maximum amplitude attenuation coefficient (DA) (a) and total energy dissipation coefficient (DE) (b) under different porosity
图 14 不同堤顶宽度条件下最大波幅衰减系数（DA）（a）和总能量耗散系数（DE）（b）变化
Fig. 14 Variations of maximum amplitude attenuation coefficient (DA) (a) and total energy dissipation coefficient (DE) (b) under different crest width of submerged breakwater
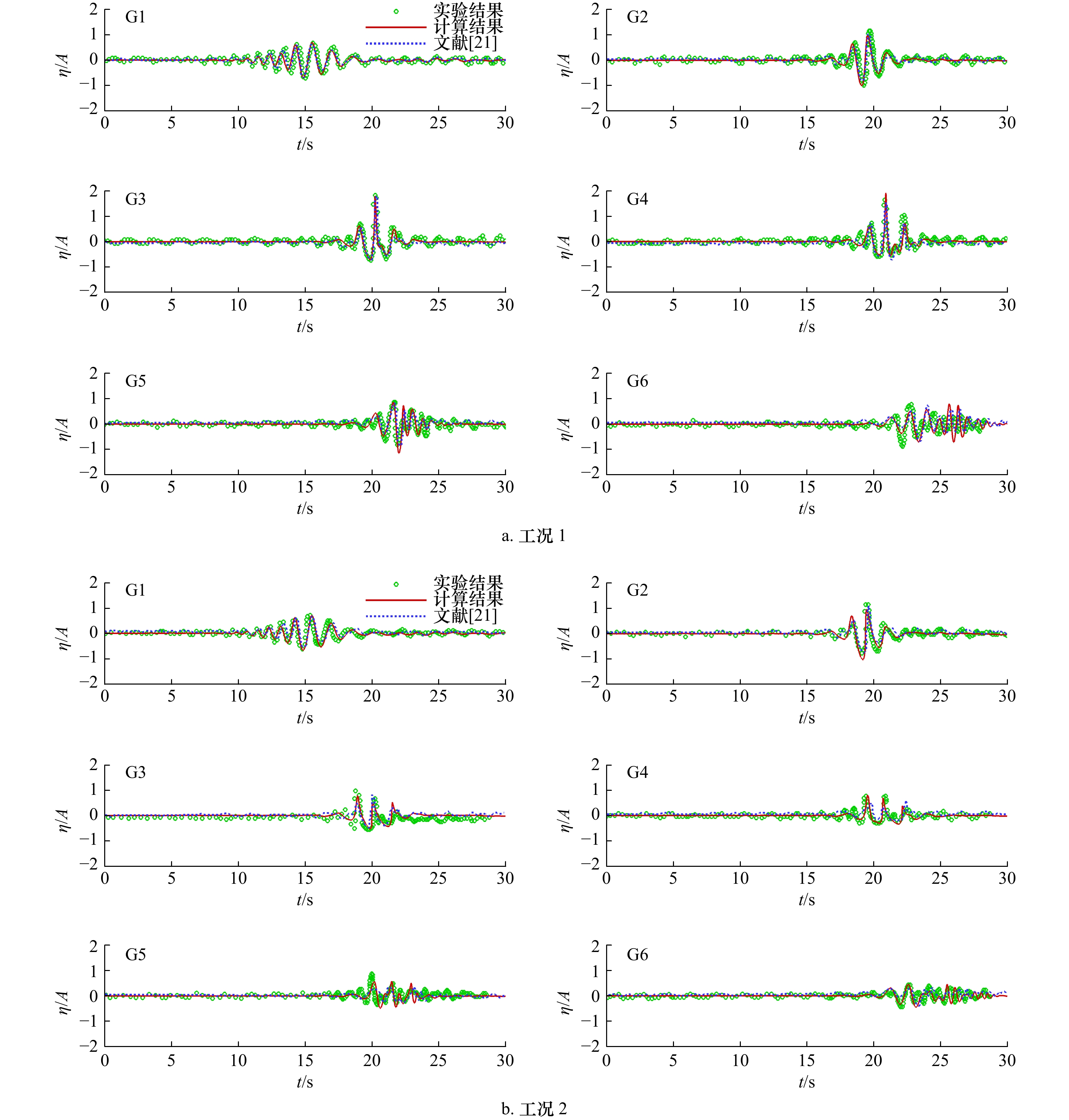
表 1 验证工况参数
Tab. 1 Parameter setup of verification conditions
工况 频率范
围$f{\text{/} }{ {\rm{H} }{\rm{z} } }$中值频
率${f_c}{\text{/} }{ {\rm{H} }{\rm{z} } }$聚焦波
幅A/m波陡
$ {k_c}A $色散系
数$kh$1 0.53, 1.13 0.83 0.03 0.092 0.83, 2.60 2 0.53, 1.13 0.83 0.06 0.184 0.83, 2.60 
下载: 导出CSV
-
[1] Kharif C, Pelinovsky E, Slunyaev A. Rogue Waves in the Ocean[M]. Berlin: Springer, 2009. [2] Nikolkina I, Didenkulova I. Rogue waves in 2006−2011[C]//Proceedings of EGU General Assembly 2012. Vienna: EGU, 2012: 2913−2924. [3] Nikolkina I, Didenkulova I. Catalogue of rogue waves reported in media in 2006–2010[J]. Natural Hazards, 2012, 61(3): 989−1006. doi: 10.1007/s11069-011-9945-y [4] Cummins W E. The impulse response function and ship motions[J]. Schiffstechnik, 1962, 9: 101−109. [5] Kharif C, Pelinovsky E, Talipova T. Freak wave generation in shallow water[J]. Comptes Rendus de l Académie des Sciences-Series IIB-Mechanics, 2000, 328(11): 801−807. [6] Kriebel D L, Alsia M V. Simulation of extreme waves in a background random sea[C]//Proceedings of the Tenth International Offshore and Polar Engineering Conference. Seattle: OnePetro, 2000: 31−37. [7] 裴玉国. 畸形波的生成及基本特性研究[D]. 大连: 大连理工大学, 2008.Pei Yuguo. The generation of freak waves and its behaviors[D]. Dalian: Dalian University of Technology, 2008. [8] Johannessen T B, Swan C. Nonlinear transient water waves—part I. A numerical method of computation with comparisons to 2-D laboratory data[J]. Applied Ocean Research, 1997, 19(5/6): 293−308. [9] 李润锋, 赵刘群, 朱良生. 畸形波的非线性生成及特性初步分析[J]. 中国造船, 2020, 61(S2): 27−36. doi: 10.3969/j.issn.1000-4882.2020.z2.004Li Runfeng, Zhao Liuqun, Zhu Liangsheng. Analysis of formation and characteristics of abnormal wave[J]. Shipbuilding of China, 2020, 61(S2): 27−36. doi: 10.3969/j.issn.1000-4882.2020.z2.004 [10] Baldock T E, Swan C, Taylor P H. A laboratory study of nonlinear surface waves on water[J]. Philosophical Transactions of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 1996, 354(1707): 649−676. doi: 10.1098/rsta.1996.0022 [11] Ning D Z, Zang J, Liu S X, et al. Free-surface evolution and wave kinematics for nonlinear uni-directional focused wave groups[J]. Ocean Engineering, 2009, 36(15/16): 1226−1243. [12] Whittaker C N, Fitzgerald C J, Raby A C, et al. Optimisation of focused wave group runup on a plane beach[J]. Coastal Engineering, 2017, 121: 44−55. doi: 10.1016/j.coastaleng.2016.12.001 [13] 刘必劲, 张振伟, 刘忠波, 等. 基于Boussinesq水波模型的聚焦波模拟[J]. 海洋学报, 2021, 43(3): 31−39.Liu Bijin, Zhang Zhenwei, Liu Zhongbo, et al. Simulating the evolution of a focused wave group by a Boussinesq-type model[J]. Haiyang Xuebao, 2021, 43(3): 31−39. [14] 卓晓玲. 聚焦波与水流及结构物作用的数值模拟[D]. 大连: 大连理工大学, 2013.Zhuo Xiaoling. Numerical investigation on the interaction of focused waves with uniform current and structures[D]. Dalian: Dalian University of Technology, 2013. [15] Beji S, Battjes J A. Experimental investigation of wave propagation over a bar[J]. Coastal Engineering, 1993, 19(1/2): 151−162. [16] 边峰, 黄哲, 琚烈红. 不同结构形式潜堤消浪性能物理模型试验研究[J]. 水运工程, 2020(8): 36−41, 58. doi: 10.3969/j.issn.1002-4972.2020.08.006Bian Feng, Huang Zhe, Ju Liehong. Physical model test study on wave resistance performance of submerged breakwaters with different structure forms[J]. Port & Waterway Engineering, 2020(8): 36−41, 58. doi: 10.3969/j.issn.1002-4972.2020.08.006 [17] 郑艳娜, 赵勇, 詹坤. 规则波作用下组合式潜堤消浪性能试验研究[J]. 水运工程, 2017(3): 40−43. doi: 10.3969/j.issn.1002-4972.2017.03.008Zheng Yanna, Zhao Yong, Zhan Kun. Experimental study on performance of combined submerged breakwaters in regular wave[J]. Port & Waterway Engineering, 2017(3): 40−43. doi: 10.3969/j.issn.1002-4972.2017.03.008 [18] Sun Jiawen, Ma Zhe, Wang Dongxu, et al. Numerical study of the run-up of a solitary wave after propagation over a saw-tooth-shaped submerged breakwater[J]. International Journal of Naval Architecture and Ocean Engineering, 2020, 12: 283−296. doi: 10.1016/j.ijnaoe.2019.11.002 [19] Han Xinyu, Dong Sheng. Interaction of solitary wave with submerged breakwater by smoothed particle hydrodynamics[J]. Ocean Engineering, 2020, 216(1/2): 108108. [20] Liang Bingchen, Wu Guoxiang, Liu Fushun, et al. Numerical study of wave transmission over double submerged breakwaters using non-hydrostatic wave model[J]. Oceanologia, 2015, 57(4): 308−317. doi: 10.1016/j.oceano.2015.07.002 [21] Li Mengyu, Zhao Xizeng, Ye Zhouteng, et al. Generation of regular and focused waves by using an internal wave maker in a CIP-based model[J]. Ocean Engineering, 2018, 167: 334−347. doi: 10.1016/j.oceaneng.2018.08.048 [22] Liu Cheng, Liu Xiaoping, Jiang Changbo. Numerical simulation of wave field near submerged bars by PLIC-VOF model[J]. China Ocean Engineering, 2005, 19(3): 509−518. [23] Sollitt C K, Cross R H. Wave transmission through permeable breakwaters[C]//Proceedings of the 13th International Conference on Coastal Engineering. Vancouver: ASCE, 1973: 1827−1846. [24] Twu S W, Liu C C. Interaction of non-breaking regular waves with a periodic array of artificial porous bars[J]. Coastal Engineering, 2004, 51(3): 223−236. doi: 10.1016/j.coastaleng.2004.01.002 [25] 蒋昌波, 刘静, 陈杰, 等. 孤立波通过透水潜堤水动力特性试验[J]. 长沙理工大学学报(自然科学版), 2013, 10(2): 40−45.Jiang Changbo, Liu Jing, Chen Jie, et al. Hydrodynamic characteristic of solitary wave passing the permeable submerged breakwater[J]. Journal of Changsha University of Science and Technology (Natural Science), 2013, 10(2): 40−45. [26] 刘胜宇, 蒋昌波, 陈杰, 等. 双列可渗潜堤消波性能实验[J]. 交通科学与工程, 2011, 27(3): 65−70. doi: 10.3969/j.issn.1674-599X.2011.03.013Liu Shengyu, Jiang Changbo, Chen Jie, et al. Experiment of wave reduction of the double permeable submerged breakwater on the slopes[J]. Journal of Transport Science and Engineering, 2011, 27(3): 65−70. doi: 10.3969/j.issn.1674-599X.2011.03.013 [27] Koraim A S, Heikal E M, Abo Zaid A A. Hydrodynamic characteristics of porous seawall protected by submerged breakwater[J]. Applied Ocean Research, 2014, 46: 1−14. doi: 10.1016/j.apor.2014.01.003 [28] Shao Songdong. Incompressible SPH flow model for wave interactions with porous media[J]. Coastal Engineering, 2010, 57(3): 304−316. doi: 10.1016/j.coastaleng.2009.10.012 [29] Huang C J, Chang H H, Hwung H H. Structural permeability effects on the interaction of a solitary wave and a submerged breakwater[J]. Coastal Engineering, 2003, 49(1/2): 1−24. [30] Hieu P D, Tanimoto K. Verification of a VOF-based two-phase flow model for wave breaking and wave–structure interactions[J]. Ocean Engineering, 2006, 33(11/12): 1565−1588. [31] Ma Gangfeng, Shi Fengyan, Hsiao S C, et al. Non-hydrostatic modeling of wave interactions with porous structures[J]. Coastal Engineering, 2014, 91: 84−98. doi: 10.1016/j.coastaleng.2014.05.004 [32] Wu Yunta, Hsiao S C. Propagation of solitary waves over a submerged permeable breakwater[J]. Coastal Engineering, 2013, 81: 1−18. doi: 10.1016/j.coastaleng.2013.06.005 [33] Behera H, Khan M B M. Numerical modeling for wave attenuation in double trapezoidal porous structures[J]. Ocean Engineering, 2019, 184: 91−106. doi: 10.1016/j.oceaneng.2019.05.006 [34] Booshi S, Ketabdari M J. Modeling of solitary wave interaction with emerged porous breakwater using PLIC-VOF method[J]. Ocean Engineering, 2021, 241: 110041. doi: 10.1016/j.oceaneng.2021.110041 [35] Zhang J S, Jeng D S, Liu P L F. Numerical study for waves propagating over a porous seabed around a submerged permeable breakwater: PORO-WSSI II model[J]. Ocean Engineering, 2011, 38(7): 954−966. doi: 10.1016/j.oceaneng.2010.10.018 [36] Hsu T J, Sakakiyama T, Liu P L F. A numerical model for wave motions and turbulence flows in front of a composite breakwater[J]. Coastal Engineering, 2002, 46(1): 25−50. doi: 10.1016/S0378-3839(02)00045-5 [37] van Gent M R A. The modelling of wave action on and in coastal structures[J]. Coastal Engineering, 1994, 22(3/4): 311−339. [38] Liu P L F, Lin Pengzhi, Chang Kangan, et al. Numerical modeling of wave interaction with porous structures[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1999, 125(6): 322−330. doi: 10.1061/(ASCE)0733-950X(1999)125:6(322) [39] Rodi W. Examples of calculation methods for flow and mixing in stratified fluids[J]. Journal of Geophysical Research: Oceans, 1987, 92(C5): 5305−5328. doi: 10.1029/JC092iC05p05305 [40] Nakayama A, Kuwahara F. A macroscopic turbulence model for flow in a porous medium[J]. Journal of Fluids Engineering, 1999, 121(2): 427−433. doi: 10.1115/1.2822227 [41] Schäffer H A. Second-order wavemaker theory for irregular waves[J]. Ocean Engineering, 1996, 23(1): 47−88. doi: 10.1016/0029-8018(95)00013-B [42] Warner J C, Geyer W R, Lerczak J A. Numerical modeling of an estuary: a comprehensive skill assessment[J]. Journal of Geophysical Research: Oceans, 2005, 110(C5): C05001. [43] Willmott C J. On the validation of models[J]. Physical Geography, 1981, 2(2): 184−194. doi: 10.1080/02723646.1981.10642213 -
计量
- 文章访问数: 297
- HTML全文浏览量: 83
- PDF下载量: 36
- 被引次数: 0
