Numerical study on influence of vegetation on bed shear stress under coastal waves
-
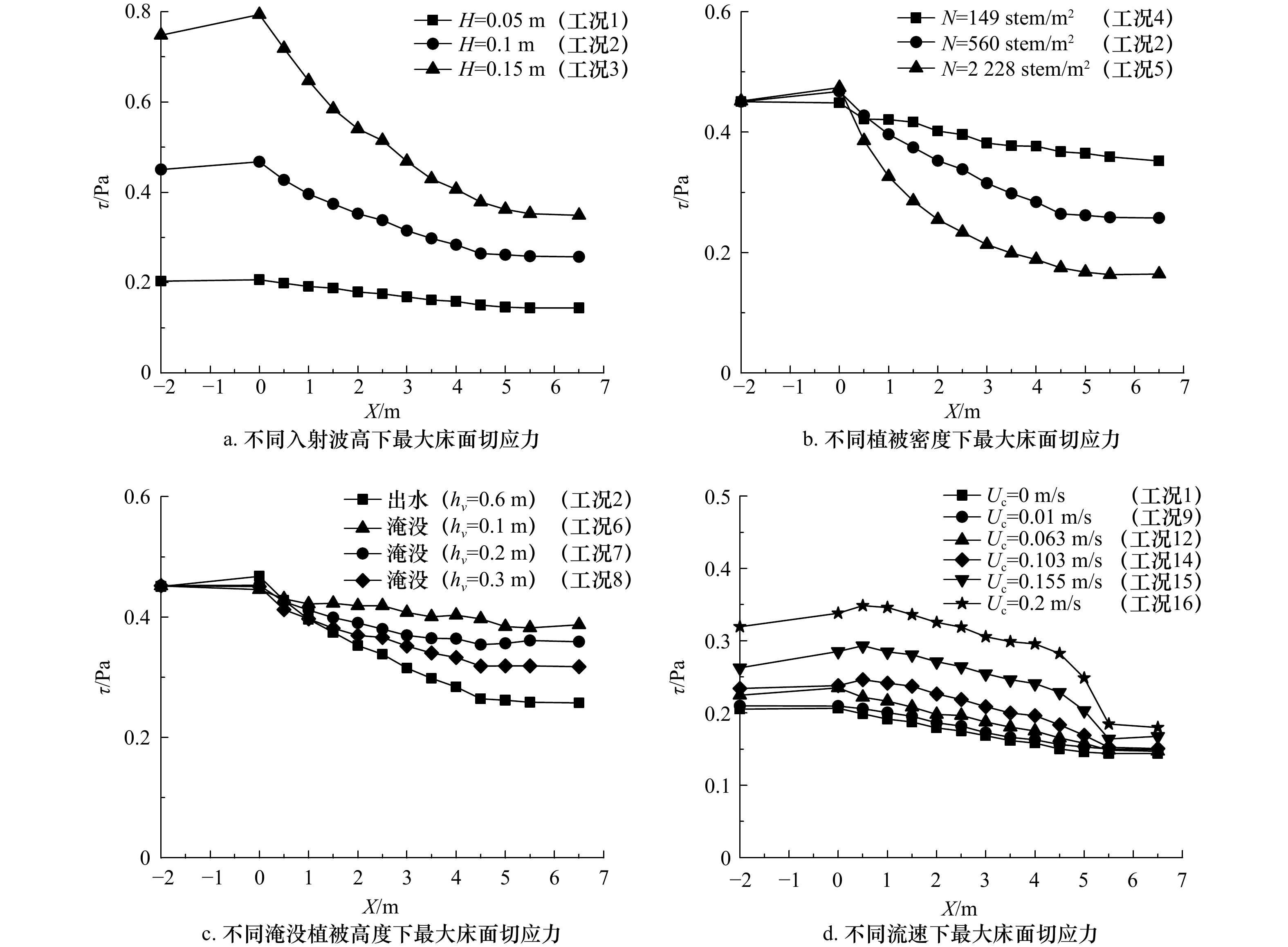
摘要: 本文基于OpenFOAM建立三维波浪数值水槽，模拟计算植被水域波浪作用下的床面切应力，分析了入射波高、植被密度、植被淹没高度、水流对植被水域波浪作用下床面切应力的影响。结果表明：纯波时，由于植被的阻水作用，植被水域床面切应力沿程衰减，其衰减程度与入射波高、植被密度及植被淹没高度呈现正相关；与纯波时相比，在波浪和同向流共同作用下正向床面切应力幅值增大，负向床面切应力幅值减小；弱水流对植被水域床面切应力的大小及分布无明显影响；强水流时，床面切应力在植被水域先增大后逐渐减小并在植被水域后显著降低。Abstract: To analyze the effects of wave height, vegetation density, submerged height of vegetation and current on the bed shear stress at vegetation zones, a three-dimensional wave-current numerical flume is established based on OpenFOAM in this study. The results show that the bed shear stress attenuates along the vegetation zones because of the blocking effect of vegetation, and the decay rate is positively correlated with the wave height, vegetation density and submerged height of vegetation. Compared with pure wave, the amplitude of positive bed shear stress increases and the amplitude of negative bed shear stress decreases under the condition of combined wave-current flows. The weak current has no obvious effect on the size and distribution of the bed shear stress at vegetation zones. In the case of strong current, the bed shear stress increases at vegetation zones and suddenly decreases after the vegetation zones.
-
Key words:
- coastal vegetation /
- wave /
- bed shear stress /
- OpenFOAM
-
图 1 考虑植被外形扰动的模拟结果
Fig. 1 Simulation results considering the disturbance of vegetation shape
图 4 理论值与模拟值对比（工况1）
Fig. 4 Comparison between theoretical and simulated values (case 1)
图 5 理论值与模拟值对比（工况2）
Fig. 5 Comparison between theoretical and simulated values (case 2)
图 10 不同流速下床面切应力变化
Fig. 10 Variation of bed shear stress under different current velocity
图 11 不同工况下植被水域最大床面切应力分布
Fig. 11 Distribution of maximum bed shear stress in vegetation zones under different conditions
图 12 不同流速下最大床面切应力衰减率
Fig. 12 Decay rate of maximum bed shear stress at different current velocities
表 1 经验系数取值
Tab. 1 Default values for the closure coefficient
经验系数 ${C_\mu }$ ${C_{\varepsilon 1}}$ ${C_{\varepsilon 2}}$ ${\sigma _\varepsilon }$ ${\lambda _2}$ ${\sigma _t}$ 值 0.09 1.44 1.92 1.3 0.05 0.85 
下载: 导出CSV
表 2 植被及波浪参数
Tab. 2 Parameters of vegetation and waves
工况 波高/
m周期/
s水深/
m流速/
（m·s−1）植被
杆径/m植被
高度/m植被水域
长度/m植被密度/
(stem·m−2)1 0.04 1.5 0.3 0 0.005 0.6 5 560 2 0.04 1.5 0.3 0.186 0.005 0.6 5 560
下载: 导出CSV
表 3 验证工况参数
Tab. 3 Parameters of verification conditions
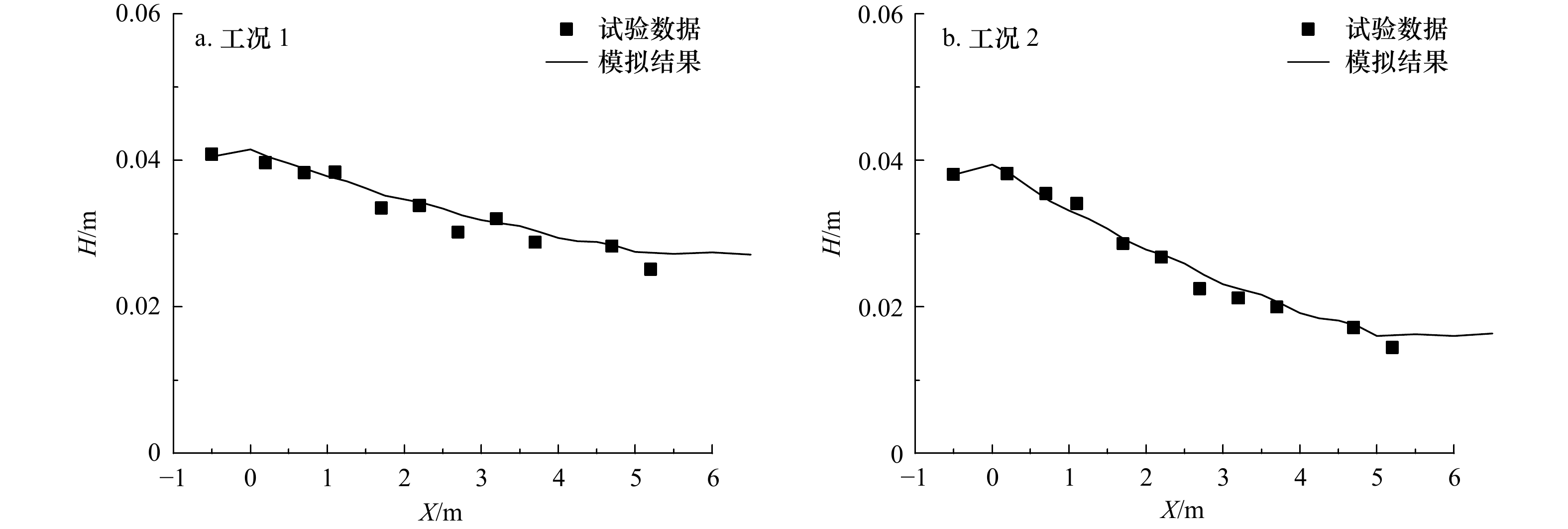
工况 波高/m 周期/s 水深/m 波浪水质点振幅/m 边界层雷诺数 1 0.05 1.5 0.4 0.022 2 103.68 2 0.1 1.5 0.4 0.045 8 414.72 3 0.15 2 0.54 0.092 26 769.86
下载: 导出CSV
表 4 模拟工况参数
Tab. 4 Parameters of numerical simulation conditions
工况 波高/m 周期/s 水深/m 流速/
(m·s−1)植被高
度/m植被水域
长度/m植被密度/
(stem·m−2)1 0.05 1.5 0.4 0 0.6 5 560 2 0.1 1.5 0.4 0 0.6 5 560 3 0.15 1.5 0.4 0 0.6 5 560 4 0.1 1.5 0.4 0 0.6 5 149 5 0.1 1.5 0.4 0 0.6 5 2 228 6 0.1 1.5 0.4 0 0.1 5 560 7 0.1 1.5 0.4 0 0.2 5 560 8 0.1 1.5 0.4 0 0.3 5 560 9 0.05 1.5 0.4 0.01 0.6 5 560 10 0.05 1.5 0.4 0.02 0.6 5 560 11 0.05 1.5 0.4 0.04 0.6 5 560 12 0.05 1.5 0.4 0.063 0.6 5 560 13 0.05 1.5 0.4 0.08 0.6 5 560 14 0.05 1.5 0.4 0.103 0.6 5 560 15 0.05 1.5 0.4 0.155 0.6 5 560 16 0.05 1.5 0.4 0.2 0.6 5 560 17 0.1 1.5 0.4 0.02 0.6 5 560 18 0.1 1.5 0.4 0.062 0.6 5 560 19 0.1 1.5 0.4 0.103 0.6 5 560 20 0.1 1.5 0.4 0.155 0.6 5 560 21 0.1 1.5 0.4 0.2 0.6 5 560 22 0.1 1.5 0.4 0.3 0.6 5 560
下载: 导出CSV
-
[1] Jonsson I G. Wave boundary layers and friction factors[C]//Proceedings of the 10th International Conference on Coastal Engineering. Tokyo: ASCE, 1966: 127−148. [2] 孔令双, 曹祖德, 焦桂英, 等. 波、流共存时的床面剪切力和泥沙运动[J]. 水动力学研究与进展(A辑), 2003, 18(1): 93−97.Kong Lingshuang, Cao Zude, Jiao Guiying, et al. The bottom shear stress and sediment movement for a wave-current coexisting system[J]. Journal of Hydrodynamics Series A, 2003, 18(1): 93−97. [3] 蔡翠苏. 波浪作用下底摩阻系数和泥沙起动实验研究[D]. 南京: 河海大学, 2007.Cai Cuisu. Laboratory investigation on wave friction factor and sediment initial motion under water waves[D]. Nanjing: Hohai University, 2007. [4] 齐富康, 边昌伟, 徐景平. 渤海海峡沉积物输运的参数化计算[J]. 海洋学报, 2020, 42(3): 83−96.Qi Fukang, Bian Changwei, Xu Jingping. Parameterization of sediment transport in the Bohai Strait[J]. Haiyang Xuebao, 2020, 42(3): 83−96. [5] Lin Pengzhi, Zhang Wenyu. Numerical simulation of wave-induced laminar boundary layers[J]. Coastal Engineering, 2008, 55(5): 400−408. doi: 10.1016/j.coastaleng.2007.12.005 [6] 滕涌, 杨永增, 芦静, 等. 波浪对泥沙作用的数值研究及在渤海区域的检验[J]. 海洋学报, 2012, 34(5): 174−182.Teng Yong, Yang Yongzeng, Lu Jing, et al. A numerical study of the wave effect on sediment transport and test in the Bohai Sea[J]. Haiyang Xuebao, 2012, 34(5): 174−182. [7] Larsen B E, Fuhrman D R. Full-scale CFD simulation of tsunamis. Part 1: model validation and run-up[J]. Coastal Engineering, 2019, 151: 22−41. doi: 10.1016/j.coastaleng.2019.04.012 [8] Larsen B E, Fuhrman D R. Full-scale CFD simulation of tsunamis. Part 2: boundary layers and bed shear stresses[J]. Coastal Engineering, 2019, 151: 42−57. doi: 10.1016/j.coastaleng.2019.04.011 [9] Wang X Y, Xie W M, Zhang D, et al. Wave and vegetation effects on flow and suspended sediment characteristics: a flume study[J]. Estuarine, Coastal and Shelf Science, 2016, 182: 1−11. doi: 10.1016/j.ecss.2016.09.009 [10] Reidenbach M A, Thomas E L. Influence of the Seagrass, Zostera marina, on wave attenuation and bed shear stress within a shallow coastal bay[J]. Frontiers in Marine Science, 2018, 5: 397. doi: 10.3389/fmars.2018.00397 [11] 陈家贵, 沈小雄. 波浪作用下柔性植物对最大床面剪切力的影响研究[J]. 中国水运(下半月), 2016, 16(4): 278−280.Chen Jiagui, Shen Xiaoxiong. Study on the effect of flexible plants on the maximum bed shear stress under waves[J]. China Water Transport, 2016, 16(4): 278−280. [12] 李勰, 陈杰, 蒋昌波, 等. 规则波下刚性植物根茎对边界层最大剪切力特性影响研究[J]. 海洋学报, 2021, 43(12): 102−110.Li Xie, Chen Jie, Jiang Changbo, et al. Study on the influence of rigid plant roots and stems on the maximum shearing characteristics of boundary layer under regular wave[J]. Haiyang Xuebao, 2021, 43(12): 102−110. [13] Luhar M, Coutu S, Infantes E, et al. Wave-induced velocities inside a model seagrass bed[J]. Journal of Geophysical Research: Oceans, 2010, 115(C12): C12005. doi: 10.1029/2010JC006345 [14] Hansen J C R, Reidenbach M A. Wave and tidally driven flows in eelgrass beds and their effect on sediment suspension[J]. Marine Ecology Progress Series, 2012, 448: 271−287. doi: 10.3354/meps09225 [15] Etminan V, Ghisalberti M, Lowe R J. Predicting bed shear stresses in vegetated channels[J]. Water Resources Research, 2018, 54(11): 9187−9206. doi: 10.1029/2018WR022811 [16] Jacobsen N G, Fuhrman D R, Fredsøe J. A wave generation toolbox for the open-source CFD library: OpenFoam®[J]. International Journal for Numerical Methods in Fluids, 2012, 70(9): 1073−1088. doi: 10.1002/fld.2726 [17] Maza M, Lara J L, Losada I J. Tsunami wave interaction with mangrove forests: a 3-D numerical approach[J]. Coastal Engineering, 2015, 98: 33−54. doi: 10.1016/j.coastaleng.2015.01.002 [18] Hu Z, Suzuki T, Zitman T, et al. Laboratory study on wave dissipation by vegetation in combined current-wave flow[J]. Coastal Engineering, 2014, 88: 131−142. doi: 10.1016/j.coastaleng.2014.02.009 [19] Devolder B, Rauwoens P, Troch P. Application of a buoyancy-modified k-ω SST turbulence model to simulate wave run-up around a monopile subjected to regular waves using OpenFOAM®[J]. Coastal Engineering, 2017, 125: 81−94. doi: 10.1016/j.coastaleng.2017.04.004 [20] Larsen B E, Fuhrman D R. On the over-production of turbulence beneath surface waves in Reynolds-averaged Navier-Stokes models[J]. Journal of Fluid Mechanics, 2018, 853: 419−460. doi: 10.1017/jfm.2018.577 [21] Hiraoka H, Ohashi M. A (k–ε) turbulence closure model for plant canopy flows[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(10/11): 2139−2149. [22] Dalrymple R A, Kirby J T, Hwang P A. Wave diffraction due to areas of energy dissipation[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1984, 110(1): 67−79. doi: 10.1061/(ASCE)0733-950X(1984)110:1(67) [23] Etminan V, Lowe R J, Ghisalberti M. Canopy resistance on oscillatory flows[J]. Coastal Engineering, 2019, 152: 103502. doi: 10.1016/j.coastaleng.2019.04.014 [24] Wang Y X, Yin Z G, Liu Y. Numerical investigation of solitary wave attenuation and resistance induced by rigid vegetation based on a 3-D RANS model[J]. Advances in Water Resources, 2020, 146: 103755. doi: 10.1016/j.advwatres.2020.103755 [25] 王倚彤. 植被水域同向水流影响下规则波传播模拟研究[D]. 大连: 大连理工大学, 2019.Wang Yitong. Simulation study of regular wave propagation under the influence of coplanar currents in vegetation zones[D]. Dalian: Dalian University of Technology, 2019. [26] 徐华, 夏云峰, 蔡喆伟, 等. 复杂水动力环境下床面切应力量测与研究初探[C]//第十八届中国海洋(岸)工程学术讨论会. 北京: 海洋出版社, 2017: 260-266.Xu Hua, Xia Yunfeng, Cai Zhewei, et al. Measurement and study of bed shear stress under complex hydrodynamic environment[C]// The 18th China Offshore Engineering Symposium. Beijing: China Ocean Press, 2017: 260−266. [27] Lamb H. Hydrodynamics[M]. Cambridge: Cambridge University Press, 1932. [28] Schaffer H A, Svendsen I A. Boundary layer flow under skew waves[J]. Int. Hydrodyn. and Hydraulic Engrg. 1986: 13−23. [29] Liu D, Diplas P, Fairbanks J D, et al. An experimental study of flow through rigid vegetation[J]. Journal of Geophysical Research Earth Surface, 2008, 113(F4): F04015. [30] 陈明, 刘曙光, 娄厦, 等. 刚性植物对波高衰减和水流结构的影响[J]. 水利水电科技进展, 2018, 38(6): 32−37.Chen Ming, Liu Shuguang, Lou Sha, et al. Impact of rigid vegetation on wave attenuation and flow structure[J]. Advances in Science and Technology of Water Resources, 2018, 38(6): 32−37. [31] Nepf H M. Hydrodynamics of vegetated channels[J]. Journal of Hydraulic Research, 2012, 50(3): 262−279. doi: 10.1080/00221686.2012.696559 [32] Tolman H L. An evaluation of expressions for wave energy dissipation due to bottom friction in the presence of currents[J]. Coastal Engineering, 1992, 16(2): 165−179. doi: 10.1016/0378-3839(92)90035-S -
计量
- 文章访问数: 390
- HTML全文浏览量: 103
- PDF下载量: 38
- 被引次数: 0
