Research on temporal and spatial variations of global tsunami based on complete catalog data
-
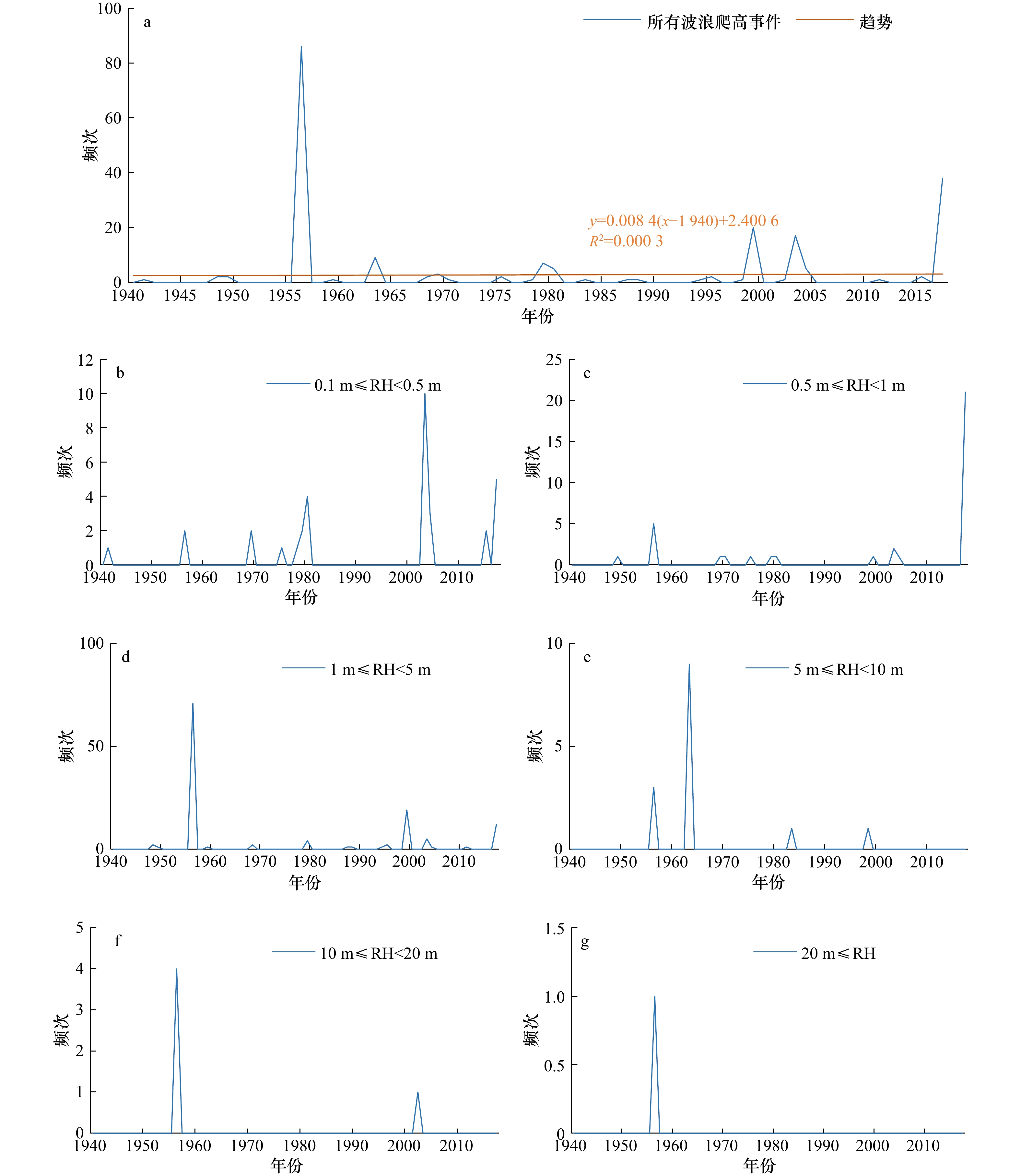
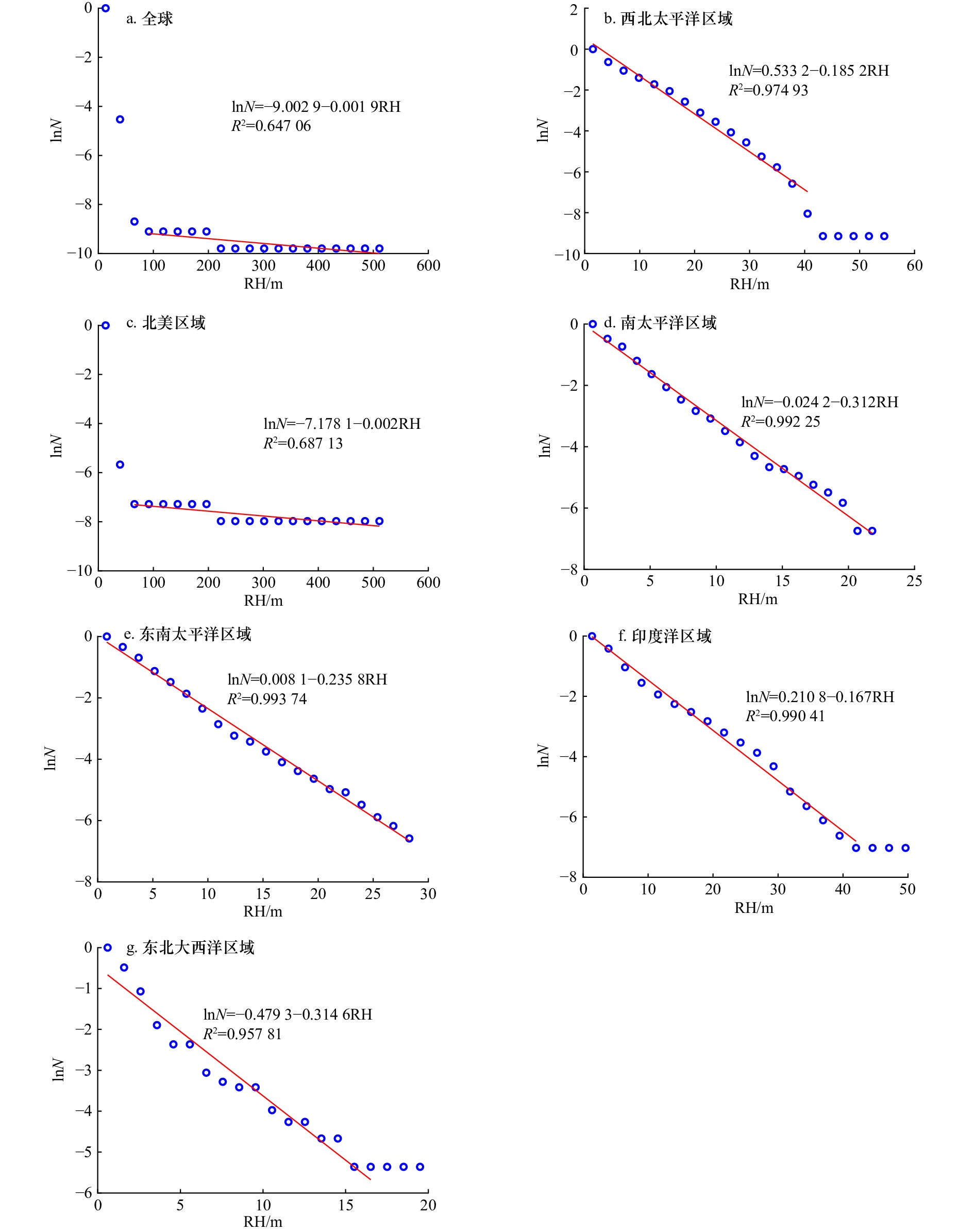
摘要: 海啸是自然灾害中对人类生命财产安全有严重威胁的灾难之一。随着全球气候变化和全球化贸易日益增强,越来越多的人口和经济暴露于海啸灾害。历史海啸灾害的时空分异分析可以帮助我们认识海啸灾害的演变规律,为灾害预警、灾害防控等提供有益参考。本文通过提取具有完整性和同质性的数据(爬高高度(RH))进行全球海啸的时空分异规律研究,结果表明:(1)对于0.1 m≤RH<0.5 m、0.5 m≤RH<1 m、1 m≤RH<5 m、5 m≤RH<10 m、10 m≤RH<20 m和20 m≤RH的间隔,海啸目录分别自1963年、1940年、1950年、1946年、1922年和1885年以来可以被认为是完整的;(2)全球海啸发生有一定的增加趋势,大约每年会多观测到7次波浪爬高事件。在0.1 m≤RH<5 m区间内,海啸发生呈现一定的周期性。当RH大于5 m时,表现出明显的增加趋势;(3)西北太平洋区域、南太平洋区域、东南太平洋区域、印度洋区域海啸发生有一定的增加趋势,而在北美区域则呈减少趋势,东北大西洋区域无显著变化;(4)除北美区域外,其他区域的海啸发生遵循一定的自组织临界行为,相比来说,东北大西洋区域更容易发生小的海啸事件,而西北太平洋区域和印度洋区域更容易发生各种强度的海啸事件。Abstract: Tsunami is one of the disasters that seriously endanger the safety of human life and property among natural disasters. In the context of global warming and increasing economic development, more and more people, infrastructure and wealth are exposed to tsunami disasters, greatly increasing the risk and vulnerability of personal and property safety in coastal and delta areas. The analysis of temporal and spatial variation of historical tsunami disasters can help us understand the evolutionary laws of tsunami disasters, and provides a useful reference for more accurate disaster warning, disaster prevention and control, etc. A study on the temporal and spatial variation of global tsunami by extracting complete and homogeneous data is conducted in this paper. The results show that: (1) for 0.1 m≤RH<0.5 m, 0.5 m≤RH<1 m, 1 m≤RH<5 m, 5 m≤RH<10 m, 10 m≤RH<20 m and 20 m≤RH intervals, the tsunami catalogues can be considered complete since 1963, 1940, 1950, 1946, 1922 and 1885 respectively; (2) from time changes it can be seen that there is a certain increasing trend in the occurrence of global tsunamis. Approximately 7 more wave runup events are observed every year. At the same time, in different intensity intervals, the frequency of tsunamis has different changes. In the intervals of 0.1 m≤RH<0.5 m, 0.5 m≤RH<1 m, and 1 m≤RH<5 m, the tsunami have a certain periodicity, showing two obvious peaks, but when the RH is greater than 5 m, the periodicity of the tsunami is no longer obvious, and it shows a clear increasing trend at this time; (3) there is a certain increasing trend in the occurrence of tsunamis in East Asia, South Pacific, South America, and Indian Ocean. However, in North America, there is a decreasing trend, and there is no significant change in Europe; (4) except for North America, tsunami events in other regions show a good power law distribution relationship, indicating that the occurrence of tsunamis follows certain self-organized critical behavior. In comparison, small tsunami events are more likely to occur in Europe, while tsunami events in East Asia and the Indian Ocean are more prone to various types of tsunami events, of which large tsunami events occupy a larger portion.
-
Key words:
- temporal and spatial variation /
- completeness analysis /
- power law /
- tsunami
-
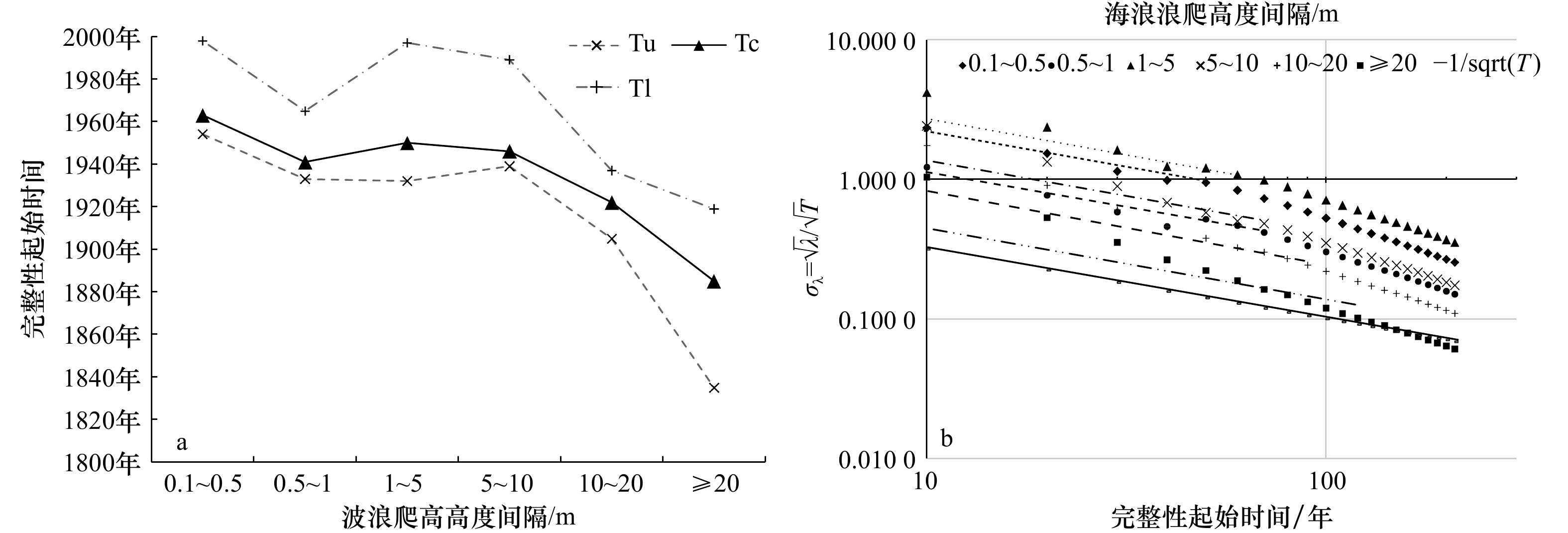
图 3 全球海啸目录的完整性分析结果
a. Albarello方法计算结果,其中Tc代表完整结果,Tu和Tl为不确定性结果;b. Steep方法分析结果,纵轴中$\lambda=\dfrac{1}{n}\displaystyle\sum x_i$,其中x为采样时间段内的事件数目,T为采样时间段
Fig. 3 The results of the complete analysis of the global tsunami catalog
a. Albarello method calculation results, where Tc represents complete results, Tu and Tl are uncertain results; b. Steep method analysis results, in vertical axis, $\lambda=\dfrac{1}{n}\displaystyle\sum x_i$, x is the number of times in the sampling time period, T is the sampling time period
-
[1] 陈颙, 史培军. 自然灾害[M]. 3版. 北京: 北京师范大学出版社, 2013.Chen Yong, Shi Peijun. Natural Disasters[M]. 3rd ed. Beijing: Beijing Normal University Press, 2013. [2] Danielsen F, Sørensen M K, Olwig M F, et al. The Asian tsunami: a protective role for coastal vegetation[J]. Science, 2005, 310(5748): 643−643. doi: 10.1126/science.1118387 [3] 刘毅, 杨宇. 历史时期中国重大自然灾害时空分异特征[J]. 地理学报, 2012, 67(3): 291−300. doi: 10.11821/xb201203001Liu Yi, Yang Yu. Spatial distribution of major natural disasters of China in historical period[J]. Acta Geographica Sinica, 2012, 67(3): 291−300. doi: 10.11821/xb201203001 [4] Liu Yi, Yang Yu, Li Li. Major natural disasters and their spatio-temporal variation in the history of China[J]. Journal of Geographical Sciences, 2012, 22(6): 963−976. doi: 10.1007/s11442-012-0976-4 [5] Strydom S, Savage M J. A spatio-temporal analysis of fires in South Africa[J]. South African Journal of Science, 2016, 112(11/12): 8. [6] Strydom S, Savage M J. A spatio-temporal analysis of fires in the southern African development community region[J]. Natural Hazards, 2018, 92(3): 1617−1632. doi: 10.1007/s11069-018-3268-1 [7] Yang Jing, Cheng Changxiu, Song Changqing, et al. Spatial-temporal distribution characteristics of global seismic clusters and associated spatial factors[J]. Chinese Geographical Science, 2019, 29(4): 614−625. doi: 10.1007/s11769-019-1059-6 [8] Karremann M K, Pinto J G, Von Bomhard P J, et al. On the clustering of winter storm loss events over Germany[J]. Natural Hazards and Earth System Sciences, 2014, 14(8): 2041−2052. doi: 10.5194/nhess-14-2041-2014 [9] Papagiannaki K, Lagouvardos K, Kotroni V. A database of high-impact weather events in Greece: a descriptive impact analysis for the period 2001−2011[J]. Natural Hazards and Earth System Sciences, 2013, 13(3): 727−736. doi: 10.5194/nhess-13-727-2013 [10] Federico S, Avolio E, Pasqualoni L, et al. Atmospheric patterns for heavy rain events in Calabria[J]. Natural Hazards and Earth System Sciences, 2008, 8(5): 1173−1186. doi: 10.5194/nhess-8-1173-2008 [11] Hossain M S, Roy K, Datta D K. Spatial and temporal variability of rainfall over the south-west coast of Bangladesh[J]. Climate, 2014, 2(2): 28−46. doi: 10.3390/cli2020028 [12] Santos J F, Pulido-Calvo I, Portela M M. Spatial and temporal variability of droughts in Portugal[J]. Water Resources Research, 2010, 46(3): W03503. [13] Reddy M J, Ganguli P. Spatio-temporal analysis and derivation of copula-based intensity-area-frequency curves for droughts in western Rajasthan (India)[J]. Stochastic Environmental Research and Risk Assessment, 2013, 27(8): 1975−1989. doi: 10.1007/s00477-013-0732-z [14] Wang Xiaoxue, Shen Huitao, Zhang Wanjun, et al. Spatial and temporal characteristics of droughts in the Northeast China Transect[J]. Natural Hazards, 2015, 76(1): 601−614. doi: 10.1007/s11069-014-1507-7 [15] Sassorova E V, Levin B W. Spatial, and temporal periodicity in the Pacific tsunami occurrence[M]. Yalçiner A C, Pelinovsky E N, Okal E. Submarine Landslides and Tsunamis. Dordrecht: Springer, 2003: 43−50. [16] Satake K, Fujii Y, Harada T, et al. Time and space distribution of coseismic slip of the 2011 Tohoku earthquake as inferred from tsunami waveform data[J]. Bulletin of the Seismological Society of America, 2013, 103(2B): 1473−1492. doi: 10.1785/0120120122 [17] Lander J F, Whiteside L S, Lockridge P A. Two decades of global tsunamis[J]. Science of Tsunami Hazards, 2003, 21(1): 3. [18] Levin B W, Sasorova E. The spatial-temporal distributions of the tsunamigenic earthquake sources[J]. Science of Tsunami Hazards, 2015, 34(1): 23. [19] Levin B W, Sasorova E V. Spatiotemporal distributions of tsunami sources and discovered periodicities[J]. Izvestiya, Atmospheric and Oceanic Physics, 2014, 50(5): 485−497. doi: 10.1134/S0001433814050065 [20] 曹罗丹, 李加林, 叶持跃, 等. 明清时期浙江沿海自然灾害的时空分异特征[J]. 地理研究, 2014, 33(9): 1778−1790.Cao Luodan, Li Jialin, Ye Chiyue, et al. Spatial-temporal variations in natural disasters of the coastal regions in Zhejiang Province during Ming and Qing dynasties[J]. Geographical Research, 2014, 33(9): 1778−1790. [21] Dunbar P K, Stroker K J, Brocko V R, et al. Long-term tsunami data archive supports tsunami forecast, warning, research, and mitigation[M]//Cummins P R, Satake K, Kong L S L. Tsunami Science Four Years after the 2004 Indian Ocean Tsunami. Birkhäuser Basel: Springer, 2008: 2275−2291. [22] Geist E L, Parsons T. Assessing historical rate changes in global tsunami occurrence[J]. Geophysical Journal International, 2011, 187(1): 497−509. doi: 10.1111/j.1365-246X.2011.05160.x [23] Ning Lixin, Cheng Changxiu, Cruz A M, et al. Exploring of the spatially varying completeness of a tsunami catalogue[J]. Natural Hazards, 2022, 111(1): 191−212. [24] Albarello D, Camassi R, Rebez A. Detection of space and time heterogeneity in the completeness of a seismic catalog by a statistical approach: an application to the Italian area[J]. Bulletin of the Seismological Society of America, 2001, 91(6): 1694−1703. doi: 10.1785/0120000058 [25] Kanamori H, Abe K. Reevaluation of the turn-of-the-century seismicity peak[J]. Journal of Geophysical Research: Solid Earth, 1979, 84(B11): 6131−6139. [26] Pérez O J, Scholz C H. Heterogeneities of the instrumental seismicity catalog (1904−1980) for strong shallow earthquakes[J]. Bulletin of the Seismological Society of America, 1984, 74(2): 669−686. [27] Smit A, Kijko A, Stein A. Probabilistic tsunami hazard assessment from incomplete and uncertain historical catalogues with application to tsunamigenic regions in the Pacific Ocean[J]. Pure and Applied Geophysics, 2017, 174(8): 3065−3081. doi: 10.1007/s00024-017-1564-4 [28] Zúñiga F R, Wyss M. Inadvertent changes in magnitude reported in earthquake catalogs: their evaluation through b-value estimates[J]. Bulletin of the Seismological Society of America, 1995, 85(6): 1858−1866. doi: 10.1785/BSSA0850061858 [29] Gutenberg B, Richter C F. Frequency of earthquakes in California[J]. Bulletin of the Seismological Society of America, 1944, 34(4): 185−188. doi: 10.1785/BSSA0340040185 [30] Schorlemmer D, Woessner J. Probability of detecting an earthquake[J]. Bulletin of the Seismological Society of America, 2008, 98(5): 2103−2117. doi: 10.1785/0120070105 [31] Mignan A, Jiang C, Zechar J D, et al. Completeness of the mainland China earthquake catalog and implications for the setup of the China Earthquake Forecast Testing Center[J]. Bulletin of the Seismological Society of America, 2013, 103(2A): 845−859. doi: 10.1785/0120120052 [32] Mignan A, Werner M J, Wiemer S, et al. Bayesian estimation of the spatially varying completeness magnitude of earthquake catalogs[J]. Bulletin of the Seismological Society of America, 2011, 101(3): 1371−1385. doi: 10.1785/0120100223 [33] Anbazhagan P, Vinod J S, Sitharam T G. Evaluation of seismic hazard parameters for Bangalore region in South India[J]. Disaster Advances, 2010, 3(3): 5−13. [34] Kafka A L, Levin S Z. Does the spatial distribution of smaller earthquakes delineate areas where larger earthquakes are likely to occur?[J]. Bulletin of the Seismological Society of America, 2000, 90(3): 724−738. doi: 10.1785/0119990017 [35] Mulargia F, Gasperini P, Tinti S. A procedure to identify objectively active seismotectonic structures[J]. Bollettino Di Geofisica Teorica ed Applicata, 1987, 29(114): 147−164. [36] 徐伟进, 高孟潭. 中国大陆及周缘地震目录完整性统计分析[J]. 地球物理学报, 2014, 57(9): 2802−2812. doi: 10.6038/cjg20140907Xu Jinwei, Gao Mengtan. Statistical analysis of the completeness of earthquake catalogs in China mainland[J]. Chinese Journal of Geophysics, 2014, 57(9): 2802−2812. doi: 10.6038/cjg20140907 [37] Khan M M, Kumar G K. Statistical completeness analysis of seismic data[J]. Journal of the Geological Society of India, 2018, 91(6): 749−753. doi: 10.1007/s12594-018-0934-6 [38] Stepp J C. Analysis of completeness of the earthquake sample in the Puget Sound area and its effect on statistical estimates of earthquake hazard[C]// Proceedings of the International Conference on Microzonazion. Seattle: [s.n.], 1972, 2: 897−910. [39] Guzzetti F, Malamud B D, Turcotte D L, et al. Power-law correlations of landslide areas in central Italy[J]. Earth and Planetary Science Letters, 2002, 195(3/4): 169−183. [40] Li Changjiang, Ma Tuhua, Zhu Xingsheng, et al. The power-law relationship between landslide occurrence and rainfall level[J]. Geomorphology, 2011, 130(3/4): 221−229. [41] Turcotte D L, Malamud B D. Landslides, forest fires, and earthquakes: examples of self-organized critical behavior[J]. Physica A: Statistical Mechanics and its Applications, 2004, 340(4): 580−589. [42] Hantson S, Pueyo S, Chuvieco E, et al. Global fire size distribution: from power law to log-normal[J]. International Journal of Wildland Fire, 2016, 25(4): 403−412. doi: 10.1071/WF15108 [43] Bak P, Tang Chao. Earthquakes as a self-organized critical phenomenon[J]. Journal of Geophysical Research: Solid Earth, 1989, 94(B11): 15635−15637. [44] Bak P, Tang Chao, Wiesenfeld K. Self-organized criticality[J]. Physical Review A, 1988, 38(1): 364−374. doi: 10.1103/PhysRevA.38.364 [45] 程昌秀, 史培军, 宋长青, 等. 地理大数据为地理复杂性研究提供新机遇[J]. 地理学报, 2018, 73(8): 1397−1406. doi: 10.11821/dlxb201808001Cheng Changxiu, Shi Peijun, Song Changqing, et al. Geographic big-data: a new opportunity for geography complexity study[J]. Acta Geographica Sinica, 2018, 73(8): 1397−1406. doi: 10.11821/dlxb201808001 -




 下载:
下载: