Study on flow and sediment dynamics and deposition characteristics of hollow block
-
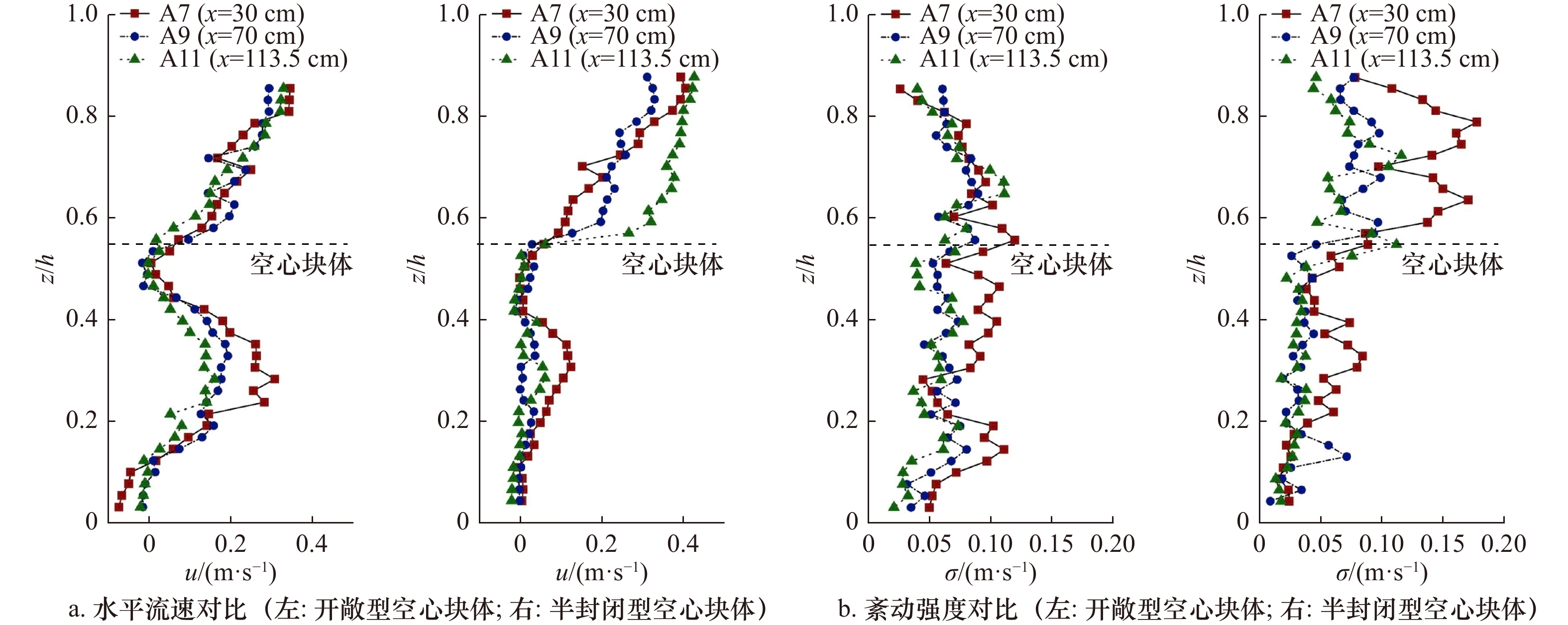
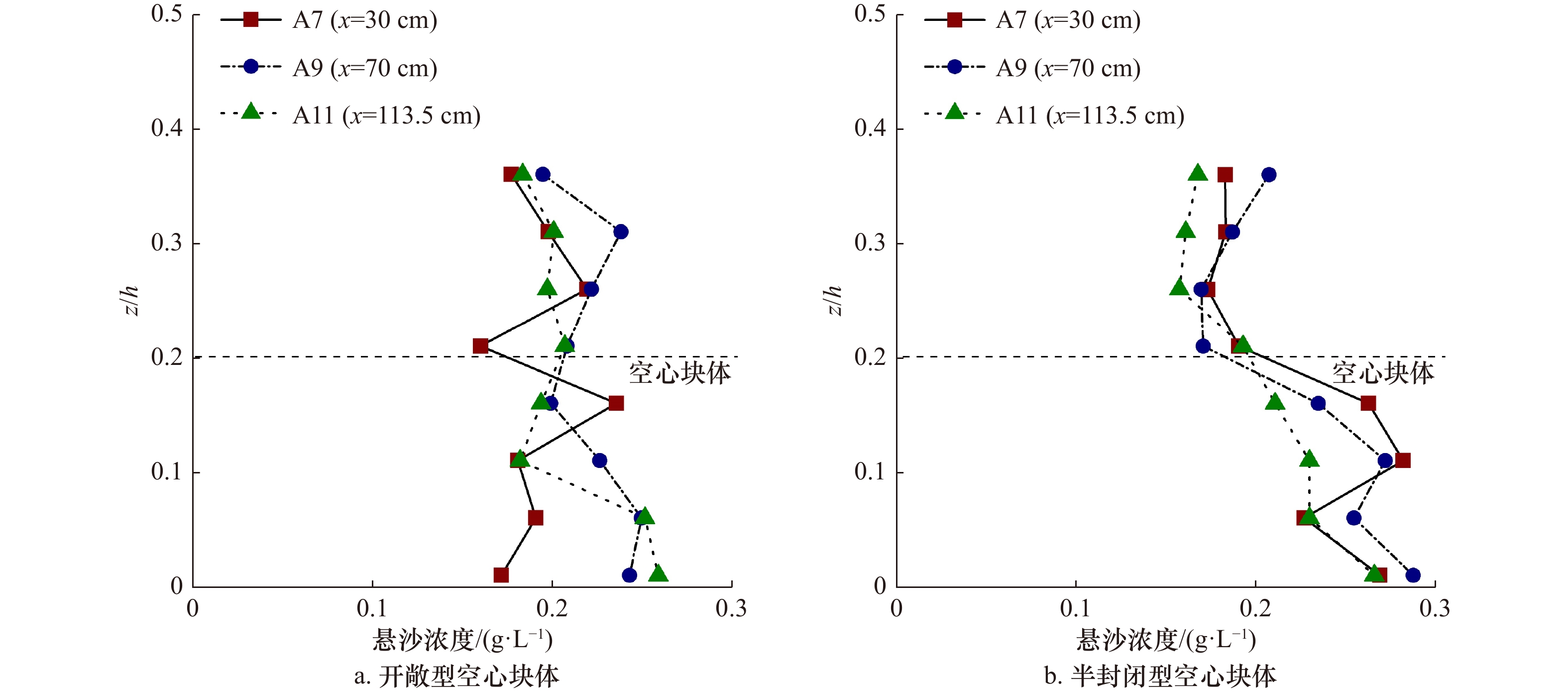
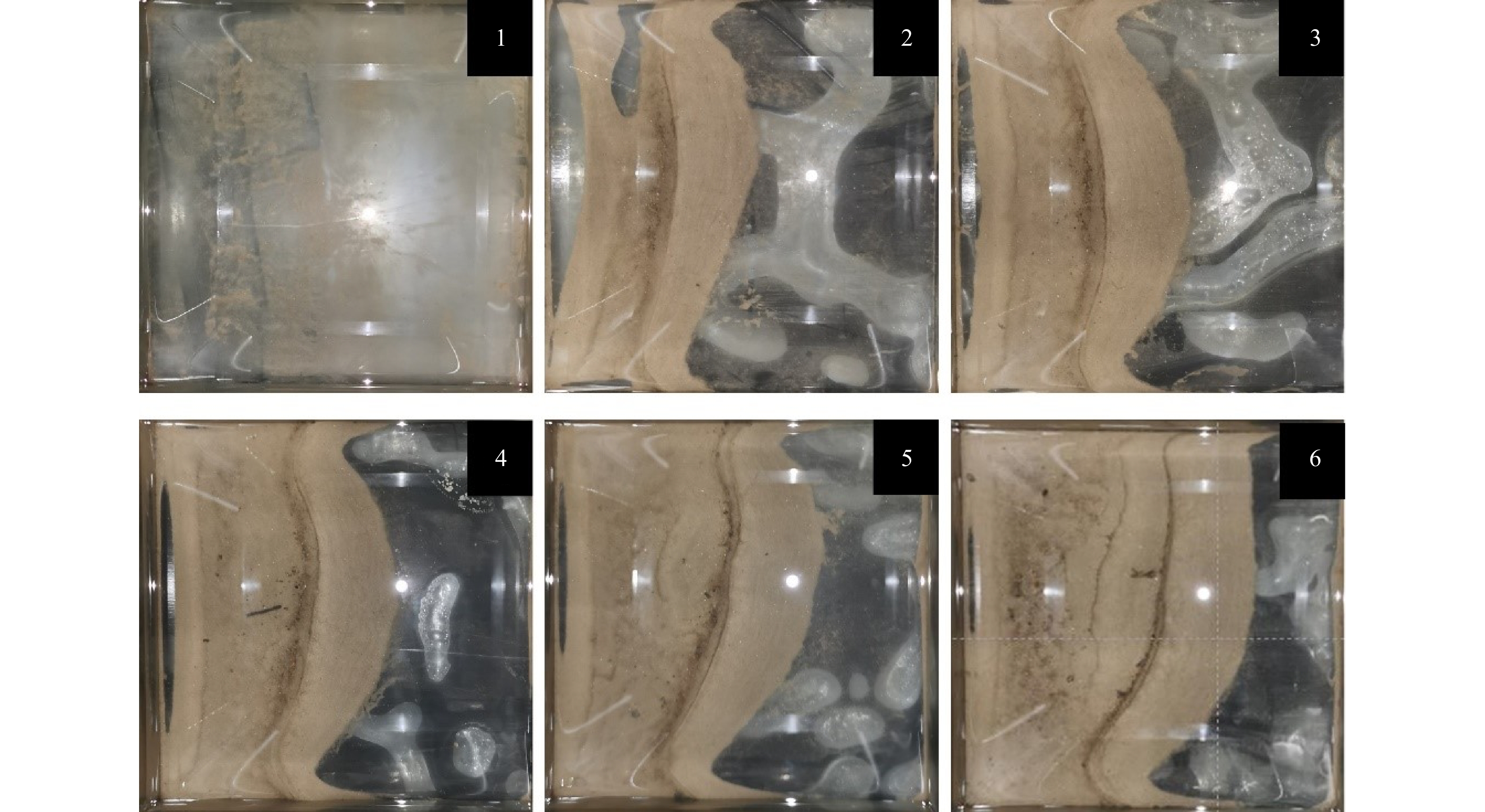
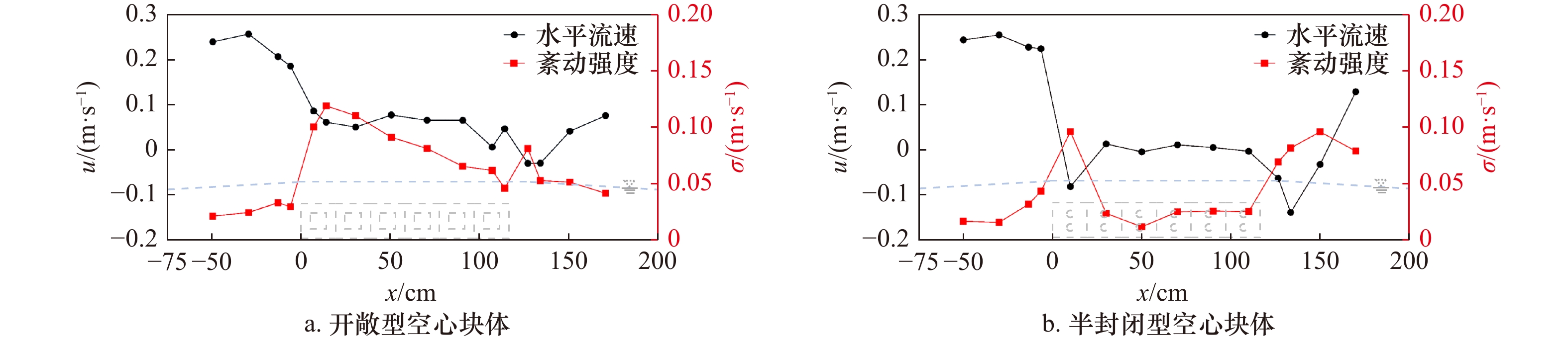
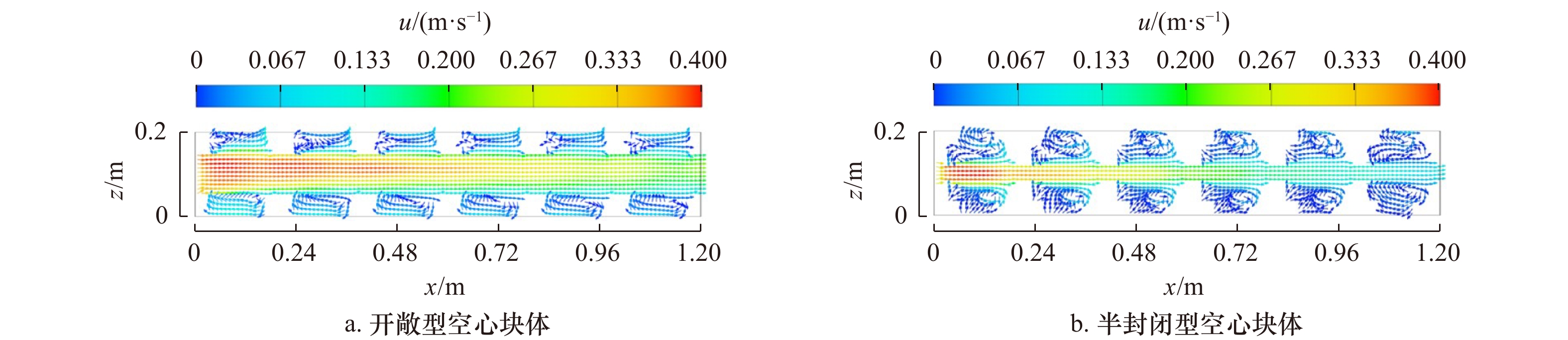
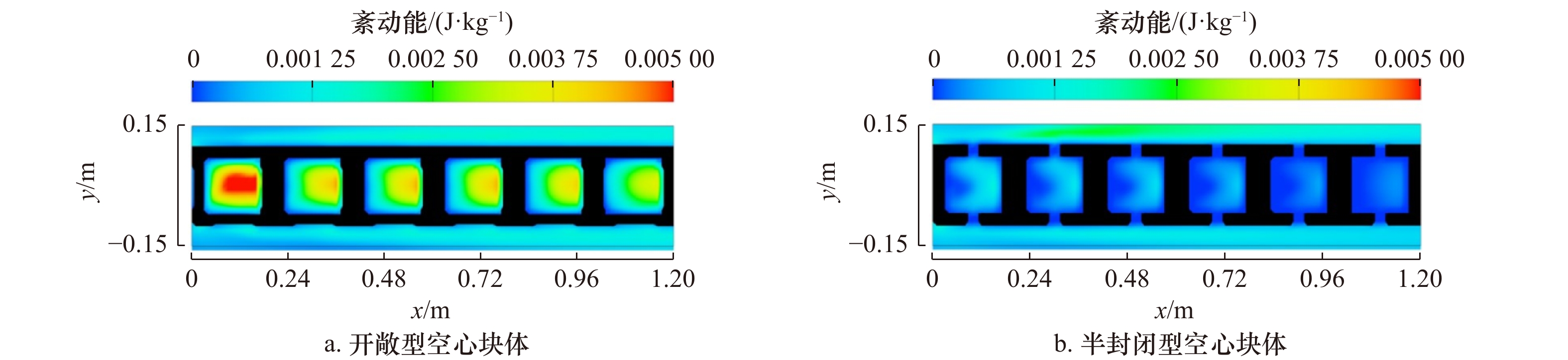
摘要: 空心块体具有良好的阻水和促淤功能，近年来被广泛用于生态修复工程。本文结合水槽试验及Flow-3D数值模拟，分析了开敞型和半封闭型空心块体的阻水效应和泥沙淤积特性。结果表明：空心块体的开孔率对内部水流流速、紊动强度起主导作用，开孔率较小的半开敞型空心块体减速、制紊效果更强；开敞型和半封闭型空心块体近底层悬沙浓度分别增大56%和75%，两者均有利于促进泥沙在块体内部淤积，近底层水流紊动越强，泥沙淤积形态差异越大；空心块体所营造的低流速、泥沙微淤、内外连通的水沙环境是大型底栖生物的生境需求，半封闭型空心块体内部的低紊动水流结构更有利于大型底栖生物的栖息、繁衍。Abstract: Hollow blocks have good water blocking and siltation promotion functions, and have been widely used in ecological restoration projects in recent years. In this paper, combined with flume experiment and Flow-3D numerical simulation, the water blocking effect and sedimentation characteristics of open and semi-closed hollow blocks are analyzed. The results show that the permeability of the hollow block plays a leading role in the internal flow velocity and turbulence intensity, and the semi-open hollow block with small permeability has a better effect in slowing down and turbulence control. The suspended sediment concentration near the bottom of open and semi-closed hollow blocks increases by 56% and 75%, respectively. Both of them can promote the deposition of sediment in the block. The environment of low flow velocity, sediment micro-deposition and water and sediment connected inside and outside by hollow blocks is the habitat requirement of macrobenthos, the structure of low turbulent flow inside the semi-enclosed hollow block is more favorable for the habitat and reproduction of macrobenthos.
-
Key words:
- hollow block /
- flume experiment /
- Flow-3D /
- flow and sediment dynamic /
- deposition
-
1. 引言
海堤是沿海地区最为常见的整治建筑物，海堤结构主要由钢筋混凝土、块石等“硬质”材料组成。随着时代发展，海堤工程的安全性已达到较高水平，但限制了自然海岸带生态系统的发展，也对周边生态环境造成一定程度破坏。针对这些问题，诸多学者提出了兼具海岸防护与生态修复等多功能的生态海堤概念[1]。现阶段传统海堤存在的问题体现在混凝土结构功能性单一、缺乏水体交换、不利于泥沙淤积，使得海岸带水生生物、底栖生物、植被等缺乏流场稳定、泥沙微淤的生长环境[2]。目前，国内外学者给出的解决方案集中在采用空心块体结构[3]、应用生态混凝土材料[4]、引进植被[5]等几个方面，从而达到海堤生态修复的效果。
空心块体与传统的抛石、混凝土结构不同，其内部的透水结构增强了内外界水体的交换，降低水流流速，促进泥沙淤积，为底栖生物、鱼类提供相对稳定的栖息环境，在海堤生态修复中广泛应用[6]。现如今，对于空心透水结构的研究主要集中在水动力特性及泥沙淤积两个方面，诸多学者认为，结构体的形态特征、布置方式是影响其减速、促淤效果的关键因素，例如张为等[7]通过开展室内水槽试验，研究不同孔径的透水三角形促淤结构对泥沙淤积的影响，结果表明8目三角架网起到的促淤效果最佳；吴龙华等[8]基于水槽试验研究架空率、长宽比对透水框架群减速促淤影响，得到了最佳减速率对应的架空率和杆件长宽比的取值范围；崔勇等[9]通过水槽试验、风洞试验结果与数值模拟结合分析，得到礁体之间的最佳布设间距应为礁体尺寸的1～1.5倍。随着近年来生态保护理念的日益加深，部分学者开始着眼于工程结构体产生的生态效应。综合考虑水工学和生态学理论，Harris[10]通过分析生态礁球，发现礁体不仅可以防浪促淤，还发现大量藻类附着在礁体表面；日本及欧盟等国家采用混有植物纤维的混凝土应用于海堤、河堤建设，不仅提高应对极端天气的能力，还能促进海岸带、流域的生态修复[11-12]。然而，空心块体的减速、促淤与生态修复之间关系的研究尚有不足，缺乏合适的评价体系。
综上所述，国内外相关研究多着眼于空心块体结构型式和周围流场特性，然而空心块体内部的水沙动力环境及泥沙淤积是水生生物是否适宜栖息、繁衍的关键要素。本文将结合室内水槽试验及数值模拟，研究两种不同空心块体的水沙动力及淤积形态，分析两种空心块体的水沙动力结构对泥沙淤积的影响及水沙环境对生态修复的影响，探究空心块体水沙特性及泥沙淤积特性，为生态海堤工程的建设提供科学依据。
2. 研究方法
2.1 室内水槽试验
2.1.1 试验概况及量测仪器
试验采用华东师范大学河口海岸学国家重点实验室的可变坡–双向–波流水槽。试验水槽长32 m，宽0.5 m，高0.7 m，坡度为0.16%。两边及底面均为有机玻璃壁，槽首和槽尾设有消能装置和尾门，通过调节槽尾尾门得到试验水深。水槽供水通过控制室内控制面板变频调节驱动水泵，根据试验所需调节进口处流量。试验水槽配备泥沙搅拌池，加入适量泥沙搅拌均匀，改变悬沙浓度。流速测量采用三维超声波多普勒测速仪（ADV），仪器最大采样频率为100 Hz，采样时间为120 s。悬沙浓度测量采用光学后向散射浊度仪（OBS 3+），测量范围为0～4 000 NTU，最大数据传输率为10 Hz。
2.1.2 空心块体
本文采用的空心块体结构整体轮廓为20 cm
$ \text{×} $ 20 cm$ \text{×} $ 20 cm的正方体，模型尺寸及结构体型式如图1所示。空心块体型式一为开敞型结构，四面开10 cm方孔，中间区域自上而下透空形成大体积空腔结构；空心块体型式二为半封闭型结构，仅在四周开圆孔，块体顶部开80 mm小方孔，底部开140 mm大方孔，前后两侧各有直径为5 cm的孔洞，左右两侧分别有两个直径为3.5 cm的孔洞。
图 1 空心块体三视图及模型图（单位: mm）Figure 1. Three views and model diagram of the hollow block (unit: mm)如表1所示，两种空心块体在透水能力上有较大差异。由于开敞型空心块体在各个截面上的透水面积均大于半封闭型，其开孔率也明显大于半封闭型空心块体，这表明开敞型空心块体相较于半封闭型空心块体与外界水沙交换能力更强。本文将通过对比空心块体的透水能力强弱，分析两者在水沙分布及泥沙淤积上的差异。
表 1 空心块体透水能力参数Table 1. Hollow block water permeability parameter结构型式 透水截面面积/cm2 总透水面积S0/cm2 开孔率S0/S x轴方向 y轴方向 z轴方向 开敞型 100 100 196 792 33% 半封闭型 19.6 19.2 顶面64
底面196337.6 14% 注：S为包含结构体外轮廓总面积S=20$ \text{×} $20$ \text{×} $6=2 400 （cm²）。 2.1.3 试验材料
为了研究空心块体的泥沙淤积特性，试验用沙取自崇明东滩北部区域（31.543 9°N，121.966 9°E），通过Coulter-LS100Q激光粒度仪分析其沉积物特征，得到水槽实验用沙累计频率分布曲线（图2）：平均粒径为7.36 µm，黏土、粉砂、砂体积占比分别为41.91%、57.71%、0.38%，沉积物类型属黏土质粉砂，水槽试验中的初始平均悬沙浓度控制为0.16 g/L。
2.1.4 试验布置
本文水槽试验中，距水槽进流15 m处放置长度为1.2 m长的空心块体组合构成堤身结构，开敞型空心块体小方孔沿水流方向排列，半封闭型空心块体的大直径透水孔沿水流方向排列，两者皆沿水槽轴线方向连续布置。为了对比堤身结构内外侧流场差异，沿堤身轴线方向共布置16个测点（A1–A16），上、下游侧各布置4个测点，堤身布置8个测点。各测点垂线方向上的流速测量点为
${z}/{{h}}=0.05\text{、}0.1\text{、}0.15\text{、}0.2\text{、}0.25\text{、} 0.75\text{、} 0.8\text{、}0.85$ ，如图3所示，悬沙浓度的测量为在垂线方向上每隔5 cm设置一个测点。试验坐标轴以沿水流方向为x轴正方向，沿水流方向左侧为y轴正方向，以水槽槽底沿水面方向向上为z轴正方向，堤身前端底边中点为坐标原点。
图 3 空心块体水槽试验测点布置（单位：mm）Figure 3. Layout of measuring points for hollow block flume experiment (unit: mm)2.2 Flow-3D数值水槽
2.2.1 模型简介
室内水槽试验的ADV流速测量由于受到空心块体型式限制，仅可测量部分点位的流速，为研究空心块体内部水流结构特征需要借助数值模型开展分析。Flow-3D是由美国流体科学公司FlowScience.Inc开发的商业流体软件，以Naiver-Stokes方程为基本控制方程。诸多学者在研究结构体与水流相互作用时采用RNG k-ε湍流模型，通过修正紊动黏度，可以很好地处理高应变率及流线弯曲程度较大的流动，取得较好模拟效果。杨培思等[13]基于Flow-3D中的RNG k-ε湍流模型和truVOF方法，分析了设计水位下竖缝式鱼道不同高层处池室及休息池的流态分布和紊动能分布情况；侯勇俊等[14]基于Flow-3D的RNG k-ε紊流模型建立数值水槽，研究了波流场中桩柱周围的流场特性。综上，Flow-3D数值模拟在研究水流与结构体相互作用下的流场特征具有较好的效果，本文通过Flow-3D软件建立数值水槽，采用RNG k-ε湍流模型描述空心块体与水流之间的相互作用，研究空心块体内水流特性对泥沙淤积分布的影响。
Flow-3D数值模型的控制方程如下所示：
连续方程为
$$ \frac{\partial {u}_{i}}{\partial {x}_{i}}=0 \text{，} $$ (1) 动量方程为
$$ \frac{\partial {u}_{i}}{\partial t}+{u}_{j}\frac{\partial {u}_{i}}{\partial {x}_{i}}=-\frac{1}{\rho }\frac{\partial p}{\partial {x}_{i}}+\frac{\partial }{\partial {x}_{i}}\left(\upsilon \frac{\partial {u}_{i}}{\partial {x}_{i}}-\overline{{u}_{i}{u}_{j}}\right) \text{，} $$ (2) k-ε湍流方程为
$$ \frac{\partial k}{\partial t}+{u}_{j}\frac{\partial {u}_{i}}{\partial {x}_{i}}=\frac{\partial }{\partial {x}_{j}}\left({\alpha }_{\kappa }\upsilon \frac{\partial k}{\partial {x}_{j}}+2{\upsilon}_{t}{S}_{ij}{S}_{ij}-\varepsilon \right) \text{，} $$ (3) $$ \frac{\partial \varepsilon }{\partial t}+{u}_{j}\frac{\partial \varepsilon }{\partial {x}_{i}}=\frac{\partial }{\partial {x}_{j}}\left({\alpha }_{\kappa }\upsilon \frac{\partial \varepsilon }{\partial {x}_{j}}\right)-R+2{c}_{1}\frac{\varepsilon }{k}{\upsilon}_{t}{S}_{ij}{S}_{ij}-{c}_{2}\frac{{\varepsilon }^{2}}{k} \text{，} $$ (4) 式中，
$ {u}_{i} $ 、$ {u}_{j} $ 为流体的速度；p为时均压强；k为湍能量；$ \varepsilon $ 为湍能量耗散率；$ \rho $ 为水体密度；$\upsilon$ 为分子黏性系数；${\upsilon}_{t}$ 为涡黏系数，${\upsilon}_{t}={C}_{\mu }\left(\dfrac{{k}^{2}}{\varepsilon }\right)$ ；$\overline{{u}_{i}{u}_{j}}=\dfrac{2}{3k{\delta }_{ij}}- {\upsilon }_{t}\left(\dfrac{\partial {u}_{i}}{\partial {u}_{j}}+\dfrac{\partial {u}_{j}}{\partial {u}_{i}}\right)$ ，$ {\delta }_{ij} $ 为Kronecker函数；$ {C}_{\mu } $ =0.0845，$ {c}_{1} $ =1.42，$ {c}_{2} $ =1.68，$ {\alpha }_{\kappa } $ =$ {\alpha }_{\varepsilon } $ =1.39；$ {S}_{ij}=\dfrac{\partial {u}_{i}}{\partial {u}_{j}}+\dfrac{\partial {u}_{j}}{\partial {u}_{i}} $ ，$R=2\upsilon {S}_{ij}\dfrac{\overline{\partial \overline{u}_{i}'}}{\partial {x}_{j}}\dfrac{\overline{\partial \overline{u}_{i}'}}{\partial {x}_{i}}=\dfrac{{C}_{\mu }{\eta }^{3}\left(1-\dfrac{\eta }{{\eta }_{0}}\right)}{1+\beta {\eta }^{3}}\dfrac{{\varepsilon }^{3}}{k}$ ，$\overline{{u}_{i}'}$ 为脉冲速度，$ \eta $ 为湍流时间尺度与平均流时间尺度之比，$ \eta =Sk/\varepsilon $ ，$ S $ 为应变率张量范数，$S={\left(2{S}_{ij}{S}_{ij}\right)}^{\tfrac{1}{2}}$ ，$ {\eta }_{0} $ 为$ \eta $ 在均匀剪切流中典型值$ {\eta }_{0} $ =4.38，$ \beta $ =0.012。2.2.2 数值模型建立
数值水槽模型的建立通过N-S方程通过有限体积法离散将Flow-3D的FAVOR网格处理技术进行解析。空心块体模型通过AutoCAD建立三维模型，将模型保存为.stl格式文件导入至Flow-3D软件进行计算。数值水槽模型的尺寸与真实试验水槽的尺寸保持一致，空心块体放置在距进流15 m位置处，由于空心块体周围的流场变化较为复杂，故对堤身前端1 m至后端1 m范围内局部加密，网格选用5 mm正方形网格，其余部分选用1 cm正方形网格（图4）。为保证数值计算的稳定性，堤身附近至水槽其余区域过渡段网格密度渐进变化。数值水槽上边界条件选用“Specified Velocity”，流速定为恒定流0.30 m/s，下边界选用“Outflow”，数值水槽y轴两端及槽底Z Min选用“Wall”，初始水深选用0.36 m，计算时间为120 s。
2.2.3 数值模型验证
数值模型的验证采用开敞型空心块体在平均流速为0.30 m/s的工况条件下进行，分别选用堤前A1点（x=–50 cm）、堤身A7点（x=30 cm）、A10（x=90 cm）及堤后A16点（x=170 cm）垂线方向的水槽试验流速数据进行比对。如图5所示，数值模拟计算出的结果与水槽试验实测结果拟合良好，表明该三维模型可以较好地模拟空心块体内外侧的流场变化。
图 5 部分点位垂线方向流速（${u} $ ）验证Figure 5. Verification of vertical flow velocity (${u} $ ) at some points3. 试验结果
室内水槽试验工况平均流速为0.30 m/s，试验水深为0.36 m，空心块体内淤积时间为8 h。水槽试验的流速数据采用三维超声波多普勒测速仪采集，得到的流速数据需进一步处理，计算各测点的时均流速及紊动强度。悬沙浓度数据是通过标定OBS 3+得到的标定曲线，将NTU数据换算为悬沙浓度得到。
时均流速是根据瞬时流速的时间序列算术平均获得，公式如下式所示：
$$ u=\frac{1}{N}\sum _{i=1}^{N}{u}_{i} \text{，} $$ (5) 式中，
$ {u}_{i} $ 为瞬时流速；N为流速组次。紊动强度反映水流中流速脉动强弱程度，采用脉动流速的均方根表示为
$$ \sigma =\sqrt{\overline{{{u}'}^{2}}} \text{，} $$ (6) 式中，
$\overline{u'}$ 为脉动流速。紊动能是单位质量水体具有的总紊动动能，是表征湍流紊动强弱的物理量，此项由Flow-3D数值水槽模型给出，公式为
$$ {\rm TKE}=(\overline{u{'}^2}+\overline{v{'}^2}+\overline{w{'}^2})/2 . $$ (7) 3.1 空心块体垂线流速和紊动强度分布
图6给出堤身内部分点位A7（x=30 cm）、A9（x=70 cm）、A11（x=113.5 cm）的水流流速、紊动强度的垂线分布。两种空心块体在堤身与水流过渡段区域（z/h>0.5）水平流速由上而下逐渐减小，外部紊动强度均大于空心块体内紊动强度。而对于空心块体内部（z/h<0.5）的垂线流速，两种空心块体有较大差异。开敞型空心块体在z/h=0.2～0.4范围内出现先增大后减小的变化过程，在z/h=0.3位置出现局部流速最大值，近底层流速明显较小，保持在约为0.03 m/s，外界水流在开敞型空心块体作用下平均流速分别减小57%；开敞型空心块体内紊动强度分布均小于外部紊动强度，近底层的紊动强度较小，保持在约为0.025 m/s。而对于半封闭型空心块体，外部的水流流速、紊动强度和开敞型空心块体表现出相似特征，但空心块体内部的水流流速和紊动强度变化较为均匀，外界水流在半封闭型空心块体作用下平均流速分别减小72%，近底层的水流流速保持在约为0 m/s，紊动强度保持在约为0.02 m/s。
图 6 空心块体部分点位流速、紊动强度垂线分布Figure 6. Vertical distribution of velocity and turbulence intensity at some points in the hollow block3.2 空心块体垂线悬沙浓度分布
图7给出了两种空心块体在垂线方向上的悬沙浓度分布，同样选取堤身部分的A7（x=30 cm）、A9（x=70 cm）、A11（x=113.5 cm）3个点位进行对比分析。两种空心块体的悬沙浓度总体上表现为由表至底逐渐增大的变化特征，但两者在变化过程有明显差异。开敞型空心块体悬沙浓度沿垂线方向上在0.15～0.25 g/L范围内变化，在z/h>0.2的高流速区域内具有较高的悬沙浓度，在近底层位置悬沙浓度达到最大值，保持在0.25 g/L左右，整体上垂线方向上悬沙浓度变化均匀且无明显变化特征，垂线上泥沙与水体混合较为均匀；而半封闭型空心块体的悬沙浓度从水面至槽底呈线性增大变化特征，在z=0.15～0.2 m的空心块体与上方水流的过渡段部分悬沙浓度梯度增大，直至近底层达到垂线方向上悬沙浓度最大值，保持在0.28 g/L的悬沙浓度。两种空心块体近底层悬沙浓度相较于空心块体外侧平均悬沙浓度分别增大了56 %和75%。
图 7 空心块体部分点位悬沙浓度垂线分布Figure 7. Vertical distribution of suspended sediment concentration at some points of the hollow block3.3 空心块体淤积分布
图8和图9给出了两种空心块体持续淤积8 h下6个块体内部泥沙淤积图。两种空心块体内部都有不同程度的泥沙落淤，开敞型空心块体的泥沙淤积主要分布在空心块体前中端，泥沙在水流作用下卷挟堆积并向右推移，最大淤积厚度达到2 mm；沿堤身方向各个空心块体的泥沙淤积量呈现较大差异，空心块体内泥沙淤积面积逐渐增大并在水流作用下有沿水流方向不断推进的趋势。半封闭型空心块体的泥沙淤积形态与开敞型空心块体相比存在明显差异，半封闭型空心块体受结构特征影响水沙环境有较大不同，表现为泥沙淤积分布比较均匀，集中在空心块体中间位置；沿堤身方向各个空心块体泥沙淤积面积逐渐增大，最大淤积厚度约为1.5 mm。
图 8 开敞型空心块体内部泥沙淤积分布Figure 8. Distribution of sediment deposition in open hollow block
图 9 半封闭型空心块体内部泥沙淤积分布Figure 9. Distribution of sediment deposition in semi-closed hollow block4. 分析与讨论
4.1 开孔率对水流结构影响分析
空心块体开孔率强弱影响其内部的水动力特性，随着透水面积增大，块体内部的涡量增大，紊动能增大[15]。图10给出通过水槽试验得到的空心块体近底层（z=5 cm）水流流速及紊动强度的沿程分布，水流流速在空心块体影响下有不同程度的减小，半封闭型空心块体的减速效果更为明显；而开敞型空心块体的紊动强度整体大于半封闭型空心块体，半封闭型空心块体近底层的紊动强度保持在0.02 m/s左右且沿程分布较为均匀。这表明空心块体的透水面积越大，对沿程水流的阻碍作用越小，即开孔率与水流流速、紊动强度呈负相关。
图 10 空心块体近底层水流流速、紊动强度分布（截面z=5 cm）Figure 10. The distribution diagram of velocity and turbulence intensity near the bottom of the hollow block (Section z=5 cm)为了进一步分析空心块体内部的水流结构，图11给出通过Flow-3D数值模拟得到的平均流速为0.30 m/s、试验水深为0.36 m（u=0.30 m/s，h=0.36 m）工况条件下堤身结构侧视轴线切面流场分布图（y=0 cm）。可以明显发现开敞型空心块体近底层区域在壁面的阻碍作用下，区域z=0.05～0.15 m与区域z<0.05 m有较大的流速差，从而形成竖直方向上顺时针方向发展的涡旋，水流紊动强度也相应增大。然而，半封闭型空心块体由于透水面积较小，水流流速在进入空心块体内部得到削弱，近底层水流紊动强度受水体涡旋的影响较小。
图 11 空心块体侧视面流场分布（截面y=0 cm）Figure 11. The flow field distribution diagram of the hollow block in side view (Section y=0 cm)4.2 近底层紊动能分布对淤积形态影响分析
水流挟沙能力的强弱是空心块体泥沙促淤的关键要素，水流挟沙力大小与泥沙淤积量成反比，即水流挟沙力越小，泥沙淤积量越大，而水流挟沙能力的影响因素为水流流速、紊动及其泥沙特性等[16]。所以，空心块体近底层水流紊动对泥沙淤积起到重要作用。
从图8和图9的泥沙淤积结果可知，泥沙淤积形态具有不同程度的差异，主要表现在开敞型空心块体泥沙淤积主要集中在前端，而半封闭型空心块体的泥沙淤积分布较为均匀，这表明在空心内部水流紊动分布的空间差异影响泥沙淤积分布。Van Rijn[17]、Nielsen和Teakle[18]基于紊流模型对床面泥沙分布进行研究，结果表明近底层水流紊动影响底床泥沙淤积分布。所以，由于室内水槽试验的ADV流速测量仅对空心块体内部进行定点流量，空心块体内紊动反馈尚有不足，需要通过Flow-3D数值水槽对空心块体内部的水流紊动进行模拟。
在Flow-3D数值模拟工况的平均流速为0.30 m/s、试验水深为0.36 m（u=0.30 m/s，h=0.36 m）条件下，图12给出了近底层（z=5 cm）处空心块体紊动能分布，可以发现随着距离的增大，空心块体内部的平均紊动能分布逐渐减小，开敞型空心块体平均紊动能为0.003 J/kg，半封闭型空心块体平均紊动能为0.001 J/kg。堤身前端的水流与上游过渡段区域达到紊动能峰值，开敞型空心块体前端的紊动能最大值达到0.005 J/kg，半封闭型空心块体紊动能最大值达到0.002 J/kg，紊动能大小使得两种空心块体淤积形态产生差异。
图 12 空心块体近底层紊动能分布（截面z=5 cm）Figure 12. Distribution diagram of turbulent kinetic energy near the bottom of the hollow block (Section z=5 cm)4.3 水沙环境对大型底栖生物生境需求的影响
空心块体在海岸、航道工程建设中会对底床水沙动力环境产生影响，从而进一步影响底床水生生物的栖息、繁衍。大型底栖生物在食物链中为次级消费者，是底层鱼类的主要饵料，所以底栖生物群落健康程度也反映了水生生态系统的健康程度[19]。李亚等[20]根据长江口地区潮下带水域底栖生物调查研究，总结分析代表性优势大型底栖生物的生境需求。表2给出长江口目标生物的水沙生境需求，综合分析生境需求指标后可发现大型底栖生物繁衍需要营造低流速、低紊动的水沙动力环境，避免强烈的水流扰动；底部有适当的泥沙淤积，达到泥沙微淤、内外连通的生存环境。
表 2 长江口目标生物生境需求指标[20]Table 2. Target biological habitat demand indicators for the Changjiang River Estuary[20]生物类别 代表性物种 生境需求指标 双壳类 河蚬、黑龙江河篮蛤、
彩虹明樱蛤等河蚬、黑龙江河篮蛤一般栖息在底质0～5 cm深度；彩虹明樱蛤栖息深度一般在4～15 cm 甲壳类 中华绒螯蟹等 中华绒螯蟹在南槽水域主要为抱卵蟹和蚤状幼体，抱卵蟹适应流速不大于1.5 m/s，
蚤状幼体适应流速不大于0.7 m/s，幼蟹介于两者之间多毛类 沙蚕 沙蚕栖息深度在0～30 cm，基本生活在沉积底质内，
受水流作用影响相对较小根据3.1节和3.2节的试验结果，表明两种空心块体均起到良好的减速、促淤效果，同时块体的遮蔽性、连通性促进内外侧水体交换，块体底部的微淤环境为大型底栖生物提供充足养料，两种空心块体均有利于达到生态修复的效果。但从图8中近底层水流紊动对比结构中可以看出，半封闭型空心块体紊动强度小于开敞型空心块体且开敞型空心块体内部紊动强度均大于外部，较大的开孔面积虽起到较好减速效果但过流时的水流扰动较为强烈，故半封闭型空心块体更满足低流速、低紊动、促淤积的要求。
5. 结论
（1）空心块体的开孔率对内部水流流速、紊动强度起主导作用。外界水流在开敞型和半封闭型空心块体作用下平均流速分别减小57%和72%，半封闭型空心块体对水流减速效果更显著；空心块体导致水体紊动强度垂向差异明显，不同块体紊动强度分布不同，开敞型空心块体内在垂线方向紊动强度变化较大，在z/h=0.3附近出现局部峰值，而半封闭型空心块体紊动强度变化较小，流态更稳定。
（2）两种空心块体均有利于促进泥沙在块体内部淤积，开敞型和半封闭型空心块体近底层悬沙浓度分别增大56%和75%，近底层水流紊动对空心块体的淤积分布产生影响，使得两种空心块体泥沙淤积形态造成较大差异。开敞型空心块体紊动能平均为0.003 J/kg，近底层形成顺时针方向的旋涡，使得近底层紊动能峰值分布在块体后端，泥沙淤积集中在前中端部分，最大淤积厚度达到2 mm；半封闭型空心块体紊动能平均为0.001 J/kg，水流紊动能小于开敞型空心块体，在近底层分布均匀，最大淤积厚度为1.5 mm（8 h泥沙淤积试验）。
（3）大型底栖生物作为水生生物的代表性优势物种，反映水生生态系统的健康程度。空心块体所营造的低流速、泥沙微淤、内外连通的水沙环境是大型底栖生物的生境需求。半封闭型空心块体内部由于内部低紊动特点，更有利于大型底栖生物的栖息、繁衍，更好促进海岸生态系统的修复。
-
图 1 空心块体三视图及模型图（单位: mm）
Fig. 1 Three views and model diagram of the hollow block (unit: mm)
图 3 空心块体水槽试验测点布置（单位：mm）
Fig. 3 Layout of measuring points for hollow block flume experiment (unit: mm)
图 5 部分点位垂线方向流速（
${u} $ ）验证Fig. 5 Verification of vertical flow velocity (
${u} $ ) at some points
图 6 空心块体部分点位流速、紊动强度垂线分布
Fig. 6 Vertical distribution of velocity and turbulence intensity at some points in the hollow block
图 7 空心块体部分点位悬沙浓度垂线分布
Fig. 7 Vertical distribution of suspended sediment concentration at some points of the hollow block
图 9 半封闭型空心块体内部泥沙淤积分布
Fig. 9 Distribution of sediment deposition in semi-closed hollow block
图 10 空心块体近底层水流流速、紊动强度分布（截面z=5 cm）
Fig. 10 The distribution diagram of velocity and turbulence intensity near the bottom of the hollow block (Section z=5 cm)
图 11 空心块体侧视面流场分布（截面y=0 cm）
Fig. 11 The flow field distribution diagram of the hollow block in side view (Section y=0 cm)
图 12 空心块体近底层紊动能分布（截面z=5 cm）
Fig. 12 Distribution diagram of turbulent kinetic energy near the bottom of the hollow block (Section z=5 cm)
表 1 空心块体透水能力参数
Tab. 1 Hollow block water permeability parameter
结构型式 透水截面面积/cm2 总透水面积S0/cm2 开孔率S0/S x轴方向 y轴方向 z轴方向 开敞型 100 100 196 792 33% 半封闭型 19.6 19.2 顶面64
底面196337.6 14% 注：S为包含结构体外轮廓总面积S=20$ \text{×} $20$ \text{×} $6=2 400 （cm²）。 
下载: 导出CSV
表 2 长江口目标生物生境需求指标[20]
Tab. 2 Target biological habitat demand indicators for the Changjiang River Estuary[20]
生物类别 代表性物种 生境需求指标 双壳类 河蚬、黑龙江河篮蛤、
彩虹明樱蛤等河蚬、黑龙江河篮蛤一般栖息在底质0～5 cm深度；彩虹明樱蛤栖息深度一般在4～15 cm 甲壳类 中华绒螯蟹等 中华绒螯蟹在南槽水域主要为抱卵蟹和蚤状幼体，抱卵蟹适应流速不大于1.5 m/s，
蚤状幼体适应流速不大于0.7 m/s，幼蟹介于两者之间多毛类 沙蚕 沙蚕栖息深度在0～30 cm，基本生活在沉积底质内，
受水流作用影响相对较小
下载: 导出CSV
-
[1] 范航清, 何斌源, 王欣, 等. 生态海堤理念与实践[J]. 广西科学, 2017, 24(5): 427−434, 440.Fan Hangqing, He Binyuan, Wang Xin, et al. The conception and practices of ecological sea dyke[J]. Guangxi Sciences, 2017, 24(5): 427−434, 440. [2] Mitsch W J, Jørgensen S E. Ecological Engineering: An Introduction to Ecotechnology[M]. New York: John Wiley & Sons, Inc. , 1989. [3] 李泽龙, 孙林云, 唐磊, 等. 河口海岸保滩促淤方式及水沙机理研究综述[J]. 中国港湾建设, 2018, 38(11): 1−8. doi: 10.7640/zggwjs201811001Li Zelong, Sun Linyun, Tang Lei, et al. Review on beach protection and deposition promotion and water and sediment transport mechanism in estuaries and coastal area[J]. China Harbour Engineering, 2018, 38(11): 1−8. doi: 10.7640/zggwjs201811001 [4] Ido S, Shimrit P F. Blue is the new green-ecological enhancement of concrete based coastal and marine infrastructure[J]. Ecological Engineering, 2015, 84: 260−272. doi: 10.1016/j.ecoleng.2015.09.016 [5] Heatherington C, Bishop M J. Spatial variation in the structure of mangrove forests with respect to seawalls[J]. Marine and Freshwater Research, 2012, 63(10): 926−933. doi: 10.1071/MF12119 [6] 杨芳丽, 耿嘉良, 付中敏, 等. 长江中游航道整治中生态技术应用探讨[J]. 人民长江, 2012, 43(24): 68−71. doi: 10.3969/j.issn.1001-4179.2012.24.018Yang Fangli, Geng Jialiang, Fu Zhongmin, et al. Exploration on application of eco-technology in waterway regulation project at midstream of Yangtze River[J]. Yangtze River, 2012, 43(24): 68−71. doi: 10.3969/j.issn.1001-4179.2012.24.018 [7] 张为, 李义天, 王秀英, 等. 透水结构促淤试验研究[J]. 四川大学学报(工程科学版), 2005, 37(6): 31−37. doi: 10.3969/j.issn.1009-3087.2005.06.007Zhang Wei, Li Yitian, Wang Xiuying, et al. Experimental study on deposition promotion of permeable structure[J]. Journal of Sichuan University (Engineering Science Edition), 2005, 37(6): 31−37. doi: 10.3969/j.issn.1009-3087.2005.06.007 [8] 吴龙华, 周春天, 严忠民, 等. 架空率、杆件长宽比对四面六边透水框架群减速促淤效果的影响[J]. 水利水运工程学报, 2003(3): 74−77. doi: 10.3969/j.issn.1009-640X.2003.03.017Wu Longhua, Zhou Chuntian, Yan Zhongmin, et al. Effects of overhead ratio and pole’s length-width ratio on deceleration and accretion promotion of tetrahedron-like penetrating frames[J]. Hydro-Science and Engineering, 2003(3): 74−77. doi: 10.3969/j.issn.1009-640X.2003.03.017 [9] 崔勇, 关长涛, 万荣, 等. 布设间距对人工鱼礁流场效应影响的数值模拟[J]. 海洋湖沼通报, 2011, 33(2): 59−65. doi: 10.3969/j.issn.1003-6482.2011.02.008Cui Yong, Guan Changtao, Wan Rong, et al. Numerical simulation on influence of disposal space on effects of flow field around artificial reefs[J]. Transactions of Oceanology and Limnology, 2011, 33(2): 59−65. doi: 10.3969/j.issn.1003-6482.2011.02.008 [10] Harris L E. Submerged reef structures for habitat enhancement and shoreline erosion abatement[J]. Coastal Engineering Technical Note, 2001(9): 1–16. [11] Moreira J, Chapman M G, Underwood A J. Maintenance of chitons on seawalls using crevices on sandstone blocks as habitat in Sydney Harbour, Australia[J]. Journal of Experimental Marine Biology and Ecology, 2007, 347(1/2): 134−143. [12] Temmerman S, Meire P, Bouma T J, et al. Ecosystem-based coastal defence in the face of global change[J]. Nature, 2013, 504(7478): 79−83. doi: 10.1038/nature12859 [13] 杨培思, 蔡德所, 莫崇勋. 基于FLOW-3D的竖缝式鱼道水力特性研究[J]. 广西大学学报(自然科学版), 2018, 43(4): 1675−1683.Yang Peisi, Cai Desuo, Mo Chongxun. Study on hydraulic characteristics of vertical-slot fishways based on FLOW3D[J]. Journal of Guangxi University (Natural Science Edition), 2018, 43(4): 1675−1683. [14] 侯勇俊, 熊烈, 何环庆, 等. 基于FLOW-3D的三维数值波流水槽的构建及应用研究[J]. 海洋科学, 2015, 39(9): 111−116. doi: 10.11759/hykx20140902003Hou Yongjun, Xiong Lie, He Huanqing, et al. Three-dimensional wave-current numerical model and application based on FLOW-3D[J]. Marine Sciences, 2015, 39(9): 111−116. doi: 10.11759/hykx20140902003 [15] 王小明, 程永舟, 常留红, 等. 梯形透水潜坝三维水流特性的数值模拟[J]. 水利水电科技进展, 2017, 37(5): 51−56. doi: 10.3880/j.issn.1006-7647.2017.05.009Wang Xiaoming, Cheng Yongzhou, Chang Liuhong, et al. Numerical simulation of three-dimensional flow characteristics of trapezoidal permeable submerged dam[J]. Advances in Science and Technology of Water Resources, 2017, 37(5): 51−56. doi: 10.3880/j.issn.1006-7647.2017.05.009 [16] Colby B R, Hembree C H. Computations of total sediment discharge, Niobrara river near Cody, Nebraska[J]. Science, 1954, 119(3097): 657−658. doi: 10.1126/science.119.3097.657.b [17] Van Rijn L C. Principles of Sediment Transport in Rivers, Estuaries and Coastal Seas[M]. Amsterdam: Aqua Publications, 1993. [18] Nielsen P, Teakle I A L. Turbulent diffusion of momentum and suspended particles: a finite-mixing-length theory[J]. Physics of Fluids, 2004, 16(7): 2342−2348. doi: 10.1063/1.1738413 [19] Larsson P. Transport of PCBs from aquatic to terrestrial environments by emerging chironomids[J]. Environmental Pollution Series A, Ecological and Biological, 1984, 34(3): 283−289. doi: 10.1016/0143-1471(84)90123-5 [20] 李亚, 陈海峰, 黄明毅, 等. 新型聚氨酯碎石空心块体生态堤结构构建[J]. 水运工程, 2020(11): 132−137. doi: 10.3969/j.issn.1002-4972.2020.11.023Li Ya, Chen Haifeng, Huang Mingyi, et al. Structure creation of new type of ecological embankment made of PPM hollow block[J]. Port & Waterway Engineering, 2020(11): 132−137. doi: 10.3969/j.issn.1002-4972.2020.11.023 -
下载:
计量
- 文章访问数: 402
- HTML全文浏览量: 190
- PDF下载量: 37
- 被引次数: 0
