Basic geoacoustic structure and geoacoustic model for seafloor sediments
-
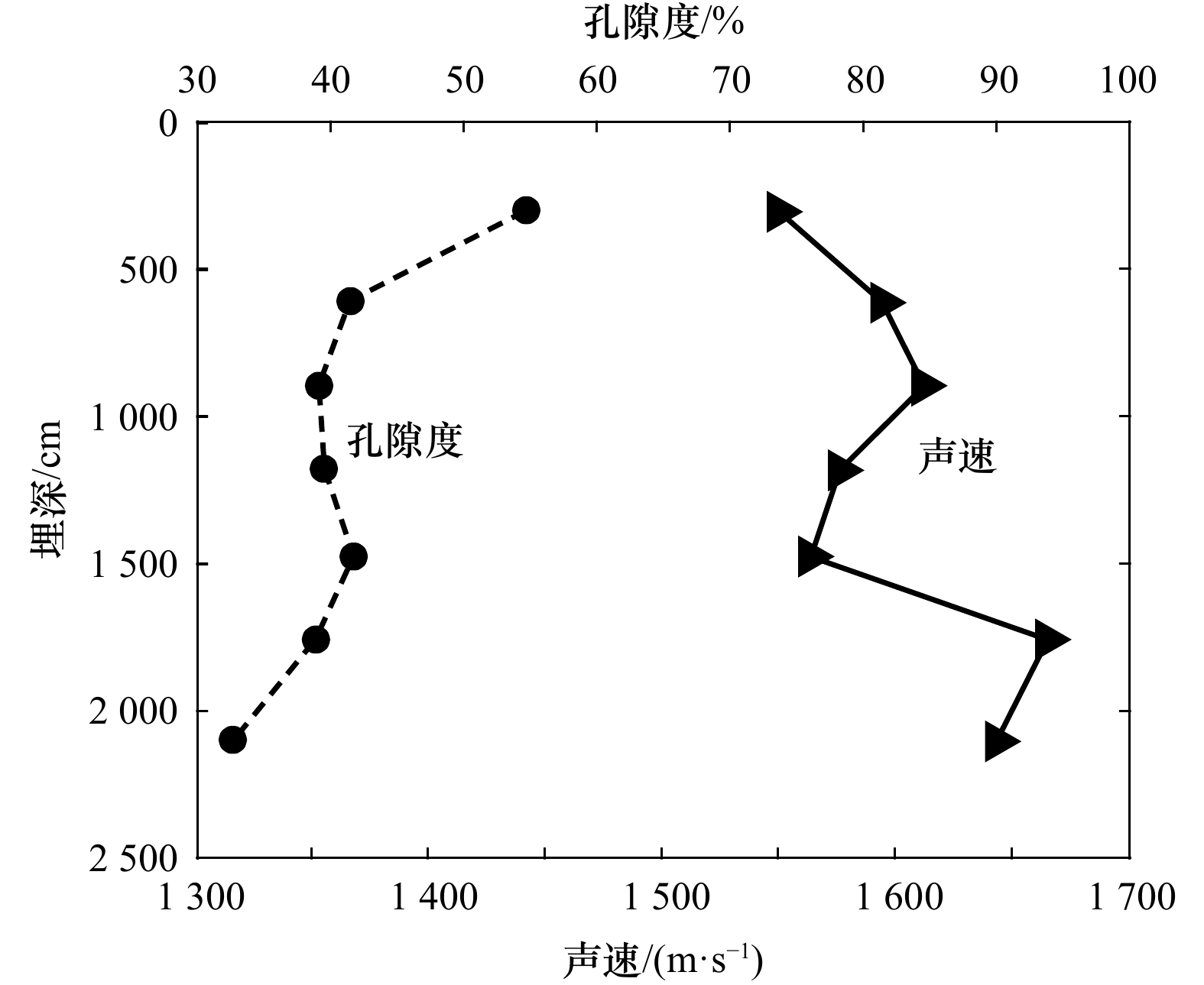
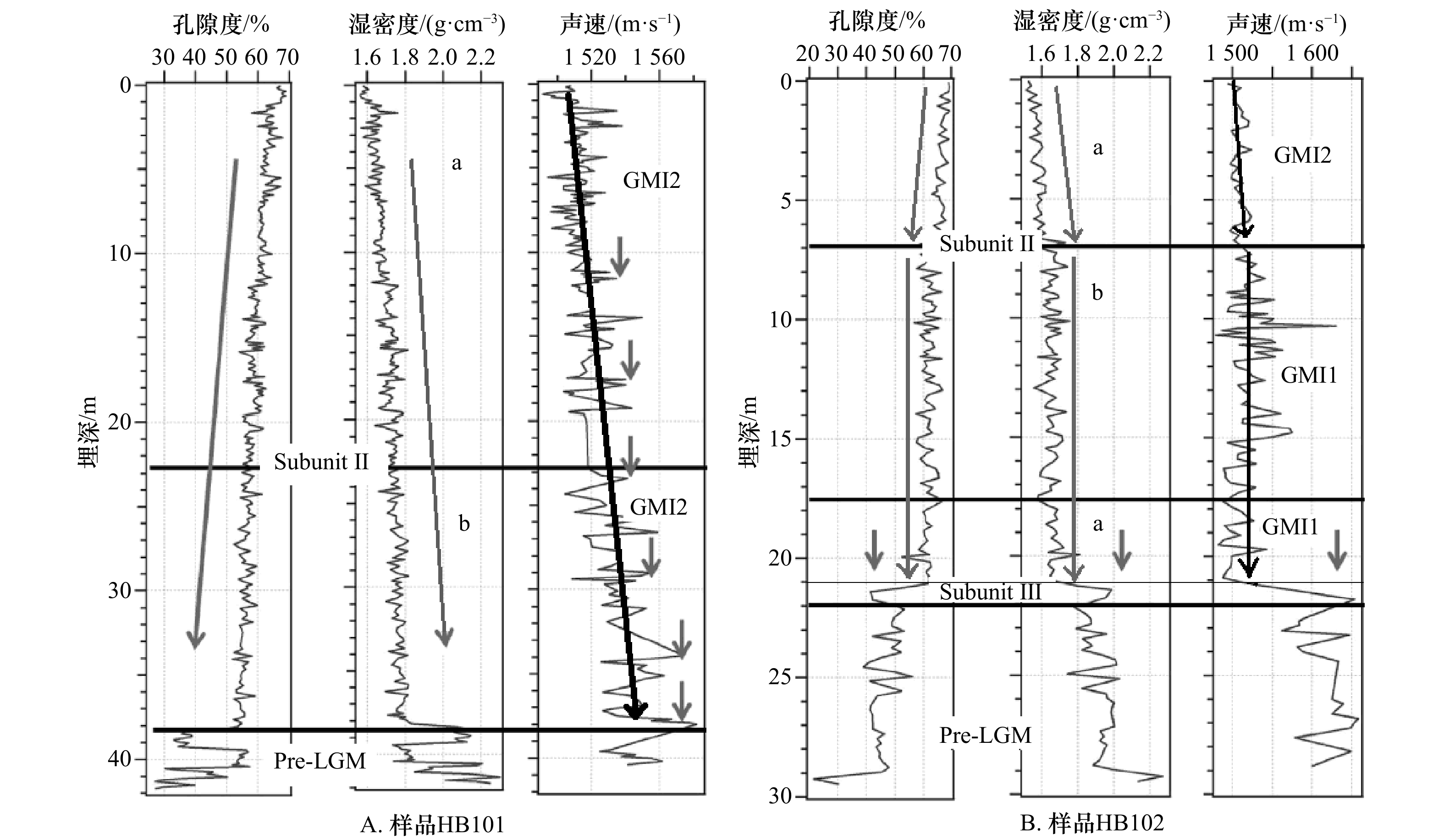
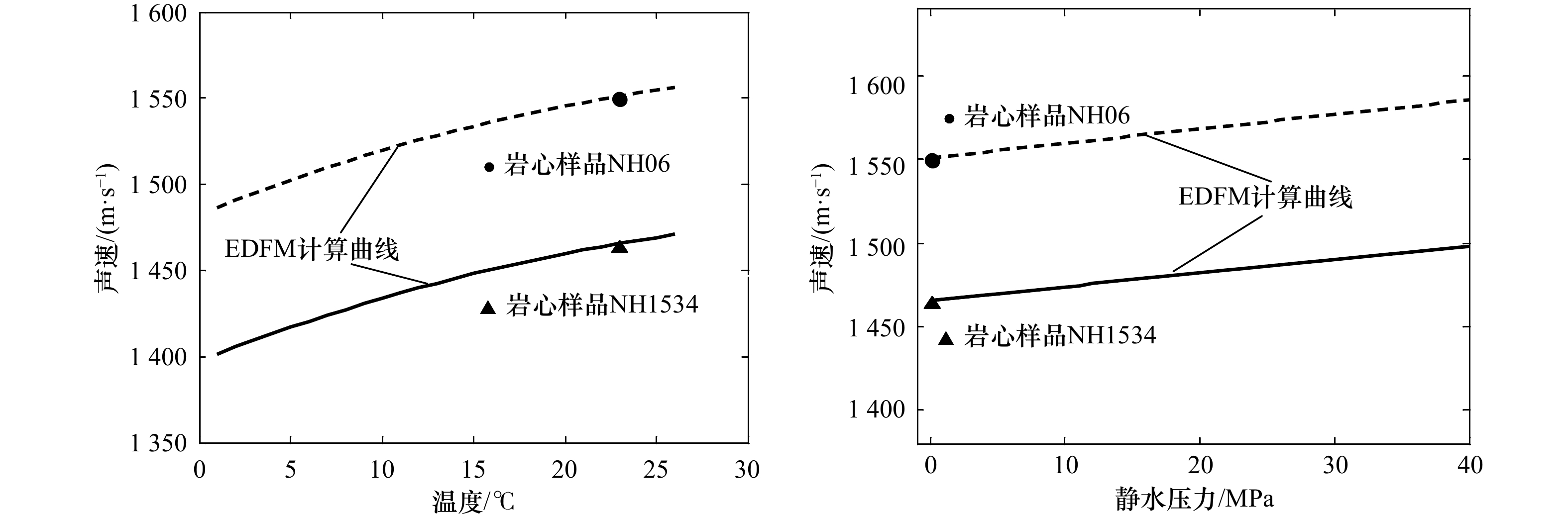
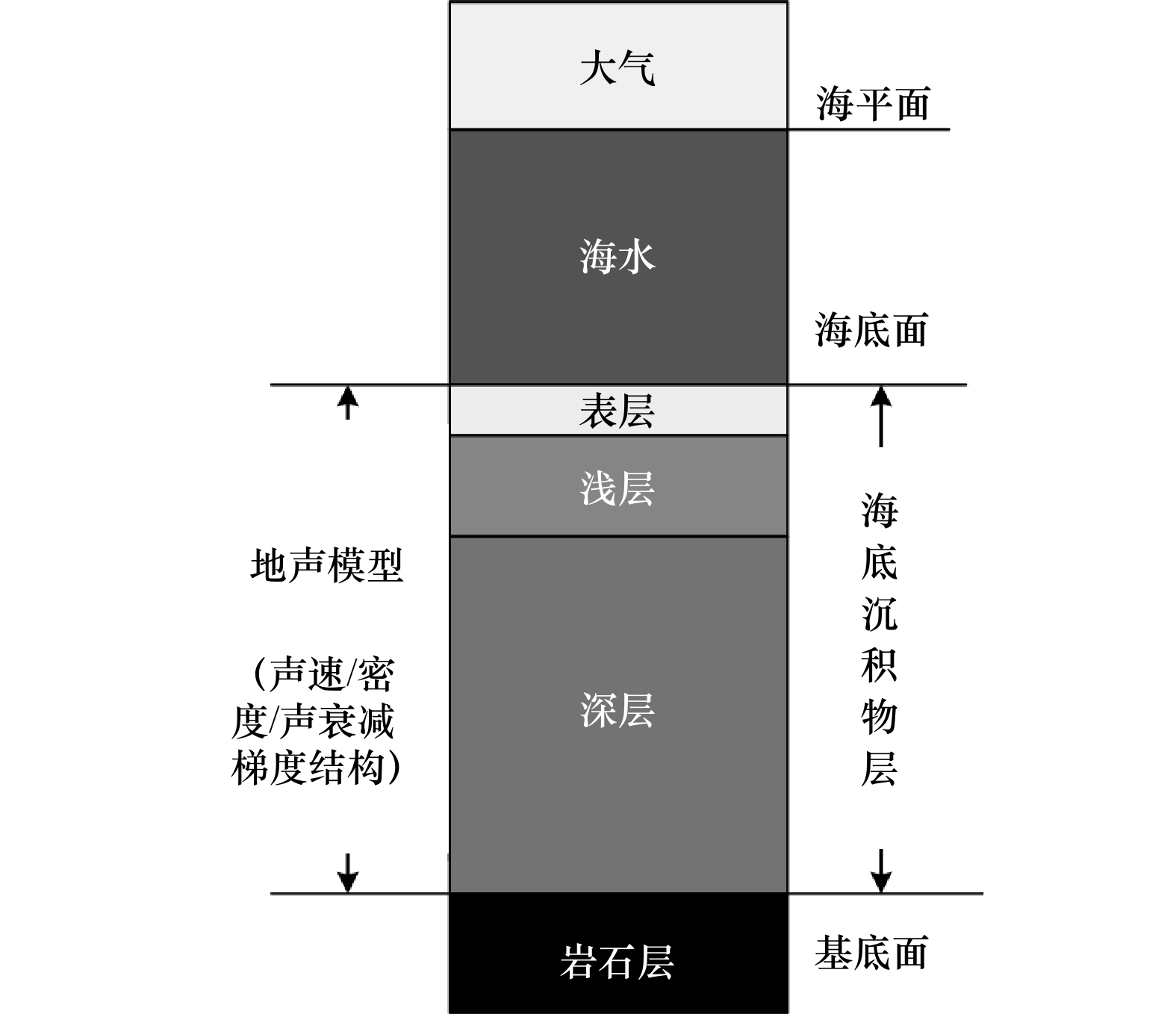
摘要: 为准确建立海底地声模型，本文探讨地声模型的基本组成和基本结构。通过样品实验室测量，分析南海海底表层沉积物的密度、孔隙度与声速随着埋深变化的关系，得出海底实际存在的低声速表面–声速缓慢变化类型、低声速表面–声速增大类型、高声速表面–声速缓慢变化类型和高声速表面–声速增大类型4种典型地声结构；对比钻探测量，分析黄海海底沉积物的密度、孔隙度与声速随埋深变化关系，得出海底地声模型分层特征与地声结构组合特征。研究表明，地声模型可以归结为4种基本地声结构的组合，通过与底层海水声速、同层内声速剖面以及与上层海底沉积物下表面声速的比较，可以建立各种海底地声模型；基于实验室测量法建立的地声模型可以作为参考地声模型，但需要考虑实际海底温度和压力梯度以及海底沉积物的频散特性等，借助于声速比校正法和频散性理论模型进行计算及修正。Abstract: To accurately establish a geoacoustic model for seafloor sediments, the elemental composition and structure of the geoacoustic model are explored in this paper. Based on the laboratory measurements of seafloor sediment samples, the buried depth relationship between density, porosity, and sound velocity of seafloor surface sediments in the South China Sea is analyzed. Four typical seafloor geoacoustic structures are obtained: low sound velocity surface-sound velocity slow change type, low sound velocity surface-sound velocity increase type, high sound velocity surface-sound velocity slow change type, and high sound velocity surface-sound velocity increase type. By comparing the drilling survey and analyzing the buried depth relationship between density, porosity, and sound velocity of seafloor sediments in the Yellow Sea, the actual layered characteristics and the combination characteristics of the geoacoustic structure are obtained. It shows that the geoacoustic model can be attributed to a combination of four basic geoacoustic structures. Various actual seafloor geoacoustic models can be derived from the comparisons between the acoustic sound speed of the bottom seawater, the sound velocity profile of seafloor sediments in the same layer, and the bottom sound velocity of the upper sediment. The geoacoustic model based on the laboratory measurement analysis of seafloor sediment samples can be used as a reference geoacoustic model. However, it should be modified with the sound velocity ratio correction method and theoretical calculation method of dispersion characteristics with the consideration of the actual seafloor temperature gradient, pressure gradient, and dispersion characteristics of seafloor sediment.
-
Key words:
- geoacoustic model /
- geoacoustic structure /
- seafloor sediments /
- sound velocity /
- frequency dispersion
-
1. 引言
海底沉积物声学特性空间结构分布是影响水下声场的重要因素之一，所有海底声学探测都与海底沉积物的声学特性及其声速剖面有关，或涉及浅表层地声模型，或涉及深层地声模型。地声模型可以提供海底声速、密度、声衰减系数和分层特征等地声属性，在声场预报、匹配场定位、地声反演中十分重要[1-4]。通过声学遥测[5-9]、理论分析[10-12]、实验室声学测量[13-19]和原位声学测量[20-23]等方法，开展海底沉积物声学与物理特性分析和地声参数反演研究，尝试建立适用于不同测量频率、不同埋深的海底声速剖面，为各种应用提供海底沉积物地声模型[12-15]，越来越成为海洋声学探测基础研究的热点和重点。
地声反演和声场预报中通常将海底声速剖面分为沉积物层和基底层的两层模型[1-8]，又根据不同需要把沉积物层等效分成深度不等的一至多层结构；对于各层声速，既有采取等声速结构[1, 3-6]，也有采取不等声速结构[2, 8]。这种采取等效方法简化建立的地声模型，为声场传播分析和地声反演带来方便。李梦竹等[1]指出负跃层起伏环境下的高声速海底的声学反演，可以采取单层等声速海底地声模型代替两层结构，与小于海底特征角的海底掠射声场等效模型相似[7]。尚尔昌[8]指出，建立在假设地声模型之上的反演得到的海底地声参数并非介质本身的固有参数，海底衰减系数的频率特性会发生严重的畸变。周志愚等[9]利用全反射射线法和折射法，获得南海浅海垂直声速剖面，指出海底表层存在低声速层，随着埋深增加既有等声速结构，也存在非等声速层结构，同时指出海底温度变化对表层声速具有影响性。Buckingham[10]基于VGS模型计算两层和3层海底的声速剖面，得出即使物理参数不随埋深变化，压缩波速度和剪切波速度都随着深度增大而增大。实际地声模型复杂多样，既有低声速结构也有高声速结构，抑或两者交错出现[12-15]。因此，水声探测和地声反演采用的等效地声模型，其存在的分层及声速剖面选择问题，即等效地声模型与实际地声模型的相互关系以及简化依据问题，需要更为深入研究得以明确。
Hamilton[13-14]运用统计分析方法研究海底沉积物样品的各物理参数之间的关系以及与声速和声阻抗的关系，建立大陆架、大陆坡、深海平原的声学特性回归模型，基于地声梯度建立地声模型，被广泛借鉴和参考。卢博[15]基于样品分析研究中国东南沿海尤其是南海海底沉积物声学特性，指出基于沉积物/海水声速比和沉积物压缩波/剪切波声速比将海底划分为液态海底、半固态海底和固态海底，在Hamilton地声模型基础上提出南海海域的3种海水–沉积物声速结构。这些根据取样测量获得的声速结构往往属于海底表层、浅层声速剖面，在各自海域具有直接指导性[13-19]。Li等[20]通过海底原位测量获得南海海底1.4 m范围内的低声速层、等声速结构，与实验室测量的声速剖面具有相似性。Kim等[21]比较原位和实验室测量获得海底沉积物声速分布，指出温度、压力、频率等不同导致声速剖面存在差异，可以进行修正。基于海底原位测量表明，海底既有等声速层结构[20-22]，也有随着埋深增大的不等声速层结构[22-23]。上述测量研究表明，沉积历史和沉积过程变化导致海底声速剖面非常复杂，也因为各种声学测量技术存在尺度不同和方法差异，导致建立的地声模型不一致。随着海底声学探测向着深远海、海底深层、高精度、高效率的方向的不断发展，如何为不同测量应用提供具有一致性解释和相互借鉴的地声模型，一直以来都是亟需探讨解决的难点。
本文通过探讨地声模型的基本组成与建立方法，分析南海海底表层沉积物样品的密度、孔隙度与声速变化关系，提出地声模型的4种基本声速结构，通过基本声速结构的组合构建和解释现有的地声模型；通过分析频散特性和环境温度与压力对声速剖面的影响性，提出将实验室测量法建立的地声模型应用于不同测量方法时，进行修正和对比，得到地声模型的解释一致性，为海底声学探测应用的各种地声模型提供建立依据。
2. 地声模型的基本组成与基本结构
2.1 地声模型的基本组成
如图1所示，海平面、海底面和基底面是物质交换、温度交换和沉积形态变化的3个重要界面，也是海洋3个最主要的声学特性传播界面。在底层海水、沉积历史和自身重力等综合作用下[24-28]，海底沉积物在海底不同埋深处形成复杂的分层特征，其特点主要有：各层既以无机质为主，又可能含有一定量的有机质；既包含硅质沉积物，也可能包含碳酸盐沉积物；既是海水饱和的两相介质沉积物，也可能因渗漏气体存在成为固液气三相混合的沉积物；还可能因为混合贝壳、油气、可燃冰、多金属结核等而成为多物质混合状态。具体应用时，需根据以上组成成分、类型、混合状态而划分为更为细致的分层。以当前取样测量[13-19, 29-31]和原位测量[20-23, 32-34]为参考，海底沉积物通常可以分为表层（0～3 m埋深）、浅层（3～10 m埋深）和深层海底沉积物（10 m以深至岩石层），部分海域深层海底沉积物可以深达千米[28]。
海底沉积物的声速、声衰减系数、密度随着海底埋深的分布结构，通常用地声模型表征。考虑到海底探测需求，根据已有的海底声速结构和地声模型的研究，得到地声模型的基本组成如下：
（1）声速结构–压缩波波速（通常称之为声速）随着埋深深度的变化关系，即声速剖面；表示成压缩波与埋深深度的梯度关系，即为声速梯度；
（2）密度结构–密度与埋深深度的关系，即密度剖面；表示成密度与埋深深度的梯度关系，即为密度梯度；
（3）空间结构–海底沉积物的埋深分层特征和水平分布范围；
（4）声衰减结构–压缩波衰减系数（通常称之为声衰减）与埋深深度的关系，即声衰减剖面；表示成压缩波衰减系数随着埋深的梯度关系，即为声衰减梯度；
（5）剪切波速度结构–剪切波速度与埋深深度的关系，即剪切波速度剖面；也可以表示成剪切波速度随着埋深的梯度关系，即为剪切波速度梯度。
其中，前3项包含海底分层的声速剖面和密度剖面，构成地声结构，可以构建海底声阻抗剖面，是一种基本地声模型关系。增加后两项可以构建扩展后的地声模型。
Hamilton[13]指出，建立地声模型还需要考虑海底沉积物层和岩石层的类型、分层厚度和形状以及弹性性质如弹性模量、剪切波衰减系数与埋深深度的关系等，更广泛意义的地声模型还包括沉积历史、沉积环境等参数。但在具体建立地声模型时，很难获得如此多的资料和数据，实际的地声模型具有多层状态、三维结构、各向异性等特性，过于复杂，需要根据需求进行简化。通过研究地声模型的基本结构，在应用时结合少量测量数据以及预报方法，可以实现构建区域性的地声模型。
2.2 地声模型的4种基本地声结构
考虑到水声探测的普遍性应用，以下针对地声模型最基本的3项组成，以压缩波波速为主，研究地声模型的基本结构，即地声结构。在地声结构研究中，只包括海底沉积物的声速剖面和密度剖面，未考虑声衰减剖面和剪切波速度剖面，主要原因有：（1）海底沉积物的声衰减特性虽然决定着测量声波在海底传播的能量、强度与距离，剪切波可以表征底质结构，却都非海底地声模型划分的决定因素；（2）海底沉积物的声衰减特性和剪切波在实验室中的测量精度都低于声速测量，仍需深入研究不同测量方法在较宽声波频率范围内精确性的关系才能建立更为准确的结构模型。
根据每一层上表面沉积物声速cpis与底层海水声速c0比较，定义为低声速表面和高声速表面，表达如式（1）；考虑到每层之间存在层间声速差异，通过比较每一层上表面沉积物声速cpis与上一层下底面沉积物声速cpjb的大小，定义分成高声速层和低声速层，表达如式（2）；考虑到每一层内存在声速变化状态因素，根据每一层声速梯度gcpi与声速梯度阈值gth0的比较，可以分为声速缓慢变化型和声速增大类型声速梯度，定义表达如式（4）。
$$ 高声速表面： c_{{\rm{p}}i{\rm{s}}}> c_0\text{；} 低声速表面： c_{{\rm{p}}i{\rm{s}}} \leqslant c_0\text{,} $$ (1) $$ 高声速层：c_{{\rm{p}}i{\rm{s}}}>c_{{\rm{p}}j{\rm{b}}} \text{；} 低声速层： c_{{\rm{p}}i{\rm{s}}} \leqslant c_{{\rm{p}}j{\rm{b}}}\text{,} $$ (2) $$ 声速梯度：g_{{\rm{cp}}i}=（c_{{\rm{p}}j{\rm{b}}} -c_{{\rm{p}}i{\rm{s}}}）/{{h}}_{{i}} , $$ (3) $$ 声速增大类型：g_{{\rm{cp}}i}>g_{\rm{th0}}\text{；}声速缓慢变化类型：g_{{\rm{cp}}i} \leqslant g_{\rm{th0}}\text{,} $$ (4) 式中，cp为声速（即压缩波波速，单位：m/s）；gcpi为声速梯度（即压缩波波速梯度，单位：s−1）；h为沉积物层厚度（单位：m），下标s、b、i、j、th0分别表示表层、底层、第i层、第i–1层、阈值，其中，i≥2。当i=1时对应着海底表层第1层，此时与底层海水c0的声速进行比较。
基于以上对应关系，得出4种地声模型的基本结构：（1）低声速表面–声速缓慢变化类型；（2）低声速表面–声速增大类型；（3）高声速表面–声速缓慢变化类型；（4）高声速表面–声速增大类型。以上4种基本地声结构，如果考虑层与层之间的过渡，还可以结合高声速层和低声速层进行细致划分，比如某海域海底第3层沉积物被定义为低声速表面–高声速层–声速增大类型，则表示第3层海底沉积物上表面声速低于底层海水声速，但高于第2层海底沉积物的下表面声速，并且第3层内声速处于增大类型。
基本地声结构定义时未考虑密度剖面，是因为虽然存在低于底层海水声速的海底沉积物类型，但其密度和声阻抗都大于底层海水的密度和声阻抗，因此只采用声速进行划分可以简化表达出海底沉积物的分层状态和结构。
海底第1层地声结构形成水声的下边界和地声的上边界，是水声学、地声学和沉积声学都关注的最重要的地声结构。表层海底沉积物的表面声速与底层海水声速c0相比较，当大于c0时，同时为高声速表面和高声速层海底，即高声速海底；小于或等于c0时，为低声速表面海底和低声速层海底，即低声速海底。对于低声速表面海底，如果属于声速缓慢变化类型时，通常整层都是低声速层，小于底层海水声速c0；如果属于声速增大类型，当沉积物层埋深增长到一定深度时会大于底层海水声速c0，由低声速层过渡成高声速层。实际海底，黏土质含量非常高的海底沉积物基本都属于低声速表面–低声速层海底，砂质含量非常高的海底沉积物基本都属于高声速表面–高声速层海底。粉砂质海底沉积物根据黏土百分含量的高低而处于高声速和低声速的过渡中。
声速梯度阈值gth0需要设定具体范围值，通常声场传播中要求声速测量精度在1%以内，以表层粉砂质海底沉积物声速为1 600 m/s计算，在16 m以浅的范围内，声速梯度阈值gth0如果设定为1 s−1，则在此16 m海底沉积物层内可以把整层海底沉积物声速当成常值1 600 m/s应用而满足精度。当某海底沉积物层的gth0设定为1 s−1，此层声速梯度平均值介于这个阈值范围时，属于声速缓慢变化类型；当声速梯度平均值大于阈值范围时，属于声速增大类型。
实际测量数据分析表明，当声速梯度较小时，海底沉积物的孔隙度基本不变或者缓慢变化，当声速梯度较大时，海底沉积物孔隙度处于减小变化；同时，海底沉积物的孔隙度与声速具有明确的一元二次相关性 [13-19, 29-31]，与密度呈现良好的线性相关。因此，引入孔隙度代替密度作为定义地声结构类型的一个基本量，在地声模型分析和实际应用中更为直观和有效。
3. 地声模型和地声结构的建立
3.1 地声模型的建立方法
当前海底沉积物声学测量方法[1-23, 29-37]，可用于建立地声模型的方法主要有4种：（1）遥测法[1-9]；（2）实验室测量法[13-19, 29-31, 37]；（3）海底原位测量法[20-23, 32-34]；（4）钻探测量法[35-37]。如表1所示，不同方法建立地声模型的测量频率和尺度各不相同。
表 1 地声模型建立方法的比较Table 1. Comparison of establishment methods of geoacoustic model建立方法 测量频率/kHz 海底埋深深度 地声参数 物理特性 遥测法 0.01～151) 通常几十米，可以至数千米 压缩波波速及其衰减系数 基于经验方程或者理论模型反演
计算获得实验室测量法 30～1 000 通常为0.5～4 m，部分
能够达到8 m压缩波波速及其衰减系数为主，部分
获得剪切波的波速及其衰减系数基于实验室测量可以获得全部所
需物理力学特性海底原位测量法 1～260 通常为0.3～3 m，部分
能够达到6～8 m压缩波波速及其衰减系数为主，部分
获得剪切波的波速及其衰减系数需要通过同站位采集样品实验室
测量获得钻探测量法 约402) 通常几十米，可以至数千米 压缩波波速和剪切波波速为主，可以
获得衰减系数随钻直接测量或者采集样品实验
室测量获得注：1)遥测法中的浅地层剖面仪、多波束测量、侧扫声呐等高频探测频率段未计入内；2)钻探取样样品的测量频率段未计入内，可参照样品采集的实验室测量法。 实验室测量法通过重力柱状取样（含活塞取样）、箱式取样、多管取样等方式取得海底沉积物样品，在实验室开展分段声学和物理特性测量。实验室测量法存在过程扰动，但可以得到海底沉积物样品的分层信息以及声学与物理特性分布结构。
海底原位测量法通过贯入式、压入式海底原位测量设备，在海底原位环境状态测量海底沉积物的声学特性和声学结构。如需要借助取样进行样品测量获得海底沉积物物理特性，因此对海底沉积物的扰动小。
遥测法通过声学反射和折射获得海底声波传播的分层走时信息和传播损失信息，结合海底沉积物的经验关系式、理论模型、搜索函数、目标函数等，获得海底沉积物的声学与物理特性的分布结构。通常需要结合实验室测量法或者海底原位测量法进行佐证。
钻探测量法通过钻探取样测量、随钻测井、钻孔测井等方式，测量深层海底沉积物的声学与物理特性。属于专有手段，能够获得实验室测量法或海底原位测量法难以提供的海底深层声速剖面特征，作为以上3种建立模型的验证、补充和支持。
实验室测量法和海底原位测量法只能获得表层和浅层海底沉积物的声速剖面分布特征，遥测法和钻探测量法可以获得深层海底沉积物的声速剖面分布特征。实验室测量法、海底原位测量法和钻探测量法都只能获得测量点的声速剖面分布，需要结合遥测法来构建区域性的地声模型。
为实现这4种建立地声模型方法的相互借鉴性和解释统一性，需要解决的共性问题有：（1）实验室测量法和原位测量法的测量频率高于遥测法中的水声测量和地声反演的探测频率，需建立有效解释从10 Hz至1 MHz测量频率范围内的海底沉积物频散特性对声速剖面影响性分析的普遍方法；（2）实验室测量法和原位测量法的测量深度远低于遥测法中的水声测量和地声反演的探测深度，需建立有效解释从表层到深层100 m深度范围内的地声模型建模的普遍方法；（3）实验室测量法的测量环境有别于其他3种方法的海底原位测量环境状态，需建立有效解释从0℃至60℃的综合温度范围内和从1.013×105 Pa至60 MPa综合压力范围内的海底沉积物声速剖面校正的普遍方法。
3.2 基于实验室测量法的地声结构建立
以重力柱状取样（含活塞取样）获得海底沉积物样品，按照可观测的分层或者定长分割分段，采用PVC管或有机玻璃管存放分段样品，在实验室测量得到海底沉积物的声学特性和物理特性。其中，砂质海底沉积物颗粒尺寸大、堆积密实、难于插入而取样长度有限，一般为1 m左右；黏土质海底沉积物因为剪切强度低而容易取得较长样品，可以达到4～8 m。海底沉积物的声速深受测量环境影响[21, 38-40]，因此参照23℃、1.013×105 Pa的实验室标准测量环境，采用此环境状态下的盐度为34.5的海水所对应的1 529.3 m/s作为底层海水实验室标准声速，用于计算建立地声模型的高低声速表层海底。
3.2.1 低声速表面的地声结构类型
海底沉积物样品NH1534取自于南海3 100 m水深海底[16]，长度为3.95 m，以黏土质类型为主，分成9段测量，声学测量主频为400 kHz。9段样品测量孔隙度为0.819±0.021，密度为（1.32±0.03） g/cm3，测量声速为（1 464.4±1.9） m/s。随着埋深深度增加，样品NH1534的孔隙度、密度、声速变化不大，整体形成比较均匀的声速剖面。实验室测量海底沉积物声速整体小于底层海水声速1 529.3 m/s，因此样品所在区域对应着低声速表面–声速缓慢变化类型的声速剖面，表层地声结构比较均匀单一。
海底沉积物样品NHB21取自南海2 843 m水深海底[17]，长度为0.9 m，以粉砂质黏土类型为主，粉砂含量高，声学测量主频为100 kHz。如图2所示，随着埋深深度增加，样品NHB21的孔隙度减小、声速增大，其中表层声速为1 430.0 m/s，低于底层海水实验室标准声速，但随着埋深增大，声速增长，属于低声速表面–声速增大类型，在0.9 m埋深处，海底沉积物的声速开始超过底层海水实验室标准声速。
图 2 海底沉积物样品NHB21的声速–孔隙度沿埋深分布Figure 2. Distribution of sound velocity and porosity along buried depth of seafloor sediment sample NHB21样品NHB21对应的地声结构表示成声速（cp
，单位：m/s）、密度（ρ，单位：kg/m3）、孔隙度（n，%）与海底埋深（z，单位：m）的拟合关系式分别如下： $$ c_{\rm p} =150.52{\textit z}+1\;401.00\quad { R}=0.953\;2\text{，} $$ (5) $$ \rho =38.095{\textit z}+1\;285.4\quad {R}=0.622\;3\text{，} $$ (6) $$ n =-3.988\;1{\textit z}+83.135\quad { R}=-0.932\;0\text{，} $$ (7) 式中，R为相关系数，表示两个量之间的相关特性及程度。
式（5）至式（7）建立的地声结构直接适用范围为取样海区一定水平区域的1 m埋深深度的范围，表示成声速梯度和密度梯度分别为150.52 s−1和38.095 kg/m4。如果向更深埋深推广应用以及向其他海区拓展应用，存在预报误差，需要进行修正和验证。
3.2.2 高声速表面的地声结构类型
海底沉积物样品NH54取自于南海1 600 m水深海底，长度为1.5 m，以黏土质粉砂类型为主，分成10段测量，声学测量主频为100 kHz。10段样品测量孔隙度为0.611±0.029，密度为（1.68±0.05） g/cm3，测量声速为（1 539.7±9.1） m/s。随着埋深深度增加，样品NH54的孔隙度、密度、声速变化不大，整体形成比较均匀的声速剖面。海底表层沉积物声速为1 533.0 m/s，大于底层海水实验室标准声速1 529.3 m/s，因此样品所在区域对应着高声速表面–声速缓慢变化类型，表层地声结构相对均匀单一。
海底沉积物样品NH06取自于南海北部大陆架附近，长度为2.2 m，以砂质粉砂类型为主，分成7段测量，声学测量主频为40 kHz。如图3所示，随着深度增加，样品NH06的孔隙度减小、密度增加、声速增大，形成声速逐渐增大趋势的声速剖面。表层海底沉积物声速为1 549.7 m/s，大于底层海水实验室标准声速，因此样品所在区域对应着高声速表面–声速增长类型。
图 3 海底沉积物样品NH06的声速–孔隙度沿埋深分布Figure 3. Distribution of sound velocity and porosity along buried depth of seafloor sediment sample NH06样品NH06对应的地声结构表示成声速、密度、孔隙度与海底埋深的拟合关系式为
$$ c_{\rm p} = 45.12{\textit z}+1\;546.60\quad { R}=0.682\;6\text{，} $$ (8) $$ \rho= 72.704{\textit z}+1\;799.3\quad {R}=0.652\;7\text{，} $$ (9) $$\qquad\qquad\;\; n = -4.917\;4{\textit z}+58.912\quad {R}=-0.874\;9. $$ (10) 式（5）建立的地声结构适用范围为取样海区一定水平区域的2.5 m埋深深度的范围，表示成声速梯度和密度梯度分别为45.12 s−1和72.704 kg/m4。
3.3 基于钻探测量法的地声结构建立
海底沉积物样品HB101和HB102取自于黄海[37]，样品平均水深为57.5 m，采取遥测法中的地震测量和钻探测量法取样测量相互结合。高频地震剖面表明两个站位具有明显的海底原位地声分层特征，HB101站位分为Subunit II-a、Subunit II-b和Pre-LGM 3层，HB102站位分为Subunit II-a、Subunit II-b、Subunit III-a、和Pre-LGM 4层。通过钻探取样获得约43 m长的样品HB101和约30 m长的样品HB102，在实验室开展声学和物理特性测量，测量频率为600 kHz。钻探测量和地震测量获得海底沉积物层的声速剖面具有较为一致的分层相似性，基于取样样品的实验室测量声速和物理特性表明海底地声结构既有单一状态，也因为沉积历史复杂和洋流运动而出现交错的复合状态。样品HB101和HB102在实验室标准环境状态下测量表层表面声速均小于底层海水实验室标准声速，都属于低声速表层类型。Pre-LGM作为最底层，因为历史沉积事件影响，组成成分复杂变化，与其他层相比出现砂质含量和砾含量的混合交错剧增，声速剖面相对异常复杂，在此不做讨论。
样品HB101的SubunitⅡ层沉积相对稳定，如图4A所示，在埋深38 m内整体呈现声速正增长的地声结构规律性，虽然在地震剖面上分为SubunitⅡ-a和SubunitⅡ-b两个子层。整个层都以粉砂质类型为主，孔隙度约从0.669减小到0.548，湿密度约从1.59 g/cm3增大到1.82 g/cm3，声速约从1 508 m/s增大到1 570 m/s，平均声速梯度为1.63 s−1，平均密度梯度为6.053 kg/m4，属于典型的低声速表面–声速增大类型。
样品HB102的Subunit-Ⅱ和Subunit-Ⅲ沉积相对稳定，都以粉砂质类型为主。如图4B所示，SubunitⅡ层分成SubunitⅡ-a和SubunitⅡ-b两个子层，地声结构存在明显差异，SubunitⅡ-a层在海底表层至7 m埋深内呈现声速正增长，孔隙度约从0.686%减小到0.598%，湿密度约从1.53 g/cm3增大到1.66 g/cm3，声速约从1 493 m/s增大到1 510 m/s，平均声速梯度为2.43 s−1，平均密度梯度为18.571 kg/m4，属于低声速表面–声速增大类型；SubunitⅡ-b层在埋深7～17 m内呈现声速缓慢变化，孔隙度、密度、声速分别围绕均值0.619、1.65 g/cm3、1 525 m/s波动，中间存在砂质薄层而出现声速偏大值，属于低声速表面–声速缓慢变化类型；Subunit Ⅲ-a层在埋深17～21 m内呈现声速缓慢变化，也属于低声速表面–声速缓慢变化类型，从地声模型上可以和SubunitⅡ-b划为同一层，整体属于低声速表面–声速缓慢变化类型。
3.4 地声结构的组合与地声模型
海底沉积物样品HB101和HB102的大深度钻探测量表明[37]，在沉积历史复杂的海底沉积物中，存在着交错的多层结构，无法采用单一的地声模型进行描述和代替，但基于以上4种基本地声结构进行划分和组合，可以将区域性复杂的地声模型描述出来。
对于同一类型海底沉积物，地声结构主要与埋深范围内存在的温度梯度和压力梯度作用有关，影响海底沉积物的物理特性参数进而影响到声学特性。邹大鹏等[12]基于FCMCM模型分析海底埋深的影响作用计算典型地声模型，将地声模型化为低声速层的GMI第一类地声模型（分为孔隙度不变的GMI1型和孔隙度减小的GMI2型两种子模型）和高声速层的GMII第二类地声模型（分为孔隙度不变的GMII1型和孔隙度减小的GMII2型两种子模型）共4类，解释了卢博[15]总结的南海地声模型。本文提出的4种基本地声结构与这4类典型地声模型具有对应性为：（1）GMI1型—低声速表面–声速缓慢变化类型；（2）GMI2型—低声速表面–声速增大类型；（3）GMII1型—高声速表面–声速缓慢变化类型；（4）GMII2型—高声速表面–声速增大类型。
将样品HB101和HB102采用4种基本地声结构组合表示成地声模型如图4所示，样品HB101的地声模型为GMI2型（0～30 m埋深范围内），样品HB101的地声模型为GMI1型（0～7 m埋深范围内）+GMI2型（7～21 m埋深范围内）。这种基于钻探取样在实验室测量建立地声结构组合而成的地声模型，与基于地震测量法获得的海底分层具有较好的一致对应性[37]，表明可以基于实验室测量法建立海底沉积物的基本地声结构，通过组合构建海底不同尺度的地声模型。
对于实验室测量法和原位测量法测量集中在表层，定义地声模型的埋深有限，如样品NH1534为GMI1型（0～4 m埋深范围内），样品NHB21为GMI2型（0～1 m埋深范围内），样品NH54为GMII1型（0～1.5 m埋深范围内），样品NHB21为GMII2型（0～2.2 m埋深范围内）。这种地声模型划分可以作为中高频海底探测声波传播的地声模型参考，虽然无法直接作为低频海底探测声波传播的地声模型，但可以结合低频探测得到的海底分层及声波传播走时剖面进行预报。
4. 讨论
4.1 频散对地声模型建立的影响
海底沉积物声波传播过程具有频散特性，在实验室测量法中，采用高频段（30～1 000 kHz），高于声学遥测法的中频和低频段（0.01～15 kHz），在如此宽频带范围内存在较为明显的频散性[29-31]；而声学遥测法中的地声反演属于低频段，频带窄，海底沉积物的声速频散性变化较小，较为关注声衰减与频率的关系[1-2, 5, 7]。当基于实验室测量法建立的地声结构和地声模型，被应用于实际水声测量和地声测量的低频率段时，应需考虑频散特性的影响性。当前基于Biot理论构建的一系列模型[5, 11, 30-31, 41]和基于VGS模型[2, 30, 42]在解释不同类型海底沉积物的频散特性规律方面并不一致，也无法全部有效解释声学遥测、原位测量、实验测量发现的频散性，但提供了一种基于理论模型计算预报及校正不同测量频率下的声速特性的方法。
应用Biot理论的EDFM简化模型[43]计算样品NH1534和样品NH06的频散性如图5所示，整体符合含砂量高的粗粒海底沉积物（如样品NH06）的频散性变化幅度大于黏土含量高的细粒海底沉积物（如样品NH1534）的规律性。两类样品的频散性变化转折点的差异较大，其原因根据Biot理论[44-45]理解为两种类型海底沉积物的渗透率差异性较大，引起特征频率的差异较大，从而导致频散特性的差异较大；而特征频率与海底沉积物的类型及其物理性质密切有关，直接导致转折频率前后范围内的声速变化特性差异较大，这种影响关系涉及海底沉积物的多个物理参数，将另文定量阐述其影响性和影响程度。从图5中可以得到，基于高频建立的声速剖面和地声结构在应用于低频时存在如下特性：（1）对于样品NH06，在中频应用时影响较小，仍属于高声速表面类型，但对于低频和甚低频测量借鉴应用时的影响较大，小于底层海水声速，将属于低声速表面类型，定义上有所改变，原因是海水不具有频散性、声速未变化；（2）对于样品NH1534，在整个频率区域内，因为频散特性变化很小，可以忽略频散特性对声速剖面和地声模型的影响；（3）当实际海底同时出现这两类样品分层时，基于高频建立的地声模型可以借鉴用于中频测量，但是在用于低频和甚低频测量时误差较大。即使如此，基于实验室测量法建立的高频地声模型仍能体现出声速剖面的差异，在很宽泛的频率段内可以借鉴使用。
图 5 基于EDFM模型计算海底沉积物频散特性Figure 5. Calculated dispersion characteristics of seafloor sediments based on EDFM基于高频建立的地声模型在应用于其他频率时，并不改变海底的实际地声结构特性和物理特征分层特性，只是可能会影响到地声模型的描述和定义类型；另一方面如果海底沉积物同层内沉积物物理性质差异不大、各层类型差异不大，则不同频率下的声速剖面变化差异较小，并不影响地声结构类型和地声模型的推广和借鉴。因此，基于实验室测量法建立的海底沉积物物理性质变化不大的同一沉积物层内的地声结构，可以直接作为建立实际的声速剖面和地声模型的参考，只是需要考虑频散影响特性对各层表面的声学特性描述和定义；在基本物理参数已知，或者可以借鉴参考，或者可以反演得到的前提下，借助于理论模型计算，可以预测和修正得到不同测量频率下所需要的地声结构。
4.2 环境温度和压力对建立地声模型的影响
实验室测量法脱离海底原位环境，产生温度变化和压力变化，直接引起测量声速的变化，需要校正。环境影响因素研究[38-40]表明，表层海底沉积物与孔隙海水的变化规律相似，在一定精度下可以采用声速比进行声速校正，得到原位测量环境状态的声速剖面。应用EDFM模型[40, 43]分析对比样品NH1534和NH06的温度和静水压力变化对声速的影响性，如图6所示。当缺乏声速比随环境变化的计算条件下，可以直接采用Hamilton固定声速比的校正法[46]进行声速，与基于EDFM模型的考虑声速比变化的校正速度趋势一致，有差异但较小。海底原位测量法和声学遥测法对应着海底原位环境的地声模型，而实验室测量法对应着实验室环境的地声模型，因此基于声速比校正法提供一种不同环境下建立地声模型进行相互校正的基本方法。大陆架海底表层沉积物主要受到温度的影响因素大，大陆坡受到温度影响性其次，深海基本处于常温状态，而压力影响作用随着海水深度的增加而呈现近似于线性增大。当海底沉积物样品采集到实验室，大陆架沉积物样品主要校正温度影响性，大陆坡和深海沉积物样品则需同时校正温度和压力的影响性。对于浅层海底沉积物，可以参考表层海底沉积物的校正方法进行校正；但是深层海底沉积物因为额外受到地热温度和埋深压力的影响作用，更为复杂，需开展深入研究和探索提出可借鉴的校正方法。
图 6 温度和静水压力对海底沉积物声速的影响特性Figure 6. Influence characteristics of temperature and hydrostatic pressure on sound velocity of seafloor sediments海底沉积物与底层海水的声学特性受到环境温度和压力的影响作用相似，两者声速比随着环境状态变化较小，基于实验室测量法获得的地声结构和建立的地声模型，可以作为其他方法的海底声速剖面和地声模型的应用参考，将不同环境建立的声速剖面校正到实际应用的海底原位环境下，建立海底原位地声模型。
5. 结论
地声模型因为海底沉积过程和沉积历史复杂而具有海底分层特性，同层内因为沉积环境影响因素具有温度和压力差异而存在地声梯度，还因为建立方法不同而存在频散性和环境差异性等引入的声速剖面差异等，通过研究地声模型的基本地声结构组成及其影响因素，得到如下结论：
（1）具有4种典型的基本地声结构：低声速表面–声速缓慢变化类型、低声速表面–声速增大类型、高声速表面–声速缓慢变化类型和高声速表面–声速增大类型，分别对应着单一结构的地声模型；
（2）地声模型可以归结为4种基本地声结构的组合，通过与底层海水声速、同层内声速剖面以及与上层海底沉积物下表面声速的比较，可以建立海底各种实际分层的地声模型；
（3）不同测量环境状态下的声速剖面具有差异性，基于实验室测量法建立的地声模型作为参考地声模型，通过考虑海底实际环境的温度和压力梯度，应用声速比校正法实现不同海底原位环境状态下的表层和浅层海底沉积物声速剖面的修正；
（4）不同测量频率下的声速剖面具有差异性，基于实验室测量法建立的地声模型作为参考地声模型，通过考虑频散性和基于理论计算相结合的基础上，修正得到不同测量频率下的声速剖面。
由于海底沉积物的沉积状态和特性复杂、声学测量方法具有多种性，建立高精度的海底沉积物地声模型仍需深入研究明晰全频域范围内海底沉积物的频散性、深层海底沉积物的声学和物理特性以及分层特性、全频域范围内的海底沉积物的声衰减特性、宽频率范围内海底沉积物的剪切波波速特性。
致谢：感谢中国科学院南海海洋研究所卢博研究员、自然资源部第一海洋研究所阚光明研究员和王景强副研究员对课题研究提供的支持和交流讨论。
-
图 2 海底沉积物样品NHB21的声速–孔隙度沿埋深分布
Fig. 2 Distribution of sound velocity and porosity along buried depth of seafloor sediment sample NHB21
图 3 海底沉积物样品NH06的声速–孔隙度沿埋深分布
Fig. 3 Distribution of sound velocity and porosity along buried depth of seafloor sediment sample NH06
图 5 基于EDFM模型计算海底沉积物频散特性
Fig. 5 Calculated dispersion characteristics of seafloor sediments based on EDFM
图 6 温度和静水压力对海底沉积物声速的影响特性
Fig. 6 Influence characteristics of temperature and hydrostatic pressure on sound velocity of seafloor sediments
表 1 地声模型建立方法的比较
Tab. 1 Comparison of establishment methods of geoacoustic model
建立方法 测量频率/kHz 海底埋深深度 地声参数 物理特性 遥测法 0.01～151) 通常几十米，可以至数千米 压缩波波速及其衰减系数 基于经验方程或者理论模型反演
计算获得实验室测量法 30～1 000 通常为0.5～4 m，部分
能够达到8 m压缩波波速及其衰减系数为主，部分
获得剪切波的波速及其衰减系数基于实验室测量可以获得全部所
需物理力学特性海底原位测量法 1～260 通常为0.3～3 m，部分
能够达到6～8 m压缩波波速及其衰减系数为主，部分
获得剪切波的波速及其衰减系数需要通过同站位采集样品实验室
测量获得钻探测量法 约402) 通常几十米，可以至数千米 压缩波波速和剪切波波速为主，可以
获得衰减系数随钻直接测量或者采集样品实验
室测量获得注：1)遥测法中的浅地层剖面仪、多波束测量、侧扫声呐等高频探测频率段未计入内；2)钻探取样样品的测量频率段未计入内，可参照样品采集的实验室测量法。 
下载: 导出CSV
-
[1] 李梦竹, 李整林, 李倩倩. 南海北部负跃层环境下海底参数声学反演[J]. 声学学报, 2019, 44(3): 321−328.Li Mengzhu, Li Zhenglin, Li Qianqian. Geoacoustic inversion for bottom parameters in a thermocline environment in the northern area of the South China Sea[J]. Acta Acustica, 2019, 44(3): 321−328. [2] Belcourt J, Holland C W, Dosso S E, et al. Depth-dependent geoacoustic inferences with dispersion at the New England mud patch via reflection coefficient inversion[J]. IEEE Journal of Oceanic Engineering, 2020, 45(1): 69−91. doi: 10.1109/JOE.2019.2900115 [3] 任群言, 朴胜春, 马力, 等. 利用渔船噪声矢量场对地声参数的估计[J]. 哈尔滨工程大学学报, 2018, 39(2): 236−240.Ren Qunyan, Piao Shengchun, Ma Li, et al. Geoacoustic inversion using ship noise vector field[J]. Journal of Harbin Engineering University, 2018, 39(2): 236−240. [4] 杨坤德, 马远良. 利用海底反射信号进行地声参数反演的方法[J]. 物理学报, 2009, 58(3): 1798−1805. doi: 10.3321/j.issn:1000-3290.2009.03.066Yang Kunde, Ma Yuanliang. A geoacoustic inversion method based on bottom reflection signals[J]. Acta Physica Sinica, 2009, 58(3): 1798−1805. doi: 10.3321/j.issn:1000-3290.2009.03.066 [5] Schock S G. A method for estimating the physical and acoustic properties of the sea bed using chirp sonar data[J]. IEEE Journal of Oceanic Engineering, 2004, 29(4): 1200−1217. doi: 10.1109/JOE.2004.841421 [6] 吴金荣, 马力, 郭圣明. 基于地声模型的浅海混响地声反演研究[J]. 哈尔滨工程大学学报, 2010, 51(7): 856−862. doi: 10.3969/j.issn.1006-7043.2010.07.007Wu Jinrong, Ma Li, Guo Shengming. Geoacoustic inversion of reverberation data by applying a geoacoustic model in shallow water[J]. Journal of Harbin Engineering University, 2010, 51(7): 856−862. doi: 10.3969/j.issn.1006-7043.2010.07.007 [7] 李风华, 张仁和. 由脉冲波形与传播损失反演海底声速与衰减系数[J]. 声学学报, 2000, 25(4): 297−302. doi: 10.3321/j.issn:0371-0025.2000.04.002Li Fenghua, Zhang Renhe. Bottom sound speed and attenuation inverted by using pulsed waveform and transmission loss[J]. Acta Acustica, 2000, 25(4): 297−302. doi: 10.3321/j.issn:0371-0025.2000.04.002 [8] 尚尔昌. 水声学中地声反演的新进展[J]. 应用声学, 2019, 38(4): 468−476. doi: 10.11684/j.issn.1000-310X.2019.04.001Shang Erchang. Progress of geoacoustic inversion in underwater acoustics[J]. Journal of Applied Acoustics, 2019, 38(4): 468−476. doi: 10.11684/j.issn.1000-310X.2019.04.001 [9] 周志愚, 杜继川, 赵广存, 等. 南海、黄海海底声速垂直分布的测量结果[J]. 海洋学报, 1983, 5(5): 543−552.Zhou Zhiyu, Du Jichuan, Zhao Guangcun, et al. Measurement results of vertical distribution of sound velocity on the seabed of the South China Sea and the Yellow Sea[J]. Haiyang Xuebao, 1983, 5(5): 543−552. [10] Buckingham M J. Wave speed and attenuation profiles in a stratified marine sediment: Geo-acoustic modeling of seabed layering using the viscous grain shearing theory[J]. The Journal of the Acoustical Society of America, 2020, 148(2): 962−974. doi: 10.1121/10.0001778 [11] Stoll R D, Bautista E O. Using the Biot theory to establish a baseline geoacoustic model for seafloor sediments[J]. Continental Shelf Research, 1998, 18(14/15): 1839−1857. [12] 邹大鹏, 阎贫, 卢博. 基于海底表层沉积物声速特征的南海地声模型[J]. 海洋学报, 2012, 34(3): 80−86.Zou Dapeng, Yan Pin, Lu Bo. A geoacoustic model based on sound speed characteristic of seafloor surface sediments of the South China Sea[J]. Haiyang Xuebao, 2012, 34(3): 80−86. [13] Hamilton E L. Geoacoustic modeling of the sea floor[J]. The Journal of the Acoustical Society of America, 1980, 68(5): 1313−1340. doi: 10.1121/1.385100 [14] Hamilton E L. Variations of density and porosity with depth in deep-sea sediments[J]. Journal of Sedimentary Petrology, 1976, 46(2): 280−300. [15] 卢博. 海水−沉积物声速结构模式[J]. 海洋通报, 1995, 14(2): 42−47.Lu Bo. Model of sound velocity structure in seawater-sediments[J]. Marine Science Bulletin, 1995, 14(2): 42−47. [16] P. Sanko, C. Lair. 中国南海的岩心分析和海底照片[J]. 海洋通报, 1975, 21(3): 1−59.P. Sanko, C. Lair. Core analysis and seafloor photographs of the South China Sea[J]. Marine Science Bulletin, 1975, 21(3): 1−59. [17] Wang Jingqiang, Guo Changsheng, Hou Zhengyu, et al. Distributions and vertical variation patterns of sound speed of surface sediments in South China Sea[J]. Journal of Asian Earth Sciences, 2014, 89: 46−53. doi: 10.1016/j.jseaes.2014.03.026 [18] 唐诚, 郑向阳, 李艳芳, 等. 北部湾南部重力柱状样的MSCL地声学性质测量及分析[J]. 海洋科学, 2019, 43(10): 88−95.Tang Cheng, Zheng Xiangyang, Li Yanfang, et al. Geoacoustic properties measurement and analysis of gravity cores using MSCL in the southern Beibu Gulf[J]. Marine Sciences, 2019, 43(10): 88−95. [19] 钱正明. 台湾东南外海海底沉积物物理、土力学和声学特性研究[D]. 台北: 台湾大学, 1989.Qian Zhengming. Study on physical, soil mechanics and acoustic characteristics of seafloor sediments off the southeast coast of Taiwan[D] Taipei: Taiwan University, 1989. [20] Li Guanbao, Wang Jingqiang, Liu Baohua, et al. In situ acoustic properties of fine-grained sediments on the northern continental slope of the South China Sea[J]. Ocean Engineering, 2020, 218: 108244. doi: 10.1016/j.oceaneng.2020.108244 [21] Kim G Y, Park K J, Lee G S, et al. KISAP: a new in situ seafloor velocity measurement tool[J]. Marine Georesources & Geotechnology, 2018, 36(3): 264−270. [22] Ballard M S, Lee K M, McNeese A R, et al. In situ measurements of compressional wave speed during gravity coring operations in the new England mud patch[J]. IEEE Journal of Oceanic Engineering, 2020, 45(1): 26−38. doi: 10.1109/JOE.2019.2924560 [23] Yang Jie, Jackson D R. Measurement of sound speed in fine-grained sediments during the seabed characterization experiment[J]. IEEE Journal of Oceanic Engineering, 2020, 45(1): 39−50. doi: 10.1109/JOE.2019.2946004 [24] 韦海伦, 蔡进功, 王国力, 等. 海洋沉积物有机质赋存的多样性与物源指标的多疑性综述[J]. 地球科学进展, 2018, 33(10): 1024−1033. doi: 10.11867/j.issn.1001-8166.2018.10.1024.Wei Hailun, Cai Jingong, Wang Guoli, et al. The diversity of organic matter in marine sediments and the suspiciousness of source parameters: a review[J]. Advances in Earth Science, 2018, 33(10): 1024−1033. doi: 10.11867/j.issn.1001-8166.2018.10.1024. [25] 段晓勇, 孔祥淮, 印萍, 等. 全球海洋地球化学调查进展[J]. 海洋地质前沿, 2020, 36(7): 1−10.Duan Xiaoyong, Kong Xianghuai, Yin Ping, et al. A progress review of the marine geochemical survey in the world[J]. Marine Geology Frontiers, 2020, 36(7): 1−10. [26] 赵绍华, 刘志飞. 海洋沉积物陆源碎屑粒度分析预处理方法研究[J]. 地球科学进展, 2017, 32(7): 769-780.Zhao Shaohua, Liu Zhifei. A study of pretreatment methods for terrigenous grain-size analysis of marine sediments[J]Advances in Earth Science, 2017, 32(7): 769−780. [27] 郑广赢, 黄益旺, 华健. 声波在水−含气沉积物界面的反射[J]. 声学学报, 2018, 43(6): 961−967.Zheng Guangying, Huang Yiwang, Hua Jian. Reflection of acoustic waves at a water-gassy sediment interface[J]. Acta Acustica, 2018, 43(6): 961−967. [28] 张正一, 范建柯, 白永良, 等. 中国海−西太平洋地区典型剖面的重−磁−震联合反演研究[J]. 地球物理学报, 2018, 61(7): 2871−2891.Zhang Zhengyi, Fan Jianke, Bai Yongliang, et al. Joint inversion of gravity-magnetic-seismic data of a typical profile in the China Sea-Western Pacific area[J]. Chinese Journal of Geophysics, 2018, 61(7): 2871−2891. [29] Zimmer M A, Bibee L D, Richardson M D. Measurement of the frequency dependence of the sound speed and attenuation of seafloor sands from 1 to 400 kHz[J]. IEEE Journal of Oceanic Engineering, 2010, 35(3): 538−557. doi: 10.1109/JOE.2010.2056230 [30] Yu Shengqi, Liu Baohua, Yu Kaiben, et al. Study on sound-speed dispersion in a sandy sediment at frequency ranges of 0.5−3 kHz and 90−170 kHz[J]. China Ocean Engineering, 2017, 31(1): 103−113. doi: 10.1007/s13344-017-0013-6 [31] Hefner B T, Jackson D R, Williams K L, et al. Mid- to high-frequency acoustic penetration and propagation measurements in a sandy sediment[J]. IEEE Journal of Oceanic Engineering, 2009, 34(4): 372−387. doi: 10.1109/JOE.2009.2028410 [32] 陶春辉, 王东, 金翔龙, 等. 海底沉积物声学特性和原位测试技术[M]. 北京: 海洋出版社, 2006.Tao Chunhui, Wang Dong, Jin Xianglong, et al. Marine Sediments Properties and in Situ Acoustic Measurements[M]. Beijing: China Ocean Press, 2006. [33] 侯正瑜, 郭常升, 王景强, 等. 一种新型海底沉积物声学原位测量系统的研制及应用[J]. 地球物理学报, 2015, 58(6): 1976−1984. doi: 10.6038/cjg20150613Hou Zhengyu, Guo Changsheng, Wang Jingqiang, et al. Development and application of a new type in-situ acoustic measurement system of seafloor sediments[J]. Chinese Journal of Geophysics, 2015, 58(6): 1976−1984. doi: 10.6038/cjg20150613 [34] 王景强, 李官保, 阚光明, 等. 深海海底沉积物声学特性原位测量试验研究[J]. 地球物理学报, 2020, 63(12): 4463−4472. doi: 10.6038/cjg2020N0427Wang Jingqiang, Li Guanbao, Kan Guangming, et al. Experiment study of the in situ acoustic measurement in seafloor sediments from deep sea[J]. Chinese Journal of Geophysics, 2020, 63(12): 4463−4472. doi: 10.6038/cjg2020N0427 [35] 汪鹏, 钟广法. 南海ODP1144站深海沉积牵引体的岩石物理模型研究[J]. 地球科学进展, 2012, 27(3): 359−366.Wang Peng, Zhong Guangfa. Applications of rock physics models to the deep-sea sediment drift at ODP site 1144, northern South China Sea[J]. Advances in Earth Science, 2012, 27(3): 359−366. [36] 王华, 陶果, 王兵, 等. 多极子随钻声波测井波场模拟与采集模式分析[J]. 地球物理学报, 2009, 52(9): 2402−2409. doi: 10.3969/j.issn.0001-5733.2009.09.027Wang Hua, Tao Guo, Wang Bing, et al. Wave field simulation and data acquisition scheme analysis for LWD acoustic tool[J]. Chinese Journal of Geophysics, 2009, 52(9): 2402−2409. doi: 10.3969/j.issn.0001-5733.2009.09.027 [37] Kim G Y, Narantsetseg B, Lee J Y, et al. Physical and geotechnical properties of drill core sediments in the Heuksan Mud Belt off SW Korea[J]. Quaternary International, 2018, 468: 33−48. doi: 10.1016/j.quaint.2017.06.018 [38] Zou Dapeng, Zeng Ziwen, Kan Guangming, et al. Influence of environmental conditions on the sound velocity ratio of seafloor surficial sediment[J]. Journal of Ocean University of China, 2021, 20(3): 573−580. doi: 10.1007/s11802-021-4628-0 [39] Kan Guangming, Zou Dapeng, Liu Baohua, et al. Correction for effects of temperature and pressure on sound speed in shallow seafloor sediments[J]. Marine Georesources & Geotechnology, 2019, 37(10): 1217−1226. [40] 邹大鹏, 吕衡生, 阚光明, 等. 海底表层沉积物声速的环境因素影响特性[J]. 声学学报, 2021, 46(2): 227−236.Zou Dapeng, Lü Hengsheng, Kan Guangming, et al. Environmental factors affecting acoustic velocity of seafloor surface sediments[J]. Acta Acustica, 2021, 46(2): 227−236. [41] Williams K L, Jackson D R, Thorsos E I, et al. Comparison of sound speed and attenuation measured in a sandy sediment to predictions based on the Biot theory of porous media[J]. IEEE Journal of Oceanic Engineering, 2002, 27(3): 413−428. doi: 10.1109/JOE.2002.1040928 [42] Buckingham M J, Richardson M D. On tone-burst measurements of sound speed and attenuation in sandy marine sediments[J]. IEEE Journal of Oceanic Engineering, 2002, 27(3): 429−453. doi: 10.1109/JOE.2002.1040929 [43] Williams K L. An effective density fluid model for acoustic propagation in sediments derived from Biot theory[J]. The Journal of the Acoustical Society of America, 2001, 110(5): 2276−2281. doi: 10.1121/1.1412449 [44] Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. Ⅰ. Low-frequency range[J]. The Journal of the Acoustical Society of America, 1956, 28(2): 168−178. doi: 10.1121/1.1908239 [45] Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. Ⅱ. Higher frequency range[J]. The Journal of the Acoustical Society of America, 1956, 28(2): 179−191. doi: 10.1121/1.1908241 [46] Hamilton E L. Prediction of in-situ acoustic and elastic properties of marine sediments[J]. Geophysics, 1971, 36(2): 266−284. doi: 10.1190/1.1440168 期刊类型引用(2)
1. 李跃金，邹大鹏，杨华勇，崔小明，吴磊，李赶先. 海底原位分层声学测量模拟装置的设计与实验. 广东海洋大学学报. 2024(01): 111-117 . 
百度学术2. 王浩森，张建兴，刘玉斌，郭常升，栾振东. 缆控式海底沉积物声温同步探测取样系统研发与应用. 海洋科学. 2024(08): 85-95 . 百度学术其他类型引用(2)
-
下载:
百度学术
计量
- 文章访问数: 466
- HTML全文浏览量: 146
- PDF下载量: 50
- 被引次数: 4
