Bathymetry estimation using ensemble adjustment Kalman filter in the numerical simulation of M2 constituent
-
摘要: 数据同化利用观测信息对模型状态场调整的同时也可以对数值模型中的不确定参数进行估计,从而改进数值模型,提高数值模拟的精度。本文基于集合调整卡尔曼滤波方法,采用广义坐标系统的美国普林斯顿大学海洋模式的外模式开展了渤海和部分黄海海域M2分潮模拟中的水深估计研究。理想数据同化试验结果表明,集合调整卡尔曼滤波方法能很好地降低模式模拟的水位误差并反演出“真实”的水深参数。而在NAO.99Jb和验潮站数据的实际数据同化试验中,与验潮站数据相比较,水深参数估计后,模式模拟的M2分潮振幅与迟角误差分别降低了40.27%和49.19%。Abstract: Data assimilation can estimate the uncertain parameters in the numerical model while adjusting the state variables with observations to improve the simulation results through enhancing the numerical model. Based on the ensemble adjustment Kalman filter (EAKF) and the external mode of the Princeton ocean model with generalized coordinate system (POMgcs), a bathymetry estimate is performed in the M2 constituent simulation of the Bohai Sea and part of the Yellow Sea. The results of the ideal data assimilation experiment or identical twin experiment show that the EAKF method can retrieve the “truth” bathymetry. In the practical data assimilation experiment of the NAO.99Jb and tide gauge data, by comparing with the 34 tide gauges, the model simulated amplitude and phase lag errors of M2 constituent are reduced by 40.27% and 49.19%, respectively, by use of the posterior estimate of the bathymetry.
-
Key words:
- data assimilation /
- EAKF /
- numerical simulation /
- Bohai Sea /
- Yellow Sea /
- M2 constituent /
- bathymetry estimation
-
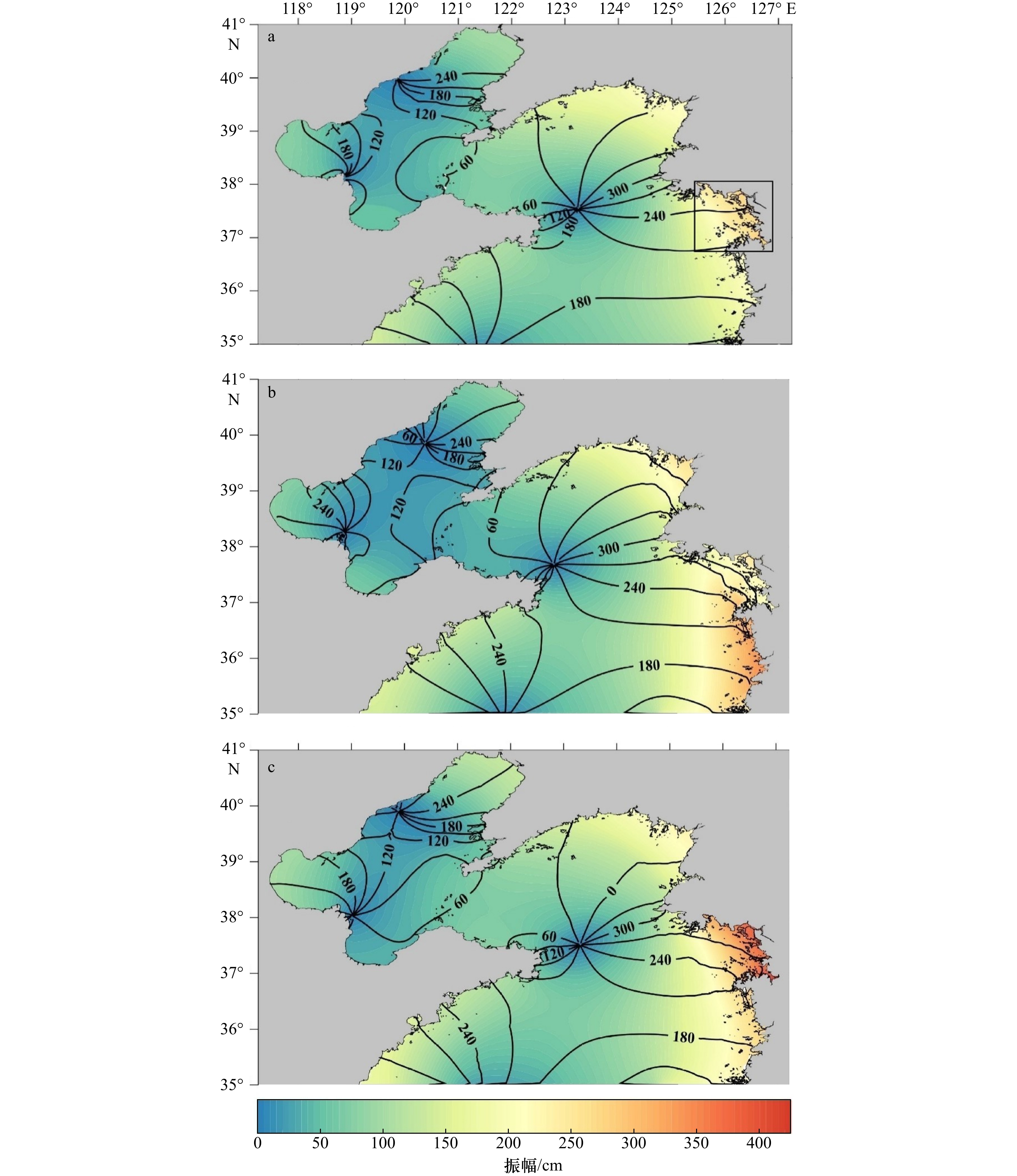
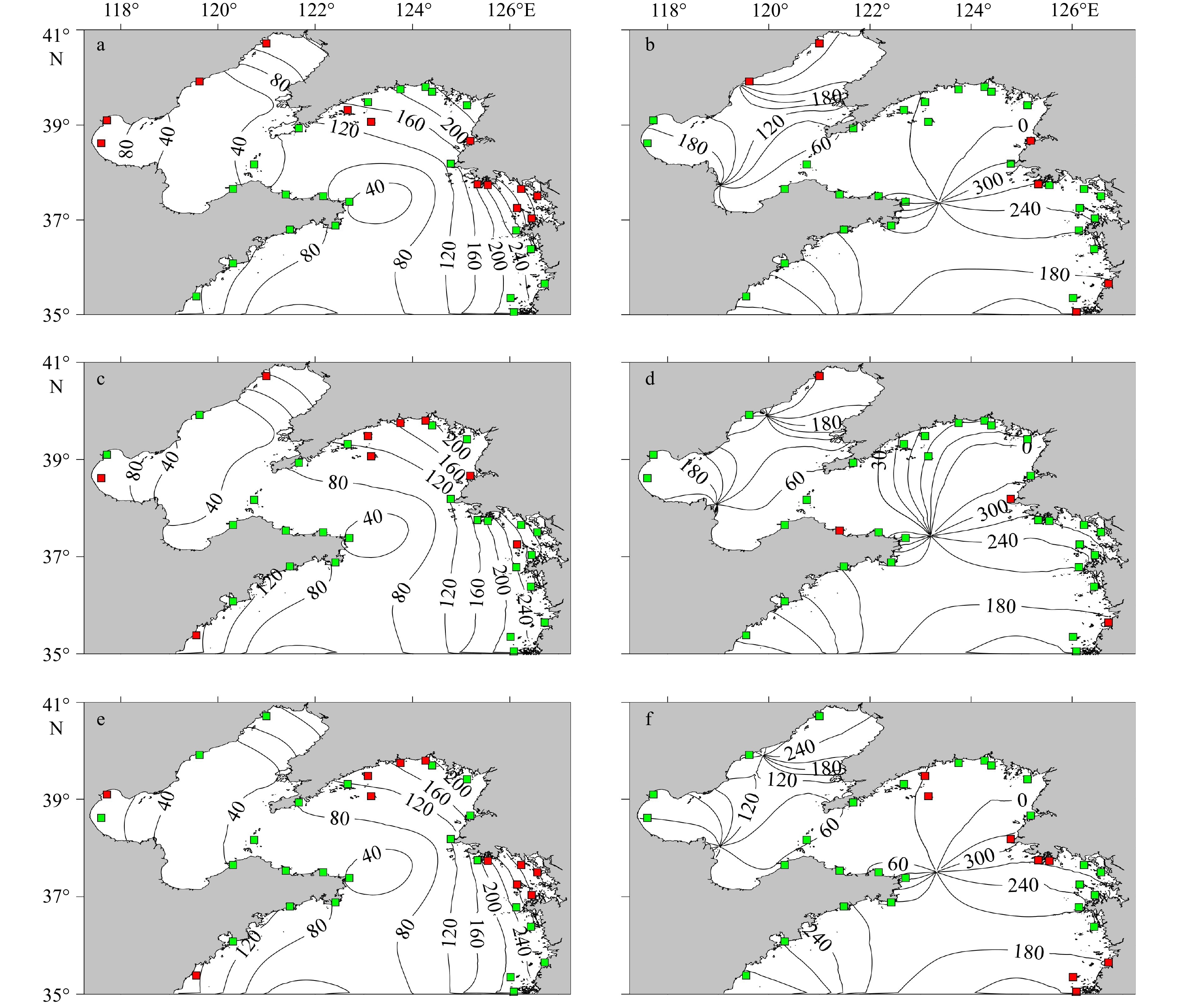
图 7 试验1(a,b)、试验2(c,d)和对比试验(e,f)的振幅(a,c,e;单位:cm)和迟角(b,d,f;单位:(°))及其在各个验潮站位置的数值相较于同化前的变化情况
绿色表示相较于同化前误差变小,而红色表示误差变大
Fig. 7 Amplitude (a, c, e; unit: cm) and phase lag (b, d, f; unit: (°)) from experiment 1 (a, b), experiment 2 (c, d) and NAO.99Jb data assimilation experiment (e, f), and change of errors at each tide gauge
Green squares represent the errors are reduced and red squares represent the errors are increased with respect the prior
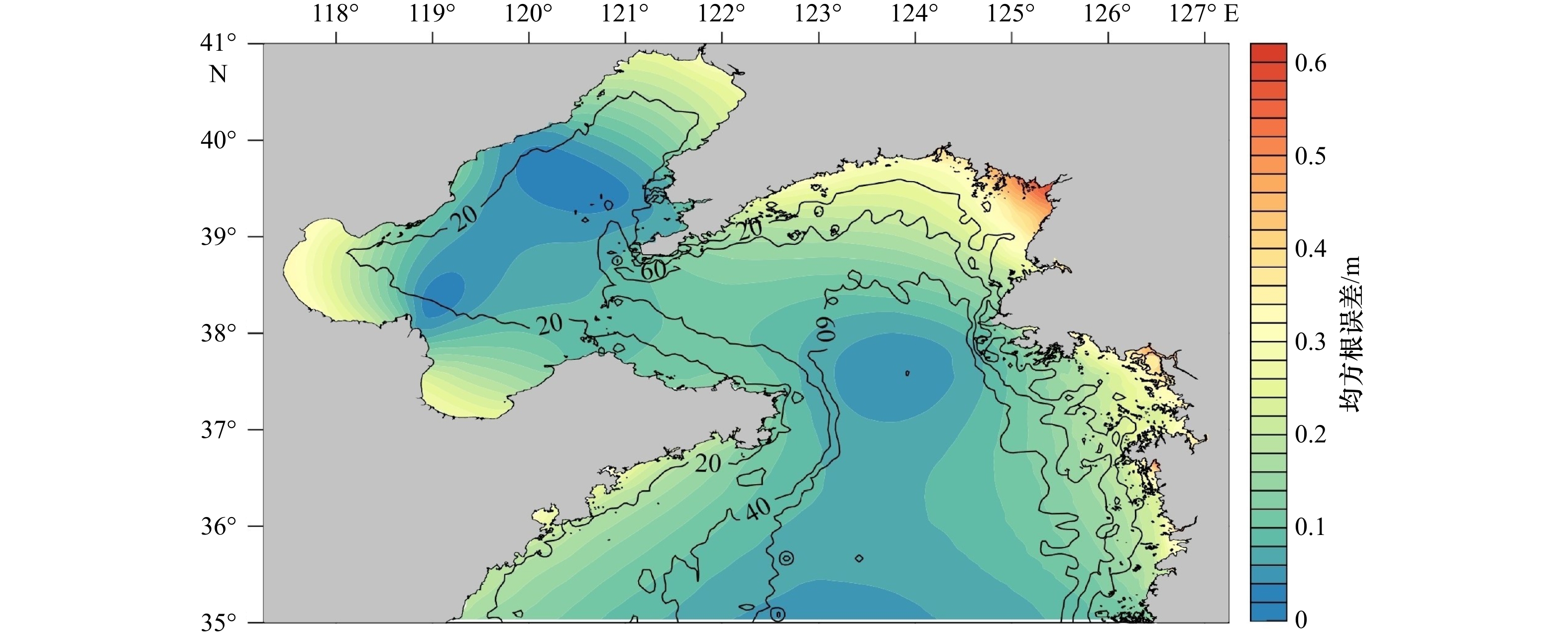
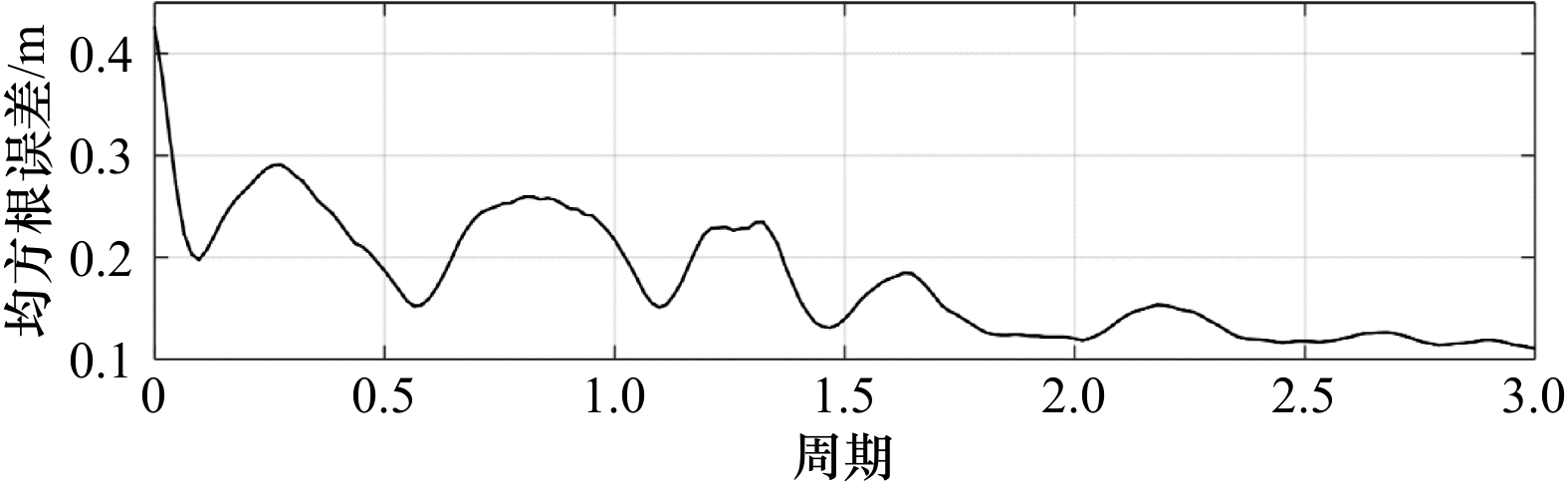
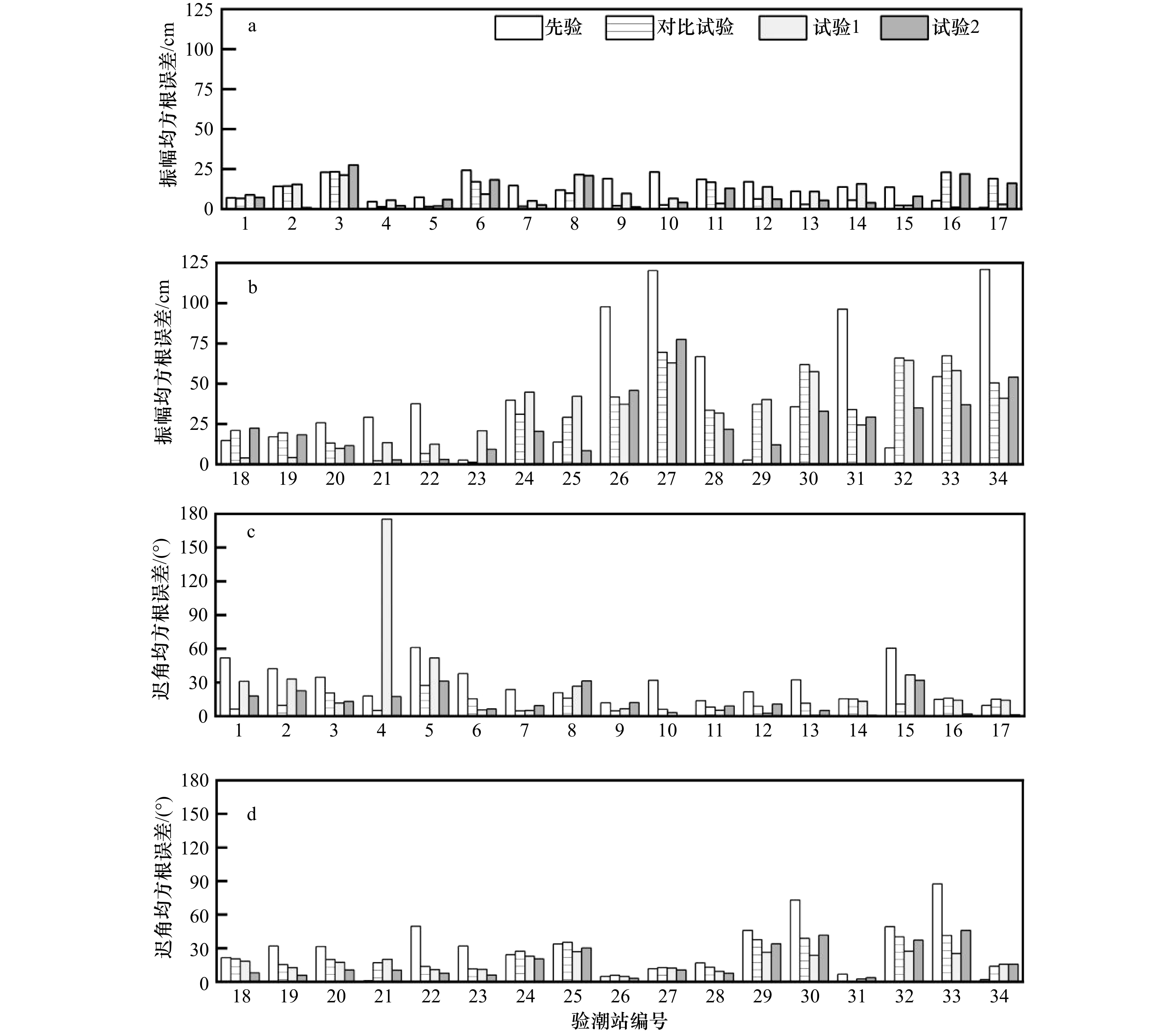
图 8 模式先验、对比试验、试验1和试验2的振幅(a, b)和迟角(c, d)在验潮站位置处的均方根误差
验潮站编号1~34与图1中对应
Fig. 8 Amplitude (a, b) and phase lag (c, d) root mean square errors of the prior, NAO.99Jb data assimilation experiment, experiment 1, and experiment 2 with respect to the tide gauges
The tidal gauge station numbers correspond to those in Fig.1
表 1 理想数据同化试验中M2分潮的先验和后验振幅与迟角空间平均误差
Tab. 1 Spatial averaged errors of amplitude and phase lag of M2 constituent from the prior and posterior in twin experiment
振幅误差/cm 迟角误差 同化前 7.6 12°54′ 同化后 0.2 18′ 表 2 NAO.99Jb实际数据同化试验中M2分潮的先验和后验振幅与迟角空间平均误差
Tab. 2 Spatial averaged errors of amplitude and phase lag of M2 constituent for the prior and posterior in the NAO.99Jb data assimilation experiment
振幅误差/cm 迟角误差 同化前 26.1 24°46′ 同化后 18.1 16°23′ 表 3 同化前、试验1、试验2和对比试验与验潮站振幅、迟角的平均空间误差
Tab. 3 Spatial averaged errors of amplitude and phase lag from the model, experiment 1, experiment 2 and NAO.99Jb data assimilation experiment with respect to those from tide gauges
振幅误差/cm 迟角误差 同化前 29.8 30°07′ 试验1 21.3 21°16′ 试验2 17.8 15°18′ 对比试验 21.8 16°56′ -
[1] Das S K, Lardner R W. Variational parameter estimation for a two-dimensional numerical tidal model[J]. International Journal for Numerical Methods in Fluids, 1992, 15(3): 313−327. doi: 10.1002/fld.1650150305 [2] Lardner R W, Al-Rabeh A H, Gunay N. Optimal estimation of parameters for a two-dimensional hydrodynamical model of the Arabian Gulf[J]. Journal of Geophysical Research: Oceans, 1993, 98(C10): 18229−18242. doi: 10.1029/93JC01411 [3] 朱江, 曾庆存, 郭冬建, 等. 利用伴随算子法从岸边潮位站资料估计近岸模式的开边界条件[J]. 中国科学(D辑: 地球科学), 1998, 41(3): 330−336.Zhu Jiang, Zeng Qingcun, Guo Dongjian, et al. Estimating open boundary conditions from coastal tidal observations by adjoint approach[J]. Science in China Series D: Earth Sciences, 1998, 41(3): 330−336. [4] 吕咸青, 张杰. 如何利用水位资料反演开边界条件(一)[J]. 水动力学研究与进展(A辑), 1999, 14(4B): 92−102.Lv Xianqing, Zhang Jie. How to invert open boundary condition from water level data (I)[J]. Chinese Journal of Hydrodynamics, 1999, 14(4B): 92−102. [5] 韩桂军, 何柏荣, 马继瑞, 等. 利用伴随法优化非线性潮汐模型的开边界条件Ⅰ: 伴随方程的建立及“孪生”数值试验[J]. 海洋学报, 2000, 22(6): 27−33.Han Guijun, He Bairong, Ma Jirui, et al. Optimizing open boundary conditions of nonlinear tidal model using adjoint method I: The establishment of adjoint model and twin-experiment[J]. Haiyang Xuebao, 2000, 22(6): 27−33. [6] 韩桂军, 方国洪, 马继瑞, 等. 利用伴随法优化非线性潮汐模型的开边界条件Ⅱ: 黄海、东海潮汐资料的同化试验[J]. 海洋学报, 2001, 23(2): 25−31.Han Guijun, Fang Guohong, Ma Jirui, et al. Optimizing open boundary conditions of nonlinear tidal model using adjoint method Ⅱ: Assimilation experiment for tide in the Huanghai Sea and the East China Sea[J]. Haiyang Xuebao, 2001, 23(2): 25−31. [7] 吕咸青, 吴自库, 殷忠斌, 等. 渤、黄、东海潮汐开边界的1种反演方法[J]. 青岛海洋大学学报, 2003, 33(2): 165−172.Lv Xianqing, Wu Ziku, Yin Zhongbin, et al. Inversion of the tides with the open boundaries of the Bohai, Huanghai and Donghai Seas[J]. Periodical of Ocean University of China, 2003, 33(2): 165−172. [8] Han Guijun, Li Wei, He Zhongjie, et al. Assimilated tidal results of tide gauge and TOPEX/POSEIDON data over the China seas using a variational adjoint approach with a nonlinear numerical model[J]. Advances in Atmospheric Sciences, 2006, 23(3): 449−460. doi: 10.1007/s00376-006-0449-8 [9] Zhang Jicai, Lu Xianqing. Parameter estimation for a three-dimensional numerical barotropic tidal model with adjoint method[J]. International Journal for Numerical Methods in Fluids, 2008, 57(1): 47−92. doi: 10.1002/fld.1620 [10] Qian Shouguo, Lv Xianqing, Sun Rencheng, et al. The estimation of open boundary conditions in the Bohai Sea with POD 4D VAR data assimilation[C]//Proceedings of 2016 International Conference on Applied Mathematics, Simulation and Modelling. Beijing: Atlantis Press, 2016: 9−11. [11] Qian Suhui, Wang Daosheng, Zhang Jicai, et al. Adjoint estimation and interpretation of spatially varying bottom friction coefficients of the M2 tide for a tidal model in the Bohai, Yellow and East China Seas with multi-mission satellite observations[J]. Ocean Modelling, 2021, 161: 101783. doi: 10.1016/j.ocemod.2021.101783 [12] Wang Daosheng, Zhang Jicai, Wang Yaping. Estimation of bottom friction coefficient in multi-constituent tidal models using the adjoint method: temporal variations and spatial distributions[J]. Journal of Geophysical Research: Oceans, 2021, 126(5): e2020JC016949. [13] Ngodock H E, Souopgui I, Wallcraft A J, et al. On improving the accuracy of the M2 barotropic tides embedded in a high-resolution global ocean circulation model[J]. Ocean Modelling, 2016, 97: 16−26. doi: 10.1016/j.ocemod.2015.10.011 [14] Wilson G, Özkan-Haller H T. Ensemble-based data assimilation for estimation of river depths[J]. Journal of Atmospheric and Oceanic Technology, 2012, 29(10): 1558−1568. doi: 10.1175/JTECH-D-12-00014.1 [15] Wilson G W, Özkan-Haller H T, Holman R A. Data assimilation and bathymetric inversion in a two-dimensional horizontal surf zone model[J]. Journal of Geophysical Research: Oceans, 2010, 115(C12): C12057. doi: 10.1029/2010JC006286 [16] Wilson G W, Özkan-Haller H T, Holman R A, et al. Surf zone bathymetry and circulation predictions via data assimilation of remote sensing observations[J]. Journal of Geophysical Research: Oceans, 2014, 119(3): 1993−2016. doi: 10.1002/2013JC009213 [17] Landon K C, Wilson G W, Özkan-Haller H T, et al. Bathymetry estimation using drifter-based velocity measurements on the Kootenai River, Idaho[J]. Journal of Atmospheric and Oceanic Technology, 2014, 31(2): 503−514. doi: 10.1175/JTECH-D-13-00123.1 [18] Moghimi S, Özkan-Haller H T, Wilson G W, et al. Data assimilation for bathymetry estimation at a tidal inlet[J]. Journal of Atmospheric and Oceanic Technology, 2016, 33(10): 2145−2163. doi: 10.1175/JTECH-D-14-00188.1 [19] An H S. A numerical experiment of the M2 tide in the Yellow Sea[J]. Journal of the Oceanographical Society of Japan, 1977, 33(2): 103−110. doi: 10.1007/BF02110016 [20] 方国洪. 黄海潮能的消耗[J]. 海洋与湖沼, 1979, 10(3): 200−213.Fang Guohong. Dissipation of tidal energy in Yellow Sea[J]. Oceanologia et Limnologia Sinica, 1979, 10(3): 200−213. [21] Matsumoto K, Takanezawa T, Ooe M. Ocean tide models developed by assimilating Topex/Poseidon altimeter data into hydrodynamical model: a global model and a regional model around Japan[J]. Journal of Oceanography, 2000, 56(5): 567−581. doi: 10.1023/A:1011157212596 [22] Egbert G D, Bennett A F, Foreman M G G. Topex/Poseidon tides estimated using a global inverse model[J]. Journal of Geophysical Research: Oceans, 1994, 99(C12): 24821−24852. doi: 10.1029/94JC01894 [23] 李大炜, 李建成, 金涛勇, 等. 利用验潮站资料评估全球海潮模型的精度[J]. 大地测量与地球动力学, 2012, 32(4): 106−110.Li Dawei, Li Jiancheng, Jin Taoyong, et al. Accuracy estimation of recent global ocean tide models using tide gauge data[J]. Journal of Geodesy and Geodynamics, 2012, 32(4): 106−110. [24] Mellor G L, Häkkinen S M, Ezer T, et al. A generalization of a sigma coordinate ocean model and an intercomparison of model vertical grids[M]//Pinardi N, Woods J. Ocean Forecasting. Berlin, Heidelberg: Springer, 2002: 55−72. [25] Anderson J L. An ensemble adjustment Kalman filter for data assimilation[J]. Monthly Weather Review, 2001, 129(12): 2884−2903. doi: 10.1175/1520-0493(2001)129<2884:AEAKFF>2.0.CO;2 [26] Gaspari G, Cohn S E. Construction of correlation functions in two and three dimensions[J]. Quarterly Journal of the Royal Meteorological Society, 1999, 125(554): 723−757. doi: 10.1002/qj.49712555417 [27] Aksoy A, Zhang Fuqing, Nielsen-Gammon J W. Ensemble-based simultaneous state and parameter estimation with MM5[J]. Geophysical Research Letters, 2006, 33(12): L12801. doi: 10.1029/2006GL026186 [28] Tong Mingjing, Xue Ming. Simultaneous estimation of microphysical parameters and atmospheric state with simulated radar data and ensemble square root Kalman filter. Part II: parameter estimation experiments[J]. Monthly Weather Review, 2008, 136(5): 1649−1668. doi: 10.1175/2007MWR2071.1 [29] Zhang Shaoqing, Liu Zhengyu, Rosati A, et al. A study of enhancive parameter correction with coupled data assimilation for climate estimation and prediction using a simple coupled model[J]. Tellus A: Dynamic Meteorology and Oceanography, 2012, 64(1): 10963. doi: 10.3402/tellusa.v64i0.10963 [30] Zhang Shaoqing, Anderson J L, Rosati A, et al. Multiple time level adjustment for data assimilation[J]. Tellus A, 2004, 56(1): 2−15. doi: 10.3402/tellusa.v56i1.14390 -





 下载:
下载: