Seawater intrusion characterization and dynamics prediction based on WA-NARX hybrid model in the south of Laizhou Bay
-
摘要: 随着我国海岸带经济的快速发展与人类活动的加剧，地下水超采现象十分严峻，由此引发的海水入侵已成为滨海地区普遍存在的地质问题。本研究以莱州湾南岸海水入侵区为研究对象，根据地下水连续监测数据分析了地下水位和电导率的动态变化特征。在此基础上，基于降雨、蒸发、潮汐及农业排灌用电量等影响地下水动态变化的因素，建立了小波分析（WA）与具有外部输入的非线性自回归神经网络（NARX）的混合模型，对地下水水位和电导率进行动态预测，并采用均方根误差和拟合度对预测结果进行评价。研究结果表明，莱州湾南岸地下水年内动态变化特征为降雨入渗–开采型，地下水位和潮汐之间在0.5 d频率上呈现较高相关性，潮汐对地下水电导率的影响要弱于对地下水位的影响；WA-NARX混合模型在训练和测试阶段的均方根误差均小于0.03且拟合度大于0.98，可有效预测研究区海水入侵的变化程度。同时，为验证模型适用性，对比了不同影响因素作为模型输入参数对预测结果的影响。结果表明，降雨和潮汐参数是影响海岸带地下水位和电导率的主要变量，蒸发以及农业排灌用电量反映的部分抽水信息对地下水位和电导率也有影响，其影响程度与观测频率相关。本文研究结果可为海岸带海水入侵的实时监测、预测、预警提供理论与技术支撑。Abstract: With the rapid economic development and increasing anthropogenic activities, the groundwater in the coastal area has been excessively exploited. The resulting seawater intrusion has become a widely distributed environmental geological problem. Taken the coastal area of Laizhou Bay as a research area, the dynamics of groundwater level (GWL) and electrical conductivity (EC) were analyzed with the continuous monitoring data. Based on the rainfall, evaporation, tide and agricultural irrigation and drainage electricity consumption that affect the groundwater variation, the hybrid model of wavelet analysis (WA) and NARX neural network was introduced to predict the dynamics of GWL and EC. The root mean square error (RMSE) and goodness of fit (R2) were used to measure the prediction accuracy. The results showed that the annual variation of GWL was characterized by a type of rainfall infiltration-exploitation. A significant correlation at the frequency of 0.5 d was observed between groundwater level and tide, and the influence of tide on EC was weaker than that on GWL. For the dynamics prediction with WA-NARX method, the RMSE was less than 0.03 and R2 was greater than 0.98 in both the training and testing stages. The results indicated the hybrid model had a good performance and could effectively predict the dynamics of GWL and EC. The effects of different influencing factors as model input parameters on the prediction results were further compared. The results showed that rainfall and tide parameters were the main variables affecting the GWL and EC variations in the coastal zone. The pumping information reflected by the evaporation and agricultural drainage and irrigation power consumption also affected the groundwater dynamics. The degree of influence was related to the observation frequency. The research results can provide theoretical and technical support for real-time monitoring, prediction and early warning of seawater intrusion in coastal zone.
-
Key words:
- seawater intrusion /
- groundwater level /
- electrical conductivity /
- wavelet analysis /
- NARX neural network /
- prediction
-
图 2 各影响因素时间序列
a. 降雨量；b. 潮汐；c. 蒸发量；d. 农业排灌用电量
Fig. 2 Time series of influencing factors
a. Precipitation; b. tide; c. evaporation; d. electricity consumption of agricultural irrigation and drainage
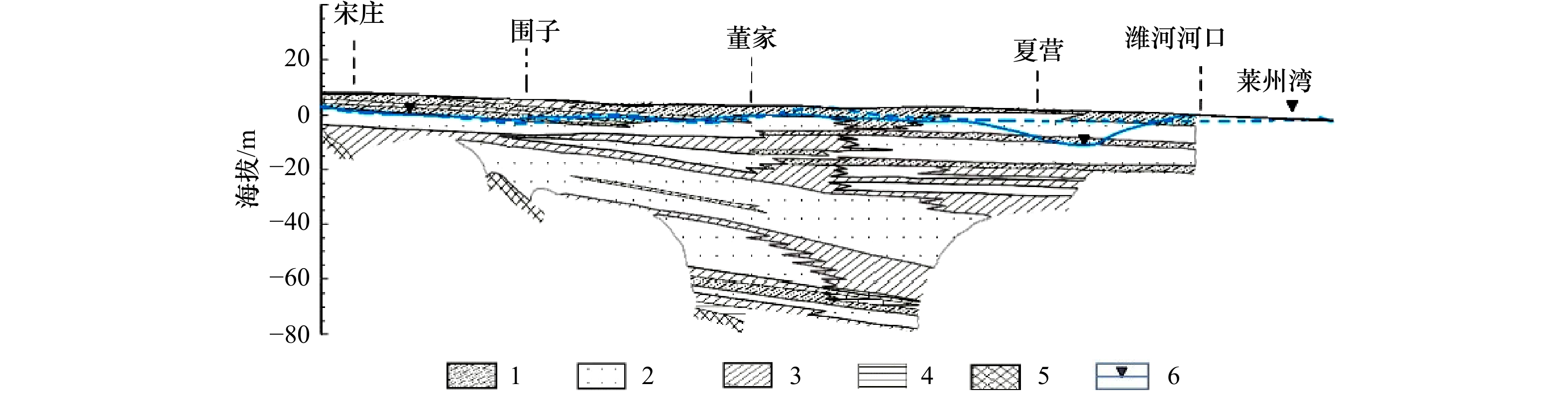
图 3 研究区剖面图（修改自文献[26]）
1. 粉质黏土；2. 中砂及砾石；3. 黏土；4. 砂质黏土；5. 基岩；6 、1992年（虚线）和2013年（实线）地下水等势面
Fig. 3 Hydrogeology of the cross section from south to north in the study area (modified from reference [26])
1. Clay sand; 2. medium sand and gravel; 3. clay; 4. sandy clay; 5. bedrock; 6. groundwater level surface in 1992 (dash line) and 2013 (solid line)
图 4 WA-NARX模型建模流程
g(n)为低通滤波器；h(n)为高通滤波器；Ci为近似分量；Wi为细节分量
Fig. 4 Flow chart of WA-NARX neural network hybrid model
g(n) is low-pass filters; h(n) is high-pass filters; Ci is low-frequency approximations; Wi is high-frequency details
图 6 监测井2011–2012年间地下水位变化曲线
Fig. 6 Groundwater level variation in monitoring wells from 2011 to 2012
图 7 监测井BH4水位与电导率变化
Fig. 7 Groundwater level and electrical conductivity variation in BH4 monitoring well
图 8 小波相干性分析
a, b. 地下水位与潮汐的相干性；c, d. 地下水电导率与潮汐的相干性
Fig. 8 Wavelet coherence analysis
a, b. Wavelet coherence between groundwater levels and tidal; c, d. wavelet coherence between electrical conductivity values and tidal
图 9 WA-NARX模型地下水位预测与观测对比
Fig. 9 Comparison of groundwater level prediction based on WA-NARX and observation
图 10 WA-NARX模型电导率预测的性能图
Fig. 10 Performance of WA-NARX model for electrical conductivity prediction
图 11 新增蒸发参数的预测和实测地下水位散点图
Fig. 11 Scatter diagrams of predicted and observed groundwater level with newly added evaporation parameters
图 12 新增用电量参数的预测和实测地下水位散点图
Fig. 12 Scatter diagrams of predicted and observed groundwater level with newly added power consumption parameters
图 13 新增蒸发参数的预测和实测电导率曲线图
Fig. 13 Curve diagrams of predicted and observed electrical conductivity with newly added evaporation parameters
图 14 新增用电量参数的预测和实测电导率曲线图
Fig. 14 Curve diagrams of predicted and observed electrical conductivity with newly added power consumption parameters
表 1 监测井地下水位统计特征分析（单位：m）
Tab. 1 Analysis on statistical characteristics of groundwater level in monitoring wells (unit: m)
监测井 最大值 最小值 平均值 标准差 BH1 1.451 –0.854 0.270 0.422 BH2 2.681 –0.230 1.504 0.633 BH3 4.092 –0.266 2.865 0.516 BH4 6.378 3.230 5.033 0.689 BH5 4.014 2.124 3.259 0.403 BH6 4.371 3.196 3.750 0.246 
下载: 导出CSV
表 2 监测井电导率统计特征分析（单位：mS/cm）
Tab. 2 Analysis on statistical characteristics of electrical conductivity in monitoring wells (unit: mS/cm)
监测井 最大值 最小值 平均值 标准差 标准离散率 BH1 2.08 0.63 1.22 0.505 41.39% BH2 1.69 1.53 1.65 0.021 1.27% BH3 1.62 1.01 1.20 0.121 10.08% BH4 13.17 2.39 4.70 2.252 47.91% BH5 16.95 3.68 8.95 3.196 35.71% BH6 15.32 4.12 6.61 3.143 47.55%
下载: 导出CSV
表 3 地下水位预测时WA-NARX模型的均方根误差（RMSE）和拟合度（R2）统计表
Tab. 3 The WA-NARX model performance metrics of RMSE and R2 for groundwater level prediction
监测井 训练数据 测试数据 RMSE R2 RMSE R2 BH1 0.004 1 0.999 9 0.003 9 0.999 8 BH2 0.004 2 1.000 0 0.004 3 0.999 9 BH3 0.028 1 0.997 1 0.014 7 0.998 3 BH4 0.004 9 0.999 9 0.005 4 0.999 9 BH5 0.003 0 0.999 9 0.006 0 0.999 6 BH6 0.003 4 0.999 8 0.003 9 0.998 7
下载: 导出CSV
表 4 电导率预测时WA-NARX模型的均方根误差（RMSE）和拟合度（
$ {{R}}^{2} $ ）统计Tab. 4 The WA-NARX model performance metrics of RMSE and R2 for electrical conductivity prediction
监测井 训练数据 测试数据 RMSE R2 RMSE R2 BH1 0.001 3 1.000 0 0.001 5 0.999 4 BH2 0.000 78 0.998 5 0.000 89 0.989 7 BH3 0.005 1 0.998 4 0.005 0 0.993 6 BH4 0.007 4 1.000 0 0.005 3 0.999 5 BH5 0.003 9 1.000 0 0.002 6 0.990 5 BH6 0.008 5 1.000 0 0.004 4 0.997 8
下载: 导出CSV
表 5 新增蒸发参数的地下水位预测误差及网络性能统计表
Tab. 5 The prediction error of groundwater level and network performance with newly added evaporation parameters
监测井 输入降雨、潮汐参数 输入降雨、潮汐、蒸发参数 网络性能 RMSE R2 网络性能 RMSE R2 BH1 1.619 3×10–5 0.004 0 0.957 1 1.526 1×10–5 0.004 4 0.948 4 BH2 2.569 7×10–5 0.005 1 0.961 9 3.006 6×10–5 0.005 5 0.955 4 BH3 8.991 8×10–5 0.009 5 0.935 7 7.640 4×10–5 0.008 7 0.945 4 BH4 2.476 8×10–5 0.009 8 0.880 7 9.752 6×10–5 0.009 9 0.878 5 BH5 2.381 2×10–4 0.015 4 0.643 7 5.149 2×10–4 0.022 7 0.229 5 BH6 1.392 0×10–5 0.003 7 0.983 9 1.249 7×10–5 0.003 5 0.985 5
下载: 导出CSV
表 6 新增用电量参数的地下水位预测误差及网络性能统计
Tab. 6 The prediction error of groundwater level and network performance with newly added power consumption parameters
监测井 输入降雨、潮汐参数 输入降雨、潮汐、用电量参数 网络性能 RMSE R2 网络性能 RMSE R2 BH1 1.619 3×10–5 0.004 0 0.957 1 2.216 3×10–5 0.004 7 0.941 3 BH2 2.569 7×10–5 0.005 1 0.961 9 7.072 1×10–5 0.008 4 0.895 0 BH3 8.991 8×10–5 0.009 5 0.935 7 2.027 0×10–4 0.014 2 0.855 1 BH4 2.476 8×10–5 0.009 8 0.880 7 2.743 9×10–4 0.016 6 0.658 0 BH5 2.381 2×10–4 0.015 4 0.643 7 1.064 5×10–4 0.010 3 0.840 7 BH6 1.392 0×10–5 0.003 7 0.983 9 1.236 6×10–5 0.003 5 0.985 7
下载: 导出CSV
表 7 不同输入参数电导率预测误差及网络性能评价统计
Tab. 7 The prediction error of electrical conductivity and network performance with different input parameters
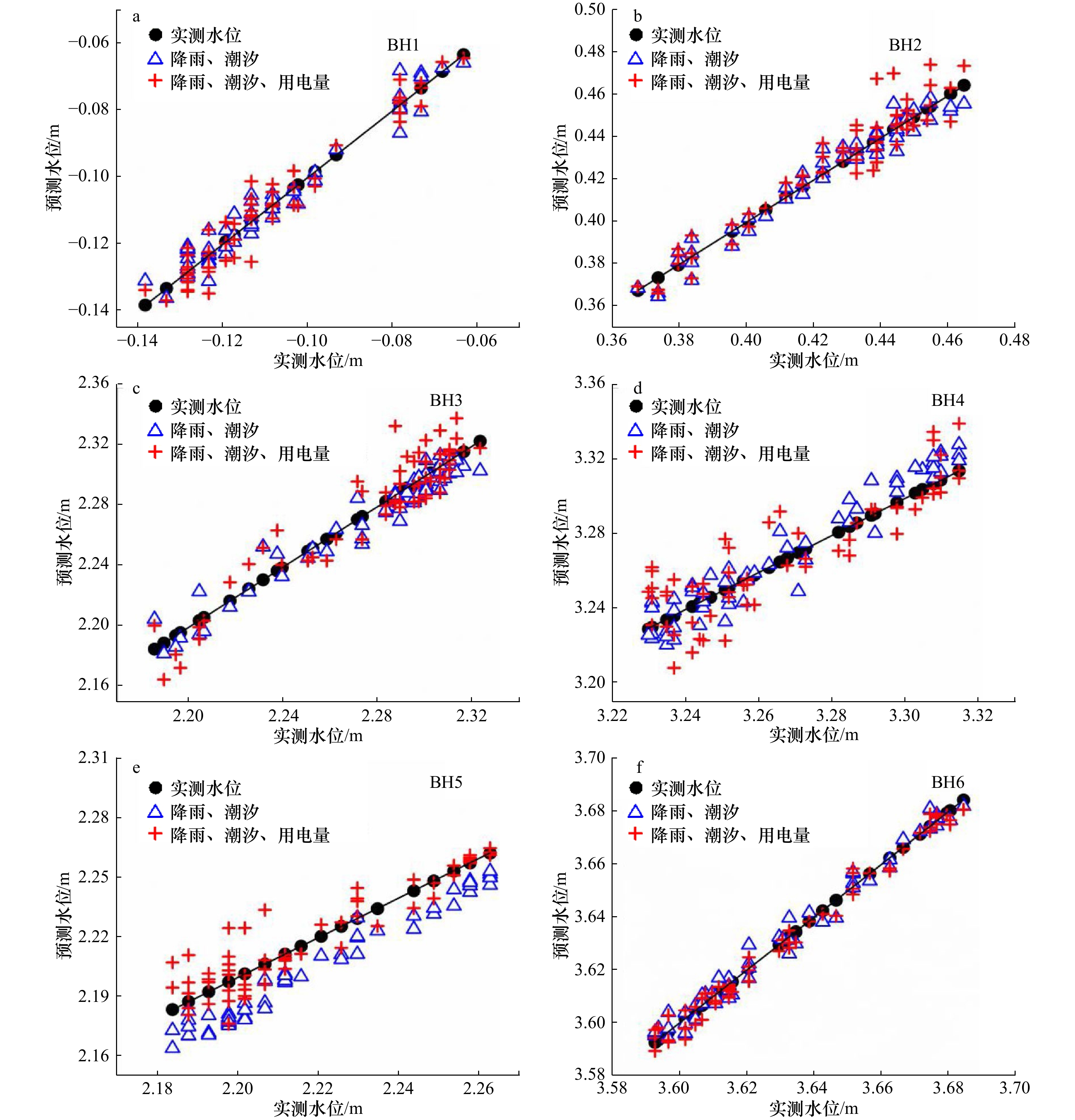
监测井 输入降雨、潮汐参数 输入降雨、潮汐、蒸发参数 输入降雨、潮汐、用电量参数 网络性能 RMSE 网络性能 RMSE 网络性能 RMSE BH1 2.005 4×10–5 0.004 5 7.984 9×10–6 0.002 8 1.383 1×10–5 0.003 7 BH2 1.086 4×10–7 0.000 33 1.086 0×10–7 0.000 30 4.927 2×10–8 0.000 31 BH3 1.409 1×10–6 0.001 2 4.998 2×10–7 0.000 71 1.637 8×10–6 0.001 3 BH4 1.072 6×10–5 0.003 3 1.946 0×10–5 0.004 4 1.368 7×10–5 0.003 7 BH5 1.100 0×10–3 0.033 9 3.371 9×10–4 0.005 8 5.466 2×10–4 0.023 4 BH6 1.136 3×10–5 0.003 4 1.161 5×10–5 0.003 4 1.007 5×10–5 0.003 2
下载: 导出CSV
-
[1] 吴吉春, 吴永祥, 林锦, 等. 黄渤海沿海地区地下水管理与海水入侵防治研究[J]. 中国环境管理, 2018, 10(2): 91−92. doi: 10.3969/j.issn.1674-6252.2018.02.017Wu Jichun, Wu Yongxiang, Lin Jin, et al. Study on the groundwater management and seawater intrusion prevention in the coastal areas of the Bohai Sea and the Yellow Sea[J]. Chinese Journal of Environmental Management, 2018, 10(2): 91−92. doi: 10.3969/j.issn.1674-6252.2018.02.017 [2] 高茂生, 骆永明. 我国重点海岸带地下水资源问题与海水入侵防控[J]. 中国科学院院刊, 2016, 31(10): 1197−1203.Gao Maosheng, Luo Yongming. Change of groundwater resource and prevention and control of seawater intrusion in coastal zone[J]. Bulletin of Chinese Academy of Sciences, 2016, 31(10): 1197−1203. [3] Zhang Xiaoying, Qi Linlin, Li Wenming, et al. Bacterial community variations with salinity in the saltwater-intruded estuarine aquifer[J]. Science of the Total Environment, 2021, 755: 142423. doi: 10.1016/j.scitotenv.2020.142423 [4] Zhang Xiaoying, Hu B X, Wang Peng, et al. Hydrogeochemical evolution and heavy metal contamination in groundwater of a reclaimed land on Zhoushan Island[J]. Water, 2018, 10(3): 316: 1−22. doi: 10.3390/w10030316 [5] 孙娜, 周建中, 朱双, 等. 基于小波分析的两种神经网络耦合模型在月径流预测中的应用[J]. 水电能源科学, 2018, 36(4): 14−17, 32.Sun Na, Zhou Jianzhong, Zhu Shuang, et al. Application of hybrid models based on wavelet analysis and two different neural networks in prediction of monthly runoff[J]. Water Resources and Power, 2018, 36(4): 14−17, 32. [6] Shoaib M, Shamseldin A Y, Melville B W, et al. A comparison between wavelet based static and dynamic neural network approaches for runoff prediction[J]. Journal of Hydrology, 2016, 535: 211−225. doi: 10.1016/j.jhydrol.2016.01.076 [7] Guzman S M, Paz J O, Tagert M L M. The use of NARX neural networks to forecast daily groundwater levels[J]. Water Resources Management, 2017, 31(5): 1591−1603. doi: 10.1007/s11269-017-1598-5 [8] Wunsch A, Liesch T, Broda S. Forecasting groundwater levels using nonlinear autoregressive networks with exogenous input (NARX)[J]. Journal of Hydrology, 2018, 567: 743−758. doi: 10.1016/j.jhydrol.2018.01.045 [9] Di Nunno F, Granata F. Groundwater level prediction in Apulia region (Southern Italy) using NARX neural network[J]. Environmental Research, 2020, 190: 110062. doi: 10.1016/j.envres.2020.110062 [10] Cannas B, Fanni A, See L, et al. Data preprocessing for river flow forecasting using neural networks: wavelet transforms and data partitioning[J]. Physics and Chemistry of the Earth, Parts A/B/C, 2006, 31(18): 1164−1171. doi: 10.1016/j.pce.2006.03.020 [11] Zhang Juan, Qiu Han, Li Xiaoyu, et al. Real-time nowcasting of microbiological water quality at recreational beaches: a wavelet and artificial neural network-based hybrid modeling approach[J]. Environmental Science & Technology, 2018, 52(15): 8446−8455. [12] Nason G P, Von Sachs R. Wavelets in time-series analysis[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical, and Engineering Sciences, 1999, 357(1760): 2511−2526. doi: 10.1098/rsta.1999.0445 [13] Moosavi V, Vafakhah M, Shirmohammadi B, et al. A Wavelet-ANFIS hybrid model for groundwater level forecasting for different prediction periods[J]. Water Resources Management, 2013, 27(5): 1301−1321. doi: 10.1007/s11269-012-0239-2 [14] Zhang Xiaoying, Dong Fan, Dai Heng, et al. Influence of lunar semidiurnal tides on groundwater dynamics in estuarine aquifers[J]. Hydrogeology Journal, 2020, 28(4): 1419−1429. doi: 10.1007/s10040-020-02136-8 [15] Kisi O, Shiri J. Precipitation forecasting using wavelet-genetic programming and wavelet-neuro-fuzzy conjunction models[J]. Water Resources Management, 2011, 25(13): 3135−3152. doi: 10.1007/s11269-011-9849-3 [16] Mohanty S, Jha M K, Raul S K, et al. Using artificial neural network approach for simultaneous forecasting of weekly groundwater levels at multiple sites[J]. Water Resources Management, 2015, 29(15): 5521−5532. doi: 10.1007/s11269-015-1132-6 [17] Nourani V, Alami M T, Vousoughi F D, et al. Wavelet-entropy data pre-processing approach for ANN-based groundwater level modeling[J]. Journal of Hydrology, 2015, 524: 255−269. doi: 10.1016/j.jhydrol.2015.02.048 [18] Adamowski J, Chan H F. A wavelet neural network conjunction model for groundwater level forecasting[J]. Journal of Hydrology, 2011, 407(1/4): 28−40. [19] Gorgij A D, Kisi O, Moghaddam A A. Groundwater budget forecasting, using hybrid wavelet-ANN-GP modelling: a case study of Azarshahr Plain, East Azerbaijan, Iran[J]. Hydrology Research, 2017, 48(2): 455−467. doi: 10.2166/nh.2016.202 [20] 张建锋, 刘见宝, 崔树军, 等. 小波–神经网络混合模型预测地下水水位[J]. 长江科学院院报, 2016, 33(8): 18−21. doi: 10.11988/ckyyb.20150474Zhang Jianfeng, Liu Jianbao, Cui Shujun, et al. A wavelet-ANN hybrid model for groundwater level forecasting[J]. Journal of Yangtze River Scientific Research Institute, 2016, 33(8): 18−21. doi: 10.11988/ckyyb.20150474 [21] Seo Y, Kim S, Kisi O, et al. Daily water level forecasting using wavelet decomposition and artificial intelligence techniques[J]. Journal of Hydrology, 2015, 520: 224−243. doi: 10.1016/j.jhydrol.2014.11.050 [22] Zhang Juan, Zhang Xiaoying, Niu Jie, et al. Prediction of groundwater level in seashore reclaimed land using wavelet and artificial neural network-based hybrid model[J]. Journal of Hydrology, 2019, 577: 123948. doi: 10.1016/j.jhydrol.2019.123948 [23] 陈广泉. 莱州湾地区海水入侵的影响机制及预警评价研究[D]. 上海: 华东师范大学, 2013.Chen Guangquan. Mechanisms underlying of seawater intrusion and evaluation of early warning systems in the Laizhou Bay area[D]. Shanghai: East China Normal University, 2013. [24] Chen Guangquan, Xiong Guiyao, Lin Jin, et al. Elucidating the pollution sources and groundwater evolution in typical seawater intrusion areas using hydrochemical and environmental stable isotope technique: a case study for Shandong Province, China[J]. Lithosphere, 2021, 2021(S3): 4227303. [25] 苗晋杰. 莱州湾南岸海(咸)水入侵动态监测及演化研究[D]. 北京: 中国地质大学(北京), 2014.Miao Jinjie. Dynamic monitoring and evolution study of saline intrusion at south coast of LaiZhou Bay[D]. Beijing: China University of Geosciences (Beijing), 2014. [26] Zhang Xiaoying, Miao Jinjie, Hu B X, et al. Hydrogeochemical characterization and groundwater quality assessment in intruded coastal brine aquifers (Laizhou Bay, China)[J]. Environmental Science and Pollution Research, 2017, 24(26): 21073−21090. doi: 10.1007/s11356-017-9641-x [27] Gedalof Z, Smith D J. Interdecadal climate variability and regime-scale shifts in Pacific North America[J]. Geophysical Research Letters, 2001, 28(8): 1515−1518. doi: 10.1029/2000GL011779 [28] Grinsted A, Moore J C, Jevrejeva S. Application of the cross wavelet transform and wavelet coherence to geophysical time series[J]. Nonlinear Processes in Geophysics, 2004, 11(5/6): 561−566. doi: 10.5194/npg-11-561-2004 [29] Mallat S G. A theory for multiresolution signal decomposition: the wavelet representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(7): 674−693. doi: 10.1109/34.192463 [30] Shensa M J. The discrete wavelet transform: wedding the a trous and Mallat algorithms[J]. IEEE Transactions on Signal Processing, 1992, 40(10): 2464−2482. doi: 10.1109/78.157290 [31] Elman J L. Finding structure in time[J]. Cognitive Science, 1990, 14(2): 179−211. doi: 10.1207/s15516709cog1402_1 [32] Lin T, Horne B G, Tino P, et al. Learning long-term dependencies in NARX recurrent neural networks[J]. IEEE Transactions on Neural Networks, 1996, 7(6): 1329−1338. doi: 10.1109/72.548162 [33] Chatterjee S, Nigam S, Singh J B, et al. Software fault prediction using Nonlinear Autoregressive with eXogenous Inputs (NARX) network[J]. Applied Intelligence, 2012, 37(1): 121−129. doi: 10.1007/s10489-011-0316-x [34] 柴琳娜, 屈永华, 张立新, 等. 基于自回归神经网络的时间序列叶面积指数估算[J]. 地球科学进展, 2009, 24(7): 756−768. doi: 10.3321/j.issn:1001-8166.2009.07.009Chai Linna, Qu Yonghua, Zhang Lixin, et al. Estimating time series leaf area index based on recurrent neural networks[J]. Advances in Earth Science, 2009, 24(7): 756−768. doi: 10.3321/j.issn:1001-8166.2009.07.009 [35] Adamowski J, Sun K R. Development of a coupled wavelet transform and neural network method for flow forecasting of non-perennial rivers in semi-arid watersheds[J]. Journal of Hydrology, 2010, 390(1/2): 85−91. [36] Tiwari M K, Chatterjee C. Development of an accurate and reliable hourly flood forecasting model using wavelet-bootstrap-ANN (WBANN) hybrid approach[J]. Journal of Hydrology, 2010, 394(3/4): 458−470. [37] 苗青. 降雨与潮汐作用对莱州湾地区海水入侵的影响机制研究[D]. 青岛: 国家海洋局第一海洋研究所, 2013.Miao Qing. Effects of precipitation and tide on seawater intrusion in the Laizhou Bay[D]. Qingdao: The First Institute of Oceanography, State Oceanic Administration, 2013. [38] 李志威, 张晓影, 张明珠, 等. 海水入侵指标对比分析与评价——以珠江口地下水含水层为例[J]. 海洋环境科学, 2020, 39(1): 16−24. doi: 10.12111/j.mes20200103Li Zhiwei, Zhang Xiaoying, Zhang Mingzhu, et al. Comparison of indicators for the assessment of saltwater intrusion in coastal aquifers—taking aquifers in Pearl River Estuary as an example[J]. Marine Environmental Science, 2020, 39(1): 16−24. doi: 10.12111/j.mes20200103 [39] 王玉广, 王传珺, 刘志华, 等. 地下水位和海平面变化对绥中砂质海岸海水入侵影响[J]. 海洋环境科学, 2019, 38(3): 347−352. doi: 10.12111/j.mes20190305Wang Yuguang, Wang Chuanjun, Liu Zhihua, et al. Impact to the the seawater intrusion around sand coast in Suizhong with the variations of groundwater level and sea level[J]. Marine Environmental Science, 2019, 38(3): 347−352. doi: 10.12111/j.mes20190305 [40] 覃光雄, 胡晓农, 张晓影, 等. 珠江河口区地下水盐分空间变异特征分析[J]. 海洋环境科学, 2018, 37(6): 835−842. doi: 10.12111/j.cnki.mes20180606Qin Guangxiong, Hu Xiaonong, Zhang Xiaoying, et al. Characterization of groundwater salinity spatial variation in the Pearl River estuary[J]. Marine Environmental Science, 2018, 37(6): 835−842. doi: 10.12111/j.cnki.mes20180606 [41] 刘启和. 辽阳市地下水电导率特性研究[J]. 水利技术监督, 2017, 25(3): 60−62, 91. doi: 10.3969/j.issn.1008-1305.2017.03.021Liu Qihe. Study on conductivity characteristics of groundwater in Liaoyang City[J]. Technical Supervision in Water Resources, 2017, 25(3): 60−62, 91. doi: 10.3969/j.issn.1008-1305.2017.03.021 [42] 章斌, 宋献方, 韩冬梅, 等. 运用数理统计和模糊数学评价秦皇岛洋戴河平原的海水入侵程度[J]. 地理科学, 2013, 33(3): 342−348.Zhang Bin, Song Xianfang, Han Dongmei, et al. Seawater intrusion degree evaluation based on mathematical statistics and fuzzy mathematics in Qinhuangdao Yangdai River plain[J]. Scientia Geographica Sinica, 2013, 33(3): 342−348. [43] 赵世彬, 陈广泉, 张晓影, 等. 潮汐影响下的海岸带地下河口水交换及其生物地球化学效应[J]. 海洋地质前沿, 2018, 34(9): 73−78.Zhao Shibin, Chen Guangquan, Zhang Xiaoying, et al. Water exchange and biogeochemical effects of subterranean estuary with tide[J]. Marine Geology Frontiers, 2018, 34(9): 73−78. -
计量
- 文章访问数: 349
- HTML全文浏览量: 113
- PDF下载量: 61
- 被引次数: 0
