Data assimilation experiments using localized particle filter and ensemble Kalman filter with community earth system model
-
摘要: 粒子滤波器(PF)是一种非常具有应用前景的非线性资料同化方法。但由于其算法本身存在的粒子退化问题,目前尚未被广泛地应用于大型地球物理模式。目前主流的集合同化系统仍然倾向于使用集合卡尔曼滤波器(EnKF)及其衍生方法。一种新近被提出的局地化粒子滤波器(LPF)在经典的粒子滤波器算法中引入局地化技术,可以使用较小的计算成本有效地避免退化问题,具有非常大的业务应用潜力。本文在全耦合的通用地球系统模式中开展了LPF和EnKF的同化实验,同化资料为模拟的卫星海表温度资料。着重考察了不同局地化参数对两种方法的不同影响,对比了局地化粒子滤波器与集合卡尔曼滤波器的同化效果差异。比较的结果表明,LPF的同化效果对于局地化参数的选择非常敏感,在使用最优局地化参数的条件下,LPF能达到与EnKF相当甚至优于后者的同化效果,并具有较大的改进空间。Abstract: Particle filter (PF) is a very promising nonlinear data assimilation method. However, due to the particle degeneracy problem, it has not been widely used in large geophysical models. In contrast, the ensemble Kalman filter (EnKF) and its derivative methods have been widely used in operational data assimilation systems in recent years. A newly proposed local particle filter (LPF) which employs the localization technique in particle filter, can effectively avoid the degeneracy problem with low computational costs and has great potential for practical applications. In this paper, data assimilation experiments using LPF and EnKF are conducted in a fully coupled Community earth system model. The sythetic satellite sea surface temperature data are assimilated with each method. Different impact of local parameters on each method is investigated, and the data assimilation performances of LPF and EnKF are compared. The comparison results show that the performance of LPF is more sensitive to localization parameter. With the optimal localization strategy, it is shown that LPF can be better than EnKF, and have a potential to be further improved.
-
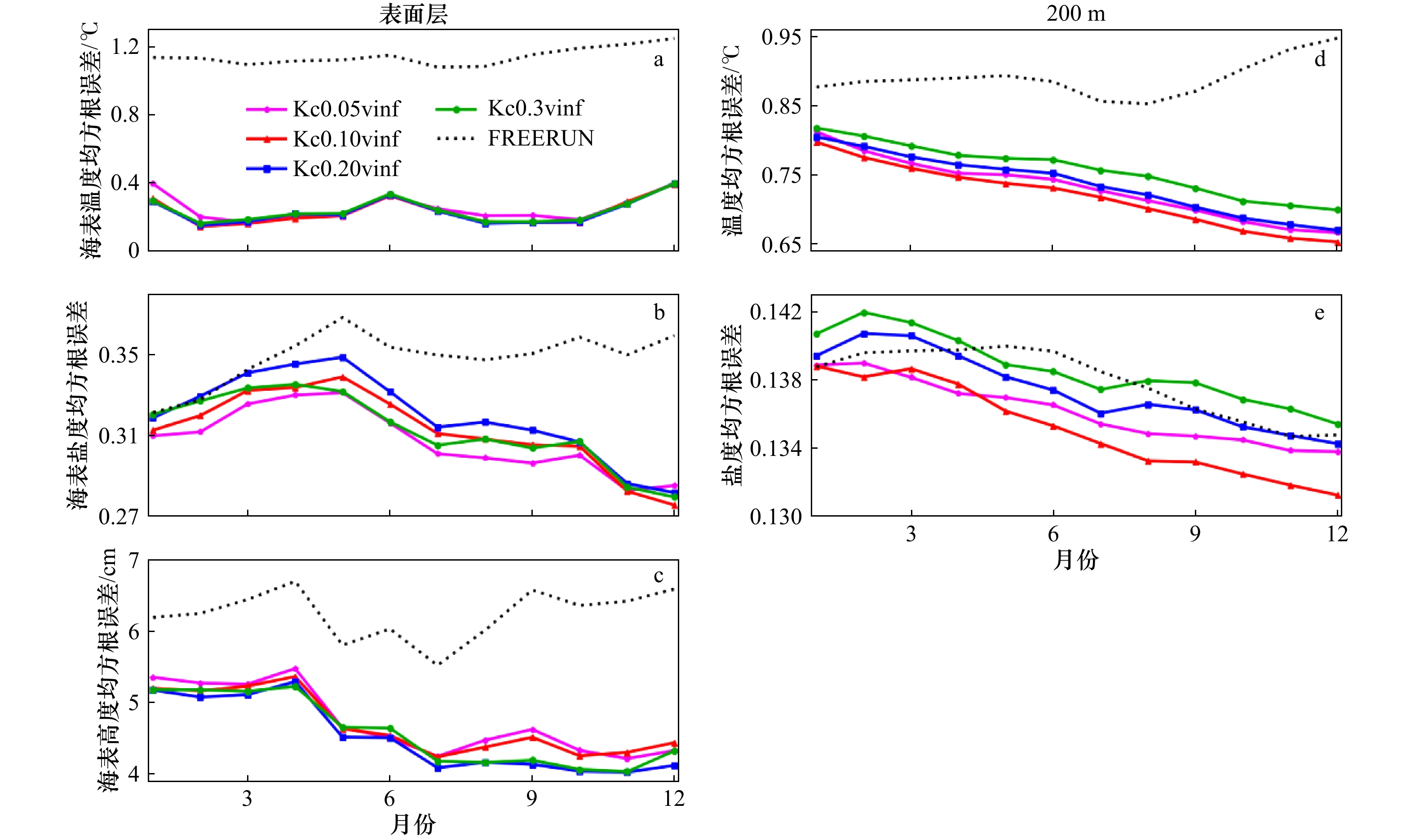
图 3 不同局地化参数EAKF实验中区域平均(60°S~60°N,环地球)的均方根误差时间序列
a. 海表温度;b. 海表盐度;c. 海表高度;d. 200 m的温度;e. 200 m的盐度
Fig. 3 RMSE time series of regional mean (60°S−60°N, ring the earth) in EAKF experiments with different local parameters
a. Sea surface temperature; b. sea surface salinity; c. sea surface height; d. temperature at 200 m; e. salinity of 200 m
图 4 海表温度相关系数
a−f. 相对于(0°,180°)位置处海表温度相关系数;g−l. 相对于(20°S,120°W)位置处海表温度相关系数;m−r. 相对于(20°S,60°E)位置处海表温度相关系数;s−x. 相对于(20°N,40°W)位置处海表温度相关系数;a, g, m, s. 局地化参数为0.05时海表温度有效相关系数;b, h, n, t. 局地化参数为0.1时海表温度有效相关系数;c, i, o, u. 局地化参数为0.2时海表温度有效相关系数;d, j, p, v.局地化参数为0.3时海表温度有效相关系数;e, k, q, w. 无局地化时海表温度样本相关系数;f, l, r, x. HadiSST资料海表温度分析相关系数。空白区域代表相关系数小于0的区域
Fig. 4 Correlation coefficient of sea surface temperature
a−f. Relative to (0°N, 180°W); g−l. relative to (20°S, 120°W); m−r. relative to (20°S, 60°E); s−x. relative to (20°N, 40°W). a, g, m, s. Effective correlation coefficient of sea surface temperature when local parameter is 0.05; b, h, n, t. effective correlation coefficient of sea surface temperature when the local parameter is 0.1; c, i, o, u. effective correlation coefficient of sea surface temperature when the local parameter is 0.2; d, j, p, v. effective correlation coefficient of sea surface temperature when the local parameter is 0.3; e, k, q, w. sample correlation coefficient of sea surface temperature without localization; f, l, r, x. analytical correlation coefficient of sea surface temperature. The areas in which correlation coefficients are smaller than 0 are blanked
表 1 实验列表
Tab. 1 Experimental list
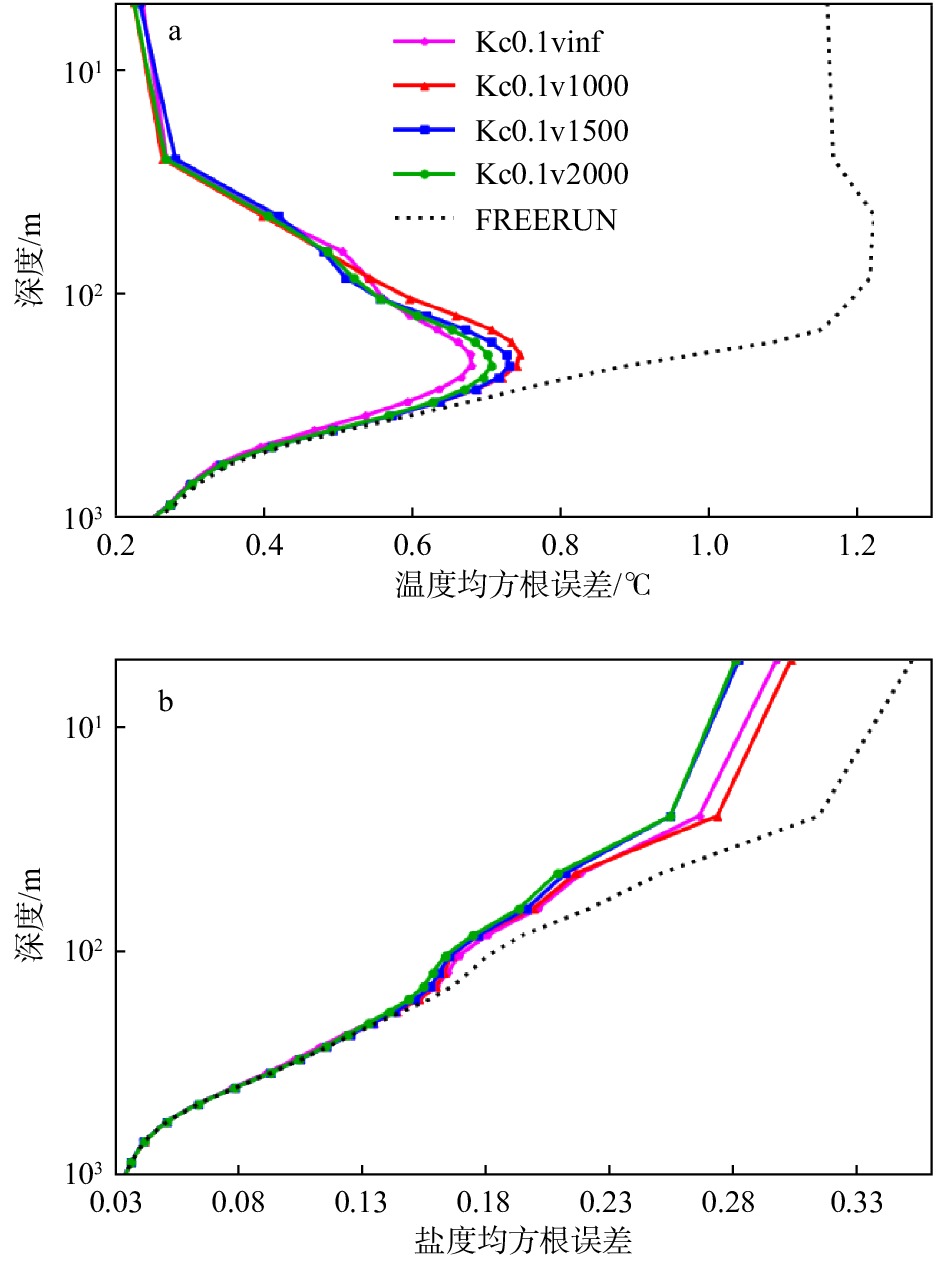
实验名称 同化方法 ν/(m·rad−1) c/rad EAKF垂向局地化
方案实验Kc0.1v1000 EAKF 1 000 0.1 Kc0.1v1500 1 500 0.1 Kc0.1v2000 2 000 0.1 EAKF局地化参数实验 Kc0.1vinf EAKF $ {\infty } $ 0.1 Kc0.05vinf $ {\infty } $ 0.05 Kc0.1vinf $ {\infty } $ 0.1 Kc0.2vinf $ {\infty } $ 0.2 Kc0.3vinf $ {\infty } $ 0.3 LPF垂向局地化
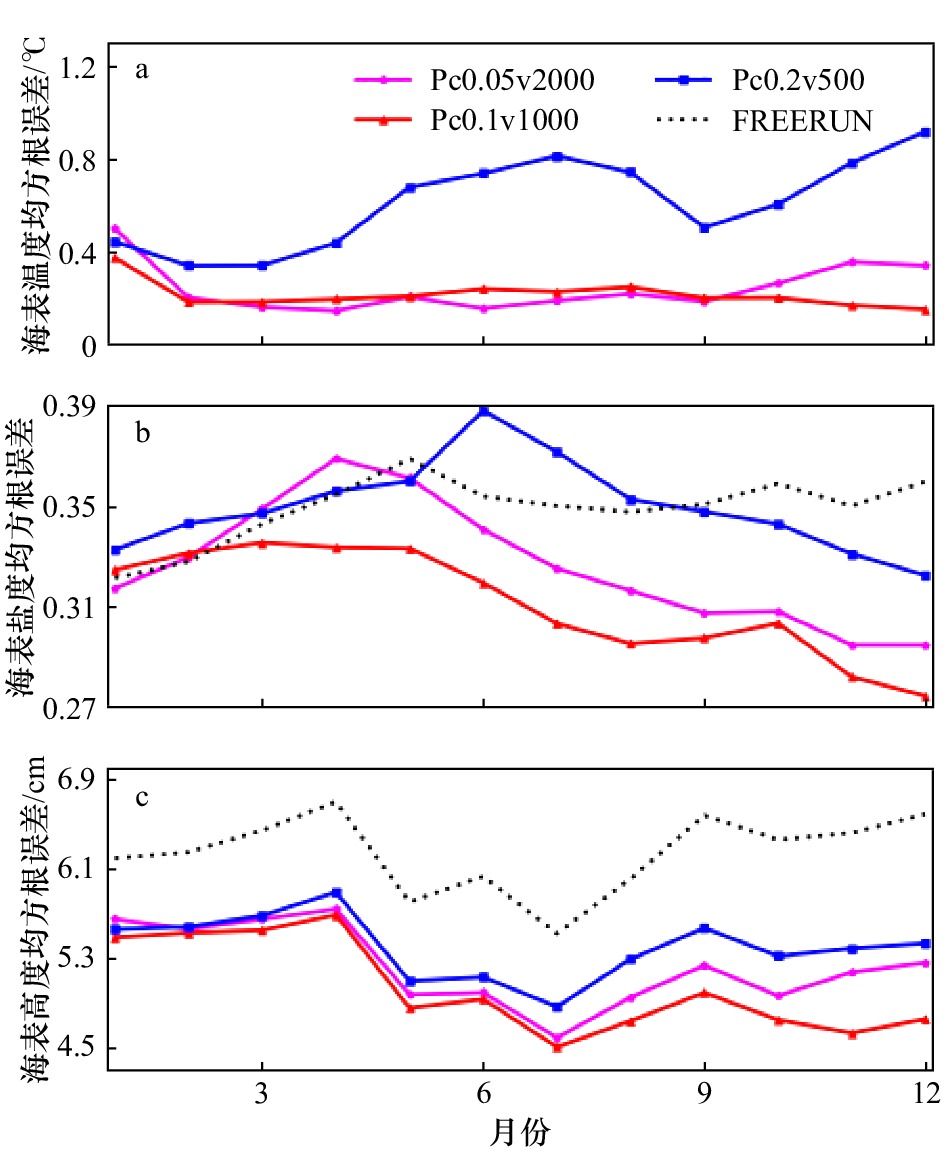
方案实验Pc0.1v500 LPF 500 0.1 Pc0.1v1000 1 000 0.1 Pc0.1v1500 1 500 0.1 LPF局地化参数实验 Pc0.1vinf LPF $ {\infty } $ 0.1 Pc0.05v2000 2 000 0.05 Pc0.1v1000 1 000 0.1 Pc0.2v500 500 0.2 控制实验 FREERUN 无同化 表 2 SST相关系数虚假相关占比
Tab. 2 Proportion of false correlation in SST correlation coefficient
虚假相关占比/% 位置 局地化参数c/rad 0.05 0.1 0.2 0.3 无局地化 (0°,180°) 0.003 4 0.000 9 3.699 6 14.947 4 264.448 6 (20°S,120°W) 0.014 4 0.004 0 0.556 4 1.110 1 381.896 4 (20°S,60°E) 0.013 9 0.004 3 0.059 3 1.045 0 258.742 8 (20°N,40°W) 0.011 0 0.006 3 0.191 7 1.565 5 250.448 1 平均 0.010 7 0.003 9 1.126 8 4.667 0 288.884 0 表 3 最优局地化参数EAKF、LPF不同区域平均均方根误差(RMSE)、同化影响(IOA)对比
Tab. 3 Comparison table of mean root mean square error (RMSE) and influence of Assimilation (IOA) of EAKF and LPF in different regions
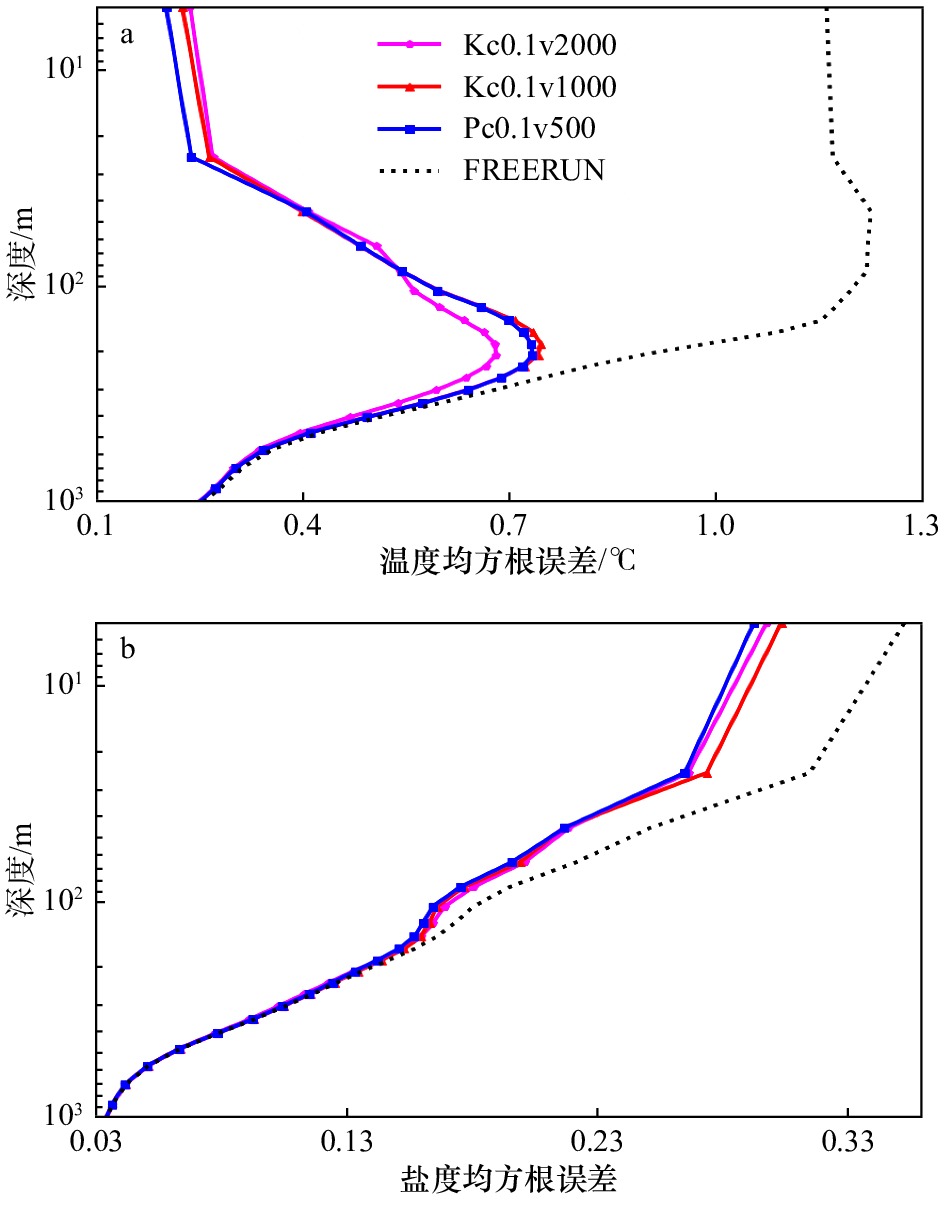
a.最优EAKF与LPF全球海洋不同区域海表温度RMSE及IOA对比表(后6个月平均) 区域 FREERUN EAKF LPF RMSE/℃ RMSE/℃ IOA/% RMSE/℃ IOA/% 全球 1.161 0.237 79.59 0.202 82.60 太平洋 1.179 0.218 81.51 0.189 83.97 大西洋 1.183 0.257 78.28 0.217 81.66 印度洋 1.038 0.251 75.82 0.204 80.35 b.最优EAKF与LPF全球海洋不同区域海表盐度RMSE及IOA对比表(后6个月平均) 区域 FREERUN EAKF LPF RMSE RMSE IOA/% RMSE IOA/% 全球 0.353 0.298 15.58 0.293 17.00 太平洋 0.382 0.312 18.32 0.314 17.80 大西洋 0.343 0.286 16.62 0.267 22.16 印度洋 0.290 0.285 1.72 0.283 2.41 c.最优EAKF与LPF全球海洋不同区域海表高度RMSE及IOA对比表(后6个月平均) 区域 FREERUN EAKF LPF RMSE/cm RMSE/cm IOA/% RMSE/cm IOA/% 全球 6.25 4.35 30.40 4.73 24.32 太平洋 7.46 5.35 28.28 5.77 22.65 大西洋 4.54 2.97 34.58 3.40 25.11 印度洋 5.25 3.43 34.67 3.74 28.76 -
[1] 李宏, 许建平. 资料同化技术的发展及其在海洋科学中的应用[J]. 海洋通报, 2011, 30(4): 463−472. doi: 10.3969/j.issn.1001-6392.2011.04.018Li Hong, Xu Jianping. Development of data assimilation and its application in ocean science[J]. Marine Science Bulletin, 2011, 30(4): 463−472. doi: 10.3969/j.issn.1001-6392.2011.04.018 [2] Evensen G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics[J]. Journal of Geophysical Research: Oceans, 1994, 99(C5): 10143−10162. doi: 10.1029/94JC00572 [3] van Leeuwen P J. Particle filtering in geophysical systems[J]. Monthly Weather Review, 2009, 137(12): 4089−4114. doi: 10.1175/2009MWR2835.1 [4] Anderson J L. An ensemble adjustment Kalman filter for data assimilation[J]. Monthly Weather Review, 2001, 129(12): 2884−2903. doi: 10.1175/1520-0493(2001)129<2884:AEAKFF>2.0.CO;2 [5] Zhang S, Harrison M J, Rosati A, et al. System design and evaluation of coupled ensemble data assimilation for global oceanic climate studies[J]. Monthly Weather Review, 2007, 135(10): 3541−3564. doi: 10.1175/MWR3466.1 [6] Le Gland F, Monbet V, Tran V D. Large sample asymptotics for the ensemble Kalman filter[M]//Crisan D. The Oxford Handbook of Nonlinear Filtering. Oxford University Press, 2011: 598−634. [7] Shen Zheqi, Zhang Xiangming, Tang Youmin. Comparison and combination of EAKF and SIR-PF in the Bayesian filter framework[J]. Acta Oceanologica Sinica, 2016, 35(3): 69−78. doi: 10.1007/s13131-015-0757-x [8] Penny S G, Miyoshi T. A local particle filter for high-dimensional geophysical systems[J]. Nonlinear Processes in Geophysics, 2016, 23(6): 391−405. doi: 10.5194/npg-23-391-2016 [9] Farchi A, Bocquet M. Review article: Comparison of local particle filters and new implementations[J]. Nonlinear Processes in Geophysics, 2018, 25(4): 765−807. doi: 10.5194/npg-25-765-2018 [10] Doucet A, Godsill S, Andrieu C. On sequential Monte Carlo sampling methods for Bayesian filtering[J]. Statistics and Computing, 2000, 10(3): 197−208. doi: 10.1023/A:1008935410038 [11] Zhu Mengbin, van Leeuwen P J, Amezcua J. Implicit equal-weights particle filter[J]. Quarterly Journal of the Royal Meteorological Society, 2016, 142(698): 1904−1919. doi: 10.1002/qj.2784 [12] Shen Zheqi, Tang Youmin. A modified ensemble Kalman particle filter for non-Gaussian systems with nonlinear measurement functions[J]. Journal of Advances in Modeling Earth Systems, 2015, 7(1): 50−66. doi: 10.1002/2014MS000373 [13] Poterjoy J. A localized particle filter for high-dimensional nonlinear systems[J]. Monthly Weather Review, 2016, 144(1): 59−76. doi: 10.1175/MWR-D-15-0163.1 [14] Whitaker J S, Hamill T M. Evaluating methods to account for system errors in ensemble data assimilation[J]. Monthly Weather Review, 2012, 140(9): 3078−3089. doi: 10.1175/MWR-D-11-00276.1 [15] Shen Zheqi, Tang Youmin, Li Xiaojing. A new formulation of vector weights in localized particle filters[J]. Quarterly Journal of the Royal Meteorological Society, 2017, 143(709): 3269−3278. doi: 10.1002/qj.3180 [16] Anderson J, Hoar T, Raeder K, et al. The data assimilation research testbed: A community facility[J]. Bulletin of the American Meteorological Society, 2009, 90(9): 1283−1296. doi: 10.1175/2009BAMS2618.1 [17] Anderson J L. Localization and sampling error correction in ensemble Kalman filter data assimilation[J]. Monthly Weather Review, 2012, 140(7): 2359−2371. doi: 10.1175/MWR-D-11-00013.1 [18] Reynolds R W. Impact of Mount Pinatubo aerosols on satellite-derived sea surface temperatures[J]. Journal of Climate, 1993, 6(4): 768−774. doi: 10.1175/1520-0442(1993)006<0768:IOMPAO>2.0.CO;2 [19] Rayner N A, Parker D E, Horton E B, et al. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century[J]. Journal of Geophysical Research: Atmospheres, 2003, 108(D14): 4407. doi: 10.1029/2002JD002670 [20] GaspriI G, Cohn S E. Construction of correlation functions in two and three dimensions[J]. Quarterly Journal of the Royal Meteorological Society, 1999, 125(554): 723−757. doi: 10.1002/qj.49712555417 [21] 沈浙奇, 唐佑民, 高艳秋. 集合资料同化方法的理论框架及其在海洋资料同化的研究展望[J]. 海洋学报, 2016, 38(3): 1−14.Shen Zheqi, Tang Youmin, Gao Yanqiu. The theoretical framework of the ensemble-based data assimilation method and its prospect in oceanic data assimilation[J]. Haiyang Xuebao, 2016, 38(3): 1−14. [22] Evensen G. The ensemble Kalman filter: Theoretical formulation and practical implementation[J]. Ocean Dynamics, 2003, 53(4): 343−367. doi: 10.1007/s10236-003-0036-9 [23] Hamill T M, Whitaker J S, Snyder C. Distance-dependent filtering of background error covariance estimates in an ensemble Kalman filter[J]. Monthly Weather Review, 2001, 129(11): 2776−2790. doi: 10.1175/1520-0493(2001)129<2776:DDFOBE>2.0.CO;2 [24] Frei M, Künsch H R. Bridging the ensemble Kalman and particle filters[J]. Biometrika, 2013, 100(4): 781−800. doi: 10.1093/biomet/ast020 -





 下载:
下载: