Analytical solution for waves propagating over a local permeable seabed
-
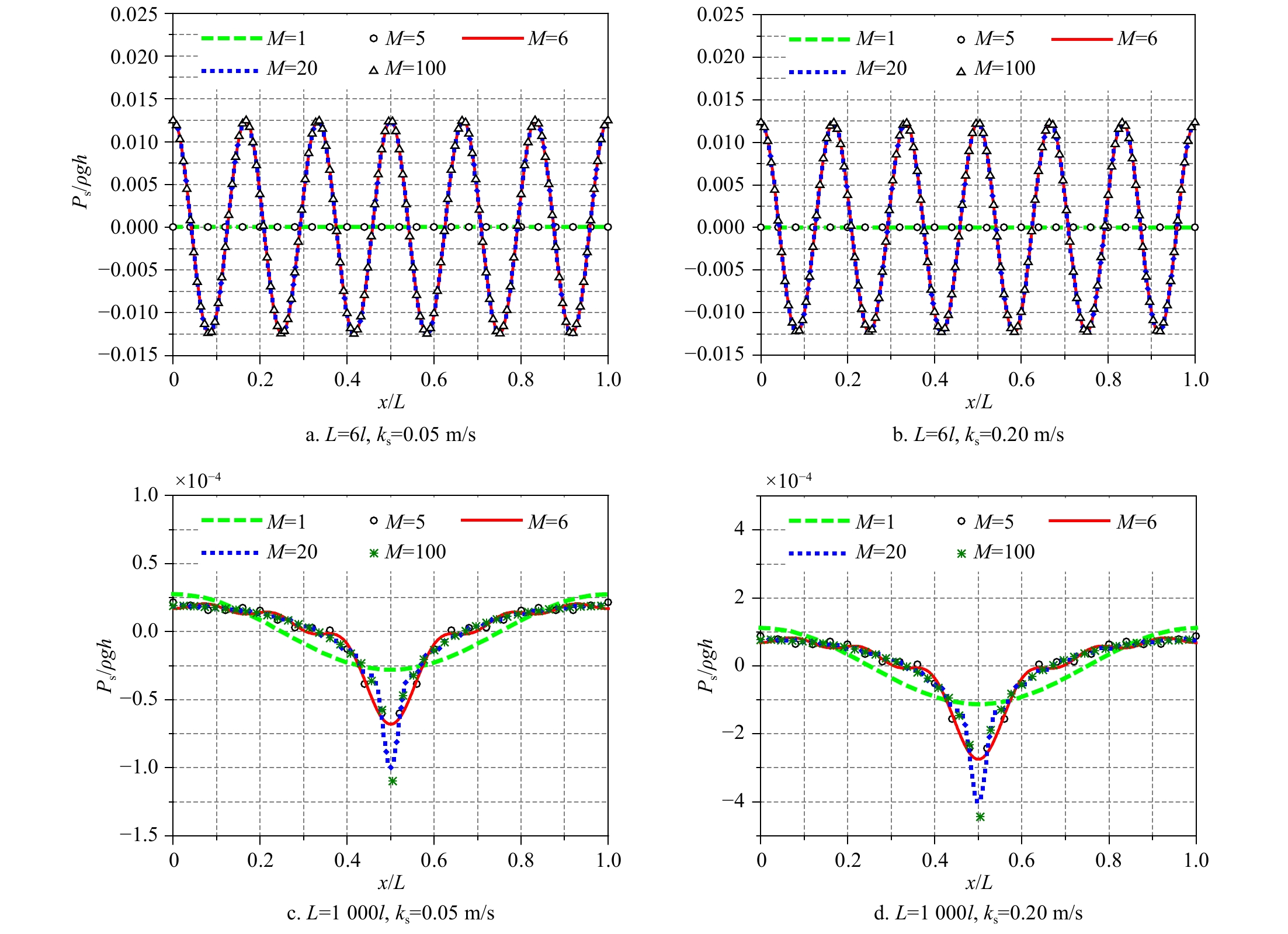
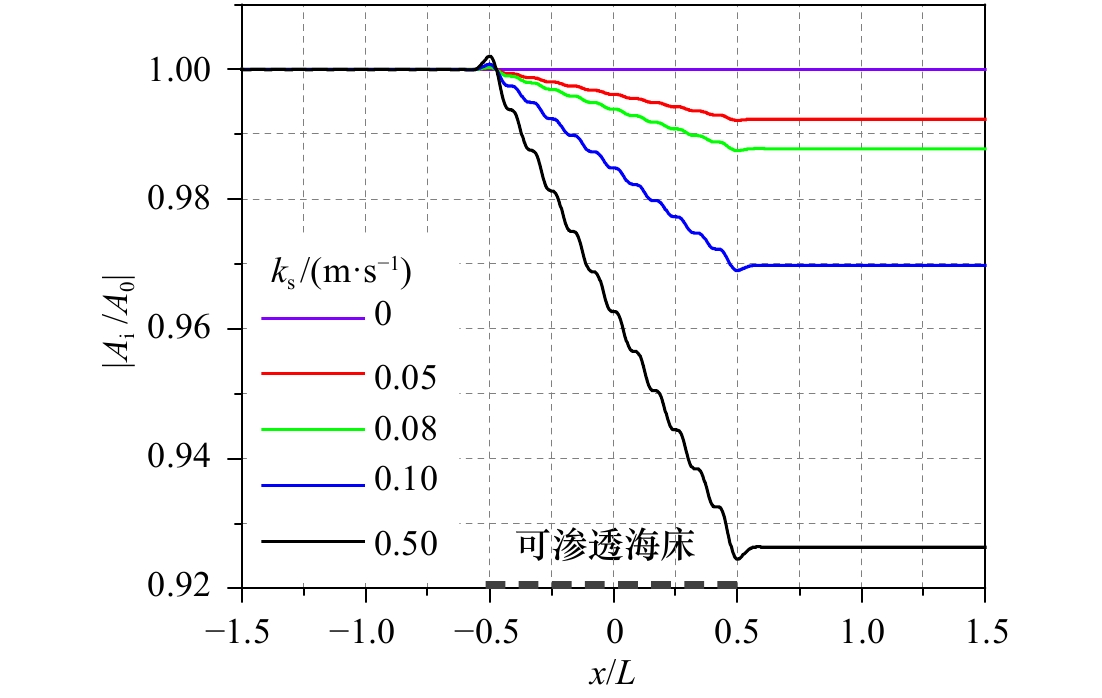
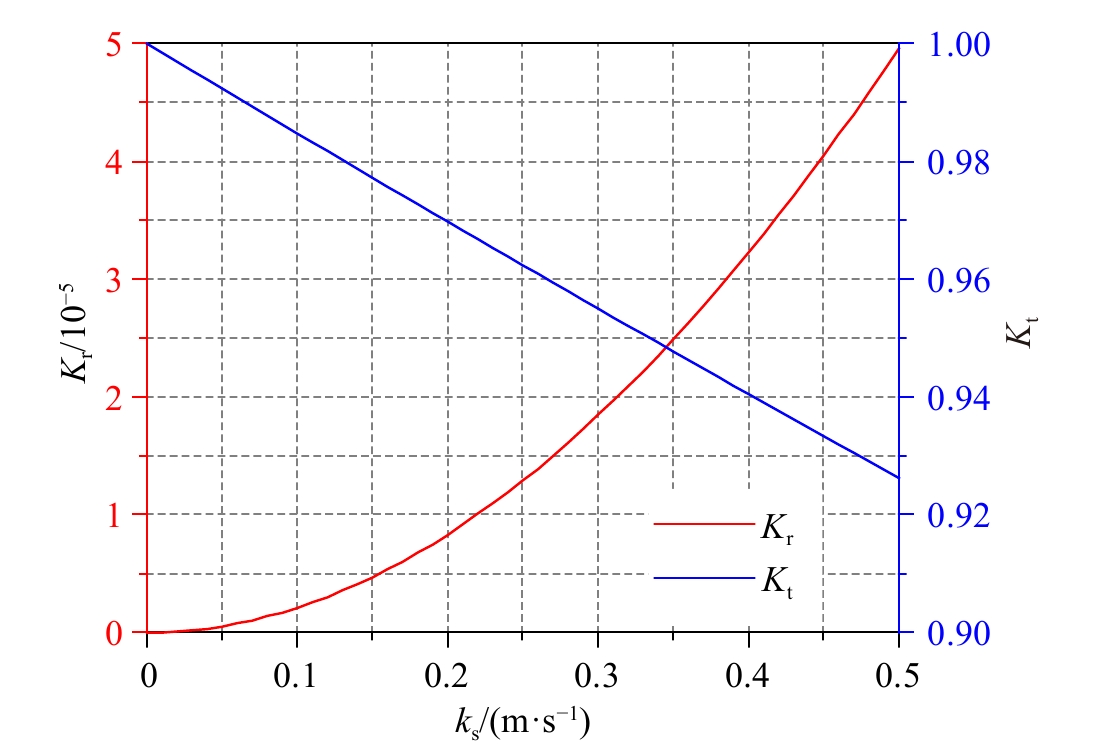
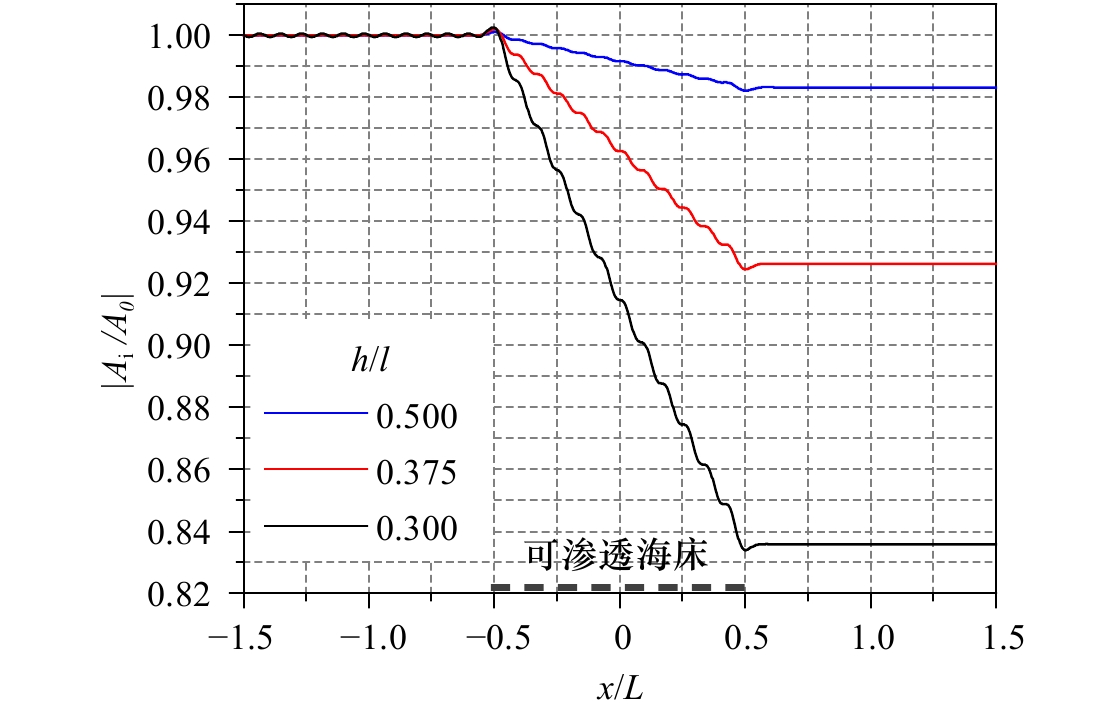
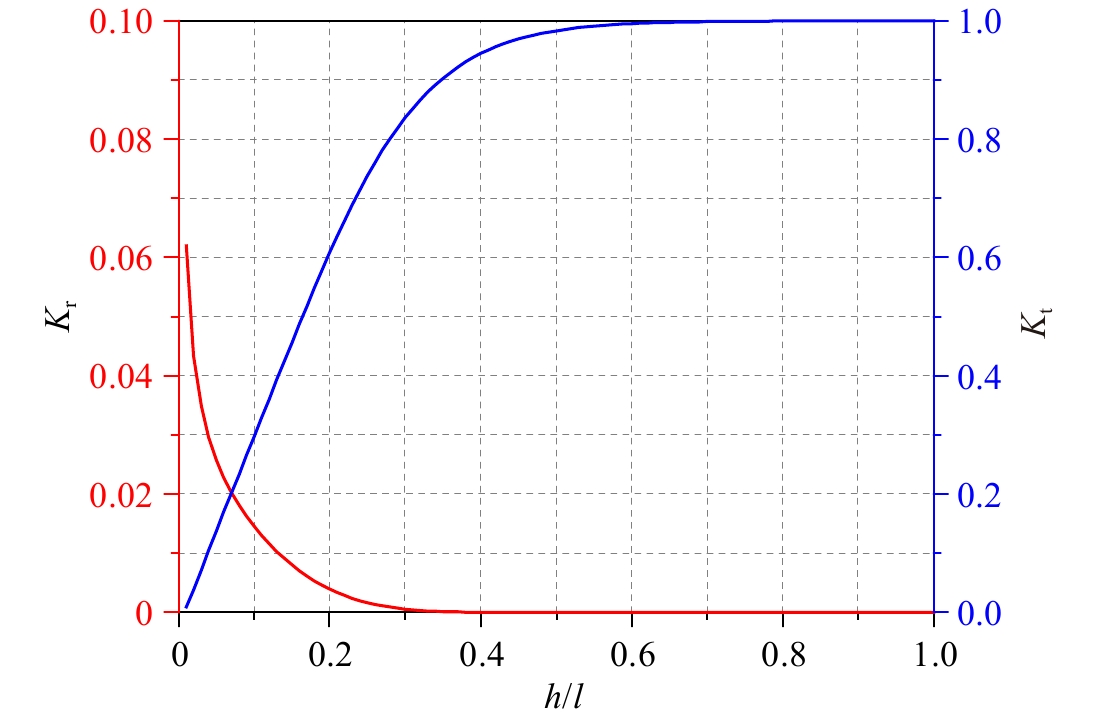
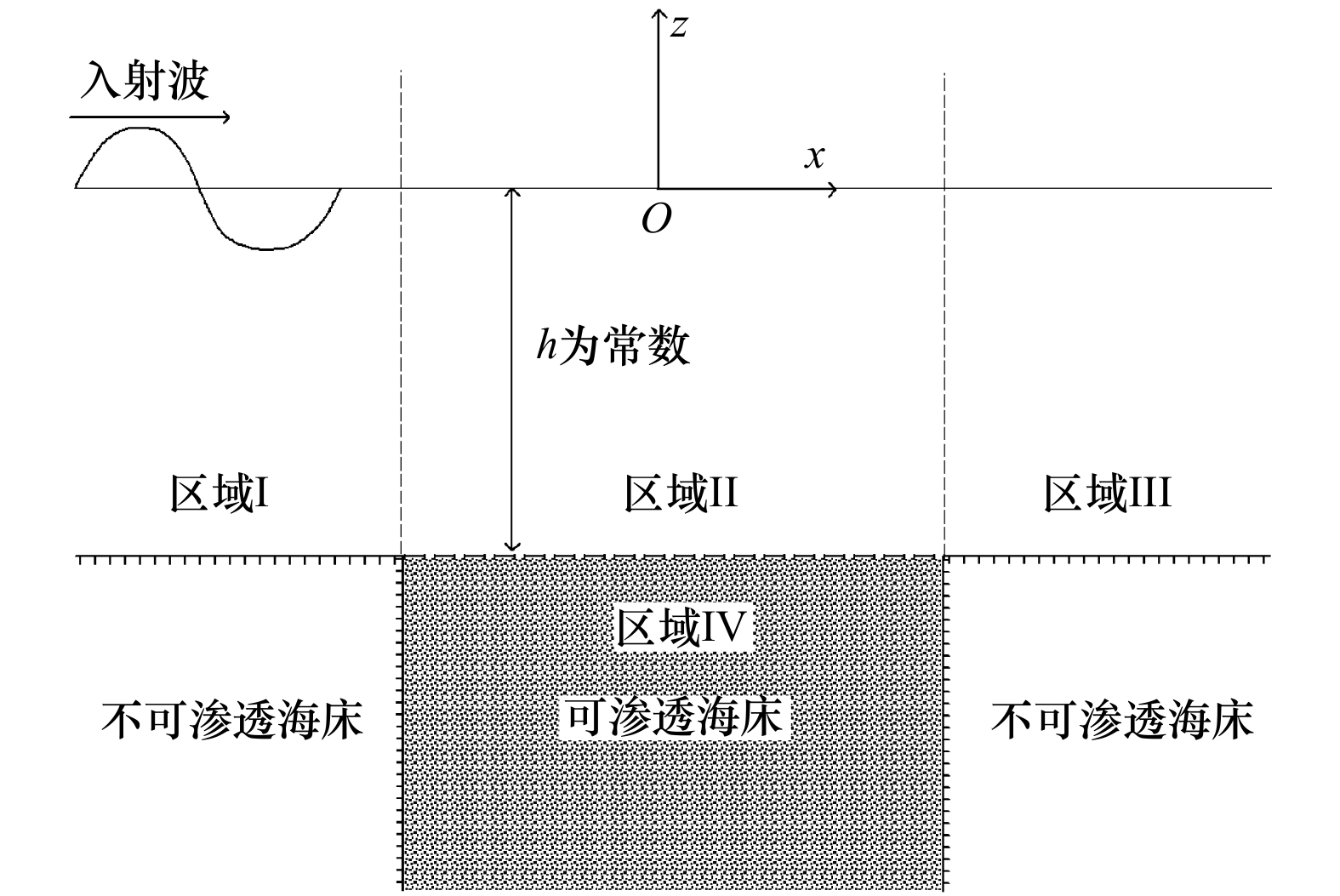
摘要: 本文建立了波浪在局部可渗透水平海床上传播的解析解,并研究了波浪在局部可渗透海床上的透射、反射问题。研究中将计算域划分为4个区域,中间区域为流域,海底可渗透,其下区域为多孔介质海床,左右两个区域也为流域,但海底不可渗透。应用线性波浪理论,建立了各流域包含非传播模态的速度势表达式,给出了海床内部的压强表达式,并利用交界面上匹配条件,求解了表达式中的待定系数。基于该解析模型,探讨了海床渗透系数、相对水深、渗透海床长度对波浪传播变形的影响。结果表明,波高沿程衰减,强度随渗透系数、渗透海床长度的增加以及相对水深的减小而变大;局部可渗透海床会引起波浪的反射和透射,随着海床长度的增加,反射系数振荡变化,并最终趋于常数,透射系数指数衰减,并最终趋于0。Abstract: The present study is concerned with the analytical solution for waves propagating over a local permeable seabed and wave reflection and transmission by the local permeable seabed. The computational domain is decomposed into four subdomains of which the middle subdomain is permeable, with the porous seabed beneath it, and the left and right subdomains are impermeable. Applying the linear wave theory, the velocity potential of each fluid subdomain is set up, including the effect of evanescent mode, and the pressure inside the porous seabed is given. The unknowns are solved by the continuous conditions at the interfaces between the neighboring subdomains. The effect of permeability coefficient, water depth and length of permeable seabed on wave transformation is discussed. The results indicate the wave height attenuates increasingly with the increase of permeability coefficient, the length of permeable seabed, and decrease of water depth. Wave reflection and transmission will occur due to the local permeable seabed. The reflection coefficient oscillates, and tends to be constant eventually, while the transmission coefficient reduces exponentially, and tends to be zero with the increase in the length of permeable seabed.
-
表 1 不同渗透系数情况下复波数计算结果
Tab. 1 Complex wavenumber calculated for different permeability coefficients
水深h
/mh/l 波浪圆频率
ω/Hz渗透系数ks
/(m·s−1)实部kr
/m−1虚部ki
/m−115 0.375 1.229 6 0 0.157 08 0 15 0.375 1.229 6 0.05 0.157 08 0.000 03 15 0.375 1.229 6 0.08 0.157 08 0.000 05 15 0.375 1.229 6 0.20 0.157 07 0.000 13 15 0.375 1.229 6 0.50 0.157 06 0.000 32 表 2 不同相对水深情况下复波数计算结果
Tab. 2 Complex wavenumber calculated for different water depth
水深h
/mh/l 波浪圆频率
ω/Hz渗透系数ks
/(m·s−1)实部kr
/m−1虚部ki
/m−120 0.500 1.238 4 0.5 0.157 08 0.000 07 15 0.375 1.229 6 0.5 0.157 06 0.000 32 12 0.300 1.212 4 0.5 0.157 05 0.000 75 -
[1] Savage R P, Fairchild J C. Laboratory study of wave energy losses by bottom friction and percolation[J]. Beach Erosion Board, 1953, 31: 1−25. [2] Özhan E, Shi-Igai H. On the development of solitary waves on a horizontal bed with friction[J]. Coastal Engineering, 1977, 1: 167−184. doi: 10.1016/0378-3839(77)90013-8 [3] Gu Zhihao, Wang H. Gravity waves over porous bottoms[J]. Coastal Engineering, 1991, 15(5/6): 497−524. [4] Sawaragi T, Deguchi I. Waves on permeable layers[C]//Proceedings of the 23rd Coastal Engineering Conference. Venice: ASCE, 1992: 1531−1544. [5] Putnam J A. Loss of wave energy due to percolation in a permeable sea bottom[J]. Eos, Transactions American Geophysical Union, 1949, 30(3): 349−356. doi: 10.1029/TR030i003p00349 [6] Reid R O, Kajiura K. On the damping of gravity waves over a permeable sea bed[J]. Eos, Transactions American Geophysical Union, 1957, 38(5): 662−666. doi: 10.1029/TR038i005p00662 [7] Murray J D. Viscous damping of gravity waves over a permeable bed[J]. Journal of Geophysical Research, 1965, 70(10): 2325−2331. doi: 10.1029/JZ070i010p02325 [8] Dean R G, Dalrymple R A. Water Wave Mechanics for Engineers and Scientists[M]. Singapore Teaneck, NJ: World Scientific, 1991. [9] Rojanakamthorn S, Isobe M, Watanabe A. Modeling of wave transformation on submerged breakwater[C]//22nd International Conference on Coastal Engineering. Virginia: ASCE, 1991: 1060−1073. [10] Silva R, Salles P, Palacio A. Linear waves propagating over a rapidly varying finite porous bed[J]. Coastal Engineering, 2002, 44(3): 239−260. doi: 10.1016/S0378-3839(01)00035-7 [11] Tsai C P, Chen Hongbin, Lee F C. Wave transformation over submerged permeable breakwater on porous bottom[J]. Ocean Engineering, 2006, 33(11/12): 1623−1643. [12] Cruz E C, Isobe M, Watanabe A. Boussinesq equations for wave transformation on porous beds[J]. Coastal Engineering, 1997, 30(1/2): 125−156. [13] Méndez F J, Losada I J, Losada M A. Wave-induced mean magnitudes in permeable submerged breakwaters[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2001, 127(1): 7−15. doi: 10.1061/(ASCE)0733-950X(2001)127:1(7) [14] Huang C J, Chang H H, Hwung H H. Structural permeability effects on the interaction of a solitary wave and a submerged breakwater[J]. Coastal Engineering, 2003, 49(1/2): 1−24. [15] Mendez F J, Losada I J. A perturbation method to solve dispersion equations for water waves over dissipative media[J]. Coastal Engineering, 2004, 51(1): 81−89. doi: 10.1016/j.coastaleng.2003.12.007 [16] Kirby J T, Dalrymple R A. Propagation of obliquely incident water waves over a trench[J]. Journal of Fluid Mechanics, 1983, 133: 47−63. doi: 10.1017/S0022112083001780 [17] Bender C J, Dean R G. Wave transformation by two-dimensional bathymetric anomalies with sloped transitions[J]. Coastal Engineering, 2003, 50(1/2): 61−84. [18] 宋岩新. 砂质海床上海底管线稳定性的数值分析[D]. 大连: 大连理工大学, 2008.Song Yanxin. Numerical analysis of stability of submarine pipelines on a sandy seabed[D]. Dalian: Dalian University of Technology, 2008. [19] 钱琨, 王新志, 陈剑文, 等. 南海岛礁吹填钙质砂渗透特性试验研究[J]. 岩土力学, 2017, 38(6): 1557−1564, 1572.Qian Kun, Wang Xinzhi, Chen Jianwen, et al. Experimental study on permeability of calcareous sand for islands in the South China Sea[J]. Rock and Soil Mechanics, 2017, 38(6): 1557−1564, 1572. -




 下载:
下载: