Numerical simulation for wave climbing process on woody plants covered slope
-
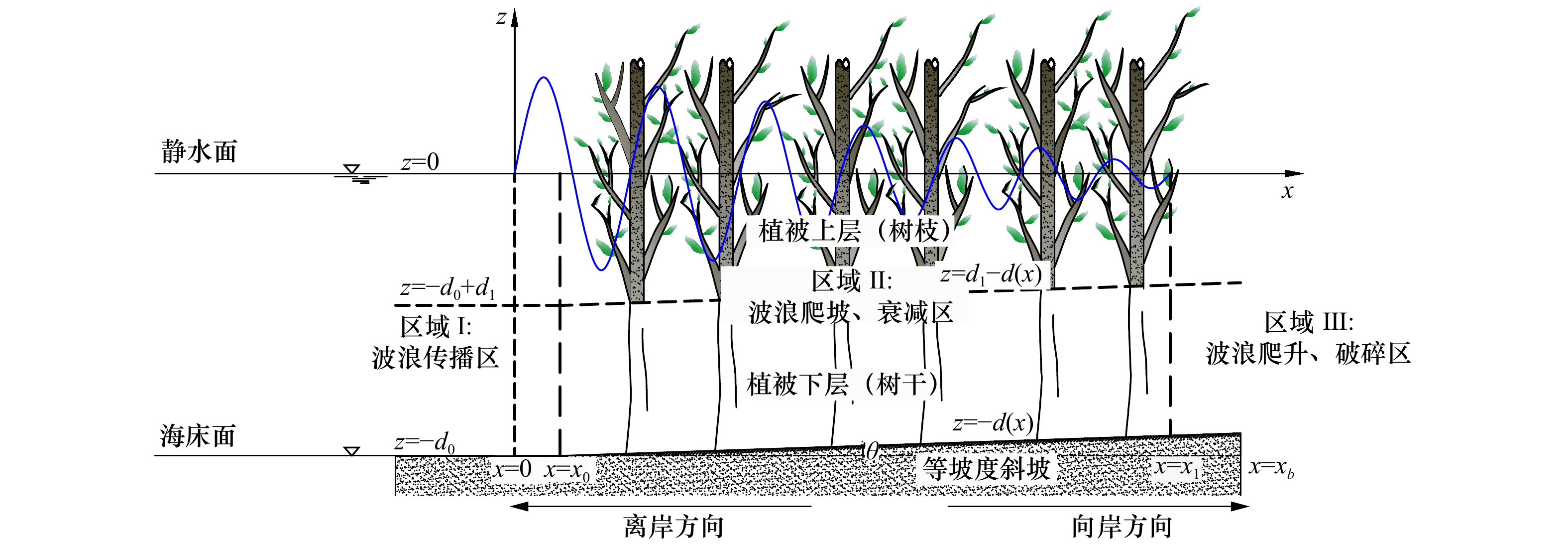
摘要: 近岸木本植物构成的生态缓冲带作为新型的海岸软防护结构，兼具功能性和生态友好性，在沿海工程建设中愈发受到关注，如何深入开展其防护效果的机理研究是目前亟待解决的问题。本文采用数值模拟方法，在N-S方程中分别考虑树枝和树干的拖曳力影响，提出了木本植被作用下波浪沿斜坡爬升的表面波衰减的连续介质等效模型，并采用MAC法来跟踪自由曲面上的水颗粒轨迹。本文以波浪沿1/30的斜坡爬升为算例，对比讨论了有无植被作用下波浪的传播过程，并将算例结果与以往试验结果规律进行对照，验证了数值模型的有效性。最后，分别讨论了植物枝干的高度、密度、树枝倾斜角度等植被特性和波浪因素对植被消浪效果的影响，得到植被消浪的基本规律。文中的计算结果也可为实际的护岸工程和生态景观设计提供参考。Abstract: As a new type of coastal ecological protection measure, ecological buffer zone formed by woody plants in coastal areas has attracted more and more attention in coastal engineering projects. It is an urgent problem to be solved that how to carry out the research on the protection effect of woody plants. The numerical simulation method is used in this paper. Firstly, a theoretical model of surface wave attenuation for wave climbing along a slope under the protection of woody vegetation is proposed by including the drag forces of branches and trunks in the N-S equation. Next, the MAC method is used to track the trajectories of water particles on the free surface. Then, taking the wave climbing along a slope of 1/30 as an example, the wave propagation process along an inclined beach with or without vegetation is discussed. The validity of the numerical model is verified by comparing the numerical result and those of the previous experiments. Finally, influences of the vegetation characteristics, such as height, density and tilt angle of plant branches and those of wave factors on wave dissipation are discussed and analyzed, respectively. Additionally, the rules of wave dissipation are summarized. The calculation results of this model can also be applicable to the design of revetment structures and ecological landscape.
-
图 1 海南岛文昌海岸近岸木本植被缓冲带
Fig. 1 Nearshore woody vegetation at Wenchang coast in Hainan Island
图 5 无植被作用下波浪沿斜坡（i=1/30）传播波形
Fig. 5 The wave form of the wave propagation along slope (i=1/30) without vegetation
图 6 无植被作用下波浪沿斜坡（i=1/30）传播流场
Fig. 6 The flow field of the wave propagation along slope (i=1/30) without vegetation
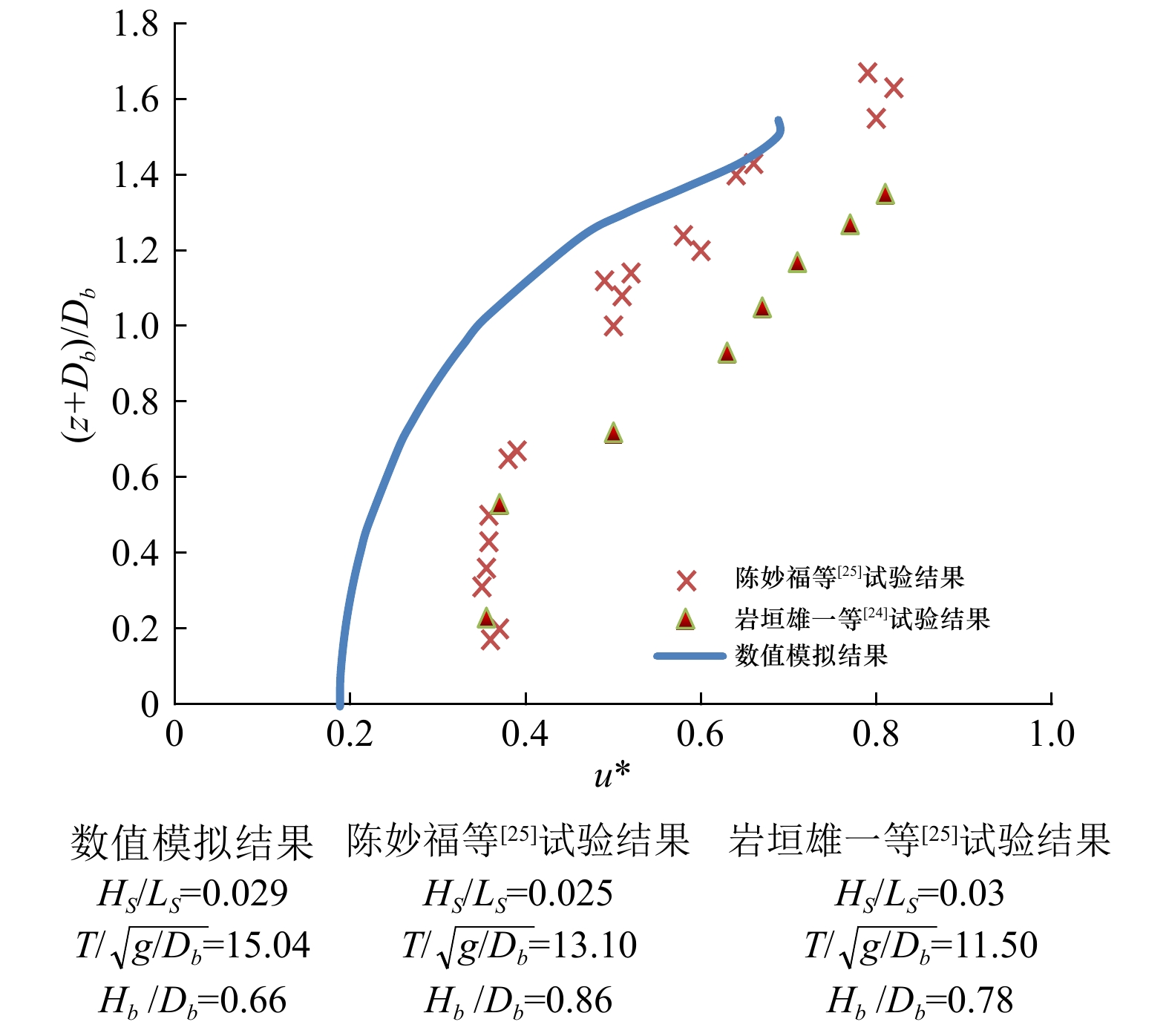
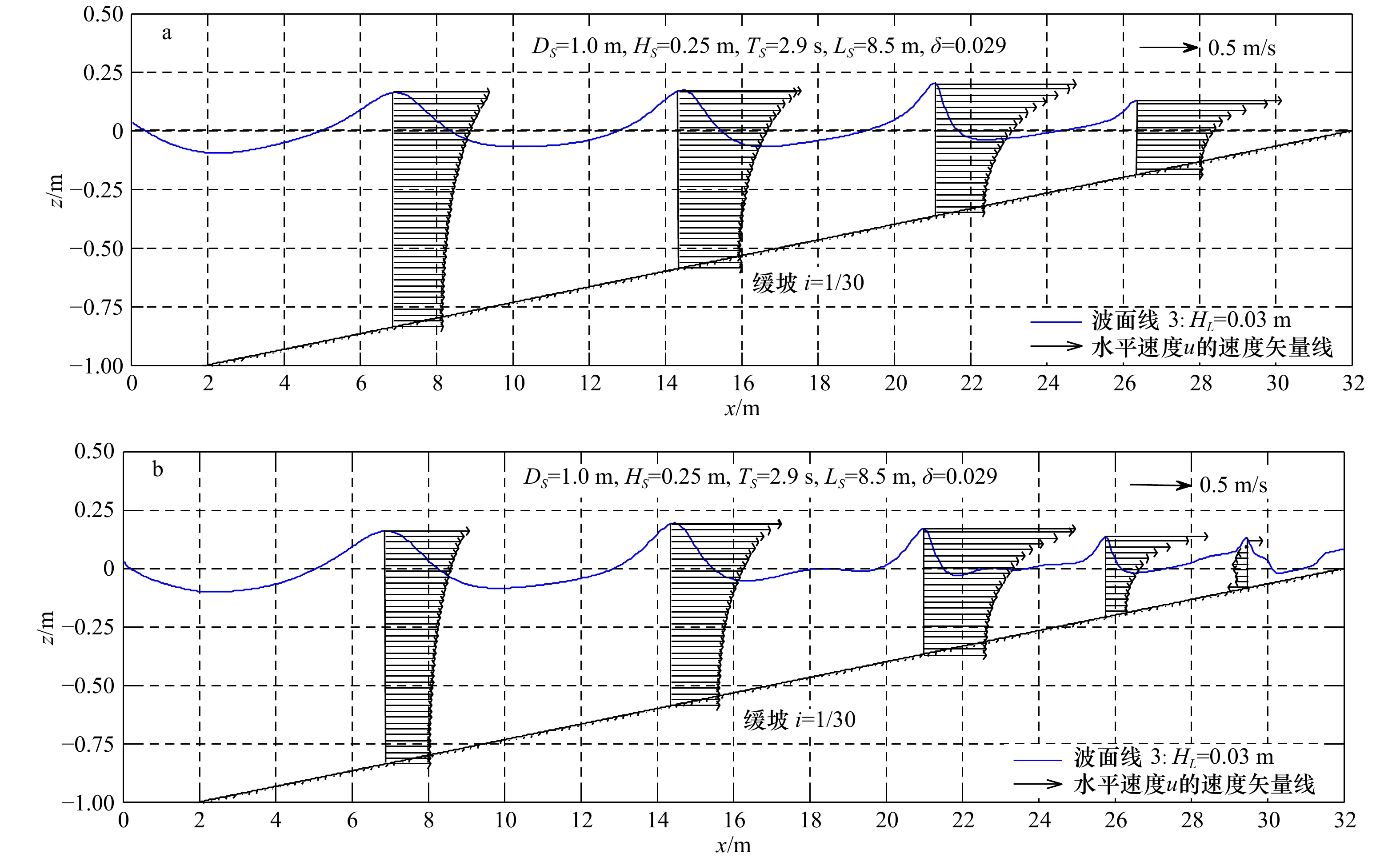
图 8 濒临破碎波峰下水平速度垂向分布比较
下标b表示濒临破碎的波峰下的相应参数，Hb表示濒临破碎的波峰所在波形内的波高值，Db表示濒临破碎的波峰位置处的水深，T为波浪周期
Fig. 8 Comparison of vertical distribution of horizontal velocity under breaking wave crest field
The subscript b represents the corresponding parameter under the crest of the wave that is on the verge of breaking, Hb represents the wave height in the waveform where the wave crest is on the verge of breakage, Db represents the depth of water at the position of the wave crest that is on the verge of breaking, T is the wave period
图 9 二阶Stokes波模拟结果验证
d为沿程水深，L为沿程波长
Fig. 9 Verification of second-order Stokes wave simulation results
d is water depth along the course, and L is wave length along the course
图 10 植被作用下波浪沿斜坡（i=1/30）传播波形
Fig. 10 The wave form diagram of the wave propagation along slope (i=1/30) with vegetation
图 11 植被作用下波浪沿斜坡（i=1/30）传播流场
Fig. 11 The flow field diagram of the wave propagation along slope (i=1/30) with vegetation
图 12 无植被作用（a）和有植被作用（b）波峰下水平速度垂向分布对比
Fig. 12 Comparison of vertical distribution of horizontal velocity under wave crest field with vegetation (a) and without vegetation (b)
图 13 无植被作用（a）和有植被作用（b）波峰位置波面高度沿程变化
Fig. 13 The variation of wave surface height on wave crest along distance with vegetation (a) and without vegetation (b)
图 14 植被密度与波面位置关系
Fig. 14 The relationship between vegetation density and wave surface position
图 15 树枝密度与波面位置关系
Fig. 15 The relationship between branch density and wave surface position
图 16 树干高度与波面位置关系
Fig. 16 The relationship between vegetation density and wave surface position
图 17 树枝角度与波面位置关系
Fig. 17 The relationship between branch tilt angle and wave surface position
图 18 相对波高与透浪系数关系
Fig. 18 The relationship between relatively wave height and transmitted coefficient
图 19 相对波高与沿程波高关系
Fig. 19 The relationship between relatively wave height and wave height along the path
图 20 波陡与透浪系数关系
Fig. 20 The relationship between wave steepness and transmitted coefficient
图 21 波陡与沿程波高关系
Fig. 21 The relationship between wave steepness and wave height along the path
表 1 植被特性模拟工况表
Tab. 1 The arrangement of simulation condition about vegetation characteristics
工况 树干数
NL树枝数
NU树干高度
hL/m树干直径
DL/m树枝直径
DU/m树枝平均
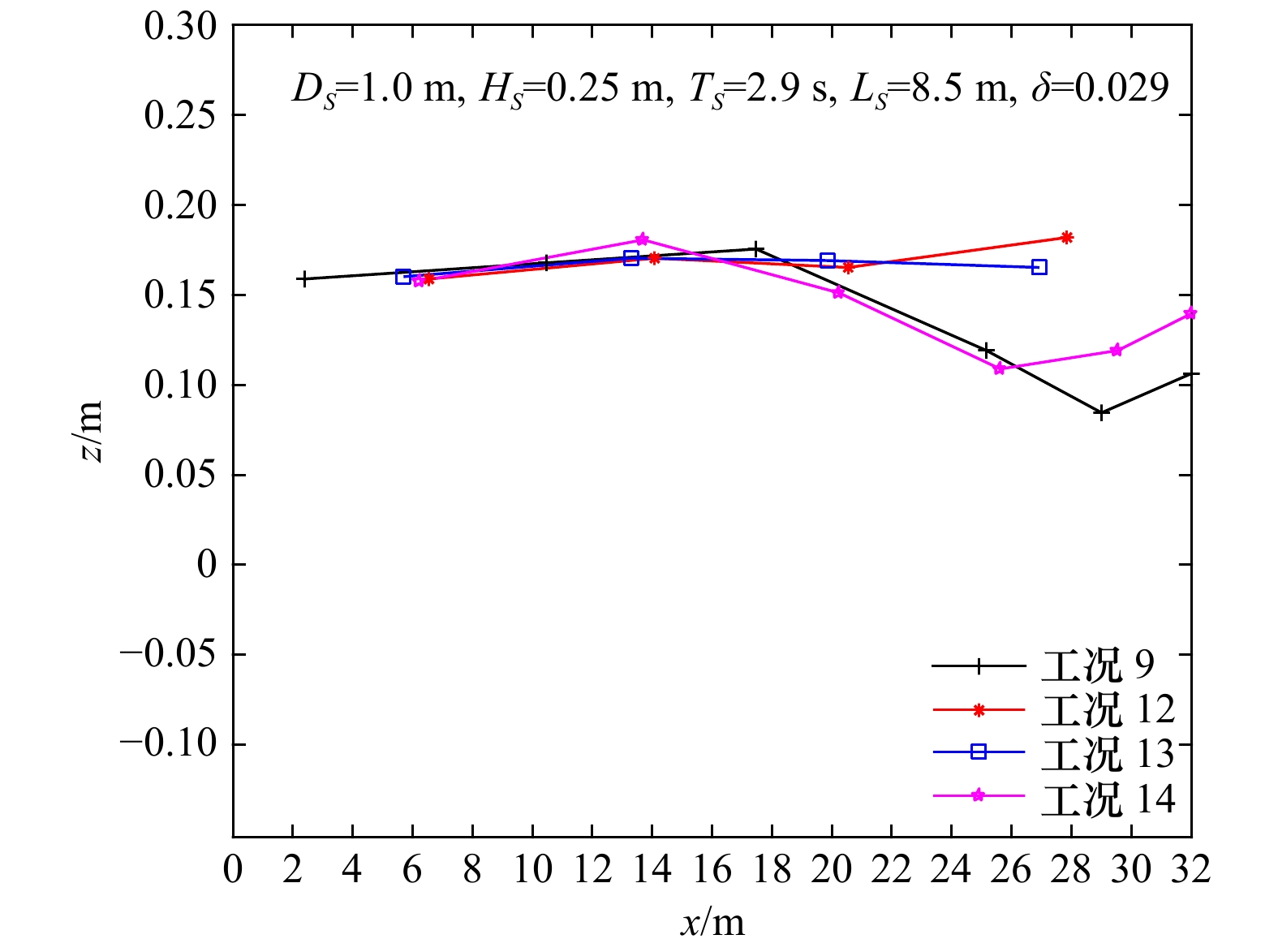
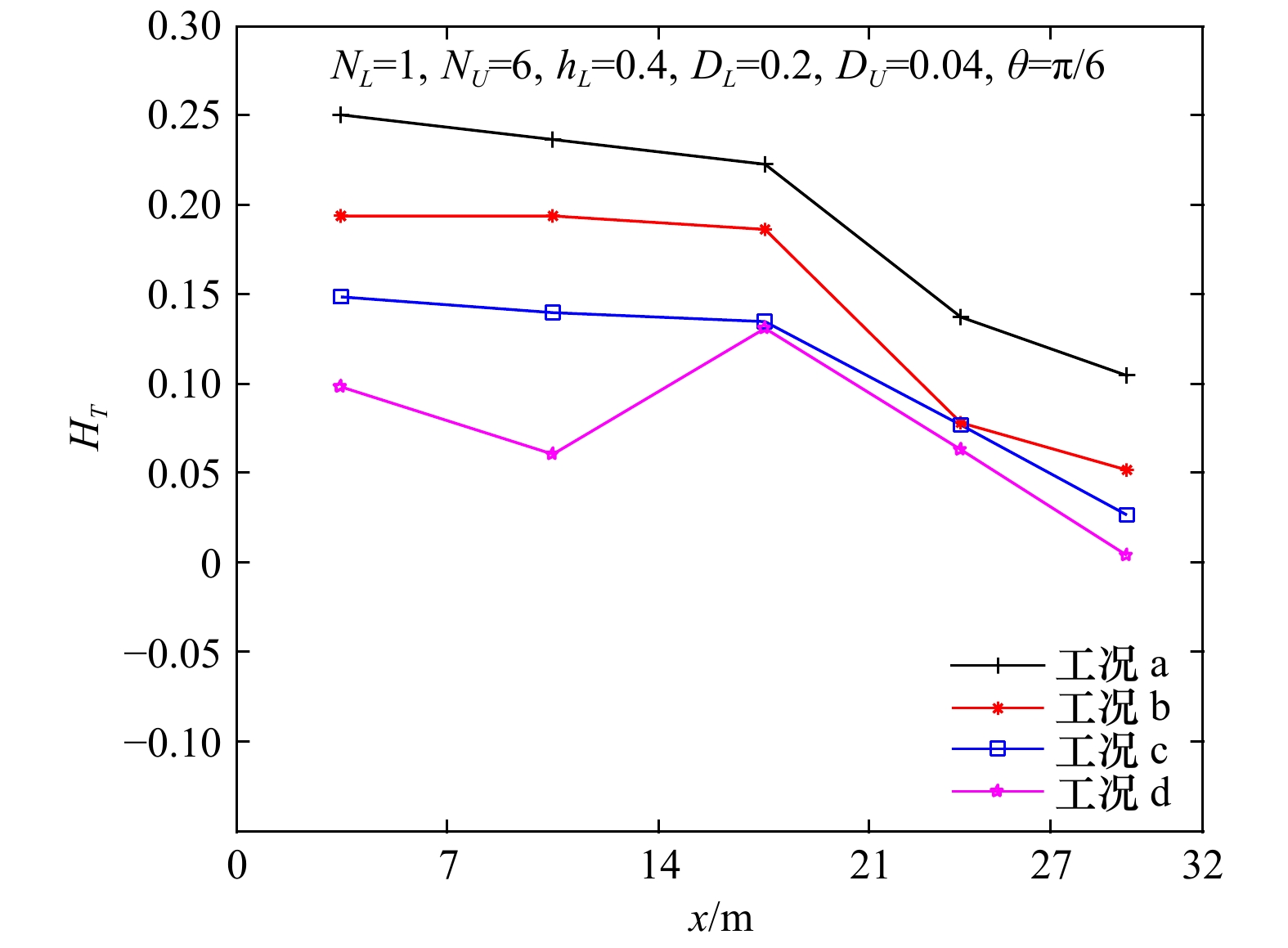
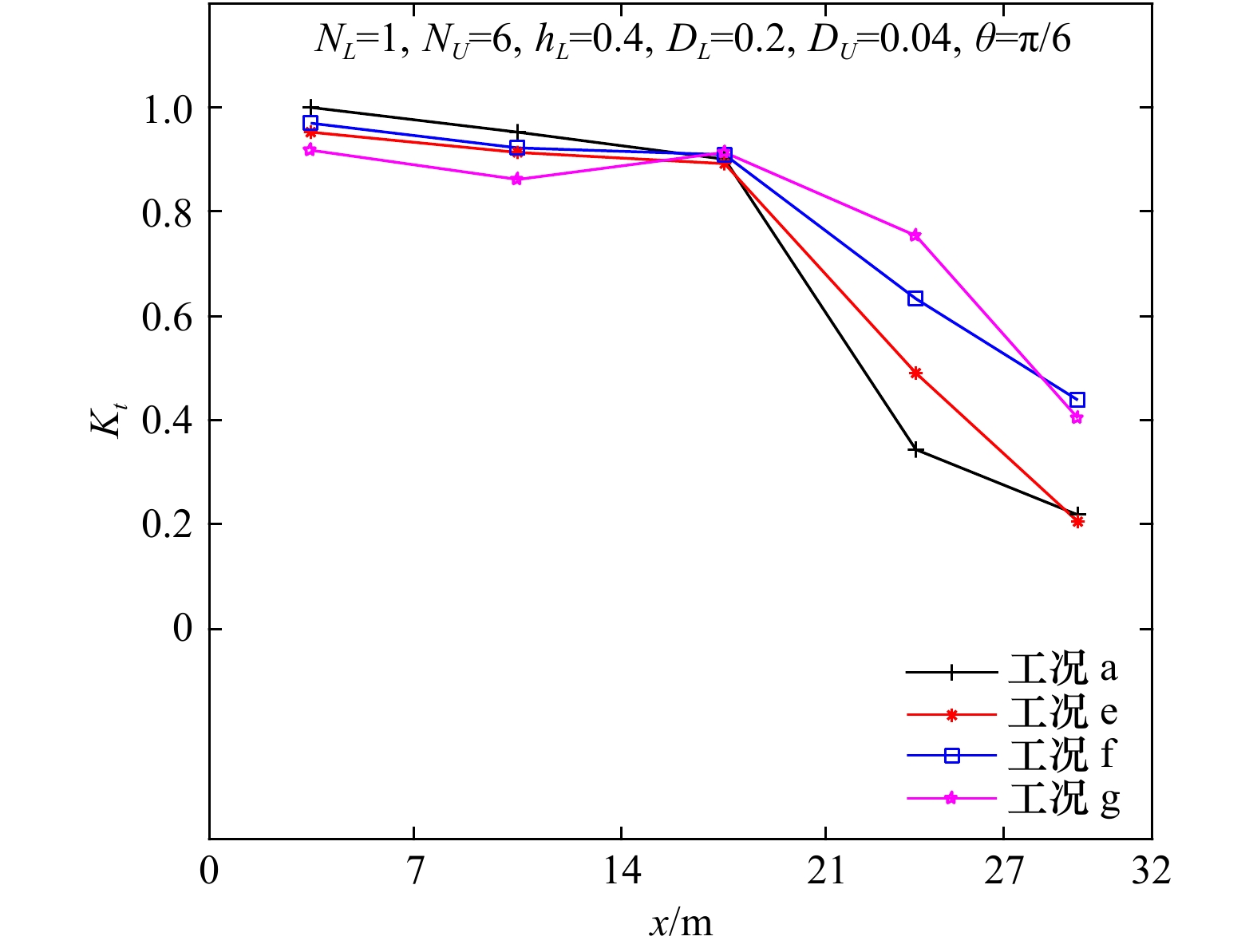
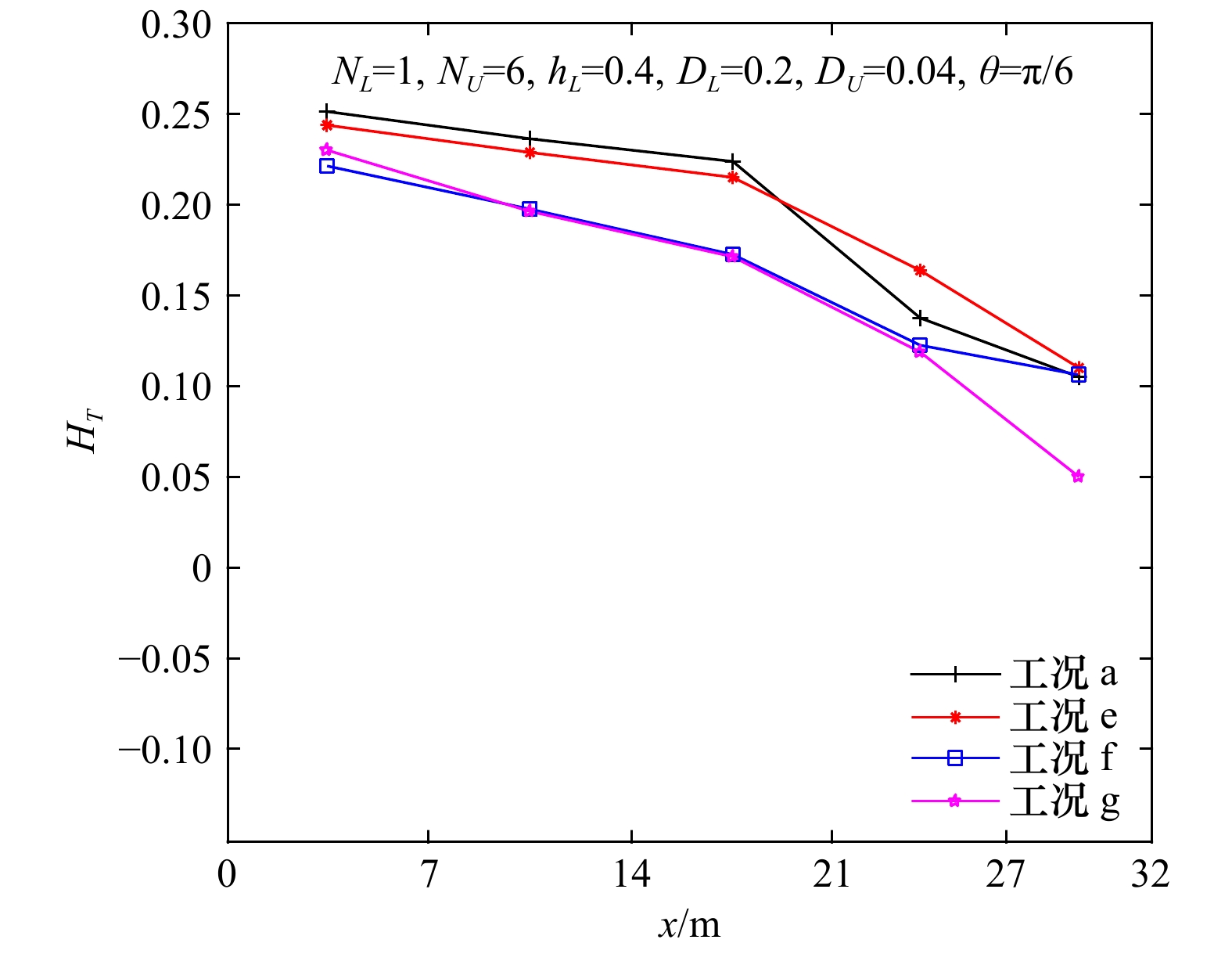
角度$\theta $1 0.1 0.6 0.6 0.2 0.04 ${\text π} $/6 2 1 6 0.6 0.2 0.04 ${\text π} $/6 3 2 12 0.6 0.2 0.04 ${\text π} $/6 4 3 18 0.6 0.2 0.04 ${\text π} $/6 5 1 3 0.6 0.2 0.04 ${\text π} $/6 6 1 4 0.6 0.2 0.04 ${\text π} $/6 7 1 5 0.6 0.2 0.04 ${\text π} $/6 8 1 6 0.2 0.2 0.04 ${\text π} $/6 9 1 6 0.4 0.2 0.04 ${\text π} $/6 10 1 6 0.8 0.2 0.04 ${\text π} $/6 11 1 6 1.0 0.2 0.04 ${\text π} $/6 12 1 6 0.4 0.2 0.04 ${\text π} $/5 13 1 6 0.4 0.2 0.04 ${\text π} $/4 14 1 6 0.4 0.2 0.04 ${\text π} $/3 注：表中各参数均指单位宽度、单位长度内的植被特性。 
下载: 导出CSV
表 2 植被特性模拟工况表
Tab. 2 The arrangement of simulation condition about vegetation characteristics
工况 入射水深/m 入射波高/m 入射波浪
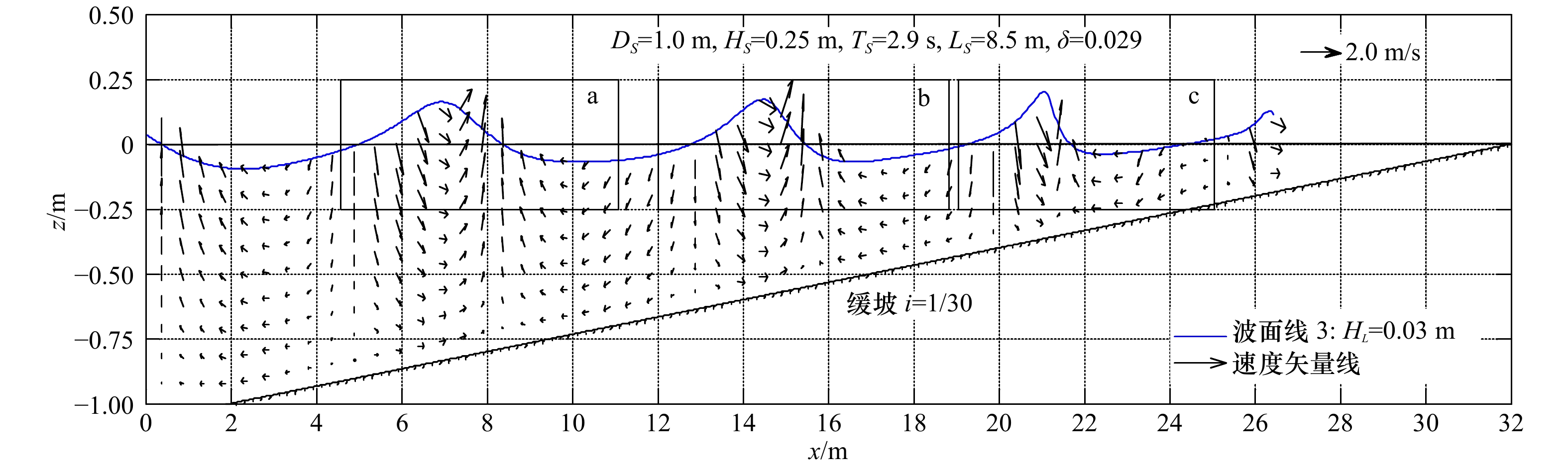
周期/s入射波长/m 相对波高/m 入射波陡 a 1 0.25 2.9 8.5 0.25 0.029 b 1 0.20 2.9 8.5 0.20 0.024 c 1 0.15 2.9 8.5 0.15 0.018 d 1 0.10 2.9 8.5 0.10 0.012 e 1 0.25 2.6 7.5 0.25 0.033 f 1 0.25 2.3 6.3 0.25 0.039 g 1 0.25 2.0 5.2 0.25 0.048
下载: 导出CSV
-
[1] Young I R, Zieger S, Babanin A V. Global trends in wind speed and wave height[J]. Science, 2011, 332(6028): 451−455. doi: 10.1126/science.1197219 [2] 吉红香, 黄本胜, 邱秀云. 植物消波消浪研究综述[J]. 水利水运工程学报, 2005(1): 75−78. doi: 10.3969/j.issn.1009-640X.2005.01.015Ji Hongxiang, Huang Bensheng, Qiu Xiuyun. Review on research of wave absorption by vegetation[J]. Hydro-Science and Engineering, 2005(1): 75−78. doi: 10.3969/j.issn.1009-640X.2005.01.015 [3] Zhang Mingliang, Zhang Hongxing, Zhao Kaibin, et al. Evolution of wave and tide over vegetation region in nearshore waters[J]. Ocean Dynamics, 2017, 67(8): 973−988. doi: 10.1007/s10236-017-1068-x [4] 白玉川, 杨建民, 胡嵋, 等. 植物消浪护岸模型实验研究[J]. 海洋工程, 2005, 23(3): 65−69. doi: 10.3969/j.issn.1005-9865.2005.03.011Bai Yuchuan, Yang Jianmin, Hu Mei, et al. Model test of vegetation on the bank to attenuate waves and protect embankments[J]. The Ocean Engineering, 2005, 23(3): 65−69. doi: 10.3969/j.issn.1005-9865.2005.03.011 [5] 吉红香. 植物消浪护岸试验研究[D]. 乌鲁木齐: 新疆农业大学, 2005.Ji Hongxiang. Experiment research on damping waves for vegetation embankment[D]. Urumqi: Xinjiang Agricultural University, 2005. [6] 周悦, 董增川, 曹海锦, 等. 刚柔组合型植被消浪特性的试验研究[J]. 水力发电学报, 2019, 38(3): 32−39. doi: 10.11660/slfdxb.20190304Zhou Yue, Dong Zengchuan, Cao Haijin, et al. Experimental study on wave attenuation characteristics of rigid-flexible combined wavebreak forests[J]. Journal of Hydroelectric Engineering, 2019, 38(3): 32−39. doi: 10.11660/slfdxb.20190304 [7] Yao Peng, Chen Hui, Huang Bensheng, et al. Applying a new force-velocity synchronizing algorithm to derive drag coefficients of rigid vegetation in oscillatory flows[J]. Water, 2018, 10(7): 906. doi: 10.3390/w10070906 [8] Mazda Y, Magi M, Kogo M, et al. Mangroves as a coastal protection from waves in the Tong King delta, Vietnam[J]. Mangroves and Salt Marshes, 1997, 1(2): 127−135. doi: 10.1023/A:1009928003700 [9] Quartel S, Kroon A, Augustinus P G E F, et al. Wave attenuation in coastal mangroves in the Red River Delta, Vietnam[J]. Journal of Asian Earth Sciences, 2007, 29(4): 576−584. doi: 10.1016/j.jseaes.2006.05.008 [10] 曹大正, 王银生, 张冬然, 等. 互花米草在吹填筑挡工程上的试验与应用[J]. 中国工程科学, 2005, 7(7): 14−23. doi: 10.3969/j.issn.1009-1742.2005.07.003Cao Dazheng, Wang Yinsheng, Zhang Dongran, et al. Application of Spartina alterniflora on blow-fill-construct sea wall engineering[J]. Engineering Science, 2005, 7(7): 14−23. doi: 10.3969/j.issn.1009-1742.2005.07.003 [11] 李志强, 谢石昌, 张会领, 等. 湛江市观海长廊红树林种植对岸滩影响初步研究[C]//中国海洋学会海洋工程分会. 第十四届中国海洋(岸)工程学术讨论会论文集(上册). 北京: 海洋出版社, 2009, 3: 745−747.Li Zhiqiang, Xie Shichang, Zhang Huiling, et al. Preliminary study on the influence of mangrove planting on the bank of Guanhai promenade in Zhanjiang City[C]//Chinese Ocean Society. Proceedings of the 14th China Ocean (Ashore) Engineering Symposium (Volume I). Beijing: China Ocean Press, 2009, 3: 745−747. [12] 田野. 广东湛江红树林消波效应初步研究[D]. 咸阳: 西北农林科技大学, 2014.Tian Ye. The preliminary study of wave attenuation by mangrove forest in Guangdong Province, Zhanjiang City[D]. Xianyang: Northwest A&F University, 2014. [13] Bai Yuchuan, Jiang Changbo, Shen Huanting. Large eddy simulation for wave breaking in the surf zone[J]. China Ocean Engineering, 2001, 15(4): 541−552. [14] Bai Yuchuan, Ng C O. Large eddy simulation for plunge breaker and sediment suspension[J]. China Ocean Engineering, 2002, 16(2): 151−164. [15] 李绍武, 李春颖, 谷汉斌, 等. 一种改进的近岸波浪破碎数值模型[J]. 水科学进展, 2005, 16(1): 36−41. doi: 10.3321/j.issn:1001-6791.2005.01.008Li Shaowu, Li Chunying, Gu Hanbin, et al. Improved numerical model for nearshore wave breaking[J]. Advances in Water Science, 2005, 16(1): 36−41. doi: 10.3321/j.issn:1001-6791.2005.01.008 [16] Dalrymple R A, Kirby J T, Hwang P A. Wave diffraction due to areas of energy dissipation[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1984, 110(1): 67−79. doi: 10.1061/(ASCE)0733-950X(1984)110:1(67) [17] Mendez F J, Losada I J. An empirical model to estimate the propagation of random breaking and nonbreaking waves over vegetation fields[J]. Coastal Engineering, 2004, 51(2): 103−118. doi: 10.1016/j.coastaleng.2003.11.003 [18] 杨建民. 海岸带边坡防浪林消浪理论与实验研究[J]. 海洋通报, 2008, 27(2): 16−21. doi: 10.3969/j.issn.1001-6392.2008.02.003Yang Jianmin. Analytical solution and physical model test of wave protection forest on coastal zones[J]. Marine Science Bulletin, 2008, 27(2): 16−21. doi: 10.3969/j.issn.1001-6392.2008.02.003 [19] 唐军, 沈永明, 崔雷. 基于抛物型缓坡方程模拟近岸植被区波浪传播[J]. 海洋学报, 2011, 33(1): 7−11.Tang Jun, Shen Yongming, Cui Lei. Modeling coastal water wave propagation in vegetation field based on parabolic mild slope equation[J]. Haiyang Xuebao, 2011, 33(1): 7−11. [20] Maza M, Lara J L, Losada I J. Tsunami wave interaction with mangrove forests: a 3-D numerical approach[J]. Coastal Engineering, 2015, 98: 33−54. doi: 10.1016/j.coastaleng.2015.01.002 [21] Zhu Ling, Chen Qin. Effects of triad interactions on wave attenuation by vegetation[J]. Journal of Engineering Mechanics, 2017, 143(9): 04017100. doi: 10.1061/(ASCE)EM.1943-7889.0001328 [22] Massel S R, Furukawa K, Brinkman R M. Surface wave propagation in mangrove forests[J]. Fluid Dynamics Research, 1999, 24(4): 219−249. doi: 10.1016/S0169-5983(98)00024-0 [23] Coastal Engineering Research Center, U. S. Shore Protection Manual[S]. Washington: Army Corps of Engineers, 1984. [24] 岩垣雄一, 酒井哲郎. Steam Function Theory による斜面上の碎波の水粒子速度の表现について[C]//第21回海岸工学讲演会论文集. 神户: 日本土木工程学会, 1974: 27−32.Iwagkai Y, Sakai T. The velocity representation of water particles breaking waves on a slope based on Steam Function Theory[C]//Proceedings of the 21st Lecture on Coastal Engineering. Kobe: Japan Society of Civil Engineering, 1974: 27−32. [25] 陈妙福, 赵耀南, 王常生. 倾斜底坡上波浪的传播与破碎[J]. 水动力学研究与进展, 1992, 7(2): 192−199.Chen Miaofu, Zhao Yaonan, Wang Changsheng. Propagation and breaking of waves on sloping beaches[J]. Journal of Hydrodynamics, 1992, 7(2): 192−199. [26] 郭晓宇, 王本龙, 刘桦. 波浪在滨海生态防护植物群落内传播特性的实验研究[C]//第二十五届全国水动力学研讨会暨第十二届全国水动力学学术会议文集. 北京: 海洋出版社, 2013: 602−607.Guo Xiaoyu, Wang Benlong, Liu Hua. Experimental study on the propagation characteristics of waves in coastal ecological protection plant communities[C]//The 25th National Hydrodynamics Symposium and the 12th National Hydrodynamics Academic Conference. Beijing: China Ocean Press, 2013: 602−607. -
计量
- 文章访问数: 492
- HTML全文浏览量: 411
- PDF下载量: 97
- 被引次数: 0
