适于模拟不规则水域波浪的缓坡方程两种数值模型比较

李巧生; 唐军; 吕义港

doi:10.3969/j.issn.0253-4193.2020.01.004

适于模拟不规则水域波浪的缓坡方程两种数值模型比较

doi: 10.3969/j.issn.0253-4193.2020.01.004

1.
苏州市航道管理处，江苏苏州 215008
2.
大连理工大学海岸和近海工程国家重点实验室，辽宁大连 116023
3.
嘉兴市交通工程质量安全管理服务中心，浙江嘉兴 314001

基金项目: 国家重点研发计划（2017YFC1404200）；国家自然科学基金（51579036）；中央高校基本科研业务费（DUT19LAB13）。

详细信息

作者简介:
李巧生（1985—），男，江苏省盐城市人，从事港口与航道整治工程及近岸水动力研究。E-mail：LQS20056789@163.com

中图分类号: P731.22
计量
- 文章访问数: 354
- HTML全文浏览量: 71
- PDF下载量: 86
- 被引次数: 0
出版历程
- 收稿日期: 2018-11-14
- 修回日期: 2018-12-21
- 网络出版日期: 2021-04-21
- 刊出日期: 2020-01-25

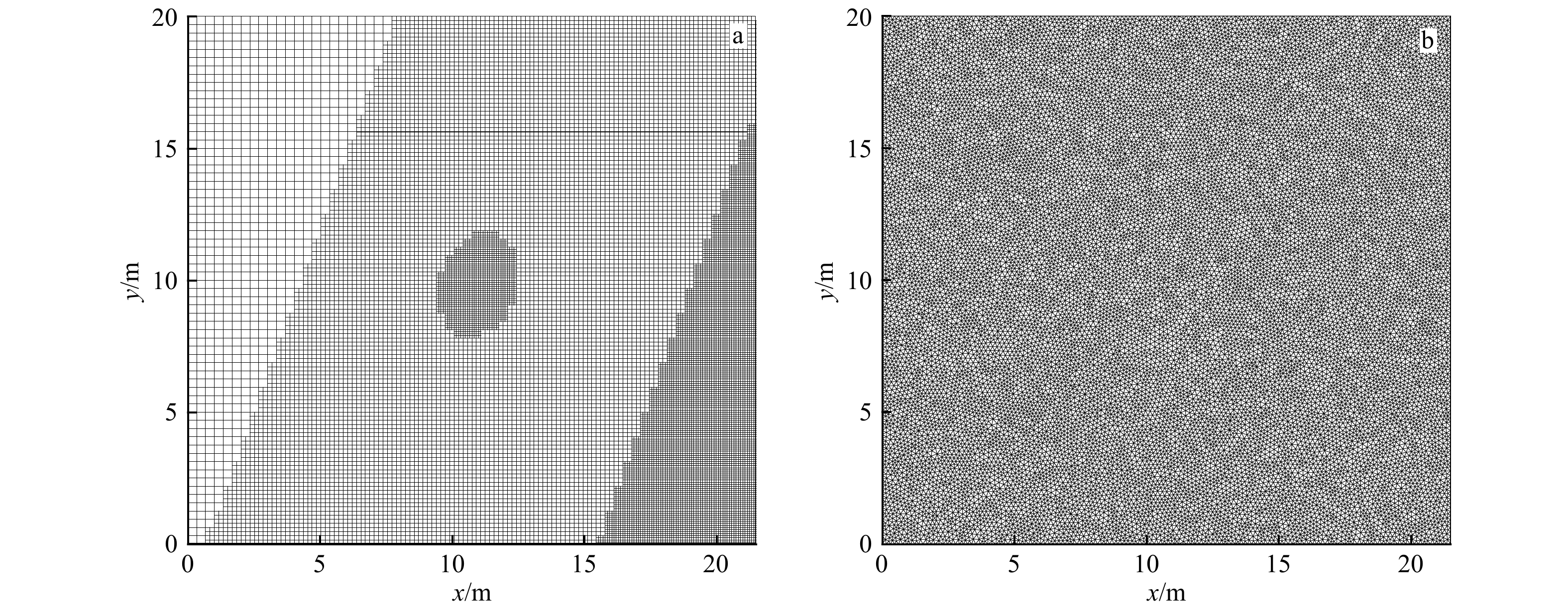
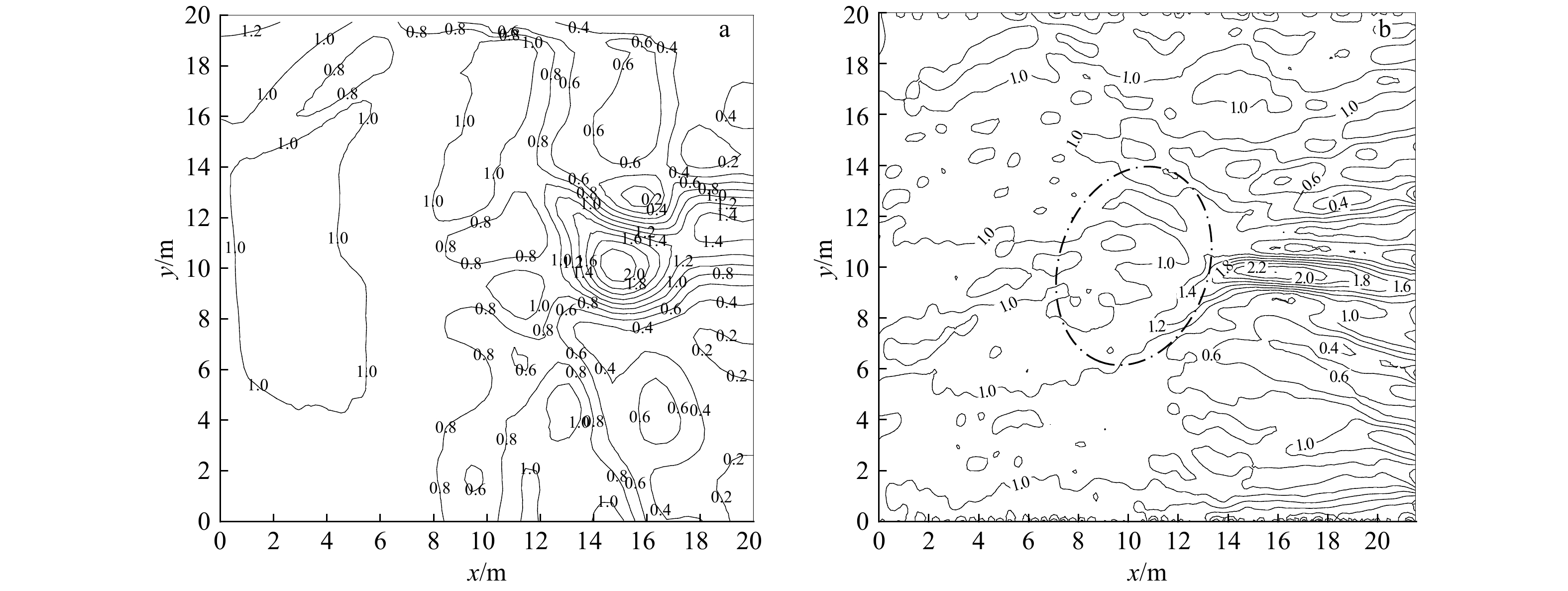
Comparisons of the two numerical models of elliptic mild-slope equation for wave propagation in irregular coastal zones

1.
Suzhou Waterway Administration Office, Suzhou 215008, China
2.
State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116023, China
3.
Jiaxing City Traffic Engineering Quality and Safety Management Service Center, Jiaxing 314001, China

摘要

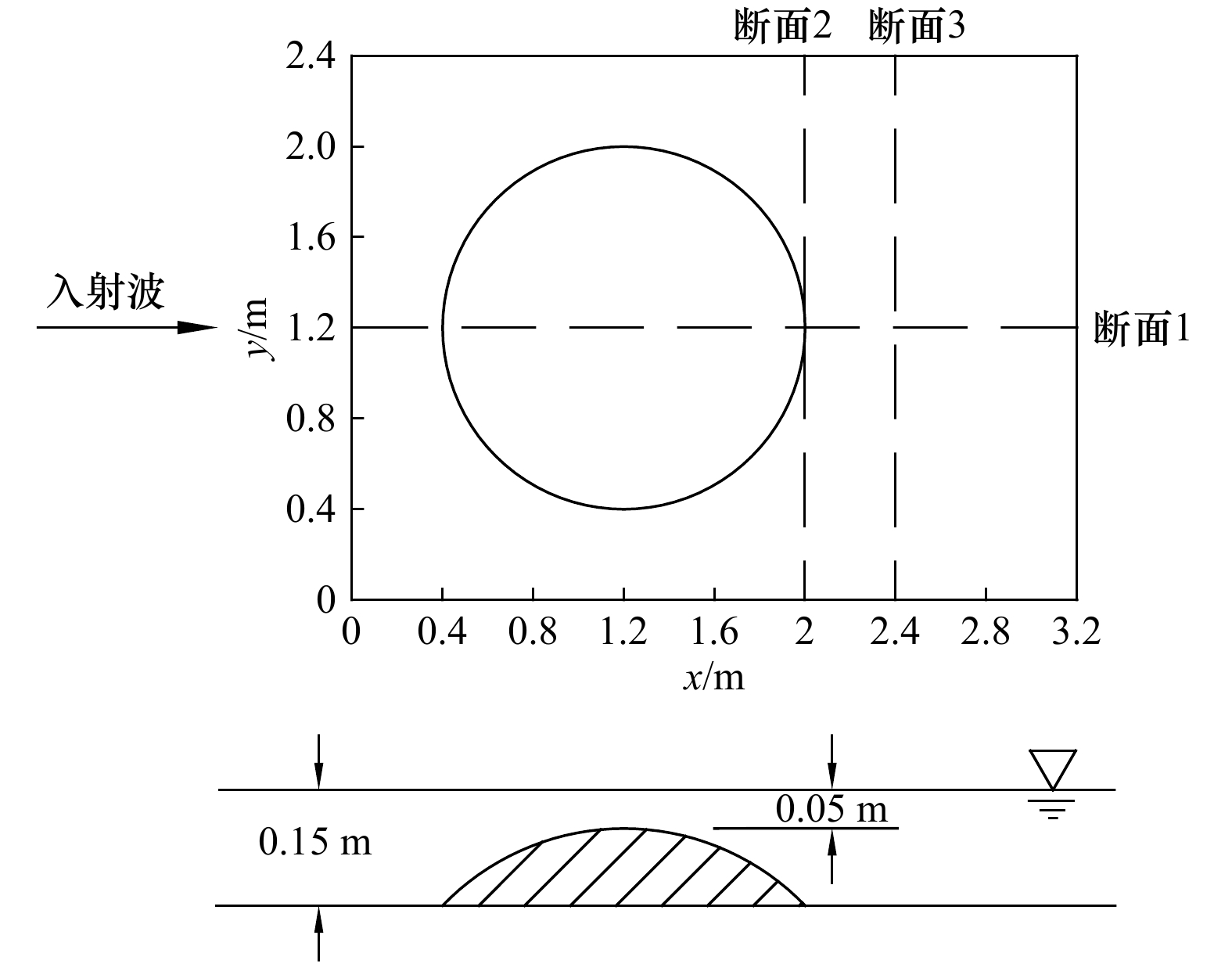
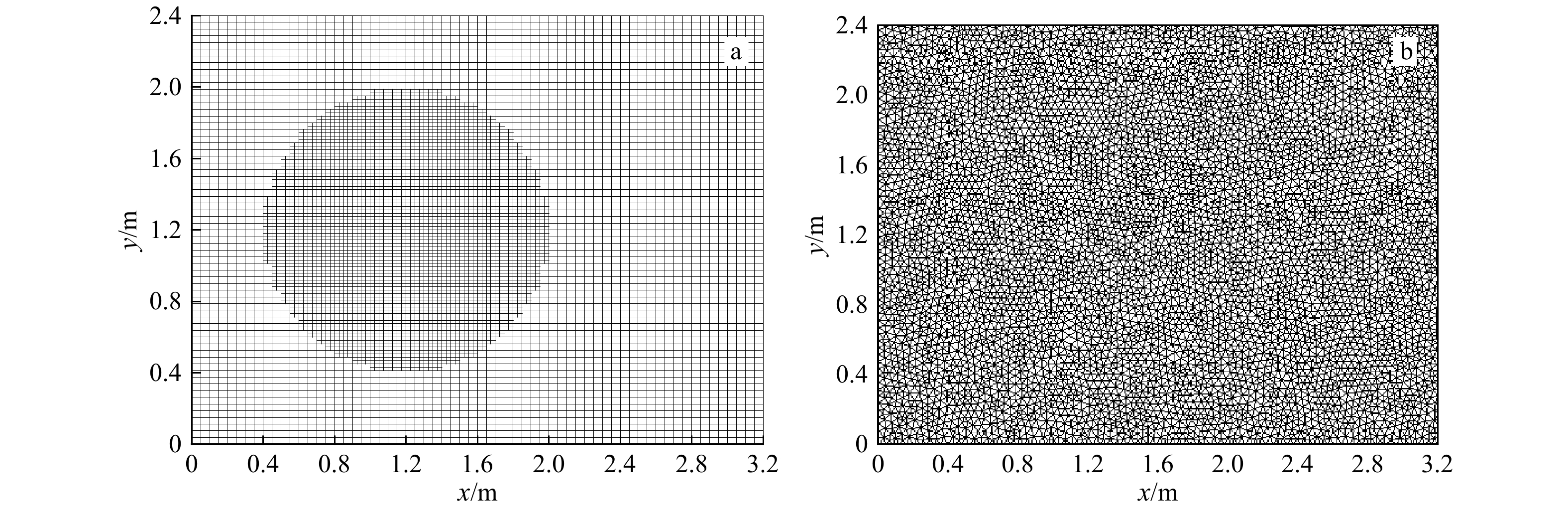
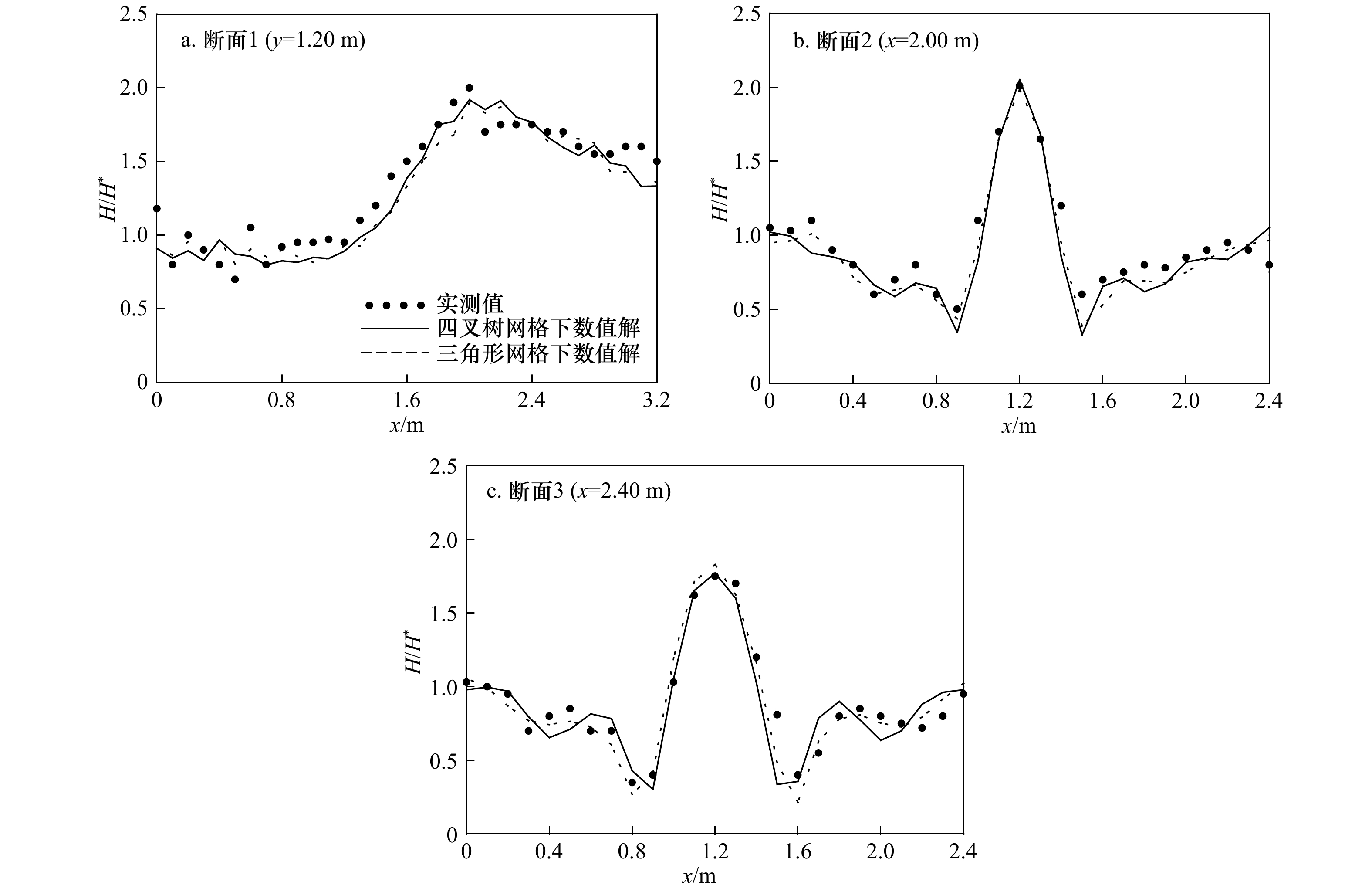
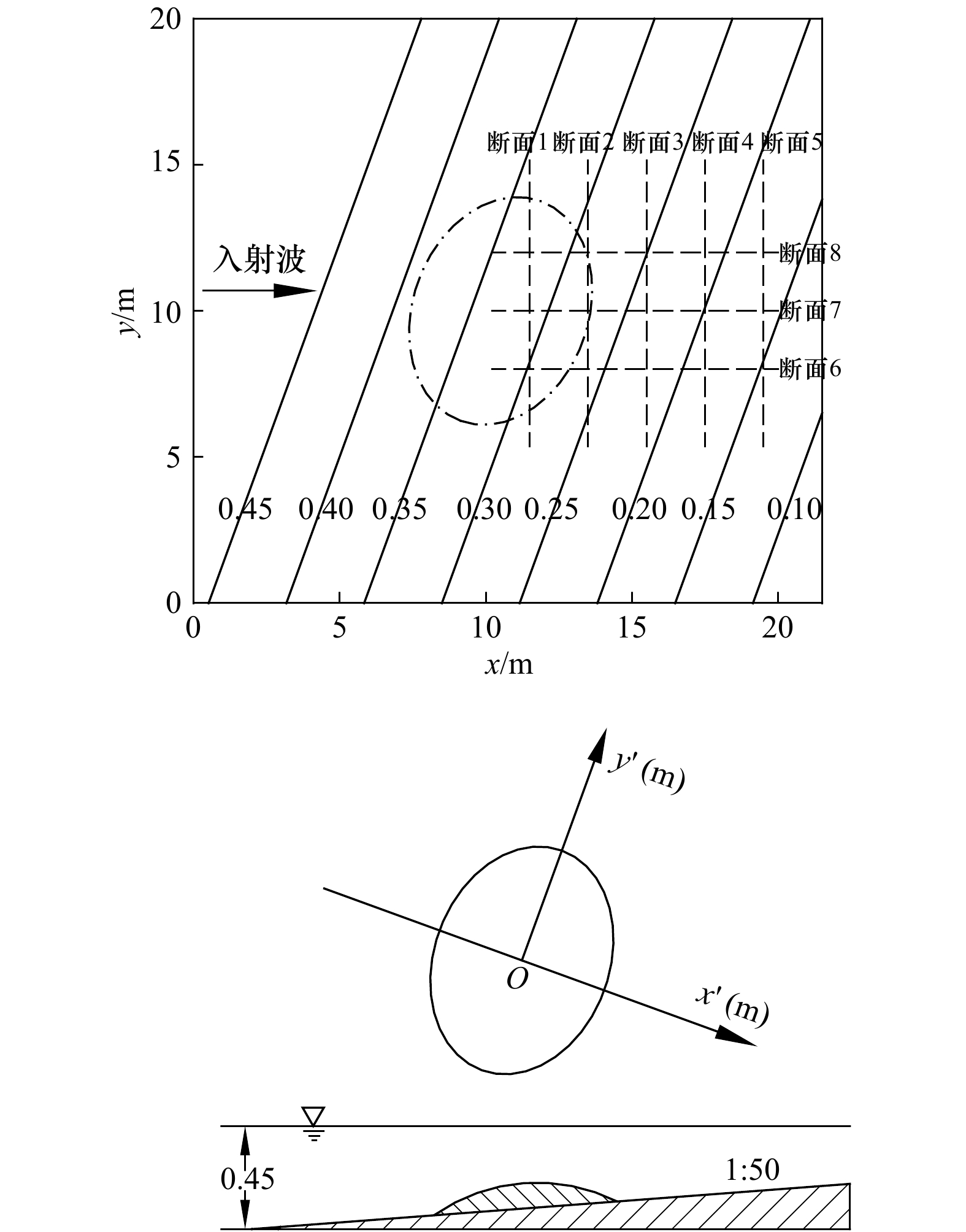
摘要: 本文分析比较了适于不规则水域波浪模拟的椭圆型缓坡方程两种数值模型。两种数值模型均采用有限体积法离散，分别基于四叉树网格和非结构化三角形网格建立。首先结合近岸缓坡地形上波浪传播的经典物理模型实验对两种数值模型分别进行了验证，并结合计算结果对比分析了两种模型的计算精度和效率。计算结果表明，两种数值模型均可有效地模拟近岸波浪的传播变形；相对非结构化三角形网格下的模型，基于四叉树网格建立的数值模型在数值离散和求解过程中无需引入形函数、不产生复杂的交叉项，离散简单，易于程序实现，且节约计算存储空间，计算效率高。
- 波浪 /
- 数值模拟 /
- 椭圆型缓坡方程 /
- 四叉树网格 /
- 非结构化网格
Abstract: In this paper, two numerical models of elliptic mild-slope equation for coastal wave propagation in coastal zones are compared and analyzed. The two numerical models are developed by using finite volume method respectively on adaptive quadtree mesh and triangular unstructured mesh. The numerical models are firstly used to simulate wave propagation and deformation on circle and elliptic shores, and the computational efficiencies are compared and analyzed based on the numerical results. The numerical results show that both of the two numerical models are effective in simulating coastal wave propagation and deformation. Compared with the numerical model on unstructured triangular mesh, the numerical model on quadtree mesh is more concise and easy for numerical implementation as it does not involve complex cross-terms due to model transformation in the process of numerical discretization. What’s more, the numerical model on quadtree mesh is more efficiency in saving computing time and storage space.
- wave /
- numerical simulation /
- elliptic mild-slope equation /
- quadtree grid /
- unstructured grid

HTML全文

图 1 四叉树网格不同分级单元间的通量计算

Fig. 1 Flux across different graded cell interfaces

下载: 全尺寸图片幻灯片

图 2 格林函数法计算示意图

Fig. 2 Diagram of Green function method

下载: 全尺寸图片幻灯片

图 3 圆形浅滩计算域地形示意图

Fig. 3 Topography of a circular shoal zone

下载: 全尺寸图片幻灯片

图 4 圆形浅滩计算域网格图

a. 自适应四叉树网格图；b. Delaunay三角化网格图

Fig. 4 Numerical grids of a circular shoal zone

a. Adaptive quadtree grid graph; b. Delaunay triangulated grid graph

下载: 全尺寸图片幻灯片

图 5 圆形浅滩数值模拟相对波高等值线图

a. 自适应四叉树模拟的相对波高；b. Delaunay三角化模拟相对波高

Fig. 5 Contours of simulated wave height for wave propagation on a circular shoal

a. Relative wave height of adaptive quadtree simulation; b. relative wave height of Delaunay triangulated simulation

下载: 全尺寸图片幻灯片

图 6 圆形浅滩地形上波高数值解与实测值^[16]的比较

Fig. 6 Comparison between numerical simulated and measured^[16] wave heights on a circular shoal

下载: 全尺寸图片幻灯片

图 7 椭圆形浅滩计算域地形

Fig. 7 Topography of a elliptic shoal zone

下载: 全尺寸图片幻灯片

图 8 椭圆形浅滩计算域网格图

a. 自适应四叉树网格图；b. Delaunay三角化网格图

Fig. 8 Numerical grids of an elliptic shoal zone

a. Adaptive quadtree grid graph; b. Delaunay triangulated grid graph

下载: 全尺寸图片幻灯片

图 9 椭圆形浅滩数值模拟相对波高等值线图

a. 自适应四叉树模拟的相对波高图；b. Delaunay三角化模拟相对波高图

Fig. 9 Contours of simulated wave height for wave propagation on an elliptic shoal

a. Relative wave height of adaptive quadtree simulation; b. relative wave height of Delaunay triangulated simulation

下载: 全尺寸图片幻灯片

图 10 椭圆形浅滩地形上波高数值解与实测值^[17]的比较

Fig. 10 Comparison between numerical simulated and measured ^[17] wave heights on an elliptic shoal

下载: 全尺寸图片幻灯片

表 1 圆形浅滩地形上两种计算网格下的模型效率比较

Tab. 1 Comparison of the efficiency for the model in two kind of numerical grids on a circular shoal

	网格个数	网格步长/m	迭代步数	计算时间/s	计算精度
自适应网格下的模型	7 288	0.025×0.018 75， 0.05×0.037 5	445	4.906	1.0×10⁻⁷
Delaunay三角化网下的模型	8 278	0.03	630	6.51	1.0×10⁻⁷

下载: 导出CSV

表 2 椭圆形浅滩地形上两种计算网格下的模型效率比较

Tab. 2 Comparison of the efficiency for the model in two kind of numerical grids on an elliptic shoal

	网格个数	网格步长/m	迭代步数	计算时间/s	计算精度
自适应网格下的模型	11 308	0.335 937 5×0.312 5， 0.167 968 75×0.156 25， 0.083 984 375×0.078 125	445	97.109	1.0×10⁻⁷
非结构化网格下的模型	30 618	0.12	630	151.14	1.0×10⁻⁷

下载: 导出CSV

参考文献(17)

[1]	Berkhoff J C W. Computation of combined refraction-diffraction[C]//Proceeding of the 13th International Conference on Coastal Engineering. Vancouver: ASCE, 1972: 471−490.
[2]	Tang Jun, Shen Yongming, Zheng Yonghong, et al. An efficient and flexible computational model for solving the mild slope equation[J]. Coastal Engineering, 2004, 51(2): 143−154. doi: 10.1016/j.coastaleng.2003.12.005
[3]	魏美芳, 唐军, 沈永明. 非结构化网格下椭圆型缓坡方程的数值求解[J]. 海洋学报, 2009, 31(2): 159−164. Wei Meifang, Tang Jun, Shen Yongming. Numerical simulation of elliptic mild-slope equation on unstructured grid[J]. Haiyang Xuebao, 2009, 31(2): 159−164.
[4]	唐军, 李巧生, 沈永明. 四叉树网格下的椭圆型缓坡方程数值模型研究[J]. 海洋学报, 2013, 35(5): 162−168. Tang Jun, Li Qiaosheng, Shen Yongming. Numerical study of the elliptic mild-slope equation for water wave in quadtree grid system[J]. Haiyang Xuebao, 2013, 35(5): 162−168.
[5]	倪云林, 滕斌, 丛龙飞. 修正型缓坡方程的有限元模型[J]. 海洋学报, 2017, 39(1): 104−110. Ni Yunlin, Teng Bin, Cong Longfei. FEM model of the modified mild slope equation[J]. Haiyang Xuebao, 2017, 39(1): 104−110.
[6]	Tang Jun, Li Qiaosheng, Meng Xiangyu, et al. Numerical modeling of coastal waves and nearshore currents on adaptive quadtree grids[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2018, 144(5): 04018011. doi: 10.1061/(ASCE)WW.1943-5460.0000463
[7]	Guo Yakun, Wu Xiuguang, Pan Cunhong, et al. Numerical simulation of the tidal flow and suspended sediment transport in the Qiantang Estuary[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2011, 138(3): 192−202.
[8]	林伟波, 王义刚. 瓯江口海域悬浮泥沙输运特性研究[J]. 水力发电学报, 2013, 32(2): 119−128. Lin Weibo, Wang Yigang. Study on characteristics of suspended sediment transport in Oujiang River Estuary[J]. Journal of Hydroelectric Engineering, 2013, 32(2): 119−128.
[9]	Zhang Mingliang, Wu Weiming, Lin Lihua, et al. Coupling of wave and current numerical model with unstructured quadtree grid for nearshore coastal waters[J]. Science China Technological Sciences, 2012, 55(2): 568−580. doi: 10.1007/s11431-011-4643-2
[10]	Wu Teng, Li Xiuxia. Vertical 2-d mathematical model of sediment silting in dredged channel[J]. Journal of Hydrodynamics, Series B, 2010, 22(S5): 628−632.
[11]	华祖林, 刘晓东, 王童远, 等. 嵌套叉树网格的FDS数值模式在近海水域污染混合区计算中的应用[J]. 水科学进展, 2003, 14(3): 305−310. doi: 10.3321/j.issn:1001-6791.2003.03.011 Hua Zulin, Liu Xiaodong, Wang Tongyuan, et al. Application of the nested adaptive quadtree grids FDS numerical model to the pollution zone for inshore water region[J]. Advances in Water Science, 2003, 14(3): 305−310. doi: 10.3321/j.issn:1001-6791.2003.03.011
[12]	刘晓东, 华祖林, 赵玉萍. 基于四叉树网格的Godunov型二维水流数值计算模式[J]. 河海大学学报: 自然科学版, 2002, 30(6): 6−10. Liu Xiaodong, Hua Zulin, Zhao Yuping. Quad-tree meshes based Godunov-type 2-D flow numerical model[J]. Journal of Hohai University: Natural Sciences, 2002, 30(6): 6−10.
[13]	付仲良, 胡玉龙, 翁宝凤, 等. M-Quadtree索引: 一种基于改进四叉树编码方法的云存储环境下空间索引方法[J]. 测绘学报, 2016, 45(11): 1342−1351. Fu Zhongliang, Hu Yulong, Weng Baofeng, et al. M-Quadtree Index: a spatial index method for cloud storage environment based on Modified Quadtree coding approach[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(11): 1342−1351.
[14]	陶文栓. 计算传热学的近代进展[M]. 北京: 科学出版社, 2001. Tao Wenshuan. Recent Advances in Computational Heat Transfer[M]. Beijing: Science Press, 2001.
[15]	高晓沨. 2D-Delaunay三角网格的数据结构与遍历[J]. 天津理工大学学报, 2006, 22(2): 66−69. Gao Xiaofeng. Data structure and traverse of 2D-Delaunay triangulation[J]. Journal of Tianjin University of Technology, 2006, 22(2): 66−69.
[16]	Ito Y, Tanimoto K. A method of numerical analysis of wave propagation-application to wave diffraction and refraction[C]//Proceeding of the 13th Coastal Engineering Conference. Vancouver: ASCE, 1972, 1: 503–522.
[17]	Berkhoff J C W, Booy N, Radder A C. Verification of numerical wave propagation models for simple harmonic linear water waves[J]. Coastal Engineering, 1982, 6(3): 255−279. doi: 10.1016/0378-3839(82)90022-9