Variational method of ocean three-dimensional thermohaline structure and its acoustic performance evaluation
-
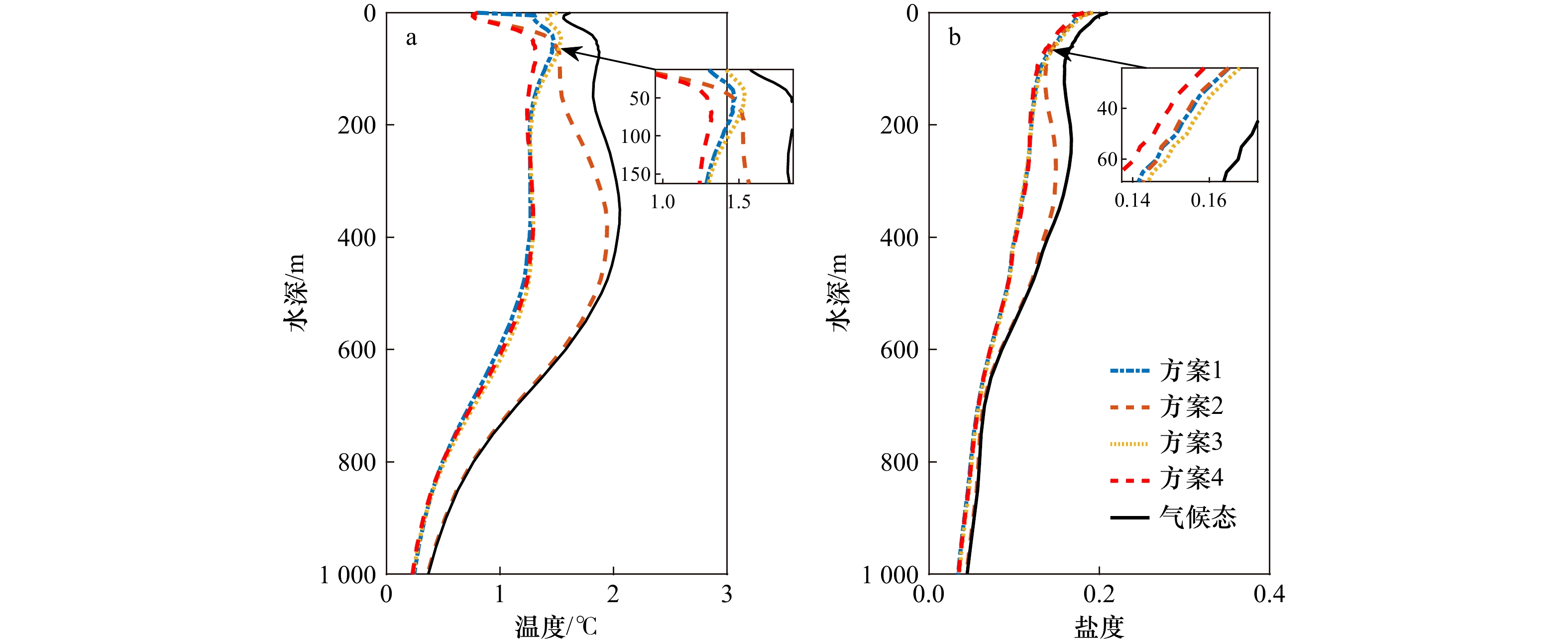
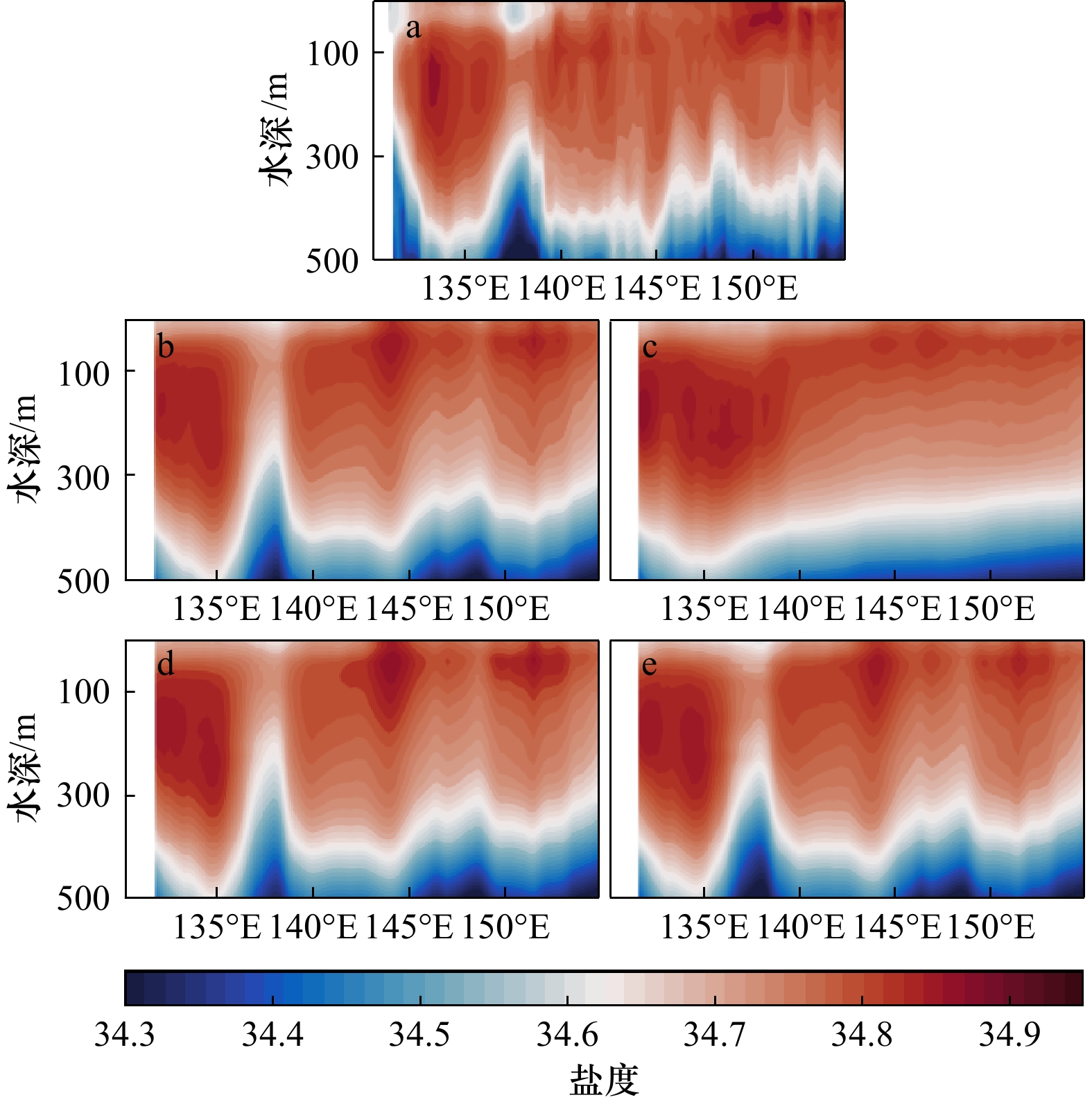
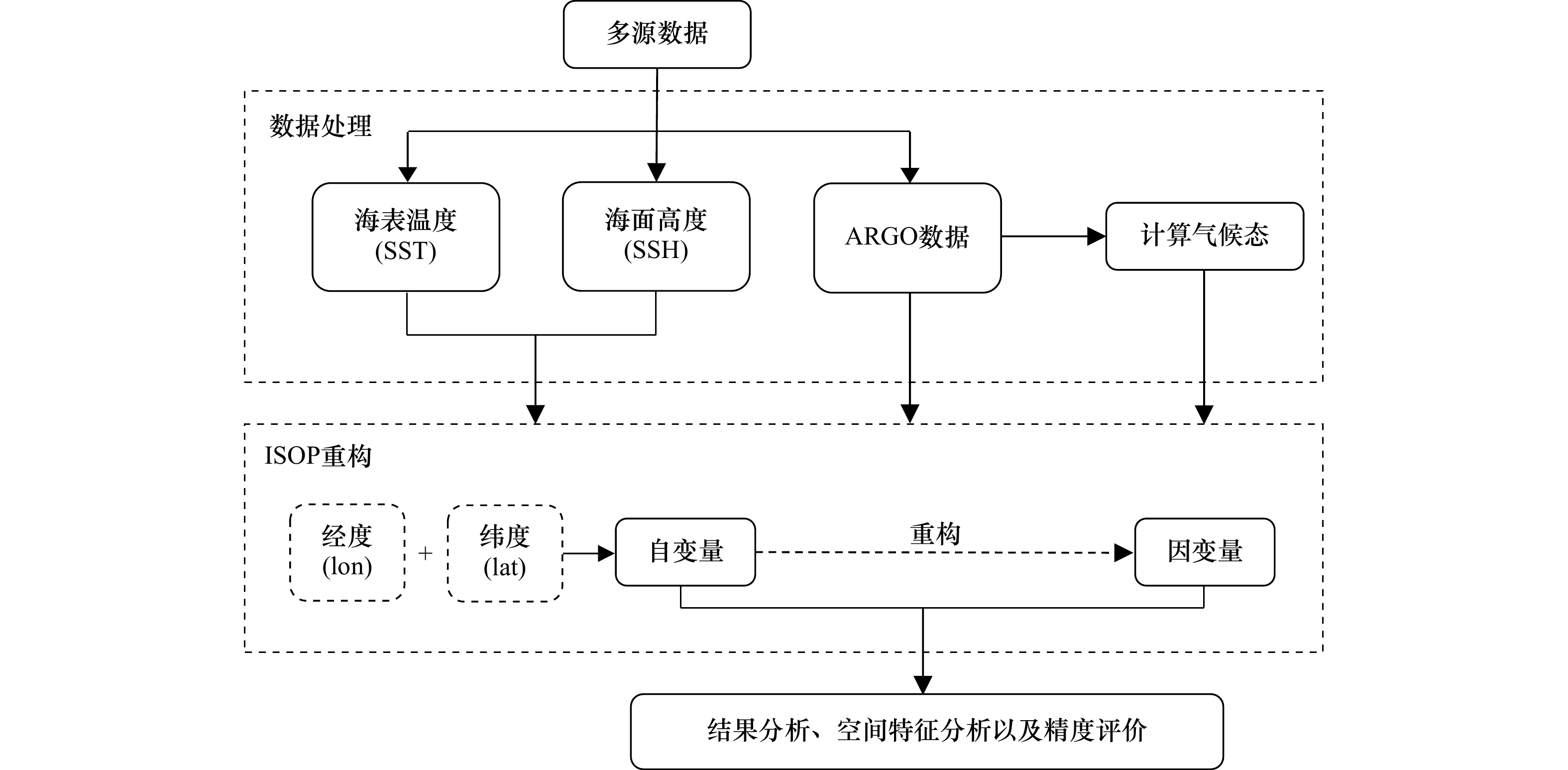
摘要: 基于卫星海面观测重构水下三维温盐场并获取声场特性的研究，在军事海洋等领域具有重要的实践应用价值，但其效果不但受到重构方法的影响，而且随所利用的卫星海面观测信息的不同而改变。本研究基于美国海军最新研发的利用变分法的温盐场重构，研究了利用卫星海面高度、海面温度或二者联合数据，及考虑温盐垂向梯度对重构三维温盐及声场特性的影响。结果发现，集合了海表温度、海表高度和温盐垂直梯度3个约束项的重构方案精度最高，其重构温度场和盐度场的平均误差分别为1.08℃、0.11，该方案也能更好地捕捉温盐场的空间特征。通过分析不同方案的空间特征，海面温度主要作用于捕捉混合层以浅区域的温盐特征，这对表面声学层（Sound Layer Depth, SLD）的影响较大；海面高度和温盐场的垂直梯度对混合层以深区域的反演精度都有较高提升，能够影响整个声速剖面的准确性。根据声学特征分析， SST、SSH与温盐垂直梯度同时约束时，SLD以浅声速与HYCOM相差最小，约为1 m/s；没有梯度约束时，SLD与HYCOM相差约为1.5 m/s，未能很好地反映海表面声道特征；表明声道特征对海表温度与梯度约束均较为敏感。Abstract: Research on the reconstruction of underwater three-dimensional temperature and salinity fields and the acquisition of acoustic field characteristics based on satellite sea surface observations has significant practical value in military oceans and other fields. However, its effectiveness not only depends on the reconstruction method but also changes with different sea surface observations used. Although there are few reports on related research, it has significant guiding value for the design of satellite sea surface observation schemes. In this study, based on the latest variational method applied by the US Navy, the influence of the vertical gradient of temperature and salinity and the sea surface height, sea surface temperature, and their joint use on the reconstruction of three-dimensional temperature and salinity and acoustic field characteristics were investigated. The results showed that the reconstruction scheme incorporating the three constraint items had the highest accuracy, with average reconstruction errors of 1.08℃ for temperature field and 0.11 for salinity field, and could better capture the spatial features of the temperature and salinity fields. By analyzing the spatial characteristics of different schemes, the sea surface temperature mainly plays a role in capturing the temperature and salinity characteristics of the shallow region of the mixing layer, which has a great influence on the Sound Layer Depth (SLD). Both the sea surface height and the vertical gradient of warm salt field can improve the inversion accuracy of mixed layer and deep area, which can affect the accuracy of the whole sound velocity profile. According to the analysis of acoustic characteristics, when SST, SSH, and the gradient were constrained simultaneously, the SLD had the smallest difference from HYCOM in the shallow sound speed, which was about 1 m/s. When there was no gradient constraint, the SLD differed significantly from HYCOM and failed to reflect the surface duct characteristics. It can be seen that the surface duct is more sensitive to sea surface temperature and gradient constraints.
-
1. 引言
海洋对于一个国家是至关重要的，在国防、涉海经济与环境等方面都有广泛且深远的影响[1–2]。对于广阔的海洋，各国已经开展了很多海洋数据的调查，比如ARGO观测计划（Array for Real time Geostrophic Oceanography）等，但其捕捉海洋信息的能力还远远不够。因为水声的折射率由温、盐、深的函数计算得到，利用三维温盐场可以获取三维声学场，在水下通信、定位等实践中有广泛的用途。因此，基于海面信息与次表面温盐场的动力约束关系，将海洋遥感海面观测映射到次表层以获取其温盐结构，成为了科研学者研究的热点之一。而三维温盐场作为重要海洋动力环境之一，其重构工作能够为深入剖析海洋环境对碳库、碳汇体的影响以及全球碳综合治理和生态环境保护提供有力支撑[3]。
目前，三维温盐场的重构方法主要有动力学方法[4]、统计学法[5–6]、人工智能法[7–8]、变分法[9–11]。其中动力学方法主要通过采用数值模型或一定的动力约束条件，将海表温度及海面高度等海表数据转化为动力模型的控制变量，实现表面数据到水下温盐的映射[12]，如SQG法[13]、iSQG法[14]等。Fox等[15]通过经验回归建立了海面高度、海面温度与次表层温盐的回归模型，并在此基础上发展为美国海军服务的MODAS（The Modular Ocean Data Assimilation System ）系统，但该系统缺乏温盐场垂直梯度的约束；在此基础上，王喜东[6]采用回归分析方法统计出海面温度异常、海面高度异常与温度剖面异常之间的关系，并利用卫星海表面温度和卫星海面高度重构了三维温度场。人工智能重构主要集中在大尺度温盐场重构上，Su等[16–17]采用支持向量机、随机森林等多种方法对全球海洋温盐场重构进行探索并取得较好的精度结果，然而对于小尺度的温盐场重构效能尚不明确。Fujii和Kamachi[18]最早开始利用变分法进行三维温盐场重构，然而其变分重构过程并未考虑梯度约束；Helber等[10]为解决垂向梯度问题，采用变分法并引入了梯度约束，以提高重构温盐场在垂向上的描述能力，该方法发展成为美国海军新一代的ISOP（Improved Synthetic Ocean Profile）系统；He等[11]基于ISOP的方法技术，对ISOP重构方法进行了改进，增加了卫星海面盐度（SSS）的约束和垂直投影算子。相对于其他方法，ISOP一方面兼顾了局部海洋的温盐特性；另一方面引入温盐梯度约束来改善温盐场的垂向特征。
重构三维温盐场的应用主要在中尺度现象的捕捉以及大尺度信息气候变化监测。汤博[19]通过经验回归模型重构三维温度场，其结果能清晰地反映出海洋断面的垂直结构及中尺度涡旋特征。王喜东[6]利用重构温盐场对吕宋海峡西侧附近由中尺度涡导致的热盐和体积的输运及其对南海上层热盐平衡的影响展开了研究。Su等[20]利用人工神经网络重构全球三维温盐场，并分析近30年来总热含量，其趋势与多种同化数据基本一致。而受海面观测精度的影响，目前三维温盐场在小尺度的捕捉能力尚未可知。此外，关于重构过程中不同输入对三维温盐场重构效能的影响探讨也较少，且缺乏对水声通信、反潜探测等声学效能方面的深入研究。
本研究首先将研究区域网格化，在每个网格内，分别计算每个月的系数矩阵，最大程度上减小了季节性差异对反演结果的影响。基于ISOP变分法，本文设计了4种重构方案（表1），并从重构精度、空间特征、声学效能等多方面评估不同参量对温盐重构的影响。通过评估不同约束项重构敏感度，为进一步细化、优化、多元化约束项，如增加海表盐度约束、海表风场约束或海表流场约束来提高重构精度。最后基于声场信息与温盐场的关系，讨论了不同方案声学反演的声道传播情况，为温盐反演在声场预报的应用提供参考。
表 1 4种研究方案及其主要约束条件Table 1. Four research schemes and their main constraints方案 主要约束条件 表达式 方案1 SST + SSH J = J1 + J3 + J5 + J7 + J9 + J10 方案2 SST + Grad J = J1 + J2 + J3 + J4 + J5 + J6 + J7 + J8 + J9 方案3 SSH + Grad J = J1 + J2 + J3 + J4 + J5 + J6 + J7 + J8 + J10 方案4 SST + SSH + Grad J = J1 + J2 + J3 + J4 + J5 + J6 + J7 + J8 + J9 + J10 2. 数据
本文使用的历史温盐场观测为ARGO数据集 （
https://data-ARGO.ifremer.fr/geo/pacific_ocean/ ），而卫星海表面输入主要有海面高度（SSH）与海面温度（SST），其中海面温度观测选择REMSS（Remote Sensing Systems）多源卫星融合的Daily SST产品（https://data.remss.com/sst/daily/mw/v05.0/netcdf/ ），其分辨率为0.25° × 0.25°。卫星观测海表面高度数据来自于Aviso+提供的Daily SSH格网产品（https://cds.climate.copernicus.eu/cdsapp#!/dataset/satellite-sea-level-global?tab=form ），分辨率为0.25° × 0.25°。本文还选择了WOA18（World Ocean Atlas 18）、GDEM3.0提供的月气候态以及高分辨率HYCOM同化数据集，来进一步评估三维温盐场的重构精度与效能，其中HYCOM分辨率为0.08°，本文将其统一插值为(1/4)°进行对比分析。本文选择黑潮延伸体附近25°～40°N, 130°～155°E区域为重构研究区，收集了从2000–2020年内总计56 000多条温度和盐度的剖面数据。因实测观测剖面会存在质量问题，在重构前对数据进行预处理，其主要包括以下8个步骤：（1）删除剖面中空值数量占比大于80%的剖面；（2）删除连续的空值数量大于10个的剖面；（3）删除气候态数据为空值的剖面；（4）删除温盐具有剧烈震荡特征的剖面，本文通过对比ARGO温盐观测和气候态温盐场相邻深度的温盐梯度，删除梯度变化不符合气候态梯度的温盐剖面；（5）删除SSH和SST数据为空的剖面；（6）线性插值温盐剖面到WOA18气候态的标准深度；（7）根据时空位置进行海面观测与温盐剖面匹配；（8）采用线性回归法消除SSH的正压信号误差以及SST的系统误差[11, 22]。
3. 方法
3.1 重构方案概述
本研究基于ISOP方法开展黑潮延伸体海域三维温盐场的重构工作。首先通过对ARGO数据集进行筛选、插值等一系列预处理，构建历史观测数据集；然后利用历史观测计算区域内月平均温盐场，并储存参与计算气候态时历史观测的协方差矩阵；在重构过程中，通过输入的经度、纬度和时间，找到对应位置和时间的协方差矩阵，并将其与相应的海面观测SST与SSH代入重构模型进行计算，得到最终的重构温盐剖面。本文使用的ISOP重构模型，构造了集合气候态、海面观测、气候态梯度、第一猜测场等多项约束的代价方程，通过将重构所需的时空相关的系数矩阵与海面观测代入代价函数，通过变分法求解最优重构剖面，使其满足代价函数值最小，具体过程见流程图（图1）。
图 1 卫星海面观测三维温盐场重建及评估的具体流程图Figure 1. The specific flow chart of reconstruction of three-dimensional temperature and salinity field and its assessment using satellite sea surface observations3.2 气候态构建
在本文重构中，温盐场的月气候态数据有非常重要的作用。通常人们都会使用WOA数据集的年/月平均气候态，但WOA气候态计算时使用了各种类型的观测数据，会与ARGO实测数据的实际平均态存在差异，从而影响重构温盐场的精确度。因此本文借助Helber等[10]的方法，通过将ARGO温盐数据加权求均值，重新计算该数据集的月平均气候态，并且将该月平均气候态的深度信息与WOA气候态进行同步，以便于“新”气候态数据在文章中的应用。
将研究区域划分为0.25°分辨率的网格，计算每个网格点的温盐气候态。利用以网格点为中心，以东西和南北长度
$\Delta X$ 、$\Delta Y$ （单位：km）为范围的矩形区域，在特定时间内的所有剖面数据，计算每个网格点的平均态。在矩形区域内，给每个标准深度处所有剖面的温度和盐度分配权重，这个权重跟观测时间和观测点位置有关。随着深度的增加，温盐场季节性信号的强度会不断减小，其计算平均态可用的时间跨度就会增加。定义一个函数
${\delta _{{b}}}\left( {d - {d_{\mathrm{m}}}} \right)$ ，且只有当观测天数$d$ 在时间跨度范围内时${\delta _b}\left( {d - {d_{\mathrm{m}}}} \right) = 1$ ，${d_{\mathrm{m}}}$ 为每个月中心在该年的天数。其次，因为观测剖面距离网格点的位置越远，对该点气候态的贡献越小，定义距离衰减比例[10]为$$ {L}_{\theta }=\Delta X/\left[110·\mathrm{cos}\left({\lambda }_{a}/180\right)\right] ,\; {L_\lambda } = {{\Delta Y} \mathord{\left/ {\vphantom {{\Delta Y} {110}}} \right. } {110}} \text{，} $$ (1) 式中，
$\Delta X$ 和$\Delta Y$ 分别表示网格点为中心矩形区域东西和南北的长度（单位：km）。由时间和空间两方面的限制，定义第
$i$ 个剖面深度为$k$ 的权重[10]为$$ {w}_{k,\;i}={\delta }_{d}\left(d-{d}_{{\mathrm{m}}}\right)·\mathrm{exp}\left[-{\left(\frac{{\theta }_{i}-{\theta }_{a}}{{L}_{\theta }}\right)}^{2}-{\left(\frac{{\lambda }_{i}-{\lambda }_{a}}{{L}_{\lambda }}\right)}^{2}\right] \text{，} $$ (2) 式中，
${\lambda _i}$ 和${\theta _i}$ 为第$i$ 个观测剖面的经度和纬度；${\lambda _a}$ 和${\theta _a}$ 为网格点的经度和纬度。对每个格网内的温盐剖面加权求平均值，作为其网格点的气候态。3.3 变分法重构三维温盐场
三维温盐场重构的ISOP法，其实质是一种变分同化过程。其变分方程如下
$$ \begin{gathered} J = \underbrace {{{\left( {{\boldsymbol{x}} - {{\boldsymbol{x}}_{cl}}} \right)}^{\text{T}}}{{\boldsymbol{B}}^{ - 1}}\left( {{\boldsymbol{x}} - {{\boldsymbol{x}}_{cl}}} \right)}_{{J_1}} + \underbrace {{{\left( {{\boldsymbol{d}} - {{\boldsymbol{d}}_{cl}}} \right)}^{\text{T}}}{\boldsymbol{B}}_g^{ - 1}\left( {{\boldsymbol{d}} - {{\boldsymbol{d}}_{cl}}} \right)}_{{J_2}}+ \\ {\text{ }}{\text{ }}{\text{ }}{\text{ }} \underbrace {{{\left( {{{\boldsymbol{x}}_{fg}} - {\boldsymbol{x}}} \right)}^{\text{T}}}{{\boldsymbol{R}}^{ - 1}}\left( {{{\boldsymbol{x}}_{fg}} - {\boldsymbol{x}}} \right)}_{{J_3}} + \underbrace {{{\left( {{{\boldsymbol{d}}_{fg}} - {\boldsymbol{d}}} \right)}^{\text{T}}}{\boldsymbol{R}}_g^{ - 1}\left( {{{\boldsymbol{d}}_{fg}} - {\boldsymbol{d}}} \right)}_{{J_4}}+ \\ {\text{ }}{\text{ }}{\text{ }} \underbrace {\sum\limits_{i \;= \;1}^N {{{\left[ {{{\left( {{T'_i} - \widehat T'} \right)} \mathord{\left/ {\vphantom {{\left( {{T'_i} - \widehat T'} \right)} {{u_i}}}} \right. } {{u_i}}}} \right]}^2}} }_{{J_5}} + \underbrace {\sum\limits_{i\; = \;1}^{N \;-\; 1} {{{\left\{ {{{\left[ {\Delta {T'_i} - \left( {{{\widehat T'}_{i \;+\; 1}} - {{\widehat T}_i'}} \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {\Delta {{T}_i'} - \left( {{{\widehat T}'_{i\; + \;1}} - {{\widehat T'}_i}} \right)} \right]} {{w_i}}}} \right. } {{w_i}}}} \right\}}^2}} }_{{J_6}}+ \\ {\text{ }} {\text{ }}{\text{ }}{\text{ }} \underbrace {\sum\limits_{i \;=\; 1}^N {{{\left[ {{{\left( {{S'_i} - {{\widehat S'}_i}} \right)} \mathord{\left/ {\vphantom {{\left( {{S'_i} - {{\widehat S'}_i}} \right)} {{u_{i + N}}}}} \right. } {{u_{i + N}}}}} \right]}^2}} }_{{J_7}} + \underbrace {\sum\limits_{i \;=\; 1}^{N\; -\; 1} {{{\left\{ {{{\left[ {\Delta {S'_i} - \left( {{{\widehat S'}_{i + 1}} - {{\widehat S'}_i}} \right)} \right]} \mathord{ \left/ {\vphantom {{\left[ {\Delta {{S'}_i} - \left( {{{\widehat S'}_{i\; +\; 1}} - {{\widehat S'}_i}} \right)} \right]} {{w_{i \;+\; N \;- \;1}}}}} \right. } {{w_{i\; +\; N \;- \;1}}}}} \right\}}^2}} }_{{J_8}} + \\ {\text{ }} {\text{ }}{\text{ }}{\text{ }} \underbrace {{{{{\left( {{{\widetilde T'}_{\rm{MLD}}} + {{\widehat T'}_{\rm{MLD}}}} \right)}^2}} \mathord{\left/ {\vphantom {{{{\left( {{{\widetilde T'}_{{\rm{MLD}}}} + {{\hat T'}_{{\rm{MLD}}}}} \right)}^2}} {\varepsilon _{{\mathrm{SST}}}^2}}} \right. } {\varepsilon _{{\mathrm{SST}}}^2}}}_{{J_9}} + \underbrace {{{{{\left( {\widetilde h' - \widehat h'} \right)}^2}} \mathord{\left/ {\vphantom {{{{\left( {\widetilde h' - \widehat h'} \right)}^2}} {\varepsilon _h^2}}} \right. } {\varepsilon _h^2}}}_{{J_{10}}}. \\[-10pt] \end{gathered} $$ (3) 在
${J_1}$ 到${J_4}$ 项中${\boldsymbol{x}}$ 是温盐剖面的组合向量，$ {\boldsymbol{x}} = {\left( {{{\widehat T}_1},\;{{\widehat T}_2},\; \cdots ,\;{{\widehat T}_N},\;{{\widehat S}_1},\;{{\widehat S}_2},\; \cdots ,\;{{\widehat S} _N}} \right)^{\text{T}}} $ ；${\boldsymbol{d}}$ 是由剖面相邻深度的温度和盐度垂直差的组合向量；$N$ 为剖面深度数；${{\boldsymbol{x}}_{cl}}、{{\boldsymbol{d}}_{cl}}$ 表示气候态的温盐度和温盐垂直差；${{\boldsymbol{x}}_{fg}}、{{\boldsymbol{d}}_{fg}}$ 表示第一猜测场的温盐度和温盐垂直差；${\boldsymbol{B}}、{{\boldsymbol{B}}_g}$ 分别是由观测温盐场和其相邻深度差计算的协方差矩阵；${\boldsymbol{R}}、{{\boldsymbol{R}}_g}$ 是由第一猜测场及其相邻深度差计算的协方差矩阵；${u_i}$ 和${w_i}$ 分别是${\boldsymbol{B}}、{{\boldsymbol{B}}_g}$ 对角标准差矩阵的对角元素。${J_5}$ 到${J_8}$ 项中，$m$ 是EOF分解保留的模态数，用温度和盐度的$m$ 模态EOF来约束合成剖面。这4项中，${T_i}^\prime $ 和${S' _i}$ 分别是观测剖面温度和盐度异常，且${T_i}^\prime = {T_i} - {T_{cl,\;i}}$ ，${S' _i} = {S _i} - {S _{cl,\;i}}$ ，${\widehat T'_i}$ 和${\widehat S'_i}$ 分别表示待求的分析剖面温度异常和盐度异常；同理，$\Delta {T'_i}$ 和$\Delta {S' _i}$ 分别表示温度和盐度相邻深度的梯度异常。${J_9}$ 中，$ {\widetilde T'_{{\mathrm{MLD}}}} $ 表示MLD位置的观测温度异常；$ {\widehat T'_{{\mathrm{MLD}}}} $ 表示MLD位置处待求温度场的异常；${\varepsilon _{{\mathrm{SST}}}}$ 表示海表面温度的观测误差。${J_{10}}$ 中，$ \widetilde h' $ 表示观测温盐场海表面的动态高度；$ \widehat h' $ 表示待求温盐场海表面的动态高度；${\varepsilon _h}$ 表示SSHA观测误差。在式（3）中，
${J_1}$ 和${J_3}$ 项分别将本文合成的温盐场限制到月气候态和第一猜测场；${J_2}$ 和${J_4}$ 项分别将合成温盐场的梯度限制到月气候态和第一猜测场的垂直梯度；${J_5}$ 和${J_7}$ 项分别将合成温度和盐度限制到观测温度和盐度的EOF分解第$m$ 模态；${J_6}$ 和${J_8}$ 项分别将合成温度和盐度的垂直梯度限制到观测温度和盐度垂直梯度的EOF分解第$m$ 模态；${J_9}$ 项将合成温度场在混合层深度处的温度限制到观测场混合层温度；${J_{10}}$ 项将合成剖面的海表面高度异常限制到观测场的海表面高度异常。根据Helber等[10]关于代价函数式（3）的计算过程，可以将
${J_1}$ −${J_{10}}$ 项化简为如下的形式：$$ {J_1} = \sum\limits_{i \;= \;1}^m {\frac{{a_i^2}}{{{\lambda _i}}}} \text{，} $$ (4) $$ {J_2} = \sum\limits_{i \;= \; 1}^m {\frac{{b_i^2}}{{{\mu _i}}}} \text{，} $$ (5) $$ {J_3} = {{\boldsymbol{F}}_{fg}}\sum\limits_{i \;= \; 1}^m {\frac{{a_i^2 + a_{fg,\;i}^2 - 2{a_i}{a_{fg,\;i}}}}{{{\lambda _i}}}} \text{，} $$ (6) $$ {J_4} = {{\boldsymbol{G}}_{fg}}\sum\limits_{i \;= \; 1}^m {\frac{{b_i^2 + b_{fg,\;i}^2 - 2{b_i}{b_{fg,\;i}}}}{{{\mu _i}}}} \text{，} $$ (7) 式中，
${a_i}$ 和${b_i}$ 分别表示观测温盐场和观测温盐场垂直梯度第$i$ 模态的EOF振幅；${a_{fg,\;i}}$ 和${b_{fg,\;i}}$ 分别表示第一猜测温盐场及其垂直梯度第$i$ 模态的EOF振幅；$ {\lambda _i} $ 和$ {\mu _i} $ 分别表示观测温盐场及其垂直梯度的相关矩阵的第$i$ 个特征值。在此我们假设矩阵${\boldsymbol{R}}$ 和${\boldsymbol{B}}$ 成正比，${R_g}$ 和${B_g}$ 成正比，并且${\boldsymbol{R }}= {{\boldsymbol{B}} \mathord{\left/ {\vphantom {B {{F_{fg}}}}} \right. } {{F_{fg}}}}$ ，${{\boldsymbol{R}}_g} = {{{{\boldsymbol{B}}_g}} \mathord{\left/ {\vphantom {{{B_g}} {{G_{fg}}}}} \right. } {{G_{fg}}}}$ ，在本文中，设置${F_{fg}} = {G_{fg}} = 1$ 。$$ {J_5} = \sum\limits_{i \;= \; 1}^N {{{\left( {\frac{{\sum\limits_{k \;= \; 1}^m {{u_i}{a_k}{{\boldsymbol{\gamma}} _{i,\;k}}} - {{\widehat T'}_i}}}{{{u_i}}}} \right)}^2}} \text{，} $$ (8) $$ {J_6} = \sum\limits_{i \;= \; 1}^N {{{\left( {\frac{{\sum\limits_{k \;= \; 1}^m {{u_{i \;+ \;N}}{a_k}{{\boldsymbol{\gamma}} _{i + N,\;k}}} - {{\widehat S'}_i}}}{{{u_{i\; +\; N}}}}} \right)}^2}} \text{，} $$ (9) $$ {J_7} = \sum\limits_{i\;= \; 1}^{N - 1} {{{\left[ {\frac{{\sum\limits_{k \;= \; 1}^m {{w_i}{b_k}{{\boldsymbol{\varphi}} _{i,\;k}}} - \left( {{{\widehat T'}_{i \;+\; 1}} - {{\widehat T'}_i}} \right)}}{{{w_i}}}} \right]}^2}} \text{，} $$ (10) $$ {J_8} = \sum\limits_{i \;= \; 1}^{N - 1} {{{\left[ {\frac{{\sum\limits_{k \;= \; 1}^m {{w_{i\; +\; N \;-\; 1}}{b_k}{{\boldsymbol{\varphi}} _{i \;+\; N \;- \;1,k}}} - \left( {{{\widehat S'}_{i \;+\; 1}} - {{\widehat S'}_i}} \right)}}{{{w_{i \;+\; N \;-\; 1}}}}} \right]}^2}} \text{，} $$ (11) 式中，
${{\boldsymbol{\gamma}} _{i,k}}$ 和$ {{\boldsymbol{\varphi}} _{i,k}} $ 分别表示观测温盐矩阵及其垂直梯度矩阵的第$k$ 组特征向量。$$ {J_9} = \frac{{{{\left( {{{\widetilde T'}_{{\mathrm{MLD}}}} - \sum\limits_{k \;= \; 1}^N {{Q_i}{{\widehat T'}_i}} } \right)}^2}}}{{\varepsilon _{{\mathrm{SST}}}^2}} \text{，} $$ (12) 式中，
$Q$ 是混合层深度（MLD）处观测温度和盐度的线性插值向量。$$ {J_{10}} = \frac{{{{\left[ {\widetilde h' - \sum\limits_{k \;=\; 1}^N {\left( {\alpha {{\widehat T'}_i} + \beta {{\widehat S'}_i}} \right)d{z_i}} } \right]}^2}}}{{\varepsilon _h^2}}\text{，} $$ (13) 式中，
$\alpha $ 和$\beta $ 分别是热膨胀系数和盐度膨胀系数。将式（3）分别对变量
${a_i}$ 、${b_i}$ 、${\widehat T'_i}$ 、${\widehat S'_i}$ 求导，令其分别等于0，即$$ \frac{{\partial J}}{{\partial { * _i}}}\;=\; \sum\limits_{k \;=\; 1}^{10} {\frac{{\partial {J_k}}}{{\partial { * _i}}}} = 0\text{，} $$ (14) 式中，
$ * $ 分别表示变量${a_i}$ 、${b_i}$ 、${\widehat T'_i}$ 、${\widehat S'_i}$ 。得到（$2m + 2N$ ）个拥有（$2m + 2N$ ）个未知量的线性方程组$ D·{\boldsymbol{g}}={\boldsymbol{e}} $ ，${\boldsymbol{g}}$ 是（$2m + 2N$ ）个未知量组成的向量${\boldsymbol{g}} = \Big( {a_1},\; \cdots ,\;{a_m},\;{b_1},\; \cdots ,\;{b_m},\; {{\widehat T'}_1},\; \cdots ,\; {{\widehat T'}_N},\;{{\widehat S'}_1},\; \cdots ,\;{{\widehat S'}_N} \Big)^{\text{T}}$ 。最后，将网格化后0.25° × 0.25°区域内的SST和SSH代入上面的线性方程组，即可求得某一时间和位置处的温盐剖面。
为了确保有足够多的历史温盐剖面，本文只重构到1 000 m深度，但是在这个深度范围内，不能获取足够多的声学信息，所以要对重构剖面继续向更深处延伸，WOA18的气候态数据只有1 500 m，因此选取GDEM3.0数据集的温盐气候态
${T_G}\left( z \right)$ 和${S_G}\left( z \right)$ 。下面以温度剖面为例进行数据延伸：$$ {T}_{s}(z)={T}_{G}(z) + [{T}_{s}(700) - {T}_{G}(700)] \times {F}_{T}\left(z\right),\text{ }z > 700\;\text{m} \text{，} $$ (15) 式中，
${F_T}\left( z \right)$ 是在深度$z$ 处的衰减函数，随着深度增加，衰减函数越来越小，当深度$z$ 在700 ～1 000 m时，$$ {F}_{T}\left(z\right)={C}_{T}\left(z\right)\times \left[{\sigma }_{T}\left(z\right)/{\sigma }_{T}\left(700\right)\right] \text{，} $$ (16) 式中，
$ {C_T}\left( z \right) $ 表示在深度$z$ 处的温度相关性，根据Helber等[10]中式（70）进行计算。当深度
$z > 1\;000\;{\text{m}}$ 时，$$ \begin{array}{l}{F}_{T}\left(z\right)=\text{sgn}\left[{C}_{T}\left(1\;000\right)\right]\mathrm{exp}\left[\left(700-z\right)/{L}_{Tv}\right]\times\\ \qquad\quad \text{ }\left[{\sigma }_{T}\left(z\right)/{\sigma }_{T}\left(700\right)\right],\end{array} $$ (17) 式中，
$ {L_{Tv}} $ 表示垂直长度尺度[10]，且$$ {L_{Tv}} = - 400/\ln \left[ {\left| {{C_T}\left( {1\;000} \right)} \right|} \right]. $$ (18) 4. 重构结果分析
为了评估不同约束项在ISOP重构中所主导的作用，需要对不同约束项进行敏感度实验。为了研究SST、SSH和温盐梯度对重构温盐场的影响，本文提出了表1的4种重构方案，以探索SST、SSH、温盐梯度3项约束重构效能的差异。其中方案1只考虑SST和SSH对重构温盐场的影响，除去了式（3）中的温度和盐度梯度项，包括
${J_2}$ 、${J_4}$ 、${J_6}$ 和${J_8}$ 项；方案2只考虑SST和温度和盐度梯度对重构温盐场的影响，除去了${J_{10}}$ 的SSH项；方案3只考虑SSH和温度和盐度梯度对重构温盐场的影响，除去了${J_9}$ 的SST项。4.1 重构温盐场精度分析
为了探索不同约束条件对ISOP算法的影响状况，本文计算了4种重构方案2015–2020年13 000多条Argo测试剖面与重构温盐剖面的均方根误差（图2）和平方相关系数（图3）。
图 2 4种重构方案与Argo观测均方根误差对比Figure 2. Comparison of the root mean square error (RMSE) of the four reconstruction schemes with Argo observations
图 3 4种重构方案与Argo观测数据平方相关系数对比Figure 3. Comparison of the square correlation coefficient of the four reconstruction schemes with Argo observations如图2a所示，在0 m处，方案3的表层均方根误差达到了1.5℃，而其他3个方案表层均方根误差仅有0.8℃。在0～100 m内，方案4的均方根误差约为1.3℃，方案1、2、3的均方根误差分别达到1.47℃、1.5℃、1.52℃，方案4的精度比其他方案提高了约0.2℃。在100～200 m内，均方根误差从大到小分别是方案2、方案3、方案1、方案4。200 m以深，方案1、3、4的均方根误差接近，方案2的均方根误差较大。这表明海面温度项在反演温度场时主要作用于0～100 m，能很好地改善混合层的温度结构，海面高度项主要作用于混合层以下位置的温度结构，而温盐梯度项能改善表层到混合层位置的温盐重构精度。
图2b表示盐度的均方根误差，在0～100 m，4种方案的均方根误差从大到小排序为方案3、方案1、方案2、方案4。在100 m以深，方案2的均方根误差急剧增大，而其他3个方案的均方根误差非常接近，这表明海面高度对100 m以下的盐度剖面有很大的影响。且对比所有方案的重构场均方根误差，方案4的平均均方根误差都最小，分别为1.08℃、0.11。
图3分析了4种重构方案与Argo观测数据的平方相关系数。在0～100 m，重构场温度和盐度的平方相关系数从大到小排序为方案4、方案2、方案1和方案3，SST对温盐场的重构影响程度最低；在100 m以深区域，随着深度增加，方案2的温度和盐度平方相关系数骤降，而其他3个方案都比较接近；在整个深度范围内，方案4温度和盐度的平均
${r^2}$ 系数都达到最大，分别为0.89、0.78。综合重构温盐剖面的精度分析，方案4的重构精度最佳。4.2 重构温盐场空间特征分析
本文以HYCOM模式数据为参考，与4种方案的重构温盐场在垂向截面和水平切面进行对比，以此评估重构温盐场对实际海洋的信息捕捉能力。本文选取30°N，130°～150°E的垂向截面，观测时间随机选取为2019年12月20日。由上述分析可知，方案1、3和4在深层区域的均方根误差和平方相关系数都较接近，因此主要分析0～500 m的深度截面。
图4为不同方案重构温度剖面的垂直断面。如图4a所示，HYCOM温度数据在132°～140°E的表层位置，存在一处高温区域，在135°～140°E处，温度有明显的凸起，在145°～150°E处，存在温度的震荡。对比4种重构方案，方案1（图4b）与方案3（图4d）能清楚的描述深处的凸起和震荡变化，但不能反映海洋表层到混合层深度处的温度特征，说明SSH和温盐梯度项约束深层区域的温度场。相比于方案1和方案3，方案2（图4c）能反映由表面温度引起的混合层上方的温度变化特征，但未能反映出混合层以下温度场的真实结构。对于方案4（图4e），既能反映表层温度的变化特征，还能反映混合层以下的凸起和振荡现象，除了能够反应其他方案的结构特征，还能捕捉到表层的SST信号。混合层以下温度场的真实结构。对于方案4（图4e），既能反映表层温度的变化特征，还能反映混合层以下的凸起和振荡现象，除了能够反应其他方案的结构特征，还能捕捉到表层的SST信号。
图 4 温度垂直断面对比a: HYCOM；b: 方案1；c: 方案2；d: 方案3；e: 方案4Figure 4. Comparison of vertical sections of temperaturea: HYCOM; b: Scheme 1; c: Scheme 2; d: Scheme 3; e: Scheme 4图5是不同方案重构盐度剖面的垂直截面，方案1（图5b）、方案3（图5d）和方案4（图5e）的重构盐度场与HYCOM盐度断面（图5a）具有良好的吻合度， 且其重构场与HYCOM之间的平均均方根误差分别为1.32、1.35、1.34，能够反映盐度场的真实结构，且3种重构方案的重构结果十分接近；但对于方案2（图5c）整体，盐度分布与HYCOM的差别较大，均方根误差达到1.63，不能反映出盐度场的变化特征。
图 5 盐度垂直断面对比a: HYCOM；b: 方案1；c: 方案2；d: 方案3；e: 方案4Figure 5. Comparison of vertical sections of salinitya: HYCOM; b: Scheme 1; c: Scheme 2; d: Scheme 3; e: Scheme 4为了检验重构模型在不同季节对温盐特征的反映能力，以及选取具体某一天重构温盐场的偶然性，本文又选取了2019年3月20日、6月20日和9月20日的温盐场数据对重构温盐场和HYCOM温盐场的垂直空间特征进行了对比。
图 8 2019年9月20日温盐垂直断面对比a: HYCOM；b: 方案1；c: 方案2；d: 方案3；e: 方案4Figure 8. Comparison of vertical sections of temperature and salinity on September 20, 2019a: HYCOM; b: Scheme 1; c: Scheme 2; d: Scheme 3; e: Scheme 4如图6至图8所示，分别给出了2019年3月20日、6月20日以及9月20日3天，4种重构方案的重构温盐场和HYCOM温盐场在30°N，130°～150°E所示垂向截面温盐场对比图。通过观察3张图可以发现，重构温盐场的空间特征都符合HYCOM模式数据的温盐空间变化，并且方案4的能更好地反映HYCOM温盐场的空间特征。
图 6 2019年3月20日温盐垂直断面对比a: HYCOM；b: 方案1；c: 方案2；d: 方案3；e: 方案4Figure 6. Comparison of vertical sections of temperature and salinity on March 20, 2019a: HYCOM; b: Scheme 1; c: Scheme 2; d: Scheme 3; e: Scheme 4
图 7 2019年6月20日温盐垂直断面对比a: HYCOM；b: 方案1；c: 方案2；d: 方案3；e: 方案4Figure 7. Comparison of vertical sections of temperature and salinity on June 20, 2019a: HYCOM; b: Scheme 1; c: Scheme 2; d: Scheme 3; e: Scheme 4通过对比4种重构方案与HYCOM模式数据的温盐场，方案4 能够更好地反映温盐场的真实变化特征，接下来针对方案4，进一步分析重构温盐场获取水平方向温盐变化特征的能力。
本文随机选择2019年12月20日，研究区域内的HYCOM数据和方案4的重构温盐场进行水平切面的对比，对比的深度选取100 m、500 m和900 m。综合对比100 m、500 m和900 m深度处HYCOM模式温盐场数据和方案4重构温盐场的平面结果（图9），方案4重构的温盐场与HYCOM模式数据的温盐场在同一深度处的分布特征大致保持一致，能反映出丰富的温盐变化特征，符合海洋真实温盐场的变化趋势，并且方案4的重构结果中，温度的分布情况更加符合真实温盐场。
图 9 100 m、500 m、900 m深度处方案4和HYCOM模式数据的温盐度切面对比Figure 9. Comparison of temperature and salinity sections at depths of 100 m, 500 m and 900 m for Scheme 4 and HYCOM model data5. 声学效能评估
温盐场与声场息息相关，提高温盐场的反演精度，才能够更准确的对水声特性进行仿真预报。声波在海水中的传播速度与海水的温度、盐度和压力等因素有关。其中任何一个参数的改变都会导致声速的变化，并且海水的温度对声速的影响最大。
根据上一节的分析，方案4重构温度场的精度最高，因此通过方案4重构的温盐场，其声速剖面也会更接近于海洋的实际声速剖面，接下来通过温盐场与声速之间计算公式，对比4种重构方案与HYCOM对照组的声速剖面。本文利用Mackenzie声速经验公式[21]对HYCOM、WOA18和4种反演方案得到的温盐场数据计算声速剖面（图10）。
图 10 4种方案的反演数据与WOA18以及HYCOM数据计算的声速剖面对比Figure 10. Comparison of the sound velocity profiles calculated from the inversion data of the four schemes and WOA18 and HYCOM data从60 m以浅的正声速梯度剖面可以看出，方案1和方案3与HYCOM存在较大偏差，且两者偏差方案1小于方案3，而方案2和方案4的反演结果与HYCOM最为接近；且4种方案的声学层深度（Sonic Layer Depth，SLD）均为50 m，与HYCOM一致，其中方案2和方案4与HYCOM偏差更小；在60 m深度附近，方案2与HYCOM的声速剖面偏差达到最大。从声速方面来看，方案2与方案4与HYCOM的声速最为接近，相差约为1 m/s，且方案4的声速更接近于HYCOM；方案1和方案3与HYCOM的声速剖面相差较大，约为1.5 m/s。接下来分别讨论4种方案的声传播特性。
利用BELLHOP模型，设置声源深度为20 m，发射角度为–15°～15°，发射频率为1 000 Hz，得到5组声速剖面的声传播损失场（图11）。
图 11 声传播损失场（0~30 km）a: HYCOM；b: 方案1；c: 方案2；d: 方案3；e: 方案4Figure 11. acoustic wave transmission loss field (0−30 km)a: HYCOM; b: Scheme 1; c: Scheme 2; d: Scheme 3; e: Scheme 44组方案的反演结果计算的深海声传播与HYCOM基本一致，第一会聚区为61.5 km，第二会聚区在124.3 km；方案2、3、4均可反映表面声道特征，方案1由于20 m以浅声速剖面的偏差，原本表面声道存在的深度变为声影区。
在深海的声传播中，会聚区是判断声纳接收信号较强的区域，4组方案均可较为准确的反演出会聚区位置，而在表面声道的研究中，方案1无法捕捉表面声道。综上，增加梯度以及表面温度的方案2与方案4计算的声学层深度以及声传播情况与HYCOM的结果更吻合。表面声道的存在可以使频率大于截止频率的声信号在管道内传输，减少传播损失，有利于声的远距离传播，更精确地反演声学层深度在潜艇路径规划、反潜探测以及水声通信中都具有重要意义。
6. 结论
本文利用多年的海洋遥感海表面信息与历史观测次表面温盐观测，开展了基于ISOP变分法的三维温盐场重构工作，其本质是通过建立表面观测约束、气候态温盐约束、垂向温盐梯度等多项约束的T−S变量的代价方程，最后通过最小化代价函数来得到最优重构温盐剖面的变分同化过程。在ISOP[10]的基础上，本文在（1/4）°网格内计算每个月的系数矩阵，以此在最大的程度上减小季节性差异带来的误差。为了探索不同约束的重构敏感度，本文制定4种方案并重新设计代价函数进行重构，并与实测数据Argo以及模式数据HYCOM进行对比，结果显示方案4（SSH + SST + Grad）的重构精度最高，同时得到海面温度约束能提高混合层重构能力，而海面高度约束对温跃层的重构有较重要的作用。
本文还评估了重构温盐场的声学效能，利用不同方案重构温盐场，并计算其声学剖面、声学通道以及声传播损失。结果显示，海面温度对SLD的影响较大；海面高度和温盐场的垂直梯度能够影响整个声速剖面的准确性。并且SST、SSH与梯度同时约束时，SLD以浅声速与HYCOM相差最小；没有梯度约束时，SLD与HYCOM相差较大，未能反映出表面声道特征，这表明梯度约束重构温盐场在声学应用上有重要价值。
综合各项约束进行多角度评估结果，三维温盐场重构精度与海表面信息息息相关，特别是海面温度与海面高度对三维温盐场重构有着至关重要的作用，卫星海面观测重构水下三维温盐场并获取声场特性的研究，在军事海洋等领域具有重要的实践应用价值。另外，从海洋动力学的角度来看，海面风场、盐度以及流场与水下温盐场的变化也有一定的联系，随着卫星技术的发展，更高精度的卫星遥感数据对表面流和盐度的长时空的监测都将成为现实，这将进一步提高海洋三维温盐场重构的精度。而海洋三维温盐场重构的进展也能为海洋三维流场的重构提供借鉴，同时本文也为重构温盐场在声学方面的应用提供了参考。
-
图 1 卫星海面观测三维温盐场重建及评估的具体流程图
Fig. 1 The specific flow chart of reconstruction of three-dimensional temperature and salinity field and its assessment using satellite sea surface observations
图 2 4种重构方案与Argo观测均方根误差对比
Fig. 2 Comparison of the root mean square error (RMSE) of the four reconstruction schemes with Argo observations
图 3 4种重构方案与Argo观测数据平方相关系数对比
Fig. 3 Comparison of the square correlation coefficient of the four reconstruction schemes with Argo observations
图 4 温度垂直断面对比
a: HYCOM；b: 方案1；c: 方案2；d: 方案3；e: 方案4
Fig. 4 Comparison of vertical sections of temperature
a: HYCOM; b: Scheme 1; c: Scheme 2; d: Scheme 3; e: Scheme 4
图 5 盐度垂直断面对比
a: HYCOM；b: 方案1；c: 方案2；d: 方案3；e: 方案4
Fig. 5 Comparison of vertical sections of salinity
a: HYCOM; b: Scheme 1; c: Scheme 2; d: Scheme 3; e: Scheme 4
图 8 2019年9月20日温盐垂直断面对比
a: HYCOM；b: 方案1；c: 方案2；d: 方案3；e: 方案4
Fig. 8 Comparison of vertical sections of temperature and salinity on September 20, 2019
a: HYCOM; b: Scheme 1; c: Scheme 2; d: Scheme 3; e: Scheme 4
图 6 2019年3月20日温盐垂直断面对比
a: HYCOM；b: 方案1；c: 方案2；d: 方案3；e: 方案4
Fig. 6 Comparison of vertical sections of temperature and salinity on March 20, 2019
a: HYCOM; b: Scheme 1; c: Scheme 2; d: Scheme 3; e: Scheme 4
图 7 2019年6月20日温盐垂直断面对比
a: HYCOM；b: 方案1；c: 方案2；d: 方案3；e: 方案4
Fig. 7 Comparison of vertical sections of temperature and salinity on June 20, 2019
a: HYCOM; b: Scheme 1; c: Scheme 2; d: Scheme 3; e: Scheme 4
图 9 100 m、500 m、900 m深度处方案4和HYCOM模式数据的温盐度切面对比
Fig. 9 Comparison of temperature and salinity sections at depths of 100 m, 500 m and 900 m for Scheme 4 and HYCOM model data
图 10 4种方案的反演数据与WOA18以及HYCOM数据计算的声速剖面对比
Fig. 10 Comparison of the sound velocity profiles calculated from the inversion data of the four schemes and WOA18 and HYCOM data
图 11 声传播损失场（0~30 km）
a: HYCOM；b: 方案1；c: 方案2；d: 方案3；e: 方案4
Fig. 11 acoustic wave transmission loss field (0−30 km)
a: HYCOM; b: Scheme 1; c: Scheme 2; d: Scheme 3; e: Scheme 4
表 1 4种研究方案及其主要约束条件
Tab. 1 Four research schemes and their main constraints
方案 主要约束条件 表达式 方案1 SST + SSH J = J1 + J3 + J5 + J7 + J9 + J10 方案2 SST + Grad J = J1 + J2 + J3 + J4 + J5 + J6 + J7 + J8 + J9 方案3 SSH + Grad J = J1 + J2 + J3 + J4 + J5 + J6 + J7 + J8 + J10 方案4 SST + SSH + Grad J = J1 + J2 + J3 + J4 + J5 + J6 + J7 + J8 + J9 + J10 
下载: 导出CSV
-
[1] 赖积保, 康旭东, 鲁续坤, 等. 新一代人工智能驱动的陆地观测卫星遥感应用技术综述[J]. 遥感学报, 2022, 26(8): 1530−1546. doi: 10.11834/j.issn.1007-4619.2022.8.ygxb202208004Lai Jibao, Kang Xudong, Lu Xukun, et al. A review of land observation satellite remote sensing application technology with new generation artificial intelligence[J]. National Remote Sensing Bulletin, 2022, 26(8): 1530−1546. doi: 10.11834/j.issn.1007-4619.2022.8.ygxb202208004 [2] 汪文杰, 贾东宁, 许佳立, 等. 全球海洋遥感卫星发展综述[J]. 测绘通报, 2020(5): 1−6.Wang Wenjie, Jia Dongning, Xu Jiali, et al. Review of the development of global marine remote sensing satellite[J]. Bulletin of Surveying and Mapping, 2020(5): 1−6. [3] 张庆君. 面向碳综合治理的卫星海洋遥感体系展望[J]. 前瞻科技, 2022, 1(1): 126−145.Zhang Qingjun. Prospect of satellite ocean remote sensing system for comprehensive carbon management[J]. Science and Technology Foresight, 2022, 1(1): 126−145. [4] Cooper M, Haines K. Altimetric assimilation with water property conservation[J]. Journal of Geophysical Research: Oceans, 1996, 101(C1): 1059−1077. doi: 10.1029/95JC02902 [5] Fiedler P C. Surface manifestations of subsurface thermal structure in the California current[J]. Journal of Geophysical Research: Oceans, 1988, 93(C5): 4975−4983. doi: 10.1029/JC093iC05p04975 [6] 王喜冬. 西北太平洋三维温盐场重构及其应用[D]. 广州: 中国科学院南海海洋研究所, 2011.Wang Xidong. Reconstruction of three-dimensional temperature and salinity fields and their applications in Northwest Pacific[D]. Guangzhou: South China Sea Institute of Oceanology, Chinese Academy of Sciences, 2011. [7] Ali M M, Swain D, Weller R A. Estimation of ocean subsurface thermal structure from surface parameters: a neural network approach[J]. Geophysical Research Letters, 2004, 31(20): L20308. [8] Wu Xiangbai, Yan Xiaohai, Jo Y H, et al. Estimation of subsurface temperature anomaly in the north Atlantic using a self-organizing map neural network[J]. Journal of Atmospheric and Oceanic Technology, 2012, 29(11): 1675−1688. doi: 10.1175/JTECH-D-12-00013.1 [9] Fujii Y, Kamachi M. A reconstruction of observed profiles in the sea east of Japan using vertical coupled temperature-salinity EOF modes[J]. Journal of Oceanography, 2003, 59(2): 173−186. doi: 10.1023/A:1025539104750 [10] Helber R W, Townsend T L, Barron C N, et al. Validation test report for the improved synthetic ocean profile (ISOP) system, part I: synthetic profile methods and algorithm[J]. Naval Research Laboratory, 2013, 7320−13−9364. [11] He Zikang, Wang Xidong, Wu Xinrong, et al. Projecting three-dimensional ocean thermohaline structure in the North Indian Ocean from the satellite sea surface data based on a variational method[J]. Journal of Geophysical Research: Oceans, 2021, 126(1): e2020JC016759. doi: 10.1029/2020JC016759 [12] 孙春健, 张晓爽, 张寅权, 等. 卫星遥感重构海洋次表层研究进展[J]. 海洋信息, 2018, 33(4): 21−28.Sun Chunjian, Zhang Xiaoshuang, Zhang Yinquan, et al. Progress in reconstruction of ocean subsurface by satellite remote sensing data[J]. Marine Information, 2018, 33(4): 21−28. [13] Ponte A L, Klein P. Reconstruction of the upper ocean 3D dynamics from high-resolution sea surface height[J]. Ocean Dynamics, 2013, 63(7): 777−791. doi: 10.1007/s10236-013-0611-7 [14] Wang Jinbo, Flierl G R, LaCasce J H, et al. Reconstructing the ocean’s interior from surface data[J]. Journal of Physical Oceanography, 2013, 43(8): 1611−1626. doi: 10.1175/JPO-D-12-0204.1 [15] Fox D N, Teague W J, Barron C N, et al. The modular ocean data assimilation system (MODAS)[J]. Journal of Atmospheric and Oceanic Technology, 2002, 19(2): 240−252. doi: 10.1175/1520-0426(2002)019<0240:TMODAS>2.0.CO;2 [16] Su Hua, Wu Xiangbai, Yan Xiaohai, et al. Estimation of subsurface temperature anomaly in the Indian Ocean during recent global surface warming hiatus from satellite measurements: a support vector machine approach[J]. Remote Sensing of Environment, 2015, 160: 63−71. doi: 10.1016/j.rse.2015.01.001 [17] Su Hua, Wu Xiangbai, Lu Wenfang, et al. Inconsistent subsurface and deeper ocean warming signals during recent global warming and hiatus[J]. Journal of Geophysical Research: Oceans, 2017, 122(10): 8182−8195. doi: 10.1002/2016JC012481 [18] Fujii Y, Kamachi M. Three-dimensional analysis of temperature and salinity in the equatorial Pacific using a variational method with vertical coupled temperature-salinity EOF modes[J]. Journal of Geophysical Research: Oceans, 2003, 108(C9): 3297. [19] 汤博. 中尺度涡旋的统计特征及其温盐场的反演方法研究[D]. 青岛: 中国科学院大学(中国科学院海洋研究所), 2019.Tang Bo. A study on the statistical characteristic of mesoscale eddies and the inversion method of their temperature and salinity[D]. Qingdao: Institute of Oceanology, Chinese Academy of Science, 2019. [20] Su Hua, Zhang Haojie, Geng Xupu, et al. OPEN: a new estimation of global ocean heat content for upper 2000 meters from remote sensing data[J]. Remote Sensing, 2020, 12(14): 2294. doi: 10.3390/rs12142294 [21] Mackenzie K V. Nine-term equation for sound speed in the oceans[J]. The Journal of the Acoustical Society of America, 1981, 70(3): 807−812. doi: 10.1121/1.386920 [22] Guinehut S, Le Traon P Y, Larnicol G. What can we learn from global altimetry/hydrography comparisons?[J]. Geophysical Research Letters, 2006, 33(10): L10604. -
下载:
计量
- 文章访问数: 323
- HTML全文浏览量: 203
- PDF下载量: 41
- 被引次数: 0
