Numerical investigation on the turbulent structures in the bottom boundary layers under the effects of waves
-
摘要: 本文基于
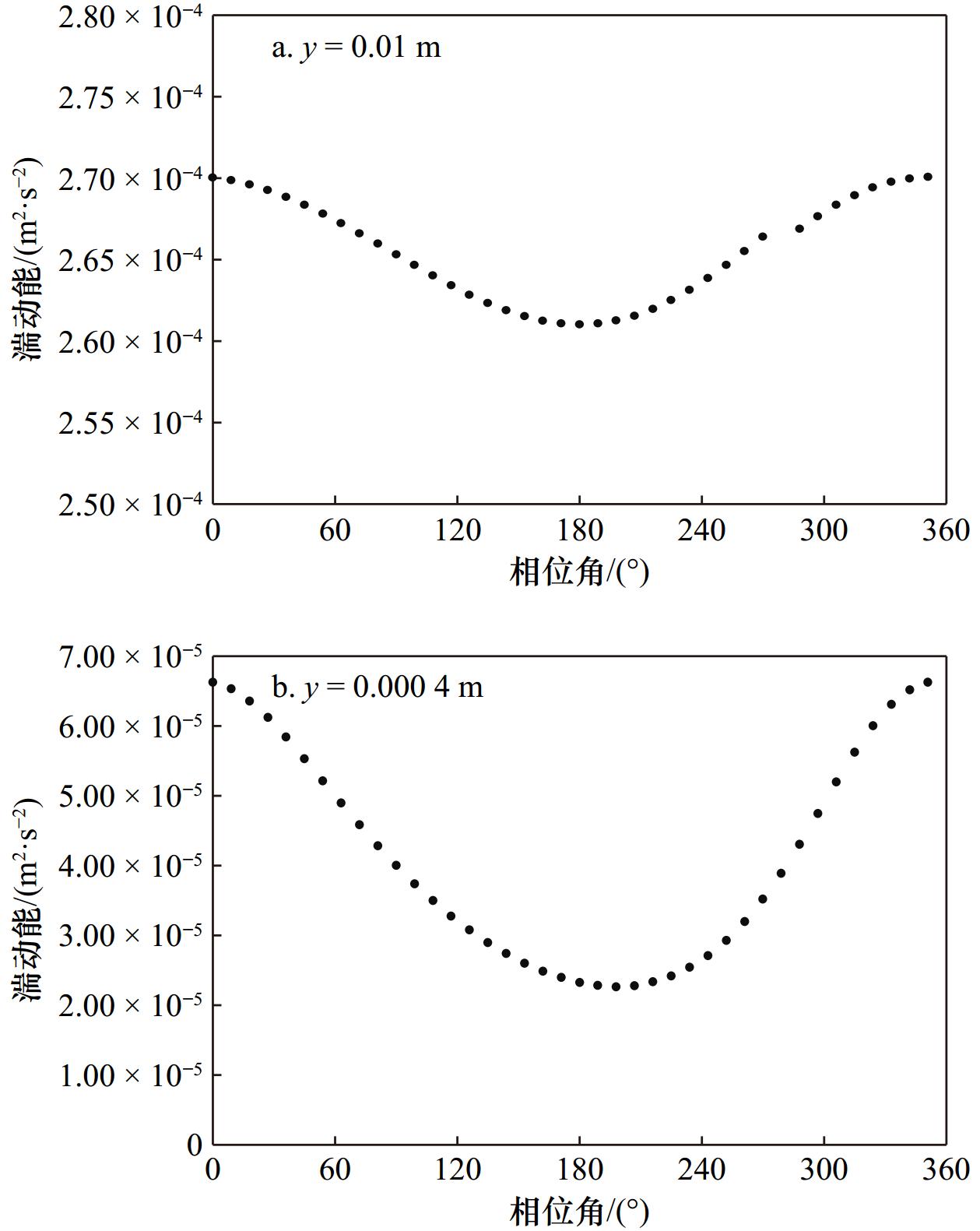
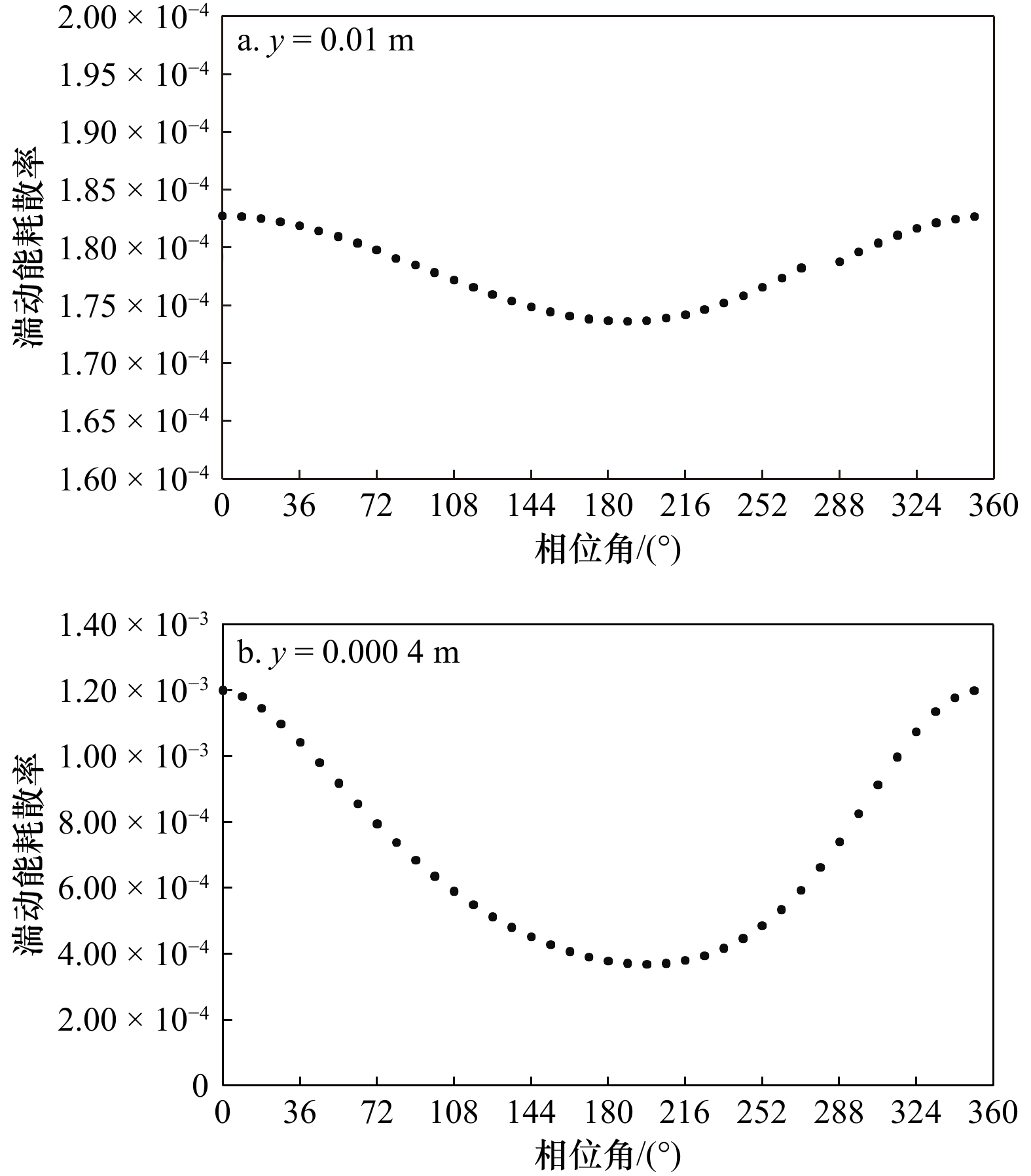
$ k $ -$ \varepsilon $ 模型研究了波流边界层内湍流结构特征。研究结果表明，时均流速分布数值解与实验结果高度吻合。一个波周期内湍流结构特征（如：涡量、湍动能、湍动能耗散率等）呈周期性变化规律，波浪作用引起涡量、湍动能及湍动能耗散率均在减速阶段减小，在波谷处达到最低值，而后在加速阶段增大，并在波峰处达到最大值。近壁面处湍流结构变化幅值较大（湍动能耗散率变化可达53%），远离壁面处变化幅值较平均值较小（仅3%）。波流边界层厚度在减速阶段增加，在加速阶段减小。本文所建立的数值模型克服了现有模型因采用“高雷诺数方法”引起的近壁区精度不高问题，可较好地描述波浪作用下湍流结构演变过程的物理机制，为河口海岸地区泥沙运动、岸滩演变及海洋可再生能源的开发利用提供一些指导意义。Abstract: This paper investigates the characteristics of turbulent structures in combined wave-current boundary layers based on the standard$ k $ -$ \varepsilon $ model. Good agreements were found between the numerical results and experimental data of the time-averaged mean velocity profiles. Periodic variations of turbulence parameters within a wave cycle (i.e. vorticity magnitudes, TKE and TKE dissipation rates etc.) were observed. The vorticity magnitudes, TKE and TKE dissipation rates all decrease during the deceleration phase, reach their minimum values during the wave trough, increase during the acceleration phase and reach their maximum values during the wave crest. The variations of turbulent structures are very high in the near-wall regions (53% for TKE dissipation rates), and are quite low in the outer regions (3% for TKE dissipation rates). The wave-current boundary layer thickness increases (decreases) during the deceleration phase (acceleration phase). The model developed in this study has solved the existing issue of low accuracy in the near-bed region by previous models based on the “high Reynolds number methods”. The present model performs well in describing the physical process of turbulence variations under the effects of wave-current interaction. This can provide some guidance for the sediment transport in coastal areas, beach erosion prediction and developments of marine renewable energy.-
Key words:
- wave-current interaction /
- bottom boundary layer /
- turbulence /
- CFD /
- k-ε model
-
图 2 波浪底摩擦系数与粗糙系数变化关系
Fig. 2 Friction factors versus the roughness in wave bottom boundary layers
图 3 波流同向作用下时均流速剖面图，WCA1，时均流速0.185 m/s
a. 线性坐标；b. 半对数坐标
Fig. 3 Time-averaged mean velocity profiles in combined wave-current flows, WCA1，mean velocity of 0.185 m/s
a. Linear axis；b. semi-log scale
图 4 WCA1工况下底部边界层内波致流速
数值结果用实线表示；实验结果通过点表示
Fig. 4 Wave-induced velocity profiles in the bottom boundary layers of WCA1
Lines for the numerical results; dots for the experimental results
图 5 WCA1工况下全水深范围内相位平均流速分布（18°时间间隔）
Fig. 5 Phase-averaged mean velocity profiles in the whole water column (18° time intervals) of WCA1
图 6 自由液面（a）及底部剪应力时间序列（b），
$ {d} $ = 200 mm,$ {T} $ = 1 s,$ {H} $ = 0.02 m,$ {U} $ = 0.185 m/sFig. 6 Free surface elevations (a) and the time series of the bed shear stress (b),
$ {d} $ = 200 mm,$ {T} $ = 1 s,$ {H} $ = 0.02 m,$ {U} $ = 0.185 m/s
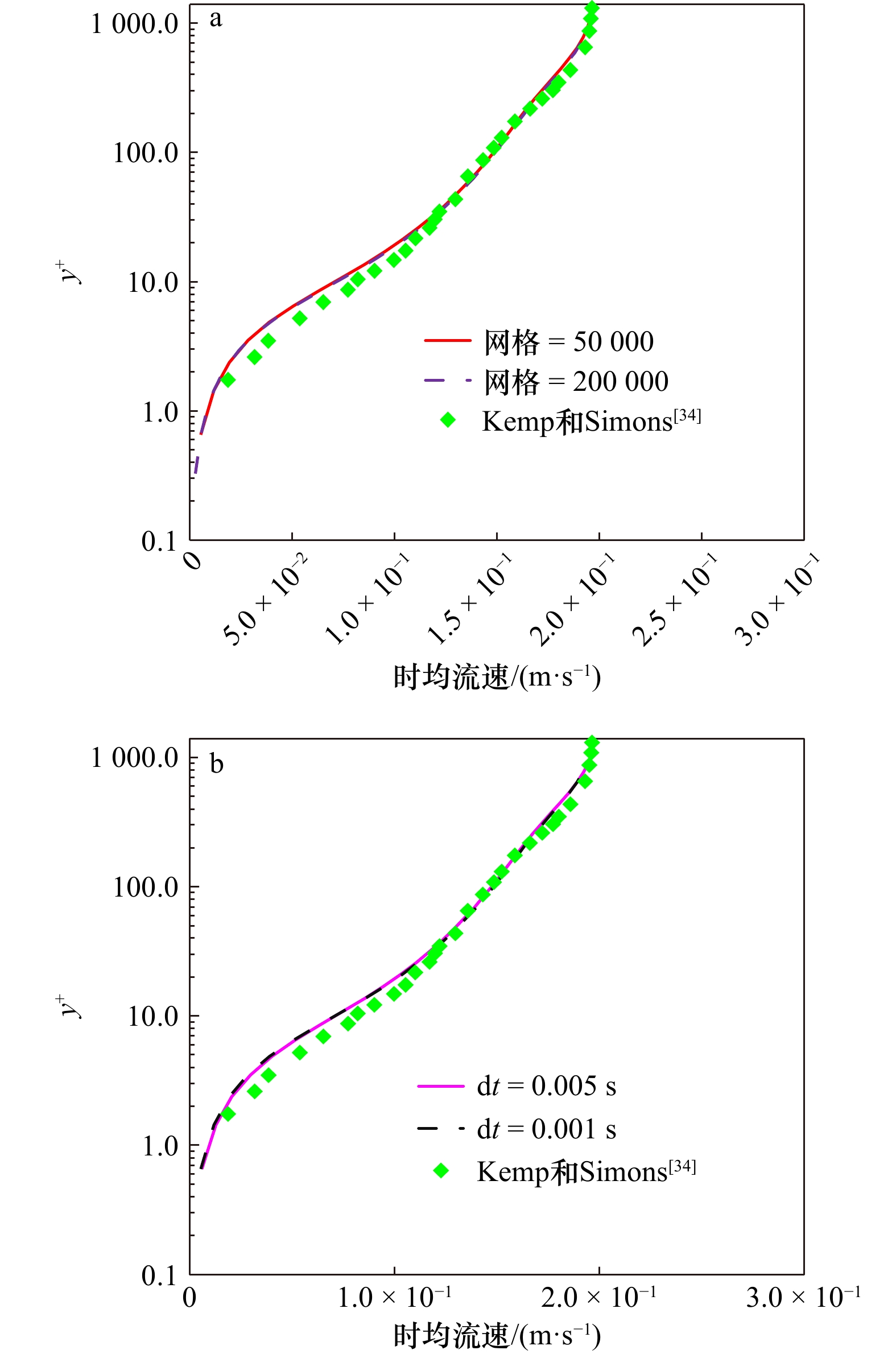
图 7 时间、空间分辨率对时均流速剖面计算结果影响，WCA1测试
a. 网格敏感性测试，时间步长为0.001 s，网格分别为50 000和200 000；b. 时间步长敏感性测试，网格为50 000，时间步长分别为0.005 s和0.001 s
Fig. 7 Sensitivity tests of the temporal and spatial resolution for the mean velocity profiles, WCA1
a. Meshing tests, time step of 0.001 s, meshing of 50 000和200 000；b. time step tests，meshing of 50 000，time steps of 0.005 s and 0.001 s
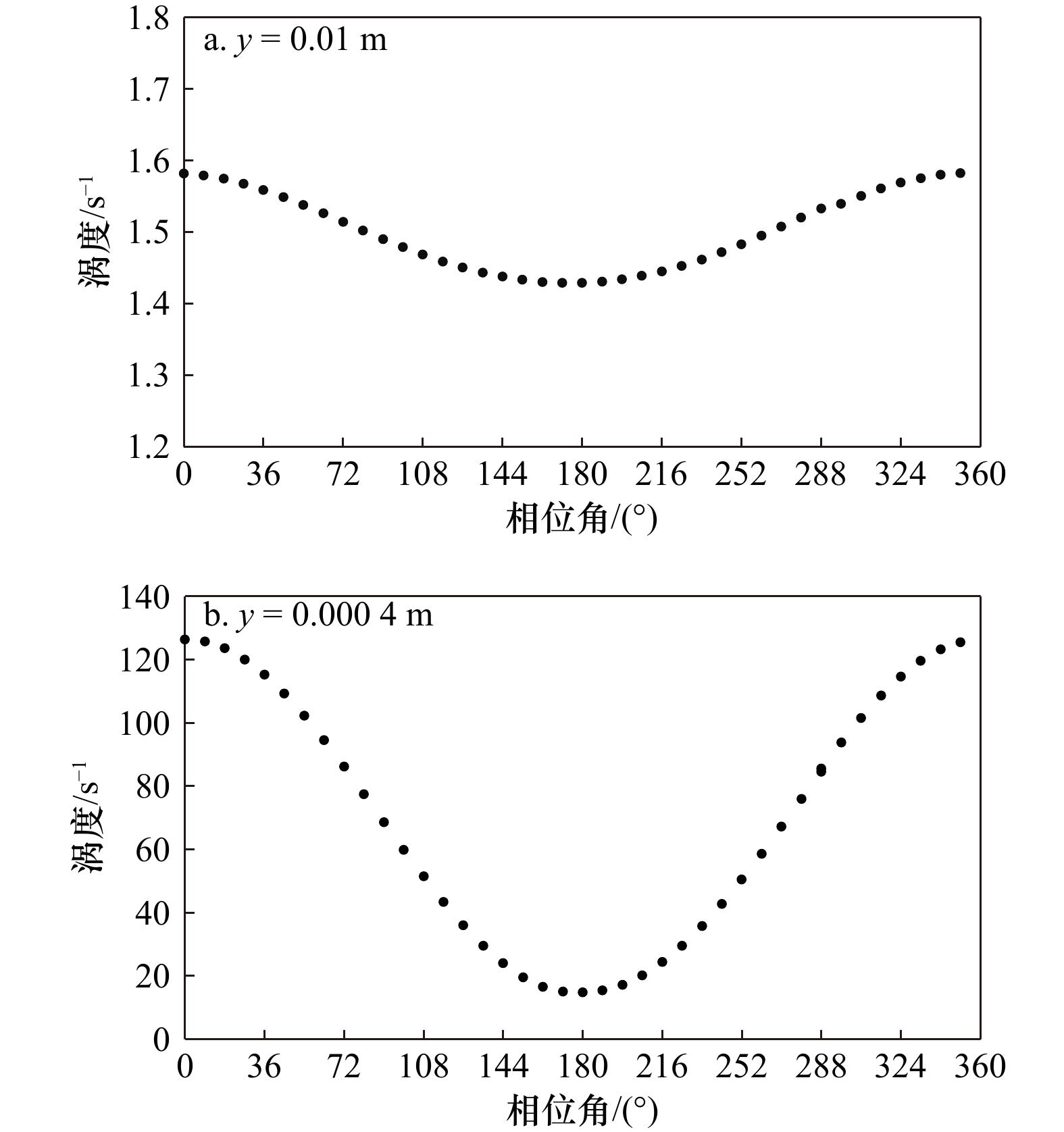
图 8 WCA1工况下不同相位时期涡度大小分布
a. 减速阶段全水深范围内涡度分布；b. 减速阶段近壁处涡度分布；c. 加速阶段全水深范围内涡度分布；d. 加速阶段近壁处涡度分布
Fig. 8 Vorticity distributions at different phases of WCA1
a. Vorticity distributions during deceleration phases in the whole water column; b. vorticity distributions during deceleration phases near the wall; c. vorticity distributions during acceleration phases in the whole water column; d. vorticity distributions during acceleration phases near the wall
纯流工况CA 波流工况WCA1 摩阻流速 $ {u}_{*} $ /（mm·s−1） 8.66 8.89 底摩擦力 $ {\tau }_{{\mathrm{b}}} $ /（$ {{10}^{-3}} $ Pa） 75.0 79.1 边界层动量厚度 $ \theta $/mm 11.6 8.1 外层流速 $ \overline{u}_{{\infty }} $ /（mm·s−1） 205 196 黏度系数${\nu } $ /（mm·s−2） 1.16 1.02 雷诺数$ {Re}_{\theta }=\;\overline{u}_{{\infty }}\theta /{\nu } $ 2 060 1 550 
下载: 导出CSV
-
[1] Lundgren H. Turbulent currents in the presence of waves[C]//13th International Conference on Coastal Engineering. Vancouver: ASCE, 1972: 623−634. [2] Grant W D, Madsen O S. Combined wave and current interaction with a rough bottom[J]. Journal of Geophysical Research: Oceans, 1979, 84(C4): 1797−1808. doi: 10.1029/JC084iC04p01797 [3] Myrhaug D. On a theoretical model of rough turbulent wave boundary layers[J]. Ocean Engineering, 1982, 9(6): 547−565. doi: 10.1016/0029-8018(82)90002-6 [4] Christoffersen J B, Jonsson I G. Bed friction and dissipation in a combined current and wave motion[J]. Ocean Engineering, 1985, 12(5): 387−423. doi: 10.1016/0029-8018(85)90002-2 [5] Myrhaug D, Slaattelid O H. Combined wave and current boundary layer model for fixed rough seabeds[J]. Ocean Engineering, 1989, 16(2): 119−142. doi: 10.1016/0029-8018(89)90002-4 [6] Myrhaug D, Slaattelid O H. A rational approach to wave-current friction coefficients for rough, smooth and transitional turbulent flow[J]. Coastal Engineering, 1990, 14(3): 265−293. doi: 10.1016/0378-3839(90)90027-T [7] You Zaijin, Wilkinson D L, Nielsen P. Velocity distributions of waves and currents in the combined flow[J]. Coastal Engineering, 1991, 15(5/6): 525−543. [8] You Zaijin, Wilkinson D L, Nielsen P. Velocity distribution in turbulent oscillatory boundary layer[J]. Coastal Engineering, 1992, 18(1/2): 21−38. [9] You Zaijin. A simple model for current velocity profiles in combined wave-current flows[J]. Coastal Engineering, 1994, 23(3/4): 289−304. [10] You Zaijin. Eddy viscosities and velocities in combined wave-current flows[J]. Ocean Engineering, 1994, 21(1): 81−97. doi: 10.1016/0029-8018(94)90031-0 [11] Yuan Jing, Madsen O S. Experimental and theoretical study of wave-current turbulent boundary layers[J]. Journal of Fluid Mechanics, 2015, 765: 480−523. doi: 10.1017/jfm.2014.746 [12] Malarkey J, Davies A G. Modelling wave–current interactions in rough turbulent bottom boundary layers[J]. Ocean Engineering, 1998, 25(2/3): 119−141. [13] Umeyama M. Reynolds stresses and velocity distributions in a wave-current coexisting environment[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2005, 131(5): 203−212. doi: 10.1061/(ASCE)0733-950X(2005)131:5(203) [14] Fredsøe J. Turbulent boundary layer in wave-current motion[J]. Journal of Hydraulic Engineering, 1984, 110(8): 1103−1120. doi: 10.1061/(ASCE)0733-9429(1984)110:8(1103) [15] Soulsby R L, Hamm L, Klopman G, et al. Wave-current interaction within and outside the bottom boundary layer[J]. Coastal Engineering, 1993, 21(1/3): 41−69. [16] Holmedal L E, Myrhaug D, Rue H. Seabed shear stresses under irregular waves plus current from Monte Carlo simulations of parameterized models[J]. Coastal Engineering, 2000, 39(2/4): 123−147. [17] Davies A G, Soulsby R L, King H L. A numerical model of the combined wave and current bottom boundary layer[J]. Journal of Geophysical Research: Oceans, 1988, 93(C1): 491−508. doi: 10.1029/JC093iC01p00491 [18] Son H T, André T. A numerical model of the rough turbulent boundary layer in combined wave and current interaction[C]//22nd International Conference on Coastal Engineering. Delft: ASCE, 1991: 853−866. [19] 吴永胜, 练继建, 张庆河, 等. 波浪和水流共同作用下水流时均流速分布[J]. 水利学报, 2001(1): 35−41.Wu Yongsheng, Lian Jijian, Zhang Qinghe, et al. Distribution of time average velocity in wave-current combined flow[J]. Journal of Hydraulic Engineering, 2001(1): 35−41. [20] 孙红, 韩光, 陶建华. 波流相互作用下沿垂向的水流结构及其实验验证[J]. 水利学报, 2001(7): 63−68.Sun Hong, Han Guang, Tao Jianhua. The flow structure along the vertical line under the interaction of current and wave[J]. Journal of Hydraulic Engineering, 2001(7): 63−68. [21] 张卓, 宋志尧, 孔俊. 波流共同作用下流速垂线分布及其影响因素分析[J]. 水科学进展, 2010, 21(6): 801−807.Zhang Zhuo, Song Zhiyao, Kong Jun. Wave-current interaction effects on velocity profiles and influencing factor analysis[J]. Advances in Water Science, 2010, 21(6): 801−807. [22] Holmedal L E, Myrhaug D, Rue H. The sea bed boundary layer under random waves plus current[J]. Continental Shelf Research, 2003, 23(7): 717−750. doi: 10.1016/S0278-4343(03)00020-7 [23] Teles M J, Pires-Silva A A, Benoit M. The influence of the turbulence closure model on wave-current interaction modeling at a local scale at a local scale[C]//Proceedings of 33rd Conference on Coastal Engineering. Santander: ASCE, 2012: 1−12.Teles M J, Pires-Silva A A, Benoit M. The influence of the turbulence closure model on wave-current interaction modeling at a local scale at a local scale[C]//Proceedings of 33rd Conference on Coastal Engineering. Santander: ASCE, 2012: 1−12. [24] Klopman G. Vertical structure of the flow due to waves and currents: laser-Doppler flow measurements for waves following or opposing a current[R]. Delft: Deltares, 1994: 32. [25] Zhang Chi, Zheng Jinhai, Wang Yigang, et al. Comparison of turbulence schemes for prediction of wave-induced near-bed sediment suspension above a plane bed[J]. China Ocean Engineering, 2011, 25(3): 395−412. doi: 10.1007/s13344-011-0033-6 [26] Zhang Chi, Zheng Jinhai, Wang Yigang, et al. Modeling wave-current bottom boundary layers beneath shoaling and breaking waves[J]. Geo-Marine Letters, 2011, 31(3): 189−201. doi: 10.1007/s00367-010-0224-9 [27] 陈丹丹, 林鹏智. 波浪作用下紊流边界层数值模拟[C]//第十七届中国海洋(岸)工程学术讨论会论文集(上). 南宁: 中国海洋工程学会, 2015: 498−501.Chen Dandan, Lin Pengzhi. Numerical simulation of turbulent wave boundary layers[C]//Proceedings of the 17th China Marine (Coastal) Engineering Academic Symposium. Nanning: Chinese Ocean Engineering Society, 2015: 498−501. [28] 郑金海, 范文彰, 张弛, 等. 波流边界层内外流速剖面的数值模拟[J]. 中国科技论文, 2016, 11(7): 746−750.Zheng Jinhai, Fan Wenzhang, Zhang Chi, et al. Numerical simulation of velocity profiles inside and outside the wave-current bottom boundary layer[J]. China Sciencepaper, 2016, 11(7): 746−750. [29] 张弛, 劳伯村, 郑金海. 加速度不对称波浪作用下的底部边界层动力特性[J]. 河海大学学报(自然科学版), 2016, 44(3): 258−264.Zhang Chi, Lao Bocun, Zheng Jinhai. Hydrodynamic characteristics of bottom boundary layer under acceleration-skewed waves[J]. Journal of Hohai University (Natural Sciences), 2016, 44(3): 258−264. [30] 伍志元, 蒋昌波, 邓斌, 等. 波流耦合模式及其在理想潮汐通道中的应用[J]. 哈尔滨工程大学学报, 2019, 40(8): 1420−1426.Wu Zhiyuan, Jiang Changbo, Deng Bin, et al. SWAN-ROMS coupling model and its application in idealized tidal inlets[J]. Journal of Harbin Engineering University, 2019, 40(8): 1420−1426. [31] 李诚, 张弛, 隋倜倜. 浅化波浪层流边界层流速分布特性的数值分析[J]. 海洋学报, 2016, 38(5): 141−149.Li Cheng, Zhang Chi, Sui Titi. Numerical investigation on velocity distribution in the shoaling laminar wave bottom boundary layer[J]. Haiyang Xuebao, 2016, 38(5): 141−149. [32] 吴丹, 张弛. 随机波浪边界层的数值模拟与分析[J]. 水动力学研究与进展, 2016, 31(3): 303−310.Wu Dan, Zhang Chi. Numerical investigation of random wave boundary layer[J]. Chinese Journal of Hydrodynamics, 2016, 31(3): 303−310. [33] Grigoriadis D G E, Dimas A A, Balaras E. Large-eddy simulation of wave turbulent boundary layer over rippled bed[J]. Coastal Engineering, 2012, 60: 174−189. doi: 10.1016/j.coastaleng.2011.10.003 [34] Kemp P H, Simons R R. The interaction between waves and a turbulent current: waves propagating with the current[J]. Journal of Fluid Mechanics, 1982, 116: 227−250. doi: 10.1017/S0022112082000445 [35] Kemp P H, Simons R R. The interaction of waves and a turbulent current: waves propagating against the current[J]. Journal of Fluid Mechanics, 1983, 130: 73−89. doi: 10.1017/S0022112083000981 [36] Lodahl C R, Sumer B M, Fredsøe J. Turbulent combined oscillatory flow and current in a pipe[J]. Journal of Fluid Mechanics, 1998, 373: 313−348. doi: 10.1017/S0022112098002559 [37] Umeyama M. Coupled PIV and PTV measurements of particle velocities and trajectories for surface waves following a steady current[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2011, 137(2): 85−94. doi: 10.1061/(ASCE)WW.1943-5460.0000067 [38] Singh S K, Debnath K. Combined effects of wave and current in free surface turbulent flow[J]. Ocean Engineering, 2016, 127: 170−189. doi: 10.1016/j.oceaneng.2016.10.014 [39] Xie Mingxiao, Zhang Chi, Li Jinzhao, et al. Flow structure and bottom friction of the nonlinear turbulent boundary layer under stormy waves[J]. Coastal Engineering, 2021, 164: 103811. doi: 10.1016/j.coastaleng.2020.103811 [40] Wolfshtein M. The velocity and temperature distribution in one-dimensional flow with turbulence augmentation and pressure gradient[J]. International Journal of Heat and Mass Transfer, 1969, 12(3): 301−318. doi: 10.1016/0017-9310(69)90012-X [41] Chen H C, Patel V C. Near-wall turbulence models for complex flows including separation[J]. AIAA Journal, 1988, 26(6): 641−648. doi: 10.2514/3.9948 [42] Kajiura K. A model of the bottom boundary layer in water waves[J]. Bulletin of the Earthquake Research Institute, 1968, 46: 75−123. [43] Swart D H. Offshore sediment transport and equilibrium beach profiles[R]. Delft: W. D. Meinema, 1974: 131. [44] Sleath J F A. Sea Bed Mechanics[M]. New York: Wiley, 1984. [45] Schlichting H. Boundary Layer Theory[M]. Kestin J, trans. New York: McGraw-Hill, 1960. -
图(11) / 表(1)
计量
- 文章访问数: 416
- HTML全文浏览量: 207
- PDF下载量: 61
- 被引次数: 0
