Effect of sea ice deformation on winter ice thickness in Arctic based on CICE model simulation results
-
摘要: 海冰数值模式是研究海冰动力热力状态参量及之间联系的有效途径。目前对冰厚数值模拟结果的分析远远少于对海冰范围/面积和密集度的研究，对冰速与海冰形变对冰厚分布影响的研究也尚欠缺。本文利用Los Alamos sea ice model（CICE）海冰模式模拟了1980−2018年的北极海冰变化，并使用遥感、同化冰厚数据进行比对验证，分析了模拟冰速和海冰形变对冰厚的影响，计算了冰速的散度和切变偏差对冰厚偏差的贡献。结果显示，CICE对北极70°N以北区域平均冰厚和冰速的年际变化模拟基本合理，但模拟的平均冰厚和冰速多年变化趋势均小于同化数据的变化率；模拟和观测冰厚的空间分布差异与冰速和形变率的偏差有密切联系，主要表现为波弗特海的正偏差和北极中央区至弗拉姆海峡的负偏差。泛北极区域散度和切变偏差在3月之前对冰厚偏差的贡献在13%～16%之间变化，3−4月则由16%跃变至27%。散度偏差主导了11月、12月波弗特海区域的冰厚正偏差，切变偏差主导了冬季加拿大群岛以北海域和穿极流区域的冰厚负偏差。Abstract: Sea ice numerical model is an effective way to study the dynamical and thermal state parameters of sea ice and the connections between them. The current assessment of the results of numerical ice thickness simulation is much less than the sea ice extent/area and concentration, and the study of the influence of ice velocity and sea ice deformation on ice thickness distribution is still lacking. We simulated the Arctic sea ice variability from 1980 to 2018 using the Los Alamos sea ice model (CICE), and validated and comparison the CICE simulation results using remote sensing and assimilated ice thickness data. We further analyzed the effects of simulated ice velocity and sea ice deformation on ice thickness, and calculated the contributions of ice velocity divergence and shear bias to ice thickness bias. The results show that the interannual variability of the mean ice thickness and ice speed in the Arctic north of 70°N is reasonable, but the multi-year trends of the simulated mean ice thickness and ice speed are smaller than the variability of the assimilated data; the differences in the spatial distribution of the simulated and observed ice thickness are closely related to the deviations of the ice speed and deformation rate, mainly in the positive deviation in the Beaufort Sea and the negative deviation in the Arctic central zone to Fram Strait. The contribution of divergence and shear deviation to ice thickness deviation in the pan-Arctic region fluctuates between 13% and 16% before March, and jumps from 16% to 27% in March-April. The divergence bias dominates the positive bias of ice thickness in the Beaufort Sea region in November and December, while the shear bias dominates the negative ice thickness bias in the winter in the ocean north of the Canadian archipelago and in the region of the Arctic transpolar drift.
-
Key words:
- Arctic /
- ice thickness /
- ice velocity /
- deformation /
- simulation results
-
1. 引言
海冰作为北极海洋系统中的重要组成部分，对大气环流、海洋环流、全球热平衡和温盐平衡起到了至关重要的作用[1]。北极海冰的加速减退是近年来全球气候变化的重要现象之一，其显著变化包括多个方面，比如北极海冰范围和海冰密集度的减小[2-3]、海冰厚度迅速减小[4-5]和海冰漂移速度的增大[6-7]等。无论从观测数据还是模拟结果方面，目前有关北极海冰密集度和海冰范围的研究已经相当丰富，本文主要关注北极冰厚及冰速对其影响。
多种观测数据都显示出了北极海冰厚度减小的现象。最初的大范围海冰厚度观测方法为潜艇声呐探测，Rothrock等[8]通过比较1958−1976年与1990年潜艇声呐数据，得出北冰洋海冰吃水深度（海冰水下部分的厚度）由3.1 m减小到了1.8 m，1975−2000年北极海冰厚度平均变化率为−0.08 m/a。通过综合分析潜艇数据、ICESat数据和CryoSat-2数据，Kwok[9]指出融冰季末（10−11月）的平均冰厚在1958−2018年这60年间减小了2.0 m，即66%。对2018−2021年北极海冰生长季节（10月至翌年4月）ICESat和CryoSat-2干舷数据的分析结果显示，在此期间4月北极海冰平均冰厚下降了0.28 m[5]。多年冰在北极海冰中所占比例及其冰厚的显著减小是1999年至今北极平均冰厚变薄的重要表现[5, 9]。
国际北极浮标计划（The International Arctic Buoy Programme, IABP）1979−2007年的浮标数据分析显示，北极海冰的漂移速度在1979−2007年期间冬季增长率为17%·(10 a)−1，夏季为8.5%·(10 a)−1[6]。SSM/I（Special Sensor Microwave/Image）卫星遥感海冰漂移数据和10 m风场再分析数据的分析表明，1992−2009年海冰漂移速度增长率为（10.6±0.9）%·(10 a)−1，远大于风速在对应时间内的增长率（约1.5%）[10]。使用Polar Pathfinder海冰漂移数据，Zhang等[11]指出1979−2019年北极冰速在所有季节都表现为显著增大趋势，其中秋季和冬季增速最大，分别为0.13 km/(d·a)和0.11 km/(d·a)，相当于21%·(10 a)−1和20%·(10 a)−1。冰厚的变化会对海冰漂移产生影响，冰厚减小导致的强度减小、流动性增强也是冰速增大的原因之一[6, 12-13]。
冰速与海冰形变能引发局地海冰体积和厚度的快速变化，对冰厚的重分布具有重要影响[14]。2010–2015年冬季格陵兰和加拿大群岛以北的冰厚季节变化的42%～56%可归因于海冰的形变（冰速的散度和切变）[15]。2015年4月斯瓦尔巴群岛北部的一次风暴事件中，海冰形变中的散度部分解释了64%的海冰干舷变化[14]。von Albedyll等[16]研究了2018年冬末的一次冰间湖海冰形变事件，强烈的辐聚导致冰间湖重冻结的薄冰在仅1个月后平均冰厚达到了1.96 m。北极气候多学科漂流冰站观测计划（Multidisciplinary Drifting Observatory for the Study of Arctic Climate, MOSAiC）揭示了海冰动力学过程对冰厚的影响，2019年秋季至2020年初夏海冰动力学过程令MOSAiC观测区域的平均冰厚增加了0.4 m，占总变化的30%[17]。在天气时间尺度上，海冰形变的特点是长时间的平静，偶尔出现强形变事件[18]，而年际与季节尺度下的冰速、海冰形变对冰厚变化的影响还有待详细研究。
数值模式是研究冰厚和冰速变化的有效手段，使用观测、同化数据对模式结果进行验证能够给模式改进提供思路。现有的海冰模式研究普遍验证了海冰范围/面积和密集度[19-22]，例如Shu等[21]指出与观测相比，第六次耦合模式比较计划（Coupled Model Intercomparison Project, CMIP6）低估了北极9月海冰范围的下降趋势（二者分别为（−0.82 ± 0.18）×106 km2/（10 a）和（−0.70 ± 0.06）×106 km2/（10 a））；Wang等[22]指出CICE6.0对于北极海冰密集度和海冰面积季节性变化的模拟与观测值最吻合，优于其他版本，CICE4.0和CICE5.0低估了多年冰范围，高估了季节性海冰的范围，而CICE6.0解决了这个问题，与观测值最接近。但是，对于模式冰厚的分析远少于海冰范围/面积和密集度，对模式冰厚的验证多将同化数据作为观测数据使用，例如王松等[23]使用泛北极冰海洋建模和同化系统（Pan-Arctic Ice Ocean Modeling and Assimilation System, PIOMAS）数据评估了模式模拟的冰厚结果，CMIP6的模拟较CMIP5略厚且在夏季有所改进，但在4月和9月的模拟结果仍然严重偏薄（平均误差分别为−0.5～−1.0 m和−0.2～−1.5 m），并指出原因主要为净短波辐射偏大引起的冰面热收支偏大；Wang等[22]未直接给出冰厚评估结果，但CICE6.0对北极海冰体积的模拟与之前版本基本一致。另外，在对冰速的模拟的验证方面，Yu等[24]分析了北极区域气候耦合模式HIRHAM-NAOSIM 2.0的模拟结果，该模式较好地模拟了夏秋季的冰速，但高估了冬春季的冰速，12月至翌年5月的平均偏差为1.52 km/d；房永杰等[25]将CICE5.0引入BCC-CSM2.0，较旧版耦合模式海冰流速减慢，与观测更加一致，对波弗特流涡模拟的改善尤其显著； Docquier等[12]评估了NEMO-LIM3.6模拟冰速结果，相比OSISAF（Ocean and Sea Ice Satellite Application Facility）冰速数据1−3月平均误差为0.91 km/d。
综上，以往对模式结果的验证多针对海冰结冰范围、面积、密集度，对冰厚和海冰漂移速度的验证仅针对变量本身，未和分析结果中冰厚和冰速的模拟偏差联系起来。本研究将利用观测数据验证CICE海冰数值模式的海冰厚度和海冰漂移速度及其散度与切变模拟结果，并分析海冰形变对于海冰厚度的分布产生的影响。这一方面将有利于解释模拟冰厚的误差原因，另一方面也可以了解冰速模拟结果的不足，为改进海冰模式动力学提供一些思路。本文重点研究冬季的北极海冰，主要原因是缺乏可靠的大范围夏季海冰厚度和冰速遥感数据，难以对夏季的模拟结果进行验证，且冬季北极海冰覆盖范围更广、海冰漂移更强，有助于更好地分析形变与冰厚的关系。
2. 数据、模式和分析方法
2.1 冰厚、冰速和海冰密集度遥感数据
本文使用阿尔弗雷德·韦格纳研究所（Alfred Wegener Institute，AWI）提供的CryoSat-2/SMOS（Soil Moisture and Ocean Salinity）北极冬季海冰厚度融合产品[26]作为验证数据（下简称CS2SMOS），该产品将CryoSat-2在观测厚冰（厚度大于1 m）上的优势与SMOS在观测薄冰（厚度小于1 m）上的优势相结合。时间范围为2011–2018年的10月至翌年4月，2010年的11月至翌年4月，时间分辨率为每周平均，空间分辨率为25 km。另外，为了对更长时间序列的冰厚进行验证，本文采用了泛北极冰海建模和同化系统（Pan-Arctic Ice Ocean Modeling and Assimilation System，PIOMAS）的海冰厚度数据[27]，该产品时间范围为1979–2021年全年，时间分辨率为月平均，空间分辨率约为1°。冰速的验证数据为美国国家冰雪中心（National Snow and Ice Data Center，NSIDC）发布的Polar Pathfinder冰速产品[28]，该产品时间范围为1978−2021年全年，时间分辨率为逐日，空间分辨率为25 km。此外，本研究还使用了欧洲气象卫星应用组织的海洋和海冰分部（OSISAF）提供的全球低分辨率海冰漂移数据[29]，时间范围为2009年12月至翌年4月，2010年至今每年的10月至翌年4月，时间分辨率为2 d，空间分辨率为62.5 km。本文使用NSIDC提供的由扫描多通道微波辐射计（Scanning Microwave Multiband Radiometr，SMMR）、特殊传感器微波成像仪（Special Sensor Microwave Imager，SSM/I）和特殊传感器微波成像探测仪（Special Sensor Microwave Imager Sounder，SSMIS）亮温数据反演的海冰密集度数据[30]，时间范围为1978–2021年全年，时间分辨率为逐日，空间分辨率为25 km。
为了与模式结果进行比较，以上数据均采用与1980−2018年的交集时段。该研究中的海冰厚度和冰速的时间序列计算与误差统计统一为70°N以北的所有数据平均，这一纬度能将北极海冰漂移的波弗特流涡与穿极流包括在内，同时排除一些纬度较低的边缘海。
2.2 CICE模式设置及强迫数据
CICE是美国Los Alamos国家实验室开发的海冰模式，具有较复杂的参数化过程[31]。本研究使用CICE6.0版本，大气强迫采用ERA5（ECMWF Reanalysis v5）再分析数据的6 h平均10 m风速、2 m气温、总降水量、降雪量、总云量、露点温度和海表面气压[32]；海洋强迫采用并行海洋计划（Parallel Ocean Program，POP）试验的气候态月平均海流速度、海表面倾斜与混合层底海洋热通量结果[33]，以及极地科学中心水温气候态（Polar Science Center Hydrographic Climatology，PHC）气候态海表面温度和盐度数据[34]。对应大气强迫，模式试验结果的时间范围为1980−2018年全年，时间步长为1 d，空间分辨率约为1°，空间范围为全球。这里主要分析冬季北极海冰70°N以北的试验结果，对模式数据的处理方式与2.1节一致。CICE模式中的主要参数基本采用默认设置，具体见表1。
表 1 CICE模式主要参数化方案与参数设置Table 1. Main parameterization schemes and parameter settings of CICE model主要方案 方案设置 主要参数 参数设置 网格 gx1（320 × 384） 海冰厚度类别（ncat） 5 流变学方案 弹性–黏性–塑性流变学（EVP） 海冰垂直分层（nilyr） 7 海冰强度方案 Rothrock强度参数化 子周期数(ndte) 120 反照率参数化 Delta-Eddington辐射计算方案 成脊参数(μ) 3 热力学参数化 糊状层热力学方案 大气边界层迭代次数（natmiter） 5 融池参数化 地形学方案（Topographic scheme） 近红外海冰反照率（albicei） 0.36 海气拖曳参数化 组合拖曳方案 可见光海冰反照率（albicev） 0.78 注：gx1代表分辨率约为1°。 2.3 冰速散度、切变的计算
海冰漂移速度的散度与切变是描述海冰形变的常用参量，为了研究海冰形变对冰厚分布的影响，本文使用遥感海冰漂移数据计算了海冰漂移的散度和切变，计算方法采用了Kwok等[35]使用的方法，其中冰速散度（
$ {D_{{\rm{div}}}} $ ）的公式为$$ {D_{{\rm{div}}}} = \nabla \cdot {{\boldsymbol{u}}} = \frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} , $$ (1) 冰速切变
$ {D_{{\rm{shear}}}} $ 的公式为$$ {D_{{\rm{shear}}}} = {\left[{\left(\frac{{\partial u}}{{\partial x}} - \frac{{\partial v}}{{\partial y}}\right)^2} + {\left(\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}}\right)^2}\right]^{1/2}} \text{，} $$ (2) 式中，
${{\boldsymbol{u}}}$ 为海冰漂移速度矢量；u、v分别代表沿网格x和y方向的海冰漂移速度。微商计算以
$\dfrac{{\partial u}}{{\partial x}} = \dfrac{1}{A}\oint {u{\rm{d}}y}$ 为例，近似为$$ \frac{{\partial u}}{{\partial x}} = \frac{1}{A}\sum\limits_{i = 1}^N {\frac{1}{2}} ({u_{i + 1}} + {u_i})({y_{i + 1}} - {y_i}) \text{，} $$ (3) 上述公式对于任意多边形区域有效，式中，N为多边形区域顶点的个数；A为区域面积；yi为多边形第i个格点的y坐标。在OSISAF冰速数据使用的d =62.5 km的正方形网格中，有N = 4、A = 3 906.25 km2，以4点坐标分别为(0, 0)、(0, d)、(d, d)、(d, 0)的正方形网格为例，按顺时针将4点的u代入式（3）计算可以得到：
$$ {u_x} = \frac{1}{2}\{ [u(0,d) - u(d,d)]/d + [u(0,0) - u(d,0)]/d\} , $$ (4) 即两条x方向边上u梯度的平均值。本文计算的冰速散度代表了网格边界海冰面积通量，正/负值代表了海冰辐散/辐聚；切变为垂直于冰速方向的冰速梯度大小，高切变的区域可能与海冰的断裂相对应[35]。值得注意的是，先计算每天的冰速散度、切变，再计算月平均值与先计算月平均冰速再计算冰速散度、切变，得出的结果存在差异，前者会保留大量的短期海冰形变，可用于短期海冰的变化分析，但计算结果会出现较多的极端值。本研究更关注海冰形变在季节尺度上对冰厚的影响，因此采用先计算月平均冰速再计算冰速散度、切变的计算方式。
3. CICE模式模拟结果分析与讨论
本节将对模拟冰厚进行验证，并使用观测数据计算海冰的形变特征，分析模拟冰速及海冰形变（冰速的散度与切变）对模拟冰厚的影响。在进行冰厚的验证之前，我们首先简单分析一下CICE模拟的1980–2018年北极冬季海冰密集度和海冰范围分布（图1）。总体上，北极冬季海冰覆盖范围的模拟与观测结果基本一致（图1a，图1b），大部分密集冰区（观测海冰密集度大于90%的区域）的模拟与观测一致性较好（图1c，图1d）。模拟结果的高估主要出现在格陵兰海、巴伦支海、巴芬湾的边缘冰区和12月的楚科奇海，而在格陵兰海海冰外缘线附近、巴芬湾的密集冰区低估了海冰密集度。
图 1 1980–2018年北极冬季（12月、2月、4月）气候态月平均海冰密集度（a1−b3）、海冰密集度差异（c1−c3）和相对误差（d1−d3）数据来源：a. SSM/I；b. CICE；c. CICE−SSM/I。c、d中的黑线为SSM/I海冰密集度90%等值线；图中纬线为70°NFigure 1. Monthly mean sea ice concentration (a1−b3), sea ice concentration difference (c1−c3) and relative error of sea ice concentration (d1−d3) of Arctic winter (December, February, April) climatic regimes from 1980 to 2018Date source: a. SSM/I; b. CICE; c. CICE−SSM/I. The black lines in c and d are the 90% contours of SSM/I sea ice density; the latitude line in the graph is 70°N3.1 冰厚
本文使用CS2SMOS遥感海冰厚度和PIOMAS冰厚产品验证了北极冬季海冰厚度模拟结果，模拟结果的统计误差如表2、表3所示。相比CS2SMOS冰厚数据，CICE模拟结果的平均误差、平均绝对误差、均方根误差和相对误差分别为0.16 m、0.47 m、0.65 m和37.07%，除平均绝对误差之外的3种冰厚误差均在11月至翌年3月减小，4月开始增大。冰厚的平均误差较小但平均绝对误差、均方根误差和相对误差较大，这意味着与观测相比，模拟冰厚的空间分布存在较大偏差。
表 2 2010−2018年冬季（11月至翌年4月）70°N以北模拟海冰厚度相对CS2SMOS观测数据的月各项误差统计结果Table 2. Monthly errors statistics of simulated sea ice thickness north of 70°N relative to CS2SMOS observations for winter (from November to April of the following year), 2010−2018误差类型 11月 12月 1月 2月 3月 4月 总计 ME/m 0.24 0.19 0.17 0.13 0.10 0.15 0.16 MAE/m 0.48 0.46 0.47 0.47 0.47 0.48 0.47 RMSE/m 0.69 0.65 0.65 0.64 0.64 0.64 0.65 RE/% 49.98 38.00 33.93 30.64 30.52 40.03 37.07 注：ME：平均误差；MAE：平均绝对误差；RMSE：均方根误差；RE：相对误差。 表 3 2010−2018年70°N以北模拟海冰厚度相对CS2SMOS观测的冬季（11月至翌年4月）各项误差统计结果Table 3. Average winter (from November to April of the following year) errors statistics of simulated sea ice thickness north of 70°N relative to CS2SMOS observations, 2010−2018误差类型 2010−2011年 2011−2012年 2012−2013年 2013−2014年 2014−2015年 2015−2016年 2016−2017年 2017−2018年 ME/m 0.19 0.32 0.27 0.08 0.07 0.21 0.02 0.06 MAE/m 0.53 0.56 0.50 0.44 0.47 0.59 0.45 0.45 RMSE/m 0.73 0.80 0.71 0.57 0.66 0.79 0.58 0.62 RE/% 39.72 45.73 41.74 34.53 30.24 57.83 30.77 39.93 注：ME：平均误差；MAE：平均绝对误差；RMSE：均方根误差；RE：相对误差；2010−2011年代表2010年11月至2011年4月，以此类推。 从2010−2018年北极冬季（11月至翌年4月）的气候态CICE冰厚模拟结果的空间分布与观测数据的差别（图2a至图2c）来看，的确具有较大的空间分布差异。图2a显示了观测数据中11月至翌年4月的冬季海冰逐渐增厚的过程。由图2a1至图2a6可知，冬季北极冰厚的空间分布规律为从加拿大北极群岛和格陵兰岛沿岸向欧亚大陆方向逐渐减小。模拟冰厚相对观测的空间分布差异较大，图2b、图2c表明，CICE的模拟结果与CS2SMOS相比最明显的差异出现在波弗特海、北极中央区和弗拉姆海峡区域。波弗特海至新西伯利亚群岛之间为正偏差区域，正偏差区域形状为蝌蚪形，其中心正偏差最强，这一区域的正偏差存在随时间减小的趋势。除此之外，在加拿大群岛和格陵兰岛的北部沿岸也存在正偏差区域，且较波弗特海更强，但不随时间变化。北极中央区至弗拉姆海峡存在一个漏斗形的负偏差区域，其中弗拉姆海峡所在的一角负偏差最大，这一区域的负偏差随时间增大。这种显著的空间分布差异解释了冰厚平均误差较小而相对误差较大的原因。图2d表明，蝌蚪形正偏差区域模式对冰厚的高估十分明显，正偏差区域中心的相对误差在11月至翌年2月均超过了100%。漏斗形负偏差区域模式对冰厚的低估则弱一些，负偏差区域的相对误差则始终小于50%。
图2e给出了2010–2018年的冬季月平均冰厚季节变化，PIOMAS冰厚同化了大量冰厚实测数据，因此与观测十分接近。模拟结果相比CS2SMOS观测冰厚明显高估了2010−2018年70°N以北的气候态冬季冰厚，相比PIOMAS冰厚数据，在除4月、5月之外的所有月份高估了冰厚。图2f为冬季平均冰厚的年际变化，相比CS2SMOS观测冰厚，模拟结果在2010年11月至2018年4月的8个冬季高估了北极海冰冰厚。相比PIOMAS冰厚数据，模拟结果在1998年之前的冬季低估了北极海冰冰厚，在2002年之后的冬季高估了北极海冰冰厚，且模拟冰厚的减小趋势偏小。CICE和PIOMAS的冰厚减小趋势分别为−0.08 m/（10 a）和−0.22 m/（10 a），但CICE与PIOMAS冬季冰速的年际变化显著相关，相关系数约为0.85，通过了99%置信度的显著性检验。Wang等[22]对多个版本的CICE模式的评估结果显示，CICE6.0版本相比CICE 5.0对海冰体积的年际变化模拟并无显著改善。因此，CICE对北极冬季冰厚季节变化和年际变化趋势模拟能力有待提高。
为了解释图2c中蝌蚪形正偏差区域和漏斗形负偏差区域，我们检查了大气强迫中直接影响海冰生长与消融的2 m气温。图3表明，2 m气温的分布情况与CICE冰厚和CS2SMOS冰厚之间的冰厚差异并不对应（图2c），冰厚正偏差区域和负偏差区域的2 m气温并不存在显著差异。另外，不使用ERA5作为大气强迫，而是通过与区域海洋建模系统（Regional Ocean Modeling System, ROMS）耦合驱动CICE，模拟冰厚结果依旧出现了与本文类似的正、负偏差区域，但其正偏差区域要向北极点方向弯曲一些[36]。可以推测，蝌蚪型正偏差与漏斗型负偏差主要是由模式本身的动力学过程而非热力学因素导致，应该与CICE对海冰漂移的模拟有关。因此，接下来本文将对CICE冰速以及海冰形变（冰速的散度和切变）进行研究。
图 3 2010−2018年11月至翌年4月ERA5月平均2 m气温图中纬线为70°NFigure 3. ERA5 monthly average 2 m temperature from November to April of the following year from 2010 to 2018The latitude line in the graph is 70°N3.2 冰速
本研究使用OSISAF和Polar Pathfinder冰速数据验证了模拟的北极冬季海冰漂移速度结果，由于Polar Pathfinder冰速产品与观测相比均值偏小[37-38]，且2009−2016年冬季与浮标数据相比平均误差约为−3.83 cm/s[38]，因此仅用于验证模拟冰速的年际变化。模拟冰速相对OSISAF冰速数据的误差统计结果如表4、表5所示，总平均误差、总平均绝对误差、总均方根误差和总相对误差分别为−0.84 cm/s、2.94 cm/s、4.13 cm/s和99.55%。与冰厚误差类似，冰速的平均误差较小，但平均绝对误差、均方根误差和相对误差较大，相对误差接近100%，这引起了我们的重视。因此接下来本研究将重点关注模拟冰速与观测之间空间分布的差异，并分析冰速差异与冰厚偏差的联系。
表 4 2010−2018年冬季（11月至翌年4月）70°N以北模拟冰速相对OSISAF冰速的月各项误差统计结果Table 4. Monthly errors statistics of simulated ice velocity north of 70°N relative to OSISAF ice velocity for each month of winter (from November to April of the following year) from 2010 to 2018误差类型 11月 12月 1月 2月 3月 4月 总计 ME/（cm·s−1） −1.55 −1.26 −0.73 −0.45 −0.68 −0.52 −0.84 MAE/（cm·s−1） 2.96 2.99 3.23 2.93 2.95 2.58 2.94 RMSE/（cm·s−1） 4.18 4.17 4.43 4.24 4.20 3.50 4.13 RE/% 67.40 68.80 105.02 105.19 121.02 121.51 99.55 注：ME：平均误差；MAE：平均绝对误差；RMSE：均方根误差；RE：相对误差。 表 5 2010−2018年逐年70°N以北模拟冰速相对OSISAF观测冰速的冬季（11月至翌年4月）各项误差统计结果Table 5. Winter (from November to April of the following year) errors statistics of simulated ice velocity north of 70°N relative to OSISAF observed ice velocity year by year from 2010 to 2018误差类型 2010−2011年 2011−2012年 2012−2013年 2013−2014年 2014−2015年 2015−2016年 2016−2017年 2017−2018年 ME/（cm·s−1） −0.43 −1.04 −2.04 −0.58 −0.37 −0.91 −0.77 −0.72 MAE/（cm·s−1） 2.41 2.98 3.34 2.37 3.29 3.21 2.90 3.17 RMSE/（cm·s−1） 3.33 3.84 4.64 3.36 4.42 4.86 4.19 4.43 RE/% 86.63 107.90 94.17 82.87 133.20 123.65 77.61 91.91 注：ME：平均误差，MAE：平均绝对误差，RMSE：均方根误差，RE：相对误差；2010−2011年代表2010年11月至201年4月，以此类推。 海冰漂移速度会影响冰厚的重分布。由图4a、图4b可知，模拟冰速场在冬季空间分布上可以呈现出明显的穿极流与波弗特流涡形态，但与遥感冰速仍有所差异。模拟冰速较观测数据的波弗特流涡范围偏大，且流涡的中心偏向西伯利亚一侧，具体表现为高估了波弗特流涡南侧向西的冰速，同时高估了加拿大群岛以北海域向南的冰速，穿极流区域模拟冰速也偏大（图4c）。格陵兰岛和加拿大群岛以北海域的冰速偏大，整个冬季由波弗特海向西的冰速偏大，这样的海冰漂移形态会导致加拿大群岛以北的厚冰更多地向波弗特海西北输出并积累，形成图2c所示正偏差区域。除此之外，OSISAF数据的海冰漂移在弗拉姆海峡区域运动方向接近正南（图4a），受到斯瓦尔巴群岛的阻碍更大；而模拟结果在该区域的海冰漂移方向偏向西南（图4b），海冰可更顺利地通过弗拉姆海峡输出，再加上模拟结果在冬季所有月份均高估了穿极流的冰速（图4c），以上因素可能导致了图2c所示的冰厚负偏差区域的产生。
图4d、图4e为北极气候态月平均冰速季节变化和冬季冰速的年际变化的模拟与观测数据比较，模拟冰速12月至翌年4月的平均值与OSISAF冰速较为接近，10月、11月则明显偏小；Polar Pathfinder冰速相比OSISAF明显偏小。冬季各月OSISAF和Polar Pathfinder冰速的季节变化基本一致，均在10月、12月和翌年3月存在峰值，而模拟冰速的两个峰值则出现于12月和翌年3月。10月模拟冰速异常的原因可能与10月海冰的明显偏厚有关（图2e），冰厚偏大导致了一定大气强迫下的冰速偏小。原因也可能是遥感冰速受到部分未冻结的冰表面信号的影响产生的反演误差，Polar Pathfinder是同化了观测数据的结果[28]，同样存在该问题。由于本文的分析仅限于冬季，因此对于夏秋季的季节变化问题，有待今后进一步讨论。
模拟冬季冰速的年际变化趋势为0.11 cm/(s·(10 a))，并不显著，而Polar Pathfinder数据存在明显增大趋势，约为0.66 cm/(s·(10 a))，但CICE与Polar Pathfinder冬季冰速的年际变化显著相关，相关系数约为0.45，去趋势后为0.51，通过了99%置信度的显著性检验。模拟冰速变化率仅相当于Polar Pathfinder数据的1/6，在3.1节中1980−2018年模拟冰厚减小趋势为−0.08 m/（10 a），仅为PIOMAS数据的36%。模拟冰厚和冰速对于年际变化趋势的低估可能存在联系，而海冰形变是海冰漂移速度影响北极冰厚的变化的重要方式，下面将进一步分析表征海冰形变的主要参量：冰速的散度与切变。
3.3 海冰形变
本文使用OSISAF月平均冰速计算了北极冬季各月月平均冰速的散度和切变，如图5所示，OSISAF的冬季海冰辐散（正散度）主要位于波弗特海至拉普捷夫海之间的连线、喀拉海等区域，辐聚区域（负散度）主要位于波弗特海、楚科奇海和大西洋扇区的海冰边缘区域与北极中央区（图5a）。除1月外，模拟结果相比OSISAF冰速散度在波弗特海海冰边缘的正散度偏大，即模式中此处的辐散相对于观测偏强，而在楚科奇海以北区域的正散度偏小甚至为负散度（图5b），即此处辐散较弱、辐聚偏强，导致了波弗特流涡向西输出的海冰在此积累，造成了图2c所示的冰厚的正偏差区域。此外，OSISAF在斯瓦尔巴特群岛以北至弗拉姆海峡区域为较强的负散度，而CICE在弗拉姆海峡区域则同时存在正散度和负散度，即模拟结果中此处的辐聚不足，有助于更多海冰从弗拉姆海峡输出，因此产生了冰厚的负偏差区域[39]，这也与前文对OSISAF和CICE在弗拉姆海峡区域海冰漂移差异的分析一致。
图 5 2010–2018年北极冬季（11月至翌年4月）OSISAF遥感观测冰速散度场（a1−a6）和CICE冰速散度场（b1−b6）图中纬线为70°NFigure 5. OSISAF remotely observed ice velocity divergence fields (a1−a6) and CICE ice velocity divergence fields (b1−b6) for the Arctic winter (from November to April of the following year) from 2010 to 2018The latitude line in the graph is 70°N图6显示，OSISAF数据的冬季冰速切变高值区域集中在波弗特海、巴芬湾和弗拉姆海峡、巴伦支海等大西洋扇区的海冰边缘区域。CICE模拟的切变场要高于观测数据，其中在波弗特海和弗拉姆海峡尤为明显，这意味着模式中海冰在此处的漂移存在更强的水平梯度。在波弗特海，这种更强的冰速水平梯度源于CICE模拟结果中更大、范围更宽的波弗特流涡，而在弗拉姆海峡，切变更强的原因一方面是更强的穿极流，另一方面是模拟的海冰范围比观测更大（图4b）。切变偏大会令海冰具有更强的流动性，从而导致更多的海冰输运。
图 6 2010–2018年北极冬季（11月至翌年4月）OSISAF遥感观测冰速切变场（a1−a6）和CICE冰速切变场（b1−b6）图中纬线为70°NFigure 6. OSISAF remotely observed ice velocity shear fields (a1−a6) and CICE ice velocity shear fields (b1−b6) for the Arctic winter (from November to April of the following year) from 2010 to 2018The latitude line in the graph is 70°N为了进一步分析散度和切变对模式冰厚偏差的贡献，研究动力学因素对CICE试验中冰厚变化的影响，本研究将冰速散度偏差、切变偏差与冰厚偏差进行了线性回归。图7为散度偏差和切变偏差对冰厚偏差的线性回归决定系数的空间分布与季节变化，其中冰厚偏差以CS2SMOS冰厚为标准，冰速散度和切变偏差以OSISAF数据为标准。综合来看，CICE冬季海冰形变的偏差对冰厚偏差的贡献在波弗特海和加拿大群岛以北海域最强，穿极流区域次之（图7a1）。图7a2显示，CICE北极冬季冰速散度偏差对冰厚偏差的贡献高值区对应了图2b、图2c中的波弗特海的冰厚正偏差区域，而图7a3则表明冬季冰速切变偏差对冰厚偏差的贡献高值区对应了加拿大群岛以北海域和穿极流区域的冰厚负偏差区域。
图 7 2010−2018年北极冬季（11月至翌年4月）平均冰速散度偏差和切变偏差对冰厚偏差（a1）、散度偏差对冰厚偏差（a2）、切变偏差对冰厚偏差（a3）的线性回归决定系数R2空间分布、11月至翌年4月泛北极区域的 R2时间序列（b）、a2中红线划定的波弗特海区域 R2时间序列（c）和a3中黑线划定的加拿大群岛以北海域 R2时间序列（d）仅显示和统计通过99%显著性检验的数据Figure 7. Spatial distribution of the linear regression coefficients of determination (R2) of the mean ice velocity divergence bias and shear bias on ice thickness bias (a1), divergence bias on ice thickness bias (a2), shear bias on ice thickness bias (a3), R2 time series for the pan-Arctic region from November to April (b); R2 time series for the Beaufort Sea region delineated by the red line in a2 (c) and R2 time series of the sea north of the Canadian archipelago delineated by the black line in a3 (d) for the Arctic winter (from November to April of the following year) from 2010 to 2018Only data that pass the 99% significance test are shown and counted泛北极区域冬季11月至翌年4月每个月散度偏差和切变偏差对冰厚偏差的线性回归决定系数如图7b所示，11月至翌年3月散度偏差和切变偏差对冰厚偏差的线性回归决定系数变化较小，维持在0.13～0.16，3–4月的变化尤为显著，由0.16增大至0.27，这可能与图2d和表1中显示的3–4月模拟与观测平均冰厚差异的剧烈变化有关，切变偏差的贡献整体高于散度偏差。它们的贡献存在明显的季节变化，散度偏差对冰厚偏差的贡献在11月至翌年1月和2−3月减弱、1−2月和3−4月增强；切变偏差对冰厚偏差的贡献在11−12月和2−3月减弱、12月至翌年2月和3−4月增强。
为了进一步研究海冰形变与冰厚偏差之间的关系，这里采取了图7a2、图7a3所示的分区，分别对应图2c的蝌蚪形正偏差区域和漏斗形的负偏差区域。图7c显示，波弗特海区域散度偏差与切变偏差对冰厚偏差的贡献在11月至翌年1月减弱、2−4月增强，其中11−12月由散度偏差主导，1月、2月、4月二者贡献接近，3月则是切变偏差对冰厚偏差的贡献高于散度偏差。加拿大群岛以北海域切变偏差对冰厚偏差存在显著贡献（图7d），整个冬季海冰形变偏差对冰厚偏差的贡献逐渐增大，切变偏差对冰厚偏差的贡献显著高于散度偏差。Kwok和Cunningham[15]的研究也指出了2010–2015年冬季加拿大群岛以北海域冰速切变对冰厚变化的显著贡献，线性回归决定系数在0.28～0.39之间。
4. 结论与展望
本文使用ERA5再分析数据作为大气强迫，POP和PHC气候态试验结果作为海洋强迫，利用CICE6.0海冰模式模拟了1980−2018年的北极海冰，使用SSMI海冰密集度、CS2SMOS和PIOMAS海冰厚度、Polar Pathfinder和OSISAF冰速数据对模拟结果进行了比对验证，进而分析了模拟海冰漂移和海冰形变对冰厚的影响，研究并解释了模拟冰厚出现误差的原因。
整体而言，模拟结果能够大致还原出1980−2018年PIOMAS冰厚数据中北极空间平均冬季冰厚的年际变化，冰厚平均误差约为0.16 m。但是与CS2SMOS冰厚数据相比，2010−2018年模式冰厚的气候态空间分布很不理想，空间平均相对误差为37.07%。冰厚在波弗特海至新西伯利亚群岛的蝌蚪形区域内明显被高估，北极中央区与弗拉姆海峡的漏斗形区域则被严重低估。这种冰厚偏差主要由力学因素造成，因此本文侧重于在动力学角度进行进一步分析。
与OSISAF冰速数据相比，2010−2018年模式冰速的平均误差和相对误差分别为−0.84 cm/s和99.55%。空间分布上，CICE模拟的波弗特流涡范围偏大，中心位置偏向西伯利亚一侧，这样的海冰漂移形态会导致加拿大群岛以北的厚冰更多地向波弗特海输出并在此累积，且冬季楚科奇海以北存在冰速散度的负偏差，即CICE模拟的海冰漂移相比于观测的辐散不足，海冰在此累积，导致CICE模拟结果高估了该区域的冰厚。另一方面，CICE模拟的北极中央区和穿极流存在西南向的冰速正偏差，且模拟结果中弗拉姆海峡区域的海冰漂移辐聚不足，过量的海冰从北极中央区向弗拉姆海峡漂移最终离开北极。
我们进一步研究了海冰形变对CICE模拟结果中冰厚偏差的贡献。泛北极区域散度偏差和切变偏差在北极冬季3月之前对冰厚偏差的贡献波动于0.13～0.16之间，3–4月突然由0.16增大至0.27，这符合冰厚越薄受到冰速及形变影响越大的物理认识。切变偏差的贡献整体高于散度偏差。散度偏差对冰厚偏差的贡献主导了11月、12月波弗特海的冰厚正偏差区域，切变偏差对冰厚偏差的贡献主导了整个冬季加拿大群岛以北海域和穿极流区域的冰厚负偏差区域。
限于遥感数据时间序列长度，这里仅使用PIOMAS同化冰厚数据和Polar Pathfinder冰速数据验证了冰厚和冰速的多年变化趋势，模拟结果均明显低估。1980−2018年模拟冰厚减小趋势为−0.08 m/(10 a)，仅为PIOMAS数据的36%，而模拟冰速变化率为0.11 cm/(s·(10 a))，相当于Polar Pathfinder数据的1/6。
CICE模拟冰厚和冰速的空间分布上的偏差与多年变化趋势的低估可能部分来源于强迫场本身，也有可能是源于模式的物理过程[36]，包括海冰对于海洋、大气强迫的响应与海冰内部的相互作用。现有模式中不少参数化方案的建立基于早期的观测数据[40-41]，不能再现近年来北极海冰性质的快速变化，例如与大气强迫相关的海冰表面粗糙度的改变[42]、与形变相关的海冰强度的减小[6]、碎冰和水道比例的增加[43]等。因此未来需要利用更高分辨率和更大时空范围的观测数据对相关的北极海冰的动力学参数进行改进，最终实现对未来北极海冰的有效预测。本研究分析了冬季模式中海冰形变对冰厚变化贡献的气候态季节变化，而随着北极海冰物理性质的加速变化，海冰形变与冰厚关系的年际变化有待进一步研究。
-
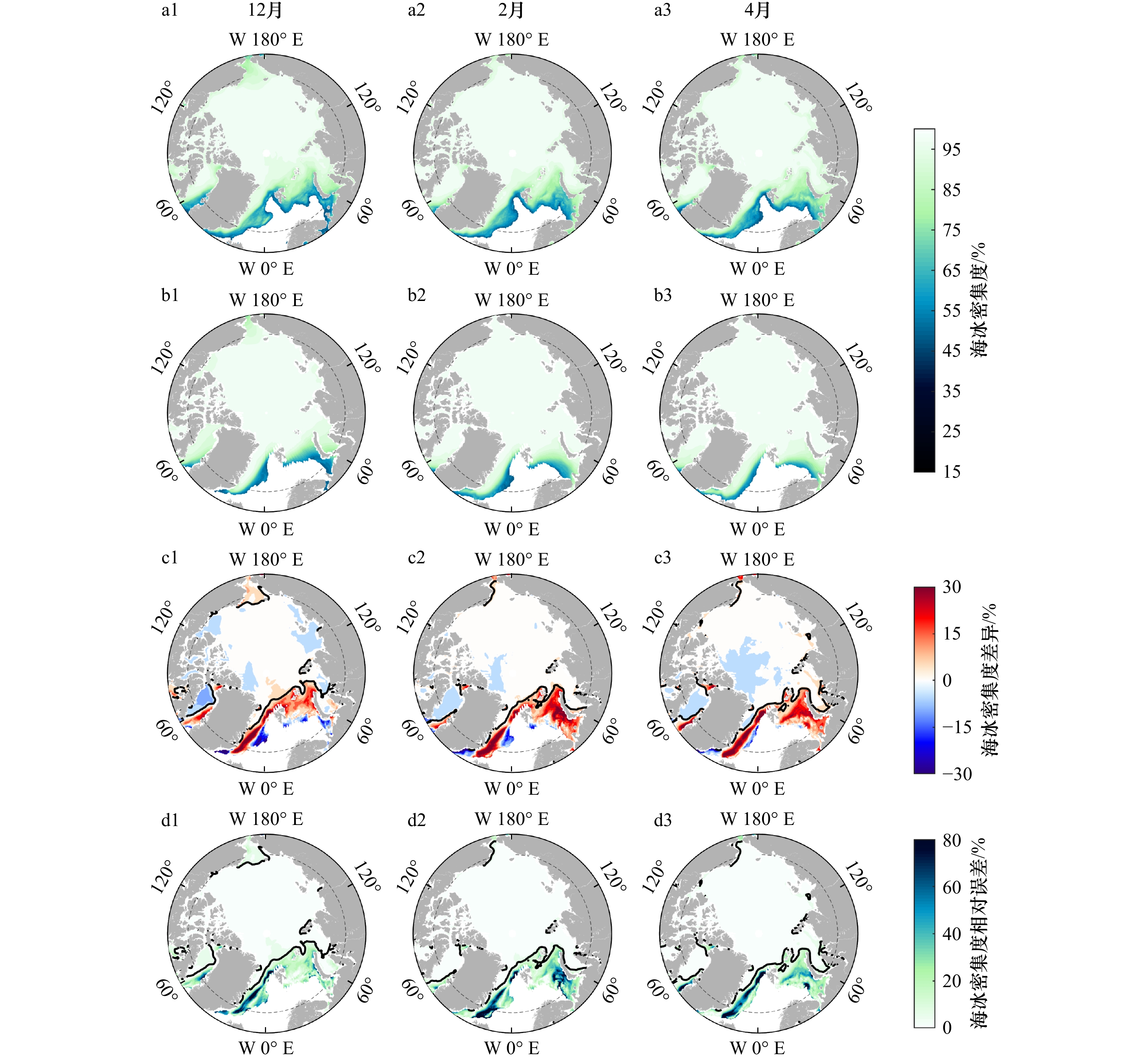
图 1 1980–2018年北极冬季（12月、2月、4月）气候态月平均海冰密集度（a1−b3）、海冰密集度差异（c1−c3）和相对误差（d1−d3）
数据来源：a. SSM/I；b. CICE；c. CICE−SSM/I。c、d中的黑线为SSM/I海冰密集度90%等值线；图中纬线为70°N
Fig. 1 Monthly mean sea ice concentration (a1−b3), sea ice concentration difference (c1−c3) and relative error of sea ice concentration (d1−d3) of Arctic winter (December, February, April) climatic regimes from 1980 to 2018
Date source: a. SSM/I; b. CICE; c. CICE−SSM/I. The black lines in c and d are the 90% contours of SSM/I sea ice density; the latitude line in the graph is 70°N
图 3 2010−2018年11月至翌年4月ERA5月平均2 m气温
图中纬线为70°N
Fig. 3 ERA5 monthly average 2 m temperature from November to April of the following year from 2010 to 2018
The latitude line in the graph is 70°N
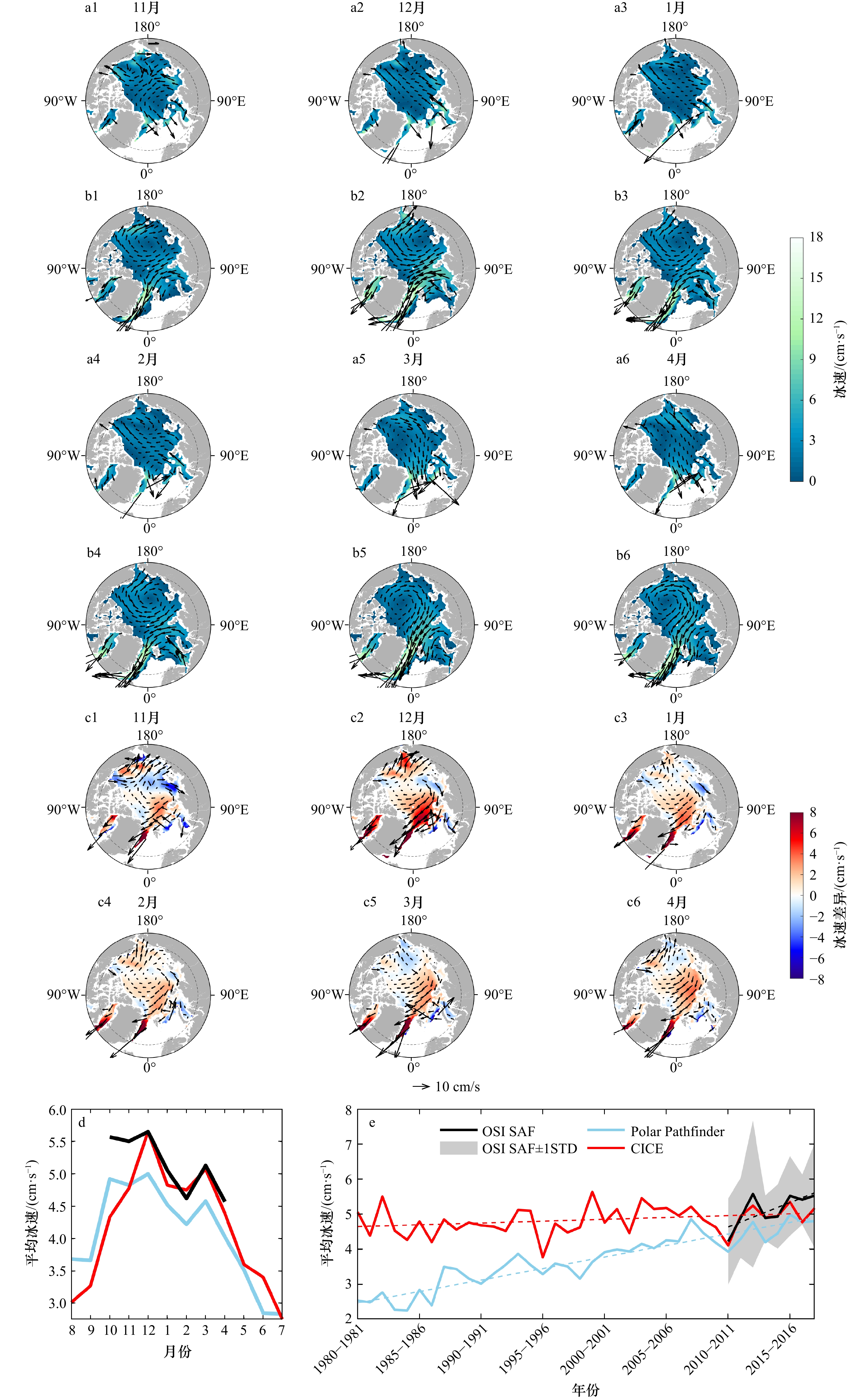
图 5 2010–2018年北极冬季（11月至翌年4月）OSISAF遥感观测冰速散度场（a1−a6）和CICE冰速散度场（b1−b6）
图中纬线为70°N
Fig. 5 OSISAF remotely observed ice velocity divergence fields (a1−a6) and CICE ice velocity divergence fields (b1−b6) for the Arctic winter (from November to April of the following year) from 2010 to 2018
The latitude line in the graph is 70°N
图 6 2010–2018年北极冬季（11月至翌年4月）OSISAF遥感观测冰速切变场（a1−a6）和CICE冰速切变场（b1−b6）
图中纬线为70°N
Fig. 6 OSISAF remotely observed ice velocity shear fields (a1−a6) and CICE ice velocity shear fields (b1−b6) for the Arctic winter (from November to April of the following year) from 2010 to 2018
The latitude line in the graph is 70°N
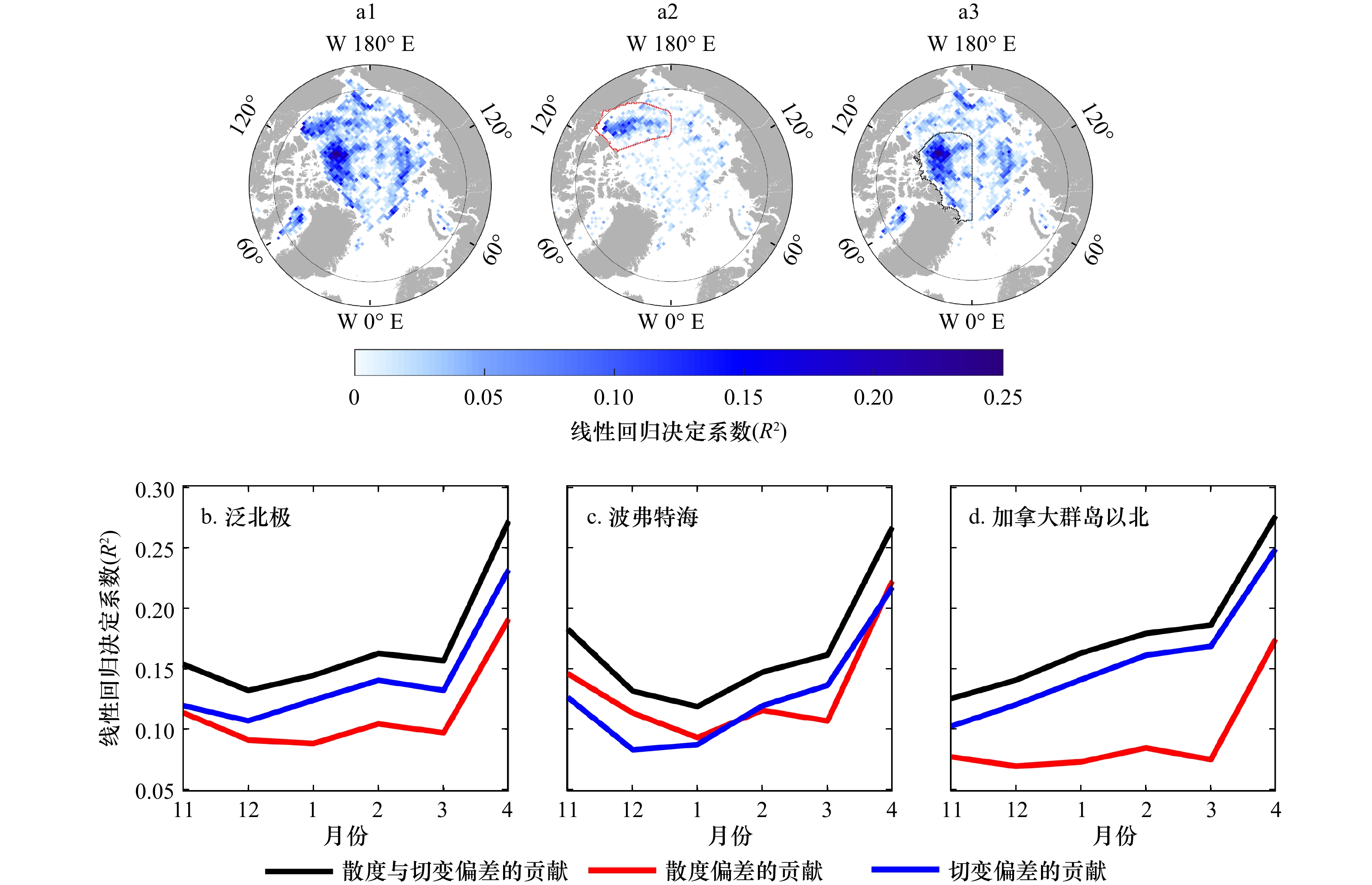
图 7 2010−2018年北极冬季（11月至翌年4月）平均冰速散度偏差和切变偏差对冰厚偏差（a1）、散度偏差对冰厚偏差（a2）、切变偏差对冰厚偏差（a3）的线性回归决定系数R2空间分布、11月至翌年4月泛北极区域的 R2时间序列（b）、a2中红线划定的波弗特海区域 R2时间序列（c）和a3中黑线划定的加拿大群岛以北海域 R2时间序列（d）
仅显示和统计通过99%显著性检验的数据
Fig. 7 Spatial distribution of the linear regression coefficients of determination (R2) of the mean ice velocity divergence bias and shear bias on ice thickness bias (a1), divergence bias on ice thickness bias (a2), shear bias on ice thickness bias (a3), R2 time series for the pan-Arctic region from November to April (b); R2 time series for the Beaufort Sea region delineated by the red line in a2 (c) and R2 time series of the sea north of the Canadian archipelago delineated by the black line in a3 (d) for the Arctic winter (from November to April of the following year) from 2010 to 2018
Only data that pass the 99% significance test are shown and counted
表 1 CICE模式主要参数化方案与参数设置
Tab. 1 Main parameterization schemes and parameter settings of CICE model
主要方案 方案设置 主要参数 参数设置 网格 gx1（320 × 384） 海冰厚度类别（ncat） 5 流变学方案 弹性–黏性–塑性流变学（EVP） 海冰垂直分层（nilyr） 7 海冰强度方案 Rothrock强度参数化 子周期数(ndte) 120 反照率参数化 Delta-Eddington辐射计算方案 成脊参数(μ) 3 热力学参数化 糊状层热力学方案 大气边界层迭代次数（natmiter） 5 融池参数化 地形学方案（Topographic scheme） 近红外海冰反照率（albicei） 0.36 海气拖曳参数化 组合拖曳方案 可见光海冰反照率（albicev） 0.78 注：gx1代表分辨率约为1°。 
下载: 导出CSV
表 2 2010−2018年冬季（11月至翌年4月）70°N以北模拟海冰厚度相对CS2SMOS观测数据的月各项误差统计结果
Tab. 2 Monthly errors statistics of simulated sea ice thickness north of 70°N relative to CS2SMOS observations for winter (from November to April of the following year), 2010−2018
误差类型 11月 12月 1月 2月 3月 4月 总计 ME/m 0.24 0.19 0.17 0.13 0.10 0.15 0.16 MAE/m 0.48 0.46 0.47 0.47 0.47 0.48 0.47 RMSE/m 0.69 0.65 0.65 0.64 0.64 0.64 0.65 RE/% 49.98 38.00 33.93 30.64 30.52 40.03 37.07 注：ME：平均误差；MAE：平均绝对误差；RMSE：均方根误差；RE：相对误差。
下载: 导出CSV
表 3 2010−2018年70°N以北模拟海冰厚度相对CS2SMOS观测的冬季（11月至翌年4月）各项误差统计结果
Tab. 3 Average winter (from November to April of the following year) errors statistics of simulated sea ice thickness north of 70°N relative to CS2SMOS observations, 2010−2018
误差类型 2010−2011年 2011−2012年 2012−2013年 2013−2014年 2014−2015年 2015−2016年 2016−2017年 2017−2018年 ME/m 0.19 0.32 0.27 0.08 0.07 0.21 0.02 0.06 MAE/m 0.53 0.56 0.50 0.44 0.47 0.59 0.45 0.45 RMSE/m 0.73 0.80 0.71 0.57 0.66 0.79 0.58 0.62 RE/% 39.72 45.73 41.74 34.53 30.24 57.83 30.77 39.93 注：ME：平均误差；MAE：平均绝对误差；RMSE：均方根误差；RE：相对误差；2010−2011年代表2010年11月至2011年4月，以此类推。
下载: 导出CSV
表 4 2010−2018年冬季（11月至翌年4月）70°N以北模拟冰速相对OSISAF冰速的月各项误差统计结果
Tab. 4 Monthly errors statistics of simulated ice velocity north of 70°N relative to OSISAF ice velocity for each month of winter (from November to April of the following year) from 2010 to 2018
误差类型 11月 12月 1月 2月 3月 4月 总计 ME/（cm·s−1） −1.55 −1.26 −0.73 −0.45 −0.68 −0.52 −0.84 MAE/（cm·s−1） 2.96 2.99 3.23 2.93 2.95 2.58 2.94 RMSE/（cm·s−1） 4.18 4.17 4.43 4.24 4.20 3.50 4.13 RE/% 67.40 68.80 105.02 105.19 121.02 121.51 99.55 注：ME：平均误差；MAE：平均绝对误差；RMSE：均方根误差；RE：相对误差。
下载: 导出CSV
表 5 2010−2018年逐年70°N以北模拟冰速相对OSISAF观测冰速的冬季（11月至翌年4月）各项误差统计结果
Tab. 5 Winter (from November to April of the following year) errors statistics of simulated ice velocity north of 70°N relative to OSISAF observed ice velocity year by year from 2010 to 2018
误差类型 2010−2011年 2011−2012年 2012−2013年 2013−2014年 2014−2015年 2015−2016年 2016−2017年 2017−2018年 ME/（cm·s−1） −0.43 −1.04 −2.04 −0.58 −0.37 −0.91 −0.77 −0.72 MAE/（cm·s−1） 2.41 2.98 3.34 2.37 3.29 3.21 2.90 3.17 RMSE/（cm·s−1） 3.33 3.84 4.64 3.36 4.42 4.86 4.19 4.43 RE/% 86.63 107.90 94.17 82.87 133.20 123.65 77.61 91.91 注：ME：平均误差，MAE：平均绝对误差，RMSE：均方根误差，RE：相对误差；2010−2011年代表2010年11月至201年4月，以此类推。
下载: 导出CSV
-
[1] Walsh J E. The role of sea ice in climatic variability: theories and evidence[J]. Atmosphere-Ocean, 1983, 21(3): 229−242. doi: 10.1080/07055900.1983.9649166 [2] Stroeve J, Holland M M, Meier W, et al. Arctic sea ice decline: faster than forecast[J]. Geophysical Research Letters, 2007, 34(9): L09501. [3] Ding Qinghua, Schweiger A, L’Heureux M, et al. Influence of high-latitude atmospheric circulation changes on summertime Arctic sea ice[J]. Nature Climate Change, 2017, 7(4): 289−295. doi: 10.1038/nclimate3241 [4] Renner A H H, Gerland S, Haas C, et al. Evidence of Arctic sea ice thinning from direct observations[J]. Geophysical Research Letters, 2014, 41(14): 5029−5036. doi: 10.1002/2014GL060369 [5] Kacimi S, Kwok R. Arctic snow depth, ice thickness, and volume from ICESat-2 and CryoSat-2: 2018–2021[J]. Geophysical Research Letters, 2022, 49(5): e2021GL097448. [6] Rampal P, Weiss J, Marsan D. Positive trend in the mean speed and deformation rate of Arctic sea ice, 1979–2007[J]. Journal of Geophysical Research: Oceans, 2009, 114(C5): C05013. [7] Kwok R, Spreen G, Pang S. Arctic sea ice circulation and drift speed: Decadal trends and ocean currents[J]. Journal of Geophysical Research: Oceans, 2013, 118(5): 2408−2425. doi: 10.1002/jgrc.20191 [8] Rothrock D A, Zhang J, Yu Youran. The Arctic ice thickness anomaly of the 1990s: a consistent view from observations and models[J]. Journal of Geophysical Research: Oceans, 2003, 108(C3): 3083. doi: 10.1029/2001JC001208 [9] Kwok R. Arctic sea ice thickness, volume, and multiyear ice coverage: losses and coupled variability (1958–2018)[J]. Environmental Research Letters, 2018, 13(10): 105005. doi: 10.1088/1748-9326/aae3ec [10] Spreen G, Kwok R, Menemenlis D. Trends in Arctic sea ice drift and role of wind forcing: 1992−2009[J]. Geophysical Research Letters, 2011, 38(19): L19501. [11] Zhang Fanyi, Pang Xiaoping, Lei Ruibo, et al. Arctic sea ice motion change and response to atmospheric forcing between 1979 and 2019[J]. International Journal of Climatology, 2022, 42(3): 1854−1876. doi: 10.1002/joc.7340 [12] Docquier D, Massonnet F, Barthélemy A, et al. Relationships between Arctic sea ice drift and strength modelled by NEMO-LIM3.6[J]. The Cryosphere, 2017, 11(6): 2829−2846. doi: 10.5194/tc-11-2829-2017 [13] Chikhar K, Lemieux J F, Dupont F, et al. Sensitivity of ice drift to form drag and ice strength parameterization in a coupled ice–ocean model[J]. Atmosphere-Ocean, 2019, 57(5): 329−349. doi: 10.1080/07055900.2019.1694859 [14] Itkin P, Spreen G, Hvidegaard S M, et al. Contribution of deformation to sea ice mass balance: a case study from an N-ICE2015 storm[J]. Geophysical Research Letters, 2018, 45(2): 789−796. doi: 10.1002/2017GL076056 [15] Kwok R, Cunningham G F. Contributions of growth and deformation to monthly variability in sea ice thickness north of the coasts of Greenland and the Canadian Arctic archipelago[J]. Geophysical Research Letters, 2016, 43(15): 8097−8105. doi: 10.1002/2016GL069333 [16] von Albedyll L, Haas C, Dierking W. Linking sea ice deformation to ice thickness redistribution using high-resolution satellite and airborne observations[J]. The Cryosphere, 2021, 15(5): 2167−2186. doi: 10.5194/tc-15-2167-2021 [17] von Albedyll L, Hendricks S, Grodofzig R, et al. Thermodynamic and dynamic contributions to seasonal Arctic sea ice thickness distributions from airborne observations[J]. Elementa: Science of the Anthropocene, 2022, 10(1): 00074. doi: 10.1525/elementa.2021.00074 [18] Krumpen T, von Albedyll L, Goessling H F, et al. MOSAiC drift expedition from October 2019 to July 2020: sea ice conditions from space and comparison with previous years[J]. The Cryosphere, 2021, 15(8): 3897−3920. doi: 10.5194/tc-15-3897-2021 [19] Barnhart K R, Miller C R, Overeem I, et al. Mapping the future expansion of Arctic open water[J]. Nature Climate Change, 2016, 6(3): 280−285. doi: 10.1038/nclimate2848 [20] DuVivier A K, Holland M M, Kay J E, et al. Arctic and Antarctic sea ice mean state in the community earth system model version 2 and the influence of atmospheric chemistry[J]. Journal of Geophysical Research: Oceans, 2020, 125(8): e2019JC015934. [21] Shu Qi, Wang Qiang, Song Zhenya, et al. Assessment of sea ice extent in CMIP6 with comparison to observations and CMIP5[J]. Geophysical Research Letters, 2020, 47(9): e2020GL087965. [22] Wang Huazhao, Zhang Lijun, Chu Min, et al. Advantages of the latest Los Alamos sea-ice model (CICE): evaluation of the simulated spatiotemporal variation of Arctic sea ice[J]. Atmospheric and Oceanic Science Letters, 2020, 13(2): 113−120. doi: 10.1080/16742834.2020.1712186 [23] 王松, 苏洁, 储敏, 等. BCC_CSM对北极海冰的模拟: CMIP5和CMIP6历史试验比较[J]. 海洋学报, 2020, 42(5): 49−64.Wang Song, Su Jie, Chu Min, et al. Comparison of simulation results of the Arctic sea ice by BCC_CSM: CMIP5 and CMIP6 historical experiments[J]. Haiyang Xuebao, 2020, 42(5): 49−64. [24] Yu Xiaoyong, Rinke A, Dorn W, et al. Evaluation of Arctic sea ice drift and its dependency on near-surface wind and sea ice conditions in the coupled regional climate model HIRHAM–NAOSIM[J]. The Cryosphere, 2020, 14(5): 1727−1746. doi: 10.5194/tc-14-1727-2020 [25] 房永杰, 储敏, 吴统文, 等. CICE5.0与BCC_CSM2.0模式的耦合及对北极海冰的模拟评估[J]. 海洋学报, 2017, 39(5): 33−43.Fang Yongjie, Chu Min, Wu Tongwen, et al. Couping of CICE5.0 with BCC_CSM2.0 model and its performance evaluation on Arctic sea ice simulation[J]. Haiyang Xuebao, 2017, 39(5): 33−43. [26] Ricker R, Hendricks S, Kaleschke L, et al. A weekly Arctic sea-ice thickness data record from merged CryoSat-2 and SMOS satellite data[J]. The Cryosphere, 2017, 11(4): 1607−1623. doi: 10.5194/tc-11-1607-2017 [27] Zhang Jinlun, Rothrock D A. Modeling global sea ice with a thickness and enthalpy distribution model in generalized curvilinear coordinates[J]. Monthly Weather Review, 2003, 131(5): 845−861. doi: 10.1175/1520-0493(2003)131<0845:MGSIWA>2.0.CO;2 [28] Tschudi M A, Meier W N, Stewart J S. An enhancement to sea ice motion and age products at the National Snow and Ice Data Center (NSIDC)[J]. The Cryosphere, 2020, 14(5): 1519−1536. doi: 10.5194/tc-14-1519-2020 [29] Lavergne T, Eastwood S, Teffah Z, et al. Sea ice motion from low-resolution satellite sensors: an alternative method and its validation in the Arctic[J]. Journal of Geophysical Research: Oceans, 2010, 115(C10): C10032. [30] Cavalieri D J, Parkinson C L, Gloersen P, et al. Deriving long-term time series of sea ice cover from satellite passive-microwave multisensor data sets[J]. Journal of Geophysical Research: Oceans, 1999, 104(C7): 15803−15814. doi: 10.1029/1999JC900081 [31] Wu Shuqiang, Zeng Qingcun, Bi Xunqiang. Modeling of Arctic sea ice variability during 1948–2009: validation of two versions of the Los Alamos sea ice model (CICE)[J]. Atmospheric and Oceanic Science Letters, 2015, 8(4): 215−219. doi: 10.1080/16742834.2015.11447262 [32] Hersbach H, Bell B, Berrisford P, et al. The ERA5 global reanalysis[J]. Quarterly Journal of the Royal Meteorological Society, 2020, 146(730): 1999−2049. doi: 10.1002/qj.3803 [33] Kerbyson D J, Jones P W. A performance model of the parallel ocean program[J]. The International Journal of High Performance Computing Applications, 2005, 19(3): 261−276. doi: 10.1177/1094342005056114 [34] Steele M, Morley R, Ermold W. PHC: a global ocean hydrography with a high-quality Arctic Ocean[J]. Journal of Climate, 2001, 14(9): 2079−2087. doi: 10.1175/1520-0442(2001)014<2079:PAGOHW>2.0.CO;2 [35] Kwok R, Hunke E C, Maslowski W, et al. Variability of sea ice simulations assessed with RGPS kinematics[J]. Journal of Geophysical Research: Oceans, 2008, 113(C11): C11012. doi: 10.1029/2008JC004783 [36] Kumar R, Li Junde, Hedstrom K, et al. Intercomparison of Arctic sea ice simulation in ROMS-CICE and ROMS-Budgell[J]. Polar Science, 2021, 29: 100716. doi: 10.1016/j.polar.2021.100716 [37] Sumata H, Lavergne T, Girard-Ardhuin F, et al. An intercomparison of Arctic ice drift products to deduce uncertainty estimates[J]. Journal of Geophysical Research: Oceans, 2014, 119(8): 4887−4921. doi: 10.1002/2013JC009724 [38] 施骞, 苏洁. 三种国际主流的北极卫星遥感冰速产品评估和分析[J]. 遥感学报, 2020, 24(7): 867−882.Shi Qian, Su Jie. Assessment of Arctic remote sensing ice motion products based on ice drift buoys[J]. Journal of Remote Sensing, 2020, 24(7): 867−882. [39] Hansen E, Gerland S, Granskog M A, et al. Thinning of Arctic sea ice observed in Fram Strait: 1990–2011[J]. Journal of Geophysical Research Oceans, 2013, 118: 5202−5221. [40] Rothrock D A. The energetics of the plastic deformation of pack ice by ridging[J]. Journal of Geophysical Research, 1975, 80(33): 4514−4519. doi: 10.1029/JC080i033p04514 [41] Thorndike A S, Rothrock D A, Maykut G A, et al. The thickness distribution of sea ice[J]. Journal of Geophysical Research, 1975, 80(33): 4501−4513. doi: 10.1029/JC080i033p04501 [42] Martin T, Tsamados M, Schroeder D, et al. The impact of variable sea ice roughness on changes in Arctic Ocean surface stress: a model study[J]. Journal of Geophysical Research: Oceans, 2016, 121(3): 1931−1952. doi: 10.1002/2015JC011186 [43] Hoffman J P, Ackerman S A, Liu Yinghui, et al. A 20-year climatology of sea ice leads detected in infrared satellite imagery using a convolutional neural network[J]. Remote Sensing, 2022, 14(22): 5763. doi: 10.3390/rs14225763 -
下载:
计量
- 文章访问数: 366
- HTML全文浏览量: 207
- PDF下载量: 54
- 被引次数: 0
