对称指数地形水槽内纵波和横波解析解研究

谢蓉; 熊焱; 童朝锋; 王岗

doi:10.12284/hyxb2023081

对称指数地形水槽内纵波和横波解析解研究

doi: 10.12284/hyxb2023081

谢蓉^{1, 2,},
熊焱^{1, 2, ,},
童朝锋^{1, 2},
王岗^{1, 2}

1.
河海大学海岸灾害及防护教育部重点实验室，江苏南京 210098
2.
河海大学港口海岸与近海工程学院，江苏南京 210098

基金项目: 江苏省自然科学基金杰出青年基金（BK20220082）；国家自然科学基金（52071128）

详细信息

作者简介:
谢蓉（1998—），女，四川省内江市人，主要从事水动力数值模拟研究。E-mail：395162775@qq.com

通讯作者:
熊焱（1992—），女，江苏省南京市人，讲师，主要从事极端水灾害数值模拟研究。E-mail：xiongyan@hhu.edu.cn

中图分类号: TV139
计量
- 文章访问数: 341
- HTML全文浏览量: 133
- PDF下载量: 26
- 被引次数: 0
出版历程
- 收稿日期: 2022-11-11
- 修回日期: 2023-01-12
- 网络出版日期: 2023-05-16
- 刊出日期: 2023-06-30

Analytic solutions of longitudinal and cross waves in the wave flume with an exponential symmetric shoal

Xie Rong^{1, 2
,},
Xiong Yan^{1, 2
, ,},
Tong Chaofeng^{1, 2},
Wang Gang^{1, 2}

1.
Key Laboratory of Coastal Disaster and Defence, Ministry of Education, Hohai University, Nanjing 210098, China
2.
College of Harbour, Coastal and Offshore Engineering, Hohai University, Nanjing 210098, China

摘要

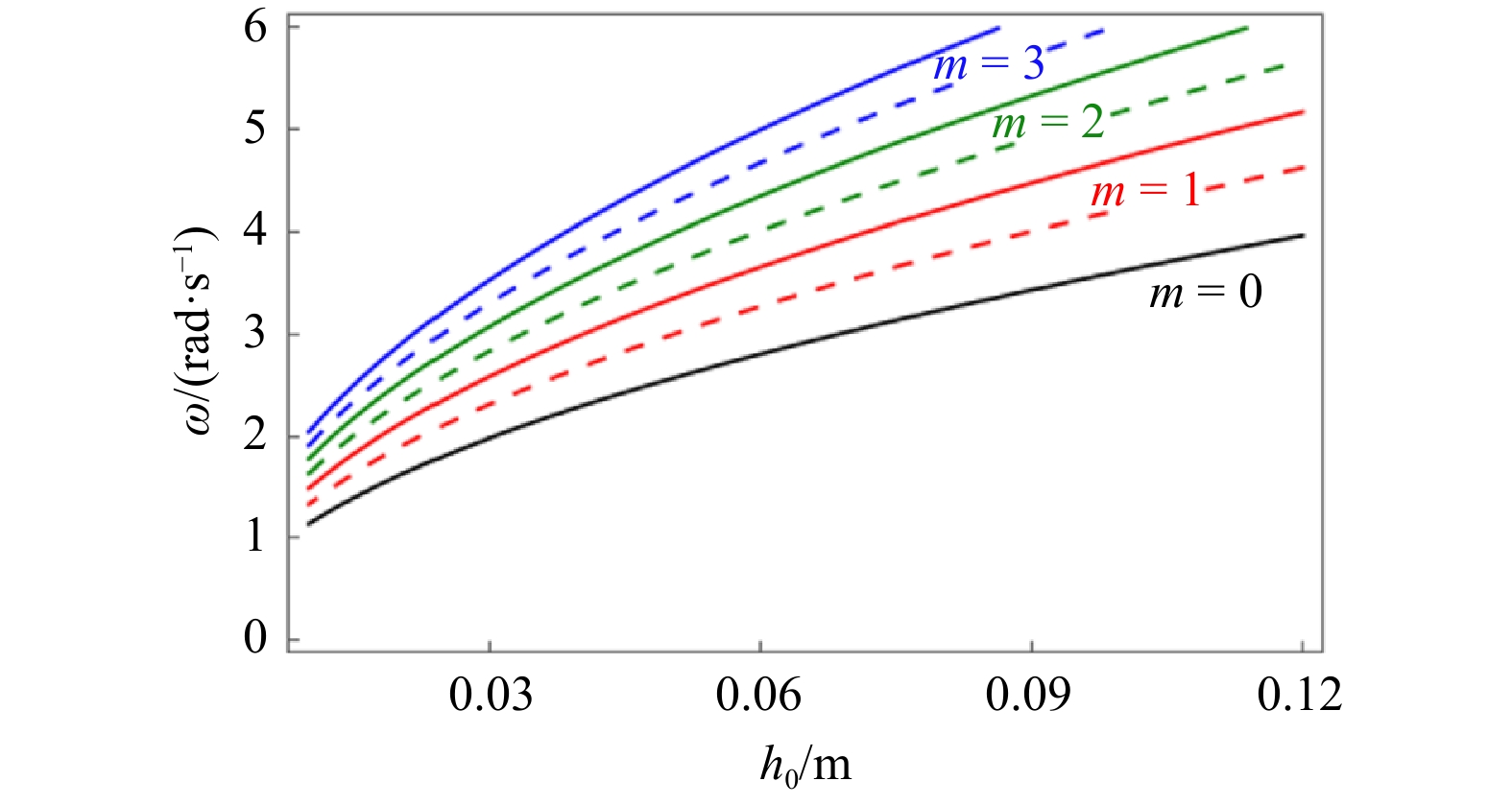
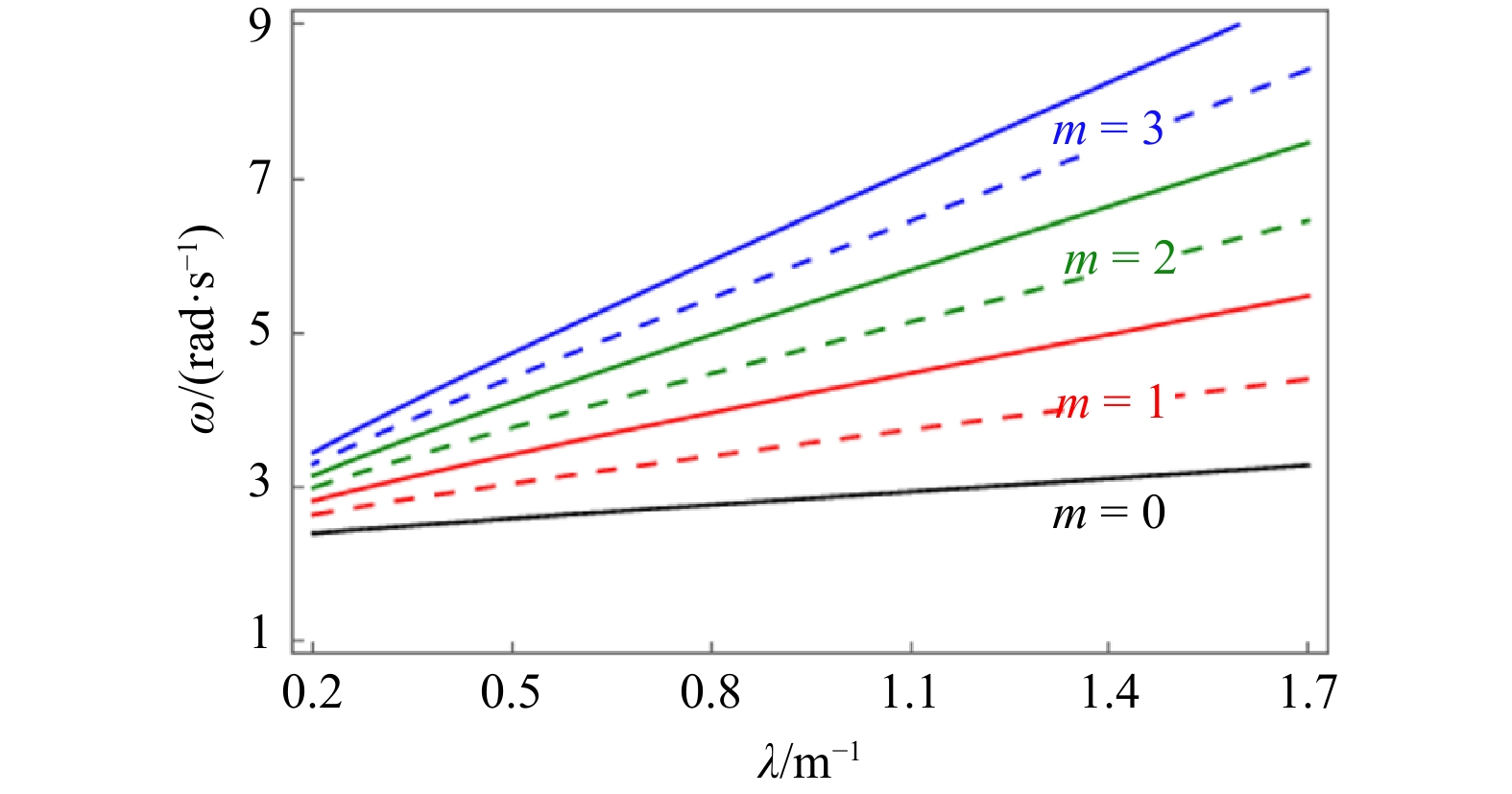
摘要: 水槽实验通常用于波浪传播变形及防波堤护面块体稳定性等研究，涉及的波要素沿水槽纵向变化且在垂直于水槽的横向保持不变。然而实验中当波长与水槽宽度满足一定关系时，可能出现明显的横向波动现象。本文针对对称指数型隆起地形，基于线性长波方程分别推导了其内沿水槽方向的纵波与垂直于水槽方向的横波的解析表达。水槽内对称指数地形上的纵波可以表示为第一类和第二类一阶贝塞尔函数的形式，并结合自由水面及速度连续条件最终得到其完整解。对称指数地形上分别存在偶对称和奇对称模态的横波，可表示为第一类ν阶贝塞尔函数的形式。偶对称模态(n, m)沿水槽方向有n条波节线，在垂直于水槽方向存在2m条波节线；奇对称模态(n, m)沿水槽方向存在n条波节线而在垂直方向有2m − 1条波节线。
- 横波 /
- 解析理论 /
- 波浪水槽 /
- 指数地形
Abstract: The flume experiment is commonly used to investigate the wave propagation deformation and the stability of the breakwater armor block, with the wave elements changing along the longitudinal direction of the flume while remaining unchanged in the cross direction perpendicular to the flume. However, when the wavelength has a certain relationship with the flume width, visible cross fluctuations may occur. In this paper, the analytical expressions of longitudinal wave along the flume direction and cross wave perpendicular to the flume direction on an exponential symmetric shoal are derived respectively based on the linear long wave equation. The longitudinal waves on symmetric exponential topography in the flume can be expressed as the first and second kinds of first order Bessel function, and the complete solution can be obtained by combining with the conditions of free surface and velocity continuity. Cross waves with even symmetric and odd symmetric modes in the flume with an exponential symmetric shoal can be expressed as the first kind of ν order Bessel function. The even symmetric (n, m) mode has n nodal lines along the direction of the flume and 2m nodal lines perpendicular to the direction of the flume; odd symmetric (n, m) mode has n nodal lines along the direction of the flume and 2m−1 nodal lines in the cross direction.
- cross waves /
- analytical theory /
- wave flume /
- exponential terrain

HTML全文

图 1 波浪水槽示意图

Fig. 1 Definition sketch of the wave flume

下载: 全尺寸图片幻灯片

图 2 归一化波幅沿波浪水槽的变化

阴影部分标识隆起地形区域，其中L = 5 m，T = 4.6 s，λ = 0.46 m⁻¹，h₁= 0.5 m，h₀= 0.05 m

Fig. 2 Variation of normalized amplitudes along the wave flume

Shaded areas denotes the hump shoal, where L = 5 m, T = 4.6 s, λ = 0.46 m⁻¹, h₁= 0.5 m and h₀= 0.05 m

下载: 全尺寸图片幻灯片

图 3 反射系数和透射系数随隆起地形顶部水深h₀的变化

T = 4.6 s，h₁= 0.5 m，L = 5.0 m，λ = ln（h₁/h₀）/L，ω = 1.37 rad/s

Fig. 3 Reflection and transmission parameters versus the depth at the top of hump shoal h₀

T = 4.6 s, h₁= 0.5 m, L = 5.0 m, λ = ln (h₁/h₀)/L and ω =1.37 rad/s

下载: 全尺寸图片幻灯片

图 4 反射系数和透射系数随着入射波角频率的变化

h₁= 0.5 m，h₀= 0.05 m，L = 5.0 m，λ = 0.46 m⁻¹

Fig. 4 Reflection and transmission parameters versus the angular frequency ω for the hump shoal

h₁= 0.5 m, h₀= 0.05 m, L = 5.0 m and λ = 0.46 m⁻¹

下载: 全尺寸图片幻灯片

图 5 反射系数和透射系数随着λ的变化

h₁= 0.5 m，h₀= 0.05 m，L = 5.0 m，ω = 1.37 rad/s，λ = ln（h₁/h₀）/L

Fig. 5 Reflection and transmission parameters versus the topography parameter λ for the hump shoal

h₁= 0.5 m, h₀= 0.05 m, L = 5.0 m, ω = 1.37 rad/s and λ = ln（h₁/h₀）/L

下载: 全尺寸图片幻灯片

图 6 角频率ω随波数κ的变化

2b = 1 m，h₁ = 0.5 m，h₀ = 0.05 m和λ = 0.46 m⁻¹，实心圆是偶对称，空心圆是奇对称

Fig. 6 Angular frequency ω versus wave number κ

2b = 1 m, h₁= 0.5 m, h₀= 0.05 m and λ = 0.46 m⁻¹, where the solid circles indicate the symmetrical mode and the hollow circles the anti-symmetrical mode

下载: 全尺寸图片幻灯片

图 7 角频率ω随着顶部水深h₀的变化

λ = 0.46 m⁻¹，κ₁ = π m⁻¹，实线是偶对称，虚线是奇对称

Fig. 7 Angular frequency ω versus the top depth h₀

λ = 0.46 m⁻¹ and κ₁ = π m⁻¹, where the solid lines indicate the symmetrical mode and the dash lines indicate the anti-symmetrical mode

下载: 全尺寸图片幻灯片

图 8 角频率ω随着地形参数λ的变化

h₀= 0.05 m，κ₁ = π m⁻¹，实线是偶对称，虚线是奇对称

Fig. 8 Angular frequency ω versus depth profile parameter λ

h₀ = 0.05 m and κ₁ = π m⁻¹, where the solid lines indicate the symmetrical mode and the dash lines indicate the anti-symmetrical mode

下载: 全尺寸图片幻灯片

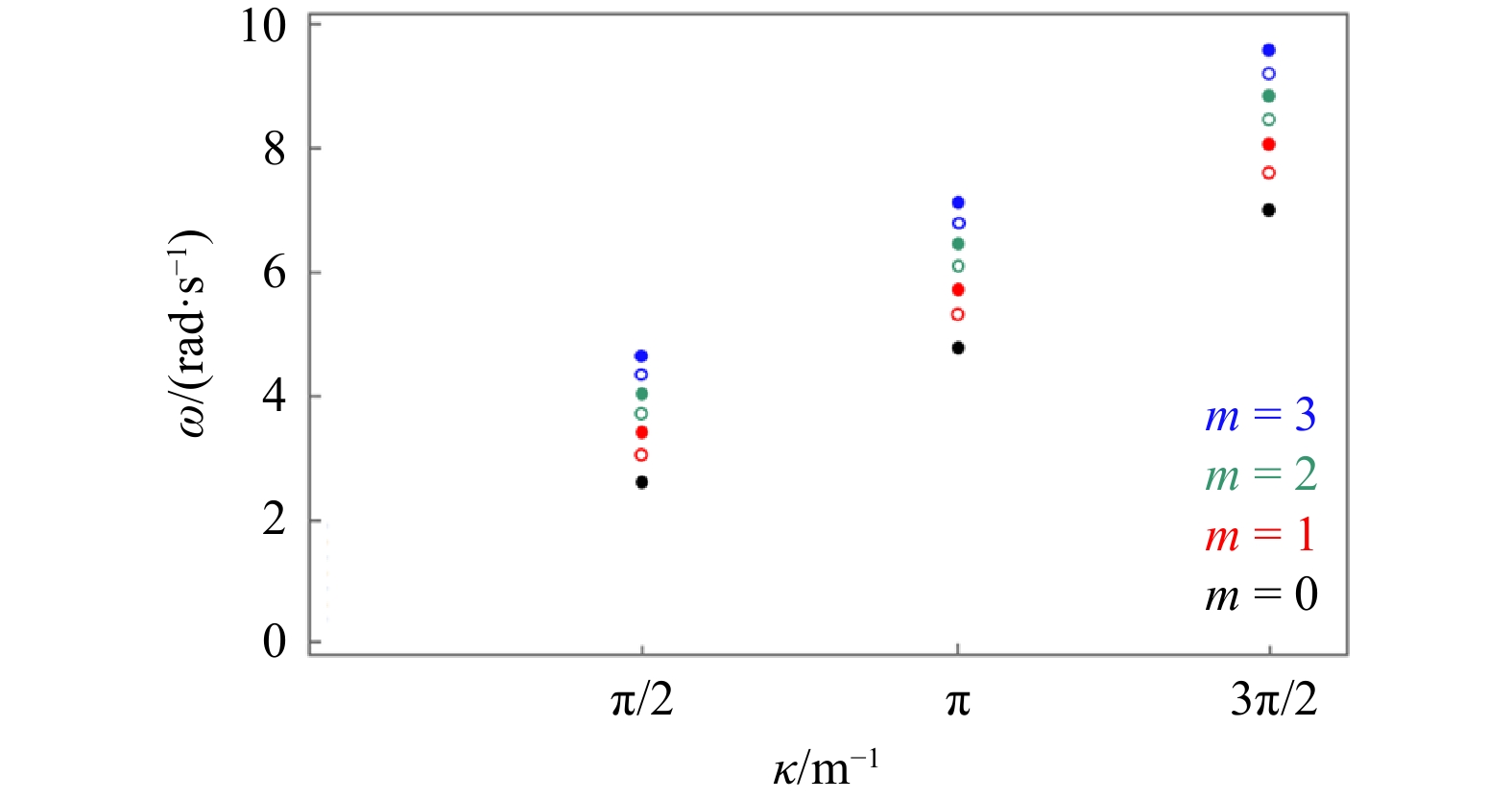
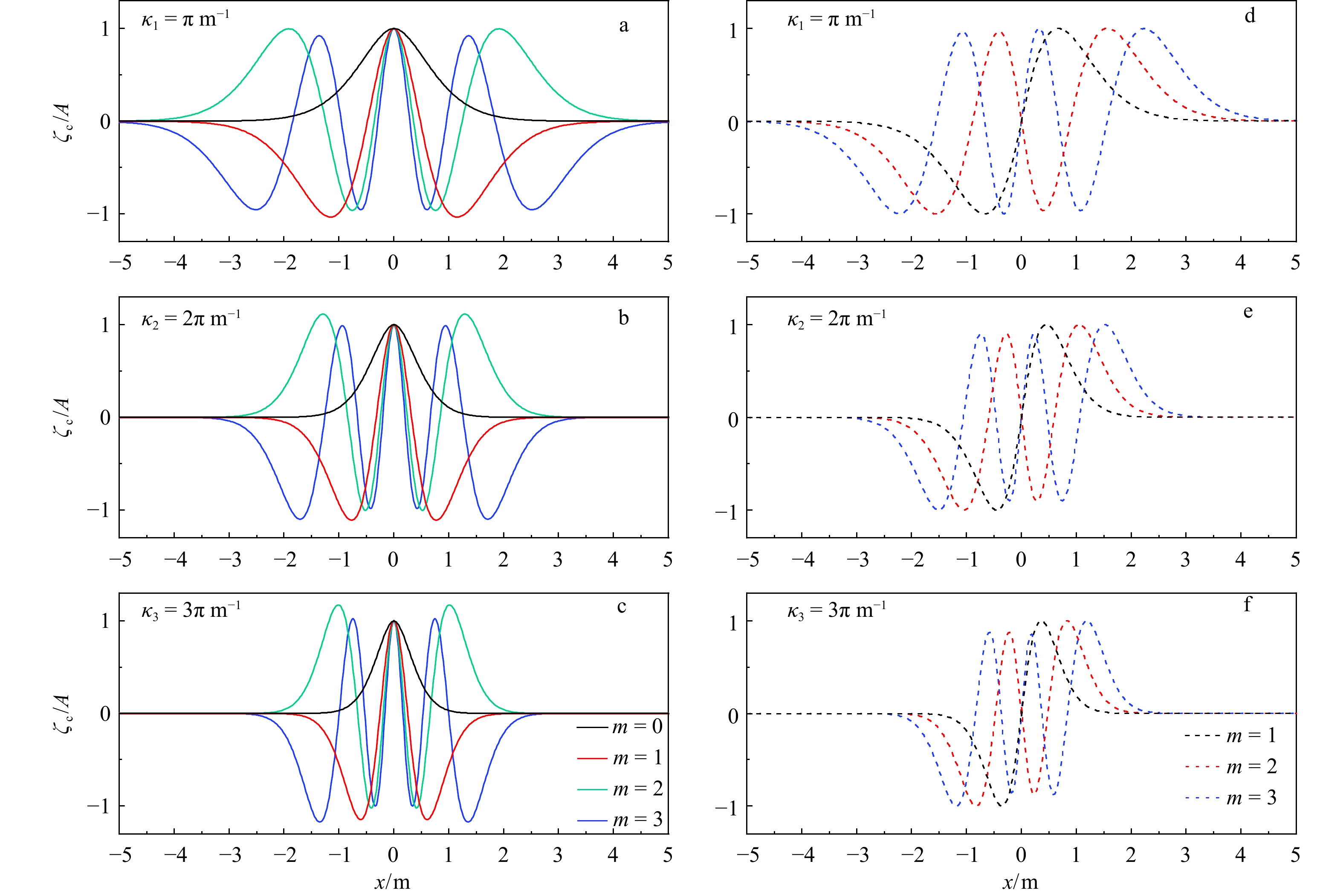
图 9 波数κ₁= π m⁻¹、κ₂= 2π m⁻¹、κ₃= 3π m⁻¹时偶对称模态（左侧）和奇对称模态（右侧）横波沿水槽方向的波幅分布

h₀= 0.05 m，h₁= 0.5 m，λ = 0.46 m⁻¹，L = 5.0 m

Fig. 9 Amplitude profiles of cross waves along the wave flume for symmetrical patterns (left column) and anti-symmetrical patterns (right column) with κ₁= π m⁻¹, κ₂= 2π m⁻¹ and κ₃= 3π m⁻¹ respectively

h₀= 0.05 m, h₁= 0.5 m, λ = 0.46 m⁻¹ and L = 5.0 m

下载: 全尺寸图片幻灯片

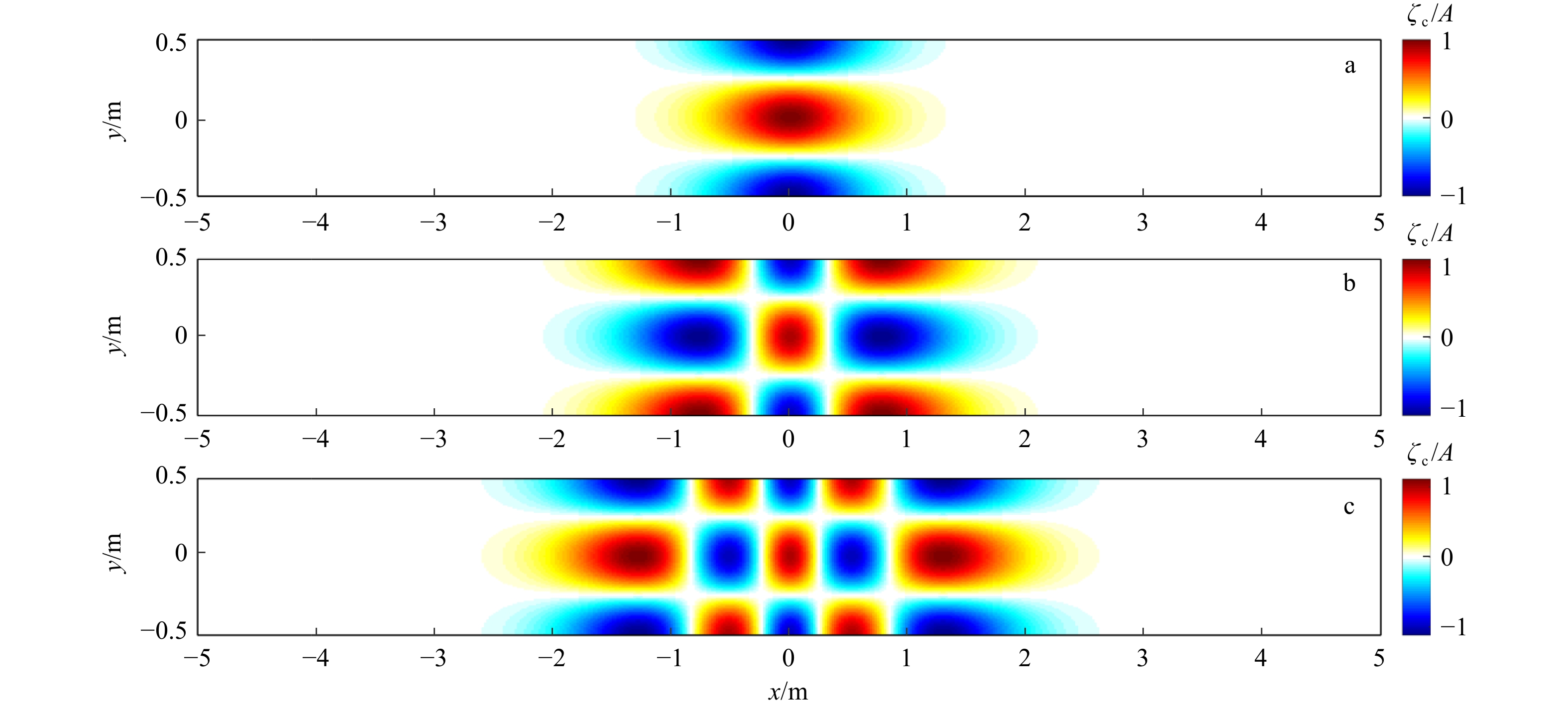
图 10 偶对称模态的横波的空间分布

宽2b = 1 m，长L = 5.0 m，顶部水深h₀= 0.05 m，地形参数λ = 0.46 m⁻¹，隆起地形上波数κ₂= 2π m⁻¹，m = 0（a），m = 1（b），m = 2（c）

Fig. 10 Spatial structure of the cross-wave amplitudes for symmetrical patterns over the exponential symmetric shoal

2b = 1 m, L = 5.0 m, h₀= 0.05 m, h₁= 0.5 m and λ = 0.46 m⁻¹ corresponding κ₂= 2π m⁻¹, where m = 0(a）, m = 1(b), m = 2(c)

下载: 全尺寸图片幻灯片

图 11 奇对称模态的横波的空间分布

宽2b = 1 m、长L = 5.0 m、顶部水深h₀= 0.05 m、地形参数λ = 0.46 m⁻¹隆起地形上波数κ₂= 2π m⁻¹，m = 1（a），m = 2（b），m = 3（c）

Fig. 11 Spatial structure of the cross-wave amplitudes for anti-symmetrical patterns over the exponential symmetric shoal

2b = 1m, L = 5.0 m, h₀= 0.05 m, h₁= 0.5 m and λ = 0.46 m⁻¹ corresponding κ₂= 2π m⁻¹, where m = 1(a), m = 2(b), m = 3(c)

下载: 全尺寸图片幻灯片

参考文献(20)

[1]	陶爱峰, 沈至淳, 李硕, 等. 中国灾害性海浪研究进展[J]. 科技导报, 2018, 36(14): 26−34. Tao Aifeng, Shen Zhichun, Li Shuo, et al. Research progrecs for disastrous waves in China[J]. Science & Technology Review, 2018, 36(14): 26−34.
[2]	王岗, 高俊亮, 王培涛, 等. 港湾共振研究综述[J]. 海洋学报, 2017, 39(11): 1−13. Wang Gang, Gao Junliang, Wang Peitao, et al. Review on harbor resonance[J]. Haiyang Xuebao, 2017, 39(11): 1−13.
[3]	徐佳丽, 时健, 张弛, 等. 近40年中国近海波浪数据库的建立及极值分析[J]. 海洋工程, 2019, 37(6): 94−103. Xu Jiali, Shi Jian, Zhang Chi, et al. Establishment of China offshore wave database and analysis of wave extreme values in recent 40 years[J]. The Ocean Engineering, 2019, 37(6): 94−103.
[4]	陈松贵, 张华庆, 陈汉宝, 等. 不规则波在筑堤珊瑚礁上传播的大水槽实验研究[J]. 海洋通报, 2018, 37(5): 576−582. doi: 10.11840/j.issn.1001-6392.2018.05.011 Chen Songgui, Zhang Huaqing, Chen Hanbao, et al. Experimental study of irregular wave transformation on reefs with seawalls in large wave flume[J]. Marine Science Bulletin, 2018, 37(5): 576−582. doi: 10.11840/j.issn.1001-6392.2018.05.011
[5]	任冰, 唐洁, 王国玉, 等. 规则波在岛礁地形上传播变化特性的试验[J]. 科学通报, 2018, 63(5): 590−600. Ren Bing, Tang Jie, Wang Guoyu, et al. Experimental investigation of monochromatic wave transformation characteristics over the coral reefs[J]. Chinese Science Bulletin, 2018, 63(5): 590−600.
[6]	Lin J D, Howard L N. Non-linear standing waves in a rectangular tank due to forced oscillation[R]. Cambridge: Hydrodynamic Laboratory Technical Report, 1960.
[7]	Garrett C J R. On cross-waves[J]. Journal of Fluid Mechanics, 1970, 41(4): 837−849. doi: 10.1017/S0022112070000952
[8]	Dong Guohai, Ma Xiaozhou, Perlin M, et al. Experimental study of long wave generation on sloping bottoms[J]. Coastal Engineering, 2009, 56(1): 82−89. doi: 10.1016/j.coastaleng.2008.10.002
[9]	Mahony J J. Cross-waves. Part 1. Theory[J]. Journal of Fluid Mechanics, 1972, 55(2): 229−244. doi: 10.1017/S002211207200182X
[10]	Barnard B J S, Pritchard W G. Cross-waves. Part 2. Experiments[J]. Journal of Fluid Mechanics, 1972, 55(2): 245−255. doi: 10.1017/S0022112072001831
[11]	Bernoff A J, Kwok L P, Lichter S. Viscous cross-waves: an analytical treatment[J]. Physics of Fluids A: Fluid Dynamics, 1989, 1(4): 678−688. doi: 10.1063/1.857361
[12]	Ayanle H, Bernoff A J, Lichter S. Spanwise modal competition in cross-waves[J]. Physica D: Nonlinear Phenomena, 1990, 43(1): 87−104. doi: 10.1016/0167-2789(90)90018-K
[13]	Deng Limei. A study of transverse waves[D]. Hong Kong, China: University of Hong Kong, 2005.
[14]	Yao Yu, He Fang, Tang Zhengjiang, et al. A study of tsunami-like solitary wave transformation and run-up over fringing reefs[J]. Ocean Engineering, 2018, 149: 142−155. doi: 10.1016/j.oceaneng.2017.12.020
[15]	Zhu Gancheng, Ren Bing, Dong Ping, et al. Experimental investigation on the infragravity wave on different reef systems under irregular wave action[J]. Ocean Engineering, 2021, 226: 108851. doi: 10.1016/j.oceaneng.2021.108851
[16]	王岗, 郑金海. 梯形底床波浪水槽内横波解析表达[C]//第十五届中国海洋(岸)工程学术讨论会论文集(中). 北京: 海洋出版社, 2011: 29-32. Wang Gang, Zheng Jinhai. Analysis of cross waves in a trapezoidal bed wave flume[C]//Proceedings of the 15th China Marine (Coastal) Engineering Academic Symposium. Beijing: China Ocean Press, 2011: 29−32.
[17]	Wang Gang, Yu Ying, Tao Aifeng, et al. An analytic investigation of primary and cross waves in the flume with a shoal[J]. Ocean Engineering, 2022, 244: 110428. doi: 10.1016/j.oceaneng.2021.110428
[18]	王竹溪, 郭敦仁. 特殊函数概论[M]. 北京: 北京大学出版社, 2012. Wang Zhuxi, Guo Dunren. Special Functions[M]. Beijing: Peking University Press, 2012.
[19]	Wang Gang, Liang Qiuhua, Shi Fengyan, et al. Analytical and numerical investigation of trapped ocean waves along a submerged ridge[J]. Journal of Fluid Mechanics, 2021, 915: A54. doi: 10.1017/jfm.2020.1039
[20]	Zhang Di, Wang Gang, Feng Xi, et al. Analytical and numerical investigation of edge waves near a vertical breakwater over a convex bottom[J]. Ocean Engineering, 2022, 266: 112923. doi: 10.1016/j.oceaneng.2022.112923