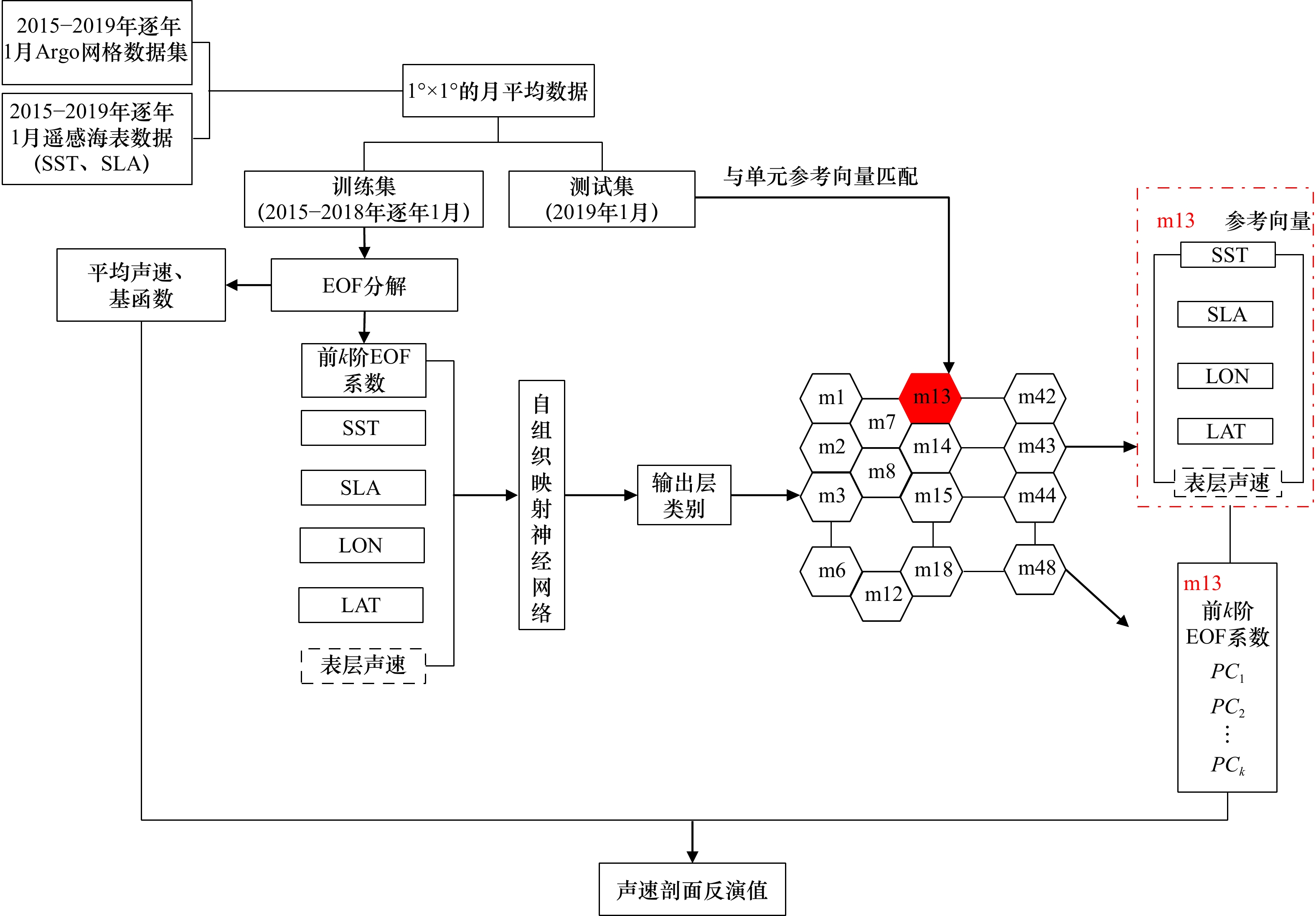
Inversion of the full-depth sound speed profile based on remote sensing data and surface sound speed
-
摘要: 海洋声速剖面严重影响着水下声传播特性，近实时地获取声速剖面对水下声通信、水下定位、鱼群探测等都有重要意义。单经验正交函数回归（single Empirical Orthogonal Function regression，sEOF-r）方法通过建立声速剖面的经验正交系数与海面遥感数据之间的线性回归关系来反演声速剖面。但是，海洋是一个复杂的动力系统，声速与海面遥感数据并不是简单的线性关系，因此，本文基于Argo历史网格数据，通过自组织映射（Self-Organizing Map，SOM）生成海平面高度异常（Sea Level Anomaly，SLA）、海表面温度（Sea Surface Temperature，SST）等海表遥感数据以及表层声速仪测量的表层声速与声速剖面异常之间的非线性映射；然后利用近实时的海表遥感数据和表层声速反演三维海洋声速场。声速剖面反演的结果表明，在多源信息融合的优势下，本文方法的反演性能最稳定且精度最高，声速剖面的平均反演精度比经典sEOF-r方法提高约2 m/s，比未考虑表层声速的经典SOM方法提高约1 m/s。Abstract: The ocean sound speed profile (SSP) determines the underwater acoustic propagation, and it is very important to obtain SSP in near real-time for underwater acoustic communication, positioning, and fish detecting. The single Empirical Orthogonal Function regression (sEOF-r) method inverts the SSP by establishing a linear regression relationship between the empirical orthogonal coefficient of the SSP and the sea surface remote sensing data. However, the ocean is a complex dynamical system, and the SSP and the remote sensing data are not simple linear. Therefore, based on the Argo historical gridded dataset, self-organizing map (SOM) was used to establish the nonlinear mapping between sea surface data, such as sea level anomaly (SLA), sea surface temperature (SST) and surface sound speed measured by surface velocimeter, and SSP anomaly. The three-dimensional sound speed field is then inverted by the near real-time remote sensing data and the surface sound speed. The results of the SSP inversion showed that, under the advantage of multi-source information fusion, the algorithm generated a smaller inversion error than linear inversion and had better robustness. It improved the average accuracy of inversion by about 2 m/s than sEOF-r method, and improved by about 1 m/s than classical SOM method that without considering the surface sound speed.
-
Key words:
- Argo dataset /
- sea surface temperature /
- sea level anomaly /
- EOF decomposition /
- surface velocimeter /
- sEOF-r method /
- SOM method
-
图 1 Argo网格数据与海表面温度、海平面高度异常数据位置匹配示意图
Fig. 1 Schematic diagram of location matching between Argo grid data and sea surface temperature and sea level anomaly data
图 2 声速剖面反演流程
黑色虚线框表示增加的先验信息，红色虚线框表示测试集中已知信息与输出层参考向量匹配
Fig. 2 Flow of sound speed profile inversion
The black dashed box indicates the added prior information, and the red dashed box indicates that the known information in the test set matches the reference vector of the output layer
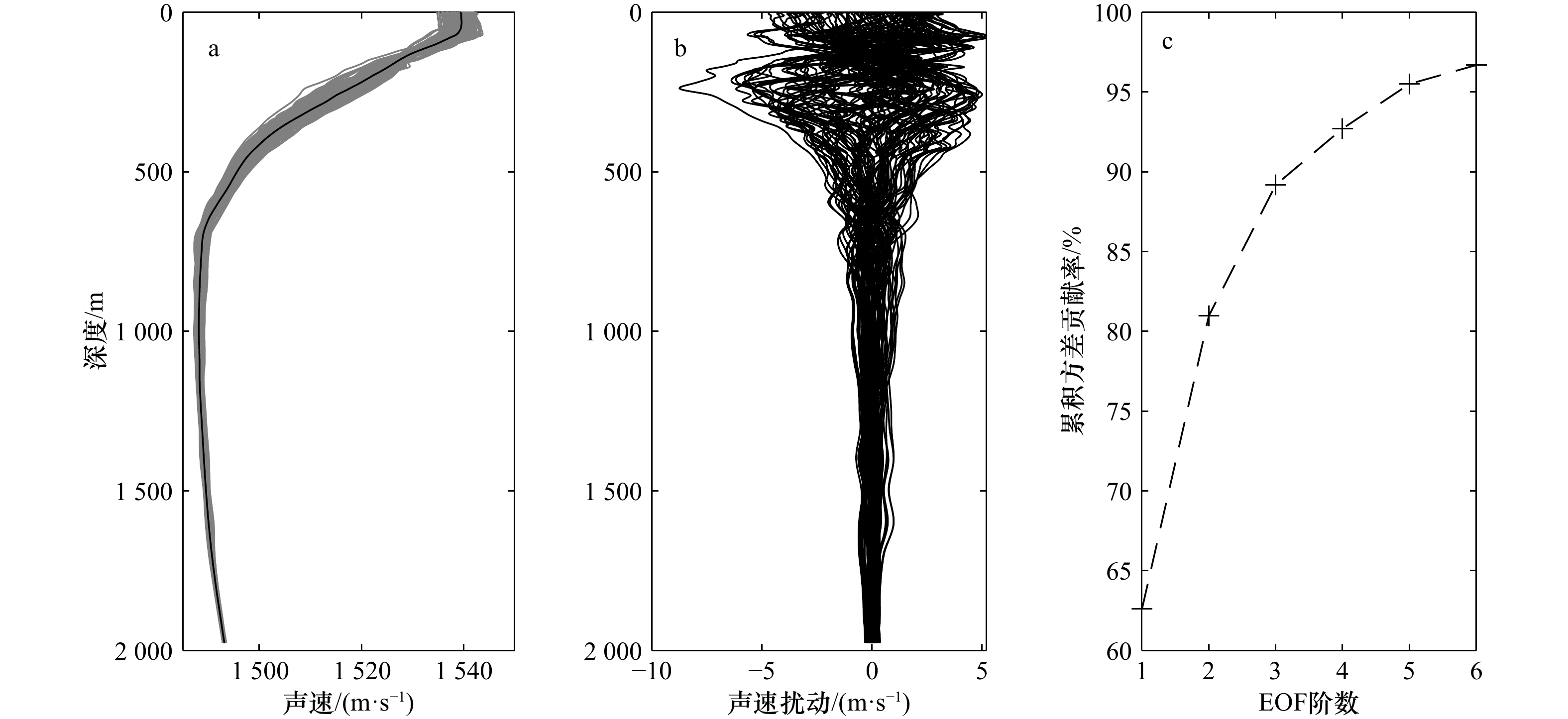
图 3 训练集中的声速剖面（灰色线为实测剖面，黑色线为平均剖面）（a）、声速扰动（b）和前6阶经验正交函数（EOF）的累积方差贡献率（c）
Fig. 3 The sound speed profile in the training set (gray lines are the measured profile, black line is the average profile) (a), residual sound speed (b) and the cumulative variance contribution rates of the first 6-order empirical orthogonal function (EOF) (c)
图 4 训练集和测试集的经验正交函数基函数之间的相关系数
Fig. 4 Correlation coefficient between empirical orthogonal function (EOF) basis functions of training set and test set
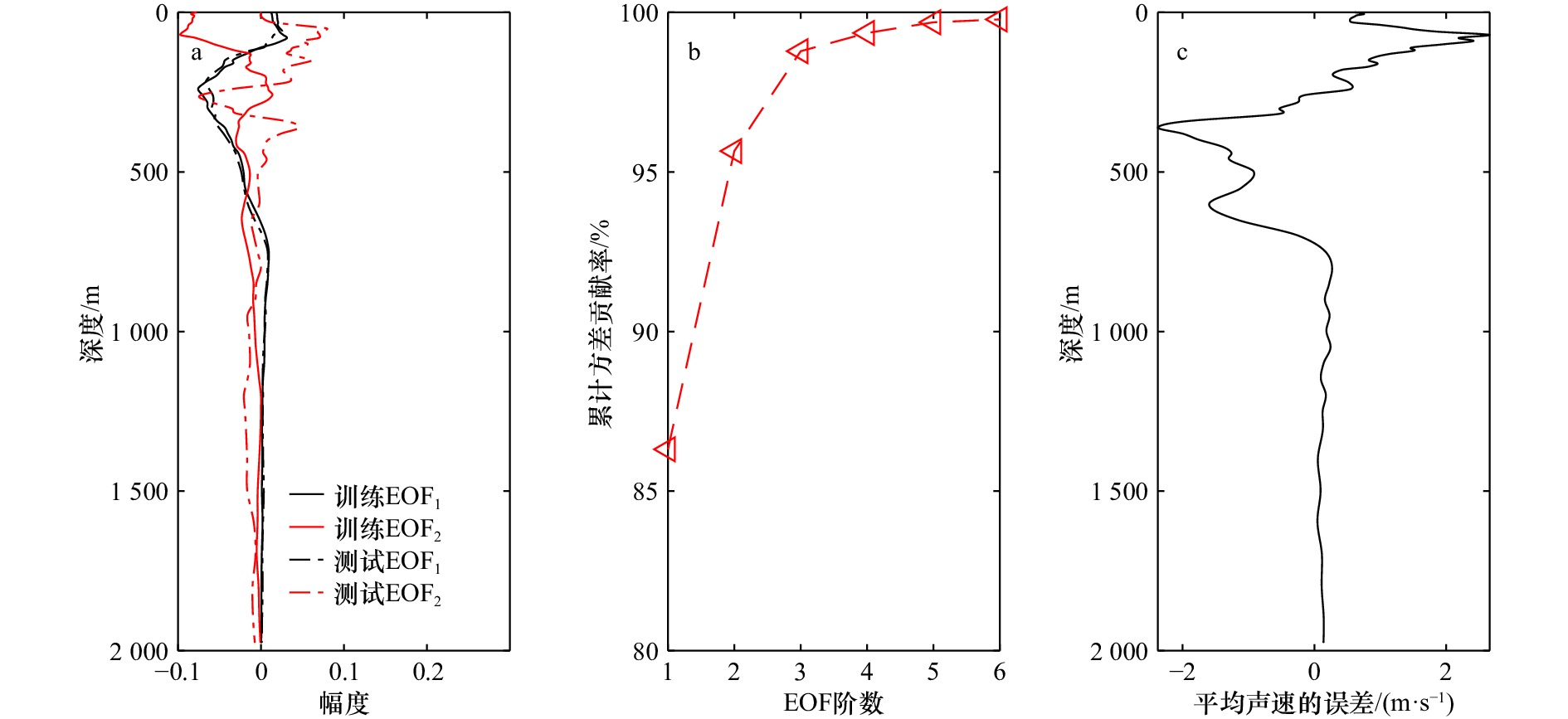
图 5 训练集和测试集的前两阶基函数（a）、测试集前6阶经验正交函数（EOF）的累积方差贡献率（b）和训练集和测试集的平均声速误差（c）
Fig. 5 The first two order basis functions of the training set and the test set (a), the cumulative variance contribution rate of the first six orders of empirical orthogonal function (EOF) in the test set (b) and the average sound speed error of the training set and test set (c)
图 6 声速剖面重构误差
白色虚线为重构声速剖面的均方根误差
Fig. 6 The reconstruction error of the sound speed profile
The white dashed line is the root mean square error of the reconstructed sound speed profile
图 7 平均声速剖面的声速梯度（a），海表面温度（SST）、海表面高度异常（SLA）和声速剖面（SSP）的相关性（b）
Fig. 7 Sound speed gradient of mean sound speed profile (a), correlation between sea surface temperature (SST), sea level anomally (SLA) and sound speed profile (SSP) (b)
图 8 测试集中声速剖面反演误差
a. SOM-c10方法；b. SOM方法；c. sEOF-r方法
Fig. 8 The inversion error of the sound speed profiles in the test set
a. SOM-c10 method; b. SOM method; c. sEOF-r method
图 11 测试集中第13号剖面（a）和第16号剖面（b）的反演情况
Fig. 11 The inversion of 13th profile (a) and 16th profile (b) in the test set
-
[1] 宋海润, 叶松, 王晓蕾, 等. 声速剖面仪测量技术综述[J]. 海洋技术学报, 2020, 39(2): 105−112.Song Hairun, Ye Song, Wang Xiaolei, et al. A review of the measurement techniques of sound velocity profilers[J]. Journal of Ocean Technology, 2020, 39(2): 105−112. [2] Li Haipeng, Qu Ke, Zhou Jianbo. Reconstructing sound speed profile from remote sensing data: nonlinear inversion based on self-organizing map[J]. IEEE Access, 2021, 9: 109754−109762. doi: 10.1109/ACCESS.2021.3102608 [3] Li Hong, Xu Fanghua, Zhou Wei, et al. Development of a global gridded Argo data set with Barnes successive corrections[J]. Journal of Geophysical Research: Oceans, 2017, 122(2): 866−889. doi: 10.1002/2016JC012285 [4] Tolstoy A, Diachok O, Frazer L N. Acoustic tomography via matched field processing[J]. The Journal of the Acoustical Society of America, 1991, 89(3): 1119−1127. doi: 10.1121/1.400647 [5] 沈远海, 马远良, 屠庆平, 等. 浅水声速剖面的反演方法与实验验证[J]. 西北工业大学学报, 2000, 18(2): 212−215. doi: 10.3969/j.issn.1000-2758.2000.02.010Shen Yuanhai, Ma Yuanliang, Tu Qingping, et al. Inversion of sound speed profile for shallow-water environment with experimental verification[J]. Journal of Northwestern Polytechnical University, 2000, 18(2): 212−215. doi: 10.3969/j.issn.1000-2758.2000.02.010 [6] Yang T T, Chen Z B, He Y J. A new method to retrieve salinity profiles from sea surface salinity observed by SMOS satellite[J]. Acta Oceanologica Sinica, 2015, 34(9): 85−93. doi: 10.1007/s13131-015-0735-3 [7] Hurlburt H E, Fox D N, Metzger E J. Statistical inference of weakly correlated subthermocline fields from satellite altimeter data[J]. Journal of Geophysical Research: Oceans, 1990, 95(C7): 11375−11409. doi: 10.1029/JC095iC07p11375 [8] Carnes M R, Mitchell J L, de Witt P W. Synthetic temperature profiles derived from Geosat altimetry: Comparison with air-dropped expendable bathythermograph profiles[J]. Journal of Geophysical Research: Oceans, 1990, 95(C10): 17979−17992. doi: 10.1029/JC095iC10p17979 [9] Carnes M R, Teague W J, Mitchell J L. Inference of subsurface thermohaline structure from fields measurable by satellite[J]. Journal of Atmospheric and Oceanic Technology, 1994, 11(2): 551−566. doi: 10.1175/1520-0426(1994)011<0551:IOSTSF>2.0.CO;2 [10] Fox D N, Teague W J, Barron C N, et al. The modular ocean data assimilation system (MODAS)[J]. Journal of Atmospheric and Oceanic Technology, 2002, 19(2): 240−252. doi: 10.1175/1520-0426(2002)019<0240:TMODAS>2.0.CO;2 [11] Chen Cheng, Ma Yuanliang, Liu Ying. Reconstructing sound speed profiles worldwide with sea surface data[J]. Applied Ocean Research, 2018, 77: 26−33. doi: 10.1016/j.apor.2018.05.002 [12] Liu Yonggang, Weisberg R H, Mooers C N K. Performance evaluation of the self-organizing map for feature extraction[J]. Journal of Geophysical Research: Oceans, 2006, 111(C5): C05018. [13] Liu Yonggang, Weisberg R H, Shay L K. Current patterns on the West Florida shelf from joint self-organizing map analyses of HF radar and ADCP data[J]. Journal of Atmospheric and Oceanic Technology, 2007, 24(4): 702−712. doi: 10.1175/JTECH1999.1 [14] Charantonis A A, Testor P, Mortier L, et al. Completion of a sparse GLIDER database using multi-iterative self-organizing maps (ITCOMP SOM)[J]. Procedia Computer Science, 2015, 51: 2198−2206. doi: 10.1016/j.procs.2015.05.496 [15] Chapman C, Charantonis A A. Reconstruction of subsurface velocities from satellite observations using iterative self-organizing maps[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(5): 617−620. doi: 10.1109/LGRS.2017.2665603 [16] Chen Cheng, Yang Kunde, Ma Yuanliang, et al. Reconstructing the subsurface temperature field by using sea surface data through self-organizing map method[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(12): 1812−1816. doi: 10.1109/LGRS.2018.2866237 [17] Chen Cheng, Yan Fenggang, Gao Ya, et al. Improving reconstruction of sound speed profiles using a self-organizing map method with multi-source observations[J]. Remote Sensing Letters, 2020, 11(6): 572−580. doi: 10.1080/2150704X.2020.1742940 [18] Jain S, Ali M M. Estimation of sound speed profiles using artificial neural networks[J]. IEEE Geoscience and Remote Sensing Letters, 2006, 3(4): 467−470. doi: 10.1109/LGRS.2006.876221 [19] Reynolds R W, Smith T M, Liu Chunying, et al. Daily high-resolution-blended analyses for sea surface temperature[J]. Journal of Climate, 2007, 20(22): 5473−5496. doi: 10.1175/2007JCLI1824.1 [20] AVISO. SSALTO/DUACS User Handbook: (M)SLA and (M)ADT near-real time and delayed time products[M]. Paris: CNES, 2012. [21] Kohonen T. The self-organizing map[J]. Neurocomputing, 1998, 21(1/3): 1−6. [22] Chen C T, Millero F J. Speed of sound in seawater at high pressures[J]. The Journal of the Acoustical Society of America, 1977, 62(5): 1129−1135. doi: 10.1121/1.381646 [23] Casagrande G, Stephan Y, Varnas A C W, et al. A novel Empirical Orthogonal Function (EOF)-based methodology to study the internal wave effects on acoustic propagation[J]. IEEE Journal of Oceanic Engineering, 2011, 36(4): 745−759. doi: 10.1109/JOE.2011.2161158 -
下载:
计量
- 文章访问数: 612
- HTML全文浏览量: 205
- PDF下载量: 70
- 被引次数: 0
