Inversion of seafloor topography in Emperor Seamount sea area by combined gravity anomalies and vertical gravity gradient anomalies data
-
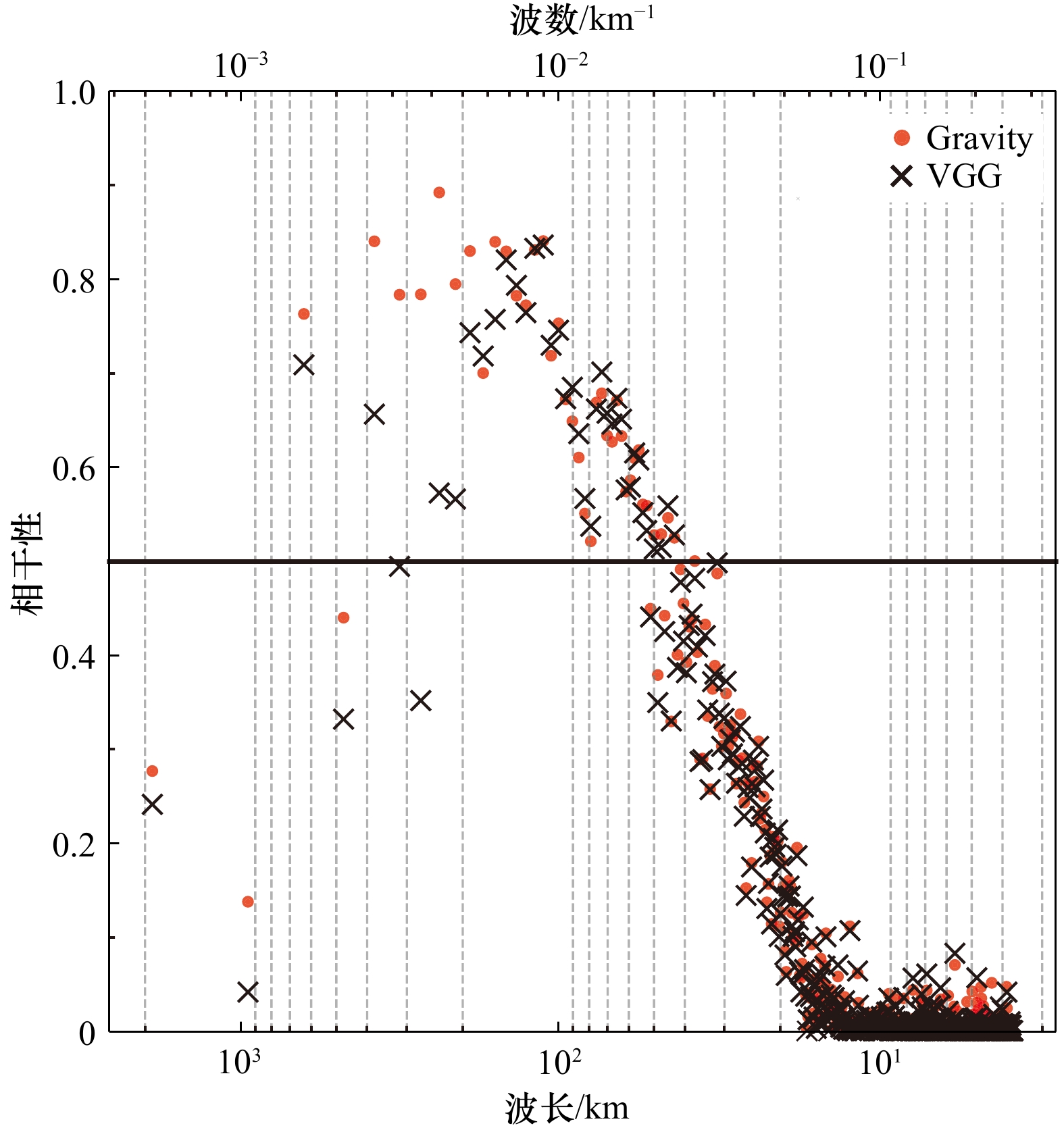
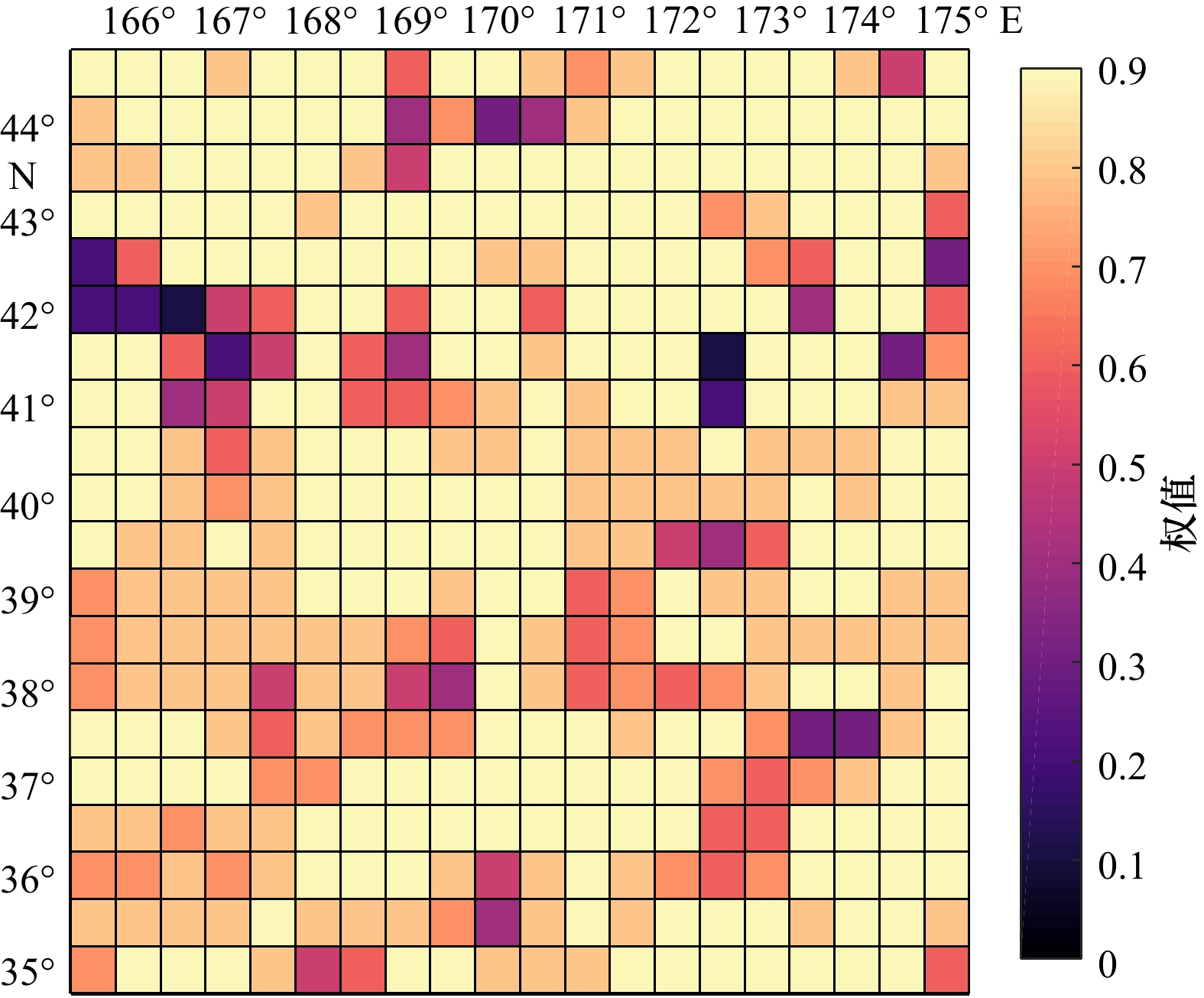
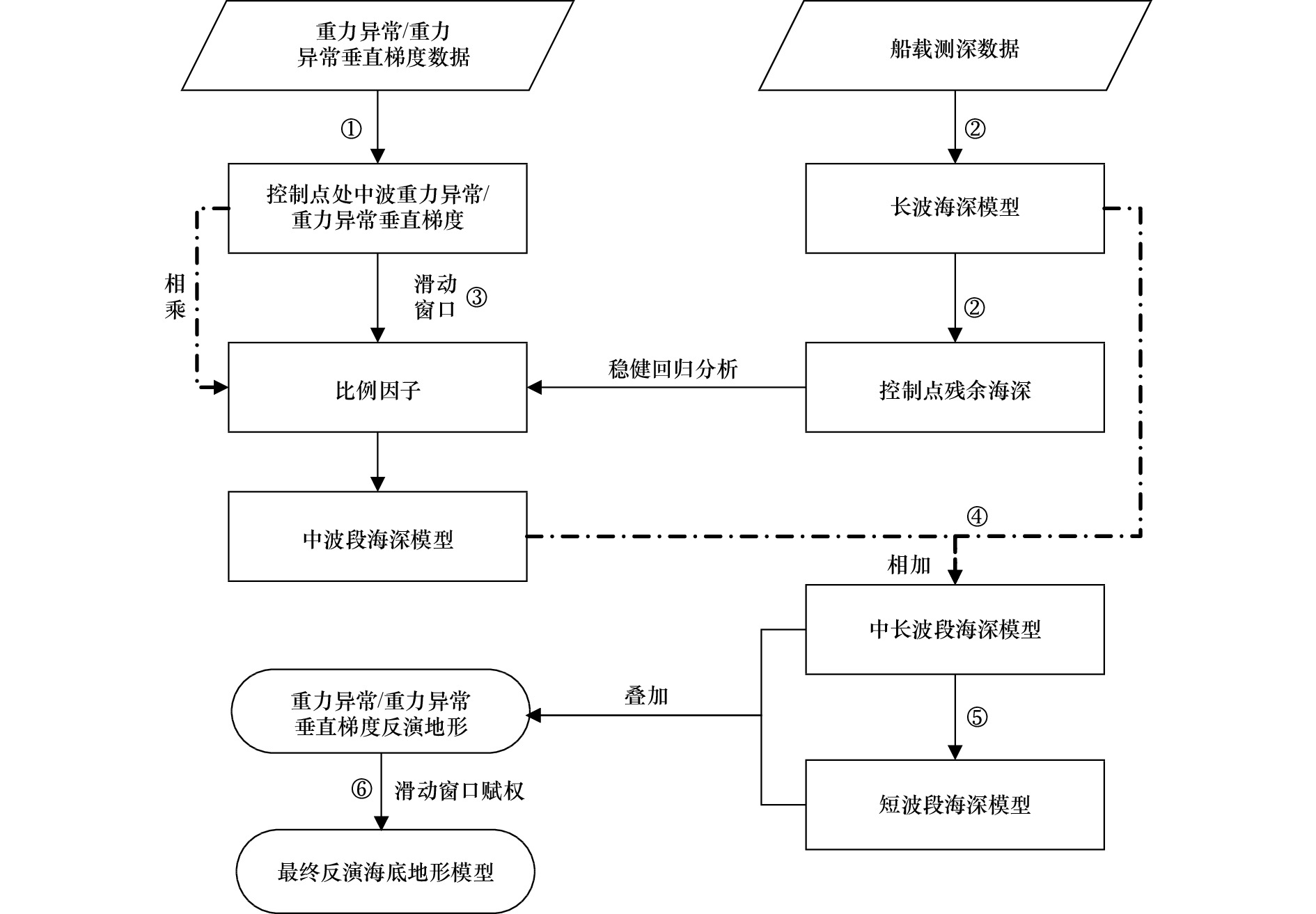
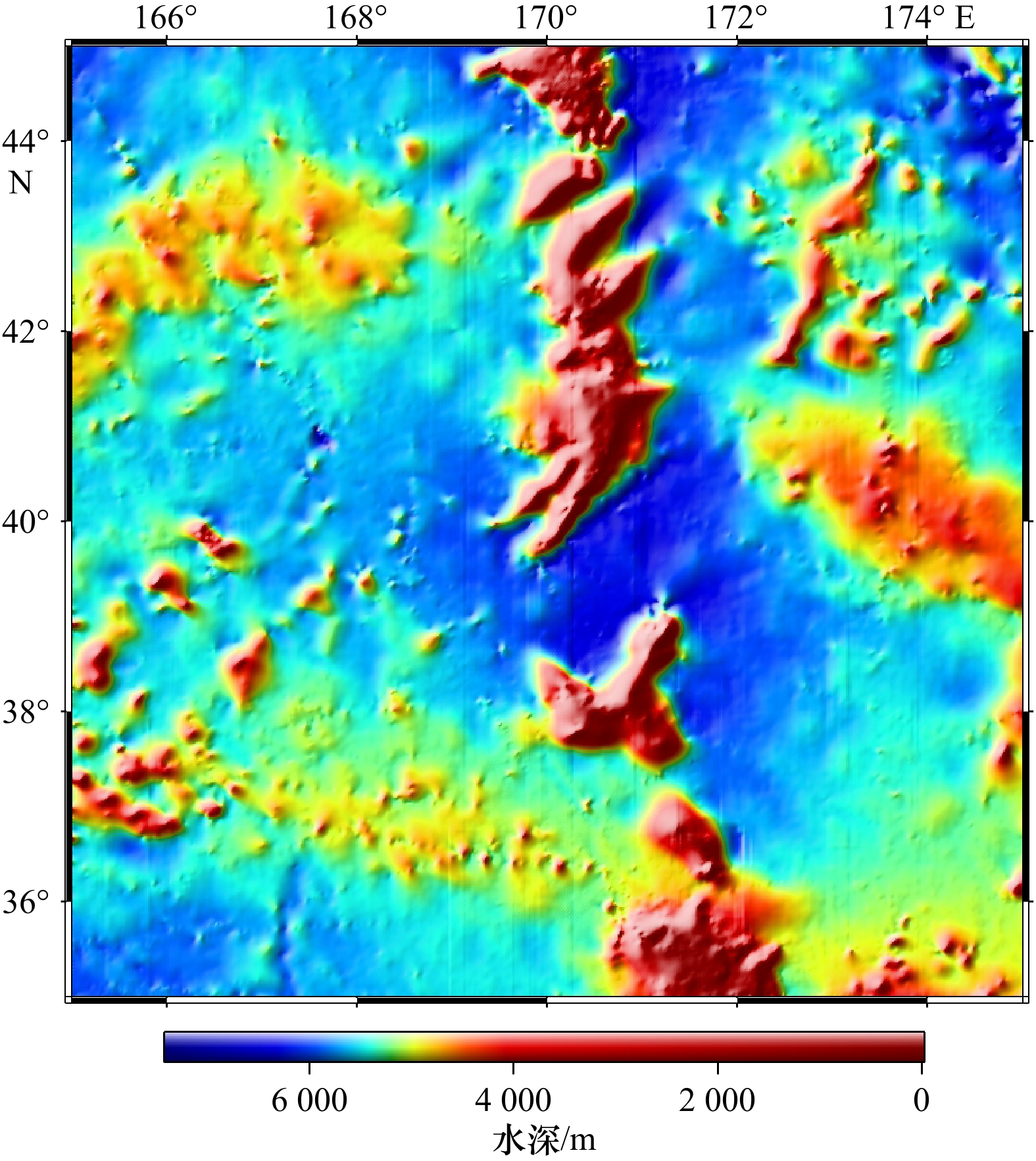
摘要: 海底地形对开展海洋科学调查和研究十分重要。以多波束为主的回声测深技术测量成本高且效率低，几十年来仅实现了全球约20%的海床测绘。对于空白区（特别是深海区域），可以借助重力异常和重力垂直梯度异常进行回归分析反演得到，但该方法得到的比例因子鲁棒性不强。为了解决这一问题，同时考虑到两种重力数据在表征海底地形长短波长的不同优势，本文结合滑动窗口赋权和稳健回归分析来反演海底地形。在太平洋皇帝山海域（35°～45°N，165°～175°E）的实验结果表明：在船测检核点处，本文构建模型的标准差为61.02 m，相比于单一重力数据反演模型，精度分别提高了14.92%（重力异常）和2.08%（重力垂直梯度异常），能较好地反映皇帝海山链的地形走势。Abstract: The topography of the seafloor is extremely important for marine scientific surveys and research. Echo-sounding technology, represented by multi-beam sounding, is costly and inefficient, and has only achieved about 20% of the world’s seabed mapping for decades. For the remaining void area, especially the deep ocean, it can be obtained by regression analysis using gravity anomalies and vertical gravity gradient anomalies, but the robustness of scale factor is poor. To address this issue, and considering the different advantages of the two kinds of gravity data in the characterization of the long and short wavelengths of the seafloor topography, a method which combining sliding window weighting and robust regression analysis was introduced in this paper. The experimental results in the Emperor Seamount in the Pacific Ocean (35°−45°N, 165°−175°E) indicate that: taking the ship test data as the checking condition, the standard deviation of the constructed model is 61.02 m, compared with the single gravity data inversion model, the accuracy was improved 14.92% (gravity anomalies) and 2.08% (vertical gravity gradient anomalies), which can better reflect the topographic trend of the Emperor Seamount Chain.
-
图 4 反演波段重力数据与残余海深线性拟合结果
Fig. 4 Results of linear fitting between gravity data of inversion band and residual sea depth
图 5 重力垂直梯度异常模型权值xi分配示意图，相应的，重力异常模型的权值分配为1−xi
Fig. 5 The schematic diagram of weight distribution xi of vertical gravity gradient anomalies model. Accordingly, the weight distribution of gravity anomalies model is 1−xi
图 9 检核点处差值结果统计直方图
Fig. 9 Statistical histogram of the difference results at the check point
图 10 异常点空间位置分布图（黑色圆点代表异常点位）
Fig. 10 Spatial distribution map of outliers (black dots represent outliers)
表 1 海底地形模型与多波束数据差值统计结果
Tab. 1 Difference statistics of seafloor topographic model with multibeam data
模型 平均值/m 标准差/m 相关系数 SGA 166.54 462.98 0.948 3 SVG 128.76 402.27 0.956 1 MGM_LS 159.01 421.55 0.949 7 MGM 139.09 393.89 0.961 1 
下载: 导出CSV
表 2 海底地形模型在检核点处差值统计结果
Tab. 2 Difference statistics of seafloor topographic model at check point
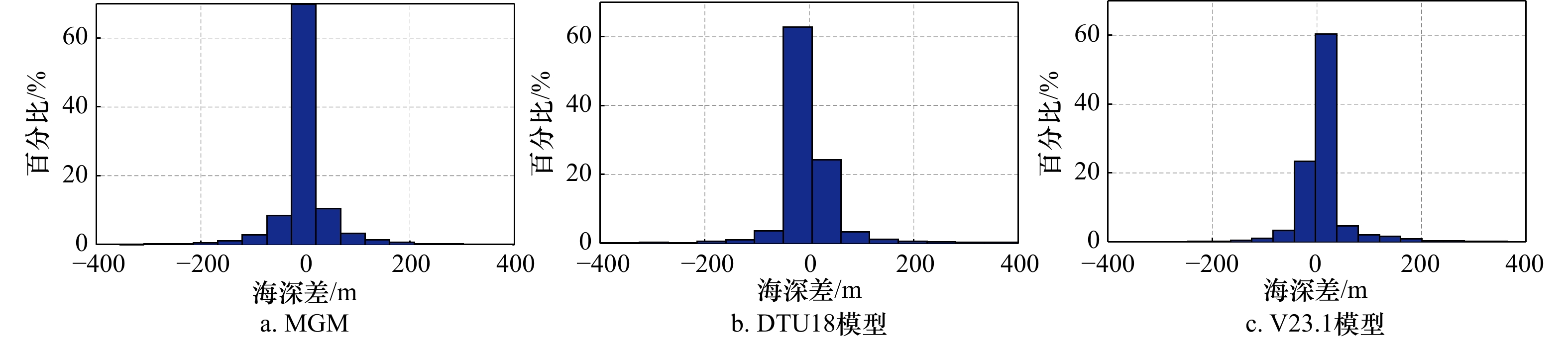
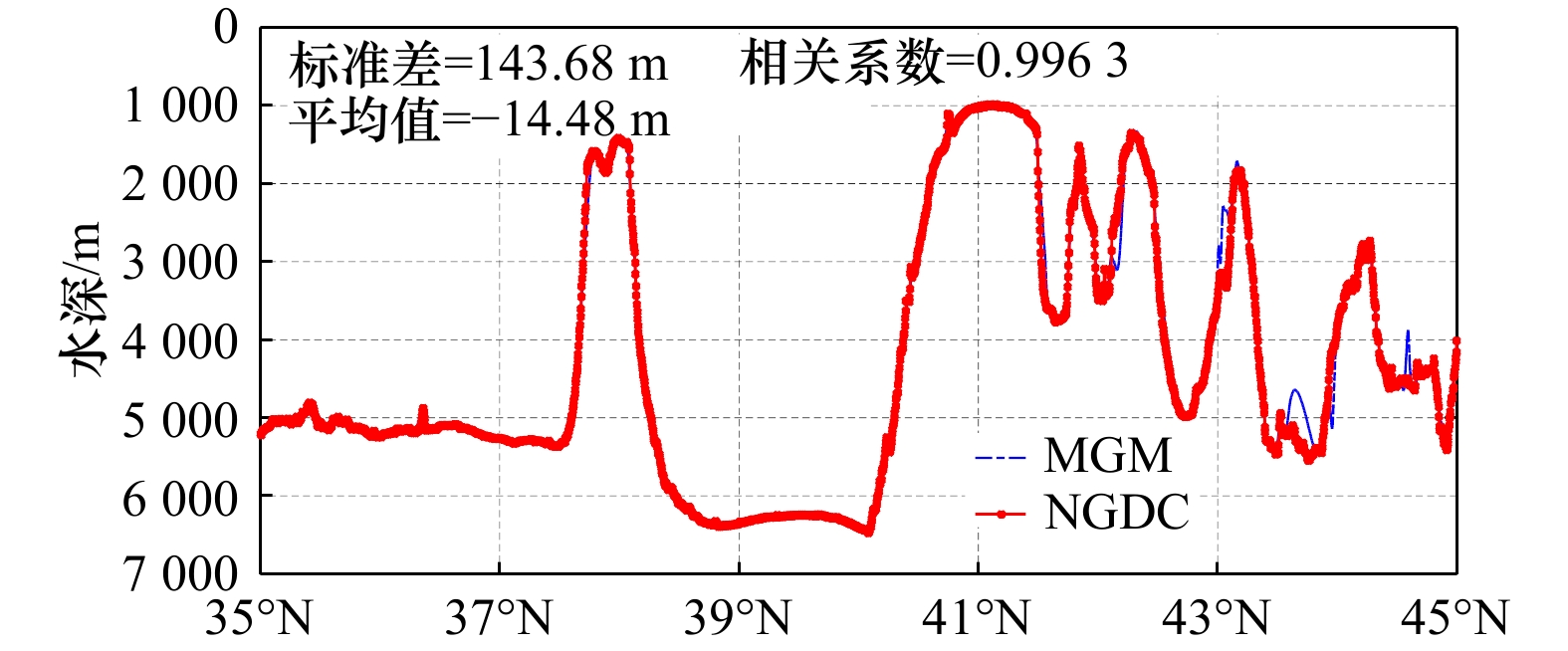
模型 最大值/m 最小值/m 平均值/m 标准差/m 相关系数 MGM 942.65 –895.09 0.64 61.02 0.998 0 DTU18 1 560.31 –1 110.94 7.74 95.41 0.996 6 V23.1 1 697.41 –2 148.33 10.46 95.52 0.996 6
下载: 导出CSV
-
[1] Weatherall P, Marks K M, Jakobsson M, et al. A new digital bathymetric model of the world’s oceans[J]. Earth and Space Science, 2015, 2(8): 331−345. doi: 10.1002/2015EA000107 [2] 欧阳明达, 孙中苗, 翟振和. 基于重力地质法的南中国海海底地形反演[J]. 地球物理学报, 2014, 57(9): 2756−2765. doi: 10.6038/cjg20140903Ouyang Mingda, Sun Zhongmiao, Zhai Zhenhe. Predicting bathymetry in South China Sea using the gravity-geologic method[J]. Chinese Journal of Geophysics, 2014, 57(9): 2756−2765. doi: 10.6038/cjg20140903 [3] 胡敏章, 李建成, 金涛勇. 应用重力地质方法反演皇帝海山的海底地形[J]. 武汉大学学报·信息科学版, 2012, 37(5): 610−612, 629. doi: 10.13203/j.whugis2012.05.008Hu Minzhang, Li Jiancheng, Jin Taoyong. Bathymetry inversion with gravity-geologic method in emperor seamount[J]. Geomatics and Information Science of Wuhan University, 2012, 37(5): 610−612, 629. doi: 10.13203/j.whugis2012.05.008 [4] Fan Diao, Li Shanshan, Meng Shuyu, et al. Bathymetric prediction from multi-source satellite altimetry gravity data[J]. Journal of Geodesy and Geoinformation Science, 2020, 2(1): 49−58. [5] Hwang C. A bathymetric model for the South China Sea from satellite altimetry and depth data[J]. Marine Geodesy, 1999, 22(1): 37−51. doi: 10.1080/014904199273597 [6] Calmant S, Berge-Nguyen M, Cazenave A. Global seafloor topography from a least-squares inversion of altimetry-based high-resolution mean sea surface and shipboard soundings[J]. Geophysical Journal International, 2002, 151(3): 795−808. doi: 10.1046/j.1365-246X.2002.01802.x [7] Smith W H F, Sandwell D T. Bathymetric prediction from dense satellite altimetry and sparse shipboard bathymetry[J]. Journal of Geophysical Research: Solid Earth, 1994, 99(B11): 21803−21824. doi: 10.1029/94JB00988 [8] Kim K B, Hsiao Y S, Kim J W, et al. Bathymetry enhancement by altimetry-derived gravity anomalies in the East Sea (Sea of Japan)[J]. Marine Geophysical Researches, 2010, 31(4): 285−298. doi: 10.1007/s11001-010-9110-0 [9] 李倩倩, 鲍李峰. 测高重力场反演海底地形方法比较[J]. 海洋测绘, 2016, 36(5): 1−4, 18. doi: 10.3969/j.issn.1671-3044.2016.05.001Li Qianqian, Bao Lifeng. Comparative analysis of methods for bathymetry prediction from altimeter-derived gravity anomalies[J]. Hydrographic Surveying and Charting, 2016, 36(5): 1−4, 18. doi: 10.3969/j.issn.1671-3044.2016.05.001 [10] 彭聪, 周兴华, 王颖. 两种测高重力异常反演海底地形方法比较[J]. 海洋通报, 2020, 39(2): 223−230.Peng Cong, Zhou Xinghua, Wang Ying. Comparison of two methods for retrieving sea bottom terrain bathymetry prediction from altimetry gravity anomalies[J]. Marine Science Bulletin, 2020, 39(2): 223−230. [11] 范雕, 李姗姗, 孟书宇, 等. 不同均衡补偿模式下海底地形反演方法比较分析[J]. 中国惯性技术学报, 2019, 27(1): 51−59.Fan Diao, Li Shanshan, Meng Shuyu, et al. Comparison and analysis on seafloor topography inversion methods with different isostatic compensation models[J]. Journal of Chinese Inertial Technology, 2019, 27(1): 51−59. [12] 郭金运, 魏志杰, 祝程程, 等. 基于重力异常迭代延拓的南海海底地形反演[J]. 山东科技大学学报(自然科学版), 2021, 40(4): 1−10.Guo Jinyun, Wei Zhijie, Zhu Chengcheng, et al. Bathymetry inversion of South China Sea based on iterative continuation of gravity anomalies[J]. Journal of Shandong University of Science and Technology (Natural Science), 2021, 40(4): 1−10. [13] 王虎彪, 肖耀飞, 武凛, 等. 重力数据融合与重力垂直梯度异常反演[J]. 海洋测绘, 2018, 38(1): 1−4, 17. doi: 10.3969/j.issn.1671-3044.2018.01.001Wang Hubiao, Xiao Yaofei, Wu Lin, et al. The fusion of gravity data and inversion of gravity vertical gradient anomaly[J]. Hydrographic Surveying and Charting, 2018, 38(1): 1−4, 17. doi: 10.3969/j.issn.1671-3044.2018.01.001 [14] Wan Xiaoyun, Ran Jiangjun, Jin Shuanggen. Sensitivity analysis of gravity anomalies and vertical gravity gradient data for bathymetry inversion[J]. Marine Geophysical Research, 2019, 40(1): 87−96. doi: 10.1007/s11001-018-9361-8 [15] Wang Yanming. Predicting bathymetry from the Earth’s gravity gradient anomalies[J]. Marine Geodesy, 2000, 23(4): 251−258. doi: 10.1080/01490410050210508 [16] Wessel P, Lyons S. Distribution of large Pacific seamounts from Geosat/ERS-1: implications for the history of intraplate volcanism[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B10): 22459−22475. doi: 10.1029/97JB01588 [17] 吴云孙, 晁定波, 李建成, 等. 利用测高重力梯度异常反演中国南海海底地形[J]. 武汉大学学报·信息科学版, 2009, 34(12): 1423−1425. doi: 10.13203/j.whugis2009.12.007Wu Yunsun, Chao Dingbo, Li Jiancheng, et al. Recovery of ocean depth model of South China Sea from altimetric gravity gradient anomalies[J]. Geomatics and Information Science of Wuhan University, 2009, 34(12): 1423−1425. doi: 10.13203/j.whugis2009.12.007 [18] 胡敏章, 李建成, 金涛勇, 等. 联合多源数据确定中国海及周边海底地形模型[J]. 武汉大学学报·信息科学版, 2015, 40(9): 1266−1273.Hu Minzhang, Li Jiancheng, Jin Taoyong, et al. Recovery of bathymetry over China Sea and its adjacent areas by combination of multi-source data[J]. Geomatics and Information Science of Wuhan University, 2015, 40(9): 1266−1273. [19] 范雕, 李姗姗, 杨军军, 等. 利用多元回归分析反演西南印度洋区域海底地形[J]. 测绘学报, 2020, 49(2): 147−161. doi: 10.11947/j.AGCS.2020.20180526Fan Diao, Li Shanshan, Yang Junjun, et al. Predicting bathymetry by applying multiple regression analysis in the Southwest Indian Ocean region[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(2): 147−161. doi: 10.11947/j.AGCS.2020.20180526 [20] Parker R L. The rapid calculation of potential anomalies[J]. Geophysical Journal International, 1973, 31(4): 447−455. doi: 10.1111/j.1365-246X.1973.tb06513.x [21] Schwarz K P, Sideris M G, Forsberg R. The use of FFT techniques in physical geodesy[J]. Geophysical Journal International, 1990, 100(3): 485−514. doi: 10.1111/j.1365-246X.1990.tb00701.x [22] 欧阳明达, 孙中苗, 翟振和, 等. 采用重力异常的导纳理论推估海底地形[J]. 测绘学报, 2015, 44(10): 1092−1099. doi: 10.11947/j.AGCS.2015.20140427Ouyang Mingda, Sun Zhongmiao, Zhai Zhenhe, et al. Bathymetry prediction based on the admittance theory of gravity anomalies[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(10): 1092−1099. doi: 10.11947/j.AGCS.2015.20140427 [23] 韩小慧. 稳健多元线性回归在地理数据处理中的应用[D]. 太原: 太原理工大学, 2012.Han Xiaohui. Application of robust multiple linear regression in geographic data processing[D]. Taiyuan: Taiyuan University of Technology, 2012. [24] Baselga S. Global optimization solution of robust estimation[J]. Journal of Surveying Engineering, 2007, 133(3): 123−128. doi: 10.1061/(ASCE)0733-9453(2007)133:3(123) [25] 陈艳国. 回归预测模型的稳健性分析[J]. 西部探矿工程, 2006, 18(2): 177−179. doi: 10.3969/j.issn.1004-5716.2006.02.083Chen Yanguo. Robustness analysis of regression prediction models[J]. West-China Exploration Engineering, 2006, 18(2): 177−179. doi: 10.3969/j.issn.1004-5716.2006.02.083 [26] 范雕, 李姗姗, 孟书宇, 等. 应用抗差估计方法构建日本海海底地形模型[J]. 中国惯性技术学报, 2020, 28(5): 576−585.Fan Diao, Li Shanshan, Meng Shuyu, et al. Applying robust estimation method to estimate seafloor topography in the Sea of Japan[J]. Journal of Chinese Inertial Technology, 2020, 28(5): 576−585. [27] 魏志杰. 基于卫星测高数据反演南海海底地形[D]. 青岛: 山东科技大学, 2021.Wei Zhijie. Bathymetry prediction of the South China Sea based on satellite altimetry data[D]. Qingdao: Shandong University of Science and Technology, 2021. [28] 范雕, 李姗姗, 孟书宇, 等. 线性回归分析技术推估海底地形[J]. 中国惯性技术学报, 2018, 26(1): 24−32.Fan Diao, Li Shanshan, Meng Shuyu, et al. Predicting submarine topography by linear regression analysis[J]. Journal of Chinese Inertial Technology, 2018, 26(1): 24−32. [29] 王永康, 周兴华, 唐秋华, 等. 应用重力地质法反演马里亚纳海沟地形[J]. 海洋科学进展, 2020, 38(4): 708−716. doi: 10.3969/j.issn.1671-6647.2020.04.014Wang Yongkang, Zhou Xinghua, Tang Qiuhua, et al. Predicting bathymetry in Mariana Trench using gravity-geologic method[J]. Advances in Marine Science, 2020, 38(4): 708−716. doi: 10.3969/j.issn.1671-6647.2020.04.014 -
图(11) / 表(2)
计量
- 文章访问数: 391
- HTML全文浏览量: 209
- PDF下载量: 52
- 被引次数: 0
