Research on inversion technology of physical properties parameters of seafloor sediments based on sub-bottom profile: Taking the Bohai Sea submarine pipeline route as an example
-
摘要: 海底浅表层（小于1 m）沉积物的物理性质，如粒度、孔隙度、密度等是海洋沉积学研究和海洋工程地质分析的重要内容，目前主要基于有限的海底取样或原位测试获取这些沉积物的物理性质。浅地层剖面是基于声学信号（频率几千赫兹）在沉积物中的传播得到可反映沉积地层结构的数据，其中的一些声学参数，如海底反射系数、波阻抗等与沉积物物理性质密切相关。如何充分而有效地利用浅地层剖面资料，反演得到剖面覆盖区海底浅表层沉积物的物理性质参数，极具科学意义和应用价值，且基于声学属性反演沉积物物理性质是当前研究的热点。为此，本文基于渤海LD16-3CEPA至LD10-1PAPD路由段的浅地层剖面数据和海底表层沉积物的实测物理参数，利用Biot-Stoll模型建立研究区海底反射系数和沉积物物理性质之间的关系，并基于浅地层剖面数据计算得到的海底反射系数，反演了研究区海底浅表层沉积物的孔隙度、密度、平均粒径等物理性质参数。其中反演的孔隙度、密度、平均粒径与实测孔隙度、密度、平均粒径基本相符，偏差度基本都在20%的偏差范围内，表明该反演方法在该区的应用是可行的。
-
关键词:
- 浅地层剖面 /
- Biot-Stoll模型 /
- 海底反射系数 /
- 沉积物物理性质 /
- 渤海
Abstract: The physical properties of seafloor sediments (less than 1 m), such as particle size, porosity and density, are an important part of marine sedimental research and marine engineering geological analysis. The acquisition of these physical properties is currently based on limited seabed sampling or in-situ testing. The sub-bottom profile is based on the propagation of acoustic signals (frequencies in thousands of Hertz) in sediments to obtain the data that can reflect the sedimentary stratigraphic structure. Some of the acoustic parameters, such as seabed reflection coefficient and wave impedance, are closely related to the physical properties of sediments. How to make full and effective use of the sub-bottom profile data to retrieve the physical property parameters of the seafloor sediments in the profile overlying area is of great scientific significance and application value. Moreover, inversion of the physical properties of sediments based on acoustic properties is a hot research topic at present. Therefore, in this paper, the Biot-Stoll model is used to establish the relationship between the seabed reflection coefficient and the physical properties of the sediments in the study area based on the measured physical parameters of the seafloor sediments from LD 16-3CEPA to LD10-1PAPD routing section of the Bohai Sea. Based on the seabed reflection coefficient calculated from the sub-bottom profile data, the physical property parameters such as porosity, density and mean grain size of the seabed sediment in the study area are retrieved. The porosity, density and mean grain size of the inversion are basically consistent with the measured, and the deviation degree is basically within the range of 20%, indicating that the application of the inversion method in this area is feasible. -
图 1 研究区位置及浅剖与取样站位分布
Fig. 1 Location of study area and distribution of sub-bottom profiles and sampling stations
图 2 浅地层剖面频谱分析特征
b和c中黑色线为剖面整体频谱特征，蓝色线为其中1道的频谱特征
Fig. 2 Spectral analysis feature of sub-bottom profile
The black lines are the overall spectral characteristics of the profile, and the blue lines are the spectral characteristics of one channel in b and c
图 3 对数分解法求取子波的过程图解
Fig. 3 Process diagram of wavelet extraction by logarithmic decomposition method
图 4 典型浅地层剖面图（a）及该剖面计算得到的海底反射系数（b）
Fig. 4 Typical sub-bottom profile (a) and the calculated seabed reflection coefficients (b)
图 5 海底反射系数与沉积物物理性质的相关关系（主频为5 kHz）
Fig. 5 Correlation between seafloor reflection coefficient and sediment physical properties, (the dominant frequency is 5 kHz)
图 6 海底表层沉积物物性反演结果与取样测试结果对比
图中坐标为TM投影，中央经线为120°E
Fig. 6 Comparison between inversion results and sampling test results of seafloor surface sediment physical properties
The coordinates in the figure are TM projection and the central meridian is 120°E
表 1 海底浅表层沉积物物理性质
Tab. 1 Physical properties of seabed shallow surface sediments
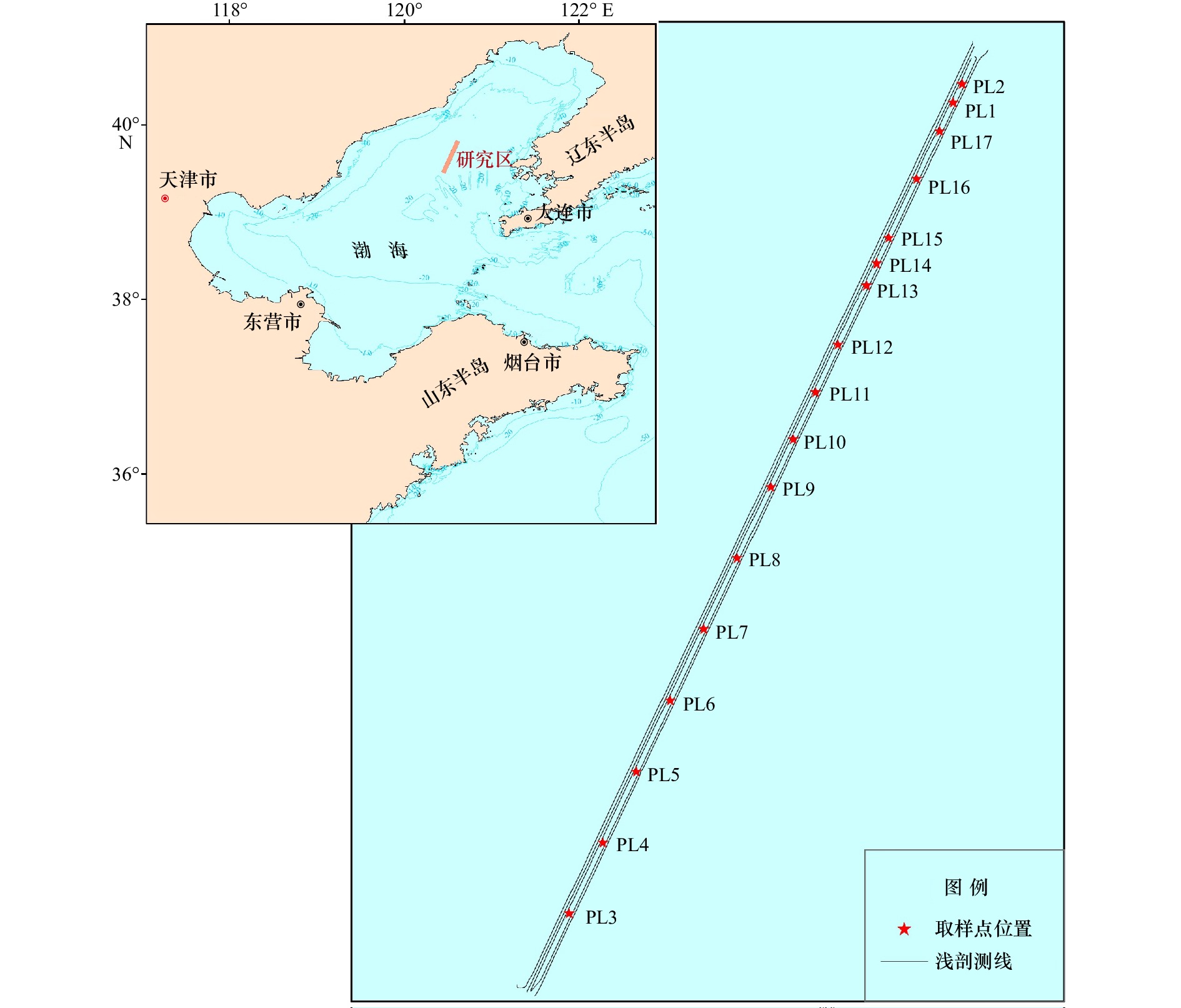
站位 纬度 经度 密度/（g·m−3) 平均粒径（Ф） 孔隙度 PL3 39.492 31°N 120.464 40°E 1 636.73 6.56 0.68 PL4 39.518 09°N 120.476 53°E 1 582.65 6.94 0.70 PL5 39.537 46°N 120.493 21°E 1 575.51 – – PL6 39.568 55°N 120.500 19°E 1 468.37 7.49 0.73 PL7 39.593 29°N 120.513 81°E 1 597.96 7.25 0.72 PL8 39.619 35°N 120.524 32°E 1 536.73 7.06 0.71 PL9 39.644 64°N 120.536 22°E 1 657.14 7.48 0.73 PL10 39.661 17°N 120.546 00°E 1 674.49 6.78 0.69 PL11 39.678 54°N 120.554 16°E 1 601.02 7.08 0.71 PL12 39.695 24°N 120.560 21°E 1 595.92 6.81 0.70 PL13 39.716 87°N 120.570 56°E 1 728.57 6.64 0.69 PL14 39.723 59°N 120.575 45°E 1 771.43 6.39 0.67 PL15 39.732 96°N 120.579 86°E 1 679.59 6.08 0.66 PL16 39.754 23°N 120.590 03°E 1 682.65 6.27 0.67 PL17 39.771 02°N 120.597 98°E 1 628.57 6.23 0.67 注：–代表无数据。 
下载: 导出CSV
表 2 Biot-Stoll模型输入的沉积物物理参数
Tab. 2 The input sediment physical parameters of the Biot-Stoll model
参数 Biot-Stoll模型取值 颗粒密度ρg /（g·m−3） 2 708 孔隙度n 0.45～0.85 孔隙曲折度α ${ \alpha = \left\{ {\begin{array}{*{20}{l}} {1.35},&{\Phi \leqslant 4}， \\ {{{ - }}0.3 + 0.412\;5\Phi },&{4 < \Phi < 8}， \\ {3.0},&{\Phi \geqslant 8} ，\end{array}} \right. }$ 式中，Φ = −log2d，Φ为平均粒径，d为颗粒直径（单位：mm） 渗透率κ/m2 ${ \kappa = \dfrac{{{d^2}{n^3}}}{{180{{(1 - n)}^2}}}\dfrac{1}{{\sqrt {10} }}} $ 海水动力黏度η/（Pa·s） 0.001 颗粒体积模量Kg/Pa 3.2×1010 海水体积模量Kw/Pa 2.395×109 海水密度ρw/（g·m−3） 102 3 框架剪切模量µ0/Pa ${{\ \mu _0} = 1.835 \times {10^5}{\left(\dfrac{n}{ {1 - n} }\right)^{ - 1.12} }\sqrt { {\tau _a}(\textit{z})}}$，
${ {\tau _a}(\textit{z}) = (1 - n)({\rho _{\rm{s}}} - {\rho _{\rm{f}}})g\textit{z} }$，
式中，$ {\tau _a}(\textit{z}) $为沉积物平均有效压力；重力加速度g=9.8 m/s2；ρs为颗粒密度；ρf为孔隙流体密度；z为沉积层厚度（单位：m） 框架体积模量K0/Pa ${ {K_0} = \dfrac{{2{\mu _0}(1 + \sigma )}}{{3(1 - 2\sigma )}}} $ ，式中，σ为沉积物骨架的泊松比 孔隙大小a $ {a = \dfrac{d}{3}\dfrac{n}{{1 - n}}\dfrac{1}{{1.8}} }$ 体积对数衰减δf ${{\delta _f}({\textit{z}_s}) = {\delta _f}({\textit{z}_0})\sqrt { \dfrac{\textit{z}_0}{\textit{z}_s}}}$，式中，z0、zs分别为第一层和特定目标层沉积物深度
下载: 导出CSV
表 3 反演结果与取样测试数据对比信息
Tab. 3 Comparison information between inversion results and sampling test data
站位 纬度 经度 样品孔隙度 反演孔隙度 偏差度/
%样品密度/
（g·m−3）反演密度/
（g·m−3）偏差度/
%样品平均粒径
（Ф）反演平均粒径
（Ф）偏差度/
%PL3 39.492 31°N 120.464 40°E 0.683 0.625 –8.37 1 636.73 1 623.65 –0.80 6.56 5.58 –14.91 PL4 39.518 09°N 120.476 53°E 0.701 0.634 –9.64 1 582.65 1 611.62 1.83 6.94 5.73 –17.46 PL6 39.568 55°N 120.500 19°E 0.727 0.711 –2.18 1 468.37 1 507.18 2.64 7.49 7.24 –3.44 PL7 39.593 29°N 120.513 81°E 0.716 0.724 1.15 1 597.96 1 477.96 –7.51 7.25 7.54 3.99 PL8 39.619 35°N 120.524 32°E 0.707 0.779 10.15 1 536.73 1 416.86 –7.80 7.06 8.69 22.97 PL9 39.644 64°N 120.536 22°E 0.727 0.796 9.54 1 657.14 1 394.14 –15.87 7.48 9.06 21.14 PL10 39.661 17°N 120.546 00°E 0.694 0.775 11.74 1 674.49 1 418.37 –15.30 6.78 8.60 26.74 PL11 39.678 54°N 120.554 16°E 0.708 0.780 10.10 1 601.02 1 414.50 –11.65 7.08 8.71 22.98 PL12 39.695 24°N 120.560 21°E 0.695 0.756 8.79 1 595.92 1 439.56 –9.80 6.81 8.19 20.23 PL13 39.716 87°N 120.570 56°E 0.687 0.751 9.29 1 728.57 1 450.71 –16.07 6.64 8.09 21.79 PL14 39.723 59°N 120.575 45°E 0.674 0.737 9.27 1 771.43 1 461.70 –17.48 6.39 7.78 21.77 PL15 39.732 96°N 120.579 86°E 0.658 0.745 13.26 1 679.59 1 455.37 –13.35 6.08 7.95 30.83 PL16 39.754 23°N 120.590 03°E 0.668 0.747 11.84 1 682.65 1 458.80 –13.30 6.27 7.95 26.70 PL17 39.771 02°N 120.597 98°E 0.666 0.722 8.41 1 628.57 1 489.09 –8.56 6.23 7.46 19.80
下载: 导出CSV
-
[1] 何起祥. 中国海洋沉积地质学[M]. 海洋出版社, 2006.He Qixiang. Marine Sedimentary Geology of China[M]. Beijing: China Ocean Press, 2006. [2] 朱长歧, 汪稔, 符策简. WR-II型海洋静力触探(SCPT)数据处理系统中的岩土力学分层模型[J]. 岩土力学, 1994, 15(2): 78−88.Zhu Changqi, Wang Ren, Fu Cejian. The identification model of soil layer used in type WR-II SCPT data processing system[J]. Rock and Soil Mechanics, 1994, 15(2): 78−88. [3] Hamilton E L. Elastic properties of marine sediments[J]. Journal of Geophysical Research, 1971, 76(2): 579−604. doi: 10.1029/JB076i002p00579 [4] Berndt C, Bünz S, Clayton T, et al. Seismic character of bottom simulating reflectors: examples from the mid-Norwegian margin[J]. Marine and Petroleum Geology, 2004, 21(6): 723−733. doi: 10.1016/j.marpetgeo.2004.02.003 [5] 阮爱国, 李家彪, 初凤友, 等. 海底天然气水合物层界面反射AVO数值模拟[J]. 地球物理学报, 2006, 49(6): 1826−1835. doi: 10.3321/j.issn:0001-5733.2006.06.031Ruan Aiguo, Li Jiabiao, Chu Fengyou, et al. AVO numerical simulation of gas hydrates reflectors beneath seafloor[J]. Chinese Journal of Geophysics, 2006, 49(6): 1826−1835. doi: 10.3321/j.issn:0001-5733.2006.06.031 [6] Li Xishuang, Liu Baohua, Liu Lejun, et al. Prediction for potential landslide zones using seismic amplitude in Liwan gas field, northern South China Sea[J]. Journal of Ocean University of China, 2017, 16(6): 1035−1042. doi: 10.1007/s11802-017-3308-6 [7] Panda S, LeBlanc L R, Schock S G. Sediment classification based on impedance and attenuation estimation[J]. The Journal of the Acoustical Society of America, 1994, 96(5): 3022−3035. doi: 10.1121/1.411266 [8] Kim G Y, Richardson M D, Bibee D L, et al. Sediment types determination using acoustic techniques in the northeastern Gulf of Mexico[J]. Geosciences Journal, 2004, 8(1): 95−103. doi: 10.1007/BF02910282 [9] Schock S G. A method for estimating the physical and acoustic properties of the sea bed using chirp sonar data[J]. IEEE Journal of Oceanic Engineering, 2004, 29(4): 1200−1217. doi: 10.1109/JOE.2004.841421 [10] 曹正良, 张叔英, 马在田. BICSQS模型与Biot-Stoll模型海底界面声波反射和散射的比较[J]. 声学学报, 2006, 31(5): 389−398. doi: 10.3321/j.issn:0371-0025.2006.05.002Cao Zhengliang, Zhang Shuying, Ma Zaitian. Comparison of reflections and interface scatterings from BICSQS model and Biot-Stoll model seafloors[J]. Acta Acustica, 2006, 31(5): 389−398. doi: 10.3321/j.issn:0371-0025.2006.05.002 [11] 朱祖扬, 王东, 周建平, 等. 基于非饱和Biot-Stoll模型的海底沉积物介质声频散特性研究[J]. 地球物理学报, 2012, 55(1): 180−188. doi: 10.6038/j.issn.0001-5733.2012.01.017Zhu Zuyang, Wang Dong, Zhou Jianping, et al. Acoustic wave dispersion and attenuation in marine sediment based on partially gas-saturated Biot-Stoil model[J]. Chinese Journal of Geophysics, 2012, 55(1): 180−188. doi: 10.6038/j.issn.0001-5733.2012.01.017 [12] 陈静, 阎贫, 王彦林, 等. 基于Biot-Stoll模型声速反演中的参数选择——以南海南部沉积物为例[J]. 热带海洋学报, 2012, 31(1): 50−54.Chen Jing, Yan Pin, Wang Yanlin, et al. Choice of parameters for Biot-Stoll model-based inversion of sound velocity of seafloor sediments in the southern South China Sea[J]. Journal of Tropical Oceanography, 2012, 31(1): 50−54. [13] 王景强, 郭常升, 刘保华, 等. 基于Buckingham模型和Biot-Stoll模型的南沙海域沉积物声速分布特征[J]. 地球学报, 2016, 37(3): 359−367. doi: 10.3975/cagsb.2016.03.13Wang Jingqiang, Guo Changsheng, Liu Baohua, et al. Sound speed distribution of seafloor sediments in Nansha Islands sea based on Buckingham model and Biot-Stoll model[J]. Acta Geoscientica Sinica, 2016, 37(3): 359−367. doi: 10.3975/cagsb.2016.03.13 [14] 陶春辉. 海底沉积物声学原位测试和特性研究[D]. 杭州: 浙江大学, 2005.Tao Chunhui. In situ acoustic experiment and properties study in marine sediments[D]. Hangzhou: Zhejiang University, 2005. [15] 陈静, 吕修亚, 陈亮, 等. 基于Chirp数据反演琼州海峡海底沉积物物性[J]. 热带地理, 2017, 37(6): 874−879.Chen Jing, Lü Xiuya, Chen Liang, et al. Physical properties of the seabed inversed by Chirp data in the Qiongzhou Strait[J]. Tropical Geography, 2017, 37(6): 874−879. [16] 董太禄. 渤海现代沉积作用与模式的研究[J]. 海洋地质与第四纪地质, 1996, 16(4): 43−53.Dong Tailu. Modern sedimentation models in the Bohai Sea[J]. Marine Geology and Quaternary Geology, 1996, 16(4): 43−53. [17] 乔淑卿, 石学法, 王国庆, 等. 渤海底质沉积物粒度特征及输运趋势探讨[J]. 海洋学报, 2010, 32(4): 139−147.Qiao Shuqing, Shi Xuefa, Wang Guoqing, et al. Discussion on grain-size characteristics of seafloor sediment and transport pattern in the Bohai Sea[J]. Haiyang Xuebao, 2010, 32(4): 139−147. [18] 王伟伟, 付元宾, 李树同, 等. 渤海中部表层沉积物分布特征与粒度分区[J]. 沉积学报, 2013, 31(3): 478−485.Wang Weiwei, Fu Yuanbin, Li Shutong, et al. Distribution on surface sediment and sedimentary divisions in the middle part of Bohai Sea[J]. Acta Sedimentologica Sinica, 2013, 31(3): 478−485. [19] Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range[J]. The Journal of the Acoustical Society of America, 1956, 28(2): 168−178. doi: 10.1121/1.1908239 [20] Stoll R D. Acoustic waves in saturated sediments[M]//Hampton L. Physics of Sound in Marine Sediments. Boston, MA: Springer, 1974: 19−39. [21] 黄绪德. 计算机在地学中的应用[J]. 物探化探计算技术, 1991, 13(2): 93−97.Huang Xude. Computer applications to geoscience[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1991, 13(2): 93−97. -
图(7) / 表(3)
计量
- 文章访问数: 439
- HTML全文浏览量: 141
- PDF下载量: 88
- 被引次数: 0
