Experimental study on the sheltering effect between ice ridges on ice-water drag force
-
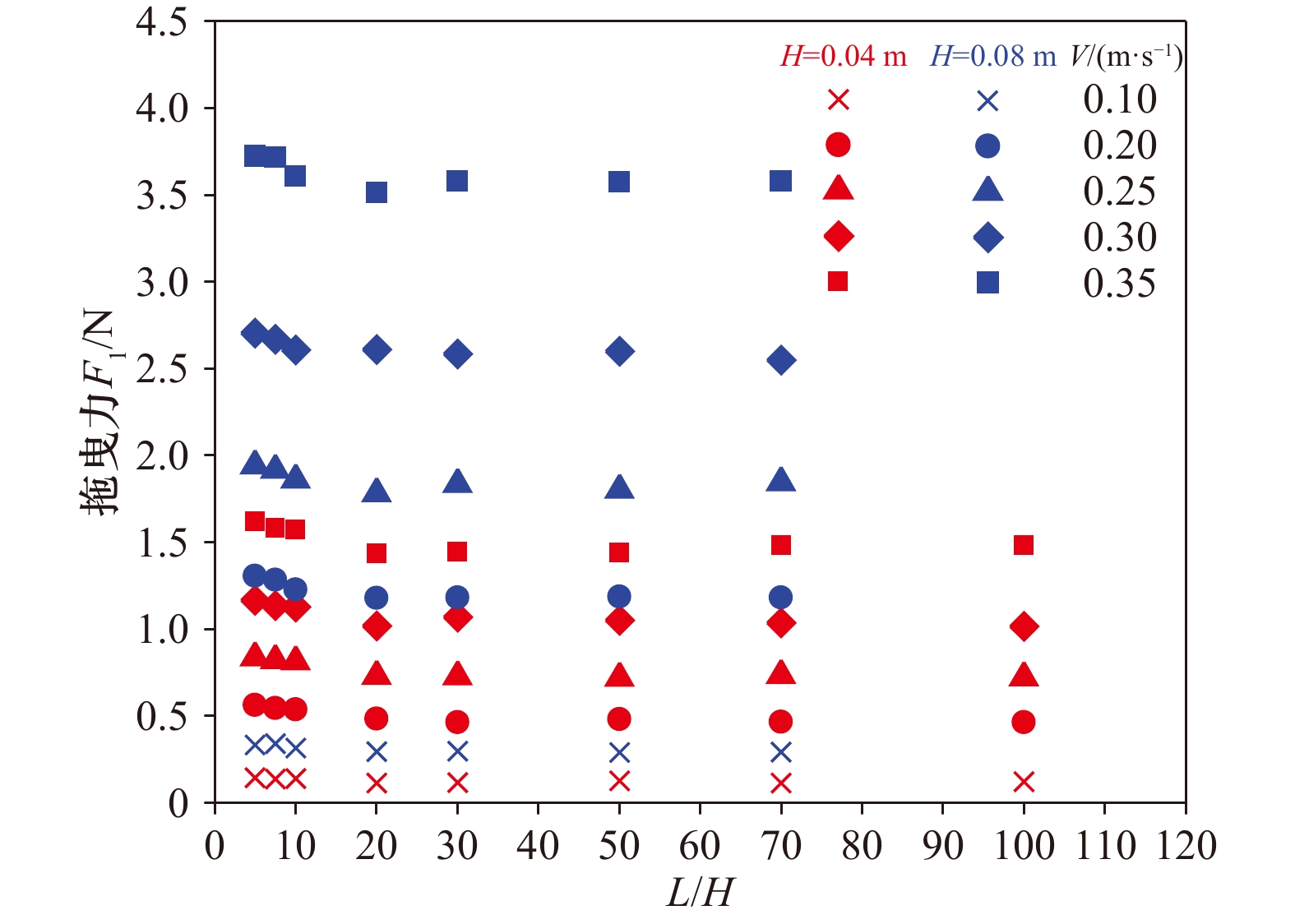
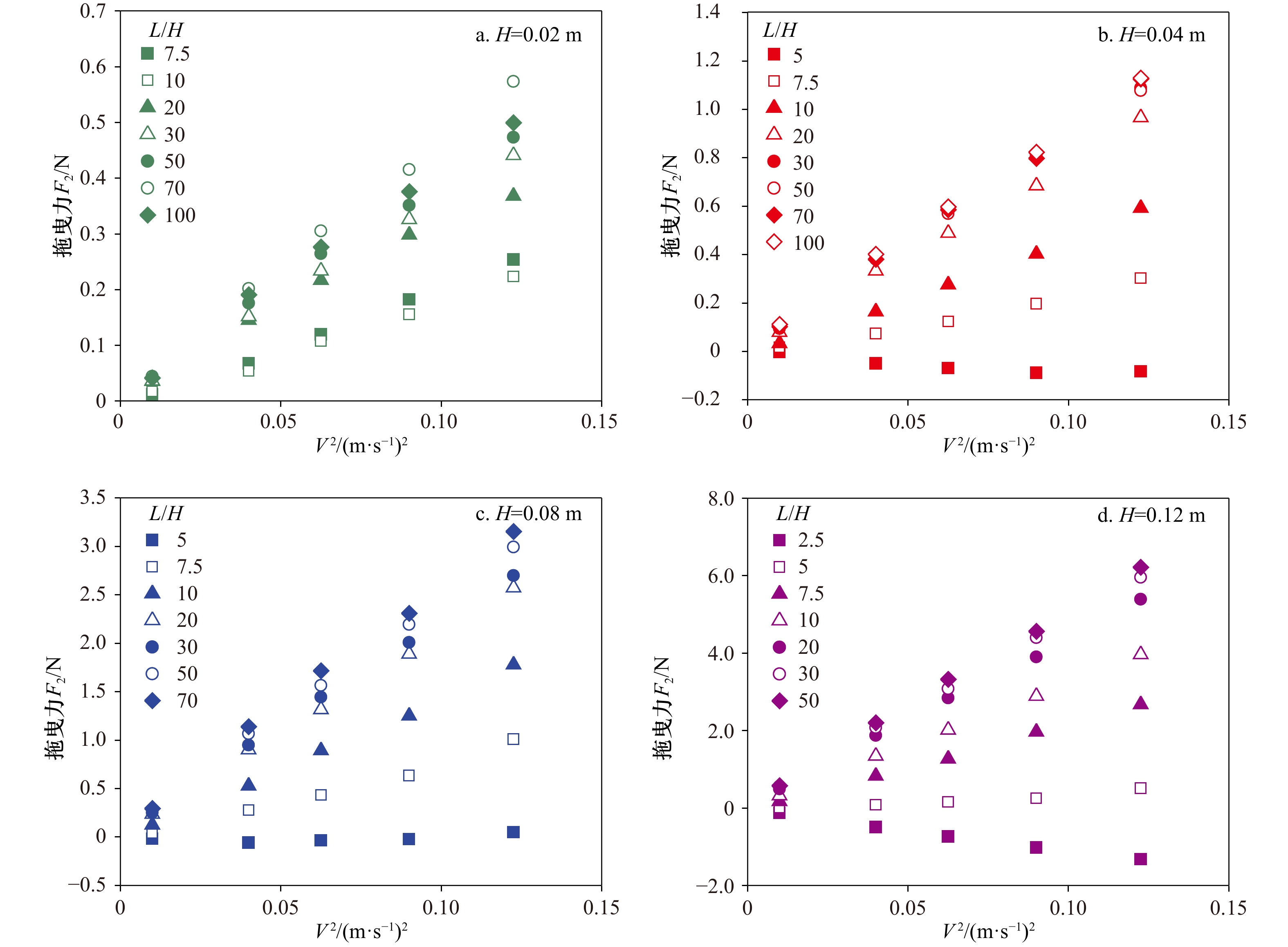
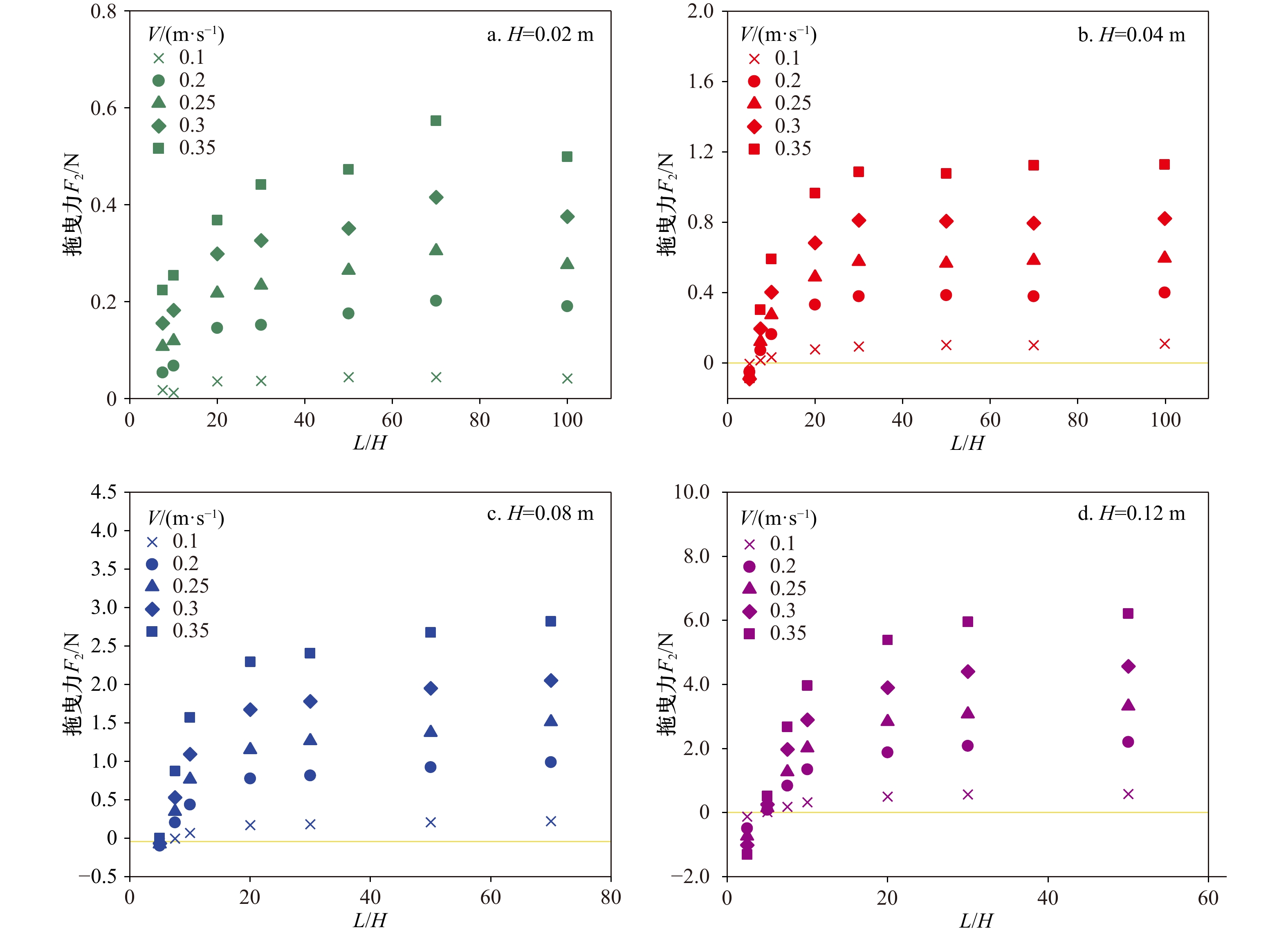
摘要: 为定量研究多冰脊之间的尾流遮掩作用对海冰漂移运动的影响，物理模型试验（试验有限水深为0.45 m）测量了多冰脊拖曳力的衰减变化。冰脊模型选用底角为45°的等腰直角三角形，选取了4种入水深度、9种冰脊间距进行测量。试验得到了前后冰脊拖曳力及其比值在尾流遮掩情况下的变化规律。前冰脊拖曳力与单冰脊情况一致，与冰脊速度的平方保持线性关系；而后冰脊在间距较小时出现了反向拖曳力，随冰脊间距的增大，后冰脊拖曳系数先减小再增大至不变。前后冰脊拖曳力比值的变化规律可以用指数遮掩函数来描述，该遮掩函数与冰脊间距和入水深度有关而与流速无关。通过与现有海冰模式中的遮掩函数对比，研究结论增强了该指数公式的适用性，加强了对海冰动力学模式中遮掩函数的理解。Abstract: In order to quantitatively study the sheltering effect between multiple ridges keel on sea ice drift, the laboratory experiment is carried out in a tank, which is 0.45 m deep. The shape of keel models is a triangle with 45° slope angle, 4 keel depths and 9 keel spacings are selected in the experiments. The variations of the front and back keel drag force and its ratio under wake effect is investigated. The drag force on the front keel is not affected by the back keel and keeps a linear relationship with the square of keel velocity; however, the drag force of back keel appears negative value (opposite direction) when the keel spacing is small. With the increase of the spacing the drag coefficient of the back keel first decreases and then increases to a constant. The variation of the ratio of drag forces between the front and back can be described by an exponential sheltering function, which is related to keel spacings and keel depths, and independent of keel velocity. Compared with the sheltering functions which are used in present sea ice models, the exponential formula is given and improves our understanding about sheltering function in sea ice dynamic model.
-
Key words:
- multiple ice ridges /
- drag force /
- the sheltering effect /
- parameterization
-
图 1 实验示意图（a）和物理模型实验装置图（b）
Fig. 1 The sketch of the experimental study (a) and physical model test device diagram (b)
图 2 前冰脊拖曳力F1随无量纲间距L/H的变化
Fig. 2 Variation of drag force of front ice ridge F1 with dimensionless distance L/H
图 3 后冰脊拖曳力F2随流速平方（V 2）
的变化情况 Fig. 3 Variation of drag force of back ice ridge F2 with the square of velocity (V 2)
图 4 后冰脊拖曳力F2随无量纲间距L/H的变化情况
Fig. 4 Variation of drag force of back ice ridge F2 with dimensionless distance L/H
图 5 拖曳力比值F2/F1随无量纲间距L/H的变化
Fig. 5 The drag force ratio F2/F1 changes with the dimensionless distance L/H
表 1 模型实验相似依据
Tab. 1 Similarity basis of model experiment
无因次数 冰脊拖曳
系数Cr无量纲
间距雷诺数Re 无量纲入水
深度冰脊底角 表达式 $ {\dfrac{F}{ {\rho}{V}^{\text{2} }{H} } }$ $ { \dfrac{{L} }{{H} } }$ $ {\dfrac{ {VH} }{ {v} } }$ $ {\dfrac{{D} }{{H} } }$ a 
下载: 导出CSV
-
[1] 吴辉碇, 白珊, 张占海. 海冰动力学过程的数值模拟[J]. 海洋学报, 1998, 20(2): 1−13.Wu Huiding, Bai Shan, Zhang Zhanhai. Numerical simulation of sea ice dynamics[J]. Haiyang Xuebao, 1998, 20(2): 1−13. [2] Wamser C, Martinson D G. Drag coefficients for winter Antarctic pack ice[J]. Journal of Geophysical Research: Atmospheres, 1993, 98(C7): 12431−12437. doi: 10.1029/93JC00655 [3] 吴岩. 冰脊对冰下流场影响的数值模拟研究[D]. 大连: 大连理工大学, 2016.Wu Yan. Numerical simulation on the influence of ice ridges on the flow field under ice[D]. Dalian: Dalian University of Technology, 2016. [4] Lu Peng, Li Zhijun, Cheng Bin, et al. A parameterization of the ice-ocean drag coefficient[J]. Journal of Geophysical Research: Oceans, 2011, 116(C7): C07019. [5] Davis N R, Wadhams P. A statistical analysis of Arctic pressure ridge morphology[J]. Journal of Geophysical Research: Oceans, 1995, 100(C6): 10915. doi: 10.1029/95JC00007 [6] Hanssen-Bauer I, Gjessing Y T. Observations and model calculations of aerodynamic drag on sea ice in the Fram Strait[J]. Tellus A, 1988, 40(2): 151−161. doi: 10.3402/tellusa.v40i2.11789 [7] Lüpkes C, Gryanik V M, Hartmann J, et al. A parametrization, based on sea ice morphology, of the neutral atmospheric drag coefficients for weather prediction and climate models[J]. Journal of Geophysical Research: Atmospheres, 2012, 117(D13): D13112. [8] Tsamados M, Feltham D L, Schroeder D, et al. Impact of variable atmospheric and oceanic form drag on simulations of arctic sea ice[J]. Journal of Physical Oceanography, 2014, 44(5): 1329−1353. doi: 10.1175/JPO-D-13-0215.1 [9] Tennekes H, Lumley J L. A First Course in Turbulence[M]. Cambridge: MIT Press, 1972. [10] Steele M, Morison J H, Untersteiner N. The partition of air-ice-ocean momentum exchange as a function of ice concentration, floe size, and draft[J]. Journal of Geophysical Research: Oceans, 1989, 94(C9): 12739−12750. doi: 10.1029/JC094iC09p12739 [11] Zu Yongheng, Lu Peng, Yu Miao, et al. Laboratory experimental study of water drag force exerted on ridge keel[J]. Advances in Polar Science, 2020, 31(1): 41−47. [12] 沈国光, 项伟征. 海洋内波的相似性分析[J]. 天津大学学报, 2002, 35(6): 691−695.Shen Guoguang, Xiang Weizheng. Similarity analyses of ocean internal wave research[J]. Journal of Tianjin University, 2002, 35(6): 691−695. [13] Waters J K, Bruno M S. Internal wave generation by ice floes moving in stratified water: Results from a laboratory study[J]. Journal of Geophysical Research Oceans, 1995, 100(C7): 13635−13639. doi: 10.1029/95JC01220 [14] Pite H D, Topham D R, Van Hardenberg B J. Laboratory measurements of the drag force on a family of two-dimensional ice keel models in a two-layer flow[J]. Journal of Physical Oceanography, 1995, 25(12): 3008−3031. doi: 10.1175/1520-0485(1995)025<3008:LMOTDF>2.0.CO;2 [15] Zu Yongheng, Lu Peng, Leppäranta M, et al. On the form drag coefficient under ridged ice: Laboratory experiments and numerical simulations from ideal scaling to deep water[J]. Journal of Geophysical Research: Oceans, 2021, 126(8): e2020JC016976. [16] Lu Peng, Li Zhijun, Han Hongwei. Introduction of parameterized sea ice drag coefficients into ice free-drift modeling[J]. Acta Oceanologica Sinica, 2016, 35(1): 53−59. doi: 10.1007/s13131-016-0796-y [17] Hoerner S F. Fluid-dynamic drag[M] Theoretical, Experimental and Statistical Information. Vancouver: SF Hoerner Fluid Dynamics, 1958. [18] 黄明海, 齐鄂荣, 李炜. PIV在二维后向台阶流实验研究中的应用[J]. 武汉大学学报(工学版), 2005, 38(2): 35−38.Huang Minghai, Qi Erong, Li Wei. Study on 2D flow over a backward facing step flow with particle image velocimetry[J]. Journal of Wuhan University, 2005, 38(2): 35−38. [19] 张俊, 张晓婷. 流体传输中流体阻力和水头损失的计算[J]. 流体传动与控制, 2011(4): 24−27. doi: 10.3969/j.issn.1672-8904.2011.04.006Zhang Jun, Zhang Xiaoting. The analysis of the fluid resistance and the pressure loss in fluid transmission system[J]. Fluicl Power Transmission and Control, 2011(4): 24−27. doi: 10.3969/j.issn.1672-8904.2011.04.006 -
计量
- 文章访问数: 340
- HTML全文浏览量: 153
- PDF下载量: 32
- 被引次数: 0
