渗透海床上矩形Bragg防波堤对波浪反射的研究

倪云林; 龚倩; 沈梦佳

doi:10.12284/hyxb2022103

渗透海床上矩形Bragg防波堤对波浪反射的研究

doi: 10.12284/hyxb2022103

浙江海洋大学海洋工程装备学院，浙江舟山 316022

基金项目: 国家自然科学基金（51879237，11572092）

详细信息

作者简介:
倪云林（1986—），男，浙江省舟山市人，博士，讲师，主要从事波浪对海上建筑物作用的研究。E-mail: nylzjou@126.com

中图分类号: P731.22
计量
- 文章访问数: 424
- HTML全文浏览量: 183
- PDF下载量: 42
- 被引次数: 0
出版历程
- 收稿日期: 2021-10-18
- 修回日期: 2022-03-03
- 网络出版日期: 2022-04-15
- 刊出日期: 2022-08-29

Study of wave reflection by the Bragg breakwater with rectangular bars on the permeable seabed

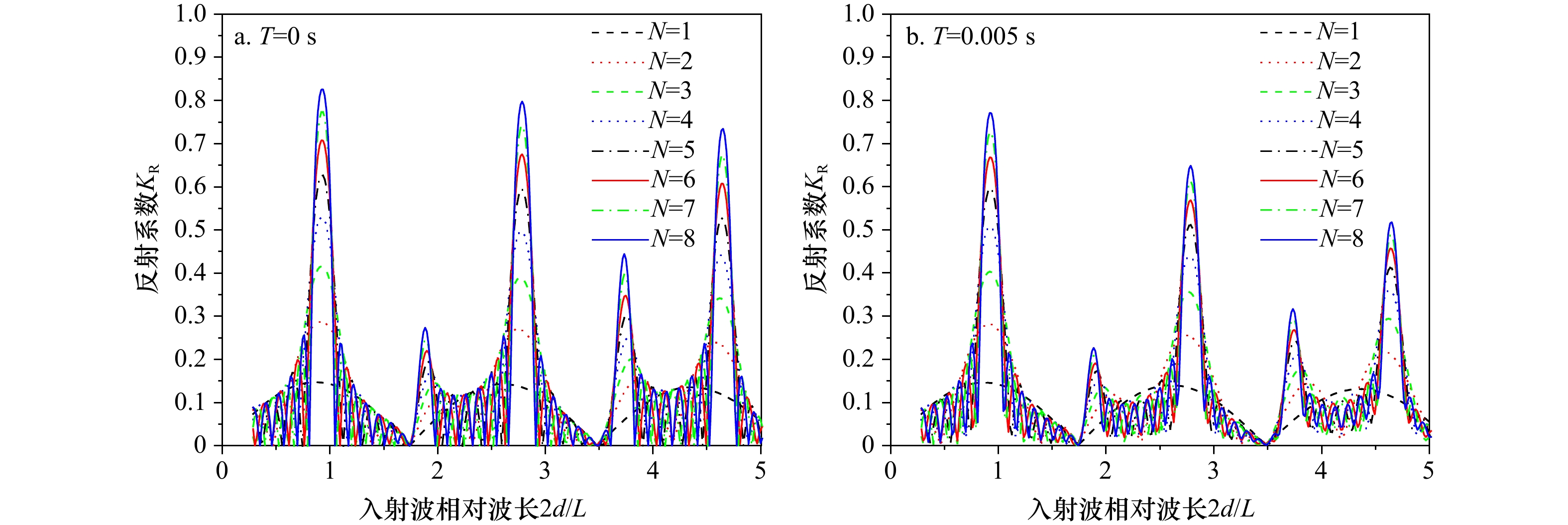
College of Marine Engineering Equipment, Zhejiang Ocean University, Zhoushan 316022, China

摘要

摘要: 与海床不可渗透的情况相比，波浪在可渗透海床上传播时会发生波能衰减。本文将基于可渗透海床上一维修正型缓坡方程，建立方程求解的有限差分模型。将通过与不可渗透海床上矩形Bragg防波堤对波浪反射系数解析解的对比，验证有限差分模型的正确性和适用性。将进一步研究海床可渗透情况下，海床的渗透性参数、坝体的相对宽度、数量、浸没度对波浪反射系数的影响及其与海床不可渗透情况下的差异。本文研究发现，Bragg共振发生时的反射系数随坝体数量的增多而增大，随海床渗透性参数和坝体浸没度的增大而减小，并且存在一个坝体相对宽度值会使Bragg共振反射达到最大。相较于海床不可渗透的情况，发生Bragg共振反射的波浪频率几乎相同，但反射系数减小，而且零反射（或全透射）现象不再存在。
- 渗透海床 /
- 矩形Bragg防波堤 /
- Bragg共振反射 /
- 修正型缓坡方程 /
- 有限差分法
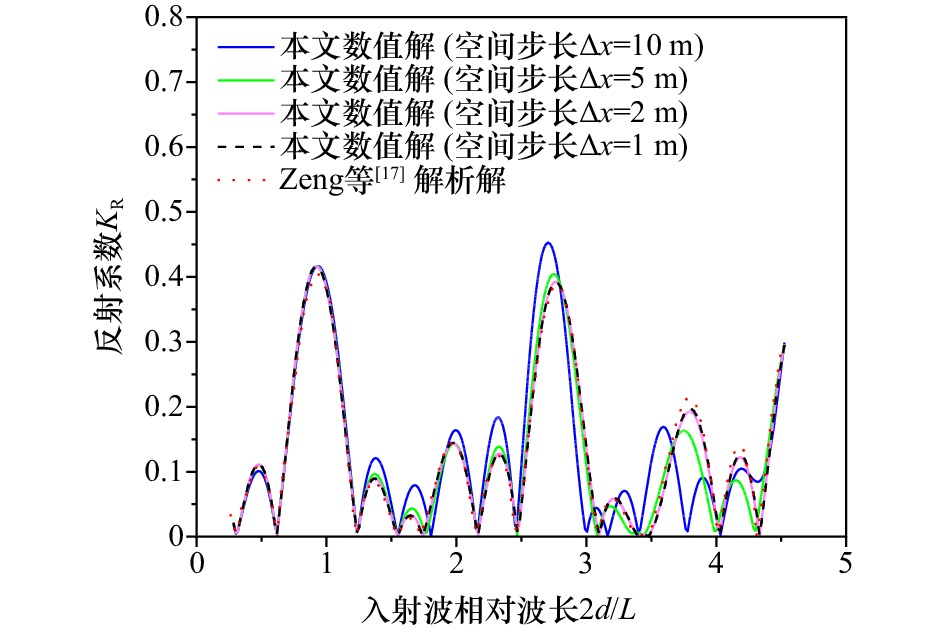
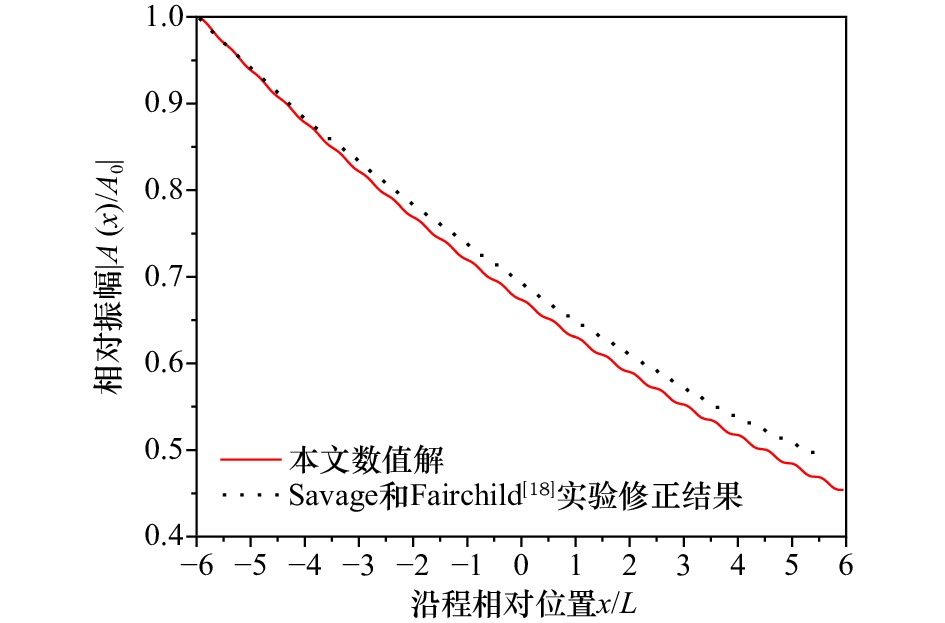
Abstract: Wave energy attenuation will occur when waves propagating over the permeable seabed, compared with the impermeable seabed. Base on the 1D modified mild slope equation for waves propagating on the permeable seabed, the finite difference model will be set up. The accuracy and applicability of the model will be verified with analytical solution for wave reflection by the rectangular Bragg breakwaters on the impermeable seabed. Furthermore, in case of a permeable seabed, the effects of the sea permeability, the bar width, the bar number and the submergence of the bars on wave reflection coefficient, as well as the difference with the case of an impermeable seabed, will be studied in details. The results show the reflection coefficient of the Bragg resonant reflection increases with the increase in the bar number, and decreases with the increase in the sea permeability and the submergence of the bars. Moreover, there exists a particular value of the bar width that maximizes the Bragg resonant reflection. Compared with the impermeable seabed, the incident wave frequency almost keep the same when Bragg resonance reflection happens, but the reflection coefficient is smaller and zero reflection or full transmission will not exit.
- permeable seabed /
- rectangular Bragg breakwater /
- Bragg resonant reflection /
- modified mild slope equation /
- finite difference method

HTML全文

图 1 渗透海床上多孔矩形Bragg防波堤平面示意图

Fig. 1 Bragg breakwaters with porous rectangular bars on a permeable seabed

下载: 全尺寸图片幻灯片

图 2 不可渗透海上矩形Bragg防波堤对波浪反射本文数值解与Zeng等^[17]解析解的比较

Fig. 2 The comparison of the present numerical solutions with Zeng et al’s^[17] analytical solutions for the wave reflection by the Bragg breakwater with rectangular bars on the impermeable seabed

下载: 全尺寸图片幻灯片

图 3 波浪在可渗透水平海床上传播相对振幅沿程变化本文数值解与Savage和Fairchild^[18]实验修正结果的比较

Fig. 3 The comparison of the present numerical solutions with Savage and Fairchild’s^[18] modified experimental results for the dimensionless wave amplitudes of waves propagation on the horizontal permeable seabed

下载: 全尺寸图片幻灯片

图 4 海床渗透性参数T对Bragg共振反射的影响

Fig. 4 Influence of the seabed permeability parameter T on Bragg resonance reflection

下载: 全尺寸图片幻灯片

图 5 坝体相对宽度w/d对Bragg共振反射的影响

Fig. 5 Influence of the bar width w/d on the Bragg resonance reflection

下载: 全尺寸图片幻灯片

图 6 坝体数量N对Bragg共振反射的影响

Fig. 6 Influence of the bar number N on the Bragg resonance reflection

下载: 全尺寸图片幻灯片

图 7 坝体浸没度S对Bragg共振反射的影响

Fig. 7 Influence of bar submergence S on Bragg resonance reflection

下载: 全尺寸图片幻灯片

表 1 不同多孔介质的渗透性参数T取值

Tab. 1 Values of the permeability parameter T for different porous media

研究人员	多孔介质	渗透性参数（T）/s
Mizutani和Mostafa^[19]	防波堤	0.018 0
Mizutani和Mostafa^[19]	粗砂	0.002 2
周李杰^[20]	防波堤	0.001 0
任玉斌等^[21]	钙质砂	0.001 2

下载: 导出CSV

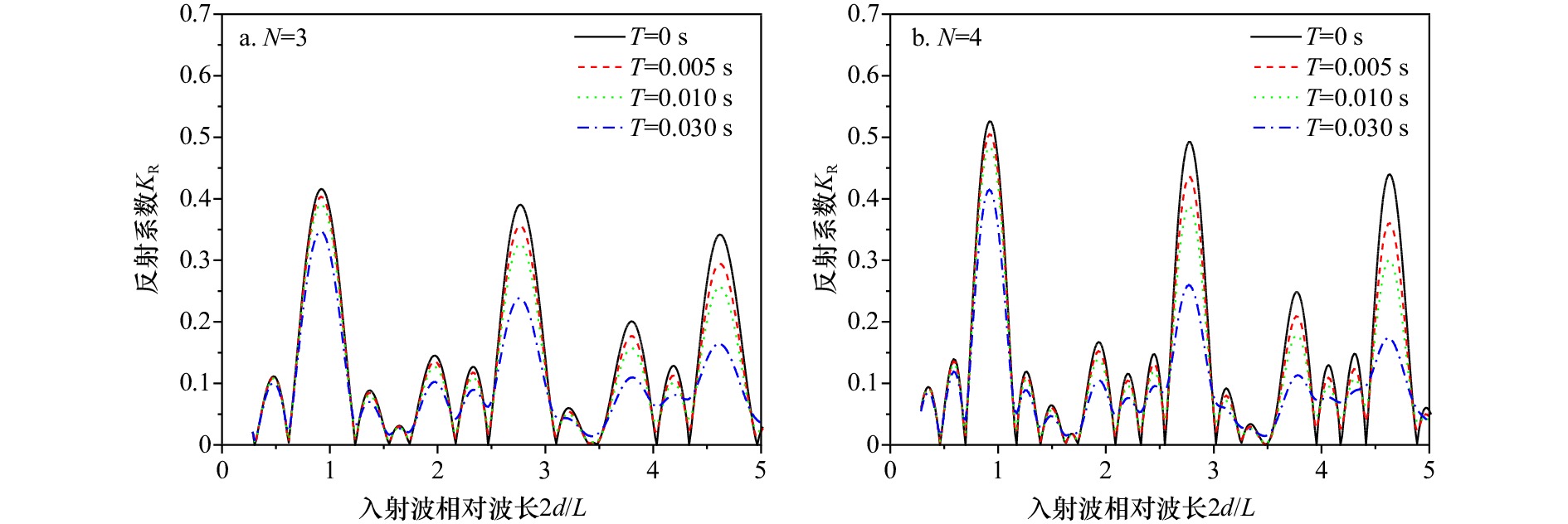
表 2 海床不同渗透性参数下Bragg共振反射的特征值

Tab. 2 Eigenvalues of Bragg resonance reflection under different permeability of seabed

坝体数量（N）	渗透性参数（T）/s	入射波相对波长（2d/L）	反射系数（K_R）
3	0	0.919	0.416
	0.005	0.919	0.403
	0.010	0.919	0.391
	0.030	0.919	0.347
4	0	0.919	0.526
	0.005	0.919	0.504
	0.010	0.919	0.484
	0.030	0.919	0.415

下载: 导出CSV

表 3 不同坝体浸没度情况下Bragg共振反射的特征值

Tab. 3 Characteristic values of Bragg resonance reflection under different bar submergence

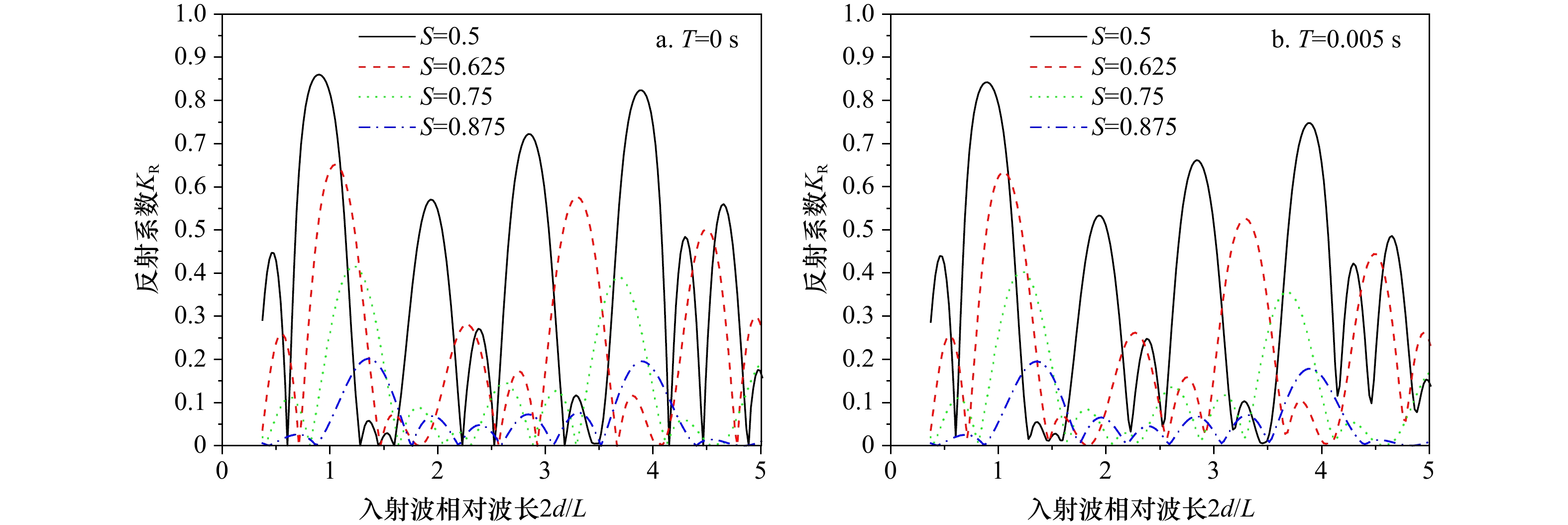
渗透性参数（T）/s	坝体浸没度（S）	入射波相对波长（2d/L）	反射系数（K_R）
0	0.5	0.909	0.860
	0.625	1.056	0.651
	0.75	1.225	0.416
	0.875	1.373	0.201
0.005	0.5	0.909	0.842
	0.625	1.056	0.634
	0.75	1.225	0.403
	0.875	1.373	0.195

下载: 导出CSV

参考文献(26)

[1]	Bragg W H, Bragg W L. The reflection of X-rays by crystals[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1913, 88(605): 428−438.
[2]	Davies A G. The reflection of wave energy by undulations on the seabed[J]. Dynamics of Atmospheres and Oceans, 1982, 6(4): 207−232. doi: 10.1016/0377-0265(82)90029-X
[3]	Mei C C, Hara T, Naciri M. Note on Bragg scattering of water waves by parallel bars on the seabed[J]. Journal of Fluid Mechanics, 1988, 186: 147−162. doi: 10.1017/S0022112088000084
[4]	Hsu T W, Chang H K, Tsai L H. Bragg reflection of waves by different shapes of artificial bars[J]. China Ocean Engineering, 2002, 16(3): 343−358.
[5]	蔡立宏. 波浪通过系列潜堤之布拉格反射研究[D]. 台南: 台湾成功大学, 2003. Cai Lihong. Study on Bragg reflection of waves passing through a series of submerged breakwaters[D]. Tainan: Cheng Kung University, 2003.
[6]	Wen C C, Tsai L H. Numerical simulation of Bragg reflection based on linear waves propagation over a series of rectangular seabed[J]. China Ocean Engineering, 2008, 22(1): 71−86.
[7]	江鸣. 波浪通过系列矩形潜堤的数值模拟[D]. 天津: 天津大学, 2012. Jiang Ming. Numerical simulation of wave propagation over a series of submerged rectangular dikes[D]. Tianjin: Tianjin University, 2012.
[8]	Liu Huanwen, Shi Yunping, Cao Dunqian. Optimization of parabolic bars for maximum Bragg resonant reflection of long waves[J]. Journal of Hydrodynamics, 2015, 27(3): 373−382. doi: 10.1016/S1001-6058(15)60495-4
[9]	Liu Huanwen, Zeng Huidan, Huang Huidong. Bragg resonant reflection of surface waves from deep water to shallow water by a finite array of trapezoidal bars[J]. Applied Ocean Research, 2020, 94: 101976. doi: 10.1016/j.apor.2019.101976
[10]	Liu Huanwen, Luo Heng, Zeng Huidan. Optimal collocation of three kinds of Bragg breakwaters for Bragg resonant reflection by long waves[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2015, 141(3): 04014039. doi: 10.1061/(ASCE)WW.1943-5460.0000278
[11]	曾慧丹. 全波谱条件下三类布拉格防波堤的最优配置[D]. 南宁: 广西民族大学, 2014. Zeng Huidan. Optimal collocation of Bragg breakwaters for Bragg resonance by water waves in the whole wave range[D]. Nanning: Guangxi University for Nationalities, 2014.
[12]	曾慧丹, 刘焕文, 唐国吉. 矩形Bragg防波堤引起线性长波共振反射的最优配置[C]//第十六届中国海洋(岸)工程学术讨论会论文集 . 北京: 海洋出版社, 2013: 663-672. Zeng Huidan, Liu Huanwen, Tang Guoji. Optimal configuration of linear long waves resonance reflection induced by rectangular Bragg breakwater[C]//Proceedings of the Sixteenth Chinese Symposium on Marine (Coastal) Engineering (Volume I). Beijing: China Ocean Press, 2013: 663−672.
[13]	Dean R G, Dalrymple R A. Water Wave Mechanics for Engineers and Scientists[M]. Singapore: World Scientific, 1984: 353.
[14]	Mendez F J, Losada I J. A perturbation method to solve dispersion equations for water waves over dissipative media[J]. Coastal Engineering, 2004, 51(1): 81−89. doi: 10.1016/j.coastaleng.2003.12.007
[15]	Ni Yunlin, Teng Bin. Bragg resonant reflection of water waves by a Bragg breakwater with porous rectangular bars on a sloping permeable seabed[J]. Ocean Engineering, 2021, 235: 109333. doi: 10.1016/j.oceaneng.2021.109333
[16]	Ni Yunlin, Teng Bin. Bragg resonant reflection of water waves by a Bragg breakwater with porous trapezoidal bars on a sloping permeable seabed[J]. Applied Ocean Research, 2021, 114: 102770. doi: 10.1016/j.apor.2021.102770
[17]	Zeng Huidan, Qin Bin, Zhang Jinghua. Optimal collocation of Bragg breakwaters with rectangular bars on sloping seabed for Bragg resonant reflection by long waves[J]. Ocean Engineering, 2017, 130: 156−165. doi: 10.1016/j.oceaneng.2016.11.066
[18]	Savage R P, Fairchild J C. Laboratory study of wave energy losses by bottom friction and percolation[J]. Beach Erosion Board, 1953, 31: 1−25.
[19]	Mizutani N, Mostafa A M. Dynamic interaction of nonlinear waves and a seawall over sand seabed[J]. International Journal of Offshore and Polar Engineering, 1998, 8(1): 30−38.
[20]	周李杰. 烟台港抛石防波堤波浪动力响应的数值分析[D]. 武汉: 武汉理工大学, 2018. Zhou Lijie. Numerical analysis of wave-induced dynamics of a rubble mould breakwater at Yantai Port[D]. Wuhan: Wuhan University of Technology, 2018.
[21]	任玉宾, 王胤, 杨庆. 颗粒级配与形状对钙质砂渗透性的影响[J]. 岩土力学, 2018, 39(2): 491−497. Ren Yubin, Wang Yin, Yang Qing. Effects of particle size distribution and shape on permeability of calcareous sand[J]. Rock and Soil Mechanics, 2018, 39(2): 491−497.
[22]	倪云林, 章哲文, 唐志波, 等. 波浪在沙质海床上传播波长变化[J]. 水利水运工程学报, 2017(3): 51−55. Ni Yunlin, Zhang Zhewen, Tang Zhibo, et al. Changes in wavelength of wave propagation over a sandy seabed[J]. Hydro-Science and Engineering, 2017(3): 51−55.
[23]	王忠涛, 栾茂田, 郑东生. 多孔介质海床对波浪传播影响理论分析[J]. 大连理工大学学报, 2009, 49(6): 891−896. doi: 10.7511/dllgxb200906020 Wang Zhongtao, Luan Maotian, Zheng Dongsheng. Dynamic analysis for effects of porous seabed on wave propagation[J]. Journal of Dalian University of Technology, 2009, 49(6): 891−896. doi: 10.7511/dllgxb200906020
[24]	Guazzelli E, Rey V, Belzons M. Higher-order Bragg reflection of gravity surface waves by periodic beds[J]. Journal of Fluid Mechanics, 1992, 245: 301−317. doi: 10.1017/S0022112092000478
[25]	Liu Huanwen, Yang Jing, Lin Pengzhi. An analytic solution to the modified mild-slope equation for wave propagation over one-dimensional piecewise smooth topographies[J]. Wave Motion, 2012, 49(3): 445−460. doi: 10.1016/j.wavemoti.2012.01.002
[26]	Liu Huanwen, Li Xiaofeng, Lin Pengzhi. Analytical study of Bragg resonance by singly periodic sinusoidal ripples based on the modified mild-slope equation[J]. Coastal Engineering, 2019, 150: 121−134. doi: 10.1016/j.coastaleng.2019.04.015