Study on the interaction between solitary waves and the non-submerged marine structures based on the SPH model
-
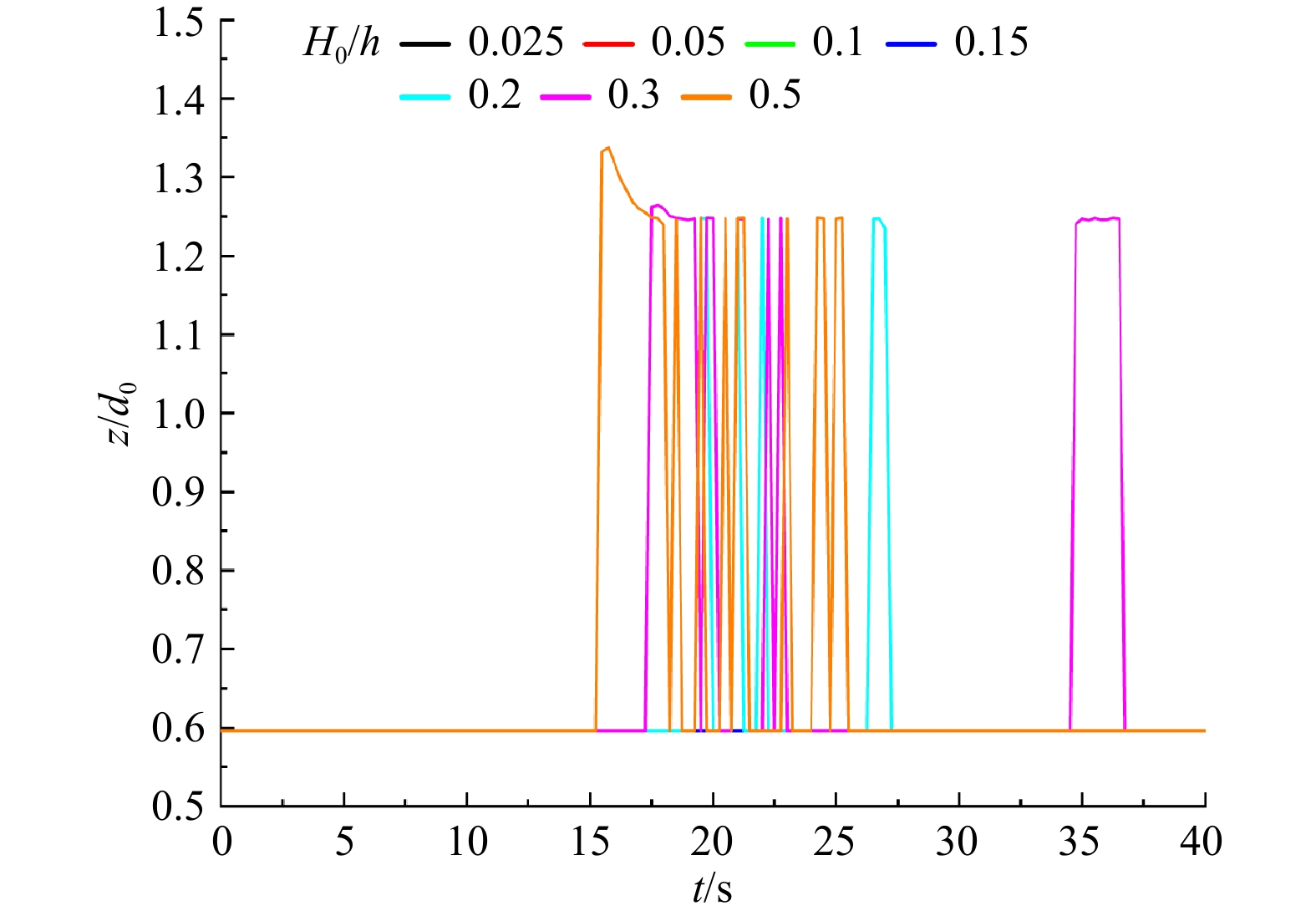
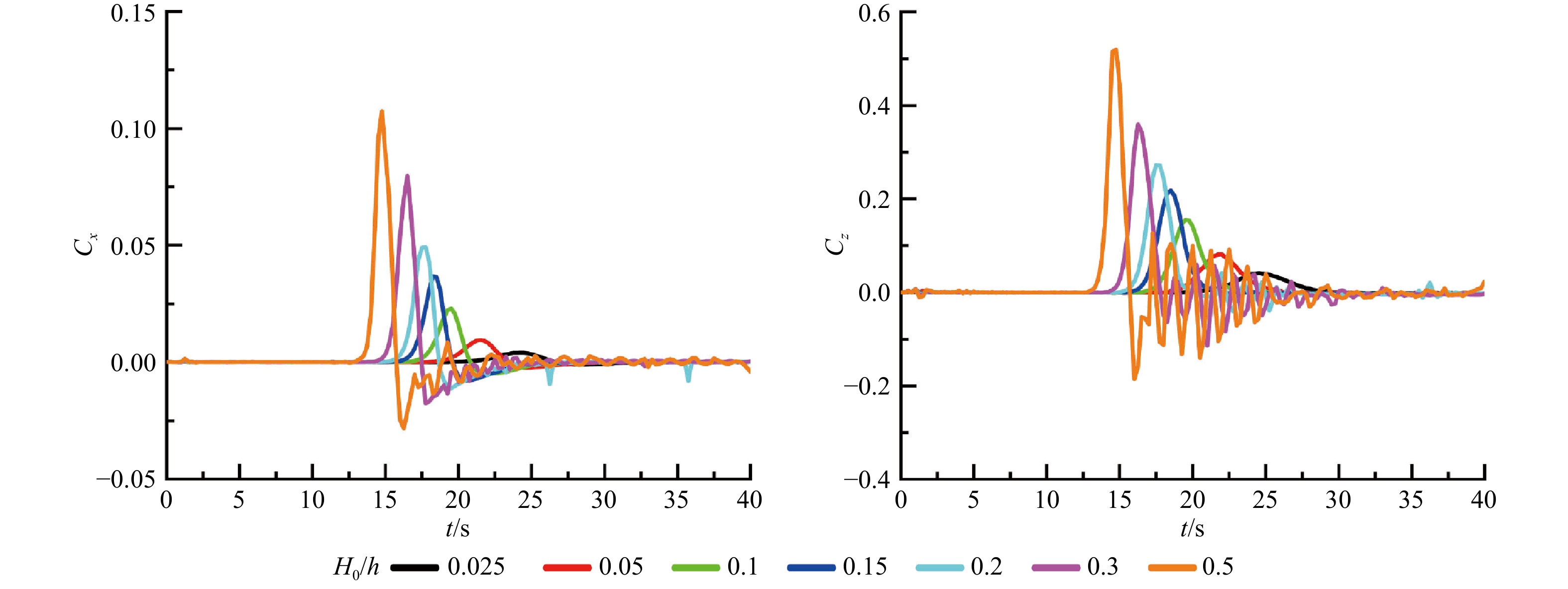
摘要: 为研究孤立波作用下结构物周围流场特征,基于无网格SPH方法,建立孤立波与海洋结构物相互作用模型,对不同波幅孤立波作用下部分淹没矩形结构物周围波面、流速、涡量及结构受力特征进行计算分析,探索了相对波高对非淹没结构物周围流场的影响规律。结果表明:流场特征与相对波高密切相关,相对波高较小时,波面、流速、涡量及结构荷载均较为光滑,相对波高在0.2以上时,波峰爬升至结构物顶部并在越过结构物后与水槽内水体碰撞造成流场波动,波面、流速、涡量及结构荷载的波动幅度随着相对波高增大而增大,流场更加复杂,结构物水平和垂向负压也越大,且结构物周围涡分布逐渐向深度方向和下游方向发展。Abstract: To investigate the characteristics of the flow field around non-submerged structures under solitary waves, a numerical model of the interaction between solitary waves and marine structures is established based on the meshless SPH method. By calculating and analyzing the characteristics of the wave surface, velocity, vorticity, and structure force under different amplitude solitary waves, the influence of relative wave height on the flow field around the non-submerged structure was explored. The results show that the flow field characteristics are closely related to the relative wave height. With a little relative wave height, the wave surface, velocity, vorticity, and structure force are smooth while the flow field fluctuate around the structure due to that the wave crest climbs to the top of the structure and collide with the water in the tank after passing the structure when the relative wave height is large than 0.2. The fluctuation amplitude of wave surface, velocity, vorticity and structure force increased with the increase of relative wave height, resulting in a more complex flow field. Meanwhile, the horizontal and vertical negative force of the structure are larger, the distribution of vorticity around the structure gradually develops to the depth and downstream direction.
-
Key words:
- solitary wave /
- non-submerged /
- SPH /
- numerical calculation
-
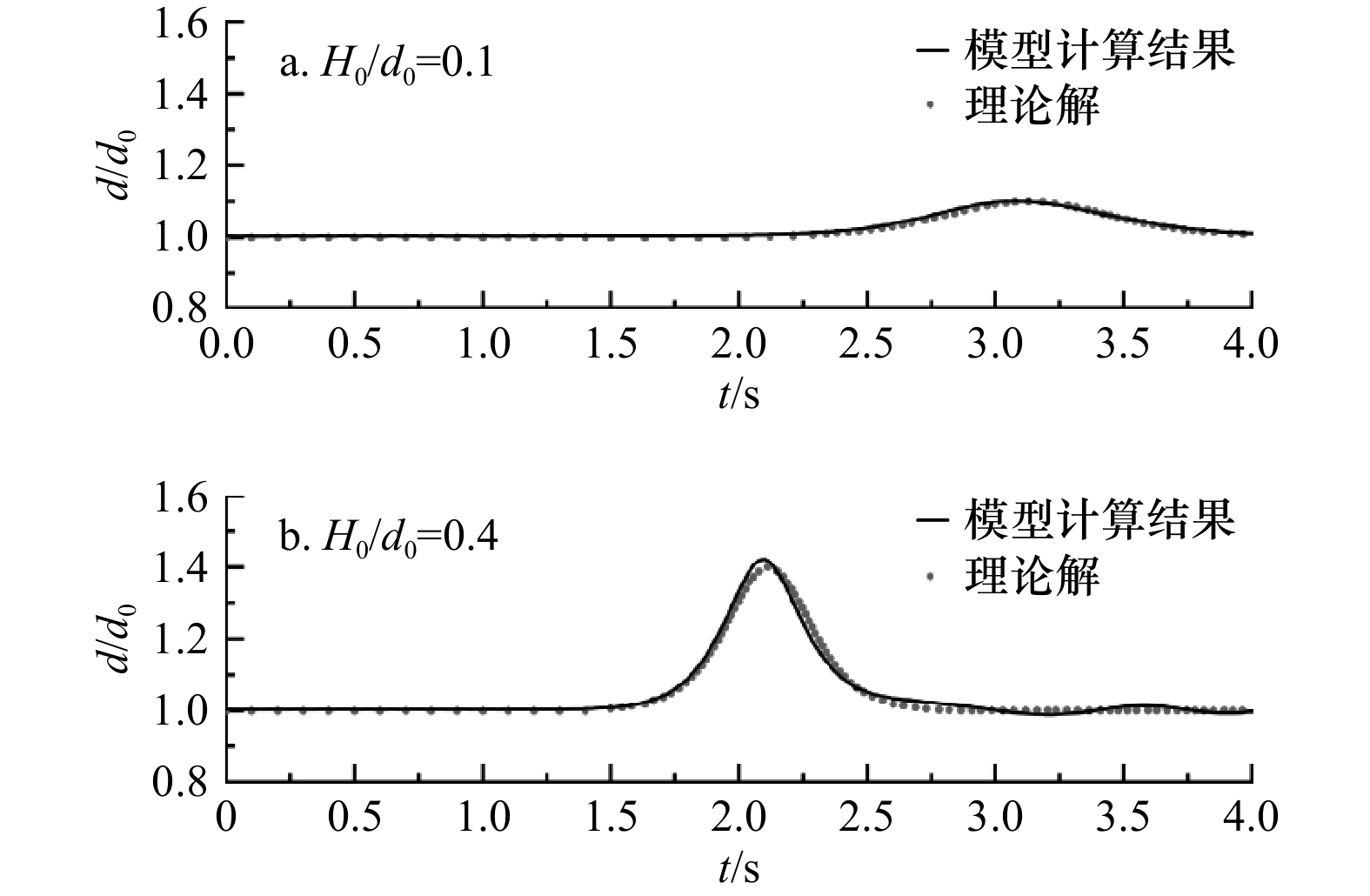
表 1 模型计算结果L2误差
Tab. 1 L2 error of the calculated results
算例 相对波高 0.1 0.4 L2误差 0.005 0.014 -
[1] Liu Xin, Xu Haihua, Shao Songdong, et al. An improved incompressible SPH model for simulation of wave-structure interaction[J]. Computers & Fluids, 2013, 71: 113−123. [2] 毛鸿飞, 李芳成, 吴光林, 等. 基于黏性流理论对平板受波浪冲击的两相流数值研究[J]. 广东海洋大学学报, 2019, 39(4): 73−80. doi: 10.3969/j.issn.1673-9159.2019.04.011Mao Hongfei, Li Fangcheng, Wu Guanglin, et al. Two-phase numerical examination of wave impact on a horizontal deck based on the viscous fluid theory[J]. Journal of Guangdong Ocean University, 2019, 39(4): 73−80. doi: 10.3969/j.issn.1673-9159.2019.04.011 [3] 毛鸿飞, 赫岩莉, 袁剑平, 等. 近水面水平圆柱在波浪作用下的水动力系数[J]. 广东海洋大学学报, 2020, 40(4): 109−115. doi: 10.3969/j.issn.1673-9159.2020.04.015Mao Hongfei, He Yanli, Yuan Jianping, et al. Hydrodynamic coefficients of a horizontal circular cylinder near free surface under wave action[J]. Journal of Guangdong Ocean University, 2020, 40(4): 109−115. doi: 10.3969/j.issn.1673-9159.2020.04.015 [4] 王佳东. 孤立波与板式结构物相互作用的数值模拟[D]. 哈尔滨: 哈尔滨工业大学, 2017.Wang Jiadong. Numerical simulation of interaction between a solitary wave and the plate structure[D]. Harbin: Harbin Institute of Technology, 2017. [5] Tripepi G, Aristodemo F, Meringolo D D, et al. Hydrodynamic forces induced by a solitary wave interacting with a submerged square barrier: Physical tests and δ-LES-SPH simulations[J]. Coastal Engineering, 2020, 158: 103690. doi: 10.1016/j.coastaleng.2020.103690 [6] 沈忠辉, 魏凯, 杨绍林. 孤立波作用下不同长宽比圆端形桥墩受力数值分析[J]. 防灾减灾工程学报, 2020, 40(6): 945−951.Shen Zhonghui, Wei Kai, Yang Shaolin. Numerical analysis of solitary wave loading on round-ended piers with different length-width ratios[J]. Journal of Disaster Prevention and Mitigation Engineering, 2020, 40(6): 945−951. [7] 刚傲, 马玉祥, 牛旭阳, 等. 孤立波与水平板相互作用过程涡演化的研究[G]//第三十届全国水动力学研讨会论文集. 合肥: 中国力学学会, 中国造船工程学会, 2019: 212-219.Gang Ao, Ma Yuxiang, Niu Xuyang, et al. Study on the vortex evolution in the interaction between solitary waves and submerged plates[G]//Proceedings of the 30th National Conference on Hydrodynamics. Hefei: Chinese Society of Theoretical and Applied Mechanics, the Chinese Society of Naval Architects and Marine Engineers, 2019: 212−219. [8] Arabi M G, Sogut D V, Khosronejad A, et al. A numerical and experimental study of local hydrodynamics due to interactions between a solitary wave and an impervious structure[J]. Coastal Engineering, 2019, 147: 43−62. doi: 10.1016/j.coastaleng.2019.02.004 [9] 王千, 刘桦, 房詠柳, 等. 孤立波与淹没平板相互作用的三维波面和水动力实验研究[J]. 力学学报, 2019, 51(6): 1605−1613. doi: 10.6052/0459-1879-19-244Wang Qian, Liu Hua, Fang Yongliu, et al. An experimental study of 3-D wave surface and hydrodynamic loads for interaction between solitary wave and submerged horizontal plate[J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(6): 1605−1613. doi: 10.6052/0459-1879-19-244 [10] 邵奇, 王千, 房詠柳, 等. 孤立波中淹没圆盘的波浪力实验研究[J]. 水动力学研究与进展, 2020, 35A(6): 681−687.Shao Qi, Wang Qian, Fang Yongliu, et al. Experimental study of wave loads on submerged disk in solitary wave[J]. Chinese Journal of Hydrodynamics, 2020, 35A(6): 681−687. [11] 宋帅. 孤立波与浮式结构物相互作用的粘性流数值模拟研究[D]. 上海: 上海交通大学, 2008.Song Shuai. The numerical simulation of interaction of solitary waves with floating structures in a viscous fluid[D]. Shanghai: Shanghai Jiao Tong University, 2008. [12] Mo W H, Liu P L F. Three dimensional numerical simulations for non-breaking solitary wave interacting with a group of slender vertical cylinders[J]. International Journal of Naval Architecture and Ocean Engineering, 2009, 1(1): 20−28. doi: 10.2478/IJNAOE-2013-003 [13] Aghili M, Ghadimi P, Maghrebi Y F, et al. Simulating the interaction of solitary wave and submerged horizontal plate using SPH method[J]. International Journal of Physical Research, 2014, 2(2): 16−26. [14] 高俊亮. 孤立波或波群诱发的港湾振荡研究[D]. 大连: 大连理工大学, 2015.Gao Junliang. Study on harbor resonance induced by solitary waves or wave groups[D]. Dalian: Dalian University of Technology, 2015. [15] Hu Zhengzheng, Greaves D, Raby A. Numerical wave tank study of extreme waves and wave-structure interaction using OpenFoam[J]. Ocean Engineering, 2016, 126: 329−342. doi: 10.1016/j.oceaneng.2016.09.017 [16] Xu Guoji, Chen Qin, Chen Jianhua. Prediction of solitary wave forces on coastal bridge decks using artificial neural networks[J]. Journal of Bridge Engineering, 2018, 23(5): 04018023. doi: 10.1061/(ASCE)BE.1943-5592.0001215 [17] 耿添, 刘桦. 孤立波对浸没平板作用的二维边界元数值分析[J]. 水动力学研究与进展, 2019, 34A(3): 275−282.Geng Tian, Liu Hua. Numerical analysis of hydrodynamic loads on submerged plate in solitary wave with 2-D boundary integral element method[J]. Chinese Journal of Hydrodynamics, 2019, 34A(3): 275−282. [18] 邹丽, 李永刚, 胡英杰, 等. 孤立波直墙反射的数值模拟[C]//第三十一届全国水动力学研讨会论文集. 厦门: 上海《水动力学研究与进展》杂志社, 2020: 2045-2051.Zou Li, Li Yonggang, Hu Yingjie, et al. Numerical simulation of solitary wave reflection at a vertical wall[C]//Proceedings of the 31th National Conference on Hydrodynamics. Xiamen: Chinese Journal of Hydrodynamics, 2020: 2045−2051. [19] 殷铭简, 赵西增, 王红伟. 孤立波与密排桩防波堤相互作用的数值模拟研究[C]//第三十一届全国水动力学研讨会论文集. 厦门: 上海《水动力学研究与进展》杂志社, 2020: 763-768.Yin Mingjian, Zhao Xizeng, Wang Hongwei. Numerical study on interactions between solitary wave and pile breakwater[C]//Proceedings of the 31th National Conference on Hydrodynamics. Xiamen: Chinese Journal of Hydrodynamics, 2020: 763−768. [20] 许彦章, 万德成. 基于MPS-FEM方法数值模拟孤立波与垂直板的相互作用[J]. 水动力学研究与进展, 2020, 35A(3): 346−355.Xu Yanzhang, Wan Decheng. Application of MPS-FEM method to numerical simulate the interaction between solitary wave and a vertical plate[J]. Chinese Journal of Hydrodynamics, 2020, 35A(3): 346−355. [21] Pan K, IJzermans R H A, Jones B D, et al. Application of the SPH method to solitary wave impact on an offshore platform[J]. Computational Particle Mechanics, 2016, 3(2): 155−166. doi: 10.1007/s40571-015-0069-0 [22] 温鸿杰, 张向, 任冰, 等. 随机波在珊瑚礁地形上传播的SPH模拟[J]. 水动力学研究与进展, 2018, 33A(6): 32−39.Wen Hongjie, Zhang Xiang, Ren Bing, et al. Numerical simulation of random wave transformation over fringing reef using SPH method[J]. Chinese Journal of Hydrodynamics, 2018, 33A(6): 32−39. [23] He Ming, Gao Xifeng, Xu Wanhai. Numerical simulation of wave-current interaction using the SPH method[J]. Journal of Hydrodynamics, 2018, 30(3): 535−538. doi: 10.1007/s42241-018-0042-5 [24] 贺铭, 徐万海, 高喜峰, 等. 基于楔体入水的孤立波制造理论及其SPH验证[C]//第十九届中国海洋(岸)工程学术讨论会论文集. 北京: 海洋出版社, 2019: 142-149.He Ming, Xu Wanhai, Gao Xifeng, et al. Solitary wave manufacturing theory based on wedge entering water and its SPH verification[C]//Proceedings of the 19th China Offshore Engineering Symposium. Beijing: China Ocean Press, 2019: 142−149. [25] Dalrymple R A, Rogers B D. Numerical modeling of water waves with the SPH method[J]. Coastal Engineering, 2006, 53(2/3): 141−147. [26] Cunningham L S, Rogers B D, Pringgana G. Tsunami wave and structure interaction: an investigation with smoothed-particle hydrodynamics[J]. Proceedings of the Institution of Civil Engineers-Engineering and Computational Mechanics, 2014, 167(3): 126−138. doi: 10.1680/eacm.13.00028 [27] Crespo A J C, Domínguez J M, Rogers B D, et al. DualSPHysics: open-source parallel CFD solver based on smoothed particle hydrodynamics (SPH)[J]. Computer Physics Communications, 2015, 187: 204−216. doi: 10.1016/j.cpc.2014.10.004 [28] Altomare C, Crespo A J C, Rogers B D, et al. Numerical modelling of armour block sea breakwater with smoothed particle hydrodynamics[J]. Computers & Structures, 2014, 130: 34−45. [29] Saghatchi R, Ghazanfarian J, Gorji-Bandpy M. Numerical simulation of water-entry and sedimentation of an elliptic cylinder using smoothed-particle hydrodynamics method[J]. Journal of Offshore Mechanics and Arctic Engineering, 2014, 136(3): 031801. doi: 10.1115/1.4026844 [30] 陈正云, 朱仁庆, 祁江涛. 基于SPH法的二维液体大幅晃荡数值模拟[J]. 船海工程, 2008, 37(2): 44−47. doi: 10.3963/j.issn.1671-7953.2008.02.013Chen Zhengyun, Zhu Renqing, Qi Jiangtao. Numerical simulation of sloshing in two dimensional liquid tank based on SPH method[J]. Ship & Ocean Engineering, 2008, 37(2): 44−47. doi: 10.3963/j.issn.1671-7953.2008.02.013 [31] Nguyen C T, Nguyen C T, Bui H H, et al. A new SPH-based approach to simulation of granular flows using viscous damping and stress regularisation[J]. Landslides, 2017, 14(1): 69−81. doi: 10.1007/s10346-016-0681-y [32] Canelas R B, Domínguez J M, Crespo A J C, et al. A Smooth Particle Hydrodynamics discretization for the modelling of free surface flows and rigid body dynamics[J]. International Journal for Numerical Methods in Fluids, 2015, 78(9): 581−593. doi: 10.1002/fld.4031 [33] Barreiro A, Crespo A J C, Dominguez J M, et al. Quasi-static mooring solver implemented in SPH[J]. Journal of Ocean Engineering and Marine Energy, 2016, 2(3): 381−396. doi: 10.1007/s40722-016-0061-7 [34] Domínguez J M, Altomare C, Gonzalez-Cao J, et al. Towards a more complete tool for coastal engineering: solitary wave generation, propagation and breaking in an SPH-based model[J]. Coastal Engineering Journal, 2019, 61(1): 15−40. doi: 10.1080/21664250.2018.1560682 [35] Katell G, Eric B. Accuracy of solitary wave generation by a piston wave maker[J]. Journal of Hydraulic Research, 2002, 40(3): 321−331. doi: 10.1080/00221680209499946 [36] Crespo A J C, Gómez-Gesteira M, Dalrymple R A. Boundary conditions generated by dynamic particles in SPH methods[J]. Computers, Materials & Continua, 2007, 5(3): 173−184. [37] Omidvar P, Stansby P K, Rogers B D. Wave body interaction in 2D using smoothed particle hydrodynamics (SPH) with variable particle mass[J]. International Journal for Numerical Methods in Fluids, 2012, 68(6): 686−705. doi: 10.1002/fld.2528 [38] Ma Yuxiang, Yuan Changfu, Ai Congfang, et al. Comparison between a non-hydrostatic model and OpenFOAM for 2D wave-structure interactions[J]. Ocean Engineering, 2019, 183: 419−425. doi: 10.1016/j.oceaneng.2019.05.002 -




 下载:
下载: