HY-1C/D卫星中国海洋水色水温扫描仪几何定位方法

刘建阳; 毛志华; 陶邦一; 马力; 朱乾坤; 黄海清; 刘建强; 丁静

doi:10.12284/hyxb2022029

HY-1C/D卫星中国海洋水色水温扫描仪几何定位方法

doi: 10.12284/hyxb2022029

刘建阳^1,,
毛志华^{1, 2, ,},
陶邦一²,
马力²,
朱乾坤²,
黄海清²,
刘建强³,
丁静³

1.
上海交通大学海洋学院，上海 200240
2.
自然资源部第二海洋研究所卫星海洋环境动力学国家重点实验室，浙江杭州 310012
3.
国家卫星海洋应用中心，北京 100081

基金项目: 国家重点研发计划（2016YFC1400901）；国家自然科学基金（41621064, 41476156）；高分辨率对地观测系统重大专项（05-Y30B01-9001-19/20-2）。

详细信息

作者简介:
刘建阳（1992-），男，江苏省泗阳县人，主要从事卫星预处理的研究。E-mail: samson_liu@sjtu.edu.cn

通讯作者:
毛志华 (1966-），男，研究员，主要从事海洋遥感的研究。E-mail: mao@sio.org.cn

中图分类号: P715.6；P714⁺.1
计量
- 文章访问数: 426
- HTML全文浏览量: 251
- PDF下载量: 34
- 被引次数: 0
出版历程
- 收稿日期: 2021-04-16
- 修回日期: 2021-11-27
- 网络出版日期: 2022-06-15
- 刊出日期: 2022-06-15

Geometric positioning method of HY-1C/D satellite Chinese ocean color and temperature scanner

1.
School of Oceanography, Shanghai Jiaotong University, Shanghai 200240, China
2.
State Key Laboratory of Satellite Marine Environment Dynamics, Second Institute of Oceanography, Ministry of Natural Resources, Hangzhou 310012, China
3.
National Satellite Ocean Application Center, Beijing 100081, China

摘要

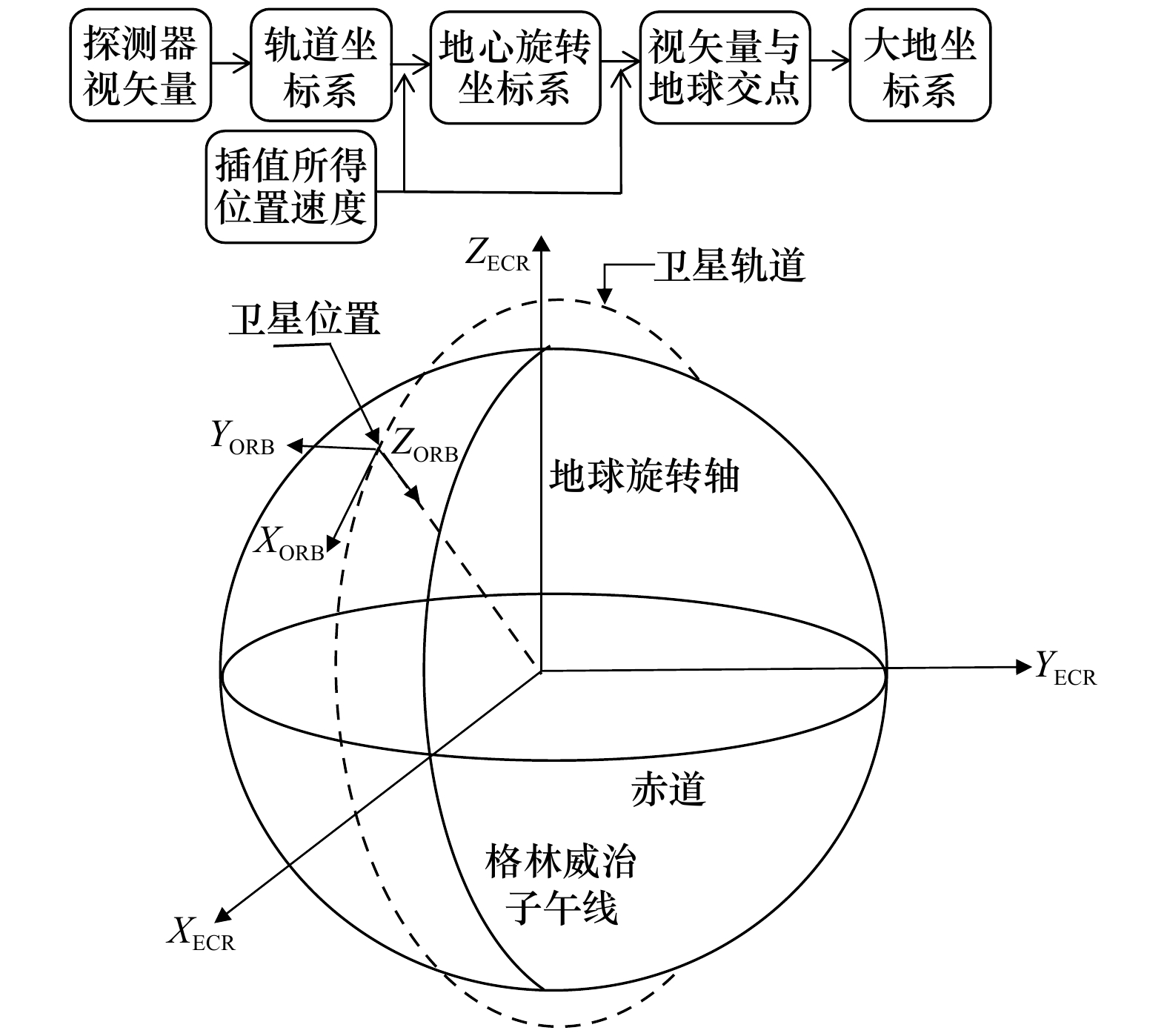
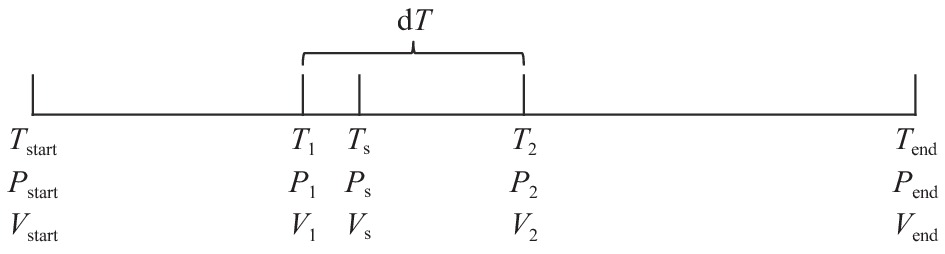
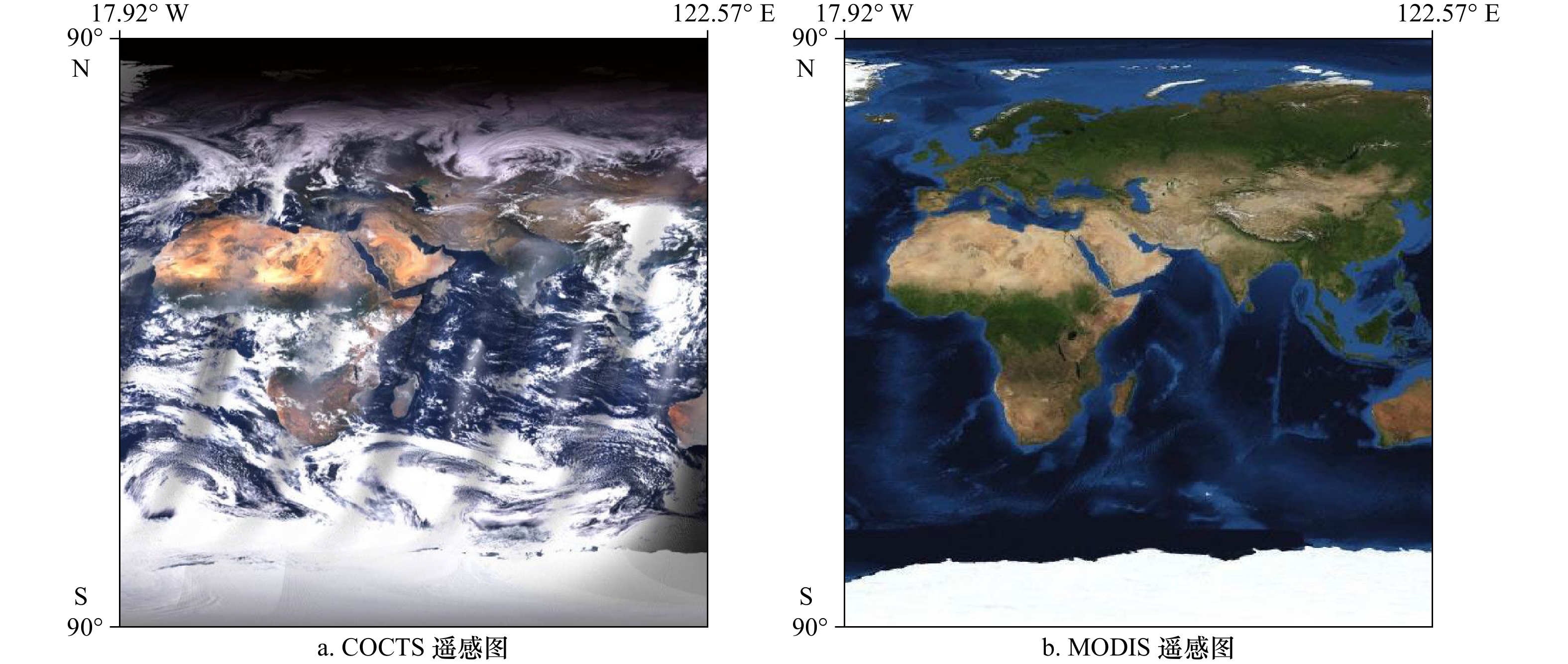
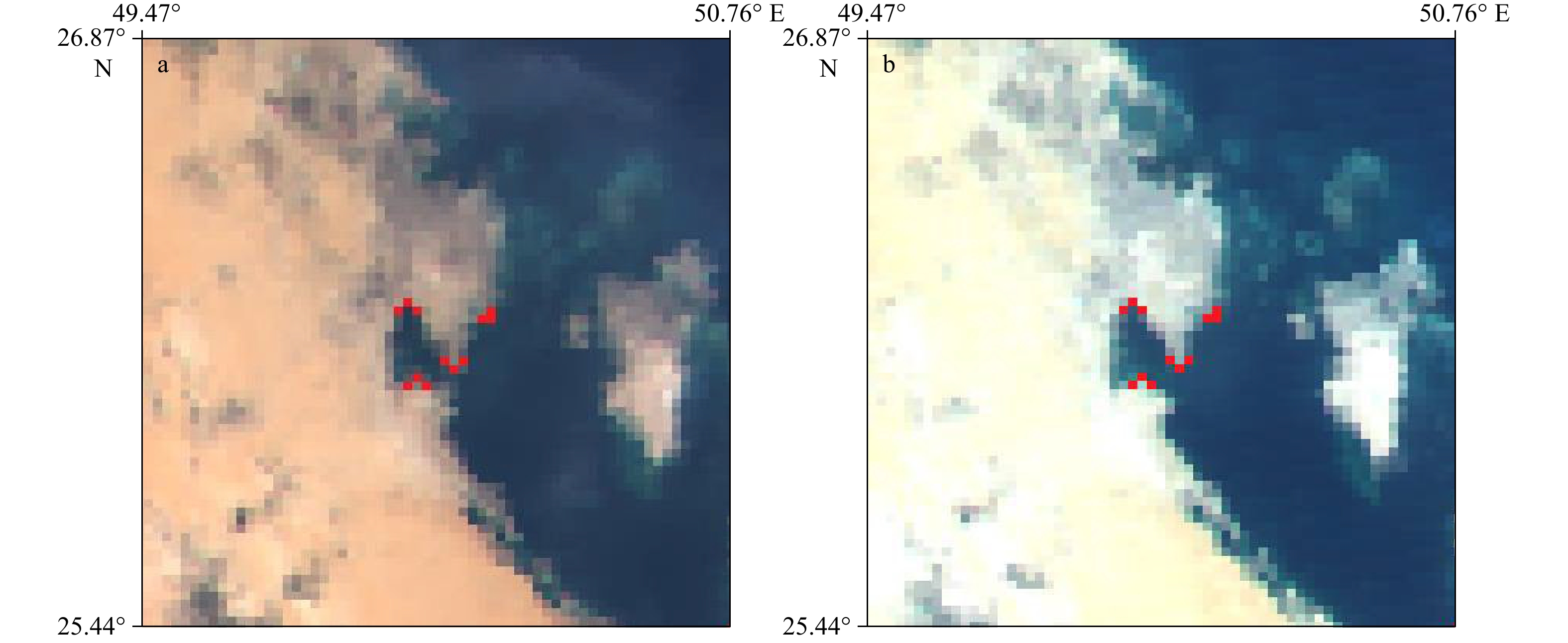
摘要: 海洋一号C/D（HY-1C/D）卫星中国海洋水色水温扫描仪（Chinese Ocean Color and Temperature Scanner，COCTS）主要用于探测海洋水色、水温等要素，这些要素需要经过卫星资料处理才能获取，而几何定位是预处理的核心，直接影响这些要素的质量。COCTS具有114°视场角和四元逐点摆扫的特征，据此研究出一套完整的几何定位方法。从0级数据中提取卫星星历，利用插值法从中获取采样时间对应的卫星位置和速度，进而得到轨道（ORB）坐标系到地心旋转（ECR）坐标系的转换矩阵。基于四元逐点摆扫的特征，中心视矢量分别绕X轴、Y轴旋转相应角度，获得扫描行各采样点ORB视矢量，建立视矢量与地球交叉点关系模型，从而对根据波段数据绘制的遥感图像进行地理定位。本文使用插值法替代了传统需要6个轨道根数来计算卫星位置的复杂方法，同时直接计算ORB到ECR的转换矩阵，而不采用传统的两步转换方法。经过多组数据计算及定性定量验证，HY-1C/D COCTS几何定位结果一致；采样像元尺度效应导致从星下点到两侧边缘、从赤道到两极，误差逐渐增大，约在两个像元内。该方法满足一定的定位精度要求，可以用于COCTS的几何定位。
- HY-1C/D卫星 /
- 中国海洋水色水温扫描仪 /
- 几何定位 /
- 逐点摆扫
Abstract: Chinese Ocean Color Temperature Scanner (COCTS) of Haiyang 1C/D (HY-1C/D) satellite is mainly used to detect ocean water color, water temperature and other elements. These elements can only be achieved by processing satellite data, and geometric positioning is the core of preprocessing, which directly affects quality of these elements. COCTS has the characteristics of 114° field of view and quaternary whisk broom point by point. A set of complete geometric positioning method has been developed based on COCTS characteristics. The satellite position and velocity corresponding to the sampling time are obtained by using the interpolation method in the satellite ephemeris extracted from 0 level data, and then the transformation matrix from orbital coordinate system (ORB) to earth-centered rotating coordinate system (ECR) will be achieved. Based on the quaternary whisk broom point by point, the ORB viewing vector of every sampling point in a sweep can be calculated by rotating center viewing vector around X and Y axis in corresponding angles. The relationship model of viewing vector and the earth intersection point can be established to carry out geolocation of remote sensing images obtained from band data. This article uses interpolation to replace the traditional complex method that requires 6 orbital elements to calculate the satellite position, and directly calculates ORB to ECR transformation matrix rather than the traditional two-step transformation method. After multiple sets of data calculation and qualitative and quantitative verification, the HY-1C/D COCTS geometric positioning results are consistent. As a result of the sampling pixel scale effect, the error increases gradually from Nadir to the edge of two sides and from the equator to two poles, all within the error of 2 pixels. This method meets certain positioning accuracy requirements and can be employed for geometric positioning of COCTS.
- HY-1C/D satellite /
- COCTS /
- geometric positioning /
- whisk broom point by point

HTML全文

图 1 水色仪COCTS周期扫描成像几何关系示意

Fig. 1 Diagram of the geometric relation of COCTS periodic scanning imaging

下载: 全尺寸图片幻灯片

图 2 COCTS几何定位方法流程

Fig. 2 Flow chart of COCTS geometric positioning method

下载: 全尺寸图片幻灯片

图 3 坐标系及几何定位示意

Fig. 3 Coordinate system and geometric positioning diagram

下载: 全尺寸图片幻灯片

图 4 插值法示意

Fig. 4 Diagram of insertion method

下载: 全尺寸图片幻灯片

图 5 水色仪降COCTS轨扫描示意

Fig. 5 Diagram of COCTS downward scanning

下载: 全尺寸图片幻灯片

图 6 欧亚非大陆遥感图

Fig. 6 Remote sensing image of Europe, Asia and Africa

下载: 全尺寸图片幻灯片

图 7 阿拉伯半岛海岸线提取与匹配

a. MODIS遥感图；b. Canny边缘检测；c, d. 人工优化；e. COCTS遥感图；f. 海岸线匹配

Fig. 7 Extraction and match of coastline in the Arabian Peninsula

a. MODIS remote sensing image; b. Canny edge detection; c, d. artificial optimization; e. COCTS remote sensing image; f. coastline match

下载: 全尺寸图片幻灯片

图 8 渤海湾海岸线提取与匹配

a. NDVI处理；b. Canny边缘检测；c. 参数调整；d. 人工优化；e. MODIS遥感图；f. 海岸线匹配

Fig. 8 Extraction and match of coastline in the Bohai Gulf

a. NDVI processing; b. Canny edge detection; c. parameter adjustment; d. artificial optimization; e. MODIS remote sensing image; f. coastline match

下载: 全尺寸图片幻灯片

图 9 阿拉伯半岛遥感图参考海岸线叠加（a），星下点附近中间放大区域（b），星下点两侧边缘放大区域（c）

Fig. 9 Reference coastline overlaying Arabian remote sensing image (a), middle enlargement area near Nadir (b), marginal enlargement area away from Nadir (c)

下载: 全尺寸图片幻灯片

图 10 HY-1C卫星（a）与HY-1D卫星（b）对应特征点采样

Fig. 10 Corresponding feature points sampled from HY-1C satellite (a) and HY-1D satellite (b)

下载: 全尺寸图片幻灯片

图 11 7对样本列距离变化趋势

Fig. 11 Distance change trends of seven pairs of adjacent sample arrays

下载: 全尺寸图片幻灯片

图 12 中间及两侧边缘特征点采样（a）及放大（b）

Fig. 12 Feature points sampled in the middle and marginal sides (a) and enlargement (b)

下载: 全尺寸图片幻灯片

图 13 赤道及两侧特征点采样（a）及放大（b）

Fig. 13 Feature points sampled near the equator and its both sides (a) and enlargement (b)

下载: 全尺寸图片幻灯片

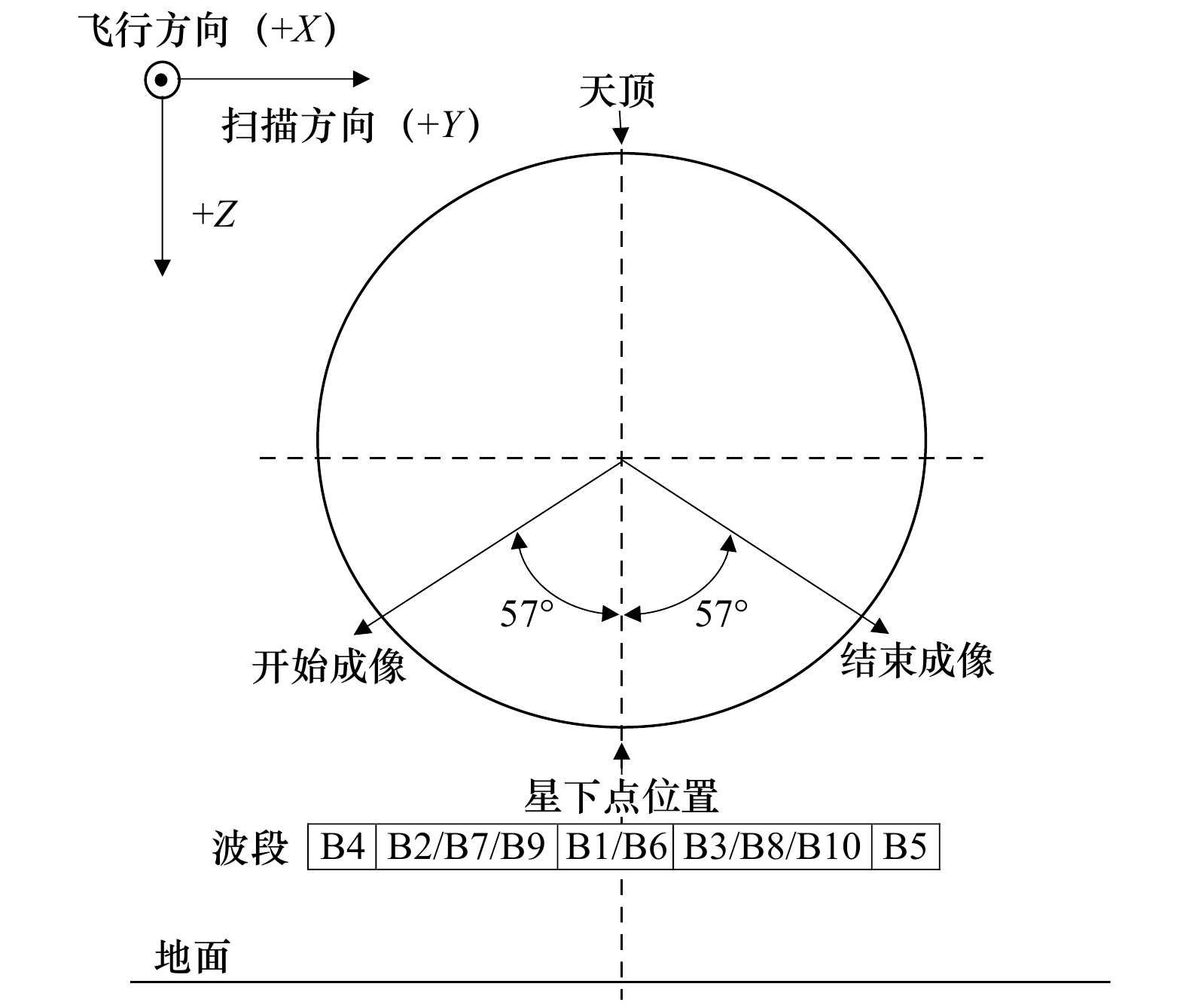
表 1 COCTS地球区图像数据传输格式

Tab. 1 COCTS earth area image data transmission format

第1元第1 采样点	…	第4元第1 采样点	…	第1元第1 664 采样点	…	第4元第1 664 采样点
B1…B10	…	B1…B10	…	B1…B10	…	B1…B10

下载: 导出CSV

表 2 计算值与参考值误差统计

Tab. 2 Error statistics between calculated and reference values

占比误差	范围
占比误差	0°～30°(S/N)	30°～60°(S/N)	60°～90°(S/N)
(−∞，0.001°)	4.17%	2.10%	0%
[0.001°，0.01°)	42.57%	34.37%	28.62%
[0.01°，0.02°)	53.26%	63.53%	71.38%

下载: 导出CSV

表 3 HY-1C/D卫星特征区域采样点比较

Tab. 3 Sampling points comparison of HY-1C/D satellite feature areas

HY-1C卫星		HY-1D卫星		偏差/像元
行号	列号	行号	列号	纬度方向	经度方向
6 389	23 013	6 389	23 013	0	0
6 390	23 014	6 390	23 014	0	0
6 389	23 015	6 389	23 015	0	0
6 384	23 017	6 384	23 017	0	0
6 384	23 018	6 384	23 018	0	0
6 383	23 018	6 383	23 018	0	0
6 392	23 009	6 392	23 009	0	0
6 391	23 010	6 391	23 010	0	0
6 392	23 011	6 392	23 011	0	0
6 383	23 008	6 383	23 008	0	0
6 382	23 009	6 382	23 009	0	0
6 383	23 010	6 383	23 010	0	0
平均偏差/像元				0	0

下载: 导出CSV

表 4 相邻样本列距离（单位：（°））

Tab. 4 Distance of adjacent sample arrays (unit: (°))

区域	样本对
区域	1/2	208/209	416/417	832/833	1247/1248	1454/1455	1663/1664
前1/3区域	0.180 6	0.1095	0.0355	0.0182	0.0206	0.0305	0.0848
中间1/3区域	0.0683	0.0206	0.0124	0.0089	0.0124	0.0205	0.0686
后1/3区域	0.0911	0.0317	0.0213	0.0190	0.0380	0.1319	0.1856
半轨区域	0.1233	0.0669	0.0250	0.0160	0.0259	0.0790	0.1243

下载: 导出CSV

表 5 靠近边缘两侧区域特征点误差

Tab. 5 Errors of feature points on both edge-nearing sides of the track

序号	行号	列号	纬度方向像元误差	经度方向像元误差	序号	行号	列号	纬度方向像元误差	经度方向像元误差
1	6 393	21 569	1	2	21	7 360	23 244	2	2
2	6 548	21 524	1	2	22	7 496	23 049	1	1
3	6 424	21 460	0	1	23	7 861	22 933	2	0
4	6 308	21 404	0	1	24	7 805	23 105	0	1
5	6 189	21 345	2	2	25	7 909	23 117	1	2
6	6 049	21 281	2	1	26	8 028	23 088	2	1
7	6 177	21 449	0	1	27	8 128	23 041	1	1
8	6 116	21 488	1	2	28	8 224	22 985	0	1
9	6 229	21 413	1	2	29	8 316	22 929	1	2
10	6 397	21 673	0	1	30	8 412	22 909	0	3
11	6 325	23 428	1	1	31	8 492	22 833	2	0
12	6 280	23 649	2	0	32	8 704	22 656	1	1
13	6 409	23 736	0	2	33	8 577	22 773	2	2
14	6 453	23 973	1	0	34	7 844	23 120	0	1
15	6 581	23 352	2	1	35	6 304	21 604	0	1
16	6 477	23 529	0	2	36	6 229	21 553	1	1
17	6 425	23 633	0	2	37	6 345	23 488	1	0
18	6 589	23 709	2	1	38	6 437	23 857	1	0
19	7 205	23 632	1	0	39	7 297	23 480	1	2
20	7 297	23 413	1	3	40	7 317	23 365	1	1
					平均误差/像元			0.95	1.25

下载: 导出CSV

表 6 中间区域特征点误差

Tab. 6 Errors of feature points in the middle area of the track

序号	行号	列号	纬度方向像元误差	经度方向像元误差	序号	行号	列号	纬度方向像元误差	经度方向像元误差
1	6293	23353	1	2	21	7648	22328	0	1
2	6212	23184	0	0	22	7721	22360	1	1
3	6109	23088	0	0	23	7732	22433	1	0
4	5985	22976	0	0	24	7696	22521	0	0
5	6117	22832	1	1	25	7897	22708	0	1
6	6292	22965	0	0	26	7909	22596	0	0
7	6477	23057	0	1	27	7953	22473	1	1
8	6489	23164	0	2	28	7881	22360	0	1
9	7676	22240	0	0	29	11408	21552	0	1
10	7601	22180	0	1	30	11552	21289	1	0
11	7553	22137	2	0	31	11849	21241	0	1
12	7460	22008	0	0	32	12049	21064	0	1
13	7000	22052	1	1	33	12232	20881	0	1
14	7124	22121	0	0	34	12351	20713	1	0
15	7244	22221	0	1	35	10757	21749	0	2
16	7445	22276	0	1	36	10385	22064	0	0
17	9001	22288	0	1	37	10117	22052	0	1
18	9129	22181	0	0	38	9836	21932	0	0
19	10605	22012	1	1	39	9312	22013	1	0
20	10953	21528	0	2	40	9553	21896	0	1
					平均误差/像元			0.30	0.65

下载: 导出CSV

表 7 赤道附近特征点误差

Tab. 7 Errors of feature points near the equator

序号	行号	列号	纬度方向像元误差	经度方向像元误差	序号	行号	列号	纬度方向像元误差	经度方向像元误差
1	8832	22472	1	1	11	8968	22317	0	0
2	8844	22453	0	2	12	8984	22304	0	0
3	8856	22440	0	0	13	8996	22293	0	1
4	8872	22421	0	0	14	9008	22281	0	0
5	8892	22397	1	0	15	9017	22272	0	0
6	8904	22384	0	1	16	9032	22257	0	0
7	8917	22365	0	0	17	9048	22241	1	1
8	8929	22353	0	0	18	9065	22228	1	0
9	8944	22340	0	0	19	9080	22217	0	1
10	8957	22325	0	1	20	9093	22204	0	0
					平均误差/像元			0.20	0.40

下载: 导出CSV

表 8 35°N附近特征点误差

Tab. 8 Errors of feature points near 35°N

序号	行号	列号	纬度方向像元误差	经度方向像元误差	序号	行号	列号	纬度方向像元误差	经度方向像元误差
1	5317	23312	0	0	11	5288	23036	0	0
2	5324	23292	0	1	12	5240	22917	1	1
3	5328	23272	0	1	13	5229	22904	1	0
4	5333	23252	2	1	14	5216	22897	0	2
5	5341	23200	1	0	15	5196	22892	0	0
6	5340	23176	0	0	16	5181	22889	1	0
7	5333	23152	1	2	17	5160	22888	0	3
8	5320	23093	1	1	18	5145	22888	2	1
9	5312	23077	1	0	19	5121	22885	0	0
10	5297	23049	0	1	20	5105	22893	0	1
					平均误差/像元			0.55	0.80

下载: 导出CSV

表 9 35°S附近特征点误差

Tab. 9 Errors of feature points near 35°S

序号	行号	列号	纬度方向像元误差	经度方向像元误差	序号	行号	列号	纬度方向像元误差	经度方向像元误差
1	12397	20529	0	2	11	12356	20697	1	1
2	12404	20552	1	0	12	12344	20724	0	3
3	12401	20572	1	2	13	12333	20741	0	0
4	12389	20564	0	0	14	12317	20765	1	0
5	12381	20568	0	1	15	12300	20793	0	1
6	12369	20585	0	0	16	12268	20840	1	1
7	12369	20604	0	0	17	12252	20860	0	0
8	12373	20629	1	0	18	12236	20877	0	1
9	12373	20656	0	1	19	12221	20896	0	0
10	12364	20676	2	0	20	12197	20916	2	1
					平均误差/像元			0.50	0.70

下载: 导出CSV

参考文献(21)

[1]	曾丽萍, 王振松. 一种新的MODIS 0级数据地理定位方法[J]. 现代电子技术, 2008, 31(2): 173−174. doi: 10.3969/j.issn.1004-373X.2008.02.057 Zeng Liping, Wang Zhensong. A new MODIS 0 level earth location algorithm[J]. Modern Electronics Technique, 2008, 31(2): 173−174. doi: 10.3969/j.issn.1004-373X.2008.02.057
[2]	Nishihama M, Wolfe R, Solomon D, et al. MODIS level 1A earth location: algorithm theoretical basis document version 3.0[EB/OL]. (1997−08−26) [2021−04−15]. https://modis.gsfc.nasa.gov/data/atbd/atbd_mod28_v3.pdf.
[3]	孙从容. 中国海洋一号卫星遥感图像GPS地理定位算法研究与实现[J]. 航天器工程, 2003, 12(3): 144−150. Sun Congrong. Research and implementation of GPS geolocation algorithm for China HY-1 satellite remote sensing image[J]. Spacecraft Engineering, 2003, 12(3): 144−150.
[4]	关敏, 杨忠东. FY-3微波成像仪遥感图像地理定位方法研究[J]. 遥感学报, 2009, 13(3): 469−474. doi: 10.11834/jrs.20090310 Guan Min, Yang Zhongdong. Geolocation method for FY-3 MWRI’s remote sensing image[J]. Journal of Remote Sensing, 2009, 13(3): 469−474. doi: 10.11834/jrs.20090310
[5]	Baker N. Joint Polar Satellite System VIIRS Geolocation Algorithm Theoretical Basis Document[R/OL]. (2011−06−31) [2021−04−15]. https://lpdaac.usgs.gov/documents/135/VNP03_ATBD.pdf
[6]	潘德炉, 毛天明, 李淑菁. 海洋卫星资料的地理定位及相关几何参数算法研究[J]. 海洋学报, 1997, 19(5): 56−68. Pan Delu, Mao Tianming, Li Shujing. Research on geolocation of marine satellite data and related geometric parameter algorithms[J]. Haiyang Xuebao, 1997, 19(5): 56−68.
[7]	柴毅. 基于多敏感器的卫星在轨高精度姿态确定技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2018. Chai Yi. Research on high accuracy attitude determination methods for on-orbit satellite based on multiple sensors[D]. Harbin: Harbin Engineering University, 2018.
[8]	边少锋, 纪兵, 李厚朴. 卫星导航系统概论[M]. 2版. 北京: 测绘出版社, 2016. Bian Shaofeng, Ji Bing, Li Houpu. Introduction to Satellite Navigation Systems[M]. 2nd ed. Beijing: Surveging and Mapping Press, 2016.
[9]	关敏, 谷松岩, 杨忠东. 风云三号微波湿度计遥感图像地理定位方法[J]. 遥感技术与应用, 2008, 23(6): 712−716. doi: 10.11873/j.issn.1004-0323.2008.6.712 Guan Min, Gu Songyan, Yang Zhongdong. Geolocation method for FY-3 MWHS’ remote sensing image[J]. Remote Sensing Technology and Application, 2008, 23(6): 712−716. doi: 10.11873/j.issn.1004-0323.2008.6.712
[10]	窦长勇, 岳昔娟. 轨道坐标系到地心固定坐标系的直接转换方法[J]. 航天返回与遥感, 2016, 37(5): 86−94. doi: 10.3969/j.issn.1009-8518.2016.05.010 Dou Changyong, Yue Xijuan. Direct transformation from orbital to earth-centered earth-fixed reference frame[J]. Spacecraft Recovery & Remote Sensing, 2016, 37(5): 86−94. doi: 10.3969/j.issn.1009-8518.2016.05.010
[11]	Noredlinger P D, Klein L. Theoretical basis of the SDP toolkit geolocation package for the ECS project. Landover: Hughes Applied Information Systems[R/OL]. (1995−05−18) [2021−04−15]. https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.131.7265&rep=rep1&type=pdf.
[12]	杨磊, 杨忠东, 张里阳, 等. 极轨气象卫星有效载荷航空校飞数据地理定位[J]. 计算机工程与应用, 2008, 44(30): 202−205. doi: 10.3778/j.issn.1002-8331.2008.30.062 Yang Lei, Yang Zhongdong, Zhang Liyang, et al. Geolocation of airborne data for polar meteorological satellite payloads[J]. Computer Engineering and Applications, 2008, 44(30): 202−205. doi: 10.3778/j.issn.1002-8331.2008.30.062
[13]	熊显名, 尧雪娟, 滕惠忠, 等. 基于遥感图像光谱特征的水陆分界线提取[C]//2007’仪表, 自动化及先进集成技术大会论文集. 重庆: 《仪器仪表学报》杂志社, 2007. Xiong Xianming, Yao Xuejuan, Teng Huizhong, et al. Shoreline extract based on spectral signatures of remote sensing images[C]//2007’ Instrumentation, Automation and Advanced Integration Technology Conference. Chongqing: Chinese Journal of Scientific Instrument, 2007.
[14]	Lykhovyd P V. Forecasting oil crops yields on the regional scale using normalized difference vegetation index[J]. Journal of Ecological Engineering, 2021, 22(3): 53−57. doi: 10.12911/22998993/132436
[15]	李继红, 焦裕欣. 东北地区归一化植被指数与环境因子间的尺度依存关系[J]. 东北林业大学学报, 2021, 49(2): 70−77. Li Jihong, Jiao Yuxin. Dependence between NDVI and environmental factors in northeast China[J]. Journal of Northeast Forestry University, 2021, 49(2): 70−77.
[16]	黄慧, 董林鹭, 何建华, 等. 强噪声下改进Canny算法的边缘检测[J]. 计算机技术与发展, 2021, 31(1): 83−87. doi: 10.3969/j.issn.1673-629X.2021.01.015 Huang Hui, Dong Linlu, He Jianhua, et al. Edge detection of an improved canny algorithm under strong noise[J]. Computer Technology and Development, 2021, 31(1): 83−87. doi: 10.3969/j.issn.1673-629X.2021.01.015
[17]	Loderer M, Beitelschmidt M. Improved edge detection based on fractional derivatives for real-time measurement systems[J]. PAMM, 2019, 19(1): e201900439.
[18]	Howard M, Hock M C, Meehan B T, et al. A locally adapting technique for edge detection using image segmentation[J]. SIAM Journal on Scientific Computing, 2018, 40(4): B1161−B1179. doi: 10.1137/17M1155363
[19]	黄祥李, 张杰, 计科峰, 等. 基于GSHHG数据库与改进CV模型的SAR图像海陆分割算法[C]//第五届高分辨率对地观测学术年会论文集. 西安: 中国科学院高分重大专项管理办公室, 2018. Huang Xiangli, Zhang Jie, Ji Kefeng, et al. Sea-land segmentation algorithm of SAR image based on GSHHG database and improved CV model[C]//The Fifth Annual Conference on High Resolution Earth Observation, Xi’an: High Score Major Project Management Office of Chinese Academy of Sciences, 2018.
[20]	王存良. 对地面某区域某时段连续覆盖的卫星轨道计算[J]. 信息与电子工程, 2012, 10(4): 421−425. doi: 10.3969/j.issn.1672-2892.2012.04.008 Wang Cunliang. Calculation of the satellite orbit covering certain area on the ground in some period of time[J]. Information and Electronic Engineering, 2012, 10(4): 421−425. doi: 10.3969/j.issn.1672-2892.2012.04.008
[21]	李跃跃, 胡彩波, 孙江艳, 等. 基于STK/Matlab的导航星座性能分析[C]//第九届中国卫星导航学术年会论文集——S08 测试评估技术. 哈尔滨: 中科北斗汇(北京)科技有限公司, 2018. Li Yueyue, Hu Caibo, Sun Jiangyan, et al. Performance analysis of navigation constellation based on STK/Matlab[C]//The Ninth China Satellite Navigation Conference. Harbin: Zhongke Beidouhui (Beijing) Technology Co., Ltd, 2018.