Morphodynamic analysis on fringing reef coasts under different damage conditions
-
摘要: 探索珊瑚礁与海滩地貌之间动力地貌联系是认识珊瑚礁海岸变化的重要一环。本文以雷州半岛徐闻西落港珊瑚礁海岸为研究对象，应用RTK-GPS和无人船开展岸滩剖面和近岸水下地形的测量、结合海滩沉积物分析，基于FUNWAVE-TVD数值模型模拟并分析不同珊瑚礁地形地貌条件下波浪动力传播过程。结果显示，研究区珊瑚礁水下地形是影响礁后海滩地貌的主要因素。礁体形态不同，导致其礁后海滩在珊瑚礁地形控制下，短波波能和次重力波波能沿程呈现不同变化规律，最终导致礁后海滩的近岸波能主控频段的差异，在较窄的珊瑚礁海岸，次重力波占比较大。在不同主控频段波浪驱动下，礁后海滩平衡剖面呈现差异性特征，Muñóz-Pérez提出的珊瑚礁后海滩平衡剖面拟合中未考虑该因素的影响，需要在此认识基础上进一步改进。
-
关键词:
- 珊瑚礁海岸 /
- FUNWAVE-TVD /
- 次重力波 /
- 动力地貌 /
- 海滩平衡剖面
Abstract: Morphodynamic relationships between fringing reefs and back-reef beach play key roles in understanding the evolution of coral coasts. The fringing reef coasts of Leizhou Peninsula, in Xiluo Port, Xuwen, are taken as the research object in this paper. RTK-GPS and unmanned-surface-vessel are used to measure and analyze the topography of the beach profile and reef as well as the sediment sampling in beach. FUNWAVE-TVD is used to simulate and analyze the hydrodynamic process of short wave and infragravity wave cross the different reef. The results show that the reef topography in the study area has significant effects on the morphology of back-reef beach. Whether the nearshore wave energy dominated by the short wave band or the infragravity band is controlled by the topography. In the narrow reef, there is a predominance of infragravity energy near the back-reef beach. The dominated wave band in the nearshore wave energy is the main factor shape the back-reef beach equilibrium profile. However, the beach equilibrium profile model of coral coast proposed by Muñóz-Pérez did not take this factor into account, it need to further research.-
Key words:
- fringing reef coasts /
- FUNWAVE-TVD /
- infragravity waves /
- morphodynamic /
- beach equilibrium profile
-
图 1 研究区域
a. 来源于ETOPO1水深数据；b. 来源于谷歌地球；c-e. 来源于野外实测
Fig. 1 Study area
a. Water depth data from ETOPO1; b. from Google Earth; c-e. from field measurements
图 2 珊瑚礁海岸剖面数值模型区域设置示意
Fig. 2 Schematic of cross-shore profiles of reef topography in the numerical experiments
图 3 有效波高（黑线）和次重力波波高（红线）实测值与数值模拟值比较
Fig. 3 Spatial variations of measured and predicted significant wave heights (black line), infragravity wave heights (red line)
图 4 网格尺寸对剖面离岸50 m和100 m处波面变化的影响
Fig. 4 Influence of grid sizes on water surface elevation at 50 m and 100 m distance from shoreline
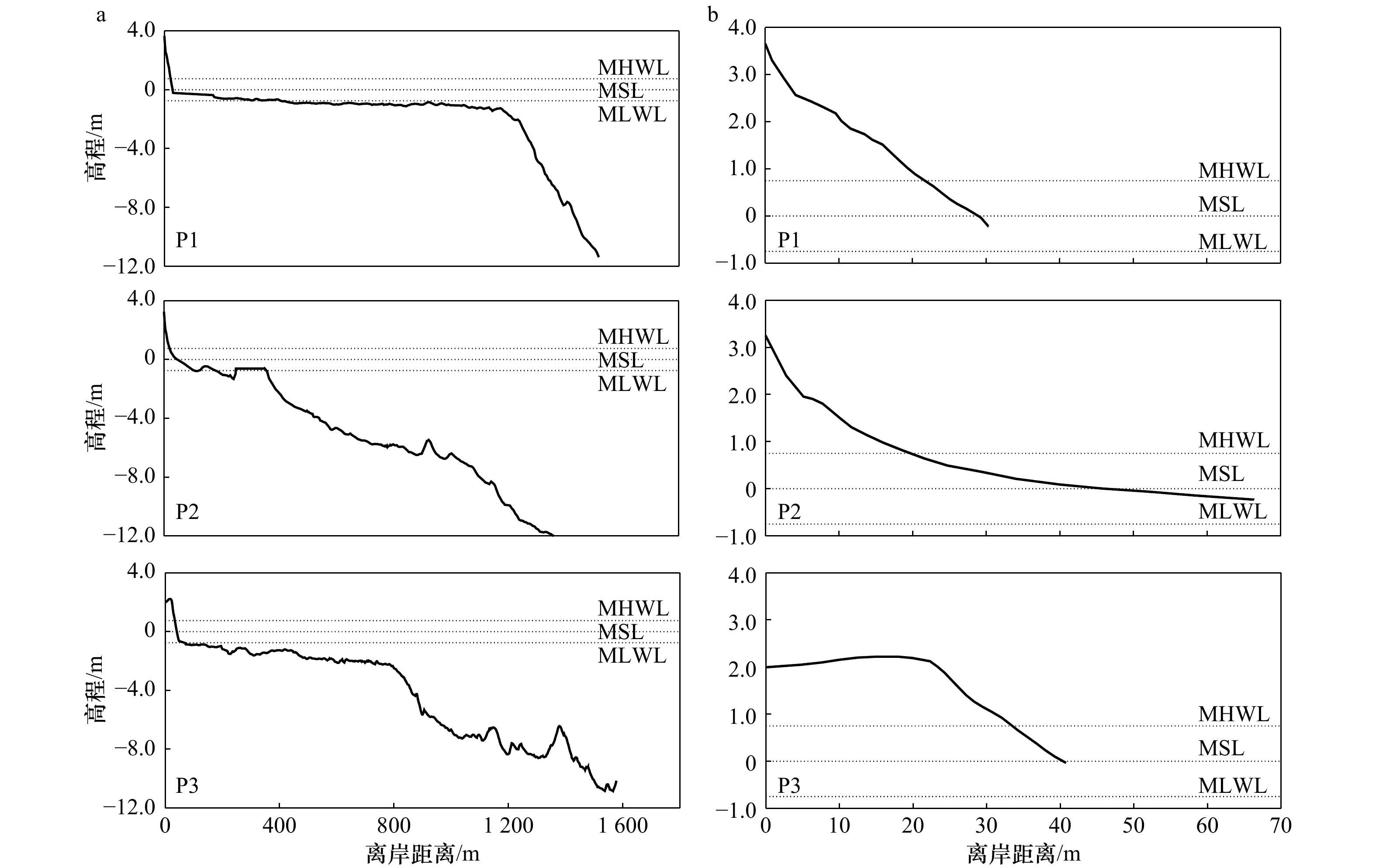
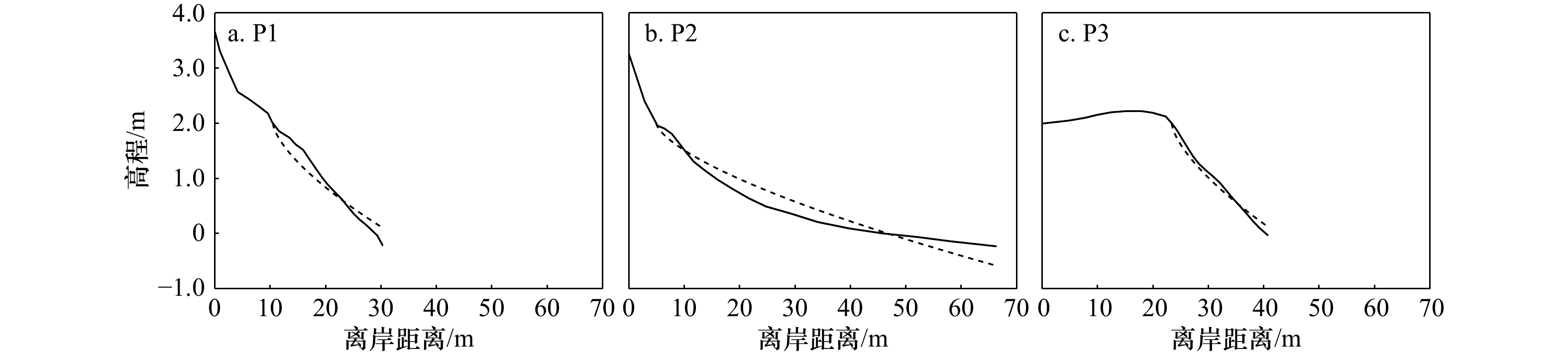
图 5 徐闻西落港珊瑚礁海岸地形
a. 海岸剖面地形；b. 礁后海滩剖面地形；MHWL表示平均高潮线，MSL表示平均海平面，MLWL表示平均低潮线
Fig. 5 Topography of fringing reef in Xiluo Port, Xuwen
a. Cross-shore profiles of reef topography; b. cross-shore profiles of back-reef beach topography; MHWL represent mean high water level, MSL represent mean sea level, and MLWL represent mean low water level
图 6 徐闻西落港海岸P1剖面粒度参数沿程分布
a. 中值粒径沿程分布；b. 分选系数沿程分布
Fig. 6 Cross-shore distribution of surface sediment grain-size parameters in the Xiluo Port, Xuwen
a. Cross-shore distribution of the median size of sediment; b. cross-shore distribution of sorting coefficient
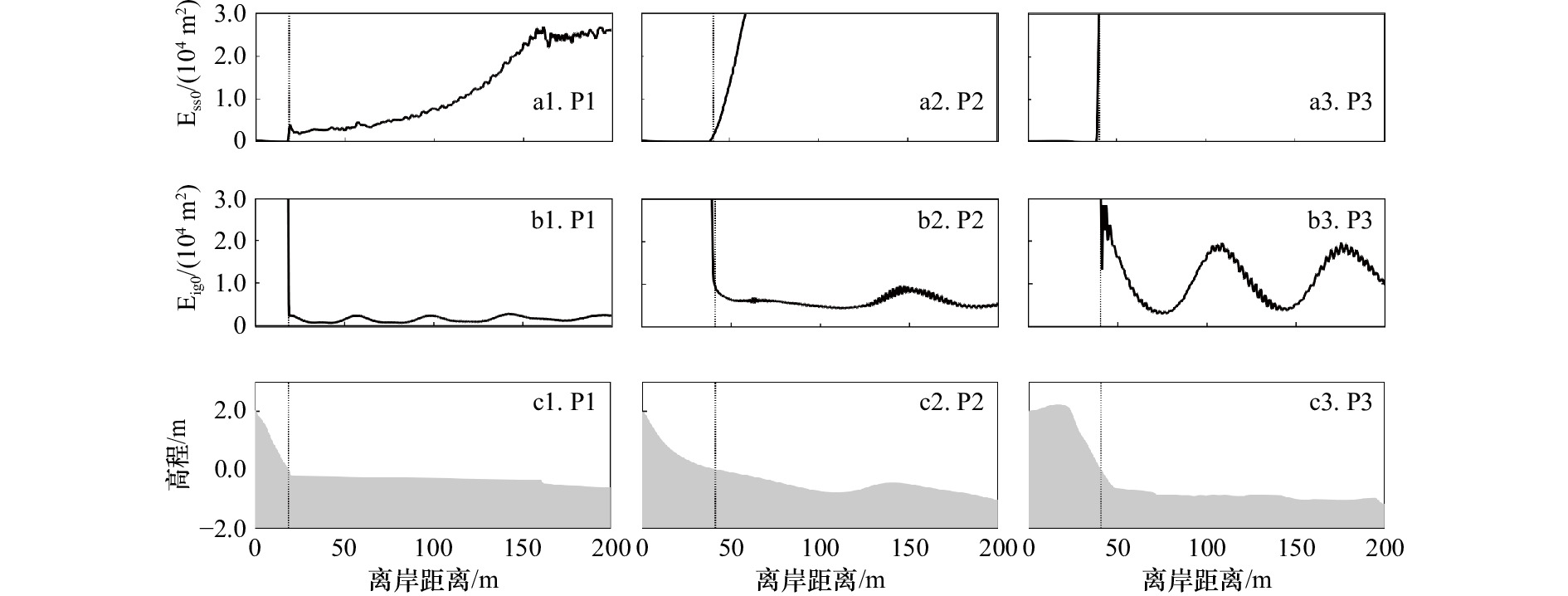
图 7 徐闻西落港珊瑚礁海岸短波波能（Ess0）（a1−a3），次重力波波能（Eig0）（b1−b3）和珊瑚礁海岸地形（c1−c3）沿程分布
范围由岸向海200 m，铅直线为0 m等深线
Fig. 7 Spatial variations of short wave energy (Ess0) (a1−a3), infragravity wave energy (Eig0) (b1−b3) and reef topography (c1−c3) in the Xiluo Port, Xuwen
The range is from 200 m from shore to sea, the vertical line means the 0 m isobaths
图 8 徐闻西落港珊瑚礁海岸剖面处岸滩平衡剖面模拟
实线为原始剖面，虚线为拟合剖面
Fig. 8 Simulation of the beach equilibrium profile in the Xiluo Port, Xuwen
The solid lines mean the original profiles, the dotted lines mean modeled profiles
表 1 徐闻西落港珊瑚礁海岸不同剖面地形参数
Tab. 1 Topographic parameters of fringing reef in the Xiluo Port, Xuwen
剖面编号 礁坪宽度/m 礁缘水深/m 礁后海滩坡度 礁后海滩宽度/m P1 1 146.00 1.27 0.13 30.31 P2 288.59 0.69 0.05 66.35 P3 731.65 2.21 0.12 40.75 
下载: 导出CSV
表 2 徐闻西落港珊瑚礁海岸0 m等深线处波能及波能成分比重
Tab. 2 Wave energy and its’ variation in different wave band along the 0 m isobaths in the Xiluo Port, Xuwen
剖面编号 Ess0/(104 m2) Eig0/(104 m2) [(Ess0−Essλ)/Essλ]/% [(Eig0−Eigλ)/Eigλ]/% (Ess0/E0)/% (Eig0/E0)/% P1 0.41 0.18 –99.59 105.21 69.58 30.42 P2 0.14 0.95 –99.85 3 729.29 13.11 86.89 P3 5.11 3.99 –95.19 9 776.25 56.14 43.86
下载: 导出CSV
表 3 各海滩平衡剖面拟合结果及误差
Tab. 3 Fitting results and errors of each beach equilibrium profile
剖面编号 $ {A}_{rp}/{m}^{1/3} $ $\varepsilon \left({A}_{rp}\right)/\text{%}$ P1 0.26 3.71 P2 0.17 9.56 P3 0.28 1.06
下载: 导出CSV
-
[1] Young I R. Wave transformation over coral reefs[J]. Journal of Geophysical Research: Oceans, 1989, 94(C7): 9779−9789. doi: 10.1029/JC094iC07p09779 [2] Beetham E, Kench P S, O’Callaghan J, et al. Wave transformation and shoreline water level on Funafuti Atoll, Tuvalu[J]. Journal of Geophysical Research: Oceans, 2016, 121(1): 311−326. doi: 10.1002/2015JC011246 [3] Nwogu O, Demirbilek Z. Infragravity wave motions and runup over shallow fringing reefs[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2010, 136(6): 295−305. doi: 10.1061/(ASCE)WW.1943-5460.0000050 [4] Su S F, Ma Gangfeng, Hsu T W. Boussinesq modeling of spatial variability of infragravity waves on fringing reefs[J]. Ocean Engineering, 2015, 101: 78−92. doi: 10.1016/j.oceaneng.2015.04.022 [5] Quataert E, Storlazzi C, Rooijen A V, et al. The influence of coral reefs and climate change on wave-driven flooding of tropical coastlines[J]. Geophysical Research Letters, 2015, 42(15): 6407−6415. doi: 10.1002/2015GL064861 [6] Shimozono T, Tajima Y, Kennedy A B, et al. Combined infragravity wave and sea-swell runup over fringing reefs by super Typhoon Haiyan[J]. Journal of Geophysical Research: Oceans, 2015, 120(6): 4463−4486. doi: 10.1002/2015JC010760 [7] De Alegria-Arzaburu A R, Mariño-Tapia I, Enriquez C, et al. The role of fringing coral reefs on beach morphodynamics[J]. Geomorphology, 2013, 198: 69−83. doi: 10.1016/j.geomorph.2013.05.013 [8] Shi Jian, Zhang Chi, Zheng Jinhai, et al. Modelling wave breaking across coral reefs using a non-hydrostatic model[J]. Journal of Coastal Research, 2018, 85(S1): 501−505. [9] Muñóz-Pérez J J, Tejedor L, Medina R. Equilibrium beach profile model for reef-protected beaches[J]. Journal of Coastal Research, 1999, 15(4): 950−957. [10] Muñóz-Pérez J J, Medina R. Comparison of long-, medium- and short-term variations of beach profiles with and without submerged geological control[J]. Coastal Engineering, 2010, 57(3): 241−251. doi: 10.1016/j.coastaleng.2009.09.011 [11] Taaouati M, Parisi P, Passoni G, et al. Influence of a reef flat on beach profiles along the Atlantic Coast of Morocco[J]. Water, 2020, 12(3): 790. doi: 10.3390/w12030790 [12] Beach R A, Sternberg R W. Suspended-sediment transport in the surf zone: response to breaking waves[J]. Continental Shelf Research, 1996, 16(15): 1989−2003. doi: 10.1016/0278-4343(96)00029-5 [13] Hughes M G, Masselink G, Brander R W. Flow velocity and sediment transport in the swash zone of a steep beach[J]. Marine Geology, 1997, 138(1/2): 91−103. [14] Butt T, Russell P. Suspended sediment transport mechanisms in high-energy swash[J]. Marine Geology, 1999, 161(2/4): 361−375. [15] Ning Yue, Liu Weijie, Sun Zhilin, et al. Parametric study of solitary wave propagation and runup over fringing reefs based on a Boussinesq wave model[J]. Journal of Marine Science and Technology, 2019, 24(2): 512−525. doi: 10.1007/s00773-018-0571-1 [16] 邵超. 海滩−珊瑚礁海岸侵蚀及适应性管理研究[D]. 厦门: 国家海洋局第三海洋研究所, 2016.Shao Chao. Study on coastal erosion of beach-coral system and its adaptive management[D]. Xiamen: Third Institute of Oceanography, State Oceanic Administration, 2016. [17] 王宝灿, 陈沈良, 龚文平, 等. 海南岛港湾海岸的形成与演变[M]. 北京: 海洋出版社, 2006.Wang Baocan, Chen Shenliang, Gong Wenping, et al. Formation and Evolution of Embayment Coast of Hainan Island[M]. Beijing: China Ocean Press, 2006. [18] Folk R L, Ward W C. Brazos River Bar: a study in the significance of grain size parameters[J]. Journal of Sedimentary Petrology, 1957, 27(1): 3−26. doi: 10.1306/74D70646-2B21-11D7-8648000102C1865D [19] Udden J A. Mechanical composition of clastic sediments[J]. GSA Bulletin, 1914, 25(1): 655−744. doi: 10.1130/GSAB-25-655 [20] Shepard F P. Nomenclature based on sand-silt-clay ratios[J]. Journal of Sedimentary Petrology, 1954, 24(3): 151−158. [21] Shi Fengyan, Kirby J T, Harris J C, et al. A high-order adaptive time-stepping TVD solver for Boussinesq modeling of breaking waves and coastal inundation[J]. Ocean Modelling, 2012, 43−44: 36−51. doi: 10.1016/j.ocemod.2011.12.004 [22] 邵超, 戚洪帅, 蔡锋, 等. 海滩−珊瑚礁系统风暴响应特征研究——以1409号台风“威马逊”对清澜港海岸影响为例[J]. 海洋学报, 2016, 38(2): 121−130.Shao Chao, Qi Hongshuai, Cai Feng, et al. Study on storm-effects on beach-coral reef system—Taking the response of Qinglangang Coast on No. 1409 Typhoon Rammasun as an example[J]. Haiyang Xuebao, 2016, 38(2): 121−130. [23] Demirbilek Z, Nwogu O G, Ward D L. Laboratory study of wind effect on Runup over fringing reefs. Report 1. Data report[R]. Vicksburg: Coastal and Hydraulics Laboratory, 2007. [24] Reniers A J H M, MacMahan J H, Thornton E B, et al. Modelling infragravity motions on a rip-channel beach[J]. Coastal Engineering, 2006, 53(2/3): 209−222. [25] da Fontoura Klein A H, de Menezes J T. Beach morphodynamics and profile sequence for a headland bay coast[J]. Journal of Coastal Research, 2001, 17(4): 812−835. [26] Brander R W, Kench P S, Hart D. Spatial and temporal variations in wave characteristics across a reef platform, Warraber Island, Torres Strait, Australia[J]. Marine Geology, 2004, 207(1/4): 169−184. [27] Filipot J F, Cheung K F. Spectral wave modeling in fringing reef environments[J]. Coastal Engineering, 2012, 67: 67−79. doi: 10.1016/j.coastaleng.2012.04.005 [28] Pomeroy A, Lowe R, Symonds G, et al. The dynamics of infragravity wave transformation over a fringing reef[J]. Journal of Geophysical Research: Oceans, 2012, 117(C11): C11022. [29] Van Dongeren A, Lowe R, Pomeroy A, et al. Numerical modeling of low-frequency wave dynamics over a fringing coral reef[J]. Coastal Engineering, 2013, 73: 178−190. doi: 10.1016/j.coastaleng.2012.11.004 [30] Ma Gangfeng, Su S F, Liu Shugang, et al. Numerical simulation of infragravity waves in fringing reefs using a shock-capturing non-hydrostatic model[J]. Ocean Engineering, 2014, 85: 54−64. doi: 10.1016/j.oceaneng.2014.04.030 [31] Buckley M L, Lowe R J, Hansen J E, et al. Mechanisms of wave-driven water level variability on reef-fringed coastlines[J]. Journal of Geophysical Research: Oceans, 2018, 123(5): 3811−3831. doi: 10.1029/2018JC013933 [32] 邹志利. 海岸动力学[M]. 4版. 北京: 人民交通出版社, 2009.Zou Zhili. Coastal Hydrodynamics[M]. 4th ed. Beijing: China Communications Press, 2009. [33] Larson M, Kraus N C. SBEACH: Numerical model to simulate storm-induced beach change[R]. Army Corps of Engineers, Waterway Experiment, Technical Report CERC-89-9, 1989. [34] Bodge K R. Representing equilibrium beach profiles with an exponential expression[J]. Journal of Coastal Research, 1992, 8(1): 47−55. [35] Inman D L, Elwany M H S, Jenkins S A. Shorerise and bar-berm profiles on ocean beaches[J]. Journal of Geophysical Research: Oceans, 1993, 98(C10): 18181−18199. doi: 10.1029/93JC00996 [36] Lee P Z F. The submarine equilibrium profile: a physical model[J]. Journal of Coastal Research, 1994, 10(1): 1−17. [37] Kit E, Pelinovsky E. Dynamical models for cross-shore transport and equilibrium bottom profiles[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1998, 124(3): 138−146. doi: 10.1061/(ASCE)0733-950X(1998)124:3(138) [38] Wang Ping, Davis Jr R A. A beach profile model for a barred coast: case study from sand key, west-central Florida[J]. Journal of Coastal Research, 1998, 14(3): 981−991. [39] Dubois R N. An inverse relationship between the A and m coefficients in the Bruun/Dean equilibrium profile equation[J]. Journal of Coastal Research, 1999, 15(1): 186−197. [40] Nelson R C. Depth limited design wave heights in very flat regions[J]. Coastal Engineering, 1994, 23(1/2): 43−59. -
计量
- 文章访问数: 523
- HTML全文浏览量: 153
- PDF下载量: 69
- 被引次数: 0
