An iterative retrieval algorithm of ocean surface current based on SAR Doppler centroid anomaly
-
摘要: 为了克服SAR多普勒质心频移法反演海面流场时风场贡献去除困难的难题，本文提出了基于M4S模型的弦截下山法，利用其迭代计算局部区域的海面流场；然后估算整幅SAR图像中风场对多普勒速度的风贡献因子
$\gamma $ ；最后去除风场对多普勒速度的贡献。将该算法用于Radarsat-2数据反演海面径向流速，并利用匹配的实测数据验证反演精度。研究结果表明，本文提出的弦截下山法具有良好的收敛性和较高的收敛速度，而且对本文中使用的两景SAR数据，反演的海面径向流速偏差分别为0.04 m/s和0.15 m/s。Abstract: To overcome the difficulty of removing the wind field contribution in the SAR Doppler centroid anomaly method when retrieving the ocean surface current, in this paper, a secant downhill method based on the M4S model is proposed. The contribution of the wind field is removed by iteratively calculating the sea surface current field in a local area and subsequently estimating the wind contribution factor to the Doppler velocity of the whole SAR map. Our method is used to retrieve the radial velocity of sea surface from Radarsat-2 data. Its retrieval accuracy is verified by matching measured data. The results show that the proposed method not only can possess well convergence and high convergent speed, but also the deviation of the radial velocity of the surface is 0.04 m/s and 0.15 m/s respectively for two scene SAR data used in this paper.-
Key words:
- SAR /
- Doppler centroid anomaly /
- ocean surface current /
- secant downhill method
-
1. 引言
海流是海洋重要的运动形式之一，与海上污染物的扩散、海上军事活动、水产养殖和全球气候变化等密切相关[1]，所以研究其特征和变化规律具有重要的科学意义。遥感技术的快速发展使得大范围、高精度的探测海洋信息成为可能[2]。目前，利用遥感技术反演海流的方法主要有光学遥感和微波遥感。光学遥感主要是根据示踪物（叶绿素等）的位移时间关系来反演流速，其易受天气的影响[3-4]；微波遥感不受天气的影响，其海流反演手段主要有：高度计[5]、地波雷达[6-7]、多普勒雷达散射计[8-11]、合成孔径雷达（Synthetic Aperture Radar，SAR）[12-16]等。高度计反演海流覆盖范围广，但其流场产品分辨率较低，不适合小尺度海流的测量[5]；地波雷达虽具有反演分辨率高、全天候等优势[6]，但其主要是岸基测量，覆盖区域有限；多普勒雷达散射计可实现二维测流[8]，但因为其是真实孔径雷达，流场产品分辨率较低；而合成孔径雷达则具有高分辨率、全天候、全天时等优势[12]，使其成为反演海流的新手段。目前，利用SAR技术反演海流主要有两种方法：顺轨干涉（Along-Track Interferometry，ATI）法和多普勒质心频移（Doppler Centroid Anomaly，DCA）法。顺轨干涉法基于两幅沿轨天线分别获得的SAR复图像的相位差反演流场[17]；多普勒质心频移法则根据海表层运动产生的多普勒质心频移与其径向速度的关系反演海表面流速[18-21]。相比DCA方法，ATI技术反演精度、分辨率更高[22]，但其成像条件苛刻，数据不易获取，所以不具有普适性。虽然DCA方法流速产品分辨率较低，但其适用数据丰富且容易获取，如Radarsat-2、Envisat ASAR和Sentinel-1等数据都可用于DCA方法反演海面流场，具有业务化观测全球海洋表面流的潜力。
DCA方法中由多普勒质心频率异常反演的地距多普勒速度不仅与海表面流场有关还与海表面风场有关。2004年Chapron等[21]利用Envisat ASAR数据分析了全球海洋多普勒测量数据，发现多普勒频移与海面风场有很高的相关性；后来Chapron等[23]又利用Envisat ASAR数据基于多普勒质心频率异常提出了一种简单的模型：
${U_{\text{D}}} \approx \gamma {U_{10}} + {U_{\text{C}}}$ （$\gamma $ 为风贡献因子），以表示海面风场和流场对多普勒速度的影响，并发现当入射角为23°且在中风和海态完全发育时，风贡献因子$\gamma = 0.3$ 。国内学者在基于DCA法反演海面流场并去除风场影响方面也做了大量研究。杨小波[24]利用多普勒质心频移法反演海流时，分析了海表面风场对流场反演的影响，发现风对流场的分布和结构有一定的影响，并给出了SAR成像时刻研究区域风场产生多普勒速度的关系式：${U_{{\text{DW}}}} = 0.03{U_{10}}$ ；侯富城等[12]利用多普勒质心频移法提取了内波产生的海表面流，并基于Chapron等[23]提出的模型，指出在中等风速下，风贡献因子$\gamma $ 取值为0.2～0.25。虽然Chapron等[23]提出的模型给出了风场和多普勒速度的关系，可以很好地修正风场产生的反演误差，但只给出了风贡献因子$\gamma $ 在特定雷达频率、入射角下的经验值。风贡献因子$\gamma $ 与雷达频率、入射角以及雷达天线的偏航角等多个参数有关[23]，一般不能由简单的线性关系描述，并且对流场反演结果的精度影响很大，所以需找到正确估算风贡献因子$\gamma $ 的方法，以提高流场反演精度。针对以上反演过程中去除风场影响存在的问题，本文提出了一种基于M4S模型的迭代方法，用于流场反演。M4S是由德国科学家Romeiser等[25]开发的海面微波成像仿真模型，其核心程序模块主要包括海表面微尺度波波高谱计算模块和雷达海面成像仿真模块。在给定风场和流场的情况下，可仿真海浪谱、海面SAR复图像（强度、相位）以及多普勒谱等信息。因此，基于M4S模型并结合弦截下山法可估算并去除风场的影响，反演海面径向流速。首先利用频谱拟合法从SAR原始复数据中获得实测多普勒中心频率；再利用SAR数据头文件信息估算卫星和地球表面的相对运动产生的预测多普勒中心频率，继而得到多普勒质心频率异常值并将其转换为地距多普勒速度；然后基于M4S模型，利用本文提出的弦截下山法迭代反演SAR局部区域的流场，估算风场对多普勒速度的影响，继而反演整幅SAR图像的海面径向流速；最后通过与实测海面流场数据比对，验证反演算法的有效性。
2. 数据源
本文采用的实测海表流场数据和SAR数据来自作者课题组组织的星地匹配实验，用安德拉海流计现场采集海表流场数据，并与Radarsat-2 SAR卫星数据作时空匹配。采用安德拉海流计测量海表面流时，将海流计悬挂于浮体之下，使其处于海表面以下约0.4 m处，在船只停航时，用绳子牵住浮体，并在船尾将浮体和海流计放置于离船200 m的海面，记录停止放绳的时间和收绳的时间，此时间段内为有效数据。所用安德拉海流计型号为SEAGUARD，这是一种自记录海流计，具有二维流场测量能力，测量流速的分辨率为0.1 mm/s，平均误差为±0.15 cm/s ，测量流向的分辨率为0.01°，误差为±5°。现场测量海表面流时，实验海流计位于海表面以下约0.4 m处，测量的是近表面流速，通过SAR数据测量得到的流速是海表层流速。因为两者测量的深度基本匹配，所以可用此实验海流计所测的实测流场数据对SAR数据的流场反演精度进行验证。
采用的SAR数据源于Radarsat-2卫星，为标准成像模式下的单视复数据。结合星地匹配实验中现场实测数据的位置及时间信息，本文选用了两幅Radarsat-2 SAR图像进行流场反演，其UTC时间分别为2019年6月23日21时53分和2019年6月25日10时11分。数据信息如表1所示，SAR数据覆盖区域如图1所示。SAR覆盖区域内，海表面流即包括有一定规律性的地转流和潮流，也包括无规律的风生流，所以整体来说该区域的海表面流场分布无明显规律。
表 1 本文所用Radarsat-2 SAR数据信息Table 1. Radarsat-2 SAR data information used in this paper成像时间（UTC） 幅宽/km 分辨率/m 入射角范围/（°） 极化方式 升、降轨模式 2019年6月23日21时53分 102.52×109.43 4.92×11.83 41.45～46.70 垂直极化（VV） 降轨 2019年6月25日10时11分 102.91×109.93 5.04×11.83 33.51～39.74 垂直极化（VV） 升轨 
图 1 所用Radarsat-2 SAR 数据覆盖区域a. 2019年6月23日；b. 2019年6月25日Figure 1. Coverage area of Radarsat-2 SAR dataa. June 23, 2019; b. June 25, 2019风场数据采用欧洲中期天气预报中心（European Centre for Medium-Range Weather Forecasts，ECMWF）ERA5中的再分析风场数据。数据中包括海面上空10 m处风场的东向分量、北向分量和经纬度、时间信息，其空间分辨率为0.25°×0.25°，时间分辨率为1 h。在使用该风场数据时发现其时空分辨率比反演得到的SAR流速产品分辨率小，无法直接使用，所以本文通过时空插值使其与SAR流速产品匹配，以方便之后的处理。
3. 模型与方法
3.1 基于多普勒质心频率异常的多普勒速度估算方法
从SAR实测数据估算的多普勒中心频率称作实测多普勒中心频率，主要包含卫星和地球表面的相对运动导致的多普勒频移与海面水质点运动导致的多普勒频移。实测多普勒中心频率的估计方法有基于幅度的频谱拟合法和基于相位的相位增量法[26-27]。本文利用频谱拟合法从SAR复数据中估计实测多普勒中心频率。首先选取一定大小的窗口，对该窗口内的数据进行快速傅里叶变换（FFT）。然后在得到的方位向能量谱中找到多普勒中心频率。由于直接从方位向能量谱中寻找多普勒中心频率较为困难，本文结合能量均衡法，将方位向功率谱与参考函数相关，寻找相关后的过0点，并把过0点处的频率作为该窗口的多普勒中心频率[28]。最后以一定的步长移动窗口得到整幅SAR图像的多普勒中心频率。
卫星和地球表面的相对运动产生的多普勒中心频率称作预测多普勒中心频率，其计算方法主要有两种：第一种方法基于卫星姿态和速度等参数，利用几何关系估算该多普勒中心频率；第二种方法从元数据中读取多普勒系数、斜距时间、标准斜距时间等数据估算预测多普勒中心频率。由于Envisat ASAR、Radarsat-2等卫星，SAR原始数据处理时已经估算了预测多普勒中心频率，并给出了拟合多项式，所以本文基于第二种方法估算预测多普勒中心频率，表达式为[29]
$$ \begin{split} {f_{{\rm{Dp}}}} =& {\rm{dop_{coef1}}} + {\rm{dop_{coef2}}} \times \left( {t - {t_0}} \right) + {\rm{dop_{coef3}}} \times {\left( {t - {t_0}} \right)^2} \\ & +{\rm{dop_{coef4}}} \times {\left( {t - {t_0}} \right)^3} + {\rm{dop_{coef5}}} \times {\left( {t - {t_0}} \right)^4}, \end{split} $$ (1) 式中，
${\text{do}}{{\text{p}}_{{\text{coef1}}}}$ 、${\text{do}}{{\text{p}}_{{\text{coef2}}}}$ 、${\text{do}}{{\text{p}}_{{\text{coef3}}}}$ 、${\text{do}}{{\text{p}}_{{\text{coef4}}}}$ 、${\text{do}}{{\text{p}}_{{\text{coef5}}}}$ 为多普勒系数；$t$ 为斜距时间；${t_0}$ 为标准斜距时间。将卫星和地球表面的相对运动产生的预测多普勒中心频率从实测多普勒中心频率中去除之后得到的剩余频率称作多普勒质心频率异常[30]
$$ {f_{{\rm{Dca}}}} \equiv {f_{{\rm{Dc}}}} - {f_{{\rm{Dp}}}}\text{，} $$ (2) 式中，
${f_{{\rm{Dc}}}}$ 为实测多普勒中心频率。经过式（2）的运算，卫星相对地球表面的运动效应被去除，因此多普勒质心频率异常对应的只是海面水质点的运动速度。将多普勒质心频率异常转化为径向多普勒速度，再将其投影到地表局部切平面坐标系得到地距多普勒速度$$ {V_{{\rm{dop}}\_{\rm{sar}}}} = - \frac{{\text{π} {f_{{\rm{Dca}}}}}}{{k{\rm{sin}}\theta }}\text{，} $$ (3) 式中，
$k$ 为雷达电磁波波数；$\theta $ 为雷达入射角。上述计算得到的地距多普勒速度对应海面水质点运动，该运动主要包括海表面流场、海浪轨道速度等，其中海浪受到海表面风场的调制作用，即风场可间接影响多普勒速度。Chapron等[23]提出的多普勒模型通过波浪谱表示了风对多普勒速度的影响，并给出了计算风场和流场产生的多普勒速度的经验表达式。
3.2 海面流场反演的弦截下山法
3.1节获得的地距多普勒速度中既包含了流场的贡献又包含了风场的贡献，只有准确去除风场的贡献，才能获得海面流场。利用M4S模型仿真的多普勒谱信息可以计算多普勒质心偏移，进而获得M4S模拟的多普勒速度场
${V_{{\rm{dop}}\_{\rm{m4s}}}}$ ，即$$ {\rm{M4S}}\left( {{U_{\rm{C}}},{U_{\rm{W}}}} \right) = {V_{{\rm{dop}}\_{\rm{m4s}}}}. $$ (4) 当输入M4S模型的风场
${U_{\rm{W}}}$ 和流场${U_{\rm{C}}}$ 信息与真实SAR成像时海面的风场和流场信息一致时，在忽略M4S模型建模误差的条件下，M4S模拟的多普勒速度${V_{{\rm{dop}}\_{\rm{m4s}}}}$ 应与从真实SAR图像反演的多普勒速度${V_{{\rm{dop}}\_{\rm{sar}}}}$ 相等，即${V_{{\rm{dop}}\_{\rm{m4s}}}} = {V_{{\rm{dop}}\_{\rm{sar}}}}$ 。在基于多普勒质心频移法获得了真实SAR图像反演的多普勒速度${V_{{\rm{dop}}\_{\rm{sar}}}}$ 的条件下，通过M4S模型获得海面真实流场，也就是求解以下关于海面流场${U_{\rm{C}}}$ 的方程（假设海面真实风场${U_{\rm{W}}}$ 已知）$$ f\left( {{U_{\rm{C}}}} \right) = {\rm{M4S}}\left( {{U_{\rm{C}}},{U_{\rm{W}}}} \right) - {V_{{\rm{dop}}\_{\rm{sar}}}} = 0. $$ (5) 上述方程是关于海面流场
${U_{\rm{C}}}$ 的非线性方程，通过求解此方程可以获得与SAR图像对应的海面流场。这里采用迭代方法求解式（5），为了兼顾计算速度与迭代收敛性，选择弦截法并结合下山法进行求解。弦截法不需要求解函数
$f\left( {{U_{\rm{C}}}} \right)$ 的导数，容易实现；而下山法可以在一定程度上保证迭代的收敛性。弦截法求解非线性方程$f\left( {{U_{\rm{C}}}} \right) = 0$ 的迭代公式为[31]$$ {U_{k + 1}} = {U_k} - \frac{{f\left( {{U_k}} \right)}}{{f\left( {{U_k}} \right) - f\left( {{U_{k - 1}}} \right)}}\left( {{U_k} - {U_{k - 1}}} \right) \quad k = 1\text{，}2\text{，}3\text{，} \cdots \text{，} $$ (6) 式中，
${U_{k - 1}}$ 、${U_k}$ 和${U_{k + 1}}$ 分别表示第$k - 1$ 、$k$ 和$k + 1$ 次迭代的流速近似解。运算中需要首先把两个初猜值${U_0}$ 和${U_1}$ 代入式（6），开启迭代运算，直到相邻两次迭代的结果满足$\left| {{U_{k + 1}} - {U_k}} \right| < e$ ，即可停止迭代（式中$e$ 为误差阈值），并以${U_{k + 1}}$ 作为非线性方程$f\left( {{U_{\rm{C}}}} \right) = 0$ 的最终近似解。为了防止迭代发散，这里引入下山条件，即要求迭代过程具有单调性[31]，即$$ \left| {f\left( {{U_{k + 1}}} \right)} \right| < \left| {f\left( {{U_k}} \right)} \right|\text{.} $$ (7) ${U_{k + 1}}$ 、${U_k}$ 为了满足上述下山条件，在式（6）中引入下山因子$A$ ，其形式变为$$ {U_{k + 1}} = {U_k} - A\frac{{f\left( {{U_k}} \right)}}{{f\left( {{U_k}} \right) - f\left( {{U_{k - 1}}} \right)}}\left( {{U_k} - {U_{k - 1}}} \right)\text{.} $$ (8) 下山因子
$A$ 的取值为$ 1\text{，}\dfrac{1}{2}\text{，}\dfrac{1}{4}\text{，} \cdots $ ，直到使得下山条件式（7）成立为止。基于M4S模型，采用上述弦截下山法迭代反演流场的流程如图2所示，具体计算按如下步骤。
图 2 弦截下山法迭代反演流场流程Figure 2. Flow chart of iterative retrieval of current field by secant downhill method（1）基于SAR反演的海面多普勒速度
${V_{{\rm{dop}}\_{\rm{sar}}}}$ 设置迭代初猜值，弦截法需要两个初猜值，这里将${V_{{\rm{dop}}\_{\rm{sar}}}}$ 作为${U_0}$ ，${U_0} + {{{V}}'}\left( {{{{V}}'} = \pm 0.1} \right)$ 作为${U_1}$ ，并将其输入M4S模型，获得${V_{0{\rm{dop}}\_{\rm{m4s}}}}$ 、${V_{1{\rm{dop}}\_{\rm{m4s}}}}$ ，在上述4个值以及风场、初始化参数$k$ 、$A$ 的基础上，开启迭代运算。（2）将由式（5）获得的
$f\left( {{U_k}} \right)$ 和$f\left( {{U_{k - 1}}} \right)$ 的绝对值进行比较，如果满足下山条件$\left| {f\left( {{U_k}} \right)} \right| < \left| {f\left( {{U_{k - 1}}} \right)} \right|$ 则进入第（3）步处理，反之，进入第（4）步处理（当$k = 1$ 时，通过选择不同的${{{V}}'}$ 的值，使得$\left| {f\left( {{U_1}} \right)} \right| < \left| {f\left( {{U_0}} \right)} \right|$ 成立）。（3）利用式（6）计算非线性方程（5）新的近似解
${U_{k + 1}}$ ，判断$\left| {{U_{k + 1}} - {U_k}} \right|$ 是否满足误差阈值条件，满足则停止迭代，以${U_{k + 1}}$ 作为最终的流场；若不满足误差阈值条件，将${U_{k + 1}}$ 输入M4S模型获得${V_{k + 1{\rm{dop}}\_{\rm{m4s}}}}$ ，更新迭代参数$k = k + 1$ ，$A = 1$ ，转入第（5）步操作。（4）下山因子减半
$A = {A}/{2}$ ，采用式（8）基于${U_{k - 2}}$ 和${U_{k - 1}}$ 重新计算${U_k}$ ，判断$\left| {{U_k} - {U_{k - 1}}} \right|$ 是否满足误差阈值条件，满足则停止迭代，以${U_k}$ 作为最终的流场；若不满足误差阈值条件，将新的${U_k}$ 输入M4S模型获得新的${V_{k{\rm{dop}}\_{\rm{m4s}}}}$ ，转入第（5）步操作。（5）基于更新的
${U_{k - 1}}$ 、${U_k}$ 及${V_{k - 1{\rm{dop}}\_{\rm{m4s}}}}$ 、${V_{k{\rm{dop}}\_{\rm{m4s}}}}$ ，转入第（2）步，进行下一步迭代运算。3.3 风贡献因子
$\gamma $ 的估算方法由于M4S模拟仿真过程计算量较大，3.2节的弦截下山法一般只适用于SAR图像局部区域的流场反演。对于整幅SAR图像，可以通过分块迭代计算海面流场，估算每块区域的风贡献因子
$\gamma $ ，进而估算整幅SAR图像的风贡献因子$\gamma $ 。本文将从整幅SAR图像上均匀的选取大小相等的几个局部区域（本文中是5个），利用3.2节提到的方法分别迭代反演其流场。将迭代反演获得的流场、相应SAR图像反演的多普勒速度${V_{{\rm{dop}}\_{\rm{sar}}}}$ 以及外部风场数据（ECMWF风场数据）代入式（9），获得每个局部区域的风贡献因子$\gamma $ 。$$ {U_{\text{D}}} \approx \gamma {U_{10}} + {U_{\text{C}}}\text{.} $$ (9) 由于风贡献因子
$\gamma $ 与雷达频率、入射角以及雷达天线的偏航角等因素有关[23]，而在一幅SAR图像中这些参数基本保持不变，所以本文中将各局部区域的风贡献因子$\gamma $ 的平均值作为整幅SAR图像的风贡献因子$\gamma $ 。4. 结果与精度验证
4.1 反演结果
采用3.1节描述的方法，对两幅Radarsat-2 SAR数据进行处理，结果如图3和图4所示。从图3中可以发现，相比于预测多普勒中心频率，多普勒质心频率异常要小的多，这是由于两者产生的原因不同，预测多普勒中心频率由卫星和地球相对运动产生，而多普勒质心频率异常由海表层运动产生。
图 3 2019年6月23日SAR图像反演结果a. 实测多普勒中心频率fDc；b. 预测多普勒中心频率fDp；c. 多普勒质心频率异常值fDca；d. 地距多普勒速度Vdop_sar，其中红框区域为利用弦截下山法迭代反演流场的局部区域Figure 3. SAR image retrieval results on June 23, 2019a. Measured Doppler center frequency fDc; b. predicted Doppler center frequency fDp; c. Doppler centroid frequency anomaly fDca; d. ground Doppler velocity Vdop_sar, the red box area is the local area of the current field iteratively retrieved by the secant downhill method
图 4 2019年6月25日SAR数据反演的地距多普勒速度Vdop_carFigure 4. Ground range Doppler velocity retrieved from SAR data on June 25, 2019经上述处理获得的地距多普勒速度（图3d、图4）中即包含了流场贡献又包含了风场贡献，文献[23]表明风场的贡献甚至更大一些，因此只有准确的去除风场的贡献，才能获得最终的海面流场。这里首先采用3.2节提出的弦截下山法对从SAR图像中截取的小区域进行迭代计算，获得其海面流场。例如，对2019年6月23日SAR图像反演的地距多普勒速度分布图（图3d）中红框1所示局部区域（大小为方位向5 km×距离向6 km）进行迭代计算，计算3次的误差
$\left| {{U_{k{\text{ + 1}}}} - {U_k}} \right|$ 依次是0.34 m/s、0.07 m/s、0.02 m/s，已经满足误差阈值条件（${e < 0.05\;{\rm{m}}/{\rm{s}}}$ ），因此停止迭代，输出最终流场。然后，将该流场和相应SAR图像反演的多普勒速度${V_{{\rm{dop}}\_{\rm{sar}}}}$ 及风场数据代入式（9）估算该局部区域的风贡献因子$\gamma $ ，得到图3d中红框1区域的风贡献因子$\gamma $ 为0.15。用同样的方法估算其他局部区域的风贡献因子$\gamma $ ，并将所有的风贡献因子$\gamma $ 进行平均，得到整幅SAR图像的风贡献因子$\gamma $ 。2019年6月23日SAR图像的平均风贡献因子$\gamma $ 为0.15，2019年6月25日SAR图像的平均风贡献因子$\gamma $ 为0.22。将两幅SAR图像的平均风贡献因子$\gamma $ 分别代入式（9）计算风场产生的多普勒速度，并将其从地距多普勒速度${V_{{\rm{dop}}\_{\rm{sar}}}}$ 中去除，得到整幅SAR图像的海面径向流速，如图5所示。对SAR地距多普勒速度图中局部区域进行迭代计算时，通常只需迭代两三次就可以满足误差阈值条件，获得该区域的径向流速。该结果表明本文提出的弦截下山法具有良好的收敛性和较高的收敛速度。
图 5 两景SAR数据对应的海表面径向流速a. 2019年6月23日；b. 2019年6月25日。黑色五角星处是实测数据所在位置Figure 5. The radial velocity of the sea surface corresponding to the SAR data of the two scenesa. June 23, 2019; b. June 25, 2019. The black five-pointed star is the location of the measured data4.2 精度验证
为了验证本文方法，把SAR反演的海表面径向流速与星地匹配实验中安德拉海流计采集的流场实测数据比对。安德拉海流计是常用的海流测量仪器，能够准确测量海水瞬时速度。实验中将海流计悬挂于浮体之下，使其处于海表面以下约0.4 m处，保证其测量的是近表面海水的速度。获取海表流场需要对海流计所测时间序列的速度取平均，以去除海浪的速度贡献。将星地匹配实验中测得的实测数据与SAR图像进行时空匹配，得到两个实测数据分别与两幅SAR数据对应，具体数据如表2所示，表中的流速、流向是卫星过境时刻前后10 min内的平均值。
表 2 海流计实测海流数据Table 2. Current data measured by ocean current meters测量时间（UTC） 位置 平均流速/（m·s–1） 平均流向/（°） 实测数据在SAR视向方向的分量/（m·s–1） 2019年6月23日21时48–58分 21.30°N，118.51°E 0.42 336.70 0.23 2019年6月25日10时6–16分 21.80°N，118.29°E 0.15 283.90 –0.14 由于SAR DCA方法反演的流速是一维径向流速，在将海流计测得的流场与其比较时，需要将海流计所测二维流场向SAR径向作投影。2019年6月23日雷达视向角为279.93°，2019年6月25日雷达视向角为79.63°。将与之匹配的海流计所测流速分别投影到SAR径向，得到实测径向流速分别为0.23 m/s、–0.14 m/s（如表2中最后一列所示）。在SAR反演的径向流速分布图中寻找实测数据的匹配位置点，如图5a和图5b中黑色五角星所示，以该点为中心，1 km×1 km范围内对SAR反演的径向流速取平均，得到两幅SAR图像DCA方法反演的流速分别为0.19 m/s，–0.29 m/s。将DCA法反演的径向流速与实测的径向流速进行比较，得到两幅SAR图像在实测点处的反演误差分别为0.04 m/s和0.15 m/s。在比对实验中，SAR反演结果的精度与产品分辨率之间往往存在矛盾。平均范围越大流速精度越高而分辨率会越低，反之，则流速精度越低而分辨率越高。所以需在两者之间进行权衡，本文在1 km×1 km的范围内取平均，可在相对较高的分辨率（1 km×1 km）下获得较高的精度。
5. 总结
为了克服SAR复图像DCA方法反演海面流场时风场贡献去除困难的难题，本文提出了基于M4S模型的弦截下山法迭代反演海面流场。首先采用传统的DCA方法反演海面多普勒速度；然后采用本文提出的弦截下山法，迭代反演SAR地距多普勒速度分布图中局部区域的海面流场，并估算其风贡献因子
$\gamma $ ；最后对不同局部区域的风贡献因子$\gamma $ 取平均，获得整幅SAR地距多普勒速度分布图的风贡献因子$\gamma $ 。进而去除风场对多普勒速度的贡献，获得整幅SAR图像对应的海面径向流速。将两幅SAR图像的反演结果与实测近海表面流速进行比对，得到的反演海面径向流速偏差分别为0.04 m/s和0.15 m/s。研究结果表明，本文提出的弦截下山法不仅具有良好的收敛性和较高的收敛速度，而且对于本文使用的两景SAR数据，反演的海面径向流速偏差在0.2 m/s内。 -
图 1 所用Radarsat-2 SAR 数据覆盖区域
a. 2019年6月23日；b. 2019年6月25日
Fig. 1 Coverage area of Radarsat-2 SAR data
a. June 23, 2019; b. June 25, 2019
图 2 弦截下山法迭代反演流场流程
Fig. 2 Flow chart of iterative retrieval of current field by secant downhill method
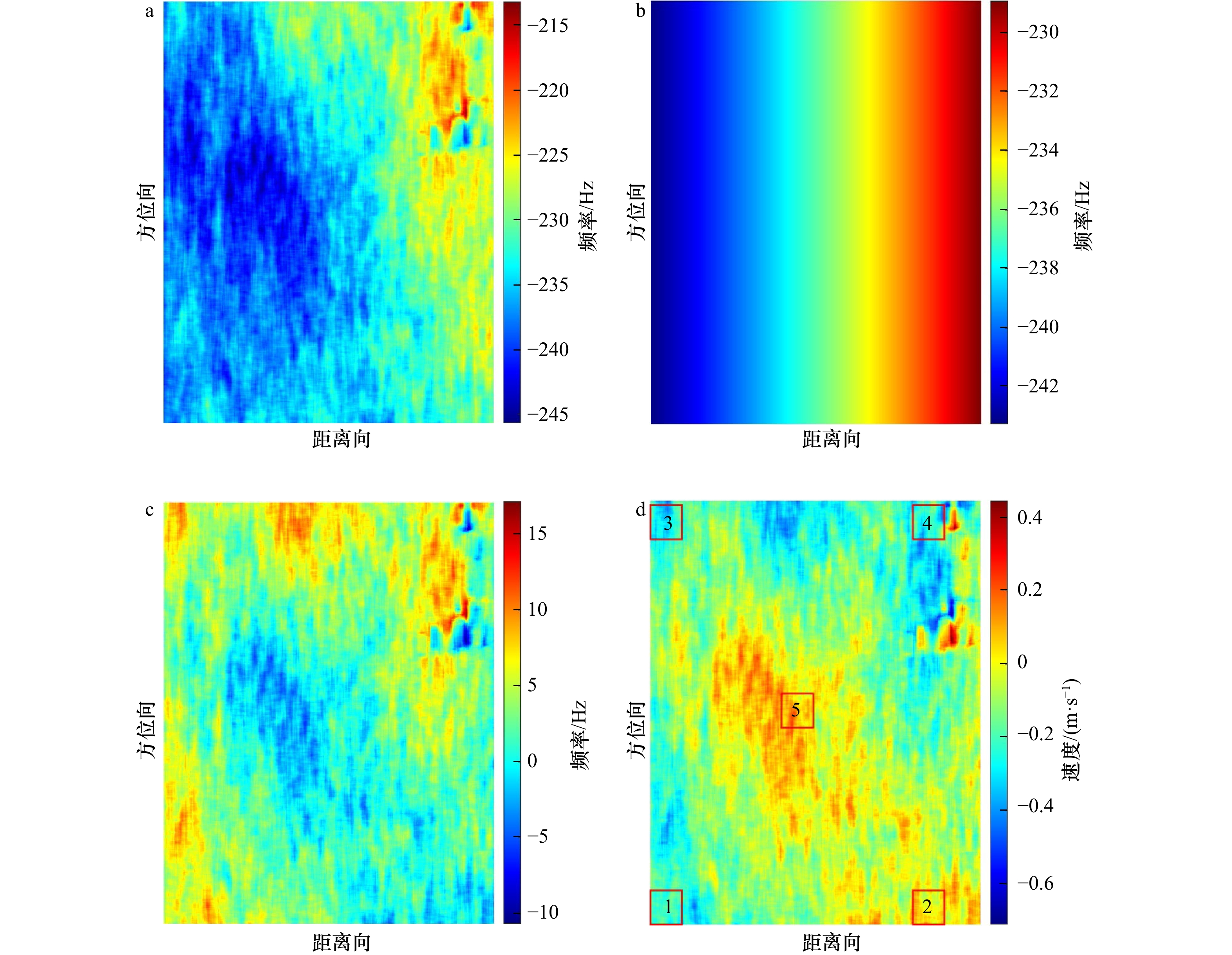
图 3 2019年6月23日SAR图像反演结果
a. 实测多普勒中心频率fDc；b. 预测多普勒中心频率fDp；c. 多普勒质心频率异常值fDca；d. 地距多普勒速度Vdop_sar，其中红框区域为利用弦截下山法迭代反演流场的局部区域
Fig. 3 SAR image retrieval results on June 23, 2019
a. Measured Doppler center frequency fDc; b. predicted Doppler center frequency fDp; c. Doppler centroid frequency anomaly fDca; d. ground Doppler velocity Vdop_sar, the red box area is the local area of the current field iteratively retrieved by the secant downhill method
图 4 2019年6月25日SAR数据反演的地距多普勒速度Vdop_car
Fig. 4 Ground range Doppler velocity retrieved from SAR data on June 25, 2019
图 5 两景SAR数据对应的海表面径向流速
a. 2019年6月23日；b. 2019年6月25日。黑色五角星处是实测数据所在位置
Fig. 5 The radial velocity of the sea surface corresponding to the SAR data of the two scenes
a. June 23, 2019; b. June 25, 2019. The black five-pointed star is the location of the measured data
表 1 本文所用Radarsat-2 SAR数据信息
Tab. 1 Radarsat-2 SAR data information used in this paper
成像时间（UTC） 幅宽/km 分辨率/m 入射角范围/（°） 极化方式 升、降轨模式 2019年6月23日21时53分 102.52×109.43 4.92×11.83 41.45～46.70 垂直极化（VV） 降轨 2019年6月25日10时11分 102.91×109.93 5.04×11.83 33.51～39.74 垂直极化（VV） 升轨 
下载: 导出CSV
表 2 海流计实测海流数据
Tab. 2 Current data measured by ocean current meters
测量时间（UTC） 位置 平均流速/（m·s–1） 平均流向/（°） 实测数据在SAR视向方向的分量/（m·s–1） 2019年6月23日21时48–58分 21.30°N，118.51°E 0.42 336.70 0.23 2019年6月25日10时6–16分 21.80°N，118.29°E 0.15 283.90 –0.14
下载: 导出CSV
-
[1] 刘巍, 张韧, 王辉赞, 等. 基于卫星遥感资料的海洋表层流场反演与估算[J]. 地球物理学进展, 2012, 27(5): 1989−1994. doi: 10.6038/j.issn.1004-2903.2012.05.020Liu Wei, Zhang Ren, Wang Huizan, et al. Sea surface flow field retrieval and estimation based on satellite remote sensing data[J]. Progress in Geophysics, 2012, 27(5): 1989−1994. doi: 10.6038/j.issn.1004-2903.2012.05.020 [2] 蒋兴伟, 林明森, 张有广. 中国海洋卫星及应用进展[J]. 遥感学报, 2016, 20(5): 1185−1198.Jiang Xingwei, Lin Mingsen, Zhang Youguang. Progress and prospect of Chinese ocean satellites[J]. Journal of Remote Sensing, 2016, 20(5): 1185−1198. [3] Emery W J, Fowler C, Clayson C A. Satellite-image-derived Gulf Stream currents compared with numerical model results[J]. Journal of Atmospheric and Oceanic Technology, 1992, 9(3): 286−304. doi: 10.1175/1520-0426(1992)009<0286:SIDGSC>2.0.CO;2 [4] 毛志华, 潘德炉, 潘玉球, 等. 利用卫星遥感SST估算海表流场[J]. 海洋通报, 1996, 15(1): 84−90.Mao Zhihua, Pan Delu, Pan Yuqiu, et al. Methods of obtaining sea surface velocities field from SST images[J]. Marine Science Bulletin, 1996, 15(1): 84−90. [5] Emery W J, Baldwin D G, Matthews D K. Sampling the mesoscale ocean surface currents with various satellite altimeter configurations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(4): 795−803. doi: 10.1109/TGRS.2003.820599 [6] 吴雄斌, 杨绍麟, 程丰, 等. 高频地波雷达东海海洋表面矢量流探测试验[J]. 地球物理学报, 2003, 46(3): 340−346. doi: 10.3321/j.issn:0001-5733.2003.03.010Wu Xiongbin, Yang Shaolin, Cheng Feng, et al. Ocean surface currents detection at the eastern China sea by HF surface wave radar[J]. Chinese Journal of Geophysics, 2003, 46(3): 340−346. doi: 10.3321/j.issn:0001-5733.2003.03.010 [7] 杨春奇. 高频地波雷达海洋回波提取及海态参数反演方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2019.Yang Chunqi. Research on wave echo extraction and high frequency ground wave radar sea-state parameters inversion method[D]. Harbin: Harbin Institute of Technology, 2019. [8] Bao Qingliu, Dong Xiaolong, Zhu Di, et al. The feasibility of ocean surface current measurement using pencil-beam rotating scatterometer[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(7): 3441−3451. doi: 10.1109/JSTARS.2015.2414451 [9] Bao Qingliu, Lin Mingsen, Zhang Youguang, et al. Ocean surface current inversion method for a Doppler scatterometer[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(11): 6505−6516. doi: 10.1109/TGRS.2017.2728824 [10] Rodríguez E, Wineteer A, Perkovic-Martin D, et al. Estimating ocean vector winds and currents using a Ka-band pencil-beam Doppler scatterometer[J]. Remote Sensing, 2018, 10(4): 576. doi: 10.3390/rs10040576 [11] Rodríguez E, Wineteer A, Perkovic-Martin D, et al. Ka-band Doppler scatterometry over a loop current eddy[J]. Remote Sensing, 2020, 12(15): 2388. doi: 10.3390/rs12152388 [12] 候富城, 孟俊敏, 张晰, 等. 利用多普勒频移反演ASAR海表面流速[J]. 海洋科学进展, 2019, 37(2): 274−283. doi: 10.3969/j.issn.1671-6647.2019.02.011Hou Fucheng, Meng Junmin, Zhang Xi, et al. Using the Doppler shift method to retrieve the ASAR sea surface velocity[J]. Advances in Marine Science, 2019, 37(2): 274−283. doi: 10.3969/j.issn.1671-6647.2019.02.011 [13] 何宜军, 杨小波, 矣娜, 等. 星载SAR测量海洋流场研究进展[J]. 南京信息工程大学学报(自然科学版), 2020, 12(2): 181−190.He Yijun, Yang Xiaobo, Yi Na, et al. Progress in sea surface current retrieval from spaceborne SAR measurements[J]. Journal of Nanjing University of Information Science and Technology (Natural Science Edition), 2020, 12(2): 181−190. [14] Liu Bochang, He Yijun, Li Xiuzhong. A new concept of full ocean current vector retrieval with spaceborne SAR based on intrapulse beam-switching technique[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(11): 7682−7704. doi: 10.1109/TGRS.2020.2983178 [15] Johannessen J A, Chapron B, Collard F, et al. Direct ocean surface velocity measurements from space: Improved quantitative interpretation of Envisat ASAR observations[J]. Geophysical Research Letters, 2008, 35(22): L22608. doi: 10.1029/2008GL035709 [16] Wang Lihua, Zhou Yunxuan, Ge Jianzhong, et al. Mapping sea surface velocities in the Changjiang coastal zone with advanced synthetic aperture radar[J]. Acta Oceanologica Sinica, 2014, 33(11): 141−149. doi: 10.1007/s13131-014-0563-x [17] Goldstein R M, Zebker H A. Interferometric radar measurement of ocean surface currents[J]. Nature, 1987, 328(6132): 707−709. doi: 10.1038/328707a0 [18] Kim J E, Kim D J, Moon W M. Enhancement of Doppler centroid for ocean surface current retrieval from ERS-1/2 raw SAR[C]// IEEE International Geoscience & Remote Sensing Symposium. Washington DC: IEEE, 2004, 5(20–24): 3118–3120. [19] Collard F, Mouche A, Chapron B, et al. Routine high resolution observation of selected major surface currents from space[C]//Proceedings of the SeaSAR 2008. Noordwijk, Netherlands: ESA Communication Production Office, 2008, SP-656. [20] Moiseev A, Johnsen H, Hansen M W, et al. Evaluation of radial ocean surface currents derived from Sentinel-1 IW Doppler shift using coastal radar and Lagrangian surface drifter observations[J]. Journal of Geophysical Research: Oceans, 2020, 125(4): e2019JC015743. [21] Chapron B, Collard F, Kerbaol V. Satellite synthetic aperture radar sea surface Doppler measurements[C]//Proceeding of the 2nd Workshop on Coastal and Marine Applications of SAR. Noordwijk, Netherlands: ESA Special Publication, 2004, 565: 133–139. [22] Romeiser R, Runge H, Suchandt S, et al. Quality assessment of surface current fields from TerraSAR-X and TanDEM-X along-track interferometry and Doppler centroid analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(5): 2759−2772. doi: 10.1109/TGRS.2013.2265659 [23] Chapron B, Collard F, Ardhuin F. Direct measurements of ocean surface velocity from space: Interpretation and validation[J]. Journal of Geophysical Research: Oceans, 2005, 110(C7): C07008. [24] 杨小波. 基于ASAR的时变海表面流场反演研究[D]. 上海: 上海海洋大学, 2016.Yang Xiaobo. Sea surface current retrieval based on ASAR data[D]. Shanghai: Shanghai Ocean University, 2016. [25] Romeiser R, Alpers W, Wismann V. An improved composite surface model for the radar backscattering cross section of the ocean surface: 1. Theory of the model and optimization/validation by scatterometer data[J]. Journal of Geophysical Research: Oceans, 1997, 102(C11): 25237−25250. doi: 10.1029/97JC00190 [26] Cumming I G, Wong F H. 合成孔径雷达成像: 算法与实现[M]. 洪文, 胡东辉, 译. 北京: 电子工业出版社, 2012.Cumming I G, Wong F H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation[M]. Hongwen, Hu Donghui, trans. Beijing: Publishing House of Electronics Industry, 2012. [27] 任圣君, 陈少昌. 基于相位增量法的合成孔径雷达多普勒中心频率估计[J]. 微型机与应用, 2017, 36(21): 81−84,89.Ren Shengjun, Chen Shaochang. Doppler center frequency estimation of synthetic aperture radar based on phase increment method[J]. Microcomputer & its Applications, 2017, 36(21): 81−84,89. [28] 王绍清. 星载SAR多普勒中心实时估计技术研究[D]. 北京: 中国科学院电子学研究所, 2005.Wang Shaoqing. Research on the Doppler centroid real-time estimation technology of space-borne SAR[D]. Beijing: Institute of Electrics, Chinese Academy of Sciences, 2005. [29] Raney R K. Doppler properties of radars in circular orbits[J]. International Journal of Remote Sensing, 1986, 7(9): 1153−1162. doi: 10.1080/01431168608948916 [30] Hansen M W, Collard F, Dagestad K F, et al. Retrieval of sea surface range velocities from Envisat ASAR Doppler centroid measurements[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3582−3592. doi: 10.1109/TGRS.2011.2153864 [31] 李庆扬, 王能超, 易大义. 数值分析[M]. 4版. 武汉: 华中科技大学出版社, 2006: 222-230.Li Qingyang, Wang Nengchao, Yi Dayi. Numerical Analysis[M]. 4th ed. Wuhan: Huazhong University of Science & Technology Press, 2006: 222−230. 期刊类型引用(0)
其他类型引用(1)
-
下载:
