Researches on statistical properties of freak waves in uni-directional random waves in deep water
-
摘要: 本文基于Longuet-Higgins随机波浪模型和JONSWAP谱，进行了大量深水随机波的模拟，获取了畸形波发生概率稳定的随机波列，并对随机波列中的畸形波进行了分析。结果表明，畸形波发生的概率小于基于Rayleigh分布预测结果，且随谱宽的减小而增大。在固定时间段内，畸形波发生的频次服从泊松分布，时间间隔服从指数分布，且随着谱宽的增大，畸形波的发生频次减小，相邻畸形波的发生时间间隔增加。通过小波变换方法分离随机波中的波群，研究了出现畸形波的波群特征，发现一个波群中最多会出现4个畸形波，但是在发生畸形波的波群中，单个畸形波的概率最大。随着谱宽减小，一个波群中包含多个畸形波的概率增加。另外，出现畸形波的波群时间长度服从广义极值分布，随着谱宽减小，畸形波波群的时间跨度增加。Abstract: Numerous random wave trains are simulated based on the JONSWAP spectrum using the Longuet-Higgins wave model, and then extreme waves are investigated based on the wave trains with stable probabilities of freak waves. The probabilities of freak waves are smaller than those of based on Rayleigh distributions. With the spectra narrower, the probability of freak waves increases. During the fixed times, the frequency of freak waves obeys the Poisson distribution and time intervals satisfy exponential distribution. The most probable occurrence frequency of freak waves decrease and intervals of freak waves are longer with the spectra wider. Wave groups are discriminated based on wavelet spectra and their characteristics are analyzed. There are no more than four freak waves in wave groups. The probability of wave groups containing merely one freak wave is the largest. Numbers of freak waves in wave groups are increasing with the spectral narrower. Furthermore, time lengths of wave groups containing freak waves satisfy Generalized extreme value distribution (GEV distribution), and with spectra narrower, the most probable lengths of the wave groups increase.
-
Key words:
- freak waves /
- wave groups /
- wave models
-
图 1 γ=1, 3, 5, 7时，时间T内畸形波发生频率的概率密度分布
Fig. 1 Probability distributions of frequency of freak waves for different peak enhancement factors (γ=1, 3, 5, 7)
图 2 泊松分布参数λ与谱宽υ的关系
Fig. 2 Relationships between Poisson distribution parameter λ and spetrum widths υ
图 3 γ=1，3，5，7时，畸形波出现时间间隔分布
Fig. 3 Probability distributions of time intervals of freak waves for different peak enhancement factors (γ=1, 3, 5, 7).
图 4 指数分布参数μ与谱宽υ的关系
Fig. 4 Relationships between exponential distribution parameter μ and spetrum wdths υ
图 5 不同谱峰因子下，不同畸形波特征所占比例
Fig. 5 Proportions of each characteristic of freak waves for different peak enhancement factors
图 6 γ=1，3，5，7时，畸形波群无量纲时间长度概率分布
Fig. 6 Probability distributions of non-dimensional time lengths of freak wave groups for different peak enhancement factors (γ=1, 3, 5, 7)
图 7 GEV系数与谱宽υ的关系
Fig. 7 Relationships between parameters of GEV distribution and spetrum widths υ
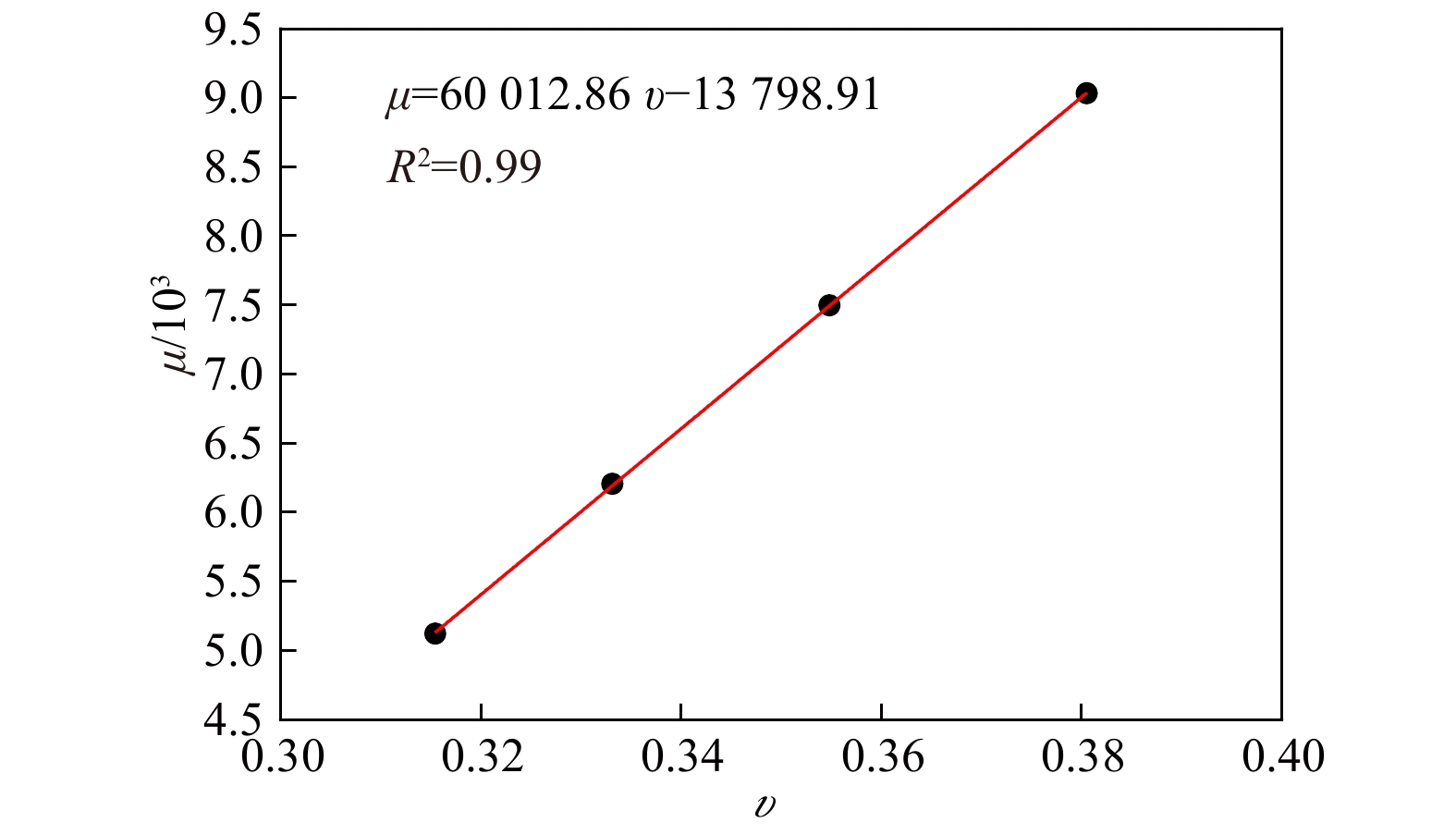
表 1 不同谱宽的时间序列长度[27]
Tab. 1 Time series lengths for different spectrum widths
γ 谱宽υ 时间序列
T0/s实际波数 波数相对
误差/%畸形波发生
概率/%1 0.381 11 988 695 1 499 724 0.018 4 0.007 5 2 0.367 12 565 184 1 499 739 0.017 4 0.009 3 3 0.355 12 959 049 1 499 760 0.016 0 0.010 7 4 0.343 13 257 563 1 499 719 0.018 7 0.012 1 5 0.333 13 496 085 1 499 696 0.020 2 0.013 3 6 0.324 13 693 145 1 499 821 0.011 9 0.014 3 7 0.315 13 859 826 1 499 880 0.008 0 0.015 2 
下载: 导出CSV
表 2 不同谱宽下畸形波出现不同频次概率的预测值与数值结果对比
Tab. 2 Comparisons of the numerical and predicted values of possibility for frequencies of freak waves
γ 谱宽υ 出现1次畸形波的概率 相对误差/% 出现2次畸形波的概率 相对误差/% 理论值 数值结果 理论值 数值结果 2 0.367 0.103 4 0.103 3 0.10 0.006 0 0.006 0 0 4 0.343 0.126 9 0.125 5 1.12 0.009 3 0.009 1 2.20 6 0.324 0.144 9 0.146 5 1.09 0.012 5 0.012 7 1.57
下载: 导出CSV
表 3 不同谱宽下相邻畸形波时间间隔预测值与数值结果对比
Tab. 3 Comparisons of the numerical and predicted values of intervals of adjacent freak waves
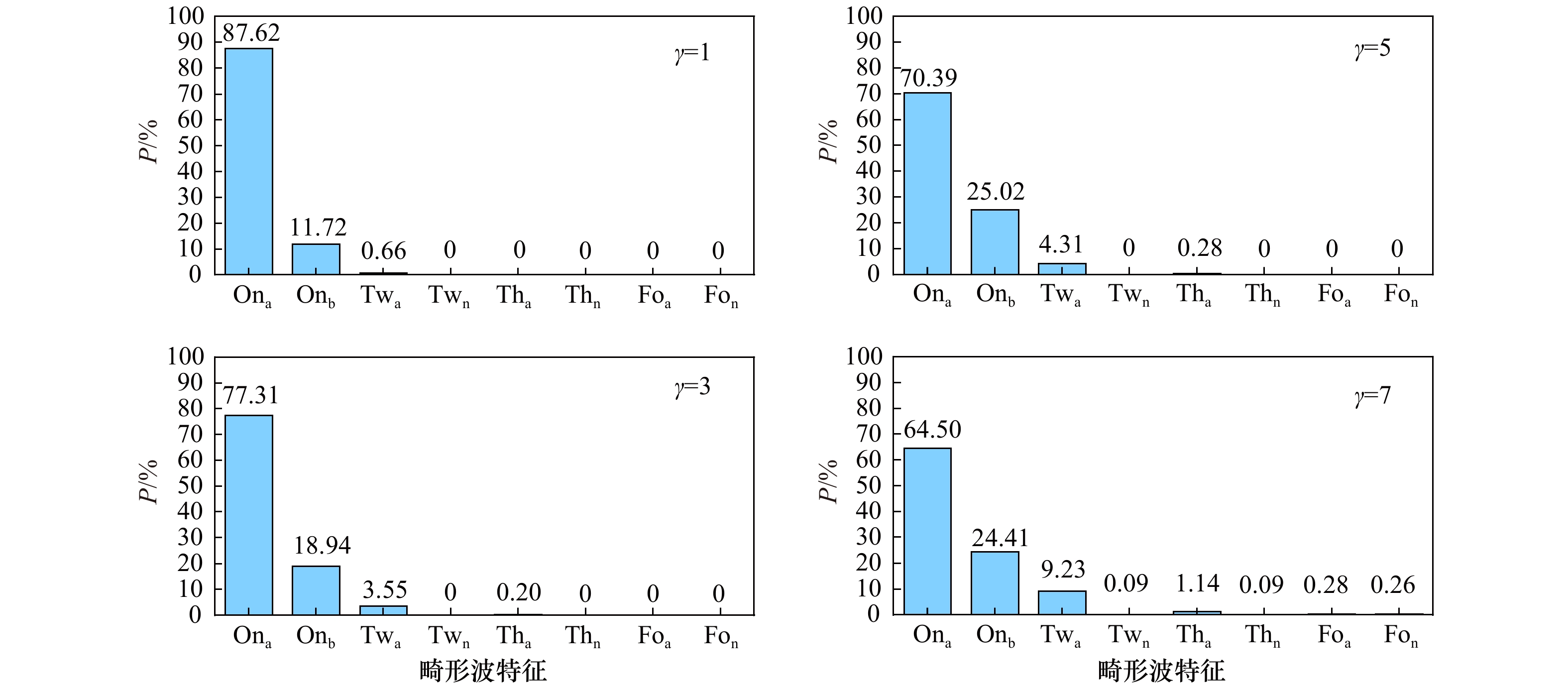
γ 谱宽υ Td /Tp=0.5×104 相对误差/% Td /Tp=1.5×104 相对误差/% 预测值/10−4 数值结果/10−4 预测值/10−4 数值结果/10−4 2 0.367 0.661 0.637 3.77 0.197 0.203 2.96 4 0.343 0.705 0.691 2.03 0.162 0.170 4.71 6 0.324 0.731 0.761 3.94 0.124 0.119 4.20
下载: 导出CSV
表 4 波群中包含畸形波的类型
Tab. 4 Classifications of freak waves in wave groups
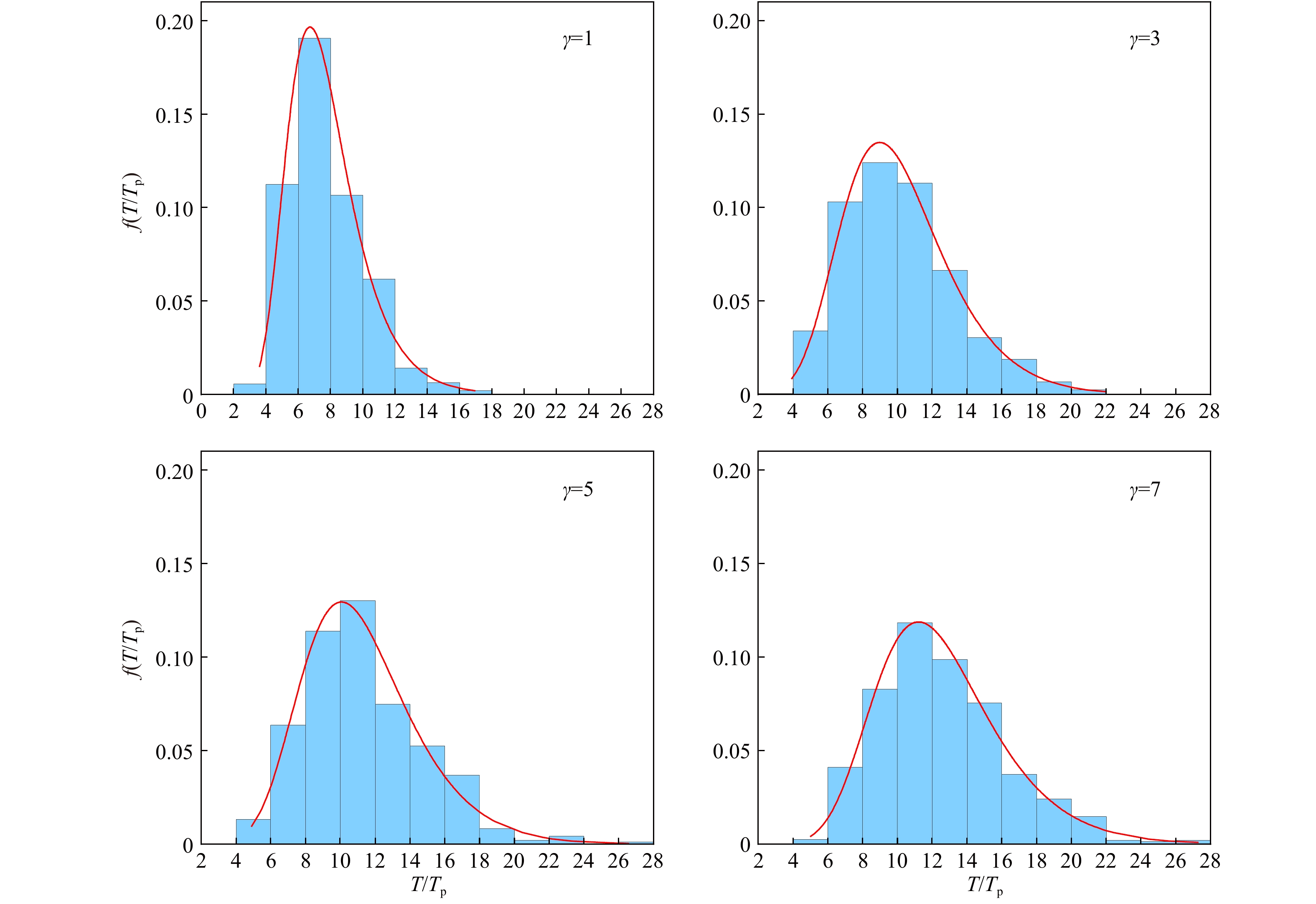
包含畸形波的个数 畸形波的特征和出现位置 命名 1 同时具有最高波峰和最深波谷 Ona 只具有最高波峰或最深波谷 Onb 2 相邻 Twa 间隔 Twn 3 相邻 Tha 间隔 Thn 4 相邻 Foa 间隔 Fon
下载: 导出CSV
表 5 畸形波群无量纲时间长度众数预测值与数值结果对比
Tab. 5 Comparisons of the numerical and predicted modes of the non-dimensional lengths of freak wave groups
γ 谱宽υ 预测值 数值结果 相对误差/% 2 0.367 8.0 8.0 0 4 0.343 9.5 9.2 3.3 6 0.324 10.5 10.5 0
下载: 导出CSV
-
[1] Dysthe K, Krogstad H E, Müller P. Oceanic rogue waves[J]. Annual Review of Fluid Mechanic, 2008, 40: 287−310. doi: 10.1146/annurev.fluid.40.111406.102203 [2] Cherneva Z, Petrova P, Andreeva N, et al. Probability distributions of peaks, troughs and heights of wind waves measured in the black sea coastal zone[J]. Coastal Engineering, 2005, 52(7): 599−615. doi: 10.1016/j.coastaleng.2005.02.006 [3] Haver S. A possible freak wave event measured at the Draupner Jacket January 1 1995[J]. Proceedings of the Rogue Waves, 2004: 1−8. [4] Kharif C, Pelinovskiĭ E N, Slunyaev A. Quasi-linear wave focusing[M]//Kharif C, Pelinovskiĭ E N, Slunyaev A. Rogue Waves in the Ocean. Berlin: Springer, 2009: 63−89. [5] Liu P C. A chronology of freauqe wave encounters[J]. Geofizika, 2007, 24(1): 57−70. [6] Waseda T. Rogue waves in the ocean[J]. Eos, Transactions American Geophysical Union, 2010, 91(11): 104. [7] Longuet-Higgins M S. On the statistical distribution of the heights of sea waves[J]. Journal of Marine Research, 1952, 11(5): 245−266. [8] 刘赞强, 张宁川. 基于Longuet-Higgins模型的畸形波模拟方法[J]. 水道港口, 2010, 31(4): 236−241. doi: 10.3969/j.issn.1005-8443.2010.04.002Liu Zanqiang, Zhang Ningchuan. Numerical methods for simulating freak waves based on the Longuet-Higgins wave model theory[J]. Journal of Waterway and Harbor, 2010, 31(4): 236−241. doi: 10.3969/j.issn.1005-8443.2010.04.002 [9] Gemmrich J, Garrett C. Unexpected waves[J]. Journal of Physical Oceanography, 2008, 38(10): 2330−2336. doi: 10.1175/2008JPO3960.1 [10] Brodtkorb P A, Johannesson P, Lindgren G, et al. WAFO-a Matlab toolbox for analysis of random waves and loads[C]//The Proceedings of the 10th (2000) International Offshore and Polar Engineering Conference v. 3. Seattle: WAFO, 2001: 343−350. [11] Gemmrich J, Garrett C. Unexpected waves: Intermediate depth simulations and comparison with observations[J]. Ocean Engineering, 2010, 37(2/3): 262−267. [12] Ghane M, Gao Zhen, Blanke M, et al. On the joint distribution of excursion duration and amplitude of a narrow-band Gaussian process[J]. IEEE Access, 2018, 6: 15236−15248. doi: 10.1109/ACCESS.2018.2816600 [13] 潘玉萍, 葛苏放, 沙文钰, 等. 由模拟波面分析双峰谱型海浪的统计特征[J]. 海洋学报, 2009, 31(4): 13−21.Pan Yuping, Ge Sufang, Sha Wenyu, et al. An analysis on the statistical characteristic of sea waves with double-peaked spectrum[J]. Haiyang Xuebao, 2009, 31(4): 13−21. [14] 毛青, 马玉祥, 袁长富. 基于数值模拟的畸形波统计特性研究[C]//第二十九届全国水动力学研讨会论文集(下册). 北京: 海洋出版社, 2018: 485−495.Mao Qing, Ma Yuxiang, Yuan Changfu. Research on statistical properties of freak wave based on numerical simulation[C]//Proceedings of the 29th National Conference on Hydrodynamics. Beijing: China Ocean Press, 2018: 485−495. [15] Veritas N. Environmental Conditions and Environmental Loads[M]. H̨vik: Det Norske Veritas, 2000. [16] Slunyaev A. Nonlinear analysis and simulations of measured freak wave time series[J]. European Journal of Mechanics-B/Fluids, 2006, 25(5): 621−635. doi: 10.1016/j.euromechflu.2006.03.005 [17] Slunyaev A, Pelinovsky E, Soares C G. Modeling freak waves from the North Sea[J]. Applied Ocean Research, 2005, 27(1): 12−22. doi: 10.1016/j.apor.2005.04.002 [18] Trulsen K. Simulating the spatial evolution of a measured time series of a freak wave[C]//Proceedings of a Workshop. Brest: IFREMER, 2001: 265−273. [19] Osborne A R, Onorato M, Serio M. The nonlinear dynamics of rogue waves and holes in deep-water gravity wave trains[J]. Physics Letters A, 2000, 275(5/6): 386−393. [20] Clauss G F. Dramas of the sea: Episodic waves and their impact on offshore structures[J]. Applied Ocean Research, 2002, 24(3): 147−161. doi: 10.1016/S0141-1187(02)00026-3 [21] 崔成, 张宁川. 畸形波生成, 演化过程时频能量结构研究[J]. 海洋工程, 2011, 29(3): 59−66.Cui Cheng, Zhang Ningchuan. Research on the time-frequency energy structure of generation and evolution of freak wave[J]. The Ocean Engineering, 2011, 29(3): 59−66. [22] Onorato M, Proment D, Toffoli A. Triggering rogue waves in opposing currents[J]. Physical Review Letters, 2011, 107(18): 184502. doi: 10.1103/PhysRevLett.107.184502 [23] Magnusson A K, Trulsen K, Aarnes O J, et al. “Three Sisters” measured as a triple rogue wave group[C]//ASME 2019 38th International Conference on Ocean, Offshore and Arctic Engineering. Glasgow: ASME, 2019: 1−8. [24] Olagnon M. Rogue Waves: Anatomy of a Monster[M]. Taylor R D, trans. London: Adlard Coles Nautical, 2017. [25] Liu P C, Hawley N. Wave grouping characteristics in nearshore Great Lakes II[J]. Ocean Engineering, 2002, 29(11): 1415−1425. doi: 10.1016/S0029-8018(01)00079-8 [26] Hasselmann K F, Barnett T, Bouws E, et al. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP)[M]. Ergänzungsheft zur Deutschen Hydrographischen Zeitschrift, 1973: 8−12. [27] Tao Aifeng, Qi Keren, Zheng Jinhai, et al. The occurrence probabilities of rogue waves in different nonlinear stages[J]. Coastal Engineering Proceedings, 2014, 34: 1−6. [28] 翟钢军, 唐东洋, 刘琨, 等. 风浪联合作用下深水半潜式平台运动响应模型试验研究[J]. 中国海洋平台, 2011, 26(6): 43−48. doi: 10.3969/j.issn.1001-4500.2011.06.010Zhai Gangjun, Tang Dongyang, Liu Kun, et al. Experimental analysis for the motion response of deep-water semi-submersible platform under wind and waves[J]. China Offshore Platform, 2011, 26(6): 43−48. doi: 10.3969/j.issn.1001-4500.2011.06.010 [29] Longuet-Higgins M S. The statistical analysis of a random, moving surface[J]. Philosophical Transactions of the Royal Society A Mathematical, Physical and Engineering Sciences, 1957, 249(966): 321−387. [30] Tao Aifeng, Peng Ji, Zheng Jinhai, et al. Discussions on the occurrence probabilities of observed freak waves[J]. Journal of Marine Science and Technology, 2015, 23(6): 923−928. [31] Wang Y, Tao A F, Zheng J H, et al. A preliminary investigation of rogue waves off the Jiangsu coast, China[J]. Natural Hazards and Earth System Sciences, 2014, 14(9): 2521−2527. doi: 10.5194/nhess-14-2521-2014 [32] 毛青. 基于数值模拟的海面突发巨浪统计特征研究[D]. 大连: 大连理工大学, 2019.Mao Qing. Study on the statistical characteristics of sudden appearance huge waves using numerical simulations[D]. Dalian: Dalian University of Technology, 2019. [33] Kharif C, Pelinovsky E. Physical mechanisms of the rogue wave phenomenon[J]. European Journal of Mechanics-B/Fluids, 2003, 22(6): 603−634. doi: 10.1016/j.euromechflu.2003.09.002 -
计量
- 文章访问数: 439
- HTML全文浏览量: 154
- PDF下载量: 30
- 被引次数: 0
