椒江河口层化动力特性研究

姚炎明; 郑逸群; 赵新宇; 袁金雄; 李莉

doi:10.12284/hyxb2021135

椒江河口层化动力特性研究

doi: 10.12284/hyxb2021135

1.
浙江大学海洋学院，浙江舟山 316021
2.
台州市港航事业发展中心，浙江台州 318001

基金项目: 国家重点研发计划项目（2020YFD0900803）；国家自然科学基金（41976157）；中央高校基本科研业务费；浙江省基金（2020C03012）

详细信息

作者简介:
姚炎明（1964-），男，浙江省嘉兴市人，主要从事河口泥沙动力学研究。E-mail：hotfireyao@163.com

通讯作者:
李莉（1982-），女，山东省青岛市人，主要从事河口动力与泥沙动力学研究。E-mail：lilizju@zju.edu.cn

中图分类号: P731.2
计量
- 文章访问数: 565
- HTML全文浏览量: 131
- PDF下载量: 33
- 被引次数: 0
出版历程
- 收稿日期: 2020-07-06
- 修回日期: 2021-04-17
- 网络出版日期: 2021-09-02
- 刊出日期: 2021-10-30

Characteristics of stratification in the Jiaojiang Estuary

1.
Ocean College, Zhejiang University, Zhoushan 316021, China
2.
Taizhou Port and Shipping Administration Bureau, Taizhou 318001, China

摘要

摘要: 基于椒江河口大、小潮期间水位、流速、盐度和悬沙浓度观测数据，研究了椒江河口主潮汐通道的水动力、盐度和悬沙浓度的时空变化特征，解释了高浊度强潮作用下的层化物理机制。椒江河口大潮期悬沙浓度和盐度均大于小潮期，主潮汐通道区域落潮期悬沙浓度大于涨潮期；盐度随潮变化，盐水锋面出现在S2测站，锋面附近出现最大浑浊带；自陆向海，悬沙浓度递减，盐度递增；随水深增加，悬沙浓度与盐度递增。Richardson数与混合参数显示，盐度和悬沙引起的层化现象，是随着潮汐的变化而变化，涨潮时的层化均强于落潮，小潮时的层化持续时间最长，区域更广。混合参数随潮周期变化，大潮期高于临界值1.0，小潮期低于临界值1.0。小潮期水体层化强于大潮期；潮汐应变项是影响势能差异变化率的重要因素；落潮期间层化向混合状态转化，涨潮相反。
- 悬沙浓度 /
- 盐度 /
- 层化 /
- 混合 /
- 椒江河口
Abstract: The elevation, current, salinity and suspended sediment concentration (SSC) data were observed during spring and neap tides in the Jiaojiang Estuary. The spatial and temporal characteristics of tides, salinity and SSC in the main tidal channel of the estuary were studied, and the stratification physical mechanism under the action of high turbidity and strong tides was explained, using the field data. SSC and salinity during spring tides were higher than those during neap tides, and SSC during ebb periods was higher than the flood periods along the main channel. Salinity varied with the tidal currents, and the salinity water front appeared around the Station S2. A turbidity maximum zone appeared near the salt water front. SSC decreased and the salinity increased towards the sea. SSC and salinity increased with the water depth. According to the Richardson number and mixing parameters, stratification caused by salinity and SSC changes with tides. Stratification during flood periods was stronger than during ebb periods. Stratification lasted the longest time and was more extensive during neap tides. The mixing parameter varied with the tidal periods, and the value was high/below the critical value of 1.0 during spring/neap tides. The tidal strain term was an important role for the change rate of the potential energy anomaly. The stratified state changed to a mixed state during neap tides, while the opposite change occurred during flood tides.
- suspended sediment concentration /
- salinity /
- stratification /
- tidal mixing /
- Jiaojiang Estuary

HTML全文

图 1 椒江河口测站位置（采用1985国家高程基准面）

Fig. 1 Locations of the field stations in the Jiaojiang Estuary (refers to the 1985 National Vertical Datum of China)

下载: 全尺寸图片幻灯片

图 2 H1、H2站潮位时间序列

Fig. 2 Time series of tide elevation at stations H1 and H2

下载: 全尺寸图片幻灯片

图 3 5个测站大潮期垂向各层流速大小和方向的时间序列（起始时间为2014年8月26日上午8点）

Fig. 3 Time series of vertical current profiles during spring tides at the 5 field stations (the x-axis is in hours from 8:00 a.m., August 26, 2014)

下载: 全尺寸图片幻灯片

图 4 5个测站小潮期垂向各层流速大小和方向的时间序列（起始时间为2014年9月3日上午8点）

Fig. 4 Time series of vertical current profiles during neap tides at the 5 field stations (the x-axis is in hours from 8:00 a.m., September 3, 2014)

下载: 全尺寸图片幻灯片

图 5 5个测站大小潮期（上为大潮期，下为小潮期）垂向悬沙浓度剖面时间序列

Fig. 5 Time series of vertical profiles of suspended sediment concentration during spring (upper panel) and neap (lower panel) tides at the 5 field stations

下载: 全尺寸图片幻灯片

图 6 5个测站大小潮期（上为大潮期，下为小潮期）垂向盐度剖面时间序列

Fig. 6 Time series of vertical profiles of salinity during spring (upper panel) and neap (lower panel) tides at the 5 field stations

下载: 全尺寸图片幻灯片

图 7 大潮期流速(a)、盐度(b)和悬沙浓度沿主潮汐通道分布(c)

矢量表示当前的方向和速度。x轴的起点是1号站

Fig. 7 Along channel distribution of current speed (a), salinity (b) and suspended sediment concentration (c) during spring tide

The vectors indicate current directions and speeds. The starting point of the x-axis is station 1

下载: 全尺寸图片幻灯片

图 8 5个测站大小潮期（上为大潮期，下为小潮期）只考虑盐度的水体密度(黑线)时和考虑盐度和悬沙浓度的水体密度的log₁₀(Ri/0.25)时间序列

Fig. 8 Time series of the Richardson number log₁₀(Ri/0.25) considering only salinity in the calculation of water density (black lines), and considering salinity and suspended sediment concentration in the calculation of water density (red lines) during spring (upper panel) and neap (lower panel) tides at the 5 stations

下载: 全尺寸图片幻灯片

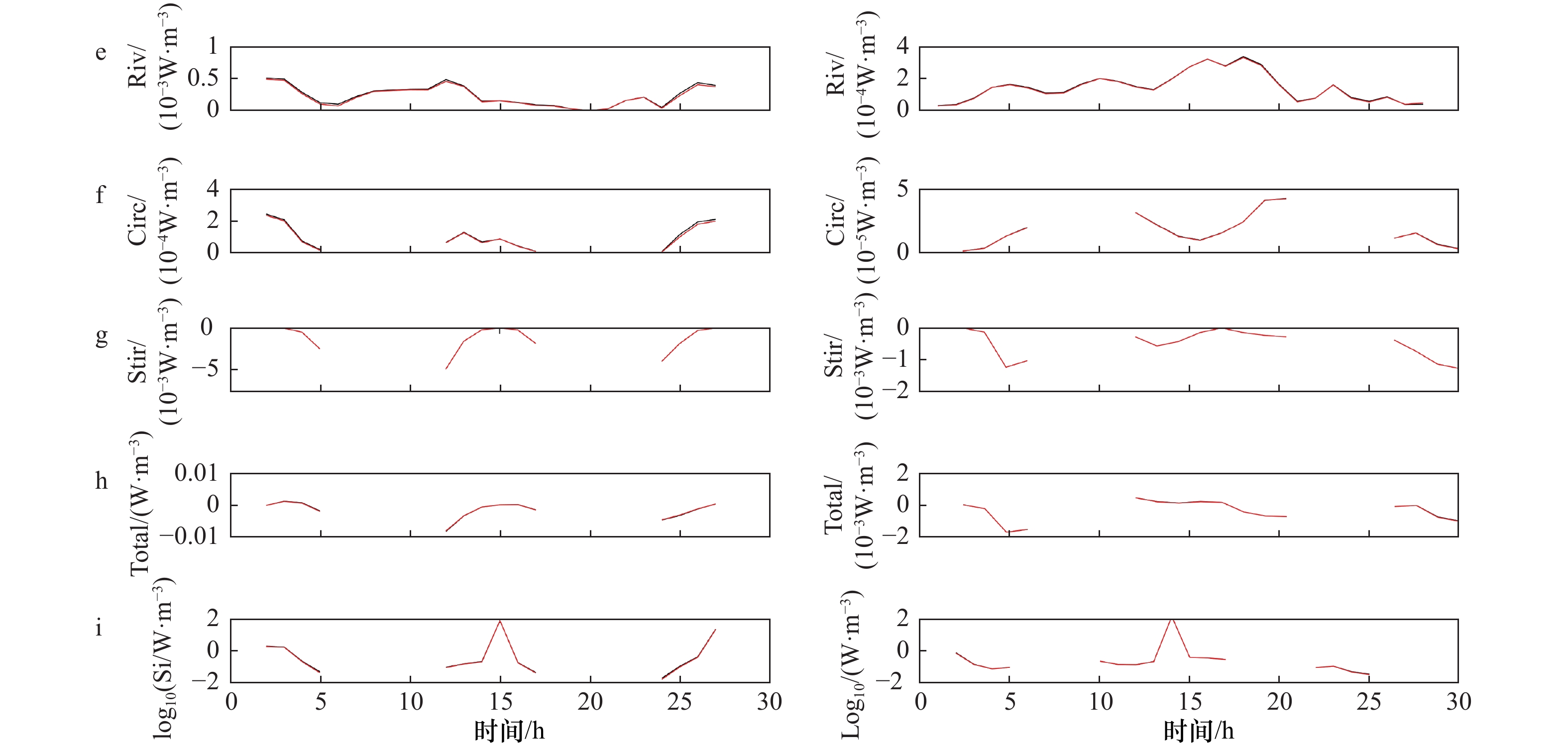
图 9 S3测站大小潮期潮位（Ele）（a）、流速（U）（b）、势能差异（φ）（c）、潮汐应变（Strain）（d）、河流效应（Riv）（e）、重力环流（Circ）（f）、潮汐搅动（Stir）（g）、势能差异的总时间导数（Total）（h）和log₁₀(Si)时间序列（i），左列为大潮期，右列为小潮期

黑色线为只考虑盐度计算水体密度，红色线为考虑盐度和悬沙浓度计算水体密度

Fig. 9 Time series of the tidal elevation (Ele) (a), current speed (U) (b), potential energy anomaly (φ) (c), tidal straining (Strain) (d), river effect (Riv) (e), gravitational circulation (Circ) (f), tidal stirring (Stir) (g), total time derivative of the potential energy anomaly (Total) (h), and the Simpson number log₁₀(Si) (i) at Station S3

Considering only salinity in the calculation of water density (black lines), and considering suspended sediment concertration and salinity in the calculation of water density (red lines)

下载: 全尺寸图片幻灯片

表 1 关于层化机制研究的部分相关文献

Tab. 1 References of stratification mechanism research

作者（年份）	名称	公式	注释
Holzman^[8]（1943）	梯度 Richardson 数（Ri）	$Ri = - \dfrac{g}{\rho } \cdot \dfrac{{\partial \rho }}{{\partial z}} \cdot {\left( {\dfrac{{\partial u}}{{\partial z}}} \right)^{ - 2}}$	反映层化与剪切之间的平衡关系和水体的整体稳定性（Monismith^[9]（2010））
Linden^[10]（1979）	通量 Richardson 数（Ri_f）	${Ri_f} = \dfrac{{g\overline {{\rho '}{w'}} }}{{\rho u_*^2\partial U/\partial Z}}$	可利用湍动能中转化为层化势能的比例，衡量混合效率
Bowden^[11]（1981）	整体 Richardson 数（Ri_o）	$R{i_o} = - \dfrac{{g\Delta \rho h}}{{\rho {{\left( {\Delta u} \right)}^2}}}$	湍流卷挟强度与Ri_o关系紧密
Simpson和 Bowers ^[12]（1981）	势能差异（Potential Energy Anomaly）	$\phi {\rm{ = } }\dfrac{1}{h}\displaystyle\int_{ - h}^0 {(\overline \rho - \rho )} gz{\rm{d}}z$，$\overline \rho = \dfrac{1}{h}\displaystyle\int_{ - h}^0 \rho {\rm{d}}z$	使水体在垂向上达到完全混合状态所需要的能量，量化层化的强度
Simpson等^[13]（1990）	一维势能差异方程	$\begin{aligned}\dfrac{{\partial \phi }}{{\partial t}} =& {\left(\dfrac{{\partial \phi }}{{\partial t}}\right)_{{\rm{strain}}}} + {\left(\dfrac{{\partial \phi }}{{\partial t}}\right)_{{\rm{cir}}}} - \\&{\left(\dfrac{{\partial \phi }}{{\partial t}}\right)_{{\rm{stir}}}} - {\left(\dfrac{{\partial \phi }}{{\partial t}}\right)_{{\rm{wind}}}}\\ = &0.031gh\overline {{u_t}} \dfrac{{\partial \rho }}{{\partial x}} + 0.003\;1\dfrac{{{g^2}{h^4}}}{{A\rho }}{\left(\dfrac{{\partial \rho }}{{\partial x}}\right)^2} -\\& \varepsilon k\rho \dfrac{{{{\left\| {\overline u } \right\|}^3}}}{h} - \delta {k_s}{\rho _a}\dfrac{{{{\overline W }^3}}}{h}\end{aligned}$	影响河口水体层化的多种物理机制，定量分析河口水体层化的形成与衰退
Monismith和Fong^[14]（1996）	Simpson 数（Si）（或水平Richardson 数(Ri_x)）	$Si = \dfrac{{\beta g{h^2}}}{{{C_D}U_T^2}}\dfrac{{\partial S}}{{\partial x}}$	表征潮汐应变与湍流混合平衡关系的无量纲参数
Verspecht等^[15]（2009）	改进的水平Richardson 数（Ri_x）	$R_x^{wt} = - \dfrac{g}{\rho }\dfrac{{\partial \rho }}{{\partial x}}\dfrac{{{H^2}}}{{u_{wt}^2}}$，${u_{wt}} = {\left( {u_{\max }^2 + \dfrac{{{\rho _a}}}{{{\rho _0}}}{W^2}} \right)^{1/2}}$	包含潮汐和风的共同作用。可以较好的指示层化发展和破坏的时间，但不能准确的判断层化的强度
Burchard和Hofmeister^[16]（2008）	三维势能差异方程	$\begin{aligned}{\partial _t}\phi =& - {\nabla _h}\left( {\overline u \phi } \right) + \dfrac{g}{D}{\nabla _h}\overline \rho \cdot \int_{ - H}^\eta z \overline u {\rm{d} }z - \\ &\dfrac{g}{D}\int_{ - H}^\eta {\left( {\eta - \dfrac{D}{2} - z} \right)} \overline u \cdot {\nabla _h}\overline \rho {\rm{d} }z-\\ & \dfrac{g}{D}\int_{ - H}^\eta {\left( {\eta - \dfrac{D}{2} - z} \right)} \overline w \cdot {\partial _z}\overline \rho {\rm{d} }z + \dfrac{ { {\rho _0} } }{D}\int_{ - H}^\eta { {P_b}{\rm{d} }z} -\\ & \dfrac{ { {\rho _0} } }{2}\left( {P_b^s + P_b^b} \right)+ \dfrac{g}{D}\int_{ - H}^\eta {\left( {\eta - \dfrac{D}{2} - z} \right)} Q{\rm{d} }z + \\ & \dfrac{g}{D}\int_{ - H}^\eta {\left( {\eta - \dfrac{D}{2} - z} \right)} {\nabla _h}\left( { {K_h}{\nabla _h}\rho } \right){\rm{d} }z\end{aligned}$	包含了经验方程中未包含但能够对势能差异产生影响的其他机制（平流、深度平均应变、非平均应变、垂向对流、垂向混合）
Song等^[17]（2013）	考虑泥沙对水体层化的影响	$\begin{aligned}{\varphi _{{\rm{tot}}} } =& \dfrac{1}{D}\int_{ - h}^\eta {\left( {\overline { {\rho _w} } - {\rho _w} } \right)} gz{ {\rm{d} } }z + \dfrac{1}{D}\int_{ - h}^\eta {\left( {\overline C - C} \right)} gz{\rm{d} }z - \\& \dfrac{1}{ { {\rho _s}D} }\int_{ - h}^\eta {\left( {\overline { {\rho _w}C} - {\rho _w}C} \right)} gz{\rm{d}}z\end{aligned}$	将泥沙浓度考虑进水体密度，进而影响势能
Pu等^[18]（2015）	改进的纵向一维势能差异方程	$\begin{aligned}\dfrac{{\partial \phi }}{{\partial t}} =& {\left(\dfrac{{\partial \phi }}{{\partial t}}\right)_{{\rm{strain}}}} + {\left(\dfrac{{\partial \phi }}{{\partial t}}\right)_{{\rm{river}}}} + {\left(\dfrac{{\partial \phi }}{{\partial t}}\right)_{{\rm{cir}}}} - \\&{\left(\dfrac{{\partial \phi }}{{\partial t}}\right)_{{\rm{stir}}}} - {\left(\dfrac{{\partial \phi }}{{\partial t}}\right)_{{\rm{wind}}}}\\ =& 0.035gh\overline {{u_t}} \dfrac{{\partial \rho }}{{\partial x}} + 0.035gh\overline {{u_r}} \dfrac{{\partial \rho }}{{\partial x}} +\\& 0.003\;1\dfrac{{{g^2}{h^4}}}{{{N_z}\rho }}{\left(\dfrac{{\partial \rho }}{{\partial x}}\right)^2} - \varepsilon k\rho \dfrac{{{{\left\| {\overline u } \right\|}^3}}}{h} - \delta {k_s}{\rho _a}\dfrac{{{{\overline W }^3}}}{h}\end{aligned}$	考虑河口效应对层化的影响
Li等^[19]（2018）	考虑泥沙对水体层化的影响，消除水深对势能差异的影响	$\begin{aligned}& {\rho _{ss}} = {\rho _0}\left( {1 + \beta {S_w}} \right) + \left[ {1 - \dfrac{{{\rho _0}\left( {1 + \beta {S_w}} \right)}}{{{\rho _s}}}} \right]C\\& Ri = - \dfrac{g}{{{\rho _{ss}}}} \cdot \dfrac{{\partial {\rho _{ss}}}}{{\partial z}} \cdot {\left( {\dfrac{{\partial u}}{{\partial z}}} \right)^{ - 2}}\end{aligned}$ $Sr = \dfrac{\varphi }{ {\overline \varphi } } \cdot 100 {\text \%} = \dfrac{ {\dfrac{1}{h}\int_{ - h}^0 {\left( {\overline { {\rho _i} } - {\rho _i} } \right)gz{\rm{d}}z} } }{ {\dfrac{1}{h}\int_{ - h}^0 { {\rho _i}gz{\rm{d}}z} } } \cdot 100 {\text \%}$	将泥沙浓度考虑进水体密度，影响Ri、Sr以及势能差异等

下载: 导出CSV

表 2 水文、泥沙观测参数及时间

Tab. 2 Hydrological, sediment observation parameters and time

测站	观测时间	观测参数
H1, H2	8月16日至9月15日，8月11日至9月15日	潮位^①
S1−S5	大、小潮期^③	流速流向、悬沙浓度、盐度、底床泥沙^②
注：①流速流向观测均采用6点法：表层，0.2H，0.4H，0.6H，0.8H，底层。②盐度采用三点法：表层，0.6H，底层。悬沙浓度采用3点法：表层，0.6H，底层。③采样时间为大潮期（8月26日08:00至8月27日11:00）和小潮期（9月3日08:00至9月4日11:00）。

下载: 导出CSV

表 3 观测仪器

Tab. 3 Observation instruments

仪器名称	类型	用途
直读海流仪、水文绞车	SLC9-2、HY-100型	定点海流观测
DGPS测量系统	DGPS-MAX	测站定位
自记式水位计	TGR-2050型	潮位观测
横式采样器	XCL型2升	悬沙、悬移质、盐度取样

下载: 导出CSV

表 4 各潮位站主要全日、半日和浅海分潮的特征

Tab. 4 Main characteristics of the tidal constituents at stations H1 and H2

分潮	H1（8月16日至9月15日）		H2（8月11日至9月15日）
分潮	振幅/m	迟角/(°)	振幅/m	迟角/(°)
K₁	0.23	230.97	0.253 8	229.06
O₁	0.23	183.97	0.236 8	172.36
M₂	1.82	256.80	1.693 9	246.79
S₂	0.83	308.50	0.767 9	293.60
M₄	0.14	103.62	0.014 2	83.61
MS₄	0.13	136.97	0.010 6	57.05
M₆	0.01	324.32	0.020 4	290.71

下载: 导出CSV

表 5 由调和常数计算的潮汐性质和潮汐特征

Tab. 5 Tidal characteristics calculated by harmonic constants

项目	H1（8月16日至9月15日）	H2（8月11日至9月15日）
潮汐性质（H_K1+H_O1）/H_M2	0.25	0.29
主要半日分潮振幅比（H_S2/H_M2）	0.46	0.45
主要浅水分潮与主要半日分潮振幅比（H_M4/H_M2）	0.08	0.01
主要半日、全日分潮迟角差：G（M₂）−[G（K₁）+G（O₁）]	201.86°	205.37°
主要半日和浅海分潮迟角差：2G（M₂）−G（M₄）	49.98°	49.97°
主要浅海分潮振幅和（M₄+MS₄+M₆）	27.92 cm	4.52 cm

下载: 导出CSV

表 6 5个测站大、小潮余流计算结果

Tab. 6 Residual currents during spring and neap tides at the 5 field stations

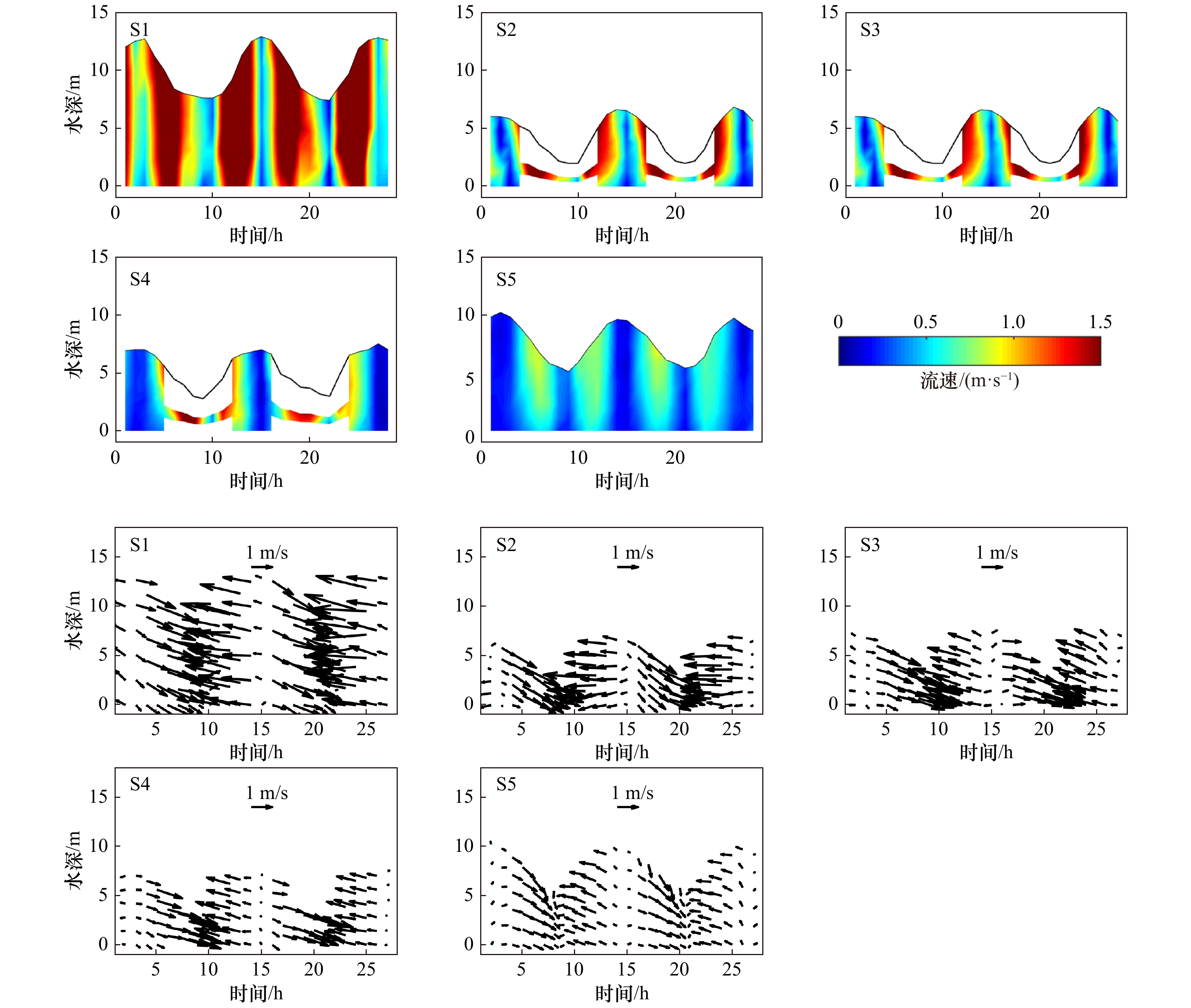
测站	层次	大潮		小潮
测站	层次	流速/(m·s⁻¹)	流向/(°)	流速/(m·s⁻¹)	流向/(°)
S1	表层	0.115	168	0.105	138
	中层	0.119	174	0.063	259
	底层	0.126	177	0.066	242
S2	表层	0.392	137	0.237	149
	中层	0.307	151	0.166	185
	底层	0.165	157	0.106	226
S3	表层	0.499	109	0.203	105
	中层	0.383	106	0.068	109
	底层	0.067	101	0.054	269
S4	表层	0.421	112	0.094	110
	中层	0.293	106	0.057	108
	底层	0.124	111	0.055	297
S5	表层	0.234	215	0.15	212
	中层	0.067	185	0.078	217
	底层	0.018	105	0.017	229

下载: 导出CSV

表 7 各测站大小潮期盐度、悬沙浓度对层化的贡献占比

Tab. 7 Contributions of salinity and suspended sediment concentration to the stratification during spring and neap tides at the 5 field stations

测站	大潮期						小潮期
	盐度贡献/%			悬沙浓度贡献/%			盐度贡献/%			悬沙浓度贡献/%
	最大	最小	平均	最大	最小	平均	最大	最小	平均	最大	最小	平均
S1	89.6	13.7	55.8	86.3	10.4	44.2	98.2	91.8	95.7	8.2	1.8	4.3
S2	85.0	35.7	63.7	64.3	15.0	36.3	97.3	91.6	95.3	8.4	2.8	4.7
S3	87.0	42.7	73.5	57.3	13.0	26.5	98.1	89.8	95.9	10.2	1.9	4.1
S4	88.7	26.1	54.5	73.9	11.3	45.5	96.8	58.5	87.9	41.5	3.2	12.1
S5	86.6	6.6	34.2	93.4	13.4	65.8	87.0	46.3	70.0	53.7	13.0	30.0

下载: 导出CSV

参考文献(33)

[1]	Allahdadi M N, Li Chunyan. Effect of stratification on current hydrodynamics over Louisiana shelf during Hurricane Katrina[J]. Water Science and Engineering, 2017, 10(2): 154−165. doi: 10.1016/j.wse.2017.03.012
[2]	Scully M E, Geyer W R. The role of advection, straining, and mixing on the tidal variability of estuarine stratification[J]. Journal of Physical Oceanography, 2012, 42(5): 855−868. doi: 10.1175/JPO-D-10-05010.1
[3]	Geyer W R. The importance of suppression of turbulence by stratification on the estuarine turbidity maximum[J]. Estuaries, 1993, 16(1): 113−125. doi: 10.2307/1352769
[4]	Shen Huanting, Mao Zhichang, Gu Yuliang. Impact of south-north water transfer (east route) on saltwater intrusion in the Changjiang Estuary with consideration of its countermeasures[J]. Resources and Environment in the Yangtza Basin, 2002, 11(2): 150−154.
[5]	Figueroa S M, Lee G H, Shin H J. Effects of an estuarine dam on sediment flux mechanisms in a shallow, macrotidal estuary[J]. Estuarine, Coastal and Shelf Science, 2020, 238: 106718. doi: 10.1016/j.ecss.2020.106718
[6]	Li Zhanhai, Jia Jianjun, Wu Yongsheng, et al. Correction to: Vertical distributions of suspended sediment concentrations in the turbidity maximum zone of the periodically and partially stratified Changjiang Estuary[J]. Estuaries and Coasts, 2019, 42(7): 1970. doi: 10.1007/s12237-019-00616-z
[7]	Thomson W. Hydrokinetic solutions and observations[J]. Philosophical Magazine, 1871, 42(281): 362−377.
[8]	Holzman B. The influence of stability on evaporation[J]. Annals of the New York Academy of Sciences, 1943, 44(1): 13−18. doi: 10.1111/j.1749-6632.1943.tb31289.x
[9]	Monismith S G. Contemporary issues in estuarine physics: Mixing in estuaries[D]. Cambridge: Cambridge University, 2010: 145−185.
[10]	Linden P F. Mixing in stratified fluids[J]. Geophysical & Astrophysical Fluid Dynamics, 1979, 13(1): 3−23.
[11]	Bowden K F. Turbulent mixing in estuaries[J]. Ocean Management, 1981, 6(2/3): 117−135.
[12]	Simpson J H, Bowers D. Models of stratification and frontal movement in shelf seas[J]. Deep-Sea Research Part A: Oceanographic Research Papers, 1981, 28(7): 727−738. doi: 10.1016/0198-0149(81)90132-1
[13]	Simpson J H, Brown J, Matthews J, et al. Tidal straining, density currents, and stirring in the control of estuarine stratification[J]. Estuaries, 1990, 13(2): 125−132. doi: 10.2307/1351581
[14]	Monismith S G, Fong D A. A simple model of mixing in stratified tidal flows[J]. Journal of Geophysical Research, 1996, 101(C12): 28583−28595. doi: 10.1029/96JC02267
[15]	Verspecht F, Rippeth T P, Simpson J H, et al. Residual circulation and stratification in the Liverpool Bay region of freshwater influence[J]. Ocean Dynamics, 2009, 59(5): 765−779. doi: 10.1007/s10236-009-0233-2
[16]	Burchard H, Hofmeister R. A dynamic equation for the potential energy anomaly for analysing mixing and stratification in estuaries and coastal seas[J]. Estuarine, Coastal and Shelf Science, 2008, 77(4): 679−687. doi: 10.1016/j.ecss.2007.10.025
[17]	Song Dehai, Wang Xiaohua, Cao Zhenyi, et al. Suspended sediment transport in the deepwater navigation channel, Yangtze River Estuary, China, in the dry season 2009: 1. Observations over spring and neap tidal cycles[J]. Journal of Geophysical Research: Oceans, 2013, 118(10): 5555−5567. doi: 10.1002/jgrc.20410
[18]	Pu Xiang, Shi J Z, Hu Guodong, et al. Circulation and mixing along the north passage in the Changjiang River Estuary, China[J]. Journal of marine systems, 2015, 148: 213−235. doi: 10.1016/j.jmarsys.2015.03.009
[19]	Li Li, He Zhiguo, Xia Yuezhang, et al. Dynamics of sediment transport and stratification in Changjiang River Estuary, China[J]. Estuarine, Coastal and Shelf Science, 2018, 213: 1−17. doi: 10.1016/j.ecss.2018.08.002
[20]	中国海湾志编纂委员会. 中国海湾志(第十四分册)[M]. 北京: 海洋出版社, 1998. China Gulf Chronicle Compilation Committee. Gulf Annals of China (Volume 14)[M]. Beijing: China Ocean Press, 1998.
[21]	张瑾, 沈先荣, 田林. 椒江河口航道整治与效果分析[J]. 水运工程, 2009(9): 131−135. doi: 10.3969/j.issn.1002-4972.2009.09.029 Zhang Jin, Shen Xianrong, Tian Lin. Improvement and effect analysis on Jiaojiang Estuary waterway[J]. Port & Waterway Engineering, 2009(9): 131−135. doi: 10.3969/j.issn.1002-4972.2009.09.029
[22]	谢钦春, 李伯根, 夏小明, 等. 椒江河口悬沙浓度垂向分布和泥跃层发育[J]. 海洋学报, 1998, 20(6): 58−69. Xie Qinchun, Li Bogen, Xia Xiaoming, et al. Vertical distributions of suspended matter and lutoclines in the Jiaojiang Estuary[J]. Haiyang Xuebao, 1998, 20(6): 58−69.
[23]	国家技术监督局, 中华人民共和国建设部. GB50159-1992, 河流悬移质泥沙测验规范[S]. 北京: 中国标准出版社, 1992: 26-39. The State Bureau of Quality and Technical Supervision, Ministry of Construction of the People’s Republic of China. GB50159-92, Code for measurements of suspended sediment in open channels[S]. Beijing: Standards Press of China, 1992: 26−39.
[24]	Wu Shuntang. A constructive approach to local linear interplation operator[J]. Mathematical Theory and Applications, 2001, 21(3): 54−58.
[25]	Ni Zhihui, Chen Hui, Dong Lixian, et al. Measurement and analysis of vertical mixing and stratification within the plume outside the Changjiang River Estuary[J]. Journal of Shanghai Jiaotong University, 2012, 46(11): 1862−1873.
[26]	Geyer W R, Maccready P. The estuarine circulation[J]. Annual Review of Fluid Mechanics, 2014, 46(1): 175−197. doi: 10.1146/annurev-fluid-010313-141302
[27]	Burchard H, Hetland R D, Schulz E, et al. Drivers of residual estuarine circulation in tidally energetic estuaries: Straight and irrotational channels with parabolic cross section[J]. Journal of Physical Oceanography, 2011, 41(3): 548−570. doi: 10.1175/2010JPO4453.1
[28]	Bigg P H. Density of water in SI units over the range 0−40°C[J]. British Journal of Applied Physics, 2002, 18(4): 521−525.
[29]	Wang Xiaohong. Tide-induced sediment resuspension and the bottom boundary layer in an idealized estuary with a muddy bed[J]. Journal of Physical Oceanography, 2002, 32(11): 3113−3131. doi: 10.1175/1520-0485(2002)032<3113:TISRAT>2.0.CO;2
[30]	Becherer J, Burchard H, Floser G, et al. Evidence of tidal straining in well-mixed channel flow from micro-structure observations[J]. Geophysical Research Letters, 2011, 38(17): L17611.
[31]	刘伟, 范代读, 涂俊彪, 等. 椒江河口春季悬沙输运特征及通量机制研究[J]. 海洋地质与第四纪地质, 2018, 38(1): 41−51. Liu Wei, Fan Daidu, Tu Junbiao, et al. Suspended transportation and flux mechanism of sediment in the Jiaojiang Estuary in spring[J]. Marine Geology & Quaternary Geology, 2018, 38(1): 41−51.
[32]	徐海, 武小勇, 张沈阳, 等. 椒江河口悬沙浓度时空变化特征分析[J]. 浙江水利科技, 2017, 45(3): 7−12. Xu Hai, Wu Xiaoyong, Zhang Shenyang, et al. Characteristics of temporal and spatial variation of suspended sediment concentration in Jiaojiang River Estuary[J]. Zhejiang Hydrotechnics, 2017, 45(3): 7−12.
[33]	赵今声, 赵子丹, 员瑛, 等. 海岸河口动力学[M]. 北京: 海洋出版社, 1993. Zhao Jinsheng, Zhao Zidan, Yuan Ying, et al. Coastal and Estuarine Dynamics[M]. Beijing: China Ocean Press, 1993.