Overtopping prediction for composite slope breakwater based on random forest method
-
摘要: 针对复坡堤越浪量的计算问题，提出了采用随机森林算法预测越浪量的方法。首先，通过对欧洲CLASH数据集进行筛选，挑选出符合复坡堤越浪量预测的数据；其次，对数据做无量纲化处理，建立以随机森林为基础的复坡堤越浪量预测模型，并通过网格搜索(GridSearchCV)方法对模型进行调参以改善模型的性能；最后，利用决定系数
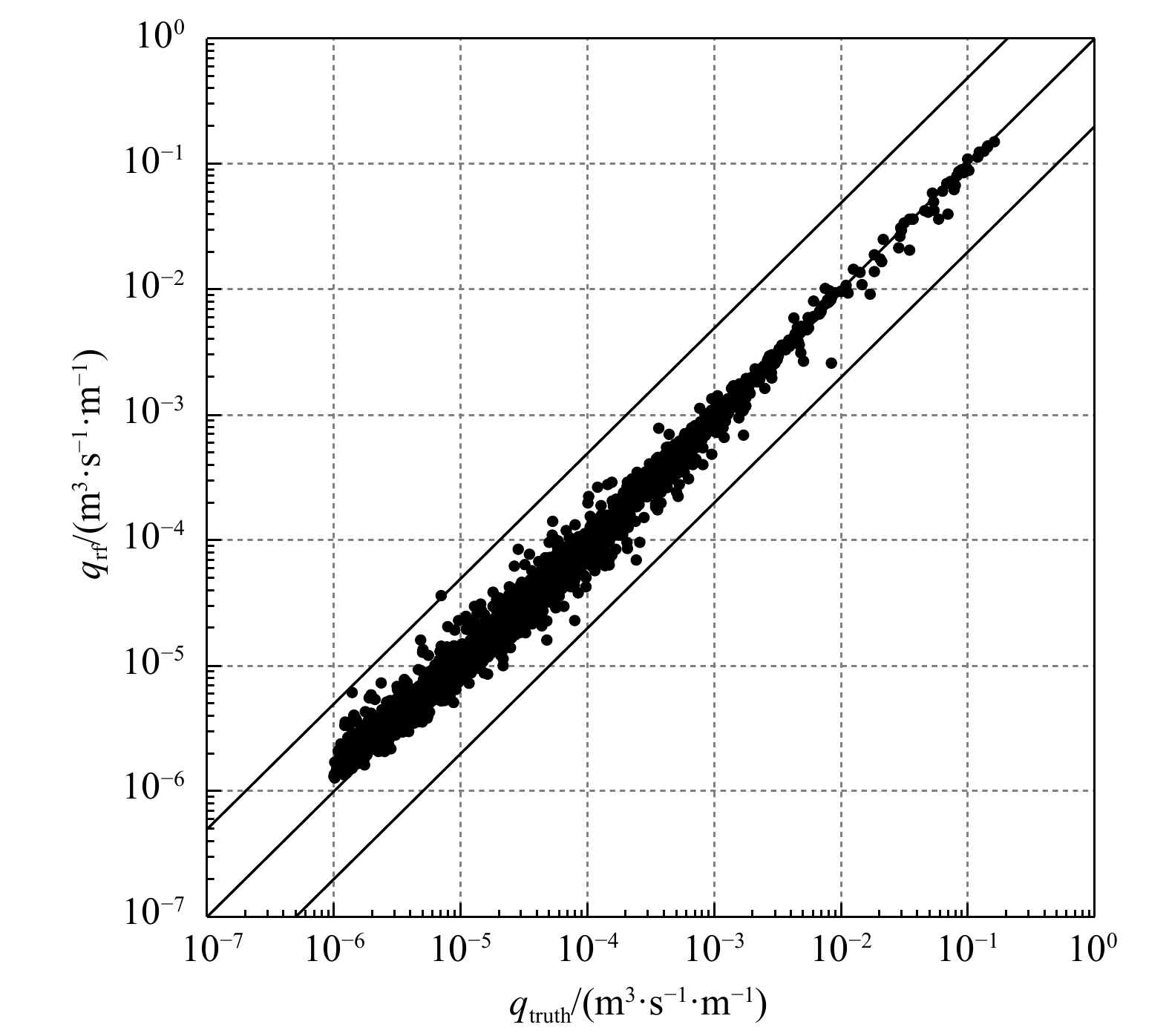
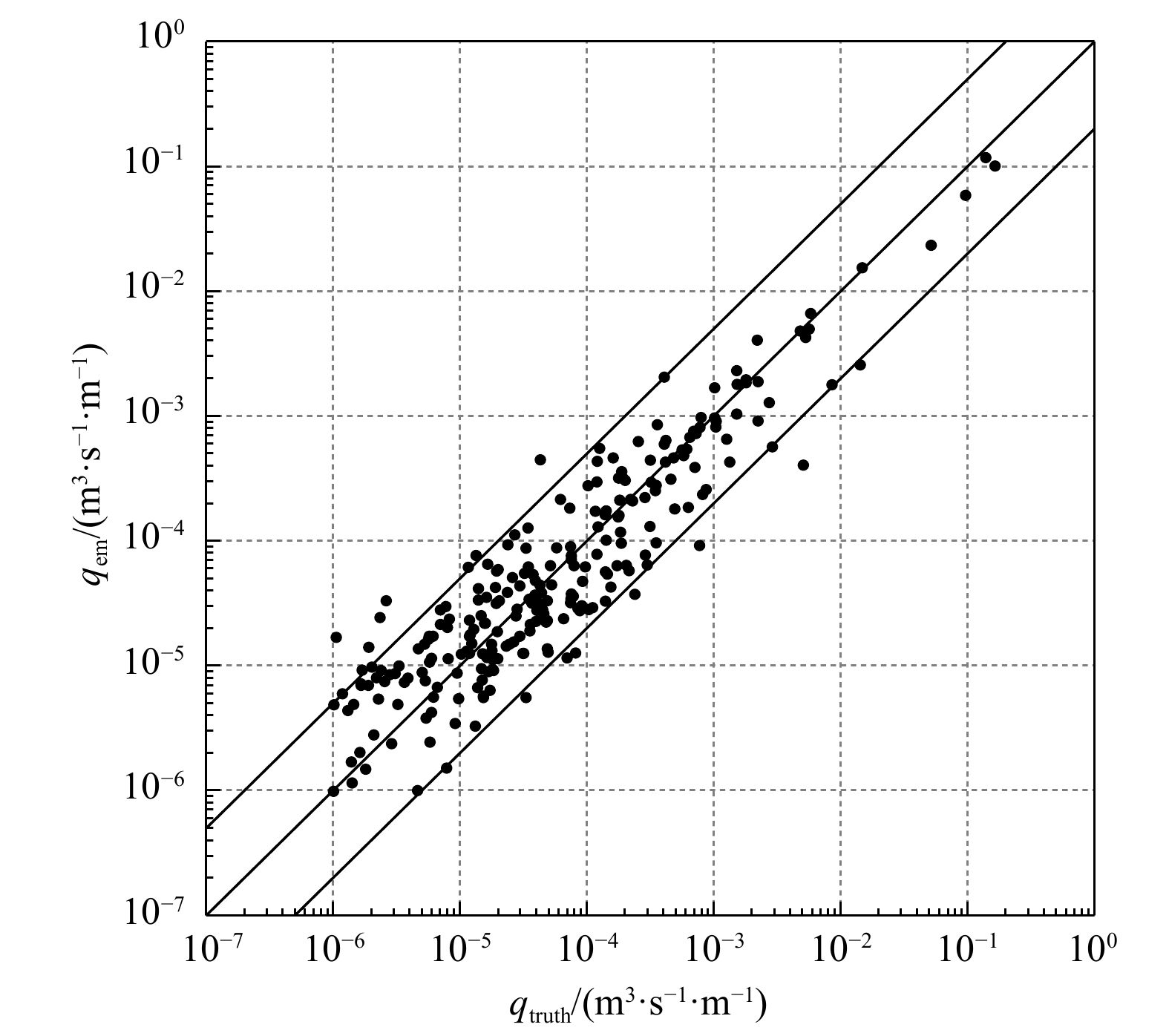
${R^2}$ 来评估模型的精度，并将随机森林模型与集成神经网络模型做了预测能力的对比，同时还给出了随机森林模型各个特征参数对预测精度的重要性。结果显示，随机森林模型的决定系数为92.7%，集成神经网络模型的决定系数为87.7%，表明随机森林模型对越浪量具有更强的学习和预测能力。通过对特征重要性的分析，墙顶高程对模型预测精度的影响最大，堤顶高程次之，堤脚宽度影响最小。Abstract: Aiming at the problem of calculating overtopping of the composite slope breakwater, a prediction model of the overtopping for the composite slope based on the random forest method is proposed. Firstly, by filtering the European CLASH data set, the data consistent with the prediction of overtopping of the composite slope breakwater are selected. Secondly, after dimensionless processing of the data, overtopping prediction model is established based on random forest method, and improved by adjusting the model parameters according to GridSearchCV. Finally, the coefficient of determination R2 is used to evaluate the accuracy of the model, and the prediction ability of the model is compared with the ensemble neural network model. The effect of each feature parameter of the random forest model on the prediction accuracy is assessed. The results show that the coefficient of determination of the random forest model is 92.7%, and the coefficient of determination of the ensemble neural network model is 87.7%, indicating the random forest model has a stronger prediction ability for predicting overtopping. Wall height with respect to static water level has the greatest influence on the prediction accuracy of the model, the height of the top of the embankment is the second, and the width of the foot of the embankment least. -
图 3 基于随机森林的复坡堤越浪量预测模型结构图
Fig. 3 Structure diagram of overtopping prediction model of composite slope breakwater based on random forest
图 6 训练集预测结果比较（集成神经网络）
Fig. 6 Prediction result of training set (ensemble neural network)
图 7 测试集预测结果比较（集成神经网络）
Fig. 7 Prediction result of testing set (ensemble neural network)
表 1 无量纲化后输入参数分布特征
Tab. 1 Distribution characteristics of input parameters after dimensionless
特征参数 平均值 最大值 最小值 标准差 ${H_{m{0 },t} }/{L_{m - 1,0,t} }$ 0.033 0.087 0.005 0.012 $\,\beta$ 0.716 80.000 0.000 4.820 $h/{L_{m - 1,0,t}}$ 0.135 0.666 0.010 0.102 ${h_t}/{H_{m0,t}}$ 3.467 22.566 0.429 2.403 ${B_t}/{L_{m - 1,0,t}}$ 0.017 0.396 0.000 0.050 ${h_b}/{H_{m0,t}}$ 0.173 7.826 –2.652 1.014 $B/{L_{m - 1,0,t}}$ 0.093 0.973 0.000 0.109 ${A_c}/{H_{m0,t} }$ 1.155 4.216 –5.242 0.581 ${R_c}/{H_{m0,t} }$ 1.246 6.032 0.000 0.531 ${G_c}/{L_{m - 1,0,t}}$ 0.023 0.257 0.000 0.039 $m$ 417.755 1 050.000 10.000 455.659 $\cot {\alpha _d}$ 1.672 7.000 0.000 1.331 $\cot {\alpha _{incl}}$ 2.584 11.299 –1.331 2.096 ${\gamma _f}$ 0.790 1.000 0.380 0.269 $D/{H_{m0,t}}$ 0.118 0.807 0.000 0.152 目标参数 $q*$ 0.001 668 0.165 0.000 001 0.010 84 
下载: 导出CSV
表 2 重要参数取值范围
Tab. 2 Value range of important parameters
重要参数 取值范围 n_estimators 10～200 max_depth 10～50 max_features auto, sqrt
下载: 导出CSV
-
[1] 王红, 周家宝, 章家昌. 单坡堤上不规则波越浪量的估算[J]. 水利水运科学研究, 1996(1): 58−63.Wang Hong, Zhou Jiabao, Zhang Jiachang. Estimating of irregular wave overtopping quantities on single sloping[J]. Journal of Nanjing Hydraulic Research Institute, 1996(1): 58−63. [2] 中华人民共和国交通运输部. JTS 145−2015, 港口与航道水文规范[S]. 北京: 人民交通出版社, 2015.Ministry of Transport of China. JTS 145−2015, Code of Hydrology for Harbour and Waterway[S]. Beijing: China Communications Press, 2015. [3] 范红霞. 斜坡式海堤越浪量及越浪流试验研究[D]. 南京: 河海大学, 2006.Fan Hongxia. Expermental study on the overtopping discharge and overtopping flow of the sloped[D]. Nanjing: Hohai University, 2006. [4] 陈国平, 周益人, 严士常. 不规则波作用下海堤越浪量试验研究[J]. 水运工程, 2010(3): 1−6. doi: 10.3969/j.issn.1002-4972.2010.03.001Chen Guoping, Zhou Yiren, Yan Shichang. Test study on wave overtopping under irregular wave action[J]. Port & Waterway Engineering, 2010(3): 1−6. doi: 10.3969/j.issn.1002-4972.2010.03.001 [5] 陈松贵, 王泽明, 张弛, 等. 珊瑚礁地形上直立式防浪堤越浪大水槽实验[J]. 科学通报, 2019, 64(28/29): 3049−3058.Chen Songgui, Wang Zeming, Zhang Chi, et al. Experiment on wave overtopping of a vertical seawall on coral reefs in large wave flume[J]. Chinese Science Bulletin, 2019, 64(28/29): 3049−3058. [6] Liu Ye, Li Shaowu, Chen Songgui, et al. Random wave overtopping of vertical seawalls on coral reefs[J]. Applied Ocean Research, 2020, 100: 102166. doi: 10.1016/j.apor.2020.102166 [7] Owen M W. Design of seawalls allowing for wave overtopping[R]. Wallingford: Hydraulics Research Station,1980. [8] Allsop N W H, Bruce T, de Rouck J, et al. EurOtop II manual on wave overtopping of sea defences and related structures[R]. Deflt: Technical Adcisory Committee on Flood Defence, 2016. [9] Ward D L, Ahrens J P. Overtopping rates for seawalls[R]. Coastal Engineering Research Center Vicksburg MS, 1992. [10] 舒叶华, 徐宇航, 谢先坤. 复式海堤结构越浪量计算方法比较[J]. 水运工程, 2019(5): 27−31. doi: 10.3969/j.issn.1002-4972.2019.05.005Shu Yehua, Xu Yuhang, Xie Xiankun. Comparison of calculation methods for overtopping discharge of composite seawall structure[J]. Port & Waterway Engineering, 2019(5): 27−31. doi: 10.3969/j.issn.1002-4972.2019.05.005 [11] Oliveira T C A, Sánchez-Arcilla A, Gironella X. Simulation of wave overtopping of maritime structures in a numerical wave flume[J]. Journal of Applied Mathematics, 2012, 2012: 246146. [12] 关大玮. 规则波与不规则波的海堤越浪数值模拟[D]. 广州: 华南理工大学, 2016.Guan Dawei. Numerical simulation of regular and irregular wave overtopping against seawalls[D]. Guangzhou: South China University of Technology, 2016. [13] 董志, 关大玮, 苗青, 等. 复式海堤上规则波和不规则波越浪数值模拟研究[J]. 中国农村水利水电, 2020(3): 112−118. doi: 10.3969/j.issn.1007-2284.2020.03.022Dong Zhi, Guan Dawei, Miao Qing, et al. Numerical simulation of regular and irregular waves overtopping on composite section sea-dike[J]. China Rural Water and Hydropower, 2020(3): 112−118. doi: 10.3969/j.issn.1007-2284.2020.03.022 [14] van Gent M R A, van den Boogaard H F P, Pozueta B, et al. Neural network modelling of wave overtopping at coastal structures[J]. Coastal Engineering, 2007, 54(8): 586−593. doi: 10.1016/j.coastaleng.2006.12.001 [15] Formentin S M, Zanuttigh B, van der Meer J W. A neural network tool for predicting wave reflection, overtopping and transmission[J]. Coastal Engineering Journal, 2017, 59(1): 1750006. [16] 刘诗学, 王收军, 陈松贵, 等. 基于人工智能的单坡式防波堤越浪量评估方法研究与应用[J]. 水道港口, 2019, 40(5): 541−546, 587. doi: 10.3969/j.issn.1005-8443.2019.05.008Liu Shixue, Wang Shoujun, Chen Songgui, et al. Research and application of artificial intelligence based method for overtopping assessment of straight slopes[J]. Journal of Waterway and Harbor, 2019, 40(5): 541−546, 587. doi: 10.3969/j.issn.1005-8443.2019.05.008 [17] Liu Ye, Li Shaowu, Zhao Xin, et al. Artificial neural network prediction of overtopping rate for impermeable vertical seawalls on coral reefs[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2020, 146(4): 04020015. doi: 10.1061/(ASCE)WW.1943-5460.0000575 [18] 孙明喆, 毕瑶家, 孙驰. 改进随机森林算法综述[J]. 现代信息科技, 2019, 3(20): 28−30. doi: 10.3969/j.issn.2096-4706.2019.20.009Sun Mingzhe, Bi Yaojia, Sun Chi. A survey of improved random forest algorithms[J]. Modern Informationn Technology, 2019, 3(20): 28−30. doi: 10.3969/j.issn.2096-4706.2019.20.009 [19] 李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012.Li Hang. Statistical Learning Methods[M]. Beijing: Tsinghua University Press, 2012. [20] 贾怀勤. 应用统计[M]. 北京: 外经济贸易大学出版社, 1998.Jia Huaiqin. Applied Statistics[M]. Beijing: University of International Business and Economics Press, 1998. [21] 林子聪, 任向宁, 朱阿兴, 等. 基于随机森林算法的耕地质量定级指标体系研究[J]. 华南农业大学学报, 2020, 41(4): 38−48. doi: 10.7671/j.issn.1001-411X.201909036Lin Zicong, Ren Xiangning, Zhu Axing, et al. Research on the index system of cultivated land quality grading based on random forest algorithm[J]. Journal of South China Agricultural University, 2020, 41(4): 38−48. doi: 10.7671/j.issn.1001-411X.201909036 [22] 陈国平, 余广明, 章家昌. 平台高程与宽度对不规则波爬高的影响[J]. 海洋工程, 1992, 10(4): 59−67.Chen Guoping, Yu Guangming, Zhang Jiachang. The effect of berm width and elevation on irregular wave run-up[J]. The Ocean Engineering, 1992, 10(4): 59−67. -
图(8) / 表(2)
计量
- 文章访问数: 385
- HTML全文浏览量: 64
- PDF下载量: 26
- 被引次数: 0
