Research on the detection effect of post-processing method of Acoustic Doppler Velocimetry data based on three-dimensional phase space thresholding method and robust estimation method
-
摘要: 水流是影响藤壶、牡蛎、藻类等水生生物能否成功附着在渔业装备上的重要环境因素，水体流速的变化会改变藻类新陈代谢过程，制约藤壶与牡蛎幼虫大面积扩散。流速测量数据的准确性对研究渔业装备上附着生物的附着机制起到至关重要的作用。声学多普勒流速仪(ADV)是测量水体流速的重要设备。然而，水体中的气泡、大颗粒悬浮物等因素会影响ADV的相关系数和信噪比，从而导致流速数据中产生野点，降低了数据的准确性。本文基于国内外主流算法稳健估算法与三维相空间法，以ADV实际测量的流速数据为例，对比研究两种后置处理方法的检测效果。结果显示，稳健估算法平均检出率为4.95%，峰度系数平均下降77.71%，三维相空间法平均检出率为14.60%，峰度系数平均下降84.05%。综合分析，三维相空间法处理效果较好，其检测准确性高于稳健估算法，但存在过处理现象。建议在处理野点含量低于5%的数据时选用相空间法，而对于野点偏离样本平均值较远的数据时，可以选用稳健估算法。本文对减小流速数据误差，为准确定量研究水流对渔业装备附着生物的附着量与种类影响有着重要的意义。Abstract: Water flow is an important environmental factor that affects whether barnacles, oysters, algae, and other aquatic organisms can successfully attach to fishing equipment. Changes in water velocity will change the metabolism of algae and restrict the spread of barnacles and oyster larvae. The accuracy of the flow velocity data plays a vital role in studying the attachment mechanism of organisms attached to fishery equipment. Acoustic Doppler Velocimetry (ADV) is an important device for measuring the flow velocity. However, factors such as bubbles and large suspended solids in the water will affect the correlation coefficient and signal-to-noise ratio of ADV, resulting in outliers in the flow velocity data and reducing the accuracy of the data. Based on the domestic and foreign mainstream algorithms—robust estimation method and the three-dimensional phase space thresholding method, actual measured flow velocity data of ADV are taken as an example to compare and study the detection effects of the two post-processing methods. The results showed that the average detection rate of the robust estimation method was 4.95%, the kurtosis coefficient decreased by 77.71%, the average detection rate of the three-dimensional phase space thresholding method was 14.60%, and the kurtosis coefficient decreased by 84.05%. Comprehensive analysis showed that the three-dimensional phase space thresholding method had a better processing effect, and its detection accuracy was higher than that of the robust estimation method, but there was a phenomenon of overprocessing. It was recommended that the three-dimensional phase space thresholding method be used when dealing with data with an outlier content of less than 5%, and for data whose outliers deviate from the sample average, the robust estimation method was recommended. This article is of great significance for reducing the error of flow velocity data and accurately and quantitatively studying the influence of water flow on the attachment amount and types of fishery equipment attached organisms. It also provides a scientific basis for the subsequent development of a post-processing algorithm with high detection accuracy and less overprocessing.
-
1. 引言
在我国渔业现代化进程不断加快，渔业科技迅猛发展的形势下，渔业装备已广泛应用于捕捞与养殖业[1]。长期在水中作业的渔业装备，常被营固着生活的水生动植物附着，如藤壶类、附着型贝类、藻类等。这些水生生物的分泌物以及死后的残留物对渔业装备性能产生较大的负面影响[2-5]。水体流速是影响固着型水生生物能否成功附着在渔业装备上的重要环境因素，例如，流速的变化会改变藻类新陈代谢过程，制约藤壶类与附着型贝类幼虫大面积扩散[2, 6-7]。声学多普勒流速仪（Acoustic Doppler Velocimetry, ADV）是测量水流速度的主要仪器[8]，根据声学多普勒移频效应原理，利用超声波探测水流速度，实现流体三维的瞬时速度、湍流特性和功率谱密度[9]测量，被广泛应用于野外和实验室水动力学实验中。相关系数和信噪比是影响ADV测量准确度的重要参数[10]。野外监测中常遇到水体产生浪花与气泡（例如，海浪、池塘水体中增氧器的使用）、水底表层出现再悬浮颗粒物（例如，在近海水动力环境紊乱区及生物扰动、人类活动的影响）等情况，会影响ADV测量的相关系数，降低信噪比，导致监测的流速数据中出现大量野点[11-12]，即产生与真实值差异较大的值。因此，进行多普勒流速仪数据后置处理，对提高流速数据准确度有着重要的意义。
目前，国内外用于多普勒流速仪后置处理的算法主要有小波阈值法[13]、稳健估算法[14]、三维相空间法[11]等。其中稳健估算法和三维相空间法是数据后置处理算法中最重要的两个方法[15]。稳健估算法通过估算定位值和尺度估算值标准化样本数据，对比所设定的最小通过值进行野点检测；三维相空间法则是基于样本平均值和标准偏差，采用迭代计算模式检测野点[11]。然而，目前关于定量化评估两种算法检测效果的研究还尚未见报道。
本文以ADV实测流速数据为例，基于稳健估算法与三维相空间法进行数据后置处理，对比分析两种方法的峰度系数与偏斜系数，评估检测效果，以期为准确定量研究水流对渔业装备附着生物的附着量与种类影响等内容提供准确的流速数据。
2. 材料与方法
2.1 研究区域
本研究使用的流速数据来自于上海市宝山区中华绒螯蟹养殖池塘（以下简称蟹塘），蟹塘内设有微孔充氧系统，间隔5 m均匀分布于塘底，由于曝气而出现气泡以及引起塘底颗粒物再悬浮，会对多普勒流速仪产生干扰，导致研究塘内渔业装备生物附着的流速测量不准确。池塘面积为15 480 m2，长为180 m，宽为86 m，水深范围为1～1.5 m。流速监测站点A（图1）位于蟹塘右下方，距最近岸边距离10 m，附近设有1个微孔充氧器。流速监测设备为声学多普勒流速仪（VECTOR, NORTEK Inc., Normay ），采样频率为1 Hz。测量深度为水面下30 cm以及离底20 cm，测量时间分别为2 min和70 min。
2.2 研究方法
2.2.1 稳健估算法
该方法最初由Rousseeuw[14]开发，利用估算定位值和尺度估算值标准化样本数据，通过标准化后的数据与所设定的检测阈值进行比较，检测阈值外的点为野点。稳健估算法的计算公式为
$$ M={{\rm{median}}}_{i=1,\cdots ,n}\left({u}_{i}\right) ,$$ (1) $$ S=e\left({{\rm{median}}}_{i=1,\cdots ,n}\left|{u}_{i}-M\right|\right), $$ (2) $$ {Z}_{i}=({u}_{i}-M)/S, $$ (3) $$ {O}_{i}=\left|{Z}_{i}\right|-c ,$$ (4) 式中，M为估算定位值（单位：m/s）；n为速度数据点的数量；u为水流速度数据（单位：m/s）；S为尺度估算值（单位：m/s）；e为估计器系数（1.483）；Zi为标准化观测值；Oi为野点判断值；c为截止值（2.5）。如果Oi的值大于0，则确定为野点并删除。通常对野点前两个数据进行外推法计算，获得的新数据作为替换值代替被删除的野点。
2.2.2 三维相空间法
三维相空间法最初由Nikora和Goring[16]开发，并由Wahl[17]进行了改进。该方法通过全局阈值将流速数据与其导数构筑成椭球体，位于椭球体外的点被视为野点，采用迭代的方式不断收缩全局阈值以进一步检测野点。三维相空间法的计算公式为
$$ U={{\rm{mean}}}_{i=1,\cdots ,n}\left({u}_{i}\right) ,$$ (5) $$ {u}_{i}'={u}_{i}-U ,$$ (6) $$ {\Delta }^{2}{u}_{i}'={\left(\Delta t\right)}^{2}\frac{{{\rm{d}}}^{2}{u}_{i}'}{{{\rm{d}}t}^{2}}, $$ (8) $$ {\sigma }_{\Delta {u}'}=\sqrt{\frac{1}{n-1}\sum _{i=1}^{n}{\left(\Delta {u}_{i}'-\overline{\Delta {u}'}\right)}^{2}} ,$$ (9) $$ {\sigma }_{{\Delta }^{2}{u}'}=\sqrt{\frac{1}{n-1}\sum _{i=1}^{n}{\left({\Delta }^{2}{u}_{i}'-\overline{{\Delta }^{2}{u}'}\right)}^{2}} ,$$ (10) $$ \lambda =\sqrt{2{{\rm{ln}}}n} ,$$ (11) $$\theta = \left\{ {\begin{array}{*{20}{c}} {{\tan^{ - 1}}\left( {\frac{{\displaystyle \sum \nolimits u_i'{\Delta ^2}u_i'}}{{\displaystyle \sum \nolimits {u_i^{'2}}}}} \right),}&{{\Delta ^2}u_i'\;{\text{与}}\;u_i'}\\ {0,}&{\Delta u_i'\;{\text{与}}\;u_i'}\\ {0,}&{{\Delta ^2}u_i'\;{\text{与}}\;\Delta u_i'} \end{array}} \right.,$$ (12) $${\left( {{\lambda _U}{\sigma _U}} \right)^2} = {a^2}{\cos^2}\theta + {b^2}{\sin^2}\theta ,$$ (13) $${\left( {{\lambda _U}{\sigma _{{\Delta ^2}U}}} \right)^2} = {a^2}{\sin^2}\theta + {b^2}{\cos^2}\theta,$$ (14) 式中，U为水流速度的平均值（单位：m/s）；n为速度数据点的数量；u为水流速度数据（单位：m/s）；ui′为脉动速度（单位：m/s）；Δui′为速度的一阶导数（单位：m/s），
$\overline{\Delta u_i}$ 为其平均数；Δ2ui′为速度的二阶导数（单位：m/s），$\overline{\Delta^2 u'_i} $ 为其平均数；σ为波动速度的标准偏差；λ为通用阈值；θ为主轴的旋转角度（rad），由于对称性，Δui′与ui′以及Δ2ui′与Δui′的旋转角度为0。由公式（12）和公式（13）构筑椭球体，位于椭球体外的点为野点，被删除的野点通常使用三阶样条式插值法进行插值。2.3 统计方法
主要采用标准偏差、峰度系数、偏斜系数等指标统计分析数据处理结果[18-19]。其中，峰度系数是表征概率密度分布曲线在平均值处峰值高低的特征数。峰度系数高说明数据存在大于或小于平均值的极端差值。偏度系数是表征概率分布密度曲线相对于平均值不对称程度的特征数。计算公式为
$${\rm{kur}} = \frac{{\displaystyle \sum \limits_{i = 1}^n {{\left( {{u_i} - \overline {{u_i}} } \right)}^4}}}{n}\Bigg/{\left[\begin{aligned} {\frac{{\displaystyle \sum \limits_{i = 1}^n {{\left( {{u_i} - \overline {{u_i}} } \right)}^2}}}{n}} \end{aligned}\right]^2},$$ (15) $${\rm{skew}} = \frac{{\displaystyle \sum \limits_{i = 1}^n {{\left( {{u_i} - \overline {{u_i}} } \right)}^3}}}{n}\Bigg/{\left[\begin{aligned} {\frac{{\displaystyle \sum \limits_{i = 1}^n {{\left( {{u_i} - \overline {{u_i}} } \right)}^2}}}{n}} \end{aligned}\right]^{\tfrac{3}{2}}},$$ (16) 式中，kur为峰度系数；skew为偏斜系数。
3. 结果
水面下30 cm处流速监测数据如图2所示。图3为稳健估算法检测结果图，虚线为标准化观测值Zi，高于Zi的数据被判断为野点。稳健估算法在3个速度分量的流速数据中检测出野点个数分别为7个、6个、5个，检出率为5.76%、4.96%、4.13%。三维相空间法检测结果如图4所示，检测出野点个数分别为18个、12个、23个，检出率14.88%、9.92%、19.01%。表1为水面下30 cm处数据及经两种方法处理后数据的统计参数值，原始数据的峰度系数分别约为16.91、27.14、23.12。经稳健估算法处理后峰度系数平均下降77.71%，速度分量v峰度系数较高，约为7.71，降幅为71.58%。经三维相空间法处理后峰度系数平均下降84.05%，速度分量w峰度系数较高，约为6.11，降幅为73.59%。经两种方法处理后偏斜系数较原始数据偏斜系数均降低。
图 2 站点A水面下30 cm处流速数据Figure 2. Flow velocity data at 30 cm below the water surface at Station A
图 3 站点A水面下30 cm处稳健估算法检测结果a. 速度分量u流速数据检测结果；b. 速度分量v流速数据检测结果；c. 速度分量w流速数据检测结果Figure 3. The detection results of the robust estimation method at 30 cm below the water surface of Station Aa. Velocity data detection result in u; b. velocity data detection result in v; c. velocity data detection result in w
图 4 站点A水面下30 cm处三维相空间法检测结果a. 速度分量u流速数据检测结果；b. 速度分量v流速数据检测结果；c. 速度分量w流速数据检测结果Figure 4. The detection results of the three-dimensional phase space thresholding method at 30 cm below the water surface of Station Aa. Velocity data detection result in u; b. velocity data detection result in v; c. velocity data detection result in w表 1 站点A水面下30 cm处流速数据统计参数值Table 1. Statistical parameter values of flow velocity data at 30 cm below the surface of Station A方法名称 速度分量 平均值/(m·s−1) 标准偏差 峰度系数 偏斜系数 最大值/(m·s−1) 最小值/(m·s−1) 实测数据 u −0.007 721 0.023 845 16.910 402 −1.113 332 0.089 9 −0.147 9 v −0.011 987 0.030 562 27.141 593 3.214 157 0.205 3 −0.107 6 w 0.001 576 0.025 555 23.118 644 3.021 304 0.178 3 −0.079 6 稳健估算法 u −0.007 051 0.011 142 3.255 587 −0.162 135 0.023 2 −0.038 3 v −0.014 798 0.017 709 7.712 472 −1.497 770 0.018 5 −0.092 8 w −0.001 415 0.015 846 4.440 737 −0.877 804 0.029 8 −0.059 1 三维相空间法 u −0.007 238 0.009 276 2.101 112 −0.011 201 0.009 6 −0.029 0 v −0.011 054 0.012 881 2.448 117 0.099 970 0.017 0 −0.040 3 w 0.003 131 0.017 945 6.105 687 1.342 966 0.068 2 −0.027 6 离底20 cm处数据及处理结果如图5所示。稳健估算法在3个速度分量流速数据中检测出野点个数分别为：52个、45个、167个，检出率为1.62%、1.36%、3.95%。三维相空间法检测出野点数分别为68个、57个、166个，检出率1.24%、1.07%、3.92%。表2为站点A离底20 cm处数据统计参数值。原始数据3个速度分量的峰度系数分别约为28.52、18.55、18.83。两种方法处理后数据峰度系数平均降幅均高于80%，分别为81.45%、84.07%。稳健估算法与三维相空间法在速度分量w数据的峰度系数降幅分别为79.72%和73.63%。原始数据3个速度分量偏斜系数分别约为0.54、0.10、0.13。稳健估算法和三维相空间法在速度分量v的偏斜系数均升高，分别上升50.01%和65.09%。
图 5 站点A离底20 cm处数据处理效果对比a. 速度分量u流速数据检测结果；b. 速度分量v流速数据检测结果；c. 速度分量w流速数据检测结果Figure 5. Comparison of data processing effects at 20 cm above the bottom of Station Aa. Velocity data detection result in u; b. velocity data detection result in v; c. velocity data detection result in w表 2 站点A离底20 cm处流速数据统计参数值Table 2. Statistical parameter values of flow velocity data at 20 cm above the bottom of Station A方法名称 速度分量 平均值/(m·s−1) 标准偏差 峰度系数 偏斜系数 最大值/(m·s−1) 最小值/(m·s−1) 实测数据 u 0.002 485 0.003 438 28.518 138 0.539 132 0.048 2 −0.039 2 v −0.000 983 0.003 137 18.550 231 0.103 749 0.030 2 −0.042 1 w −0.001 342 0.001 293 18.826 066 0.127 427 0.009 4 −0.015 1 稳健估算法 u 0.002 464 0.002 641 3.500 889 0.089 815 0.016 7 −0.006 3 v −0.001 015 0.002 607 2.824 961 0.155 629 0.008 4 −0.007 8 w −0.001 330 0.000 908 3.817 821 −0.163 720 0.002 2 −0.004 8 三维相空间法 u 0.002 486 0.002 714 3.615 697 0.032 647 0.014 2 −0.008 0 v −0.001 022 0.002 629 3.082 643 0.171 276 0.010 9 −0.009 9 w −0.001 372 0.000 935 4.963 777 −0.413 947 0.003 5 −0.006 5 4. 讨论
由水下30 cm数据处理结果可见，三维相空间法检测出野点数显著多于稳健估算法，在3个速度分量的检出率分别高于稳健估算法9.12%、4.96%、14.88%。对于离底20 cm处的数据，稳健估算法检测出野点多于三维相空间法，但在3个速度分量的检出率仅高于三维相空间法0.38%、0.29%、0.03%。三维相空间法检测率较低的主要原因是三维相空间法检测阈值的计算基于平均值和标准偏差，两者对野点值非常敏感，数据中野点超过5%时，野点的存在会显著影响两个参数的性能，导致检测阈值增大，野点被视为有效数据而未被剔除[17]。离底20 cm处的数据中野点含量高于7%，因此对三维相空间法的检测精度存在影响。这一问题可以通过迭代的方法改善，但在迭代过程中位于野点周围速度数据的一阶导数
$ \Delta {v} $ 和二阶导数$ {\Delta }^{2}{v} $ 可能超出阈值椭球边界值，将野点附近部分真实数据判断为野点[20]，出现过处理情况。经两种方法处理后数据和原始数据的峰度系数对比发现，三维相空间峰度系数降幅均高于稳健估算法。在离底20 cm处测量的流速数据中，稳健估算法与三维相空间法峰度系数在速度分量w均较高，但稳健估算法峰度系数低于三维相空间法。这是因为稳健估算法是基于样本的中位数和绝对偏差，不受平均值和标准偏差影响，只能有效检测出与样本平均值差异较大的野点，而速度分量w流速数据中的野点距离平均值较近。因此，稳健估算法无法有效检测这些野点，从而导致速度分量w数据的峰度系数较高。三维相空间法速度分量w流速数据峰度系数较高的主要原因是速度分量w流速数据中野点含量显著多于速度分量u、v，三维相空间法检测精度会随污染程度增加而下降[21-22]。因此，速度分量w数据中部分野点未被有效剔除，从而导致速度分量w数据峰度系数偏高。
以速度分量v流速数据为例，稳健估算法与三维相空间法处理后偏斜系数均升高，分别为0.16和0.17。两种方法对于污染数据偏度的处理均与污染程度无关。稳健估算法仅计算关于位置估计量的对称统计量，不处理偏度[23]。偏斜系数升高可能是由于插值法产生的新数据值导致数据右偏。
综上所述，三维相空间法综合检测效果优于稳健估算法。当野点含量低于5%时，野点对三维相空间法检测阈值的影响较小，三维相空间法通过迭代不断收缩检测阈值，能够检测出更多与真实数据相近的野点，检测精度更高。但该方法的局限性是当野点含量高于5%时，其检测精度降低，且存在过处理现象。稳健估算法能有效检测出与样本平均值差异较大的野点，但该方法不进行迭代，仅检测1次，因此无法有效检测出与真实数据相近的野点。
5. 结语
本文以实测流速数据为例，通过定量化评估了稳健估算法与三维相空间法的检测效果。对比分析了两种方法的峰度系数与偏斜系数，结果表明，三维相空间法处理效果较好，其检测准确性高于稳健估算法，但存在过处理现象。本研究对降低流速数据误差，准确定量研究水流对渔业装备附着生物的附着量与种类影响有着重要的意义，也为后续开发一种检测精度高且过处理现象少的后置处理算法提供了科学的参考。
-
图 2 站点A水面下30 cm处流速数据
Fig. 2 Flow velocity data at 30 cm below the water surface at Station A
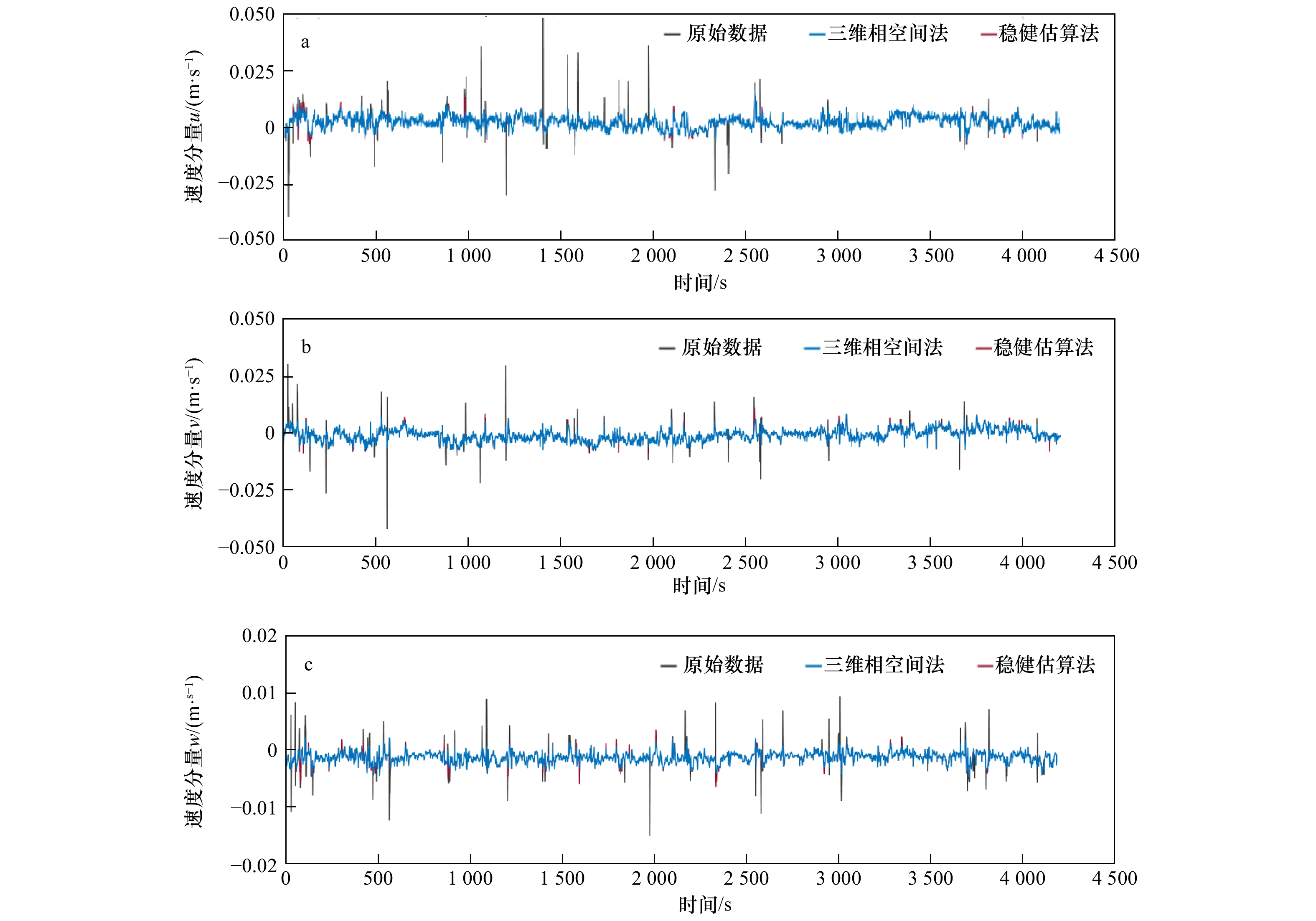
图 3 站点A水面下30 cm处稳健估算法检测结果
a. 速度分量u流速数据检测结果；b. 速度分量v流速数据检测结果；c. 速度分量w流速数据检测结果
Fig. 3 The detection results of the robust estimation method at 30 cm below the water surface of Station A
a. Velocity data detection result in u; b. velocity data detection result in v; c. velocity data detection result in w
图 4 站点A水面下30 cm处三维相空间法检测结果
a. 速度分量u流速数据检测结果；b. 速度分量v流速数据检测结果；c. 速度分量w流速数据检测结果
Fig. 4 The detection results of the three-dimensional phase space thresholding method at 30 cm below the water surface of Station A
a. Velocity data detection result in u; b. velocity data detection result in v; c. velocity data detection result in w
图 5 站点A离底20 cm处数据处理效果对比
a. 速度分量u流速数据检测结果；b. 速度分量v流速数据检测结果；c. 速度分量w流速数据检测结果
Fig. 5 Comparison of data processing effects at 20 cm above the bottom of Station A
a. Velocity data detection result in u; b. velocity data detection result in v; c. velocity data detection result in w
表 1 站点A水面下30 cm处流速数据统计参数值
Tab. 1 Statistical parameter values of flow velocity data at 30 cm below the surface of Station A
方法名称 速度分量 平均值/(m·s−1) 标准偏差 峰度系数 偏斜系数 最大值/(m·s−1) 最小值/(m·s−1) 实测数据 u −0.007 721 0.023 845 16.910 402 −1.113 332 0.089 9 −0.147 9 v −0.011 987 0.030 562 27.141 593 3.214 157 0.205 3 −0.107 6 w 0.001 576 0.025 555 23.118 644 3.021 304 0.178 3 −0.079 6 稳健估算法 u −0.007 051 0.011 142 3.255 587 −0.162 135 0.023 2 −0.038 3 v −0.014 798 0.017 709 7.712 472 −1.497 770 0.018 5 −0.092 8 w −0.001 415 0.015 846 4.440 737 −0.877 804 0.029 8 −0.059 1 三维相空间法 u −0.007 238 0.009 276 2.101 112 −0.011 201 0.009 6 −0.029 0 v −0.011 054 0.012 881 2.448 117 0.099 970 0.017 0 −0.040 3 w 0.003 131 0.017 945 6.105 687 1.342 966 0.068 2 −0.027 6 
下载: 导出CSV
表 2 站点A离底20 cm处流速数据统计参数值
Tab. 2 Statistical parameter values of flow velocity data at 20 cm above the bottom of Station A
方法名称 速度分量 平均值/(m·s−1) 标准偏差 峰度系数 偏斜系数 最大值/(m·s−1) 最小值/(m·s−1) 实测数据 u 0.002 485 0.003 438 28.518 138 0.539 132 0.048 2 −0.039 2 v −0.000 983 0.003 137 18.550 231 0.103 749 0.030 2 −0.042 1 w −0.001 342 0.001 293 18.826 066 0.127 427 0.009 4 −0.015 1 稳健估算法 u 0.002 464 0.002 641 3.500 889 0.089 815 0.016 7 −0.006 3 v −0.001 015 0.002 607 2.824 961 0.155 629 0.008 4 −0.007 8 w −0.001 330 0.000 908 3.817 821 −0.163 720 0.002 2 −0.004 8 三维相空间法 u 0.002 486 0.002 714 3.615 697 0.032 647 0.014 2 −0.008 0 v −0.001 022 0.002 629 3.082 643 0.171 276 0.010 9 −0.009 9 w −0.001 372 0.000 935 4.963 777 −0.413 947 0.003 5 −0.006 5
下载: 导出CSV
-
[1] 黄一心, 丁建乐, 鲍旭腾, 等. 中国渔业装备和工程科技发展综述[J]. 渔业现代化, 2019, 46(5): 1−8. doi: 10.3969/j.issn.1007-9580.2019.05.001Huang Yixin, Ding Jianle, Bao Xuteng, et al. Development research on China fishery equipment and engineering technology[J]. Fishery Modernization, 2019, 46(5): 1−8. doi: 10.3969/j.issn.1007-9580.2019.05.001 [2] 杨宗澄, 白秀琴, 姜欢, 等. 船体表面海洋污损生物附着规律分析[J]. 船舶工程, 2016, 38(2): 29−33, 79.Yang Zongcheng, Bai Xiuqin, Jiang Huan, et al. Analysis of biofouling occurrence trends on ship hull surface[J]. Ship Engineering, 2016, 38(2): 29−33, 79. [3] 王海涛, 张东兴, 郑岩. 防除海洋污损生物附着的技术研究进展[J]. 水产学杂志, 2018, 31(6): 47−50. doi: 10.3969/j.issn.1005-3832.2018.06.010Wang Haitao, Zhang Dongxing, Zheng Yan. A review: research progress on prevention and removal technology of marine fouling organisms[J]. Chinese Journal of Fisheries, 2018, 31(6): 47−50. doi: 10.3969/j.issn.1005-3832.2018.06.010 [4] Jadidi P, Zeinoddini M, Soltanpour M, et al. Towards an understanding of marine fouling effects on VIV of circular cylinders: aggregation effects[J]. Ocean Engineering, 2018, 147: 227−242. doi: 10.1016/j.oceaneng.2017.10.037 [5] Balasubramanian V, Rajaram R, Palanichamy S, et al. Lanosterol expressed bio-fouling inhibition on Gulf of Mannar coast, India[J]. Progress in Organic Coatings, 2018, 115: 100−106. doi: 10.1016/j.porgcoat.2017.11.009 [6] Crisp D J. The behaviour of barnacle cyprids in relation to water movement over a surface[J]. Journal of Experimental Biology, 1955, 32(3): 569−590. doi: 10.1242/jeb.32.3.569 [7] 廖平安, 胡秀琳. 流速对藻类生长影响的试验研究[J]. 北京水利, 2005(2): 12−14.Liao Ping’an, Hu Xiulin. Experimental study on the effect of flow velocity on algal growth[J]. Beijing Water Resources, 2005(2): 12−14. [8] 严松, 吴浩, 孙大鹏, 等. 声学多普勒流速仪在水槽流速测量中的应用[J]. 实验室研究与探索, 2017, 36(5): 9−13. doi: 10.3969/j.issn.1006-7167.2017.05.003Yan Song, Wu Hao, Sun Dapeng, et al. Application of acoustic Doppler velocimetry in flume flow experiment[J]. Research and Exploration in Laboratory, 2017, 36(5): 9−13. doi: 10.3969/j.issn.1006-7167.2017.05.003 [9] Sharma A, Maddirala A K, Kumar B. Modified singular spectrum analysis for despiking acoustic Doppler velocimeter (ADV) data[J]. Measurement, 2018, 117: 339−346. doi: 10.1016/j.measurement.2017.12.025 [10] Fugate D C, Friedrichs C T. Determining concentration and fall velocity of estuarine particle populations using ADV, OBS and LISST[J]. Continental Shelf Research, 2002, 22(11/13): 1867−1886. [11] Goring D G, Nikora V I. Despiking acoustic Doppler velocimeter data[J]. Journal of Hydraulic Engineering, 2002, 128(1): 117−126. doi: 10.1061/(ASCE)0733-9429(2002)128:1(117) [12] Cea L, Puertas J, Pena L. Velocity measurements on highly turbulent free surface flow using ADV[J]. Experiments in Fluids, 2007, 42(3): 333−348. doi: 10.1007/s00348-006-0237-3 [13] Donoho D L, Johnstone I M. Ideal spatial adaptation by wavelet shrinkage[J]. Biometrika, 1994, 81(3): 425−455. doi: 10.1093/biomet/81.3.425 [14] Rousseeuw P J. Robust estimation and identifying outliers[M]. 2nd ed. New York: McGraw-Hill, 1998. [15] Zhong Chunyi, Yin Fang, Zhang Junbo, et al. Optimized algorithm for processing outlier of water current data measured by acoustic Doppler velocimeter[J]. Journal of Marine Science and Engineering, 2020, 8(9): 655. doi: 10.3390/jmse8090655 [16] Nikora V I, Goring D G. ADV measurements of turbulence: can we improve their interpretation[J]. Journal of Hydraulic Engineering, 1998, 124(6): 630−634. doi: 10.1061/(ASCE)0733-9429(1998)124:6(630) [17] Wahl T L. Discussion of “Despiking Acoustic Doppler Velocimeter Data” by Derek G. Goring and Vladimir I. Nikora[J]. Journal of Hydraulic Engineering, 2003, 129(6): 484−487. doi: 10.1061/(ASCE)0733-9429(2003)129:6(484) [18] Joanes D N, Gill C A. Comparing measures of sample skewness and kurtosis[J]. Journal of the Royal Statistical Society: Series D (The Statistician), 1998, 47(1): 183−189. doi: 10.1111/1467-9884.00122 [19] Köse Ö. Various filtering algorithms used to eliminate outliers in velocity time series obtained by ADVs (acoustic Doppler velocimeter)[J]. Arabian Journal of Geosciences, 2013, 6(7): 2691−2697. doi: 10.1007/s12517-012-0523-8 [20] Parsheh M, Sotiropoulos F, Porté-Agel F. Estimation of power spectra of acoustic-Doppler velocimetry data contaminated with intermittent spikes[J]. Journal of Hydraulic Engineering, 2010, 136(6): 368−378. doi: 10.1061/(ASCE)HY.1943-7900.0000202 [21] Jesson M, Sterling M, Bridgeman J. Despiking velocity time-series—Optimisation through the combination of spike detection and replacement methods[J]. Flow Measurement and Instrumentation, 2013, 30: 45−51. doi: 10.1016/j.flowmeasinst.2013.01.007 [22] Islam M R, Zhu D Z. Kernel density-based algorithm for despiking ADV data[J]. Journal of Hydraulic Engineering, 2013, 139(7): 785−793. doi: 10.1061/(ASCE)HY.1943-7900.0000734 [23] Razaz M, Kawanisi K. Signal post-processing for acoustic velocimeters: detecting and replacing spikes[J]. Measurement Science and Technology, 2011, 22(12): 125404. doi: 10.1088/0957-0233/22/12/125404 期刊类型引用(1)
1. 李高如，龚国宁，张生乐，高美华，张伯伦，马煜曦，何培民，方淑波. 台风过程影响下的滨海湿地物理变量观测及湿地系统响应. 海洋学报. 2022(12): 116-125 . 
本站查看其他类型引用(2)
-
下载:
计量
- 文章访问数: 366
- HTML全文浏览量: 109
- PDF下载量: 27
- 被引次数: 3
