Research on the optimization method of analytical four dimensional ensemble variational data assimilation
-
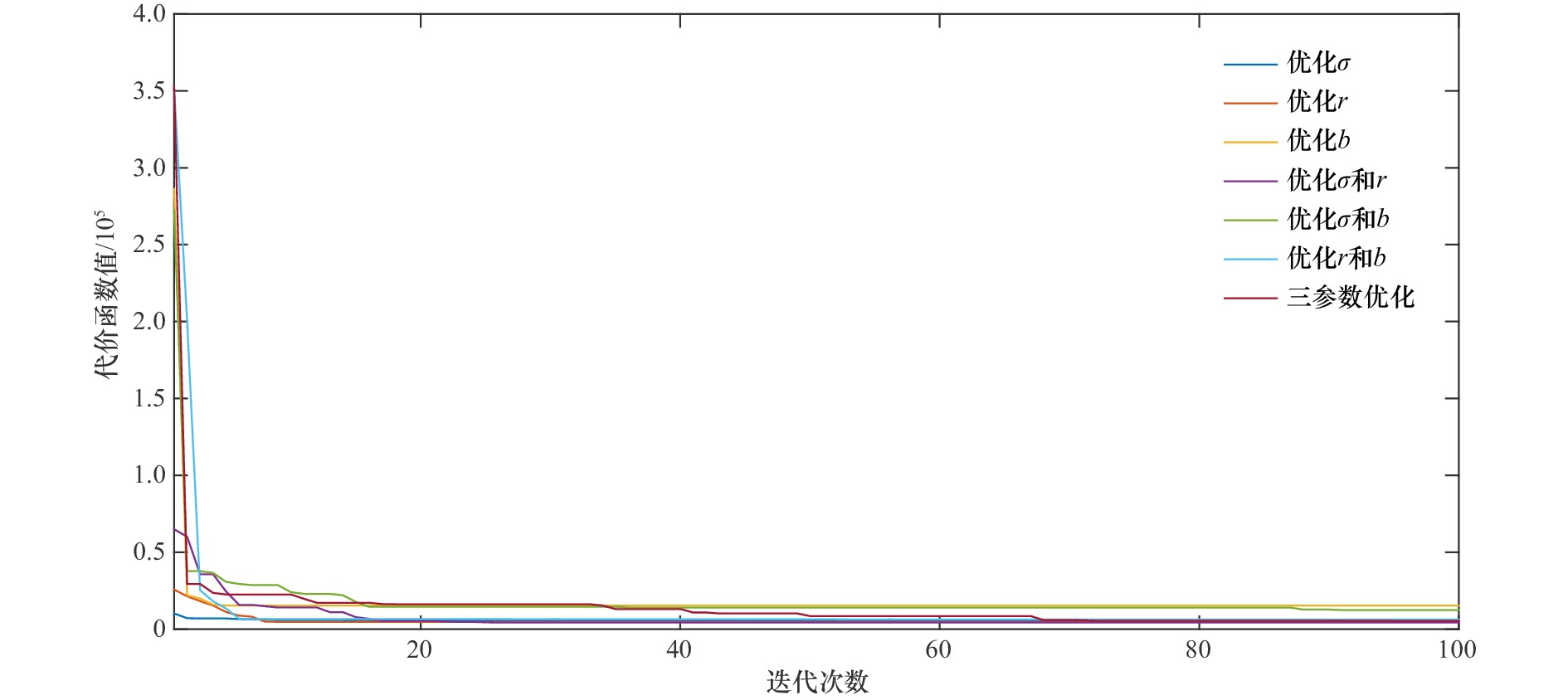
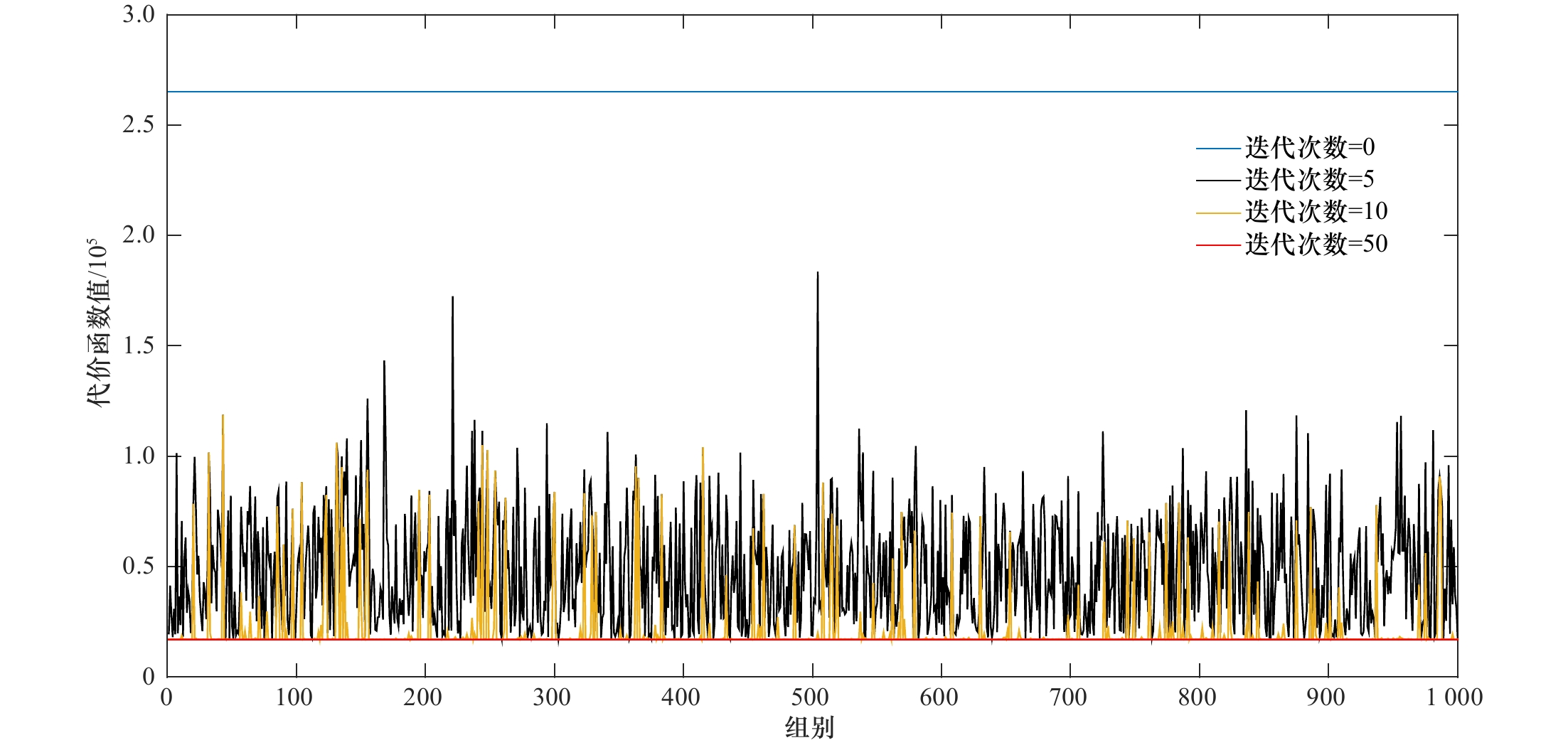
摘要: 传统的四维变分数据同化方法在同化观测资料的同时可以对数值模式参数进行优化，然而传统的四维变分方法需要针对不同的数值模式编写特有的伴随模式，因此算法的可移植性差，同时计算时耗费大量资源。本文提出了一种新的基于解析四维集合变分的参数优化方法，该方法以迭代搜索得到的模式参数为基准展开扰动并构建样本集合，由此显式地计算协方差矩阵，并得到代价函数极小值的解析解，从而避免了伴随模式的使用。基于Lorenz-63模型对该方法进行单参数和多参数数值试验和优化效果检验，并在不同的同化时间窗口长度和观测采样间隔情况下，采用传统四维变分方法与之进行对比，结果显示，新方法表现出与传统四维变分相同的优化性能，都能有效收敛到真值，而新方法不需要计算伴随模式，可移植性好。本文还测试了不同的集合成员个数和模式参数真值的情况下新方法的同化效果，结果表明，新方法对集合样本个数及模型参数真值不敏感，采用较少的集合样本即可完成数据同化。Abstract: The traditional four-dimensional variational data assimilation method can optimize the parameters of the numerical model while assimilating the observation data. However, the traditional four-dimensional variational method needs to compile special adjoint models for different numerical models, so the portability of the traditional four-dimensional variational method is poor and a lot of resources are consumed in the calculation. In this paper, a new parameter optimization method based on the analytic four-dimensional ensemble variation is proposed, which expands the perturbation and constructs the ensemble based on the model parameters obtained by iterative search, and then explicitly calculates the covariance matrix, and obtains the analytic solution of the minimum value of the cost function, so as to avoid the use of adjoint model. Using Lorenz-63 model, single-parameter and multi-parameter numerical tests and optimization effect tests were carried out on the analytic four-dimensional ensemble variation method, and in the case of different assimilation time window length and observation sampling interval, the traditional four-dimensional variational method was used to compare with the new method, the results show that the new method has the same optimization performance as the traditional four-dimensional variational method, and it can converge to the truth value effectively, and the new method does not need to calculate adjoint mode, so it has good portability. This paper also test the assimilation effect of the new method with different ensemble members and true values of model parameters, and the results show that the new method is insensitive to the number of ensemble members and the true values of model parameters, and the data assimilation can be completed with fewer ensemble members.
-
图 2 A-4DEnVar代价函数值随迭代次数的变化
Fig. 2 Changes of value of cost function of A-4DEnVar with the number of iterations
图 3 改变积分时间窗口长度和观测采样间隔之后的模型均方根误差变化
Fig. 3 Model RMSE changes after changing integral time window length and observation sampling interval
图 4 不同积分时间窗口长度和观测采样间隔组合下收敛后的平均均方根误差
Fig. 4 Convergent average RMSE under the combination of different integral time window length and observation sampling interval
图 5 改变集合成员数量后模型分析场拟合真实场轨迹
Fig. 5 Trajectory chart of analysis field fitting real field after changing the number of members of the set
图 6 改变模型参数标准值后各组代价函数值变化
Fig. 6 Changes of each group's cost functions after changing the standard values of model parameters
图 7 改变模型参数标准值后平均代价函数值变化
Fig. 7 Changes of average cost function value after changing the standard values of model parameters
表 1 A-4DEnVar和传统4DVar对Lorenz-63模型的参数优化试验设计
Tab. 1 Experimental design of Lorenz-63 model parameter optimization by A-4DEnVar and traditional 4DVar
方法 积分窗口
长度集合成员
个数观测采样
间隔参数标准值 $\sigma$ r b 解析4DEnVar 500 500 10 10 28 8/3 传统4DVar 500 0 10 10 28 8/3 
下载: 导出CSV
表 2 改变积分窗口长度和观测采样间隔条件下Lorenz-63模型参数优化试验
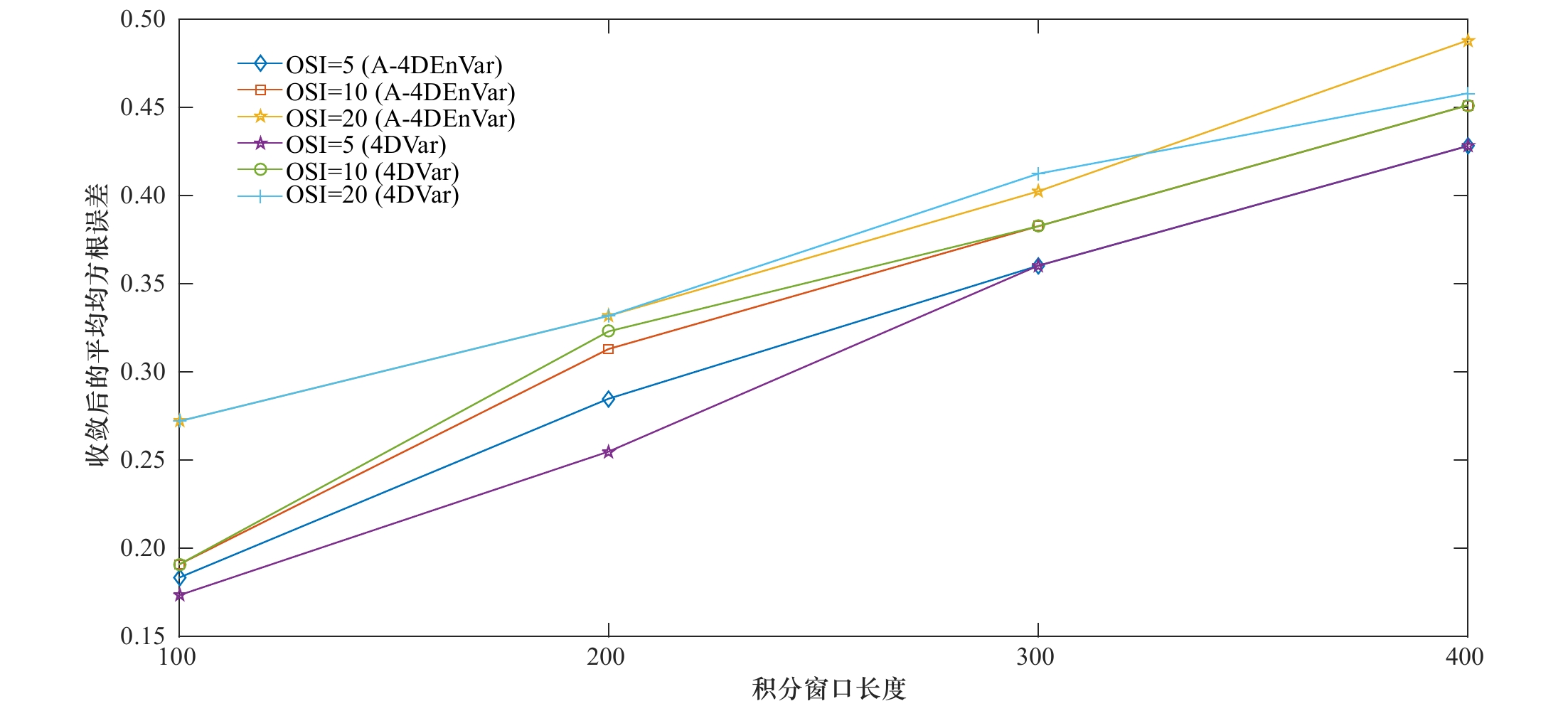
Tab. 2 Lorenz-63 model parameter optimization experiment under the changes of integral window length and observation sampling interval
方法 积分窗口长度 集合成员数量 观测采样间隔 参数标准值 $\sigma$ r b 解析4DEnVar 100 500 5 10 20 10 28 8/3 200 500 5 10 20 10 28 8/3 传统4DVar 300 0 5 10 20 10 28 8/3 400 0 5 10 20 10 28 8/3
下载: 导出CSV
表 3 不同集合成员数量情况下解析4DEnVar对Lorenz-63模型的参数优化
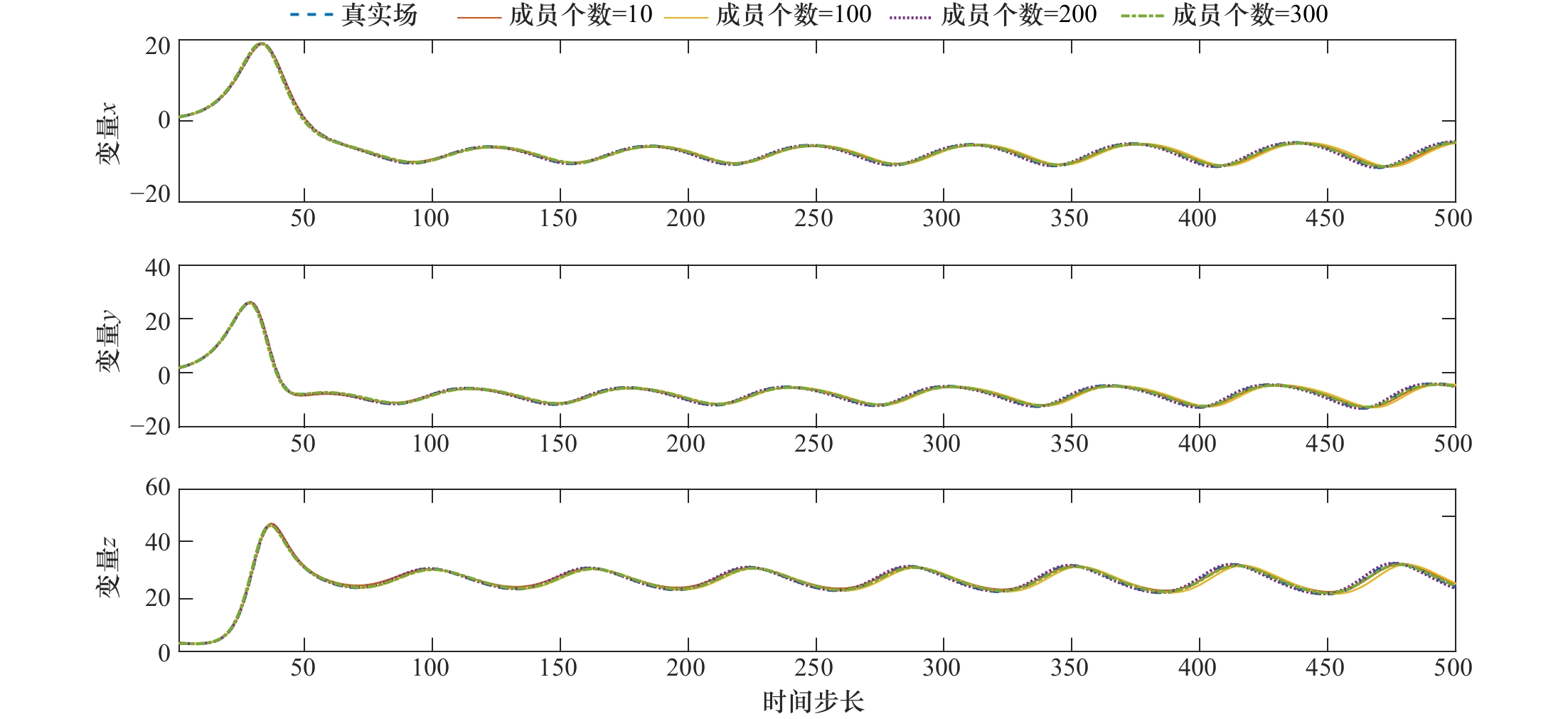
Tab. 3 Lorenz-63 parameter optimization experiment by A-4DEnVar under different number of members of the set
方法 积分窗口
长度集合成员
个数观测采样
间隔参数标准值 $\sigma $ r b 解析4DEnVar 500 10 10 10 28 8/3 500 100 10 10 28 8/3 500 200 10 10 28 8/3 500 300 10 10 28 8/3
下载: 导出CSV
表 4 不同参数标准值情况下解析4DEnVar对Lorenz-63模型的参数优化
Tab. 4 Lorenz-63 parameter optimization experiment by A-En4DVar under different standard values of parameters
方法 积分窗口长度 集合成员个数 观测采样间隔 参数标准值选取范围 $\sigma $ r b 解析4DEnVar 500 500 10 （9, 11） （25.2, 30.8） （2.4, 2.93）
下载: 导出CSV
-
[1] 魏敏. 四维变分方法在微分方程参数优化中的应用[D]. 南京: 南京师范大学, 2013.Wei Min. Applications of the four-dimensional variation methods on parameter optimization of differential equations[D]. Nanjing: Nanjing Normal University, 2013. [2] Lewis J M, Derber J C. The use of adjoint equations to solve a variational adjustment problem with advective constraints[J]. Tellus A: Dynamic Meteorology and Oceanography, 1985, 37(4): 309−322. doi: 10.3402/tellusa.v37i4.11675 [3] Le Dimet F X, Talagrand O. Variational algorithms for analysis and assimilation of meteorological observations: Theoretical aspects[J]. Tellus A: Dynamic Meteorology and Oceanography, 1986, 38(2): 97−110. doi: 10.3402/tellusa.v38i2.11706 [4] Chu Kekuan, Tan Zhemin, Ming Xue. Impact of 4DVAR assimilation of rainfall data on the simulation of mesoscale precipitation systems in a Mei-Yu heavy rainfall event[J]. Advances in Atmospheric Sciences, 2007, 24(2): 281−300. doi: 10.1007/s00376-007-0281-9 [5] Zhao Juan, Wang Bin, Liu Juanjuan. Impact of analysis-time tuning on the performance of the DRP-4DVar approach[J]. Advances in Atmospheric Sciences, 2011, 28(1): 207−216. doi: 10.1007/s00376-010-9191-3 [6] Wang Yunfeng, Wang Bin, Fei Jianfang, et al. The effects of assimilating satellite brightness temperature and bogus data on the simulation of typhoon Kalmaegi (2008)[J]. Acta Meteorologica Sinica, 2013, 27(3): 415−434. doi: 10.1007/s13351-013-0309-2 [7] Zhong Jian, Huang Sixun, Fei Jianfang, et al. Application of tikhonov regularization method to wind retrieval from scatterometer data II: Cyclone wind retrieval with consideration of rain[J]. Chinese Physics B, 2011, 20(6): 064301. doi: 10.1088/1674-1056/20/6/064301 [8] Inazu D, Higuchi T, Nakamura K. Optimization of boundary condition and physical parameter in an ocean tide model using an evolutionary algorithm[J]. Theoretical and Applied Mechanics Japan, 2010, 58: 101−112. [9] Wang Tingting, Li Wenlong, Chen Zhanghui, et al. Correcting the systematic error of the density functional theory calculation: The alternate combination approach of genetic algorithm and neural network[J]. Chinese Physics B, 2010, 19(7): 076401. doi: 10.1088/1674-1056/19/7/076401 [10] 王云峰, 顾成明, 张晓辉, 等. 优化模式物理参数的扩展四维变分同化方法[J]. 物理学报, 2014, 63(24): 12−19.Wang Yunfeng, Gu Chengming, Zhang Xiaohui, et al. Expanded four-dimensional variatiaonal data assimilation method to optimize model physical parameters[J]. Acta Physica Sinica, 2014, 63(24): 12−19. [11] Liu Chengsi, Xiao Qingnong, Wang Bin. An ensemble-based four-dimensional variational data assimilation scheme. Part I: Technical formulation and preliminary test[J]. Monthly Weather Review, 2008, 136(9): 3363−3373. doi: 10.1175/2008MWR2312.1 [12] Liu Chengsi, Xiao Qingnong, Wang Bin. An ensemble-based four-dimensional variational data assimilation scheme. Part II: Observing system simulation experiments with advanced research WRF (ARW)[J]. Monthly Weather Review, 2009, 137(5): 1687−1704. doi: 10.1175/2008MWR2699.1 [13] Liu Chengsi, Xiao Qingnong. An ensemble-based four-dimensional variational data assimilation scheme. Part III: Antarctic applications with advanced research WRF using real data[J]. Monthly Weather Review, 2013, 141(8): 2721−2739. doi: 10.1175/MWR-D-12-00130.1 [14] Arbogast É, Desroziers G, Berre L. A parallel implementation of a 4DEnVar ensemble[J]. Quarterly Journal of the Royal Meteorological Society, 2017, 143(706): 2073−2083. doi: 10.1002/qj.3061 [15] Yang Yin, Mémin E. High-resolution data assimilation through stochastic subgrid tensor and parameter estimation from 4DEnVar[J]. Tellus A: Dynamic Meteorology and Oceanography, 2017, 69(1): 1308772. doi: 10.1080/16000870.2017.1308772 [16] Song H J, Kang J H. Effects of the wind-mass balance constraint on ensemble forecasts in the hybrid-4DEnVar[J]. Quarterly Journal of the Royal Meteorological Society, 2019, 145(719): 434−449. doi: 10.1002/qj.3440 [17] 杨雨轩. 基于华南冬季暴雨的雷达资料四维集合变分同化技术研究[D]. 长沙: 国防科技大学, 2017.Yang Yuxuan. Technical research of four-dimensional ensemble variational assimilation of doppler radar data based on awinter heavy rainstorm in south China[D]. Changsha: National University of Defense Technology, 2017. [18] Lee K S, Bang S H, Chang K S. Feedback-assisted iterative learning control based on an inverse process model[J]. Journal of Process Control, 1994, 4(2): 77−89. doi: 10.1016/0959-1524(94)80026-X [19] 杜川利, 黄向宇, 俞小鼎. 变分同化方法在Lorenz系统中的简单应用研究[J]. 气象, 2005, 31(2): 23−26. doi: 10.7519/j.issn.1000-0526.2005.02.005Du Chuanli, Huang Xiangyu, Yu Xiaoding. Simple application of variational four-dimensional assimilation in Lorenz system[J]. Meteorological Monthly, 2005, 31(2): 23−26. doi: 10.7519/j.issn.1000-0526.2005.02.005 [20] Hall M C G. Application of adjoint sensitivity theory to an atmospheric general circulation model[J]. Journal of the Atmospheric Sciences, 1986, 43(22): 2644−2652. doi: 10.1175/1520-0469(1986)043<2644:AOASTT>2.0.CO;2 [21] 李建平, 丑纪范. 非线性大气动力学的进展[J]. 大气科学, 2003, 27(4): 653−673. doi: 10.3878/j.issn.1006-9895.2003.04.15Li Jianping, Chou Jifan. Advances in nonlinear atmospheric dynamics[J]. Chinese Journal of Atmospheric Sciences, 2003, 27(4): 653−673. doi: 10.3878/j.issn.1006-9895.2003.04.15 [22] 郜吉东, 丑纪范. 数值模式初值的敏感性程度对四维同化的影响——基于Lorenz系统的研究[J]. 气象学报, 1995, 53(4): 471−479.Gao Jidong, Chou Jifan. The effects of the model sensitivity to initial condition upon the variational four-diensional assimilation−the study based on Lorenz model[J]. Acta Meteorologica Sinica, 1995, 53(4): 471−479. -
计量
- 文章访问数: 725
- HTML全文浏览量: 273
- PDF下载量: 32
- 被引次数: 0
