Influence of atmospheric momentum input on Beaufort Gyre long term changes under the Arctic sea ice retreat
-
摘要: 随着北冰洋海冰快速减退，气–冰–海系统发生显著变化，波弗特流涡也发生显著变化。本文使用实测资料和海洋大气再分析数据，探讨北冰洋波弗特流涡的长期变化和大气动量输入对波弗特流涡变化的影响。波弗特流涡的长期变化可以分为3个典型时期(1980–1995年，1996–2007年，2008–2018年)。最近时期(2008–2018年)，波弗特流涡平均流涡强度达到4.39×10–7，相较于第1个时期(1980–1995年)，流涡强度增加近2倍，达到稳定的状态。波弗特流涡范围扩大，主体向西北移动；上层海洋斜压性增强。与此同时，上层海洋环流主模态已发生显著转变：1980–1995年，环流主模态为影响整个加拿大海盆的加拿大海盆模态；2008–2018年的主模态则转变为影响整个研究海域的太平洋扇区模态。最近时期，表征气–海之间动量输入的气–海应力显著增加，尤其是夏末秋初的8–10月，与冰–海应力几乎相当。增加的大气动量输入带来平均动能增加，埃克曼泵压效应增强，下盐跃层深度加深，增加的大气动量输入进而导致近年来波弗特流涡的显著增强。加拿大海盆南部是大气动量输入的关键区。Abstract: Beaufort Gyre (BG) had presented the significant changes associated with the complicated interactions between the Arctic air-ice-ocean system. In this paper, the observed McLane Moored Profiler data combined with the oceanic and atmospheric reanalysis datasets are used to discuss the influence of atmospheric momentum input on the BG long term changes. The BG exhibited the three different stages from 1980 to 2018 (1980−1995, 1996−2007, 2008−2018). The BG kept a stable state during the recent period (2008−2018). Compared with the first period (1980−1995), the BG strength reached up to 4.39×10−7, and increased nearly twice during the recent period. Meanwhile, the upper ocean processes showed the measurable discrepancies, such as the BG area expanded, gyre moved northwestward, and upper baroclinicity enhanced. Accordingly, the leading upper circulation mode had undergone a significant shift during these two periods. During the recent period, that is the leading Pacific sector mode played the main role in the upper circulation, while the basin mode receded the domination. Since the air-ocean stress represents the atmospheric momentum input process, our study indicated the summer air-ocean stress (August−October) increased remarkably and was even equivalent to the contribution of sea ice. The increased atmospheric momentum input may benefit to the mean kinetic energy increasing, together with the Ekman pumping enhancing and cold halocline deepening. Thus, the mentioned processes resulted in the BG obvious enhancement during the recent period. The southern Canada basin was the key area for the atmospheric momentum input.
-
Key words:
- Beaufort Gyre /
- leading circulation mode /
- atmospheric momentum input /
- key area /
- long term changes
-
1. 引言
近年来，北极地区显著增暖[1-2]，北冰洋夏季海冰迅速减少，开阔水和冰间水道增加[3-4]。大部分海冰消退都发生在加拿大海盆[5]。波弗特流涡（Beaufort Gyre）作为加拿大海盆，乃至北冰洋上层重要的环流系统之一，也发生着相应的转变。波弗特流涡变化会影响整个北冰洋上层海洋环流结构，改变淡水运移与释放，而后者会对北大西洋深层环流以及全球气候产生深远影响[6-8]。
随着北冰洋气–冰–海系统的显著变化，波弗特流涡也发生明显变化，流涡强度和范围均显著增大。利用实测资料和遥感数据以及模式所得结果均显示，流涡明显增强[9-11]，且近年来趋于稳定[12]，同时在海洋动力地形场上表现海洋动力地形梯度增大[13]。最近的研究[14-15]表明，近年来波弗特流涡处于自旋加速的状态，主要体现在地转流流速增加。空间上，近年来波弗特流涡核心向西北移动[14, 16]、流涡范围显著扩大[17-18]。Regan等[18]的研究表明在2003−2014年期间，波弗特流涡以每年53 000 km2的速度向北和向西扩展，波弗特流涡强度增强，形状变得不对称。冬季流涡范围大且强度大，而夏季范围小且强度弱。
关于大气环流对波弗特流涡变化的影响机理方面一直是北极研究热点。21世纪之前北冰洋风应力主要表现为多时间尺度振荡[19]。进入21世纪以来，除了多时间尺度的振荡，风应力还存在一个长期增加的趋势[20-21]。Martin等[22]的模式结果显示，相对于冰−海应力而言，气−海应力的量值很小可以忽略不计，海洋表层应力主要由冰−海应力影响。波弗特高压系统驱动着反气旋式波弗特流涡，20世纪90年代末开始，波弗特高压显著增强[23-24]。波弗特高压在不同大气环流背景下的变化会引起波弗特流涡的显著变化[25-27]进而影响弗拉姆海峡的海冰输出。直接作用于界面的气−海应力在平衡波弗特流涡的过程中有重要作用[28]。Karcher等[29]指出异常强的反气旋表面应力使得波弗特流涡自旋加速。海冰快速减退是调节气−海应力的重要因素之一[30]，Meneghello等[31]提出冰−海应力输入会调节波弗特流涡强度，自旋运动会受到应力输入的限制而趋于稳定。
近年来北冰洋海冰快速减退，波弗特流涡正处于一个新的时期[32]，在这一背景下探讨日益增加的大气动量输入对上层环流影响的研究仍待深入。本文利用实测资料和再分析数据，定量分析波弗特流涡强度的长期变化特征，探讨第1个时期和最近时期环流主模态的转变，在此基础上，提出大气动量输入影响波弗特流涡变化的关键区域。
2. 数据和方法
2.1 数据
2.1.1 实测和卫星遥感资料
实测数据主要有2003−2018年的锚定数据和船测CTD数据，其中锚定数据来自波弗特流涡勘探计划(Beaufort Gyre Exploration Project，BGEP)的A、B、C 3个锚定点的MMP（McLane Moored Profiler）数据，由加拿大圣劳伦斯破冰船提供的，锚定点（76°N，140°W）的数据只提供到2008年夏季因此没有选用。锚定数据深度范围大约为50～2 000 m，深度间隔为2 m，数据时间间隔为6 h。本文主要选取了其中的流速数据。此外，本文还采用WOD18数据，该数据由美国国家海洋和大气管理局（NOAA）的国家环境信息中心（National Centers for Environmental Information, NCEI）提供。本文选取1980−2018年加拿大海盆附近海域质量可靠的数据，结合锚定和船测数据，分析波弗特流涡的长期变化特征。
海冰密集度[33]和海冰漂流场数据由美国国家冰雪数据中心（NSIDC）提供，数据网址
https://nsidc.org/data/nsidc-0116 ，空间分辨率为 25 km×25 km。海冰漂流场资料是由AVHRR、SMMR和SSM/I多个卫星遥感数据以及国际北极浮标计划（IABP）的实测资料同化得到。本文选取的是1980−2018年月均海冰密集度和海冰漂流场数据。2.1.2 再分析数据
SODA（Simple Ocean Data Assimilation）再分析数据[34]，是由马里兰大学提供的月均和5 d数据，空间网格分辨率是0.5°×0.5°，数据范围覆盖全球，垂向分层50层，SODA3.4.2数据的强迫场是欧洲中心ERA-Interim数据。本文选取1980−2018年SODA再分析海流、海面高度和盐度数据。
本文选取由NCEP/NCAR提供的大气再分析数据集[35]提供的10 m风场数据，其空间分辨率为2.5º×2.5º，数据范围覆盖全球，用于计算1980−2018年大气对海洋的动量输入长期变化。
海洋动力地形（Dynamic Ocean Topography, DOT）数据来自Armitage等[36]的结果。该月均数据的空间覆盖范围为60°～81.5°N，环全球经度，网格分辨率为0.75°×0.25°，时间跨度为2003−2014年。本文在计算过程中分别采用2003−2011年Envisat卫星数据和2012−2014年CryoSat-2卫星数据。
2.2 方法
海面高度起伏的空间差异可以用来刻画波弗特流涡强度[18, 37]，本文利用SODA海面高度场数据给出定量分析波弗特流涡变化的强度指数S，
$$ {{S}} = \frac{{{\rm{SS}}{{\rm{H}}_{{\rm{max}}}} - {\rm{SS}}{{\rm{H}}_{{\rm{min}}}}}}{{{R}}}, $$ (1) 式中，SSHmin和SSHmax分别是围绕波弗特流涡中心海面高度的一系列闭合等值线的最小值和最大值；R是波弗特流涡平均半径，也就是上述两条闭合等值线间平均距离。为了更好地刻画该强度指数，等值线间隔取0.1 cm。同理，采用海洋动力地形数据，也可计算流涡强度指数SDOT。
上层海洋的应力来源主要有大气对上层海洋应力输入和海冰对上层海洋应力输入[31]，
$$ {{\rm{\tau }}_{{\rm{total}}}} = {a}{{\rm{\tau }}_{{\rm{io}}}} + \left( {1 - {{a}}} \right){{\rm{\tau }}_{{\rm{ao}}}}, $$ (2) 式中，a为海冰密集度；
${\tau _{{\rm{ao}}}}$ 为气−海应力，由${\rm{}}{{\rm{\tau }}_{{\rm{ao}}}} = $ $ {{\rm{\rho }}_{\rm{a}}}{{{C}}_{{\rm{Da}}}}\left| {{U_{{\rm{air}}}}} \right|{U_{{\rm{air}}}}$ 计算；$ {{\rm{\tau }}_{{\rm{io}}}}$ 为冰−海应力，由${{\rm{\tau }}_{{\rm{io}}}} = {{\rm{\rho }}_{\rm{w}}}{{{C}}_{{\rm{Di}}}} $ $ \left| {{U_{{\rm{ice}}}} - {U_{{\rm{ocean}}}}} \right|\left( {{U_{{\rm{ice}}}} - {U_{{\rm{ocean}}}}} \right)$ 计算得到。大气与开阔水域之间拖曳系数${{{C}}_{{\rm{Da}}}}$ =0.001 25，海冰与开阔水域之间拖曳系数$ {{{C}}_{{\rm{Di}}}}$ =0.005 5，ρa、ρw分别是大气和海水的密度，Uair是海面10 m处风速，Uice是海冰漂流速度，Uocean是表层海洋流速。下文所提的气−海应力与冰海应力均为考虑海冰密集度的情况。关于加拿大海盆盐跃层深度的计算方法，前人主要有双扩散系数比值法、盐度梯度法和浮力频率法等。其中，盐度梯度法可以很好地刻画波弗特流涡区域内的盐跃层，并且计算简单且结果只依赖盐度[11]。本文选取波弗特流涡区域内的CTD实测数据，采用盐度梯度法计算盐跃层深度。
3. 波弗特流涡的长期变化
3.1 波弗特流涡的长期变化
波弗特流涡强度具有较为显著的长期变化特征。本文利用加拿大海盆附近（70º～84ºN，160ºE～120ºW）的SODA海面高度数据，计算了波弗特流涡强度。本文计算的流涡强度与由卫星遥感反演的海洋动力地形[36]计算的流涡强度SDOT，都表明波弗特流涡近年来显著增强的现象，两者同步相关性很高，达到0.93（通过95%的显著性检验，图1a）。这也表明SODA同化数据可以很好地刻画波弗特流涡的长期变化。1980−2018年间流涡强度以每十年9.5×10−8的趋势显著增加。除个别年份（主要是1996年、2007年）外，流涡强度的逐年标准差、年极值均相对稳定，它们的长期变化特征不显著。对波弗特流涡强度的时间序列进行滑动t检验发现，流涡强度先后在1996年和2007年发生明显变化（图1b）。月均流涡强度也显示，1996年和2007年是波弗特流涡强度年变率最剧烈的年份。由此，波弗特流涡强度可以分为3个显著变化时期（结合同期加拿大海盆海冰范围变化）：1980−1995年（第1个时期）、1996−2007年（过渡时期）、2008−2018年（最近时期）。1980−1995年平均流涡强度为1.46×10−7，2008−2018年平均流涡强度达到4.39×10−7，增加近2倍，最近时期波弗特流涡正处于一个稳定的新状态，且叠加以显著的低频变化。本文将重点分析第1个时期和最近时期的波弗特流涡变化特征。
图 1 波弗特流涡强度的长期变化（a）及其滑动t检验（b，滑动窗口长度5年）Figure 1. Long term changes (a) and the moving 5-a t-test (b) of Beaufort Gyre strength实测和再分析数据得到较为一致的波弗特流涡变化的垂直结构。最近时期（2008−2018年），流涡内3个锚定点（A: 75ºN，150ºW；B: 78ºN，150ºW和C: 74ºN，140ºW）的上层250 m以浅流速明显增加，且存在明显的年际变化，存在准正压结构。虽然缺乏第1个时期的实测MMP海流资料，但2003−2018年锚定点50～250 m流速增加仍可超过2 cm/s（图2a），且斜压性有所增强。对比锚定点附近的实测海流资料与SODA再分析数据的结果显示，SODA再分析数据很好地捕捉到这种海流垂直结构上的变化，流速亦增大2 cm/s以上。锚定点的流速结构显示波弗特流涡结构似乎发生转变，近表层的流核均变浅，更易受表层过程的影响。锚定点流速结构显示波弗特流涡近年来年际变化较大，尤其是锚定A点和B点，这可能是由于流涡南部斜压性增强所致。流速垂直结构表明，流涡结构在最近时期显著增强，这与流涡强度在最近时期显著增强（图1a）相似，也表明近年来波弗特流涡已经进入一个新的时期。
图 2 波弗特流涡内BGEP锚定点流速、WOD盐度和SODA再分析数据的垂直结构a−c 中细绿（红）线表示锚定点 1996−2007年（2008−2018 年）的年平均流速。a−c（d−f ）中粗蓝、绿和红线表示 1980−1995 年、1996−2007年和2008−2018 年的平均流速（盐度）Figure 2. The velocity vertical structure of BGEP moorings data and SODA reanalysis datasets as well as the salinity vertical structure of WOD data and SODA reanalysis datasets in the Beaufort Gyrea−c indicate the annual mean current velocity of three moorings during 1996−2007 (2008−2018) by the thin green (red) lines. a−c (d−f) indicate the mean velocity (salinity) during 1980−1995, 1996−2007 and 2008−2018 by the thick blue, green and red lines与波弗特流涡增强密切相关的海洋层化结构也发生显著的变化。2008−2018年，加拿大海盆上层海洋盐度明显降低，盐跃层加深，强度增强（图2d至图2f）。波弗特流涡汇聚大量淡水，淡水主要集中在上400 m。实测WOD数据和SODA再分析数据清晰的显示，随着波弗特流涡近年来（2008−2018年）的显著增强（图1a），流涡内的淡水含量明显增加。流涡内盐度变化显著的深度在空间上并不一致，主要集中在两个深度上，分别是50 m以浅和150～200 m附近。这也导致近年来增加的淡水含量，在流涡西北部主要积聚在盐跃层内（锚定点B），在流涡南部则主要积聚在上盐跃层以浅的近表层（锚定点A、C）。这种垂直结构上的变化间接地支持了近年来波弗特流涡显著西北向移动的结论。
3.2 环流主模态转变
加拿大海盆及其临近海域环流主模态发生了显著转变。依据前文流涡强度的分析，为了去除全球变暖对流涡长期变化的影响，本文对1980−1995年、2008−2018年SODA月均海面高度，去除趋势和季节变化（多年逐月异常）后进行经验正交函数分解（EOF），分析其时空变化特征。两个时段的前两个模态累积方差均超过52%。结果表明，1980−2018年的环流主模态由第1个时期的加拿大海盆模态（图3a）转变为近年来的太平洋扇区模态（图3c）。1980−1995年，海面高度呈东西反相变化，主要体现了波弗特流涡和东西伯利亚海陆架陆坡流的变化，受这一海盆模态的控制，流涡主体位于加拿大海盆深水区（水深大于500 m）。2008−2018年，环流范围明显扩大，几乎影响了整个太平洋扇区，而且环流主体明显向西北移动，位于楚科奇海台−门捷列夫海岭附近，而海盆内的环流系统则集中于波弗特海陆坡附近。与环流主模态转变相呼应的是，近年来波弗特流涡流速增大，影响范围显著扩大，形状更加不对称（图4a），加拿大海盆和楚科奇海台上层海洋随环流主模态转变而共同调整。
图 3 1980−1995 年、2008−2018 年 SODA 海面高度异常EOF 分析的前两个空间模态及其对应的时间系数a, b（c, d）为1980−1995年（2008−2018年）海面高度异常EOF分解的前两个空间模态，灰色实线为500 m等深线。e,f图是空间模态对应的时间系数，其中粗实线为经过12个月低通滤波的时间系数Figure 3. First two spatial patterns and the corresponding time series of EOF analysis of SODA sea surface height anomalies during 1980−1995 and 2008−2018a, b (c, d) show the spatial patterns of EOF of the first two sea level height anomalies during 1980−1995 (2008−2018), and the gray solid line indicates the 500 m isobath. e,f show the time series corresponding to the spatial patterns, and the thick solid line indicate the 12 months low-pass filtering results of the first two modes
图 4 波弗特流涡范围（a）、断面流速垂直结构（b, c）和断面流量（d）的长期变化a中阴影代表2003−2014年的平均海洋动力地形，粗实线分别为1984年、1997年和2012年SODA数据刻画的年平均波弗特流涡范围，灰色实线为选取断面。b, c为1980−1995年和2008−2018年断面流速，负值表示海流向南Figure 4. Beaufort Gyre area (a) as well as the velocity vertical structure (b, c) and the volume transport long term changes (d) of the selected sectiona shows the mean ocean dynamic topography during 2003−2014, by the thick blue, green and red lines indicate annual mean Beaufort gyre area in 1984, 1997 and 2012 derived by SODA datasets, respectively, the gray solid line indicates the selected section. b and c show the section velocity during 1980−1995 and 2008−2018, negative values indicate southward current vector波弗特流涡空间分布变化也表明近年来流涡范围扩大且非对称性增大，上400 m经向体积输运增加48%；流涡影响深度加深，可达大西洋层，流涡次表层的层化增强。波弗特流涡主要位于深水（水深大于500 m）区域（图4a）。本文详细比较了1980−2018年的流涡影响区域，根据2003−2014年海洋动力地形数据显示的波弗特流涡的范围变化，在波弗特流涡东侧截取一条纬向断面（75°N，145°～125°W），分别选择1984年、1997年、2012年作为3个时期的代表性年份。与环流主模态转变相对应，近年来波弗特流涡范围明显增大，流涡核心明显向西北移动，并与陆坡相互作用，产生斜压不稳定，使得流涡形状非对称性增大[38]。对比1980−1995年和2008−2018年平均的断面流速垂直结构，根据39 a间断面南向流速的平均值加上一倍标准差计算得到，波弗特流涡在断面处的临界速度为0.5 cm/s。2008−2018年波弗特流涡影响深度加深明显，且上200 m的流速增加明显（图4b，图4c）。在1980−1995年，断面东侧的次表层存在一支南向的急流，此时加拿大海盆上层的层化较弱。最近时期，流轴变宽，流涡东部近表层流速大，流涡受表层作用影响显著，受到来自大气通过气−海界面作用和海冰的影响，表层速度梯度明显增大，剪切增强，靠近加拿大北极群岛附近速度剪切更强，近年来波弗特流涡汇聚了大量的淡水，导致次表层的层化显著增强（图2）。但是 2007年以后，纬向断面的体积输运明显增大，2016年达到极大值39×106 m3/s，在2008−2018年通过断面的平均的体积输运可达28×106 m3/s。在整个研究时间段上，通过断面的流量与流涡强度的同步相关性可达0.72（通过95%的显著性检验），断面流量的结果也支持近年来波弗特流涡显著增强并且达到一个稳定的时期。
盐跃层深度和淡水库深度在1980−1995年和2008−2018年的空间分布表明环流主模态近年来已经从加拿大海盆模态转变为太平洋扇区模态。盐跃层深度和淡水库是依据WOD和UDASH（Unified Database for Arctic and Subarctic Hydrography）整合的实测CTD数据计算得到，CTD站点位置在图中标示（图5中灰点）。淡水库深度取得是盐度34.8等盐线。与环流主模态转变相对应，1980−1995年淡水库深度与盐跃层深度空间分布与加拿大海盆模态相似，核心区域主要分布在加拿大海盆，2008−2018年淡水库深度与盐跃层深度的空间分布与太平洋扇区模态相似，深度深于350 m的淡水库核心区域范围明显扩大，影响到楚科奇海台−门捷列夫海岭附近。盐跃层深度的变化可以反映波弗特流涡的变化。2008−2018年，加拿大海盆及其周边海域整个区域的盐跃层深度不同程度加深，楚科奇海台盐跃层深度加深尤为明显。1980−1995年，加拿大海盆盐跃层深度和淡水库深度加深。2008−2018年，淡水库主体范围扩大，淡水库核心区域主要在加拿大海盆中部和西北部。淡水库的核心深度加深，盐跃层的最大深度也明显加深。淡水库在整个范围内加深，在楚科奇海台加深更加显著，这种调整与环流主模态改变相似，呼应了近年来波弗特流涡的范围扩大，向西北移动。
图 5 1980−1995年、2008−2018年的盐跃层深度和淡水库深度的空间分布Figure 5. Spatial characteristics of halocline depth and freshwater reservoir depth during 1980−1995 and 2008−20184. 大气动量输入对波弗特流涡的影响
4.1 大气动量输入日益显著
加拿大海盆及其周边海域气候态平均的风场、海冰运动场、表层流场在1980−1995年与2008−2018年都呈现反气旋式结构；近年来，风场矢量与表层流场矢量、海冰运动矢量与表层流场矢量夹角变小。1980−1995年，加拿大海盆和楚科奇海台气候态平均的风场反气旋式结构较弱，风速大小分布空间差异明显，楚科奇海台和加拿大海盆内部风速较小；海洋表层流速较小，小于海冰运动场速度，该时期波弗特流涡较弱（图6a），流涡边缘流速较大，尤其西南部。海冰和大气共同作用于海洋，对表层海水运动有正贡献。2008−2018年，加拿大海盆及其周边海域的表层流速相较于1980−1995年在整个研究区域都明显增加；加拿大海盆西南部流速增大尤为显著。加拿大海盆西南部和楚科奇海台上的风速增大明显。
图 6 1980−1995年、2008−2018年的10 m风场、表层流场和海冰漂流场Figure 6. Wind speed at 10 m, sea surface current and sea ice motion during 1980−1995 and 2008−2018我们计算了波弗特流涡核心区域（70.5°～81.5°N，180°～130°W）内的气−海应力和冰−海应力，用以比较大气和海冰动量输入的长期变化。大气动量输入和海冰动量输入在气−冰−海系统中共同调节上层海洋，海冰动量输入为主，海冰动量输入大约是大气动量输入的3倍（图7a）。波弗特流涡主要受到冰海调节器影响，波弗特流涡形状与海冰漂流场形状更加接近。近年来，大气动量输入呈现显著年际变化，小波分析显示，2007年前后大气动量输入和海冰动量输入都存在显著年际变化周期，其中2006−2012年大气动量输入存在更低频的变化周期 (图7b，图7c)。波弗特流涡强度在2007年迅速增强并且之后处于稳定状态，与之对应的是2007年大气动量输入增加异常显著，可达1.42×10−2 N/m2,与海冰动量输入相当。
图 7 上层海洋应力的长期变化、气−海应力和冰−海应力的小波分析Figure 7. Long term changes of upper ocean stress as well as air-ocean stress and ice-ocean stress wavelet analysis在气−冰−海系统中，大气动量输入存在明显季节变化，在夏末秋初（8−10月）海冰融化，大气动量输入明显强于其他季节（图8a），近年来，甚至成为上层海洋动量输入的主要来源，随着海冰的继续减退，甚至北冰洋会出现夏季无冰的现象，大气动量输入将日益显著。冬末春初，表层海水被海冰大面积覆盖，计算区域内大气动量输入几乎为0，这种情况一直持续到海冰开始融化。1980−1995年，夏末秋初的大气动量输入小于海冰动量输入。2008−2018年，夏末秋初的大气动量输入和海冰动量输入都有增加，大气动量输入的增加更加显著，增加大约130%（图8c），量值甚至超过海冰动量输入。此时，上层海洋受到大气动量输入的影响更加显著。海冰动量输入是上层海洋主要的动量输入来源。其中在秋末冬初更为显著（图8b）。10月份大气动量输入在最近时期增加更加显著，这可能是由于近年来海冰冻结延缓。海冰动量输入近年来在8月、9月份几乎保持不变，在2−4月增加更加显著。随着近年来海冰减退，海冰密集度减小，开阔水域面积增加，冻结延缓。夏末秋初，大气动量输入对波弗特流涡的影响日益显著。
图 8 气−海应力、冰−海应力的季节变化和夏末秋初（8−10月）上层海洋应力的长期变化Figure 8. Seasonal variations of air-ocean stress and ice-ocean stress as well as long term changes of upper ocean stress in late summer and early autumn (August, September, October)近年来（2008−2018年），海冰快速减退，气−海、冰−海应力旋度表现出显著的年际差异，气−海和冰−海应力旋度都有所增加，其中气−海应力旋度增加更为显著。气−海应力旋度和冰−海应力旋度达到年代尺度最大值，2007年气−海应力旋度达到2.9×10−8 N/m3。根据地理位置，将波弗特流涡区域分为加拿大海盆和楚科奇海台两部分，利用WOD数据来研究盐跃层深度的变化。楚科奇海台上盐跃层深度近年来有缓慢变浅的趋势，与气−海应力旋度2007年极大值相对应的是楚科奇海台上盐跃层2007年前后年变率显著（图9e），楚科奇海台下盐跃层深度在2007年这一年加深显著，出现阶跃。2007年以后，下盐跃层在200 m深度以下保持相对稳定与加拿大海盆下盐跃层深度相当，并以微小的趋势继续增加（图9h）。2008−2018年波弗特流涡更加稳定，上盐跃层的年际变化更小。在1980−1995年，加拿大海盆下盐跃层年际变化显著，2007年开始，加拿大海盆下盐跃层逐渐加深，近年来年际变化和季节变化趋于稳定。盐跃层深度结果支持波弗特流涡的范围扩大，向西北移动和环流主模态转变的结论。
图 9 应力旋度和由实测数据计算得到盐跃层深度的长期变化b−d给出了实测 CTD 站点的位置（红色点）和波弗特流涡平均范围（黑色实线）。 e−j 中蓝色误差棒为年平均值加减1倍标准差，红色实线为不同时期的变化趋势（第1个时期由于数据样本个数少，未求其趋势）Figure 9. Long term changes of stress curl and halocline depth derived from observed datab−d indicate the locations of CTD stations by red dots and the mean Beaufort Gyre area by black solid line. e−j indicate annual mean plus or minus one standard deviation by the blue bar and the trend of different periods by the red solid line (the trend of the first period was not calculated due to lacked of data samples)4.2 大气动量输入的关键区域
在最近时期大气动量输入与波弗特流涡强度变化密切相关。相较于1980−1995年，2008−2018年波弗特流涡强度显著增加的同时大气动量输入也增加1倍多，达4.8×10−3 N/m2（图10）。特别的是，2007年加拿大海盆出现异常强的大气动量输入，高于平均值约一个量级，达到
$1.5 \times {10^{ - 2}}$ N/m2，尽管此后迅速降低，但仍稳定在相对较高的平均态上振荡。与大气动量输入变化相对应，波弗特流涡强度在2007年迅速增强，此后并没有显著降低，在2008−2018年间流涡强度和范围均处于相对稳定的新状态[12]。随着北极海冰的快速减退，波弗特流涡正处于对大气风场高度敏感的状态[39]。2007年大气动量输入异常是导致近年来波弗特流涡显著增强的触发器，异常增加的大气动量输入促使流涡强度发生突变，也使得波弗特流涡进入一个新的时期。近年来，波弗特流涡强度与大气动量输入都存在低频变化，2008−2018年二者的年际变化较大，流涡的这种低频变化似乎受到大气动量输入的低频变化的影响。
图 10 上层海洋的大气动量输入和流涡强度长期变化Figure 10. Long term changes of Beaufort Gyre strength and upper ocean atmospheric momentum input加拿大海盆南部是这种增强的大气动量输入的关键区。近年来，比较两个时期的大气动量输入，大气风场异常（最近时期相较于第1个时期）主要表现为反气旋式的环流差异，大气动量输入仍显著增加（图11）。图中等值线分别指示了对应时段的主模态的核心区。第1个时期（1980−1995年）大气动量输入量值不大，流涡核心位于海盆深水海域。而2008−2018年，显著增加的大气动量输入集中在海盆南部，是导致环流主模态发生改变的重要因素。一方面，增加的气−海应力使流涡内的表层平均动能显著增加，而涡旋动能亦有所增加，会部分抵消大气动量输入造成的盐跃层加深[28, 39]，使流涡趋于稳定。平均动能在加拿大海盆南部增加显著，表明了波弗特流涡在关键区明显增强。大气动量输入的变化存在空间差异，除了关键区外，门捷列夫海岭附近大气动量输入也明显增加，但是在加拿大海盆东北部多年冰区域，大气动量输入减少。
图 11 1980−1995年、2008−2018年的气象要素和上层海洋动能的空间分布和差异图中异常指的是各物理量2008−2018年和1980−1995年气候态平均的差异。a中蓝线为加拿大海盆模态，b中绿线为太平洋扇区模态，c中灰色方框为关键区位置Figure 11. Spatial characteristics and difference of meteorological factors as well as upper ocean kinetic energy during 1980−1995 and 2008−2018The discrepancy in the figures refers to the physical characteristics difference between the mean state during 2008−2018 and 1980−1995. a. Blue line is the Canada basin mode, b. green line is Pacific sector mode, c. gray box is on behalf of the location of the key area两个时期的风场异常呈现较强的反气旋式环流结构。与近年来波弗特流涡显著增强和流涡区域内盐跃层加深相对应，大气动量输入关键区与风场异常的显著区域大体一致（图11c和图11e）。在最近时期，关键区内的气−海应力输入显著增加，是冰−海应力与表层流之间的负反馈机制[28]的重要补充，使流涡强度保持在显著增强的新状态。近年来加拿大海盆南部的东风异常有利于关键区的海冰向加拿大海盆内输运，进而加快关键区内的海冰减少，关键区的大气动量输入随之增加。大气动量输入增加带来平均动能的增加，以及埃克曼泵压效应的增强和下盐跃层加深，伴随着波弗特流涡增强，都表明加拿大海盆的局地海洋动力过程发生显著变化。随着全球变暖，加拿大海盆海冰快速变化，大气动量输入通过关键区域对波弗特流涡影响将日益显著。
5. 总结与讨论
本文使用实测资料和海洋大气再分析数据，分析波弗特流涡的长期变化，并探讨大气动量输入对波弗特流涡变化的影响，结果表明：
波弗特流涡强度的长期变化可以分为3个稳定的时期（1980−1995年，1996−2007年，2008−2018年）。波弗特流涡强度在最近时期（2008−2018年）相较于第1个时期（1980−1995年）增加近2倍，且处于一个新的稳定的状态，存在显著年际变化特征。与此同时，加拿大海盆上层海洋环流主模态发生转变：1980−1995年，环流主模态为影响加拿大海盆的加拿大海盆模态；2008−2018年，环流主模态转变为几乎影响整个研究区域的太平洋扇区模态。2008−2018年，大气动量输入的变化，是导致环流主模态发生改变和流涡强度增强并稳定的重要因素。值得注意的是，流涡对大气强迫的响应存在滞后[18, 40]，滞后时间往往在数月以内，北冰洋海冰的密集度、覆盖范围等的变化也可能会使得流涡响应的滞后时间发生变化。
上层海洋大气动量输入日益显著，海冰动量输入依然占据主导地位，近年来（2008−2018年），大气动量输入在夏末秋初显著增加，大气动量输入和海冰动量输入对波弗特流涡的调节同等重要。最近时期，冻结延缓，大气动量输入在10月份增加最为显著。大气动量输入异常是导致近年来波弗特流涡显著增强的触发器，异常增加的大气动量输入促使流涡强度发生突变，也使得波弗特流涡进入一个新的时期。波弗特流涡区域内盐跃层深度与淡水库深度呼应环流主模态改变的结论。2007年楚科奇海台下盐跃层深度明显加深，出现阶跃。大气动量输入关键区在加拿大海盆南部。我们也发现关键区域的涡旋动能增加也更加显著，这可能是因为波弗特流涡在范围扩大向西北移动的过程中，与地形发生相互作用，产生较强的斜压不稳定，斜压不稳定一方面使得流涡非对称性增大，另一方面使得涡旋动能增加显著。
最近Doddridge等[28]利用理想模型，提出大气风应力与冰−海调节器以及涡旋通量3个过程共同平衡波弗特流涡，且冰海调节器是主要的动力过程。我们将借助数值模式，定量评估三者在北冰洋夏季海冰快速减退过程中的相对重要性。此外，北冰洋夏季无冰情形下，无冰−海调节器的影响时，探究平衡流涡的关键动力过程，仍是北极物理海洋学的研究热点。
致谢：感谢北极和亚北极水文统一数据库（UDASH, Unified Database for Arctic and Subarctic Hydrography）提供的数据，该数据库包含1980−2015年65°N以北的温盐数据集（
https://www.earth-syst-sci-data.net/10/1119/2018/ ）。 -
图 1 波弗特流涡强度的长期变化（a）及其滑动t检验（b，滑动窗口长度5年）
Fig. 1 Long term changes (a) and the moving 5-a t-test (b) of Beaufort Gyre strength
图 2 波弗特流涡内BGEP锚定点流速、WOD盐度和SODA再分析数据的垂直结构
a−c 中细绿（红）线表示锚定点 1996−2007年（2008−2018 年）的年平均流速。a−c（d−f ）中粗蓝、绿和红线表示 1980−1995 年、1996−2007年和2008−2018 年的平均流速（盐度）
Fig. 2 The velocity vertical structure of BGEP moorings data and SODA reanalysis datasets as well as the salinity vertical structure of WOD data and SODA reanalysis datasets in the Beaufort Gyre
a−c indicate the annual mean current velocity of three moorings during 1996−2007 (2008−2018) by the thin green (red) lines. a−c (d−f) indicate the mean velocity (salinity) during 1980−1995, 1996−2007 and 2008−2018 by the thick blue, green and red lines
图 3 1980−1995 年、2008−2018 年 SODA 海面高度异常EOF 分析的前两个空间模态及其对应的时间系数
a, b（c, d）为1980−1995年（2008−2018年）海面高度异常EOF分解的前两个空间模态，灰色实线为500 m等深线。e,f图是空间模态对应的时间系数，其中粗实线为经过12个月低通滤波的时间系数
Fig. 3 First two spatial patterns and the corresponding time series of EOF analysis of SODA sea surface height anomalies during 1980−1995 and 2008−2018
a, b (c, d) show the spatial patterns of EOF of the first two sea level height anomalies during 1980−1995 (2008−2018), and the gray solid line indicates the 500 m isobath. e,f show the time series corresponding to the spatial patterns, and the thick solid line indicate the 12 months low-pass filtering results of the first two modes
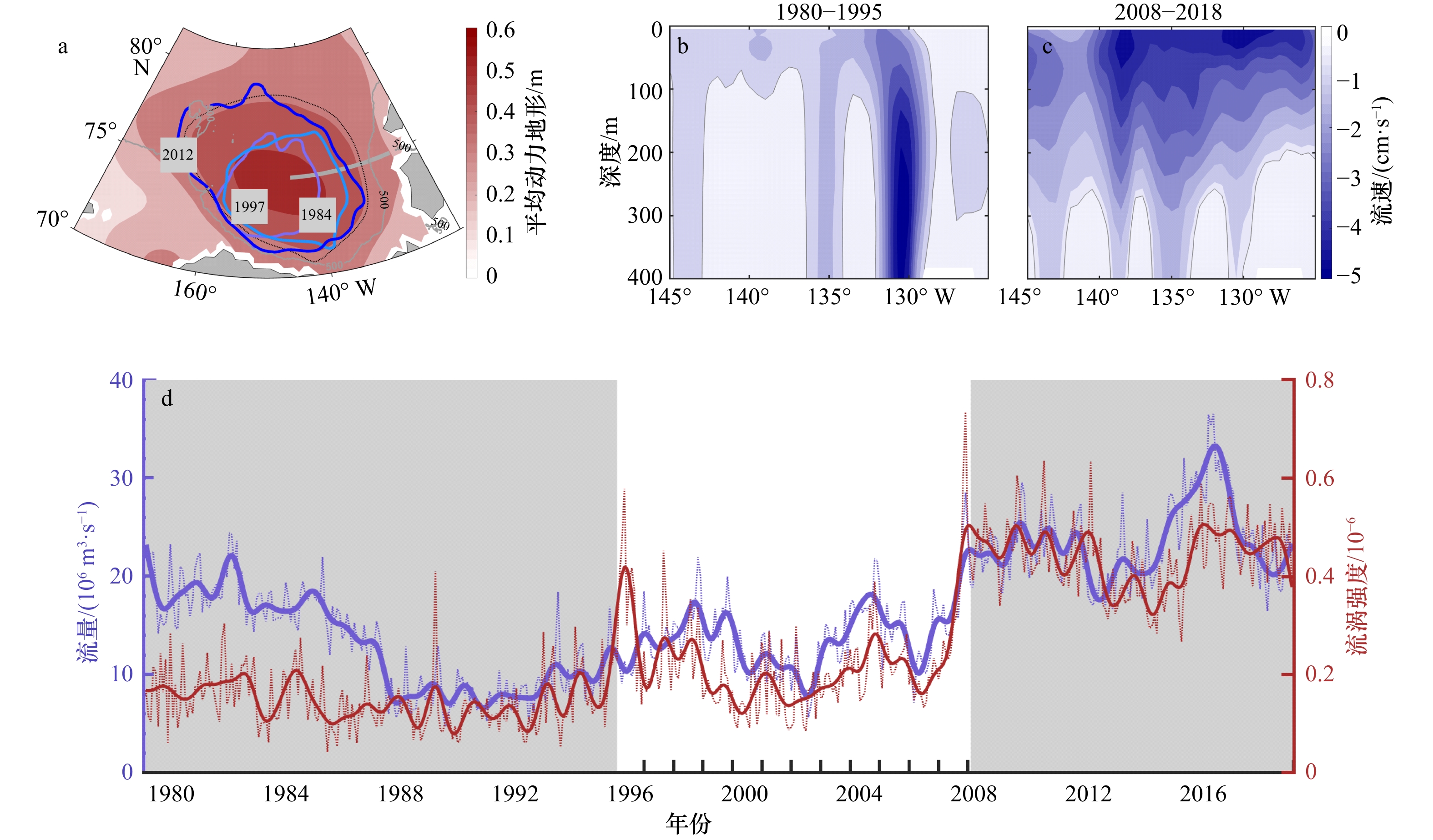
图 4 波弗特流涡范围（a）、断面流速垂直结构（b, c）和断面流量（d）的长期变化
a中阴影代表2003−2014年的平均海洋动力地形，粗实线分别为1984年、1997年和2012年SODA数据刻画的年平均波弗特流涡范围，灰色实线为选取断面。b, c为1980−1995年和2008−2018年断面流速，负值表示海流向南
Fig. 4 Beaufort Gyre area (a) as well as the velocity vertical structure (b, c) and the volume transport long term changes (d) of the selected section
a shows the mean ocean dynamic topography during 2003−2014, by the thick blue, green and red lines indicate annual mean Beaufort gyre area in 1984, 1997 and 2012 derived by SODA datasets, respectively, the gray solid line indicates the selected section. b and c show the section velocity during 1980−1995 and 2008−2018, negative values indicate southward current vector
图 5 1980−1995年、2008−2018年的盐跃层深度和淡水库深度的空间分布
Fig. 5 Spatial characteristics of halocline depth and freshwater reservoir depth during 1980−1995 and 2008−2018
图 6 1980−1995年、2008−2018年的10 m风场、表层流场和海冰漂流场
Fig. 6 Wind speed at 10 m, sea surface current and sea ice motion during 1980−1995 and 2008−2018
图 7 上层海洋应力的长期变化、气−海应力和冰−海应力的小波分析
Fig. 7 Long term changes of upper ocean stress as well as air-ocean stress and ice-ocean stress wavelet analysis
图 8 气−海应力、冰−海应力的季节变化和夏末秋初（8−10月）上层海洋应力的长期变化
Fig. 8 Seasonal variations of air-ocean stress and ice-ocean stress as well as long term changes of upper ocean stress in late summer and early autumn (August, September, October)
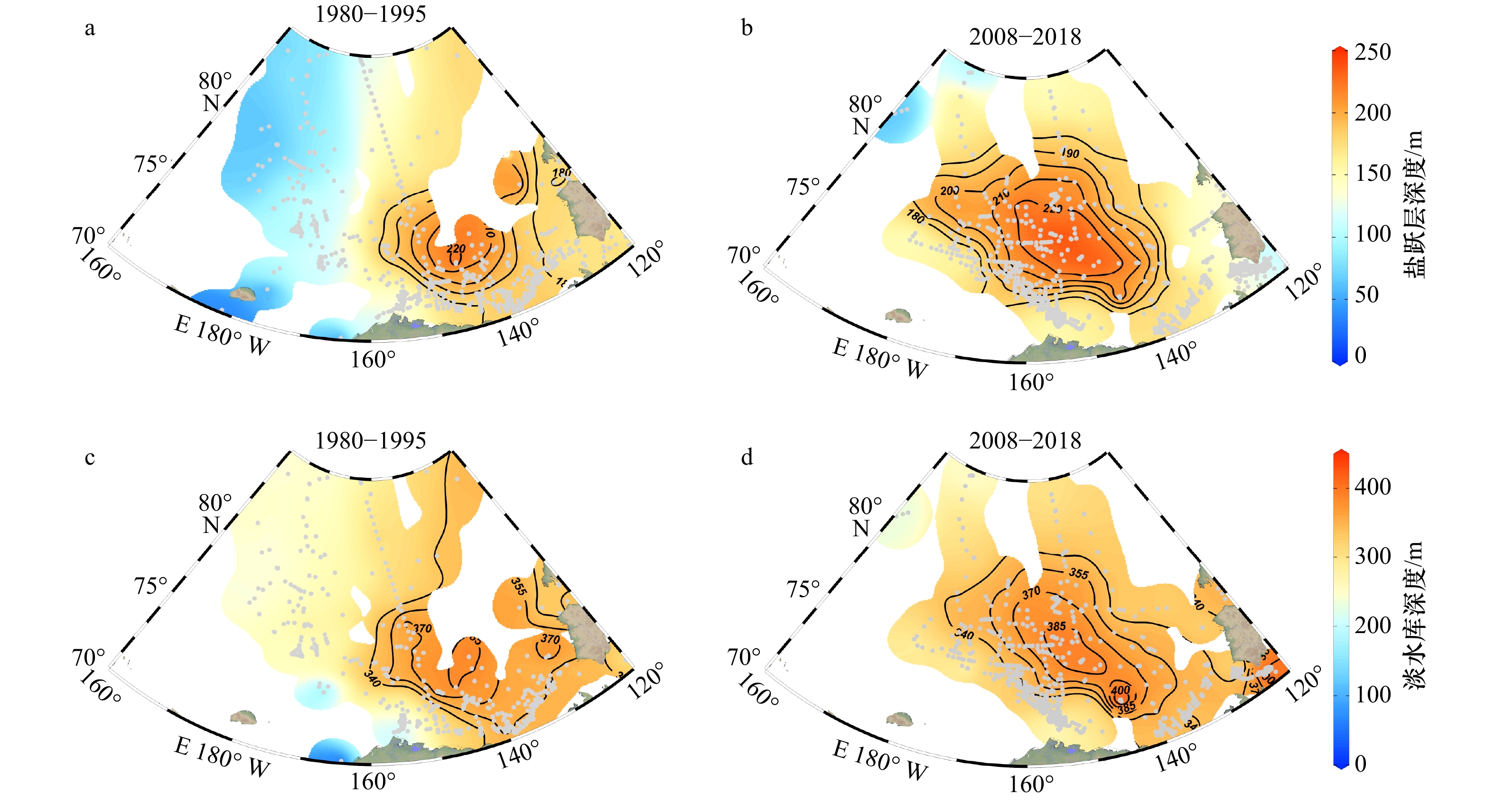
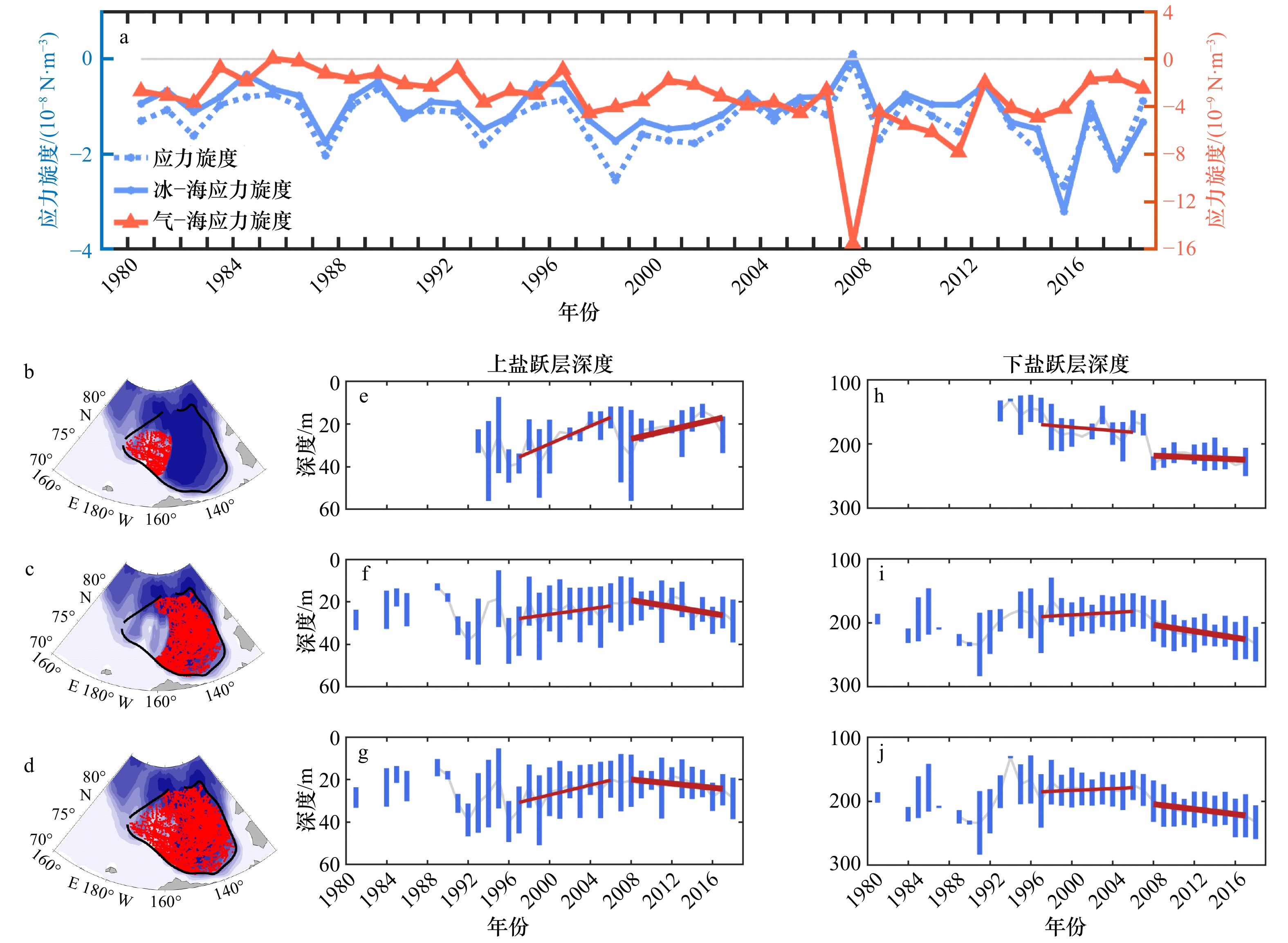
图 9 应力旋度和由实测数据计算得到盐跃层深度的长期变化
b−d给出了实测 CTD 站点的位置（红色点）和波弗特流涡平均范围（黑色实线）。 e−j 中蓝色误差棒为年平均值加减1倍标准差，红色实线为不同时期的变化趋势（第1个时期由于数据样本个数少，未求其趋势）
Fig. 9 Long term changes of stress curl and halocline depth derived from observed data
b−d indicate the locations of CTD stations by red dots and the mean Beaufort Gyre area by black solid line. e−j indicate annual mean plus or minus one standard deviation by the blue bar and the trend of different periods by the red solid line (the trend of the first period was not calculated due to lacked of data samples)
图 10 上层海洋的大气动量输入和流涡强度长期变化
Fig. 10 Long term changes of Beaufort Gyre strength and upper ocean atmospheric momentum input
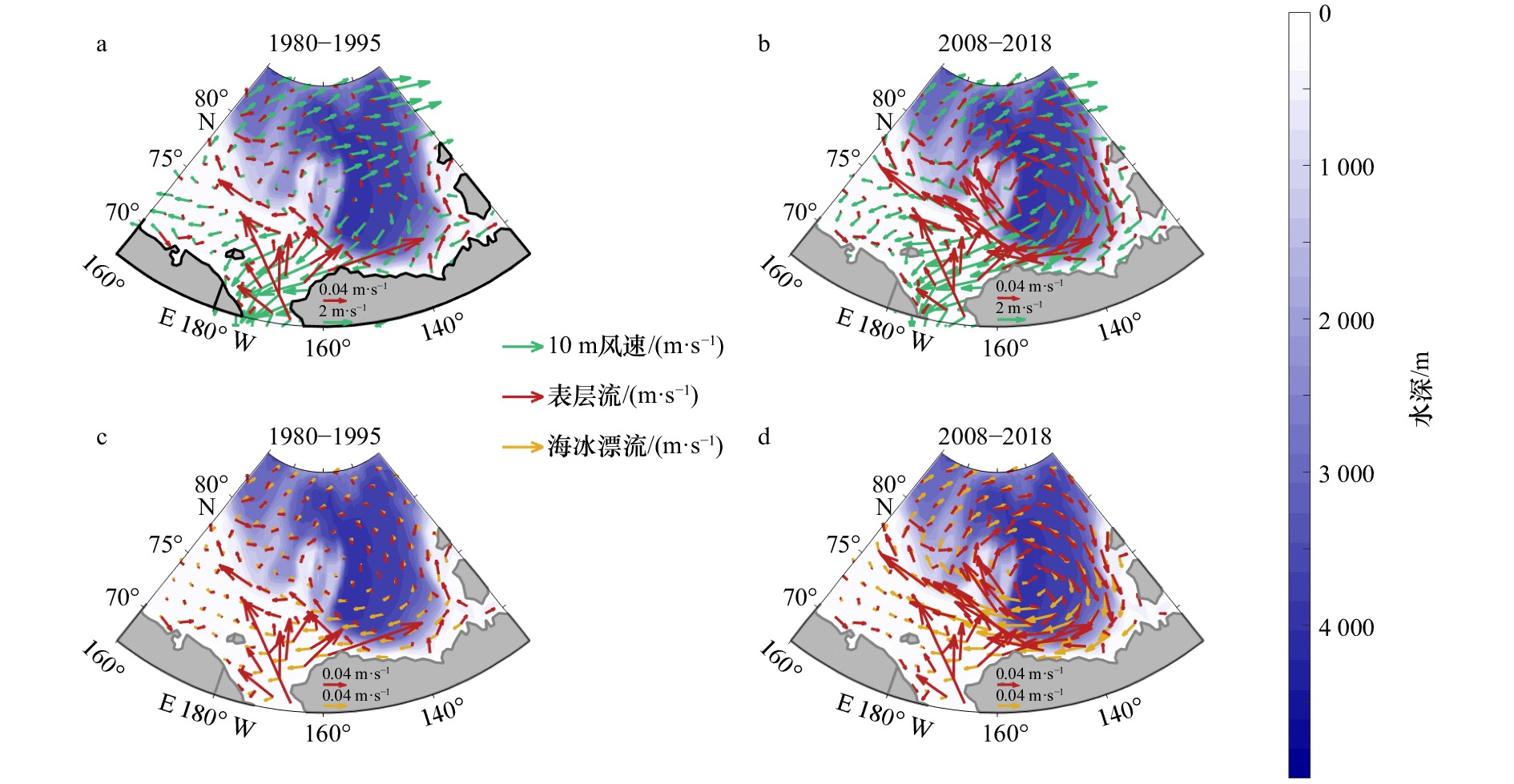
图 11 1980−1995年、2008−2018年的气象要素和上层海洋动能的空间分布和差异
图中异常指的是各物理量2008−2018年和1980−1995年气候态平均的差异。a中蓝线为加拿大海盆模态，b中绿线为太平洋扇区模态，c中灰色方框为关键区位置
Fig. 11 Spatial characteristics and difference of meteorological factors as well as upper ocean kinetic energy during 1980−1995 and 2008−2018
The discrepancy in the figures refers to the physical characteristics difference between the mean state during 2008−2018 and 1980−1995. a. Blue line is the Canada basin mode, b. green line is Pacific sector mode, c. gray box is on behalf of the location of the key area
-
[1] Screen J A, Simmonds I. The central role of diminishing sea ice in recent Arctic temperature amplification[J]. Nature, 2010, 464(7293): 1334−1337. doi: 10.1038/nature09051 [2] Previdi M, Janoski T P, Chiodo G, et al. Arctic amplification: A rapid response to radiative forcing[J]. Geophysical Research Letters, 2020, 47(17): e2020GL089933. [3] Meier W N, Stroeve J, Barrett A, et al. A simple approach to providing a more consistent Arctic sea ice extent time series from the 1950s to present[J]. The Cryosphere, 2012, 6(6): 1359−1368. doi: 10.5194/tc-6-1359-2012 [4] Perovich D, Meier W, Tschudi M, et al. [The Arctic] sea ice cover [in “State of the Climate in 2018”][J]. Bulletin of the American Meteorological Society, 2019, 100(9): S146−S150. [5] Davis P E D, Lique C, Johnson H L, et al. Competing effects of elevated vertical mixing and increased freshwater input on the stratification and sea ice cover in a changing Arctic Ocean[J]. Journal of Physical Oceanography, 2016, 46(5): 1531−1553. doi: 10.1175/JPO-D-15-0174.1 [6] Aagaard K, Swift J H, Carmack E C. Thermohaline circulation in the Arctic mediterranean seas[J]. Journal of Geophysical Research: Oceans, 1985, 90(C3): 4833−4846. doi: 10.1029/JC090iC03p04833 [7] Curry R, Mauritzen C. Dilution of the northern North Atlantic Ocean in recent decades[J]. Science, 2005, 308(5729): 1772−1774. doi: 10.1126/science.1109477 [8] Proshutinsky A, Krishfield R, Toole J M, et al. Analysis of the Beaufort Gyre freshwater content in 2003–2018[J]. Journal of Geophysical Research: Oceans, 2019, 124(12): 9658−9689. doi: 10.1029/2019JC015281 [9] Proshutinsky A, Krishfield R, Timmermans M L, et al. Beaufort Gyre freshwater reservoir: State and variability from observations[J]. Journal of Geophysical Research: Oceans, 2009, 114(C1): C00A10. [10] Zhao Mengnan, Timmermans M L, Cole S, et al. Evolution of the eddy field in the Arctic Ocean's Canada Basin, 2005–2015[J]. Geophysical Research Letters, 2016, 43(15): 8106−8114. doi: 10.1002/2016GL069671 [11] Armitage T W K, Manucharyan G E, Petty A A, et al. Enhanced eddy activity in the Beaufort Gyre in response to sea ice loss[J]. Nature Communications, 2020, 11(1): 1−8. doi: 10.1038/s41467-020-14449-z [12] Zhang Jinlun, Steele M, Runciman K, et al. The Beaufort Gyre intensification and stabilization: A model-observation synthesis[J]. Journal of Geophysical Research: Oceans, 2016, 121(11): 7933−7952. doi: 10.1002/2016JC012196 [13] Giles K A, Laxon S W, Ridout A L, et al. Western Arctic Ocean freshwater storage increased by wind-driven spin-up of the Beaufort Gyre[J]. Nature Geoscience, 2012, 5(3): 194−197. doi: 10.1038/ngeo1379 [14] Armitage T W K, Bacon S, Ridout A L, et al. Arctic Ocean surface geostrophic circulation 2003−2014[J]. The Cryosphere, 2017, 11(4): 1767−1780. doi: 10.5194/tc-11-1767-2017 [15] Zhong Wenli, Steele M, Zhang Jinlun, et al. Greater role of geostrophic currents in Ekman dynamics in the western Arctic Ocean as a mechanism for Beaufort Gyre stabilization[J]. Journal of Geophysical Research: Oceans, 2018, 123(1): 149−165. doi: 10.1002/2017JC013282 [16] Xie Jiping, Bertino L, Counillon F, et al. Quality assessment of the TOPAZ4 reanalysis in the Arctic over the period 1991−2013[J]. Ocean Science, 2017, 13(1): 123−144. doi: 10.5194/os-13-123-2017 [17] Kelly S J, Proshutinsky A, Popova E K, et al. On the origin of water masses in the Beaufort Gyre[J]. Journal of Geophysical Research: Oceans, 2019, 124(7): 4696−4709. doi: 10.1029/2019JC015022 [18] Regan H C, Lique C, Armitage T W K. The Beaufort Gyre extent, shape, and location between 2003 and 2014 from satellite observations[J]. Journal of Geophysical Research: Oceans, 2019, 124(2): 844−862. doi: 10.1029/2018JC014379 [19] Yang Jiayan. Seasonal and interannual variability of downwelling in the Beaufort Sea[J]. Journal of Geophysical Research: Oceans, 2009, 114(C1): C00A14. [20] Hakkinen S, Proshutinsky A, Ashik I. Sea ice drift in the Arctic since the 1950s[J]. Geophysical Research Letters, 2008, 35(19): L19704. doi: 10.1029/2008GL034791 [21] Spreen G, Kwok R, Menemenlis D. Trends in Arctic sea ice drift and role of wind forcing: 1992–2009[J]. Geophysical Research Letters, 2011, 38(19): L19501. [22] Martin T, Steele M, Zhang Jinlun. Seasonality and long-term trend of Arctic Ocean surface stress in a model[J]. Journal of Geophysical Research: Oceans, 2014, 119(3): 1723−1738. doi: 10.1002/2013JC009425 [23] Serreze M C, Barrett A P. Characteristics of the Beaufort Sea high[J]. Journal of Climate, 2011, 24(1): 159−182. doi: 10.1175/2010JCLI3636.1 [24] Moore G W K. Decadal variability and a recent amplification of the summer Beaufort Sea High[J]. Geophysical Research Letters, 2012, 39(10): L10807. [25] Proshutinsky A, Bourke R H, McLaughlin F A. The role of the Beaufort Gyre in Arctic climate variability: Seasonal to decadal climate scales[J]. Geophysical Research Letters, 2002, 29(23): 15-1−15-4. doi: 10.1029/2002GL015847 [26] Proshutinsky A, Dukhovskoy D, Timmermans M L, et al. Arctic circulation regimes[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2015, 373(2052): 20140160. doi: 10.1098/rsta.2014.0160 [27] Wu Bingyi, Johnson M A. A seesaw structure in SLP anomalies between the Beaufort Sea and the Barents Sea[J]. Geophysical Research Letters, 2007, 34(5): L05811. [28] Doddridge E W, Meneghello G, Marshall J, et al. A three-way balance in the Beaufort Gyre: The Ice-Ocean Governor, wind stress, and eddy diffusivity[J]. Journal of Geophysical Research: Oceans, 2019, 124(5): 3107−3124. doi: 10.1029/2018JC014897 [29] Karcher M, Smith J N, Kauker F, et al. Recent changes in Arctic Ocean circulation revealed by iodine-129 observations and modeling[J]. Journal of Geophysical Research: Oceans, 2012, 117(C8): C08007. [30] Davis P E D, Lique C, Johnson H L. On the link between Arctic sea ice decline and the freshwater content of the Beaufort Gyre: Insights from a simple process model[J]. Journal of Climate, 2014, 27(21): 8170−8184. doi: 10.1175/JCLI-D-14-00090.1 [31] Meneghello G, Marshall J, Campin J M, et al. The ice-ocean governor: Ice-ocean stress feedback limits Beaufort Gyre spin-up[J]. Geophysical Research Letters, 2018, 45(20): 11293−11299. [32] Timmermans M L, Marshall J. Understanding Arctic Ocean circulation: A review of ocean dynamics in a changing climate[J]. Journal of Geophysical Research: Oceans, 2020, 125(4): e2018JC014378. [33] Meier W N, Fetterer F, Savoie S, et al. NOAA/NSIDC climate data record of passive microwave sea ice concentration, Version 3[R]. Boulder, Colorado USA: National Snow and Ice Data Center, 2017. [34] Carton J A, Chepurin G A, Chen Ligang. SODA3: A new ocean climate reanalysis[J]. Journal of Climate, 2018, 31(17): 6967−6983. doi: 10.1175/JCLI-D-18-0149.1 [35] Kalnay E, Kanamitsu M, Kistler R, et al. The NCEP/NCAR 40-year reanalysis project[J]. Bulletin of the American Meteorological Society, 1996, 77(3): 437−472. doi: 10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2 [36] Armitage T W K, Bacon S, Ridout A L, et al. Arctic sea surface height variability and change from satellite radar altimetry and GRACE, 2003–2014[J]. Journal of Geophysical Research: Oceans, 2016, 121(6): 4303−4322. doi: 10.1002/2015JC011579 [37] Proshutinsky A Y, Johnson M A. Two circulation regimes of the wind-driven Arctic Ocean[J]. Journal of Geophysical Research: Oceans, 1997, 102(C6): 12493−12514. doi: 10.1029/97JC00738 [38] Manucharyan G E, Isachsen P E. Critical role of continental slopes in halocline and eddy dynamics of the Ekman-driven Beaufort Gyre[J]. Journal of Geophysical Research: Oceans, 2019, 124(4): 2679−2696. doi: 10.1029/2018JC014624 [39] Manucharyan G E, Spall M A. Wind-driven freshwater buildup and release in the Beaufort Gyre constrained by mesoscale eddies[J]. Geophysical Research Letters, 2016, 43(1): 273−282. doi: 10.1002/2015GL065957 [40] Dewey S R, Morison J H, Zhang Jinlun. An edge-referenced surface fresh layer in the Beaufort Sea seasonal ice zone[J]. Journal of Physical Oceanography, 2017, 47(5): 1125−1144. doi: 10.1175/JPO-D-16-0158.1 -
下载:
下载:
计量
- 文章访问数: 187
- HTML全文浏览量: 313
- PDF下载量: 44
- 被引次数: 0
