Development and application of a finite volume tsunami numerical model based on the well-balanced shallow water equations
-
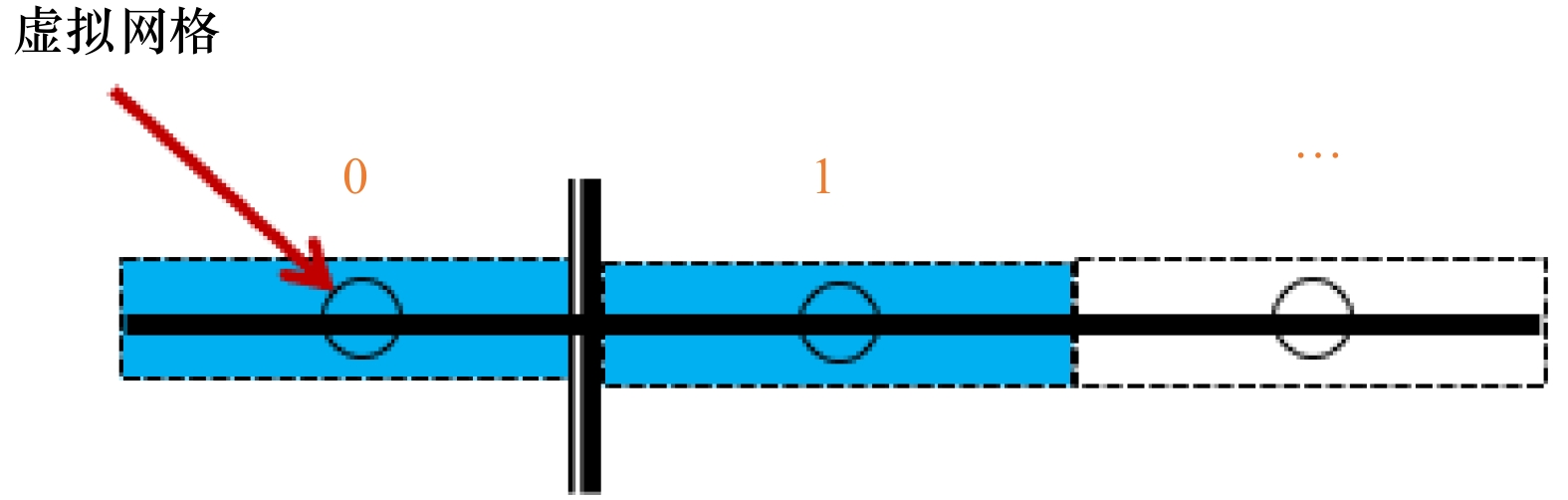
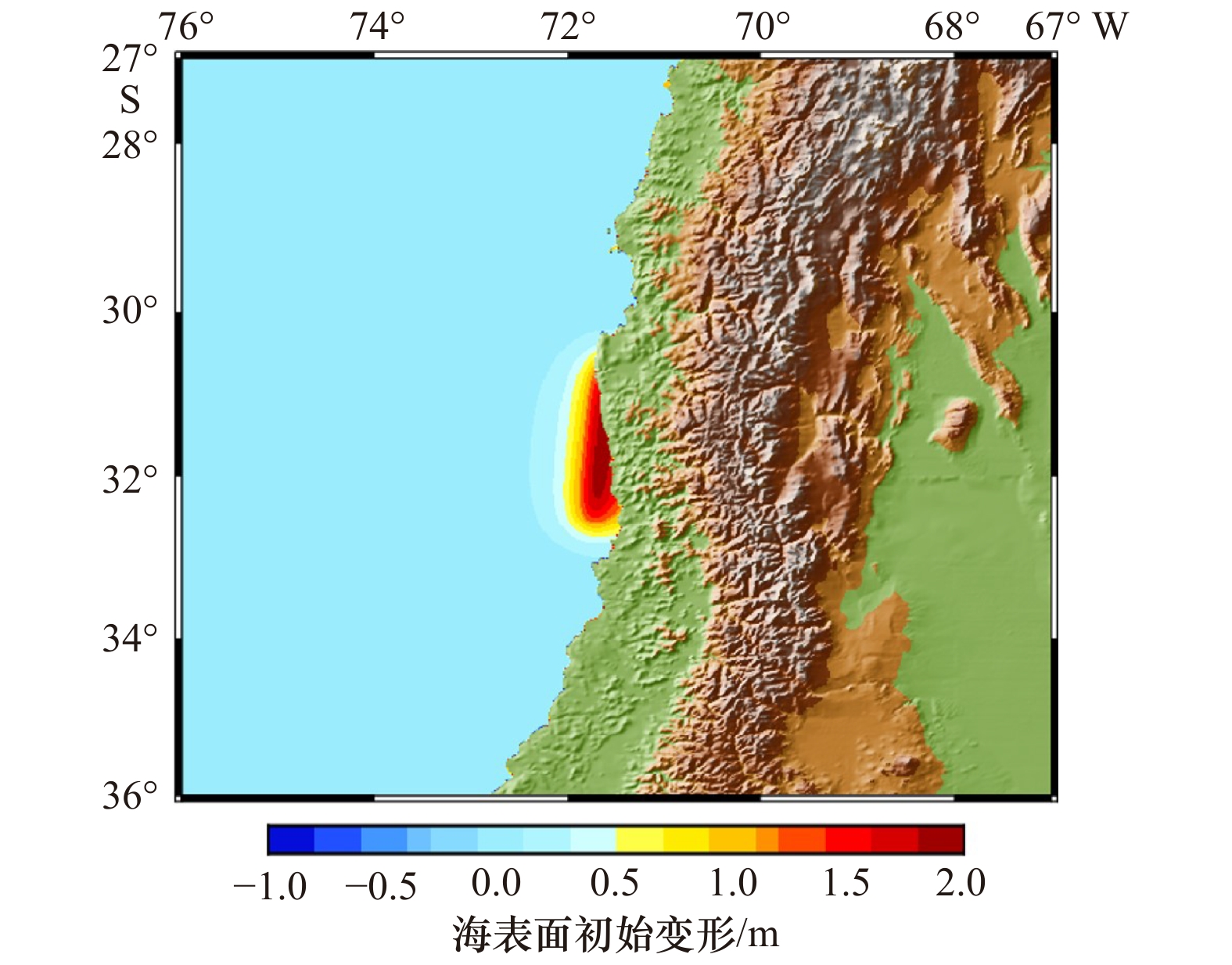
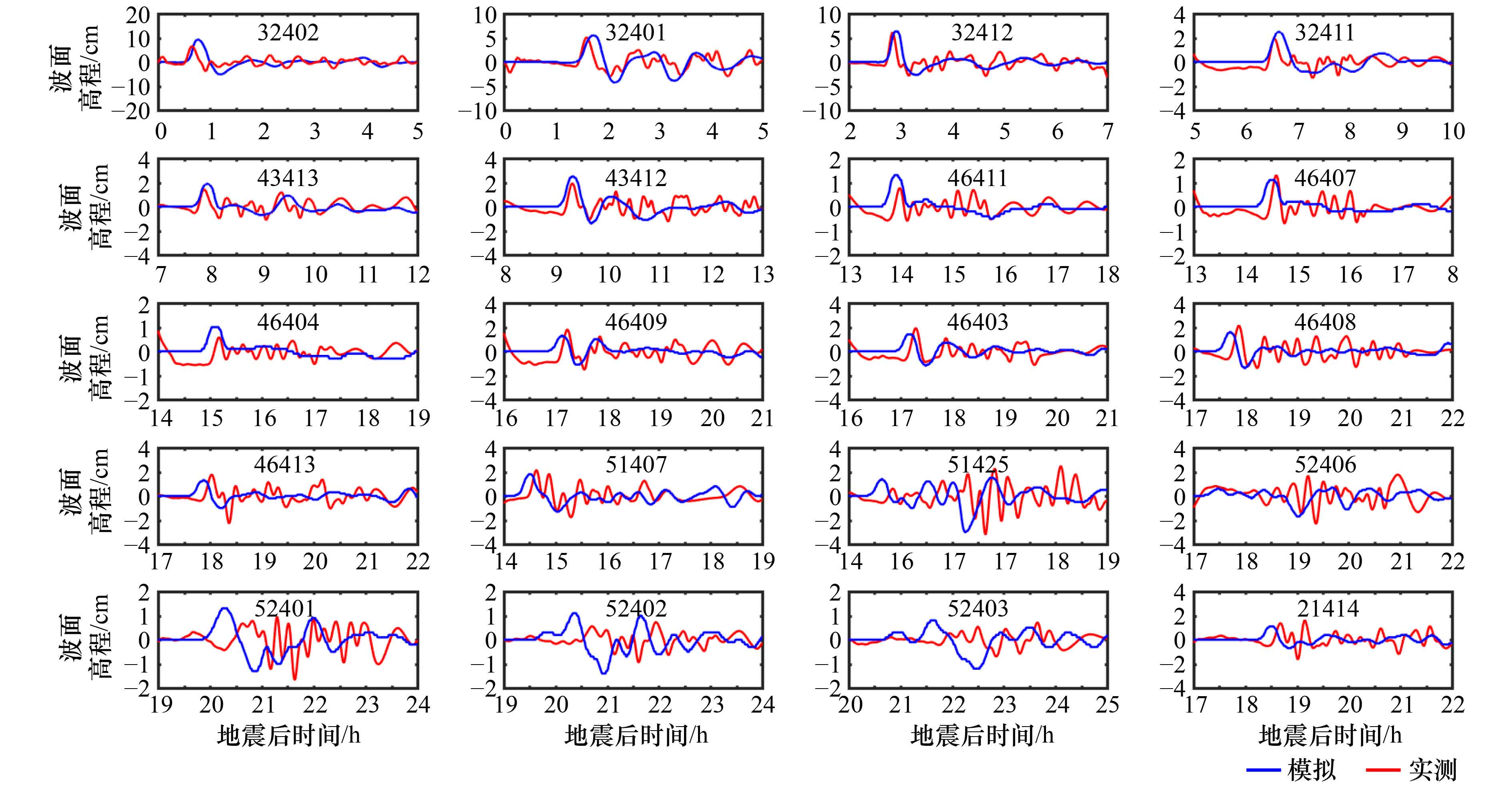
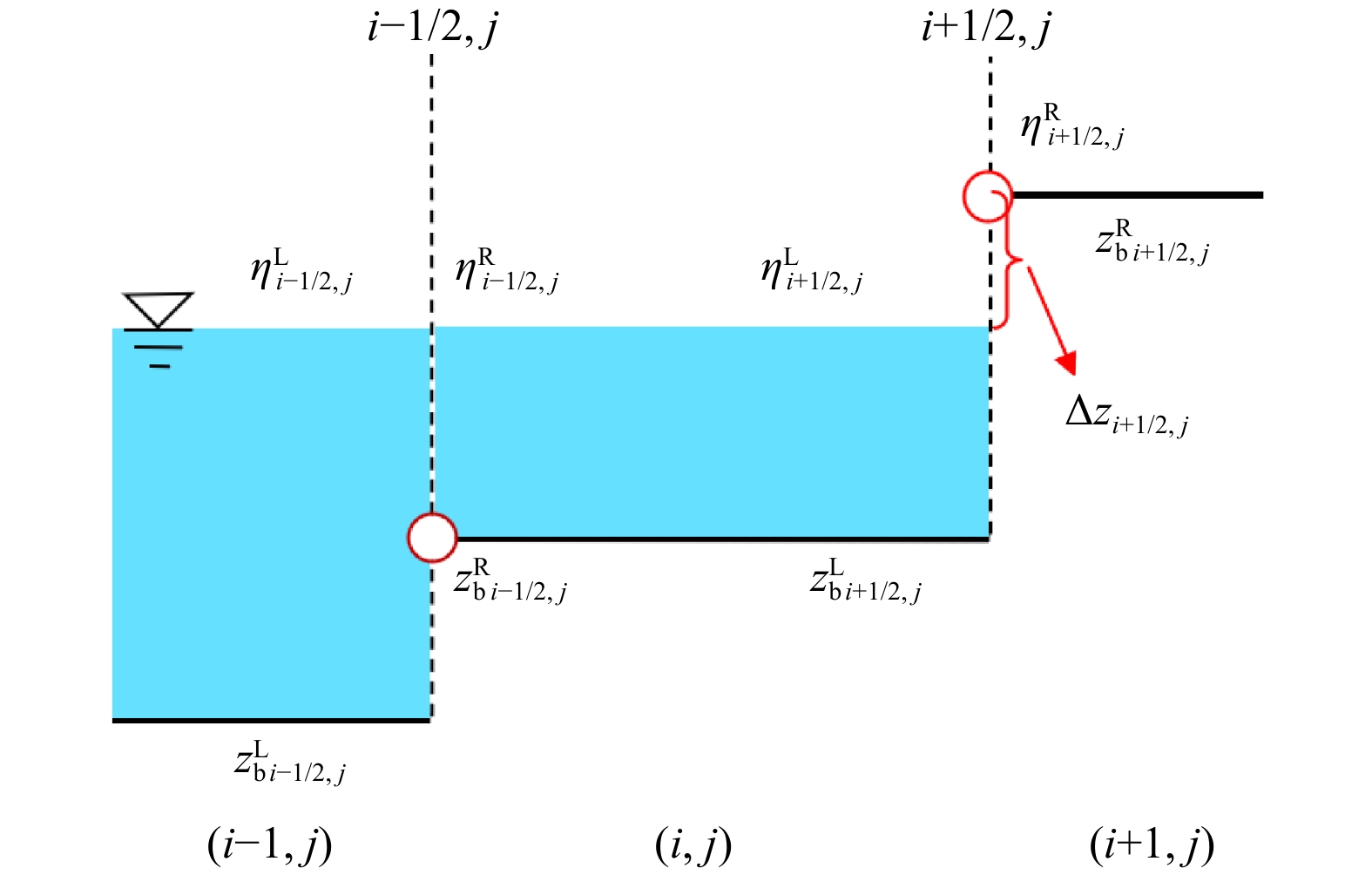
摘要: 数值模拟作为海啸预报的主要研究方法在海啸预警中起着关键作用。本文采用Godunov格式的有限体积方法，使用MUSCL-Hancock格式，并利用HLLC Riemann近似求解器计算单元界面上的流体通量，建立了球坐标系下二阶精度的海啸数值模型。模型所基于的全和谐型浅水方程保证了数值的稳定性，而地形重构方法实现了干湿边界的精准模拟。本文模拟了2015年9月16日智利Mw8.3级地震海啸，通过与智利近岸14个测站和环太平洋20个DART浮标实测数据比较，验证了模型对实际越洋海啸模拟预报的能力。Abstract: Numerical simulation, as the major research method of tsunami, plays a key role in tsunami warning. The present paper develops a second-order accuracy numerical tsunami model in the spherical coordinate using the Godunov-type finite volume method and MUSCL-Hancock scheme. An HLLC approximate Riemann solver is employed to evaluate fluxes across cell interfaces. The well-balanced expression format of shallow water equations ensures the numerical stability, while the local topography reconstruction method is used to deal with the moving shoreline boundary. The model is used to investigate the propagation of the 16 September 2015 Chile tsunami. The capability of the model is verified by comparison with the observational data from 14 coastal tidal-gauge stations near Chile and 20 DART buoys covering the Pacific Ocean.
-
图 4 智利区域海啸和泛太平洋海啸模拟范围及DART浮标与智利近岸测站位置
Fig. 4 Domains of Chile regional tsunami and the Pacific tsunami and the location of DART buoys and coastal tide-gauge stations
图 5 智利近岸测站波面过程与模拟对比
Fig. 5 Time histories of observation and simulation at Chile coastal tide-gauge stations
图 6 地震后越洋海啸瞬时波面分布
Fig. 6 Snapshots of simulated tsunami wavefields after the earthquake
图 8 DART海啸浮标实测波面过程与模拟结果对比
Fig. 8 Comparisons of the free surface elevation between DART buoys and simulations
图 9 智利海啸在太平洋的最大波幅分布
Fig. 9 Distribution of maximum wave amplitude in the Pacific for Chile tsunami
表 1 智利地震断层参数
Tab. 1 Fault parameters of Chile earthquake
断层参数 参数值 震源位置 31.57°S, 71.67°W 震源深度 22.4 km 断层长度 212 km 断层宽度 79 km 倾角 19° 滑动角 83° 走向角 353° 平均滑移量 6.3 m 
下载: 导出CSV
表 2 智利近岸测站海啸先导波到达时间和波幅模拟与实测比较
Tab. 2 Comparisons of simulation and observation of the arrival time and amplitude for the leading wave at Chile coastal tidal-gauge stations
测站名称 位置 到达时间 先导波波幅 模拟/min 实测/min 相对误差 模拟/cm 实测/cm 相对误差 COQUIMBO CL 30.0°S,71.3°W 28 32 12.5% 104.0 96.9 6.8% SAN ANTONIO CL 33.6°S,71.6°W 30 38 21.1% 73.4 65.3 11.0% BUCALEMU CL 34.6°S,72.0°W 41 49 16.3% 48.5 46.9 3.3% HUASCO CL 28.5°S,71.2°W 30 35 14.3% 46.9 46.2 1.5% CONSTITUCION CL 35.4°S,72.5°W 53 63 15.9% 68.6 49.7 27.6% CHANARAL CL 26.4°S,70.6°W 57 61 6.6% 41.8 42.5 1.6% TALCAHUANO CL 36.7°S,73.1°W 104 108 3.7% 43.4 44.0 1.4% TALTAL CL 25.4°S,70.5°W 67 67 0% 18.8 19.5 3.6% JUAN FERNANDEZ 33.6°S,78.8°W 63 60 4.8% 45.4 40.9 9.9% CORRAL CL 39.9°S,73.4°W 112 132 15.2% 26.1 24.4 6.5% TOCOPILLA CL 22.1°S,70.2°W 93 92 1.1% 12.0 10.8 10.0% SAN FELIX CL 26.3°S,80.1°W 80 81 1.2% 23.8 22.6 5.0% MATARANI PE 17.0°S,72.1°W 141 140 0.7% 13.3 13.9 4.3% CALLAO LA-PUNTA PE 12.1°S,77.2°W 206 218 5.5% 23.1 20.3 12.1%
下载: 导出CSV
表 3 DART浮标海啸先导波到达时间和波幅模拟与实测比较
Tab. 3 Comparisons of simulation and observation of the arrival time and amplitude for the leading wave at DART buoys
浮标号 位置 到达时间 先导波波幅 模拟/min 实测/min 相对误差 模拟/cm 实测/cm 相对误差 32402 26.7°S,74.0°W 46 39 15.2% 9.3 10.0 7.0% 32401 20.5°S,73.4°W 103 96 6.8% 5.5 5.1 7.3% 32412 18.0°S,86.4°W 174 171 1.7% 6.3 6.1 3.2% 32411 5.0°N,90.9°W 398 394 1.0% 2.5 1.9 24.0% 43413 11.0°N,100.1°W 476 473 0.6% 1.9 1.4 26.3% 43412 16.0°N,107.0°W 560 560 0% 2.5 1.9 24.0% 46411 39.3°N,127.1°W 837 839 0.2% 1.3 0.8 38.5% 46407 42.7°N,127.8°W 874 876 0.2% 1.1 1.3 15.4% 46404 45.8°N,128.8°W 910 910 0% 1.0 0.7 30.0% 46409 55.3°N,148.5°W 1 030 1 034 0.4% 1.2 1.8 33.3% 46403 52.7°N,157.0°W 1 032 1 038 0.6% 1.4 1.9 26.3% 46408 49.6°N,169.9°W 1 063 1 073 0.9% 1.6 2.2 27.3% 46413 48.0°N,174.2°W 1 074 1 082 0.7% 1.3 1.8 27.8% 51407 19.6°N,156.5°W 872 878 0.7% 1.8 1.9 5.3% 51425 9.5°S,176.3°W 879 891 1.3% 1.4 0.8 42.9% 52406 5.3°S,165.0°E 1 075 1 091 1.5% 0.3 0.4 25.0% 52401 19.3°N,155.8°E 1 220 1 238 1.5% 1.3 1.0 23.1% 52402 11.9°N,153.9°E 1 224 1 242 1.4% 1.1 0.7 36.4% 52403 4.0°N,145.5°E 1 300 1 318 1.4% 0.8 0.3 62.5% 21414 49.0°N,178.2°E 1 113 1 121 0.7% 1.1 1.4 21.4%
下载: 导出CSV
-
[1] Barrientos S E, Ward S N. The 1960 Chile earthquake: Inversion for slip distribution from surface deformation[J]. Geophysical Journal International, 1990, 103(3): 589−598. doi: 10.1111/j.1365-246X.1990.tb05673.x [2] Bernard E N, Meinig C. History and future of deep-ocean tsunami measurements[C]//Oceans'11 MTS/IEEE Kona. Waikoloa, HI, USA: IEEE, 2011: 1−7. [3] 董杰, 田士政, 武文, 等. 全球海啸预警系统发展及其对我国的启示[J]. 海洋通报, 2019, 38(4): 368−378.Dong Jie, Tian Shizheng, Wu Wen, et al. The development of global tsunami warning systems and their enlightenments to China[J]. Marine Science Bulletin, 2019, 38(4): 368−378. [4] Mandli K T, Ahmadia A J, Berger M, et al. Clawpack: Building an open source ecosystem for solving hyperbolic PDEs[J]. PeerJ Computer Science, 2016, 2: e68. doi: 10.7717/peerj-cs.68 [5] Berger M J, George D L, LeVeque R J, et al. The GeoClaw software for depth-averaged flows with adaptive refinement[J]. Advances in Water Resources, 2011, 34(9): 1195−1206. doi: 10.1016/j.advwatres.2011.02.016 [6] Kirby J T, Wei G, Chen Q, et al. FUNWAVE 1.0: Fully nonlinear Boussinesq wave model-documentation and user's manual[R]. Network, USA: University of Delaware, 1998. [7] Shi Fengyan, Kirby J T, Harris J C, et al. A high-order adaptive time-stepping TVD solver for Boussinesq modeling of breaking waves and coastal inundation[J]. Ocean Modelling, 2012, 43−44: 36−51. doi: 10.1016/j.ocemod.2011.12.004 [8] Yuan Ye, Shi Fengyan, Kirby J T, et al. FUNWAVE-GPU: Multiple-GPU acceleration of a Boussinesq-type wave model[J]. Journal of Advances in Modeling Earth Systems, 2020, 12(5): e2019MS001957. [9] Yamazaki Y, Kowalik Z, Cheung K F. Depth-integrated, non-hydrostatic model for wave breaking and run-up[J]. International Journal for Numerical Methods in Fluids, 2009, 61(5): 473−497. doi: 10.1002/fld.1952 [10] Zhao Binbin, Duan Wenyang, Webster W C. Tsunami simulation with Green-Naghdi theory[J]. Ocean Engineering, 2011, 38(2/3): 389−396. [11] Titov V V, Gonzalez F I. Implementation and testing of the Method of Splitting Tsunami (MOST) model[R]. Washington, USA: Pacific Marine Environmental Laboratory, NOAA, 1997. [12] 余锡平. 近岸水波的数值方法[M]. 北京: 科学出版社, 2017.Yu Xiping. Numerical Methods in Nearshore Wave[M]. Beijing: Science Press, 2017. [13] Toro E F. Shock-Capturing Methods for Free-Surface Shallow Flows[M]. Chichester, UK: John Wiley & Sons Inc, 2001. [14] Alias N A, Liang Qiuhua, Kesserwani G. A Godunov-type scheme for modelling 1D channel flow with varying width and topography[J]. Computers & Fluids, 2011, 46(1): 88−93. [15] Xia Xilin, Liang Qiuhua. A new efficient implicit scheme for discretising the stiff friction terms in the shallow water equations[J]. Advances in Water Resources, 2018, 117: 87−97. doi: 10.1016/j.advwatres.2018.05.004 [16] Harten A, Lax P D, Van Leer B. On upstream differencing and Godunov-type schemes for hyperbolic conservation laws[J]. Siam Review, 1983, 25(1): 35−61. doi: 10.1137/1025002 [17] Toro E F, Spruce M, Speares W. Restoration of the contact surface in the HLL-Riemann solver[J]. Shock Waves, 1994, 4(1): 25−34. doi: 10.1007/BF01414629 [18] Liang Qiuhua, Borthwick A G L. Adaptive quadtree simulation of shallow flows with wet-dry fronts over complex topography[J]. Computers & Fluids, 2009, 38(2): 221−234. [19] Baba T, Allgeyer S, Hossen J, et al. Accurate numerical simulation of the far-field tsunami caused by the 2011 Tohoku earthquake, including the effects of Boussinesq dispersion, seawater density stratification, elastic loading, and gravitational potential change[J]. Ocean Modelling, 2017, 111: 46−54. doi: 10.1016/j.ocemod.2017.01.002 [20] Van Leer B. Towards the ultimate conservative difference scheme[J]. Journal of Computational Physics, 1997, 135(2): 229−248. doi: 10.1006/jcph.1997.5704 [21] Liang Qiuhua. Flood simulation using a well-balanced shallow flow model[J]. Journal of Hydraulic Engineering, 2010, 136(9): 669−675. doi: 10.1061/(ASCE)HY.1943-7900.0000219 [22] Liang Qiuhua, Marche F. Numerical resolution of well-balanced shallow water equations with complex source terms[J]. Advances in Water Resources, 2009, 32(6): 873−884. doi: 10.1016/j.advwatres.2009.02.010 [23] Steketee J A. On volterra’s dislocations in a semi-infinite elastic medium[J]. Canadian Journal of Physics, 1958, 36(2): 192−205. doi: 10.1139/p58-024 [24] Steketee J A. Some geophysical applications of the elasticity theory of dislocations[J]. Canadian Journal of Physics, 1958, 36(9): 1168−1198. doi: 10.1139/p58-123 [25] Kajiura K. The leading wave of a tsunami[J]. Bulletin of the Earthquake Research Institute, 1963, 41(3): 535−571. [26] Mansinha L, Smylie D E. The displacement field of inclined faults[J]. Bulletin of the Seismological Society of America, 1971, 61(5): 1433−1440. [27] Okada Y. Surface deformation due to shear and tensile faults in a half-space[J]. Bulletin of the Seismological Society of America, 1985, 75(4): 1135−1154. [28] 于福江, 王培涛, 赵联大, 等. 2010年智利地震海啸数值模拟及其对我国沿海的影响分析[J]. 地球物理学报, 2011, 54(4): 918−925.Yu Fujiang, Wang Peitao, Zhao Lianda, et al. Numerical simulation of 2010 Chile tsunami and its impact on Chinese coasts[J]. Chinese Journal of Geophysics, 2011, 54(4): 918−925. [29] 王培涛, 于福江, 赵联大, 等. 2011年3月11日日本地震海啸越洋传播及对中国影响的数值分析[J]. 地球物理学报, 2012, 55(9): 3088−3096. doi: 10.6038/j.issn.0001-5733.2012.09.026Wang Peitao, Yu Fujiang, Zhao Lianda, et al. Numerical analysis of tsunami propagating generated by the Japan Mw9.0 earthquake on Mar. 11 in 2011 and its impact on China coasts[J]. Chinese Journal of Geophysics, 2012, 55(9): 3088−3096. doi: 10.6038/j.issn.0001-5733.2012.09.026 [30] 闪迪, 王培涛, 任智源, 等. 有限断层模型在2015年9月16日智利Mw8.3级地震海啸数值模拟中的应用与评估[J]. 海洋学报, 2017, 39(11): 49−60.Shan Di, Wang Peitao, Ren Zhiyuan, et al. Application and evaluation of the 16 September 2015 Illapel, Chile Mw8.3 earthquake finite fault rupture model from numerical simulation[J]. Haiyang Xuebao, 2017, 39(11): 49−60. [31] Wu Wennan, Zhao Li, Wu Y M. Empirical relationships between aftershock zone dimensions and moment magnitudes for plate boundary earthquakes in Taiwan[J]. Bulletin of the Seismological Society of America, 2013, 103(1): 424−436. doi: 10.1785/0120120173 [32] Hayes G P, Myers E K, Dewey J W, et al. Tectonic summaries of magnitude 7 and greater earthquakes from 2000 to 2015[R]. USA: USGS, 2016. [33] Kanamori H, Rivera L. Source inversion of W phase: Speeding up seismic tsunami warning[J]. Geophysical Journal International, 2008, 175(1): 222−238. doi: 10.1111/j.1365-246X.2008.03887.x [34] Glimsdal S, Pedersen G K, Harbitz C B, et al. Dispersion of tsunamis: Does it really matter?[J]. Natural Hazards and Earth System Sciences, 2013, 13(6): 1507−1526. doi: 10.5194/nhess-13-1507-2013 [35] Watada S, Kusumoto S, Satake K. Traveltime delay and initial phase reversal of distant tsunamis coupled with the self-gravitating elastic earth[J]. Journal of Geophysical Research: Solid Earth, 2014, 119(5): 4287−4310. doi: 10.1002/2013JB010841 [36] 王岗, 胡见, 王培涛, 等. 双曲余弦海脊上海啸俘获波的解析与数值研究[J]. 海洋学报, 2018, 40(5): 15−23.Wang Gang, Hu Jian, Wang Peitao, et al. Analytical and numerical investigation of tsunami trapped waves over a hyperbolic-cosine squared ocean ridge[J]. Haiyang Xuebao, 2018, 40(5): 15−23. -
图(9) / 表(3)
计量
- 文章访问数: 399
- HTML全文浏览量: 85
- PDF下载量: 39
- 被引次数: 0
