沿岸流不稳定运动传播特性的小波相干谱分析

任春平; 刘宇; 赵喜萍

doi:10.12284/hyxb2021092

沿岸流不稳定运动传播特性的小波相干谱分析

doi: 10.12284/hyxb2021092

太原理工大学水利科学与工程学院，山西太原 030024

基金项目: 水利工程安全与仿真国家重点实验室开放基金(HESS-2006)；中国博士后基金(2013M541179)；太原理工大学校基金(2017MS07)

详细信息

作者简介:
任春平（1978-），男，山西省祁县人，博士，副教授，主要从事河口海岸动力学研究。E-mail：chunpingren@163.com

中图分类号: P731.21
计量
- 文章访问数: 185
- HTML全文浏览量: 79
- PDF下载量: 22
- 被引次数: 0
出版历程
- 收稿日期: 2020-06-04
- 修回日期: 2020-08-08
- 网络出版日期: 2021-07-08
- 刊出日期: 2021-06-30

An analysis on the propagation of the instabilities of longshore currents using wavelet coherence spectrum

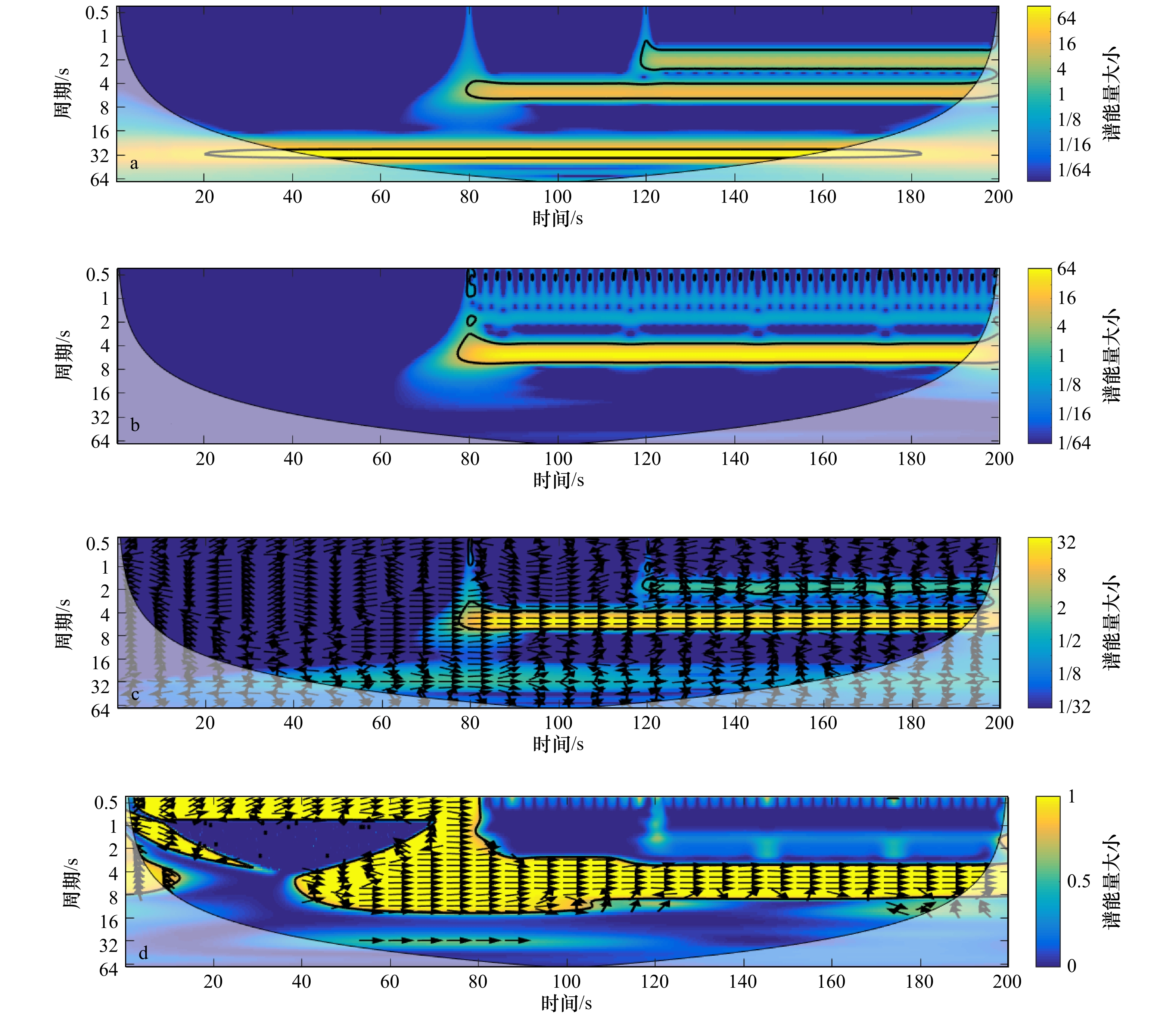
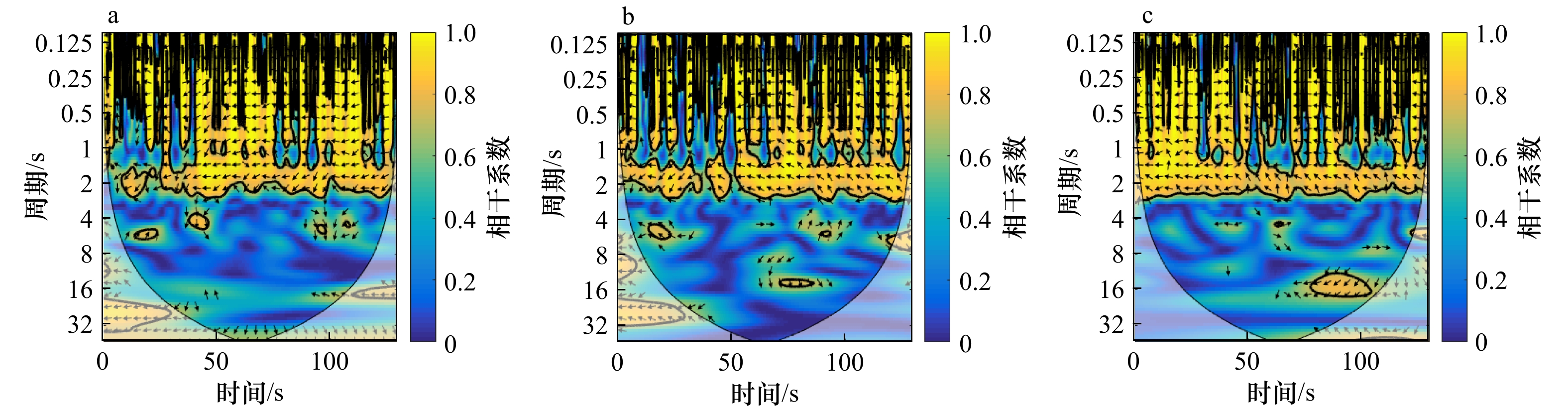
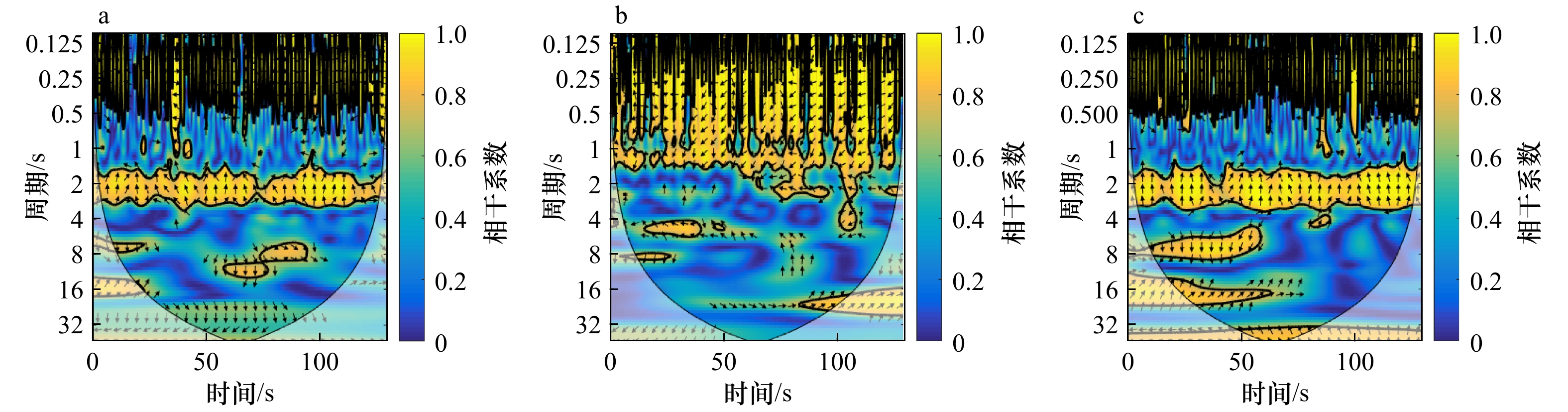
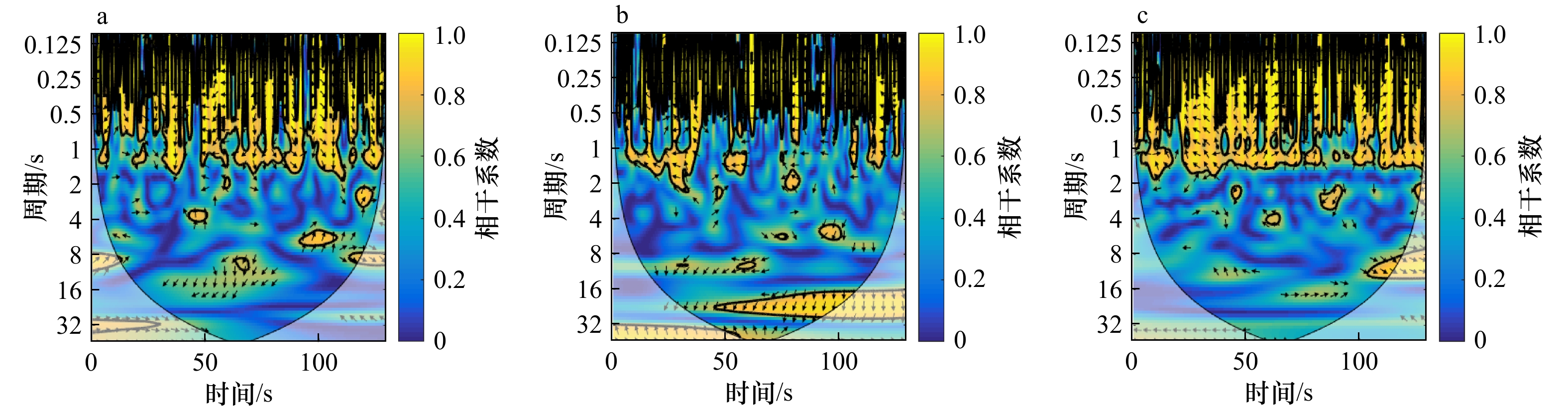
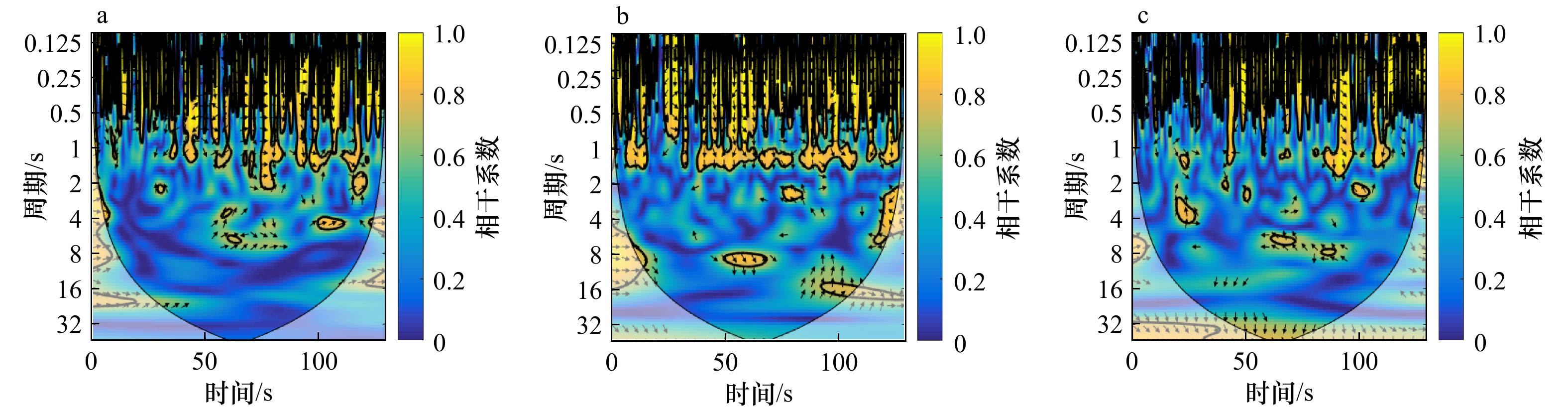
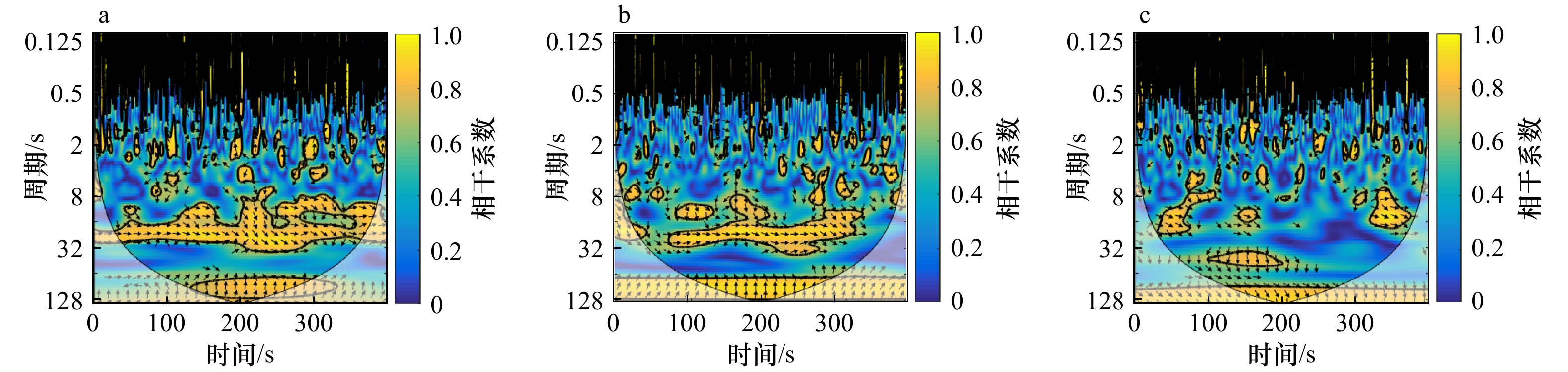
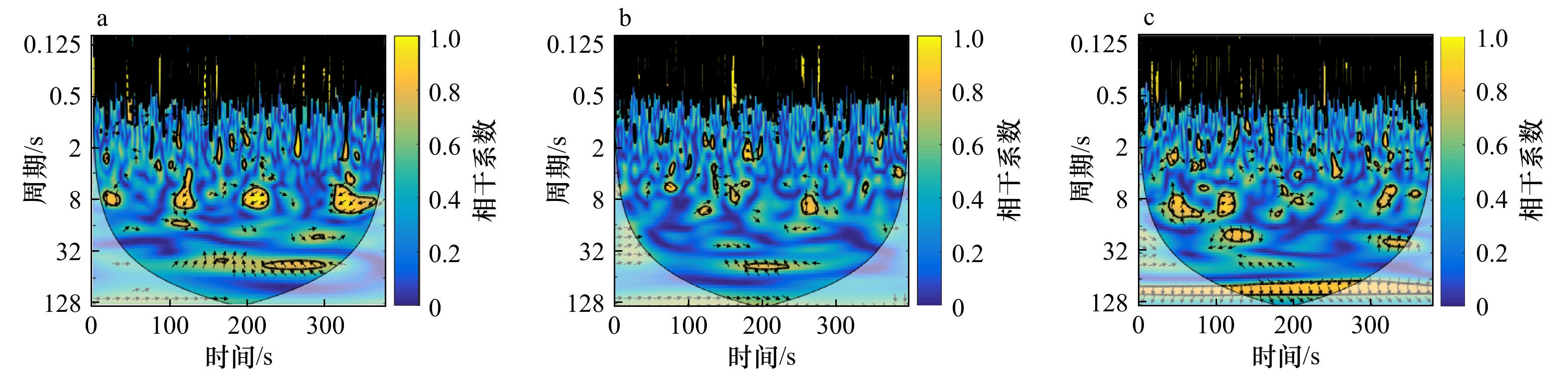
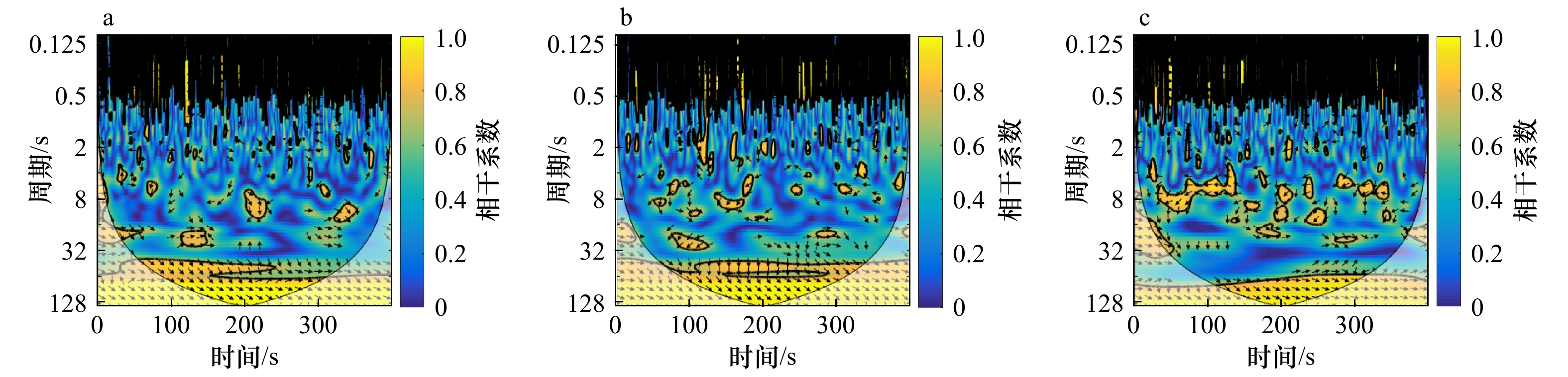
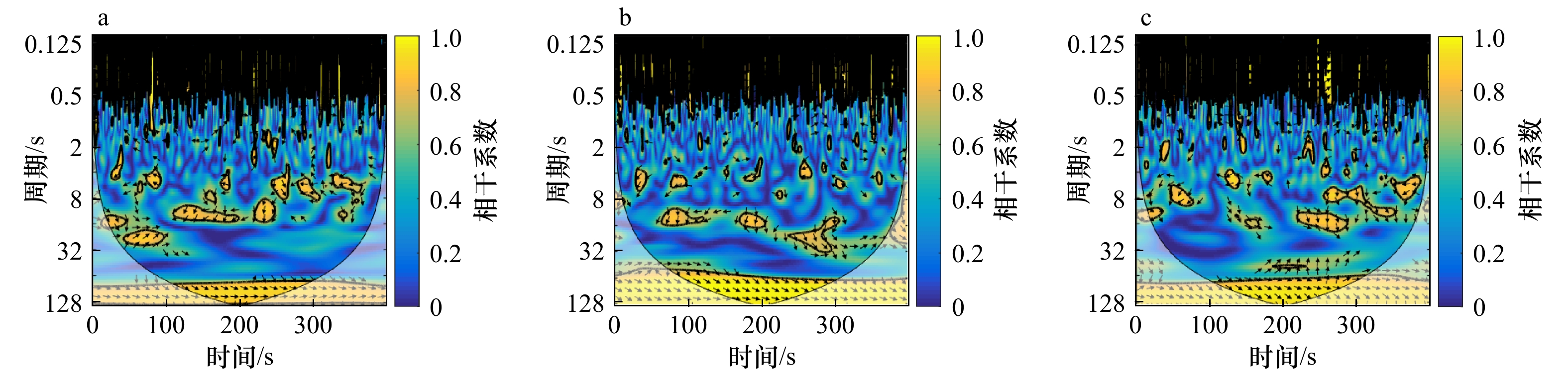
College of Water Resource Science and Engineering, Taiyuan University of Technology, Taiyuan 030024, China

摘要

摘要: 沿岸流不稳定运动属于超低频运动，研究它的传播特性，有助于深入理解其对岸滩演变、污染物、鱼卵等输移、迁移的影响。本文基于小波相干谱对所选实验波况进行了研究，分析了规则波、随机波入射情况下沿岸流不稳定运动传播特性，并讨论了入射波高、周期、坡度等对其的影响。结果表明，不规则波更易诱导出沿岸流不稳定运动，且在不规则波情况下，不稳定运动在沿岸方向相距4 m的两个断面上产生的相位差都约为±30°，与波浪入射角相近；随着入射波高的增加，非线性随之增强，更易诱导出不稳定运动，生成的沿岸流不稳定运动周期范围将增大；入射波周期对沿岸流不稳定运动的传播特性影响较小；坡度越陡越易诱导出超低频的不稳定运动。
- 沿岸流 /
- 不稳定运动 /
- 传播 /
- 小波相干 /
- 相位差
Abstract: The instabilities of longshore currents are the far infragravity band waves. The study of its propagation characteristics will help us to understand its influence on the evolution of coastal beach and the transport and migration of pollutants, fish eggs and other organisms. Based on the wavelet coherence spectrum, this paper analyzes the propagation characteristics of the unsteady motion under regular and random waves, and discusses the influence of the wave height, period and slope on it. The results show that the irregular wave is easier to induce the unsteady motion, and the positive or negative phase difference of the unsteady motion is about 30° in the case of irregular waves, which is similar to the incident angle of waves; with the increase of the incident wave height, nonlinear effects become stronger and the period range of the unsteady motion will be wider, that is to say, it is easier to induce the unsteady motion; the incident wave period has a little effect on the propagation; the steeper the slope is, the more likely it is to induce the instabilities of longshore currents.
- longshore current /
- unsteady motion /
- propagation /
- wavelet coherence /
- phase lag

HTML全文

图 1 实验布置

Fig. 1 Experimental layout

下载: 全尺寸图片幻灯片

图 2 实验地形

Fig. 2 Bottom profile

下载: 全尺寸图片幻灯片

图 3 1∶40地形流速仪布置

Fig. 3 The layout of velocity meters for slope 1∶40

下载: 全尺寸图片幻灯片

图 4 波况4和波况9分别在x=2.5 m和x=4.0 m处采集的沿岸方向流速时间历程

Fig. 4 Time series of alongshore velocity at x=2.5 m and x=4.0 m for Case 4 and Case 9

下载: 全尺寸图片幻灯片

图 5 X、y1、y2及y3信号

Fig. 5 Test signals of X, y1, y2 and y3

下载: 全尺寸图片幻灯片

图 6 X（a）和Y=y2（b）的小波谱、X-Y小波交叉谱（c）及X-Y小波相干谱（d）

Fig. 6 The wavelet power spectrum of X (a) and Y=y2 (b), and X-Y cross wavelet spectrum (c) and X-Y wavelet coherence spectrum (d)

下载: 全尺寸图片幻灯片

图 7 波况1中距离岸线2 m（a）、2.5 m（b）及3 m（c）处对应的小波相干谱

Fig. 7 Wavelet coherent spectrum at x=2.0 m (a), x=2.5 m (b) and x=3.0 m (c) under Case 1

下载: 全尺寸图片幻灯片

图 11 波况5中距离岸线3.5 m（a）、4.0 m（b）及4.5 m（c）处对应的小波相干谱

Fig. 11 Wavelet coherent spectrum at x=3.5 m (a), x=4.0 m (b) and x=4.5 m (c) under Case 5

下载: 全尺寸图片幻灯片

图 8 波况2中距离岸线3.5 m（a）、4.0 m（b）及4.5 m（c）处对应的小波相干谱

Fig. 8 Wavelet coherent spectrum at x=3.5 m (a), x=4.0 m (b) and x=4.5 m (c) under Case 2

下载: 全尺寸图片幻灯片

图 9 波况3中距离岸线4.5 m（a）、5.0 m（b）及5.5 m（c）处对应的小波相干谱

Fig. 9 Wavelet coherent spectrum at x=4.5 m (a), x=5.0 m (b) and x=5.5 m (c) under Case 3

下载: 全尺寸图片幻灯片

图 10 波况4中距离岸线2.0 m（a）、2.5 m（b）及3.0 m（c）处对应的小波相干谱

Fig. 10 Wavelet coherent spectrum at x=2.0 m (a), x=2.5 m (b) and x=3.0 m (c) under Case 4

下载: 全尺寸图片幻灯片

图 12 波况6中距离岸线5.5 m（a）、6.0 m（b）及6.5 m（c）处对应的小波相干谱

Fig. 12 Wavelet coherent spectrum at x=5.5 m (a), x=6.0 m (b) and x=6.5 m (c) under Case 6

下载: 全尺寸图片幻灯片

图 17 波况11中距离岸线2.5 m（a）、3.0 m（b）及3.5 m（c）处对应的小波相干谱

Fig. 17 Wavelet coherent spectrum at x=2.5 m (a), x=3.0 m (b) and x=3.5 m (c) under Case 11

下载: 全尺寸图片幻灯片

图 13 波况7中距离岸线2.0 m（a）、2.5 m（b）及3.0 m（b）处对应的小波相干谱

Fig. 13 Wavelet coherent spectrum at x=2.0 m (a), x=2.5 m (b) and x=3.0 m (c) under Case 7

下载: 全尺寸图片幻灯片

图 14 波况8中距离岸线2.5 m（a）、3.0 m（b）及3.5 m（c）处对应的小波相干谱

Fig. 14 Wavelet coherent spectrum at x=2.5 m (a), x=3.0 m (b) and x=3.5 m (c) under Case 8

下载: 全尺寸图片幻灯片

图 15 波况9中距离岸线3.5 m（a）、4.0 m（b）及4.5 m（c）处对应的小波相干谱

Fig. 15 Wavelet coherent spectrum at x=3.5 m (a), x=4.0 m (b) and x=4.5 m (c) under Case 9

下载: 全尺寸图片幻灯片

图 16 波况10中距离岸线2.0 m（a）、2.5 m（b）及3.0 m（c）处对应的小波相干谱

Fig. 16 Wavelet coherent spectrum at x=2.0 m (a), x=2.5 m (b) and x=3.0 m (c)under Case 10

下载: 全尺寸图片幻灯片

表 1 波况参数

Tab. 1 Wave parameters

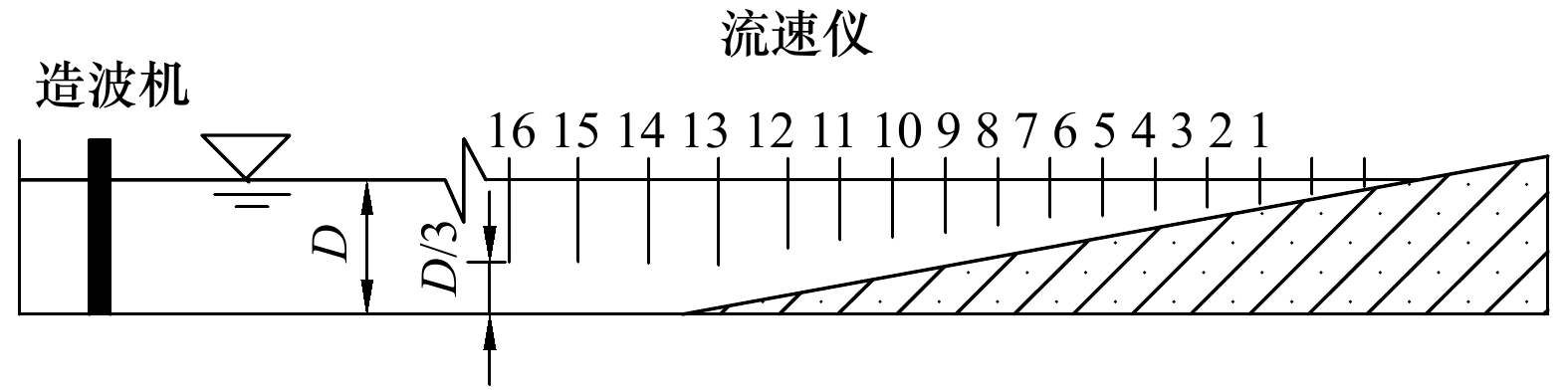
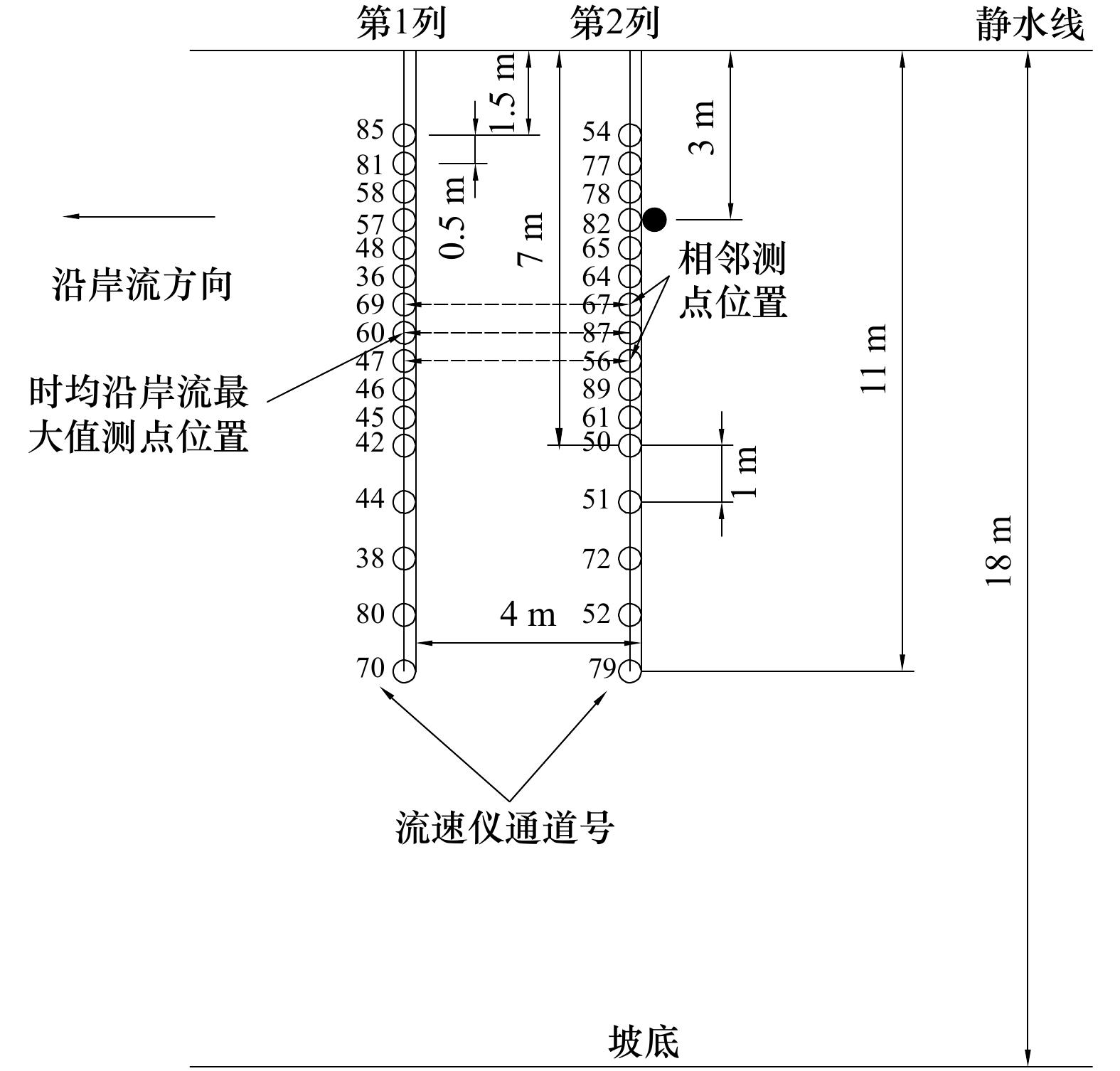
入射波	波况	坡度	静水深/ cm	入射波高/cm	入射波周期/s	x₁/m	x_n/m
规则波	1	1∶40	45	5.0	1.0	2.5	2.0	3.0
	2	1∶40	45	5.9	1.5	4.0	3.5	4.5
	3	1∶40	45	10.5	1.5	5.0	4.5	5.5
	4	1∶40	45	13.0	1.5	2.5	2.0	3.0
	5	1∶40	45	5.2	2.0	4.0	3.5	4.5
随机波	6	1∶100	18	3.4	2.0	6.0	5.5	6.5
	7	1∶40	45	3.6	1.0	2.5	2.0	3.0
	8	1∶40	45	5.5	1.0	3.0	2.5	3.5
	9	1∶40	45	7.8	1.0	4.0	3.5	4.5
	10	1∶40	45	4.0	1.5	2.5	2.0	3.0
	11	1∶40	45	3.7	2.0	3.0	2.5	3.5

下载: 导出CSV

参考文献(15)

[1]	Shanks A L, Morgan S G, Macmahan J, et al. Persistent differences in horizontal gradients in phytoplankton concentration maintained by surf zone hydrodynamics[J]. Estuaries and Coasts, 2018, 41(1): 158−176. doi: 10.1007/s12237-017-0278-2
[2]	Bowen A J, Holman R A. Shear instabilities of the mean longshore current 1. Theory[J]. Journal of Geophysical Research, 1989, 94(C12): 18023−18030. doi: 10.1029/JC094iC12p18023
[3]	Özkan-Haller H T, Kirby J T. Nonlinear evolution of shear instabilities of the longshore current: A comparison of observations and computations[J]. Journal of Geophysical Research: Oceans, 1999, 104(C11): 25953−25984. doi: 10.1029/1999JC900104
[4]	Dodd N, Iranzo V, Caballería M. A subcritical instability of wave-driven alongshore currents[J]. Journal of Geophysical Research, 2004, 109(C2): C02018. doi: 10.1029/2001JC00106
[5]	Reniers A J H M, Battjes J A, Falqués A, et al. A laboratory study on the shear instability of longshore currents[J]. Journal of Geophysical Research: Oceans, 1997, 102(C4): 8597−8609. doi: 10.1029/96JC03863
[6]	Noyes T J, Guza R T, Feddersen F, et al. Model-data comparisons of shear waves in the nearshore[J]. Journal of Geophysical Research: Oceans, 2005, 110(C5): C05019. doi: 10.1029/2004JC002541
[7]	Ren Chunping, Zou Zhili, Qiu Dahong. Experimental study of the instabilities of alongshore currents on plane beaches[J]. Coastal Engineering, 2012, 59(1): 72−89. doi: 10.1016/j.coastaleng.2011.07.004
[8]	任春平, 蒋利君, 季海嘉. 沿岸流不稳定运动对边缘波影响的实验研究[J]. 中国科学: 技术科学, 2015, 45(4): 423−433. doi: 10.1360/N092014-00028 Ren Chunping, Jiang Lijun, Ji Haijia. A laboratory study of the effects of the instability of longshore currents on the edge waves[J]. Scientia Sinica Technologica, 2015, 45(4): 423−433. doi: 10.1360/N092014-00028
[9]	沈良朵. 缓坡沿岸流不稳定性特征研究[D]. 大连: 大连理工大学, 2015. Shen Liangduo. Study of the feature of longshore current and its instability on mild beach slope[D]. Daliang: Daliang University of Technology, 2015.
[10]	Ruiz-Merchán J, Otero L, Conde M, et al. Field observations of wave and current characteristics on a microtidal reflective beach[J]. Journal of Coastal Research, 2019, 35(6): 1164−1184. doi: 10.2112/JCOASTRES-D-18-00120.1
[11]	Conde-Frias M, Otero L, Restrepo J C, et al. Experimental analysis of infragravity waves in two eroded microtidal beaches[J]. Acta Oceanologica Sinica, 2017, 36(5): 31−43. doi: 10.1007/s13131-017-1054-7
[12]	Grinsted A, Moore J C, Jevrejeva S. Application of the cross wavelet transform and wavelet coherence to geophysical time series[J]. Nonlinear Processes in Geophysics, 2004, 11(5/6): 561−566. doi: 10.5194/npg-11-561-2004
[13]	Wang Gang, Nguyena V T, Zheng Jinhai, et al. Disintegration of linear edge waves[J]. China Ocean Engineering, 2013, 27(4): 557−562. doi: 10.1007/s13344-013-0047-3
[14]	Reniers A J H M, Battjes J A. A laboratory study of longshore currents over barred and non-barred beaches[J]. Coastal Engineering, 1997, 30(1): 1−21.
[15]	Tang Jun, Lü Yigang, Shen Yongming, et al. Numerical study on influences of breakwater layout on coastal waves, wave-induced currents, sediment transport and beach morphological evolution[J]. Ocean Engineering, 2017, 141: 375−387. doi: 10.1016/j.oceaneng.2017.06.042