Laboratory study of solitary wave transformation and run-up over reefs with large reef roughness
-
摘要: 本文采用圆柱体阵列来模拟珊瑚礁面的大糙率，通过波浪水槽实验研究礁面糙率对孤立波传播变形及岸滩爬高的影响。结果表明，粗糙礁面的存在显著削弱了礁坪上孤立波的首峰和礁后岸滩反射造成的次峰，同时降低了波浪在珊瑚礁面的传播速度；垂直于岸线方向沿礁相对波高随着入射波增大而减小，随着礁坪水深的增大而增大，粗糙礁面上波高沿礁的衰减更为显著；礁前斜坡的无量纲反射波高随无量纲入射波高的变化与礁坪水深有关，当入射波高足够大时其趋于常值，粗糙礁面略微增大了礁前斜坡的反射；无量纲透射波高和岸滩爬高随着无量纲入射波高的增大而减小，特别是礁坪水深较大时更为显著，粗糙礁面时的无量纲岸滩爬高相对于光滑礁面平均减小46%；通过回归分析得出了同时适合于光滑和粗糙礁面的预测孤立波岸滩爬高的经验关系式。Abstract: A series of laboratory experiments is carried out in a wave flume to study the influence of rough reef surface on solitary wave transformation and run-up over coral reefs. The cylinder array is used to model the reef surface with large roughness. The results show that the rough reef surface significantly reduces the leading solitary wave and the secondary wave due to beach-reef beach reflection, as well as the wave speed on the reef flat. The relative cross-shore wave height decreases with the increase of dimensionless incident wave height along the reef. It also increases with the increase of reef-flat wave level. The cross-shore wave height attenuation is more evident with the rough reef surface. The variation of dimensionless reflected wave height with the dimensionless incident wave height depends on the reef-flat wave level. The dimensionless reflected wave height approaches to a constant when the incident wave height is sufficient large. The rough reef surface slightly enhances the wave reflection from the fore-reef slope. The dimensionless transmitted wave height as well as wave run-up decline with the increasing dimensionless incident wave height, particularly for the large reef-flat water level. The dimensionless wave run-up on the back-reef beach with the rough reef surface reduces by an average of 46% compared to that with the smooth surface. An empirical formula is obtained by a regression analysis to predict the wave run-up with both smooth and rough reefs.
-
Key words:
- coral reef /
- solitary wave /
- artificial roughness /
- wave run-up
-
图 1 物理实验设置
a. 实验布置图；b. 珊瑚礁模型；c. 粗糙礁面；d. 粗糙密度的排列方式
Fig. 1 Experimental setup
a. Layout of the setup; b. reef model; c. rough reef surface; d. arrangement of the roughness elements
图 2 垂直于岸线方向沿礁不同位置（G1、G5、G7、G10、G14、G18）自由液面高度(
$\eta $ )的时间序列Fig. 2 Time series of free surface elevation (
$\eta $ ) at different cross-shore locations (G1, G5, G7, G10, G14, G18) along the reef
图 3 无量纲波高
${H_i}/{H_0}$ 垂直于岸线方向的沿礁（G1−G18）变化规律a. 礁坪水深hr=0.05 m和粗糙礁面$ {\phi = 0.126}$时不同入射波高$ {{H_0}}$的影响；b. 入射波高H0=0.08 m和粗糙礁面$ {\phi = 0.126}$时不同礁坪水深$ {{h_r}}$的影响；c. 入射波高H0=0.08 m和礁坪水深hr=0.05 m时不同糙率密度（$ {\phi }$）的影响；d. 珊瑚礁物理模型剖面（礁缘处为X=0，向岸方向为正）
Fig. 3 The cross-shore variation of normalized wave heights (
${H_i}/{H_0}$ ) along the reef (G1−G18)a.Different incident wave heights ($ {{H_0}}$) under hr=0.05 m and $ {\phi = 0.126}$; b. different reef-flat submergences ($ {{h_r}}$) under H0=0.08 m and $ {\phi = 0.126}$; c. different roughness densities ($ {\phi }$) under H0=0.08 m and hr=0.05 m; d. profile of the physical reef model (X=0 indicates the location of reef edge with positive X pointing shoreward)
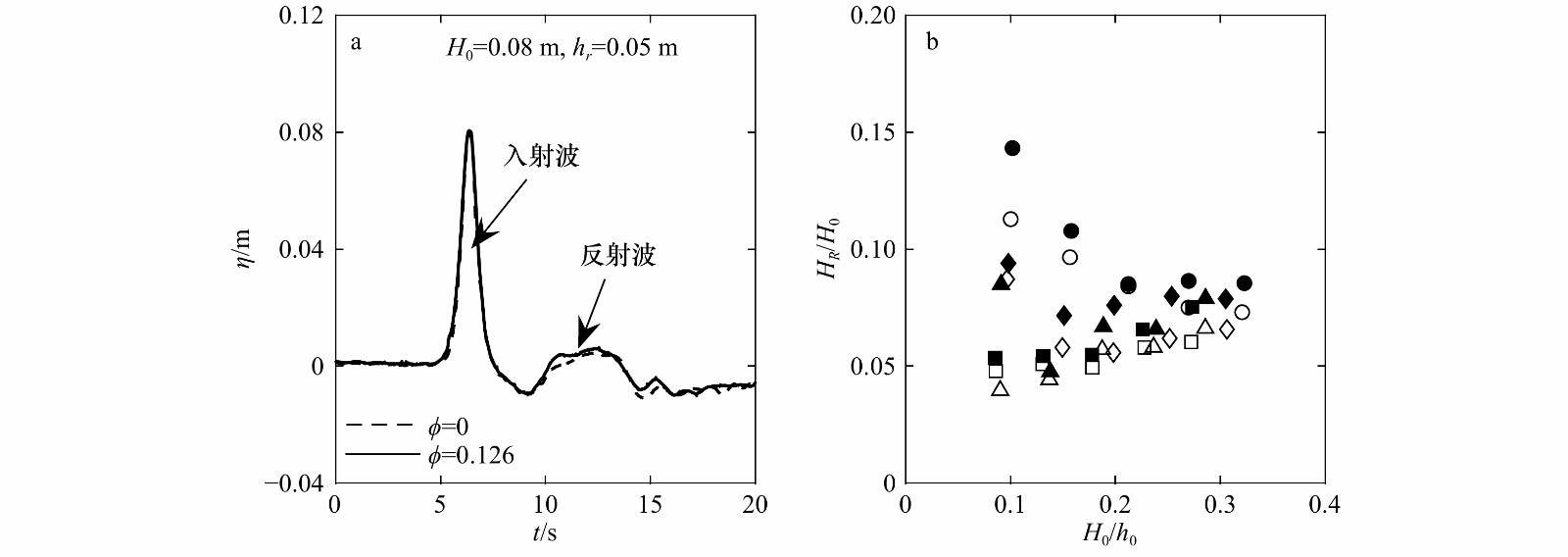
图 4 外海G1处自由液面（
$\eta $ ）的时间序列（a）和无量纲反射波高${H_{\rm{R}}}/{H_0}$ 随无量纲入射波高${H_0}/{h_0}$ 的变化（b）b图中空心：$ {\phi {\rm{ = }}0}$，实心：$ {\phi {\rm{ = }}0.126}$；圆形：hr=0.025 m，菱形：hr=0.05 m，三角形：hr=0.075 m，正方形：hr=0.10 m
Fig. 4 Time-series of the free surface elevation at offshore G1 (a), and variation of the normalized reflected wave height at G1 (
${H_{\rm{R}}}/{H_0}$ ) with the normalized incident wave height (${H_0}/{h_0}$ )（b）In figure b, white markers: $ {\phi {\rm{ = }}0}$, black markers: $ {\phi {\rm{ = }}0.126}$; circles: hr=0.025 m, diamonds: hr=0.05 m, triangles:hr=0.075 m, squares: hr=0.10 m
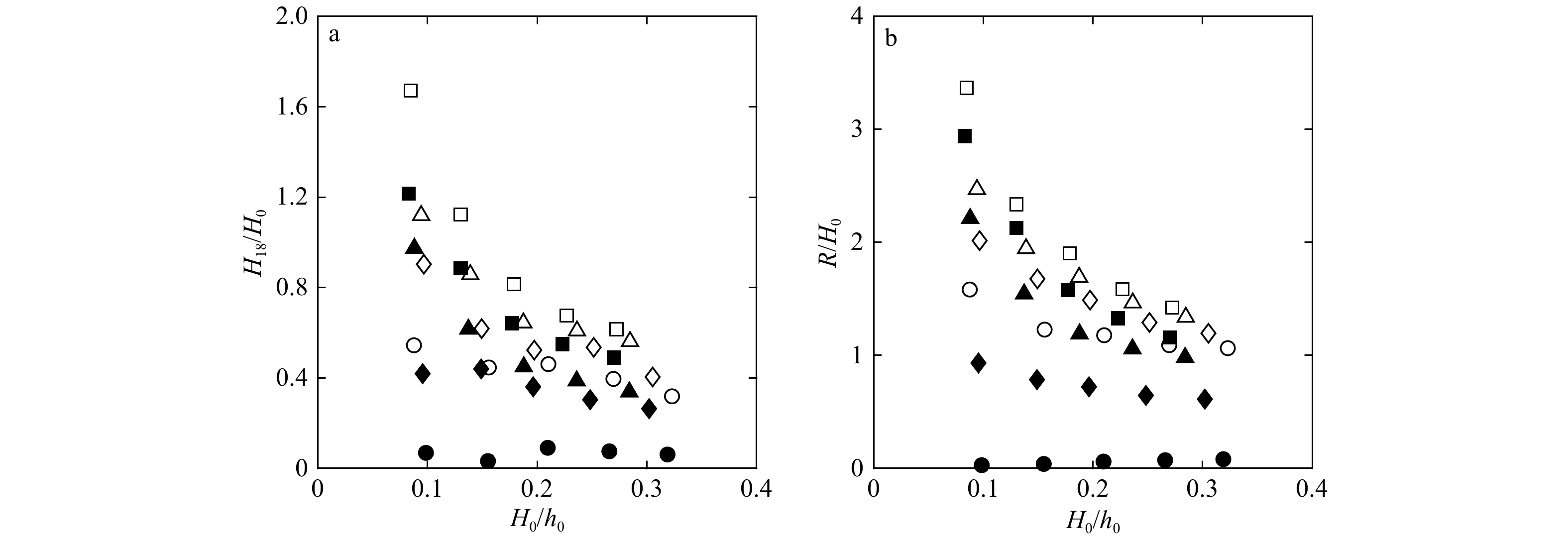
图 5 礁后岸滩坡脚（G18）处无量纲透射波高（
${H_{18}}/{H_0}$ ）随无量纲入射波高（${H_0}/{h_0}$ ）的变化（a），岸滩爬高（$R/{H_0}$ ）随无量纲入射波高（${H_0}/{h_0}$ ）的变化（b）$ {\phi {\rm{ = }}0}$，实心：$ {\phi {\rm{ = }}0.126}$；圆形：hr=0.025 m，菱形：hr=0.05 m，三角形：hr=0.075 m，正方形：hr=0.10 m
Fig. 5 Variation of the normalized transmitted wave height at the toe of back-reef beach (G18) (
${H_{18}}/{H_0}$ ) with the normalized incident wave height (${H_0}/{h_0}$ ) (a), and variation of the wave run-up on the back-reef beach ($R/{H_0}$ ) with the normalized incident wave height (${H_0}/{h_0}$ ) (b)White markers: $ {\phi {\rm{ = }}0}$, black markers: $ {\phi {\rm{ = }}0.126}$; circles: hr=0.025 m, diamonds: hr=0.05 m, triangles:hr=0.075 m, squares: hr=0.10 m
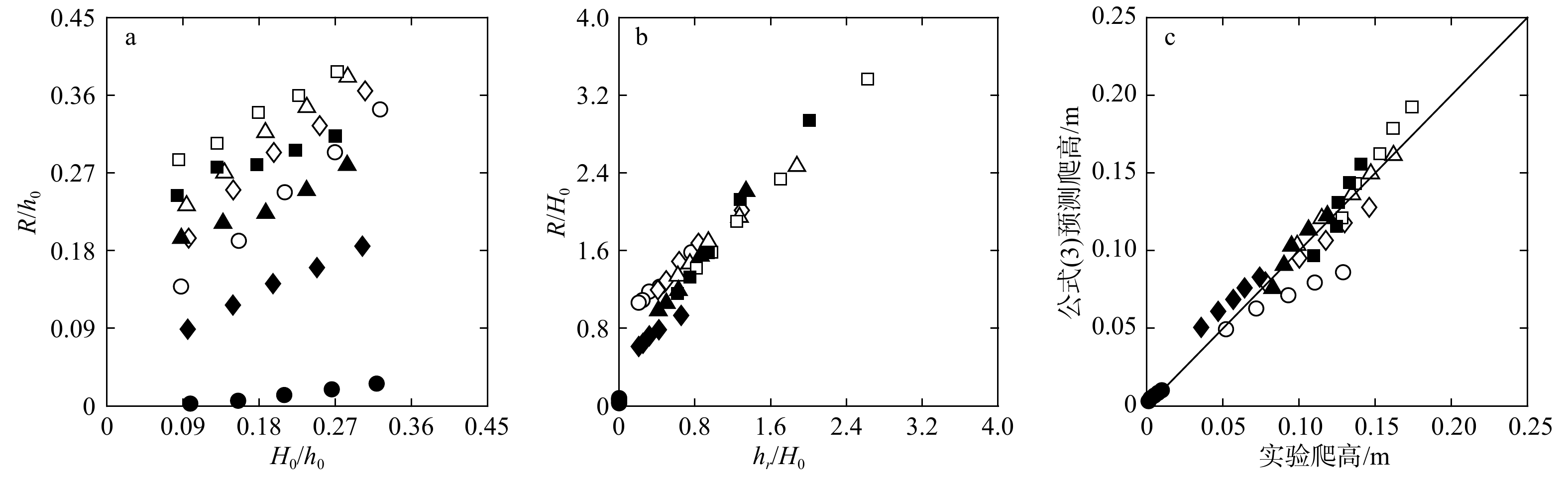
图 6 无量纲礁后岸滩爬高（
$R/{h_0}$ ）随无量纲入射波高（${H_0}/{h_0}$ ）的变化（a）；无量纲礁后岸滩爬高（$R/{H_0}$ ）随相对礁坪水深（${h_r}/{H_0}$ ）的变化（b）；基于公式（3）的预测值与实验测量爬高对比（c）$ {\phi {\rm{ = }}0}$，实心：$ {\phi {\rm{ = }}0.126}$；圆形：hr=0.025 m，菱形：hr=0.05 m，三角形：hr=0.075 m，正方形：hr=0.10 m
Fig. 6 Variation of the normalized wave run-up on the back-reef beach (
$R/{h_0}$ ) with the normalized incident wave height (${H_0}/{h_0}$ ) (a); variation of the normalized wave run-up on the back-reef beach ($R/{h_0}$ ) with the relative reef-flat water level (${h_r}/{H_0}$ ) (b); comparison between the predicted wave run-ups based on Eq. (3) and the measured wave run-ups (c)White markers: $ {\phi {\rm{ = }}0}$, black markers: $ {\phi {\rm{ = }}0.126}$; circles: hr=0.025 m, diamonds: hr=0.05 m, triangles:hr=0.075 m, squares: hr=0.10 m
-
[1] Yao Yu, Du Ruichao, Jiang Changbo, et al. Experimental study of reduction of solitary wave run-up by emergent rigid vegetation on a beach[J]. Journal of Earthquake and Tsunami, 2015, 9(5): 1540003. doi: 10.1142/S1793431115400035 [2] Titov V, Rabinovich A B, Mofjeld H O, et al. The global reach of the 26 December 2004 Sumatra tsunami[J]. Science, 2005, 309(5743): 2045−2048. doi: 10.1126/science.1114576 [3] Mori N, Takahashi T. The 2011 Tohoku Earthquake Tsunami Joint Survey Group (2012) nationwide post event survey and analysis of the 2011 Tohoku earthquake tsunami[J]. Coastal Engineering Journal, 2012, 54(1): 1250001. [4] Danielsen F, Sørensen M K, Olwig M F, et al. The Asian tsunami: a protective role for coastal vegetation[J]. Science, 2005, 310(5748): 643. doi: 10.1126/science.1118387 [5] Gourlay M R. Wave set-up on coral reefs. 1. Set-up and wave-generated flow on an idealised two dimensional horizontal reef[J]. Coastal Engineering, 1996, 27(3/4): 161−193. [6] 姚宇. 珊瑚礁海岸水动力学问题研究综述[J]. 水科学进展, 2019, 30(1): 139−152.Yao Yu. A review of the coral reef hydrodynamics[J]. Advances in Water Science, 2019, 30(1): 139−152. [7] Lin Pengzhi. A numerical study of solitary wave interaction with rectangular obstacles[J]. Coastal Engineering, 2004, 51(1): 35−51. doi: 10.1016/j.coastaleng.2003.11.005 [8] Quiroga P D, Cheung K F. Laboratory study of solitary-wave transformation over bed-form roughness on fringing reefs[J]. Coastal Engineering, 2013, 80: 35−48. doi: 10.1016/j.coastaleng.2013.05.002 [9] Yao Yu, He Fang, Tang Zhengjiang, et al. A study of tsunami-like solitary wave transformation and run-up over fringing reefs[J]. Ocean Engineering, 2018, 149: 142−155. doi: 10.1016/j.oceaneng.2017.12.020 [10] Becker J M, Merrifield M A, Ford M. Water level effects on breaking wave setup for Pacific island fringing reefs[J]. Journal of Geophysical Research: Oceans, 2014, 119(2): 914−932. doi: 10.1002/2013JC009373 [11] Synolakis C E. The runup of solitary waves[J]. Journal of Fluid Mechanics, 1987, 185: 523−545. doi: 10.1017/S002211208700329X [12] Yao Yu, Huang Zhenhua, Monismith S G, et al. Characteristics of monochromatic waves breaking over fringing reefs[J]. Journal of Coastal Research, 2013, 29(1): 94−104. [13] Yao Yu, He Wenrun, Du Ruichao, et al. Study on wave-induced setup over fringing reefs in the presence of a reef crest[J]. Applied Ocean Research, 2017, 66: 164−177. doi: 10.1016/j.apor.2017.06.002 -
下载:
计量
- 文章访问数: 332
- HTML全文浏览量: 101
- PDF下载量: 16
- 被引次数: 0
