Research on data assimilation and features analysis of storm surge in the Shanghai offshore areas
-
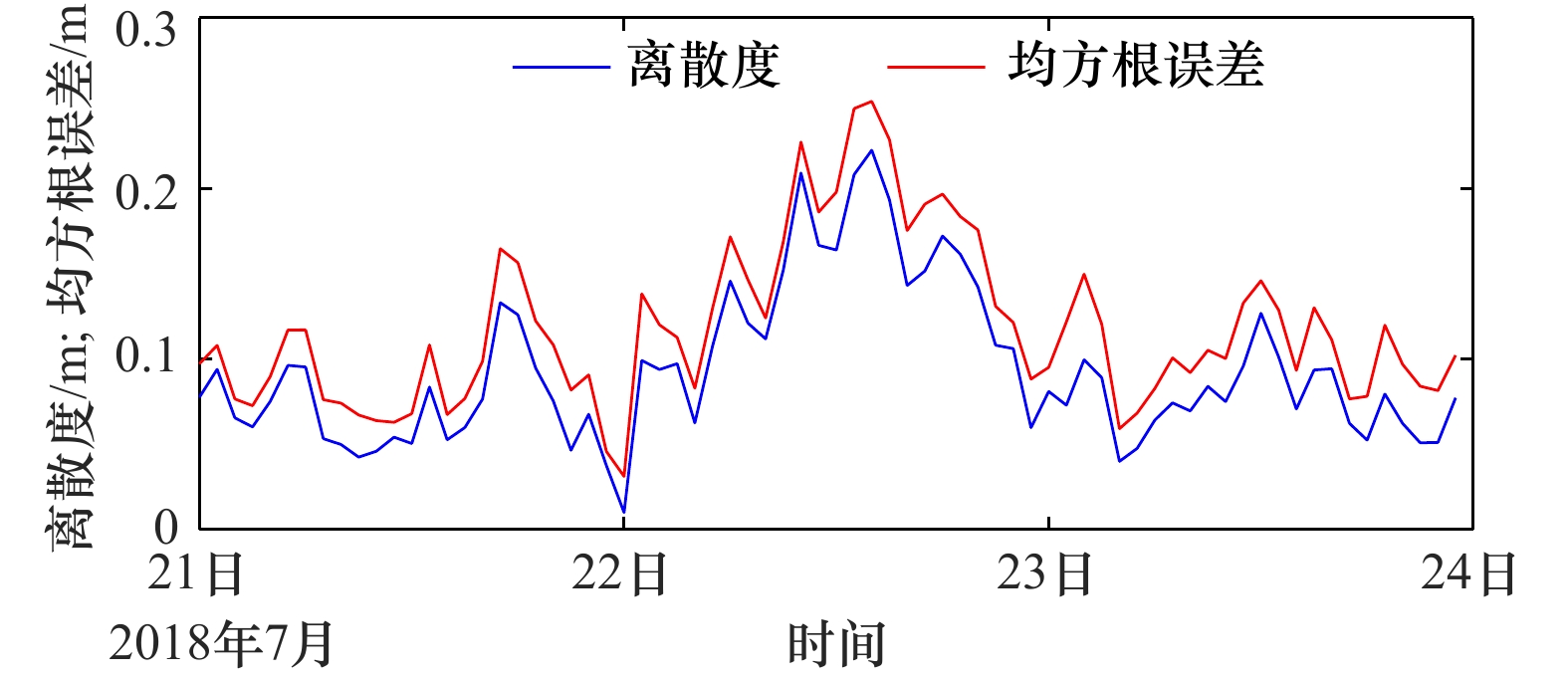
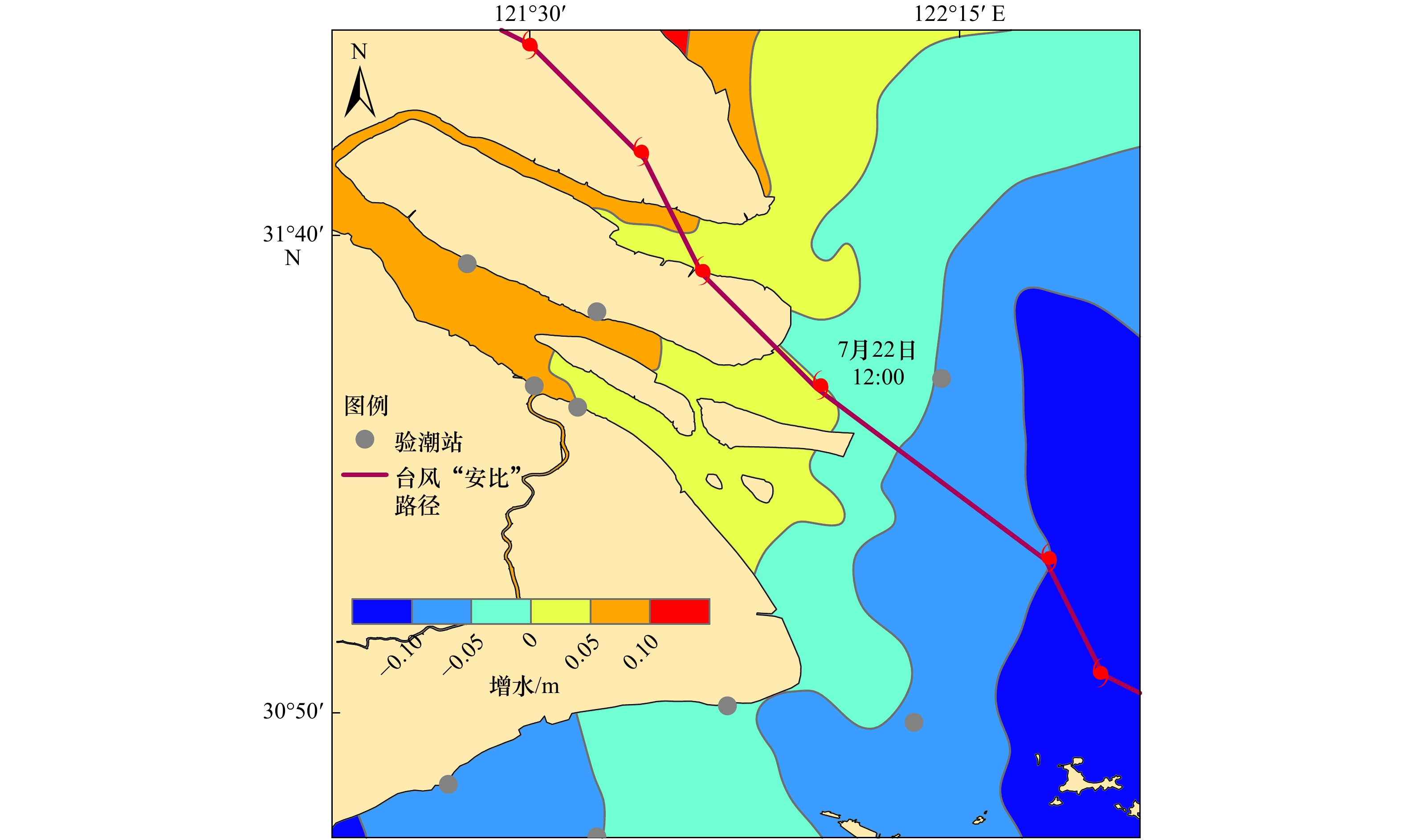
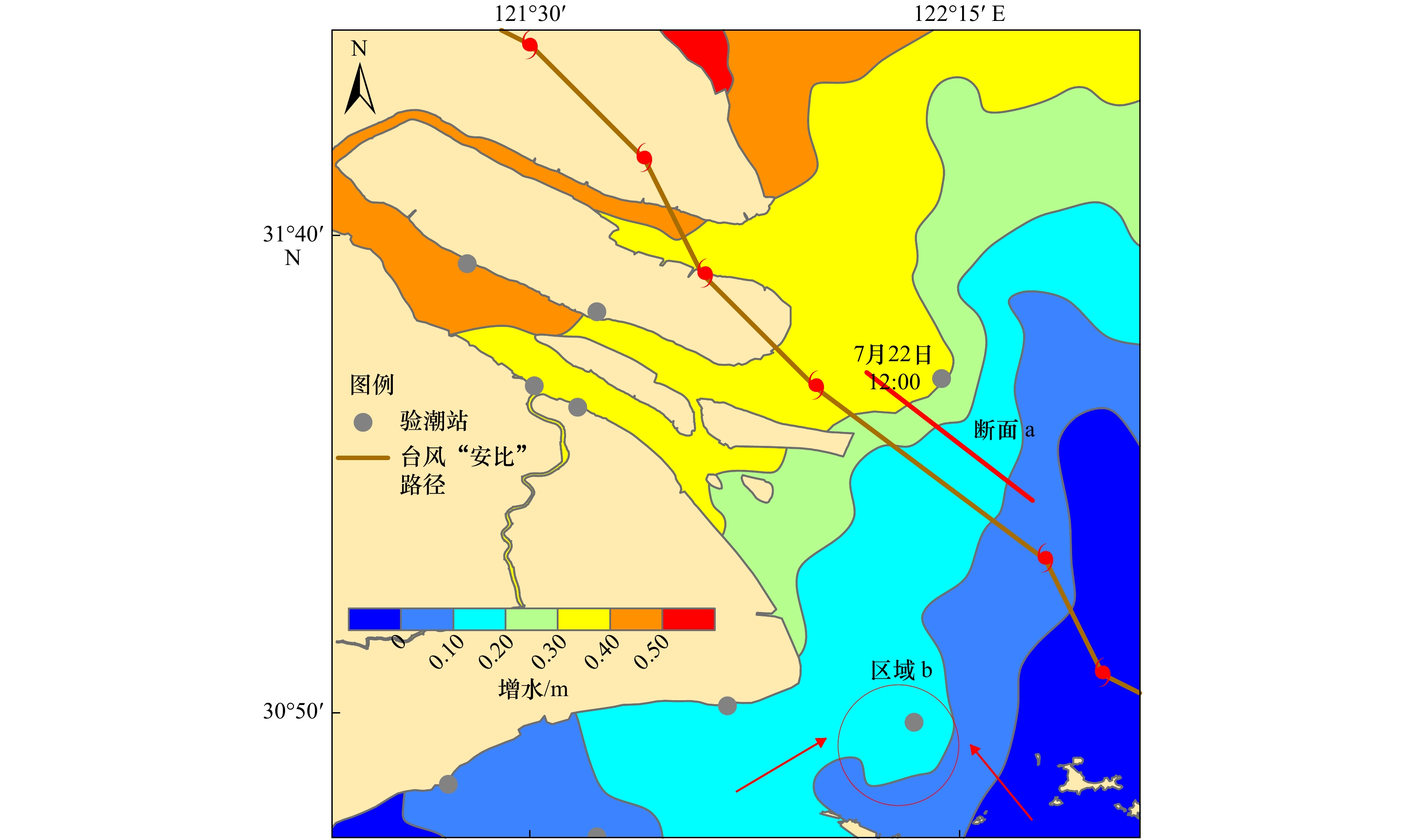
摘要: 风暴潮是一种复杂的对众多因素敏感又备受关注的海洋现象。本文基于协方差局地化的集合卡尔曼滤波方法（EnKF），选择201810号台风“安比”登陆上海的风暴潮过程，首次将海洋站和FVCOM数值模拟的不同来源、不同误差信息、不同时空分辨率的风暴潮进行数据同化融合，获得了逐72 h的上海海域风暴潮的最优解，进行了同化结果评估验证，并给出了集合样本数和Schur半径设置范围。结果表明，实测计算和数值模拟的风暴增减水之间均方根误差为0.20 m，实测和同化计算的风暴增减水之间均方根误差为0.07 m，准确度提高了65%；独立观测和同化计算的风暴增减水均方根误差为0.09 m，集合离散度与均方根误差比值为0.90，同化效果较好且可信；同化后的风暴增减水能够较好地刻画双峰增水、台风眼增水、增水锋面等特征，对于风暴潮研究、数值模拟结果订正、海洋防灾减灾等有重要意义。Abstract: Storm surge is a complex ocean phenomenon which is sensitive to many factors and has attracted much attention. In this paper, based on covariance localization method of ensemble Kalman filter(EnKF), the storm surge data of different sources, different error and different spatial and temporal resolution calculated by tide gauge stations and FVCOM model were assimilated and fused for the first time. Taking the storm surge process of typhoon 201810 landing in Shanghai for example, the optimal solution of 72-hourly storm surge in the Shanghai offshore areas was obtained and verified, the setting range of set sample number and Schur radius were given. The results show that the root mean square error of storm surge calculated by the observed stations and the model is 0.20 m, while calculated by the observed stations and assimilation is 0.07 m, which is improved by 65%, the root mean square error calculated by independent observation and assimilation is 0.09 m, the ratio of set dispersion to root mean square error is 0.90, the assimilation effect is better and credible. The assimilated storm water increment field can clearly and accurately depict the characteristics of double peaks storm surge, typhone eye surge and frontal surge which can be better used for the research of storm surge, correction of numerical simulation and marine disaster prevention.
-
Key words:
- storm tide /
- storm surge /
- data assimilation /
- EnKF /
- marine disaster /
- Shanghai offshore areas
-
图 1 数据同化区域、监测站点分布和部分台风路径
Fig. 1 Data assimilation region, monitoring stations and parts of typhoon track
图 2 长江口海域计算网格和水深
Fig. 2 Computing grids and water depth in the Changjiang River Estuary
图 3 同化实验的6个站风暴增减水时间序列
Fig. 3 Storm surge time series of 6 stations participating in assimilation
图 4 未参加同化的3个站风暴增减水时间序列
Fig. 4 Storm surge time series of 3 stations not participating in assimilation
图 6 台风登陆前数值模拟的增减水场
Fig. 6 Storm surge field calculated by model before the typhoon landing
图 7 台风登陆前同化实验的增减水场
Fig. 7 Storm surge field of assimilation before the typhoon landing
图 8 2018年7月22日12:00时长江口断面各站增水值
Fig. 8 Storm surge of the Changjiang River Estuary section stations at 12:00 July 22, 2018
图 9 2018年7月22日12:00时杭州湾北断面各站增水值
Fig. 9 Storm surge of the Hangzhou Bay section stations at 12:00 July 22, 2018
图 10 不同集合样本数及Schur半径同化误差
Fig. 10 The assimilation results error of different set samples and Schur radius
表 1 同化检验实验设计
Tab. 1 Experimental design of assimilation verification
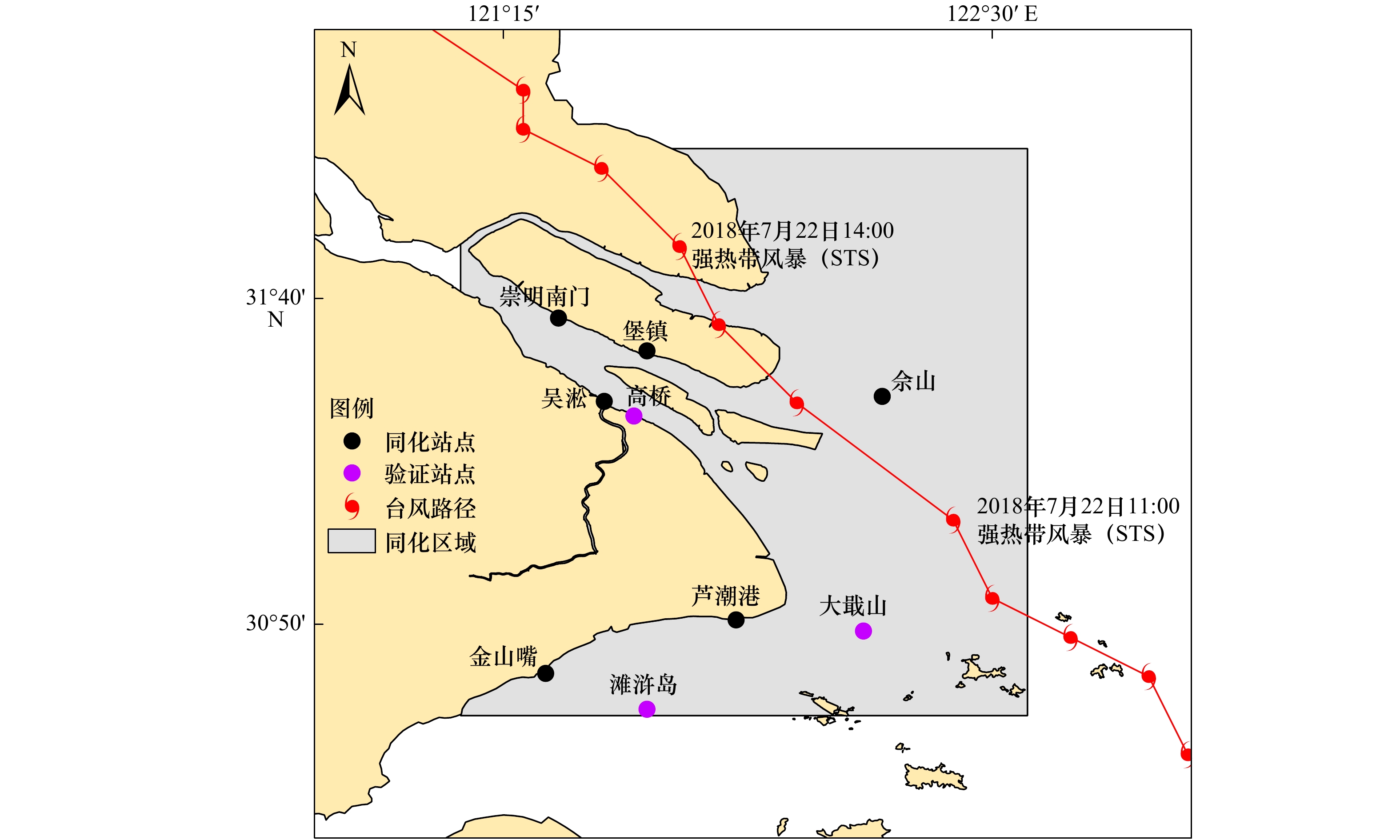
实验方案 实验名称 起始状态 观测资料 步长 方法 实验目标 A 控制实验 2018年7月20日15时（世界时）FVCOM预报结果 无 1 h FVCOM数值模拟 9个站数值模拟的风暴增减水序列（72 h）；典型时刻数值模拟的风暴增减水场 2016年1月1日00时实测水位 9个站实测水位 1 h 调和分析 9个站实测水位计算的风暴增减水序列（72 h） B 同化实验 2018年7月20日15时（世界时）FVCOM预报结果 6个站实测水位计算的风暴增减水序列 1 h EnKF 6个站同化的风暴增减水序列（72 h）；3个站同化的风暴增减水序列（72 h）；典型时刻同化的风暴增减水场 
下载: 导出CSV
表 2 典型时刻9个海洋站增减水对比
Tab. 2 Storm surge comparisons of the 9 stations as typical moment
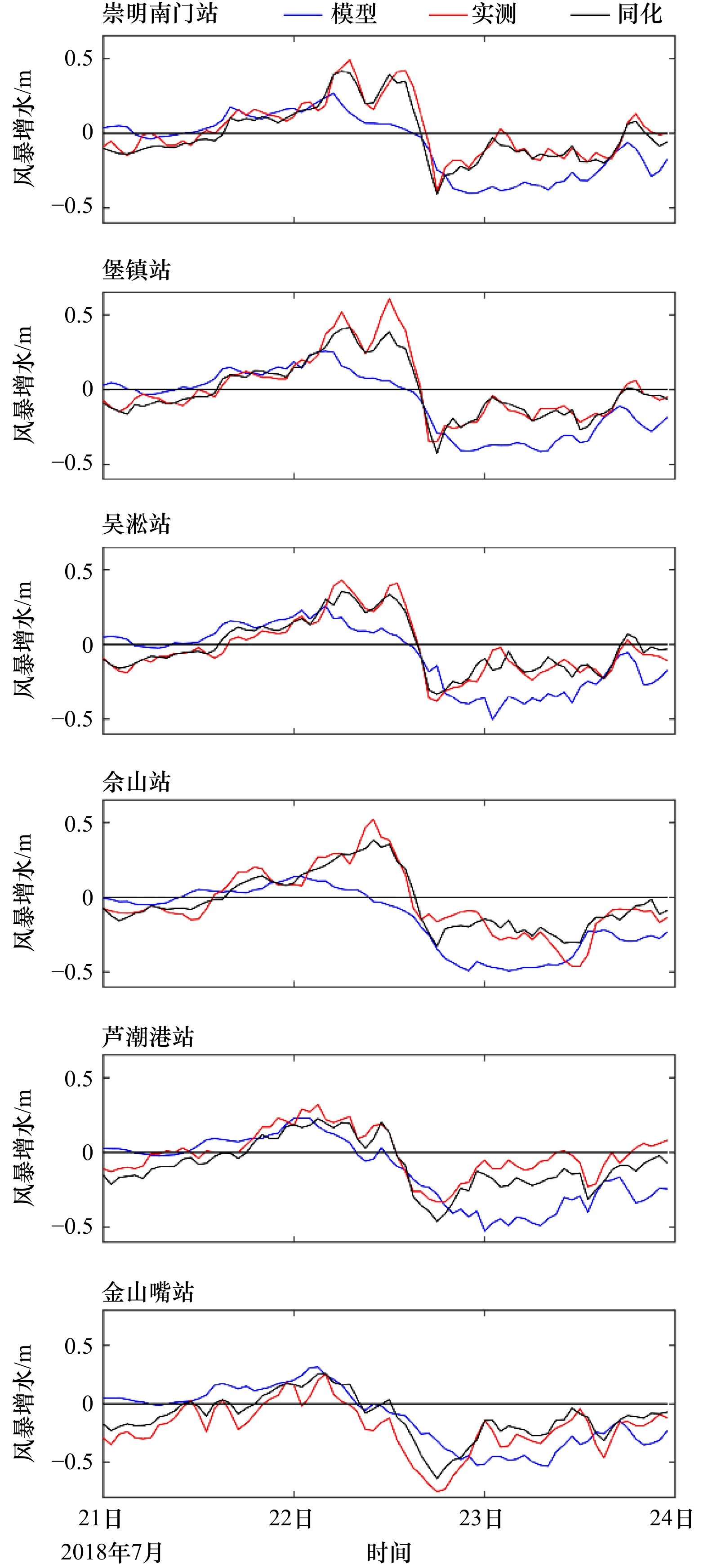
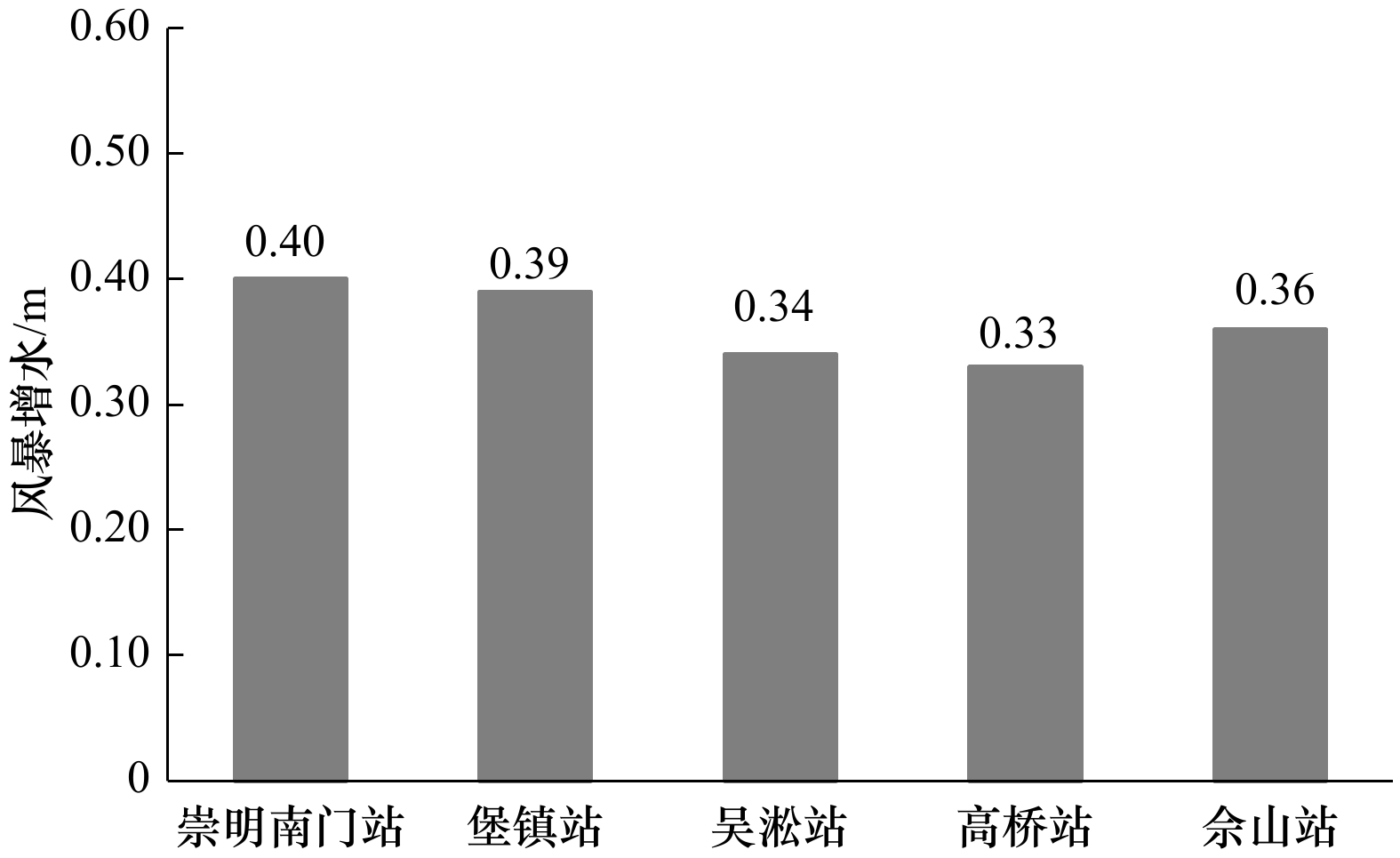
海洋站 实测水位计算的增水/m 数值模拟的增水/m 同化后的增水/m 实测水位计算与数值模拟 实测水位计算与同化 绝对偏差/m 均方根误差/m 绝对偏差/m 均方根误差/m 崇明南门 0.34 0.06 0.40 0.28 0.31 0.06 0.12 堡镇 0.61 0.06 0.39 0.55 0.22 吴淞 0.39 0.07 0.34 0.32 0.05 高桥 0.46 0.06 0.33 0.40 0.13 佘山 0.38 −0.05 0.36 0.43 0.02 大戢山 0.04 −0.06 0.13 0.10 0.09 芦潮港 0.13 −0.04 0.13 0.17 0.00 滩浒岛 −0.10 −0.05 0.07 0.05 0.17 金山嘴 −0.12 −0.08 0.04 0.04 0.16
下载: 导出CSV
-
[1] Dube S K, Rao A D, Sinha P C, et al. Storm surges: worst coastal marine hazard[M]//Murthy C R, Sinha P C, Rao Y R. Modelling and Monitoring of Coastal Marine Processes. Dordrecht: Springer, 2008: 125−140. [2] Maduwantha M G P, Wijayaratna T M N. An estimation of storm surge heights of colombo coastline[C]//Moratuwa Engineering Research Conference (MERCon). Moratuwa, Sri Lanka: IEEE, 2019. [3] NOAA. Introduction to storm surge guide[EB/OL]. [2020−11−10]. https://www.nhc.noaa.gov/surge/surge_intro.pdf. [4] 王喜年, 叶琳. 我国沿海风暴潮的监测及其预报[J]. 海洋预报, 1992, 9(3): 28−37. doi: 10.11737/j.issn.1003-0239.1992.03.004Wang Xinian, Ye Lin. Monitoring and forecasting of storm surges along the coastal areas of China[J]. Marine Forecasts, 1992, 9(3): 28−37. doi: 10.11737/j.issn.1003-0239.1992.03.004 [5] 刘俊. 关注风暴潮、巨浪、潮汐[M]. 北京: 军事科学出版社, 2011.Liu Jun. Focus on Storm Surges, Huge Waves, and Tides[M]. Beijing: Military Science Press, 2011. [6] Thuy N B, Tien T Q, Wettre C, et al. Monsoon-induced surge during high tides at the southeast coast of vietnam: a numerical modeling study[J]. Geosciences, 2019, 9(2): 72. doi: 10.3390/geosciences9020072 [7] 冯士筰, 李凤岐, 李少菁. 海洋科学导论[M]. 北京: 高等教育出版社, 1999.Feng Shizuo, Li Fengqi, Li Shaojing. An Introduction to Marine Science[M]. Beijing: Higher Education Press, 1999. [8] Chen Nan, Han Guoqi, Yang Jingsong, et al. Hurricane Sandy storm surges observed by HY-2A satellite altimetry and tide gauges[J]. Journal of Geophysical Research: Oceans, 2014, 119(7): 4542−4548. doi: 10.1002/2013JC009782 [9] 周黔生. 对风暴潮增水及其计算方法的一点见解[J]. 海洋预报, 1992, 9(3): 56−59. doi: 10.11737/j.issn.1003-0239.1992.03.007Zhou Qiansheng. Point of view on storm surge water and its calculation method[J]. Marine Forecasts, 1992, 9(3): 56−59. doi: 10.11737/j.issn.1003-0239.1992.03.007 [10] Evensen G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics[J]. Journal of Geophysical Research: Oceans, 1994, 99(C5): 10143−10162. doi: 10.1029/94JC00572 [11] Houtekamer P L, Zhang Fuqing. Review of the ensemble Kalman filter for atmospheric data assimilation[J]. Monthly Weather Review, 2016, 144(12): 4489−4532. doi: 10.1175/MWR-D-15-0440.1 [12] Houtekamer P L, Mitchell H L. Data assimilation using an ensemble Kalman filter technique[J]. Monthly Weather Review, 1998, 126(3): 796−811. doi: 10.1175/1520-0493(1998)126<0796:DAUAEK>2.0.CO;2 [13] Butler T, Altaf M U, Dawson C, et al. Data assimilation within the advanced circulation (ADCIRC) modeling framework for hurricane storm surge forecasting[J]. Monthly Weather Review, 2012, 140(7): 2215−2231. doi: 10.1175/MWR-D-11-00118.1 [14] Altaf M U, Butler T, Mayo T, et al. A comparison of ensemble Kalman filters for storm surge assimilation[J]. Monthly Weather Review, 2014, 142(8): 2899−2914. doi: 10.1175/MWR-D-13-00266.1 [15] Colle B A, Bowman M J, Roberts K J, et al. Exploring water level sensitivity for Metropolitan New York during Sandy (2012) using ensemble storm surge simulations[J]. Journal of Marine Science and Engineering, 2015, 3(2): 428−443. doi: 10.3390/jmse3020428 [16] Etala P, Saraceno M, Echevarría P, et al. An investigation of ensemble-based assimilation of satellite altimetry and tide gauge data in storm surge prediction[J]. Ocean Dynamics, 2015, 65(3): 435−447. doi: 10.1007/s10236-015-0808-z [17] 冯士筰. 风暴潮导论[M]. 北京: 科学出版社, 1982.Feng Shizuo. Introduction to Storm Surge[M]. Beijing: Science Press, 1982. [18] 赵长进. 长江口及其邻近海区无结构网格风暴潮模式的建立与应用[D]. 上海: 华东师范大学, 2014: 1−69.Zhao Changjin. Development and analysis of the unstructured numerical model for storm surge in the Changjiang Estuary[D]. Shanghai: East China Normal University, 2014: 1−69. [19] Wahl T, Mudersbach C, Jensen J. Statistical assessment of storm surge scenarios within integrated risk analyses[J]. Coastal Engineering Journal, 2015, 57(1): 1540003. [20] Houtekamer P L, Mitchell H L. A sequential ensemble Kalman filter for atmospheric data assimilation[J]. Monthly Weather Review, 2001, 129(1): 123−137. doi: 10.1175/1520-0493(2001)129<0123:ASEKFF>2.0.CO;2 [21] 庄照荣, 薛纪善, 李兴良. GRAPES集合卡尔曼滤波资料同化系统Ⅰ:系统设计及初步试验[J]. 气象学报, 2011, 69(4): 620−630.Zhuang Zhaorong, Xue Jishan, Li Xingliang. The GRAPES ensemble Kalman filter data assimilation system. Part I: design and its tentative experiment[J]. Acta Meteorologica Sinica, 2011, 69(4): 620−630. [22] Oregon State University. TPXO global tide models[DB/OL]. [2019−11−12]. http://volkov.oce.orst.edu/tides/global.html. [23] 《海洋图集》编委会. 渤海黄海东海海洋图集(水文)[M]. 北京: 海洋出版社, 1993.Editorial Board for Marine Atlas. Marine Atlas of the Bohai Sea, Yellow Sea and East China Sea (Hydrology)[M]. Beijing: China Ocean Press, 1993. [24] 林佳. 台风侵袭下的超级城市上海[J]. 中国减灾, 2018(19): 18−21. doi: 10.3969/j.issn.1002-4549.2018.19.007Lin Jia. The super city of Shanghai under the typhoon[J]. Disaster Reduction in China, 2018(19): 18−21. doi: 10.3969/j.issn.1002-4549.2018.19.007 [25] 中央气象台. 台风网[DB/OL]. [2019−11−20]. http://typhoon.nmc.cn/web.html.National Meteorological Center. The typhoon web[DB/OL]. [2019−11−20]. http://typhoon.nmc.cn/web.html. [26] 陈宗镛. 潮汐学[M]. 北京: 科学出版社, 1980.Chen Zongyong. Tidology[M]. Beijing: Science Press, 1980. [27] Chen Changsheng, Liu Hedong, Beardsley R C. An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: application to coastal ocean and estuaries[J]. Journal of Atmospheric and Oceanic Technology, 2003, 20(1): 159−186. doi: 10.1175/1520-0426(2003)020<0159:AUGFVT>2.0.CO;2 [28] Chen C, Beardsley R C, Cowles G, et al. An unstructured grid, finite-volume community ocean model FVCOM user manual[R]. Cambridge: NOAA, 2013. [29] Yang Zhaoqing, Wang Taiping, Leung R, et al. A modeling study of coastal inundation induced by storm surge, sea-level rise, and subsidence in the Gulf of Mexico[J]. Natural Hazards, 2014, 71(3): 1771−1794. doi: 10.1007/s11069-013-0974-6 [30] Leith C S. Theoretical skill of Monte Carlo forecast[J]. Monthly Weather Review, 1974, 102(6): 409−418. doi: 10.1175/1520-0493(1974)102<0409:TSOMCF>2.0.CO;2 [31] Palmer T N, Mureau R, Molteni F. The Monte Carlo forecast[J]. Weather, 1990, 45(6): 198−207. doi: 10.1002/j.1477-8696.1990.tb05619.x [32] 韩培, 舒红, 许剑辉. EnKF同化的背景误差协方差矩阵局地化对比研究[J]. 地球科学进展, 2014, 29(10): 1175−1185. doi: 10.11867/j.issn.1001-8166.2014.10.1175Han Pei, Shu Hong, Xu Jianhui. A comparative study of background error covariance localization in EnKF data assimilation[J]. Advances in Earth Science, 2014, 29(10): 1175−1185. doi: 10.11867/j.issn.1001-8166.2014.10.1175 [33] Gaspari G, Cohn S E. Construction of correlation functions in two and three dimensions[J]. Quarterly Journal of the Royal Meteorological Society, 1999, 125(554): 723−757. doi: 10.1002/qj.49712555417 [34] ECMWF. Evaluation of probabilistic prediction systems[EB/OL]. [2019−11−25]. https://www.ecmwf.int/en/elibrary/12555-evaluation-probabilistic-prediction-systems. [35] Jolliffe I T, Stephenson D B. Forecast Verification: A Practitioner's Guide in Atmospheric Science[M]. Chichester: Wiley and Sons Ltd, 2003. [36] 范宇恩. GRAPES区域集合预报侧边界及模式扰动试验[D]. 成都: 成都信息工程大学, 2019.Fan Yuen. The lateral boundary and mode disturbance test of GRAPES region ensemble prediction model[D]. Chengdu: Chengdu University of Information Engineering, 2019. [37] 高士博, 闵锦忠, 黄丹莲. EnKF局地化算法对雷达资料同化的影响研究[J]. 大气科学学报, 2016, 39(5): 633−642.Gao Shibo, Min Jinzhong, Huang Danlian. Research on the impact of localization methods on radar data assimilation using the ensemble Kalman filter[J]. Transactions of Atmospheric Sciences, 2016, 39(5): 633−642. [38] 陈吉余, 沈焕庭, 恽才兴, 等. 长江河口动力过程和地貌演变[M]. 上海: 上海科学技术出版社, 1990.Chen Jiyu, Shen Huanting, Yun Caixing, et al. The Dynamical Process and Physiognomy Evolvement in the Yangtze River[M]. Shanghai: Shanghai Scientific and Technical Publishers, 1990. [39] 张文舟, 胡建宇, 商少平, 等. 福建沿海风暴潮特征的分析[J]. 海洋通报, 2004, 23(3): 12−19. doi: 10.3969/j.issn.1001-6392.2004.03.002Zhang Wenzhou, Hu Jianyu, Shang Shaoping, et al. On the characteristics of storm surges along Fujian coast[J]. Marine Science Bulletin, 2004, 23(3): 12−19. doi: 10.3969/j.issn.1001-6392.2004.03.002 [40] 刘俊民, 余新晓. 水文与水资源学[M]. 北京: 中国林业出版社, 1999.Liu Junmin, Yu Xinxiao. Hydrology and Water Resources[M]. Beijing: China Forestry Publishing House, 1999. [41] 盖尔·埃文森. 数据同化—集合卡尔曼滤波[M]. 2版. 刘厂, 赵玉新, 高峰, 译. 北京: 国防工业出版社, 2017.Evensen G. Data Assimilation—The Ensemble Kalman Filter[M]. 2nd ed. Liu Chang, Zhao Yuxin, Gao Feng, trans. Beijing: National Defence Industry Press, 2017. [42] 王泽人, 马荣华, 段洪涛, 等. 基于集合卡尔曼滤波的太湖叶绿素a浓度同化试验系统设计及实现[J]. 中国科学院大学学报, 2013, 30(5): 628−636.Wang Zeren, Ma Ronghua, Duan Hongtao, et al. Design and implementation of an experimental data assimilation system for chlorophyll-a in Lake Taihu based on the ensemble Kalman filter[J]. Journal of University of Chinese Academy of Sciences, 2013, 30(5): 628−636. [43] Hamill T M, Whitaker J S, Snyder C. Distance-dependent filtering of background error covariance estimates in an ensemble Kalman filter[J]. Monthly Weather Review, 2001, 129(11): 2776−2790. doi: 10.1175/1520-0493(2001)129<2776:DDFOBE>2.0.CO;2 -
图(10) / 表(2)
计量
- 文章访问数: 284
- HTML全文浏览量: 64
- PDF下载量: 51
- 被引次数: 0
